Determination of stable isotope ratios using nuclear reaction analysis coupled with a particle–gamma coincidence method†
Paula Rangel Pestana
Allegro
 *a,
Márcia de Almeida
Rizzutto
a,
Nemitala
Added
a,
Vitor Ângelo Paulino de
Aguiar
*a,
Márcia de Almeida
Rizzutto
a,
Nemitala
Added
a,
Vitor Ângelo Paulino de
Aguiar
 a,
Dennis Lozano
Toufen
b,
Eduardo Luiz Augusto
Macchione
a,
Nilberto Heder
Medina
a,
Dennis Lozano
Toufen
b,
Eduardo Luiz Augusto
Macchione
a,
Nilberto Heder
Medina
 a,
Roberto Vicençotto
Ribas
a,
José Roberto Brandão de
Oliveira
a,
Rafael
Escudeiro
a,
Juan Antonio
Alcántara-Núñez
a,
Roberto Vicençotto
Ribas
a,
José Roberto Brandão de
Oliveira
a,
Rafael
Escudeiro
a,
Juan Antonio
Alcántara-Núñez
 a,
Jessica Fleury
Curado
c,
Valdir Brunetti
Scarduelli
a,
Vinicius Antonio Bocaline
Zagatto
ad,
Cléber Lima
Rodrigues
a,
Jessica Fleury
Curado
c,
Valdir Brunetti
Scarduelli
a,
Vinicius Antonio Bocaline
Zagatto
ad,
Cléber Lima
Rodrigues
 a and
Manfredo Harri
Tabacniks
a and
Manfredo Harri
Tabacniks
 a
a
aInstitute of Physics, University of São Paulo, 05508-090, São Paulo, São Paulo, Brazil. E-mail: allegro@if.usp.br
bFederal Institute of Education, Science, and Technology of São Paulo – IFSP, 07115-000, Guarulhos, São Paulo, Brazil
cPhysics Dept, Universitary Center of FEI, 09850-901, São Bernardo do Campo, São Paulo, Brazil
dPhysics Institute, Fluminense Federal University – UFF, 24210-340, Niterói Rio de Janeiro, Brazil
First published on 9th November 2020
Abstract
A non-destructive standard-free analytical method of obtaining stable isotope ratios in materials using nuclear reactions excited by an 11.75 MeV proton beam is demonstrated for a special 63Cu/65Cu target characterized traceably by Rutherford backscattering spectrometry (using 2.2 MeV protons). The method is general and is capable of being a useful alternative to standard ICP-MS methods. Relatively high energy proton beams are required to excite multiple isotopes of most elements of interest, and the many resulting nuclear reaction products are filtered by coincidence methods to characterize the desired isotope ratios. Specifically: the use of particle–gamma coincidences permits identification of specific channels populated in the nuclear reaction and avoids or minimizes typical drawbacks of this method including high backgrounds and interfering reactions. The test Cu target was a sandwich of a natural Cu and an enriched 65Cu foil, and particle–gamma coincidences were measured for the reactions 63Cu(p,πγ){63Cu,60Ni} and the corresponding reactions for 65Cu (where “π” represents the energetic charged particle reaction product: proton or alpha). Limitations of the method, and applications in cultural heritage and other fields are discussed.
1. Introduction
Isotope ratio measurements provide valuable information in archaeology,1 anthropology,2 geology,3 medicine,4 agriculture,5 forensic science,6 and cultural heritage studies.7 Several techniques are available for measuring stable isotopes: Isotope-Ratio Mass Spectrometry (IRMS),8 Inductively Coupled Plasma Mass Spectrometry (ICP-MS),9 Laser Induced Breakdown Spectroscopy (LIBS)10 and its variant Laser Ablation Molecular Isotopic Spectrometry (LAMIS),11 Accelerator Mass Spectrometry (AMS),12 Thermal Ionization Mass Spectrometry (TIMS),13 Secondary-Ion Mass Spectrometry (SIMS),14 Time-of-Flight Mass Spectrometry (TOF-MS),15 and Neutron Activation Analysis (NAA).16 The most important drawback of the mass spectrometry techniques is the need to extract samples from the material, and complex sample preparation, that can be quite elaborate since it may involve several steps that must be free from contamination. Also, in some of these mass spectrometry techniques, the sample is destroyed during the measurement and quantitative analyses rely on a standard reference material. LIBS and LAMIS can, in principle, be used without sample preparation, but the quantity of isotopes that can be determined using these techniques are, so far, small. NAA could be applied to analyze any kind of material without taking samples or using a standard reference material, but matrix activation for a long irradiation period imposes limitations on the material's composition. NAA also modifies the material composition on a part per million (ppm)–part per billion (ppb) scale, thus interfering with subsequent analysis by other sensitive techniques. In the case of cultural heritage studies and forensic science, it is of special interest to determine the isotopic concentration without taking samples or, at least, avoid sample destruction. Nuclear Reaction Analysis (NRA)17 is an alternative method to determine isotopes that can be used to avoid or minimize some of the drawbacks of the other isotope determination techniques.NRA consists of an induced nuclear reaction by an ion beam with the isotopes present in the material. Typically, gamma-rays and charged particles such as protons, deuterons, tritium, 3He, and alpha particles are detected as a result of these nuclear reactions. The reactions can be induced using a wide range of ions beams with energies varying from MeV to GeV and the measurements can be done in-vacuum or in-air. NRA does not require samples or sample preparation and the quantitative analysis can be performed without reference to a standard reference material, since it relies on fundamental principles. The technique is dependent on reaction cross-sections, interfering reactions, and background effects, that can be avoided or mitigated depending on the chosen nuclear reaction and experimental setup. NRA is already being used to study cultural heritage18 and in forensic sciences19 to determine the light elements in a material using especially the Particle-Induced Gamma-ray Emission (PIGE) technique,17,20 a special case of NRA. The modification in the material composition by using NRA techniques are typically on a sub-ppb level.
NRA measurements can also be done using a coincidence between the charged particles and the gamma-rays produced in the nuclear reactions, permitting the identification of the nuclear products produced in a complex sample. We will follow from now on the nomenclature given by Kristiansson et al.21–23 to refer to the NRA with a particle–gamma coincidence method as photon-tagged nuclear reaction analysis (pNRA).
For the implementation of pNRA, it is necessary to use a particle–gamma coincidence detection system with energy and time resolution that allows distinguishing among the diverse nuclear reactions that occur in a heterogeneous sample. Kristiansson et al.21–23 have proposed the use of particle–gamma coincidences to measure light element traces (Li to Si) by using (p,p′γ) and (p,αγ) reactions, a plastic scintillator gamma-ray detector, and a surface barrier detector. This setup increases the measurement efficiency and reduces the gamma-ray background radiation through very accurate time information of the particle–gamma coincidence, but it does not provide accurate information on the gamma-ray energies due to the low energy resolution of the plastic scintillator. This limitation was overcome by Borysiuk et al.24,25 by using a gamma-ray HPGe detector in coincidence with a double-sided silicon strip detector (DSSSD), which permits distinguishing between different nuclear reactions produced in a heterogeneous sample.
The major problem in using the pNRA for determining isotopic ratios in a material is that most of the measurements are done using small accelerators, with enough energy to surmount the Coulomb barrier only of the light elements, and it is also necessary to have resonance reactions to obtain cross-sections of hundreds of mb.26 Few reactions are known with protons, alpha-particle, and deuterium beams with low energy (up to 5 MeV) that excite all the isotopes of the same element with the same bombarding energy. In the case of heavy elements, such as Pb, the lack of known resonance reactions at low energy to simultaneously measure all of the isotopes of interest is an additional limitation.
At higher energy accelerators, it is possible to use heavier beams which allows different reaction mechanisms,27 such as complete and incomplete fusion, particle transfer, breakup, besides Coulomb excitation, inelastic scattering and resonant reactions already used in the pNRA technique. All these mechanisms of nuclear reactions allow measuring simultaneously different nuclei and isotopes, with cross-sections ranging from tens to hundreds of mb. Also, it is possible to determine the isotope depth profile by varying the beam energy, without the preoccupation to find an adequate resonance reaction.
In this article, we propose the use of the pNRA in a medium energy accelerator with a maximum terminal voltage 3–40 MV giving access to ion beams of energy 5–500 MeV to identify a specific channel in the nuclear reaction, to measure simultaneously all isotopes in the same experiment, and to avoid or minimize the pNRA drawbacks such as low production cross-section, interfering reactions and other background effects.
To test the above proposal, we measured the copper isotopes of a specially created copper sample (a mix of natural copper and enriched 65Cu foils) using an 11.75 MeV proton beam and a particle–gamma coincidence setup. Copper isotopes have a wide range of applications4,5,28–33 and the required sensitivity is strongly dependent on element prevalence and matrix effects,31,34 sample preparation procedure,35 instrumental setup36 and the specificities of the technique used to measure the isotopes, such as the instrumental mass bias effect.37 The fact that the international copper reference material NIST SRM 976 to enable the interlaboratory comparison of results is no longer commercially available38,39 also plays an important role in the development of a standardless technique. Copper isotopes have also some technical features that facilitate their use in a first test of the pNRA method: ease in obtaining high-purity natural and isotope samples at relatively low cost since both isotopes constitute a large percent fraction of the sample and ease of target production.
To test the pNRA technique, we measured the isotope ratio of an especially created copper target, a mix of natural copper and enriched 65Cu foils with different 63,65Cu isotopic concentration relative to a natural copper sample. As the pNRA depends on the reaction cross section and geometrical factors, we also measured a natural and a 99.9% enriched 65Cu to correctly address those issues. The first test of the pNRA was performed in-vacuum, mainly because the laboratory already had an experimental setup to measure particle–gamma coincidences40 and also to allow a high energy resolution beam and consequently, a univocal cross-section measurement.
To validate the 63,65Cu isotope ratio obtained for the modified copper target using the pNRA method, this target was also measured using the Rutherford Backscattering Spectrometry (RBS) technique,41,42 an especial case of the Elastic Backscattering (EBS) analytical method,43 capable of a high degree of accuracy to determine the thin target's composition.
2. Principles of the method
The pNRA technique is based on the simultaneous measurement of the particle and gamma-ray produced in a nuclear reaction. So, it is possible to define a theoretical yield for each gamma-ray that is dependent on the particle and gamma detector solid angles, when the data is recorded only when a particle and a gamma detector have fired in coincidence: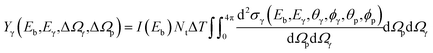 | (1) |
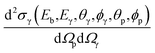 is the differential cross-section given in mb sr−2 and dΩp and dΩγ are the solid angles for the particle and gamma-ray detectors, each of them given in sr. Since the gamma-ray and particle detectors have a finite size and are placed at fixed angles, it is possible to approximate eqn (1) as:
is the differential cross-section given in mb sr−2 and dΩp and dΩγ are the solid angles for the particle and gamma-ray detectors, each of them given in sr. Since the gamma-ray and particle detectors have a finite size and are placed at fixed angles, it is possible to approximate eqn (1) as:| Yγ(Eb,Eγ,ΔΩγ,ΔΩp) ≈ I(Eb)NtΔTσγ(Eb,Eγ,ΔΩγ,ΔΩp) | (2) |
Experimentally, this yield is defined by:
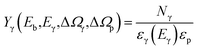 | (3) |
It is possible to determine the number of isotopes in the target (Nt) by combining eqn (1) and (3) and knowing the gamma-ray production cross-section σγ(Eb,Eγ,ΔΩγ,ΔΩp). Also, if the reference cross-sections and the sample are measured using the same experimental setup, a convenient cancellation of the parameters ΔΩp,γ, εγ(Eγ), and εp occurs, helping to avoid systematic errors, and it is possible to write:
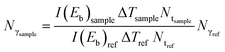 | (4) |
Eqn (4) represents the linear dependence of Nγsample on Nγref, e.g. y = ax + b, where the linear coefficient, b, is compatible with zero if all experimental conditions and corrections are taken into account. The angular coefficient, 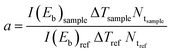 , is independent of the gamma-ray energy, so, it is possible to obtain the number of isotopes in the sample (Ntsample) by doing a fit in the Nγsample × Nγref plot. Since the pNRA technique measures the number of isotopes in the sample, the isotope ratio is obtained by:
, is independent of the gamma-ray energy, so, it is possible to obtain the number of isotopes in the sample (Ntsample) by doing a fit in the Nγsample × Nγref plot. Since the pNRA technique measures the number of isotopes in the sample, the isotope ratio is obtained by:
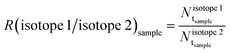 | (5) |
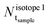 and
and 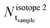 are, respectively, the number of the two isotopes one wants to determine in the sample, given in atoms cm−2.
are, respectively, the number of the two isotopes one wants to determine in the sample, given in atoms cm−2.
3. Experimental setup
3.1. Sample preparation
Three targets were produced using four self-supporting copper foils produced by using the lamination technique and 99.9% purity pellets. Two of these foils were produced using natCu pellets while the other two were produced from 65Cu 99.2% isotopically enriched pellets. The first two targets were produced by using a foil of natCu and a foil of 65Cu to measure the 63,65Cu cross-sections. To create the third target with a different isotopic ratio from the natural one, the remaining natCu and 65Cu foils were laminated together, creating a mixed film of natCu + 65Cu, hereafter named as mixedCu target. Table 1 shows the mass and dimensions of each foil used to create the three targets natCu, 65Cu, and mixedCu used in the experiment, together with the estimated number of atoms (Nt) of 63,65Cu in each target. In this paper, we report in parentheses the standard uncertainties, which correspond to one sigma or k = 1, referred to the corresponding last digits of the quoted result, when applicable.| Target | Mass (mg) | Height (cm) × width (cm) | N t (1018 atoms cm−2) | |||
|---|---|---|---|---|---|---|
| natCu | 65Cu | natCu | 65Cu | natCu | 65Cu | |
| natCu | 0.8795 (1) | 1.20 (5) × 1.00 (5) | 4.8 (6) | 2.1 (3) | ||
| 65Cu | 1.5485 (1) | 1.10 (5) × 1.10 (5) | 9.59 (14) | |||
| mixedCu | 0.8323 (1) | 1.0344 (1) | 0.90 (5) × 1.30 (5) | 1.00 (5) × 1.00 (5) | 4.7 (6) | 11.7 (14) |
| Target | N b (1013 particles) | Time (hours) | N γ–p (104 counts) | N γ–α (103 counts) | ||
|---|---|---|---|---|---|---|
| 77° | 101° | 77° | 101° | |||
| natCu | 6.663 (13) | 23.60 | 7.4786 | 12.9044 | 1.907 | 3.449 |
| 65Cu | 3.615 (10) | 24.17 | 3.4563 | 3.5518 | 0.649 | 0.635 |
| mixedCu | 5.099 (13) | 28.84 | 9.5727 | 10.2834 | 1.653 | 1.679 |
3.2. pNRA measurements
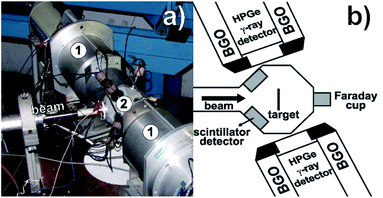
Experimental tests were performed at the 8UD Pelletron tandem accelerator of the Nuclear Physics Open Laboratory (LAFN), located at the University of São Paulo, Brazil, using a proton beam with an incident energy of 11.75 MeV and a current of 0.1 nA. The beam energy resolution is better than 0.1% (ref. 44 and 45) and its accuracy was calibrated by measuring the well-known sharp-threshold neutron emission of 27Al(p,n)27Si and 12C(α,n)15O reactions.46,47A modified configuration of the SACI-PERERE spectrometer40 was used to measure the particle and gamma-ray emission that follows a fusion-evaporation reaction, as seen in Fig. 1. Five ΔE–E plastic phoswich telescopes were positioned at 117.0° with respect to the beam direction, each of them assembled using a thin ΔE (0.1 mm) fast plastic scintillator (τ = 2.4 ns) and a thick E (10 mm) slow plastic scintillator (τ = 264 ns). Those 5 detectors cover a solid angle of 5.4 sr, ensuring about 43% efficiency for single proton detection and 8.5% for single α-particle detection. Two Compton suppressed HPGe detectors with 0.2% absolute photopeak efficiency (60Co @ 1332 keV) and 0.17 sr solid angle were positioned at 77.6° (3) and 101.2° (3) with respect to the beam direction. These angles were defined considering the geometrical layout of the charged particle detectors, and to prioritize the detection of quadrupolar (77°) and dipolar (101°) gamma-ray transitions.48 A Faraday cup with electron suppression of −320 V was positioned at 0° with respect to the beam direction to measure the incident proton beam current with nearly 100% of charge collection. The continuous beam current was integrated with an ORTEC 439 charge integrator, which has an accuracy better than 0.5%, allowing determine the total number of the beam particles that reached the target during the experiment (see Table 2).
The electronics used to perform the particle–gamma coincidence is the standard one used in gamma-ray spectroscopy, and it is described in detail in ref. 40. Basically, an event is collected when at least one of SACI's particle detectors fired in coincidence within a 400 ns time window with one of the HPGe γ-ray detectors. Due to the difference in the response time of the phoswich and the HPGe detectors, there is an immediate digital conversion of the particle information to avoid pulse degradation. The gamma-ray signal obtained by the HPGe is verified in an anti-coincidence mode with the BGO Compton suppressor, which improves the ratio of the full-energy peak to the background Compton signal. After that, the coincidence between gamma rays and particles is verified. The data acquisition dead time was measured using a pulser signal inserted in the test line of the two HPGe detectors as well as directly into one channel of the data acquisition system. The final registered information in an event consists of the energy loss (ΔE) in the fast plastic scintillation and residual energy (E) in the slow plastic scintillation of the charged particle detector, the pulser counts, and energy and time (relative to the particle detection) information of each gamma ray.
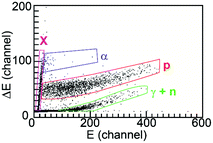
The detected evaporated charged particles are identified due to the difference in the energy loss in the ΔE region of the SACI's detectors as can be seen in a bi-parametric ΔE–E plot (Fig. 2), where the regions related to gamma-rays, neutrons, protons, and alpha-particles were marked. The region marked with “X” represents the particles that have stopped in the detector's ΔE region. The “γ + n” region represents the neutron and gamma-rays interaction with the organic plastic scintillators. As the neutron and gamma-rays cannot be distinguished in the current setup, we did not consider the neutron reaction channel to obtain the isotope ratio.
The gamma-ray photopeak areas for the gamma-rays related to 63,65Cu were obtained from the gamma-ray spectra sorted in coincidence using the proton or alpha-particle regions of the ΔE–E plot. All gamma-ray spectra were subtracted from the random coincidence background and were calibrated in energy using a standard 152Eu gamma-ray source. The 152Eu and 60Co standards were used in the detection efficiency (ε), and their energy dependence fitted using the traditional formula: 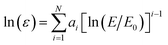 where E0 is the 60Co reference 1332 keV energy and ai are the fitted parameters. Table 2 shows the number of proton–gamma and alpha–gamma coincidence events acquired using the natCu, 65Cu, and mixedCu targets after the random coincidence subtraction.
where E0 is the 60Co reference 1332 keV energy and ai are the fitted parameters. Table 2 shows the number of proton–gamma and alpha–gamma coincidence events acquired using the natCu, 65Cu, and mixedCu targets after the random coincidence subtraction.
3.3. RBS measurements
Rutherford Backscattering Spectrometry (RBS) measurements were performed with the 1.7 MV Pelletron accelerator of the Ion Beam Analysis Laboratory of the University of São Paulo (LAMFI-USP),49 São Paulo, Brazil, to determine accurately the number of atoms per cm2 in the three targets and to have a reference isotope ratio value of the mixedCu target for comparison.A 2.2 MeV proton beam with an average intensity of the order of 15 nA was used in the measurement, as well as 2 surface-barrier detectors positioned at 120° and 170° with respect to the incident beam direction to measure the proton scattered particles. The scattering cross sections for 2.2 MeV protons on copper have been demonstrated to be indistinguishable from Rutherford for scattering angles of 135° and 165° by Nurmela et al.50 An amorphous carbon beam stopper was placed 0.5 mm behind the self-supporting copper targets and was electrically connected with the targets and with the charge integration system.
An X-ray detector, placed at 90° relative to the beam direction, was also used to determine the target's contamination by using the particle-induced X-ray emission (PIXE) technique. The Cu targets were positioned with an inclination of 10° in the center of the measurement chamber. A TiAlTa standard was used to perform energy calibration.
The uniformity of the three targets was verified by probing each one with a 0.5 mm collimated proton beam at three points: center, 1.5 mm to the right of the center, and 1.5 mm to the left of the center. These measurements have shown that the natCu and 65Cu targets have a non-uniformity of less than 2%, while the non-uniformity in the mixedCu target could be of the order of 30%. Due to the non-uniformity of the targets, a 1.8 mm Ta collimator was used to check the average atoms per cm2 value in the area to be irradiated in the pNRA experiment since its experimental setup uses also a Ta collimator with the same 1.8 mm diameter.
The complete elemental sample depth profiles were obtained using the MultiSIMNRA51 software, a program to fit simultaneously and self-consistently multiple energy spectra of scattering techniques using the traditional SIMNRA52 software for interpretation of nuclear scattering analysis. MultiSIMNRA was used to simultaneously fit the experimental data of the two particle detectors used in the RBS analysis to obtain the copper target composition (layer thickness, element concentration, isotopic composition and rugosity) considering small fluctuations in the beam energy and the uncertainties in the calibration parameters.
4. Results
4.1. RBS results
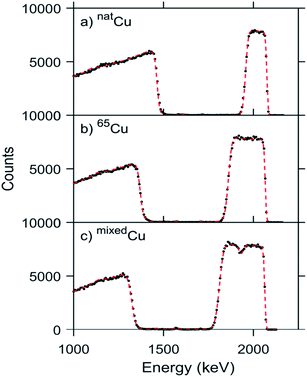
The energy spectra for the natCu, 65Cu, and mixedCu targets using the 1.8 mm collimator and the 170° detector are shown in Fig. 3. The width of the peak located near 2000 keV represents the thickness of each Cu target while the dashed line in those spectra represents the MultiSIMNRA fits to determine the composition of the targets (elements and number of atoms per cm2). The presence of a dip in the mixedCu target around 1.9 MeV (see Fig. 3c) is due a combination of effects such as the kinematic separation between the 63,65Cu isotopes (∼4 keV), the internal oxidation layer (∼2 keV), the energy straggling (σ ≈ 18 keV), and the detector resolution (13 keV). The carbon signal presented in Fig. 3 comes from the beam stopper, and its presence is used as a checker of the MultiSIMNRA calculations to determine the target composition, being included in the fit procedure with reduced weight in the ROI objective function together with a virtual hydrogen gap layer to compensate the 0.04° geometry difference. Table 3 presents the number of atoms per cm2 of 63,65Cu isotopes measured in each target with the 1.8 mm collimator.| Target | N t (1018 atoms cm−2) | R(65Cu/63Cu) | |
|---|---|---|---|
| 63Cu | 65Cu | ||
| natCu | 4.92 (7) | 2.20 (3) | |
| 65Cu | — | 12.16 (6) | |
| mixedCu | 4.75 (8) | 9.87 (10) | 2.08 (6) |
The RBS analysis has also shown a thin layer of oxidation on the surfaces of the targets due to copper's reactivity to oxygen. The number of oxygen atoms per cm2 in each target is less than 1% of the target's composition and their presence should not be a concern in the pNRA measurements due to the difference in the gamma-ray energies from these isotopes to the Cu nuclei, although the predicted nuclear cross-sections of the reactions from the proton beam with the oxygen isotopes are within the same order of magnitude as the copper reactions.
4.2. pNRA results
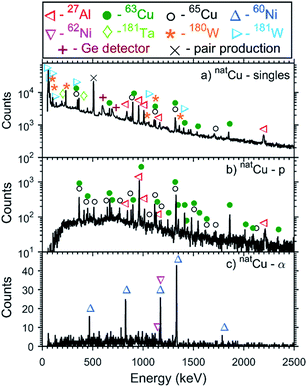
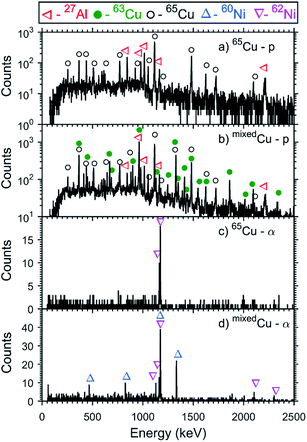
The pNRA technique was tested by using the fusion-evaporation reaction mechanism of the proton beam with the copper targets. In this kind of reaction, after fusion, highly excited compound nuclei are formed, which may emit light particles, such as neutrons, protons, and alpha-particles and the residual nuclei will decay by gamma-ray emission in cascade to the nuclear ground state. The expected populated nuclei produced in the proton reaction with the copper targets predicted by the PACE4 (ref. 53) code can be seen in Table S.1 of the ESI.† In the case of the (p,p′γ) channel, there are also contributions of the inelastic scattering cross-section of the incident proton beam and the excitation of the isotope in the target, improving the total cross-section and favoring the measurement of this channel.Fig. 4 shows the potentiality of the pNRA to differentiate between all gamma-rays from a nuclear reaction. Fig. 4a shows the gamma-ray spectrum observed directly from the natCu target, without particle–gamma coincidence (single mode). In this spectrum, there are gamma-ray peaks from different reactions than the one of interest and also the Compton background is high. Together with the 63,65Cu gamma-rays peaks, the gamma rays emitted from the 27Al chamber and 181Ta collimator reactions with the scattered beam were also observed, together with the gamma rays emitted from 180,181W, products of the fusion-evaporation reaction with the collimators, since the beam energy is higher than the proton–181Ta nucleus Coulomb barrier. The use of collimators is required to ensure that scattered beam particles, with energies different from 11.75 MeV, do not reach the target, and, also, to ensure that only the target is being irradiated. In this gamma-ray spectrum, there are also the Ge isotope gamma rays from the (n,n′) reactions with the HPGe detector by neutrons produced in the fusion-evaporation reaction. All these contamination reactions contribute to increase the background in the single mode spectrum and also make it difficult to identify the gamma-rays from the reaction channels of the Cu targets since some of the 27Al, 180,181W, and 181Ta gamma-ray peak energies are very close to the 63,65Cu gamma-rays and sometimes indistinguishable with the detector's energy resolution.
Fig. 4b and c show, respectively, the gamma-ray spectrum of the natCu target acquired in coincidence mode with protons and with alpha-particles. In these spectra, the majority of the gamma-ray peaks are from the fusion-evaporation reaction with the natCu target. In the case of the proton channel, there are also the contributions from the inelastic reaction natCu (p,p′γ) natCu. Due to the geometry of the experimental setup, the charged particle produced in the fusion reaction with the 181Ta collimator does not reach the particle detectors. Only in the proton channel is there a contamination of the 27Al gamma-rays due to the impossibility to prevent the proton beam particles to be scattered in the target and to produce a fusion-evaporation reaction with the 27Al chamber as a result to the proximity of the chamber to the particle and HPGe detectors. In Fig. 5, the gamma-ray spectra obtained in coincidence with protons and alpha-particles for the 65Cu and mixedCu targets are shown.
There are no contributions in the proton and alpha particle coincidence spectra (see Fig. 4b, c and 5) from the reactions of the beam with the oxygen isotopes, present due to the oxidation of the targets. Although the predicted nuclear fusion-evaporation cross-sections of these reactions were of the same order of magnitude as those with copper isotopes, the small amount of oxidation did not permit a proper measurement of the oxygen isotopic distribution. In such cases, the measurement time and/or efficiency should be increased to lower the pNRA detection limit, as discussed in Section 5.2.
Usually, fusion-evaporation reactions populate high angular momentum nuclear states, which will decay by emitting characteristic gamma-rays down to the ground state. The identification of several gamma-rays can indicate the nuclei to which the gamma-ray belongs and permits the extraction of the number of counts to determine the isotope quantity in a sample. Several excited nuclear states of 63,65Cu and 60,62Ni were populated in the experiments. Fig. S.1 (ESI)† shows the level scheme of each of these nuclei with all the states populated and gamma-rays observed in the experiments described in this report. Despite having identified several gamma-rays of the nuclei of interest, only the most intense gamma-rays, whose peak energies were well defined, and without contamination of other nuclei were used to determine the isotopic concentration in the mixedCu target, as shown in Table S.2 (ESI).†
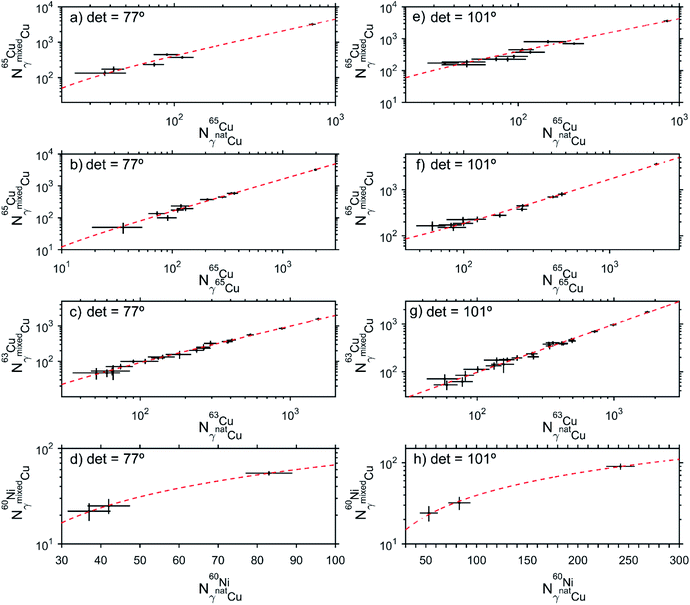
Fig. 6 shows the linear fits of the Nγsample × Nγref plots for the two reference targets (natCu and 65Cu) and the two gamma-ray detectors using the gamma-ray peaks discriminated in Table S.2 (ESI).† The angular coefficients obtained in those fits were used to determine the isotopic ratio as described in Section 2 and the results can be seen in Table 4. In the case of the 62Ni, obtained in the alpha-particle channel, only one or two gamma-rays could be used (see Table S.2 in ESI†), and the isotopic ratio was calculated using eqn (2) and (3).
| Coincidence spectrum | γ-ray detector angle (°) | R(65Cu/63Cu) | |
|---|---|---|---|
| Using 65Cu cross-sections from natCu target | Using 65Cu cross-sections from 65Cu target | ||
| γ-proton | 101.2 (3) | 1.96 (12) | 2.24 (11) |
| 77.6 (3) | 2.03 (15) | 2.17 (11) | |
| γ-alpha | 101.2 (3) | 1.9 (5) | 2.1 (7) |
| 77.6 (3) | 1.9 (6) | 2.9 (10) | |
The pNRA isotopic ratio results obtained in Table 4 are shown by the HPGe detector angle (77° or 101°), by the type of the coincidence particle (proton or alpha) and by using the 65Cu cross-sections obtained using the natural or the isotopically enriched targets. The discrimination of the results considering the detector position is to show that although the emitted gamma-rays have an angular distribution,48 implying that some transitions are better seen by one detector than the other, the isotope ratio can be obtained in any angle. The particle-type (proton or alpha) discrimination results are especially dependent on the particle detector efficiency and can increase the necessary measurement time. As seen in Fig. 4c, 5c and d, there are few counts in the alpha spectra due to the low alpha particle efficiency detection, although these spectra present only the gamma-rays of interest. However, particle discrimination is fundamental to correctly determine isotope ratios in complex samples, since depending on the measured isotope and ion beam, only the proton or alpha channel can be used to quantify an element. The results also show the possibility to determine the isotope ratios using the cross-section data measured with enriched targets. This is especially interesting for isotopes of certain elements whose natural concentration is very low (<1%) and precise measurements of the isotope cross-section are often unknown. The apparent 10% systematic difference between the results measured with the isotopically enriched 65Cu and with the natCu targets comes mainly due to the systematic error caused by the system's dead time, which will be discussed in Section 5.1. A convenient cancellation of the dead time correction occurs when all the referenced cross-sections were measured in the same experiment (Table 4, column 3), which does not occur when the cross-sections came from different experiments (Table 4, column 4). All isotopic ratios obtained with the pNRA for the mixedCu target are in good agreement with the compositional analysis performed using the RBS technique (see Table 3), showing the reliability of this new technique to measure stable isotopes.
5. Discussion
5.1. Experimental setup
The pNRA experimental setup needs to consider the beam particle elastic scattering and the gamma-ray angular distribution, whether the measurement is being done in-vacuum or in-air.The cross section of the elastic scattering can be very large depending on the beam and the analyzed material and will influence mostly the forward angles (laboratory system). It can degrade the particle and gamma detector signals due to the very high counting rates, and in the case of in-vacuum measurements, can produce reactions with the vacuum chamber that will influence the measurements (as discussed in Section 4.2) and also cause radiation damage in the detectors, if those reactions produce high energy neutrons.
The gamma-ray angular distribution needs to be considered when positioning the gamma-ray detectors.48 As pNRA measures simultaneously gamma-rays with different multipolarities, this contribution can be minimized by placing the detector at 55° or 125°. In the case when more gamma-ray detectors are used, they can be placed at different angles to maximize the dipolar and quadrupolar transition detection and reduce the beam time exposure.
Small changes are required in the SACI-PERERE setup to analyze samples using the pNRA technique. The SACI's vacuum chamber is as small as possible to maximize the detection efficiency, making the beam collimators very close to the target. Usually, this closeness is not a problem, since the SACI-PERERE was projected to work with heavy-ion beams, which results in a negligible interaction of the beam with the collimators. However, as shown in Fig. 4a, it is not true when using a proton beam, as the gamma-rays from the reaction of the beam with the Ta collimators reach the HPGe detectors, increasing by up to 50% the dead time of the system, depending on the beam intensity. Changing the collimator position or shielding the gamma-ray detectors can drastically reduce the dead time, as those gamma-rays will not reach the HPGe detectors and, consequently, making the detection system busy with spurious events. The use of digital data acquisition systems, based on the use of Field Programmable Gate Arrays (FPGA), can also be used to decrease the dead time since they are faster to perform the particle–gamma coincidences.
The gamma-ray angular distribution is already considered in the SACI-PERERE to study the fundamental physics parameters since this measurement determines the gamma-ray multipolarity and, consequently, the nuclear spin and parity can be estimated. However, modifications need to be done to consider the high cross-section of the elastic scattering. In this work, we needed to change the SACI-PERERE's Compton suppressed HPGe detector from its 37° original position to the 77° position relative to the beam direction. This angle was chosen to achieve a compromise between detection efficiency, the geometrical layout of the charged particle detectors, and maximizing the detection of the quadrupolar transitions. The forward 63° particle detectors also needed to be removed from the measurements due to the high signal degradation caused by the very high counting rates produced by the elastic scattering.
5.2. Detection limits
Detection limit determination is based upon the minimum detectable signal for a given background, composed, in this experiment, mainly by Compton events and random coincidences. The random coincidences are low and were subtracted during the construction of the coincidence spectra. The detection limit (DL) represents minimum peak count that can be distinguished from background statistical variation, calculated using Poisson statistics. As stated by Currie,54 one should consider when using an analytical technique, at least two different quantities: the detection limit (DL), defined as the reliable gamma-ray peak count to consider the isotope present in the sample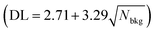 , and determination limit (QL), defined as the number of counts necessary for quantitative measurement with a 95% confidence level
, and determination limit (QL), defined as the number of counts necessary for quantitative measurement with a 95% confidence level 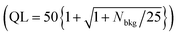 , where Nbkg is the number of counts in the background under the peak region. Both limits are defined for a given experimental setup and acquisition time.
, where Nbkg is the number of counts in the background under the peak region. Both limits are defined for a given experimental setup and acquisition time.
The minimum amount of 63,65Cu which could be detected in a sample can be evaluated using the same experimental conditions for the mixedCu target (28.84 hours of beam time and a live-time of 62%) using the modified SACI-PERERE setup. Table 5 shows the minimum amount of the copper isotopes in a sample considering the detection of only one of the most intense gamma-rays belonging to 63,65Cu and 60,62Ni. In this evaluation, the number of counts in the background (Nbkg) was considered within an energy interval of three full widths at half maximum around the gamma peak.
| Isotope | γ-ray detector angle (°) | Coincidence spectrum | γ-ray energy (keV) | N p (103 counts) | N bkg (102 counts) | DL (counts) | QL (counts) | Minimal isotope quantity (μg g−1) | |
|---|---|---|---|---|---|---|---|---|---|
| DL | QL | ||||||||
| 63Cu | 101.2 (3) | γ-proton | 1327.03 (8) | 2.87 (7) | 1.73 (21) | 46 (3) | 191 (7) | 0.72 (6) | 2.98 (11) |
| 77.6 (3) | γ-proton | 1327.03 (8) | 2.49 (12) | 0.40 (10) | 23 (3) | 131 (6) | 0.41 (6) | 2.33 (11) | |
| 101.2 (3) | γ-alpha | 1332.501 (5) | 0.144 (10) | 0 | 2.71 | 100 | 0.84 (7) | 30.9 (3) | |
| 77.6 (3) | γ-alpha | 1332.501 (5) | 0.088 (4) | 0 | 2.71 | 100 | 1.37 (9) | 50.5 (5) | |
| 65Cu | 101.2 (3) | γ-proton | 1115.546 (4) | 5.74 (16) | 3.4 (3) | 63 (3) | 241 (8) | 0.49 (4) | 1.86 (6) |
| 77.6 (3) | γ-proton | 1115.546 (4) | 5.11 (20) | 0.64 (13) | 29 (3) | 144 (7) | 0.25 (3) | 1.25 (2) | |
| 101.2 (3) | γ-alpha | 1163.50 (12) | 0.057 (9) | 0 | 2.71 | 100 | 2.1 (3) | 77.9 (8) | |
| 77.6 (3) | γ-alpha | 1163.50 (12) | 0.065 (10) | 0 | 2.71 | 100 | 1.9 (3) | 68.3 (7) | |
The detection limits reported in literature for the copper isotopes by NAA55 are 0.57 μg g−1 for 63Cu and 5 μg mg−1 for 65Cu, and 1 μg g−1 for both isotopes measured by TOF-MS.36 ICPMS results56 reported a 50 ng g−1 natural copper concentration to determine the isotope ratio. The detection limits presented in Table 5 for the pNRa technique are in good agreement with the detection limits obtaining using NAA and TOF-MS. However, with one day of acquisition time and this experimental setup, pNRA was not capable of measuring the small quantities of isotopes which can be detected with the ICP-MS technique. To perform a better isotopic ratio measurement, improvements in the experimental setup can be made to increase efficiency and live-time, as discussed in Section 5.1, but the necessary acquisition time still depends on the quantity of material to be measured.
5.3. Modification, activation, or oxidation of the sample and presence of surface impurities
No visible damage to the targets was observed after the measurements, although the use of the nuclear reactions may modify the sample composition and can also activate the sample, as is the case of neutron activation analysis. In the case of the nuclear reactions with a proton beam and the 63Cu isotope, 63Zn nuclei were produced within the neutron emission channel, while with the 65Cu isotope, 65Zn nuclei were produced in the same reaction channel. Both 63,65Zn decay back to 63,65Cu, with a lifetime of T1/2 = 38.47 (5) min (ref. 57) and T1/2 = 243.93 (9) days,58 respectively, resulting in the activation of the targets after the particle–gamma analysis was performed. All targets were monitored after the measurements to check their activity after irradiation and the results were at the same level as the laboratory background radiation, demonstrating that the pNRA technique can be safely used with low ion beam currents, even measuring for a long time.Stable 60,62Ni isotopes were also produced with reactions with 63,65Cu, respectively, as seen in Fig. 4c, 5c and d. The mixedCu target composition was modified by producing about N60Ni = 8.4 (7) × 108 60Ni atoms cm−2 and of N62Ni = 5.9 (8) × 108 62Ni atoms cm−2. It corresponds to a fraction of 1.79 (15) × 10−10 and 6.1 (9) × 10−11 to the total 63,65Cu atoms per cm2 in the target, respectively. The knowledge of the sample modification is very important to correctly interpret the sample composition if different techniques with a sub-ppb sensibility were used after the pNRA measurement.
The presence of impurities deposited in the sample surface or oxide layers are usual in some materials and are concerning only if the isotopes present in the impurity or the oxygen isotopes needed to be determined, or they are present in high concentration. In the first case, it would be necessary to vary the beam energy to determine the impurity/oxygen distribution with the depth profile to determine the isotope ratio in the sample correctly. In the second case, the presence of impurities/oxygen in high quantity will result in different reaction products together with the desired ones. This can increase the necessary measurement time to determine the desired isotope ratio, depending on the required precision of the results. It also can reduce the number of gamma-ray transitions that can be used in the isotope ratio determination, since some of the impurity/oxygen reaction products can have gamma-ray transition energies similar to the gamma-ray transitions from the desired isotope. Surface cleaning can be done to remove the impurities and oxide layers, although it is not mandatory.
In this work, all the Cu targets used were quite reactive to oxidation, so all surfaces contained a layer of copper oxide, confirmed in the RBS measurements. Although the presence of oxygen generates reactions other than the ones of interest for the determination of Cu isotopes, it does not influence the Cu isotope ratios, since the oxygen quantity in the targets was small and the gamma-rays from the oxygen reaction did not have the same energies as the Cu reaction products.
5.4. Reliability of measured reaction cross-sections
There are cross-section databases, such as IBANDL,26 where it is possible to obtain cross-section values in energies equal or close to the desired one or check for resonances that increase the population probability of a given nucleus. There are also computer codes which use analytical or Monte-Carlo methods that can be used to estimate total fusion-evaporation cross-sections, such as CASCADE,59 HIVAP,60 CNABLA,61,62 POTFUS+GEMINI++,62,63 and PACE4,53 each of them with their advantages and drawbacks, as shown by Blank et al.64 However, care must be taken to compare the calculated values with those obtained experimentally using pNRA, as the pNRA technique depends on the nuclear decay scheme, on the gamma-ray angular distribution, and on the angular correlation between the particle and gamma-ray detection, since the measurement is done in coincidence. Also, if a proton beam is being used, an enhancement in the population of the proton channel is expected, since there is the contribution of the inelastic cross-section.Fusion-evaporation reactions produce aligned nuclei, resulting in the population of states with angular momentum j and a projection m along the direction of the beam projectiles. The gamma rays emitted have an angular distribution depending on the electromagnetic properties of the initial and final states, playing an important role in the position of the HPGe detectors and in the beam time exposure.48 If the measurement is done using a coincidence method, information about the state's population can be inferred. Few experiments were done to determine the angular correlation between particle and gamma-ray emission with the necessary precision for proper quantification of cross-section, as these experiments focus on different aspects of nuclear research. Also, the theory of angular correlation relies on several assumptions that are suitable for nuclear structure descriptions but can interfere in absolute value measurements. Zagatto et al.65 have shown an approximation to calculate the particle–gamma differential cross-section taking into account the particle–gamma angular correlation to estimate these contributions. In addition, the total experimental cross section will also depend on the nuclear decay scheme, since it is necessary to consider the differential cross-sections from all gamma-ray transitions that decay to the ground state, including the isomeric transitions.
5.5. Applying the pNRA technique to cultural heritage objects
The pNRA can be applied to different materials, since it is based on fundamental principles and does not require reference standards that match the elemental composition and structure of the analyzed material. Only its flatness needs to be considered to correctly determine the depth at which the measurement is being done. Also, material restrictions like dimensions and vacuum endurance properties (mechanical strength, vapor pressure and heating) can be avoided if the measurements are done in-air. So, with all these considerations, pNRA can be a candidate to analyze cultural heritage objects.However, the main problem when measuring cultural heritage objects with ion beams is to quantify the damage caused to the object or, at least, assure that it is an acceptable one.66 Among the damages that can be caused by the ion beam, it is possible to mention the heat caused by the energy deposition, the dose effects that could be transformed in water radiolysis, the displacement of atoms in the crystalline lattice of the material, activation of long-lived isotopes, etc. Some authors66–68 choose to control the radiation effects on the sample by means of two fundamental quantities of the experiment, namely beam power and fluence. The comparison is then made in terms of these quantities.
Zucchiati68 summarizes some conditions for ion beam analysis experiments guaranteed to avoid damage of delicate organic compounds, for example, beam energies between 0.8 and 5.4 MeV and fluences in the range of 1013 to 1015 particles cm−2. Nevertheless, as demonstrated by Beck et al.,67 the same conditions harm some inorganic compounds like ZnO pigments.
To evaluate the possibility to use the present technique in the cultural heritage field, we estimate the beam power, fluence, and heat deposited in the mixedCu target. These estimates can be divided into two groups: those that consider, for the experiment shown in this work, just the energy deposited by the proton beam in the sample, as the protons had enough energy to traverse the target; and those that consider all the proton's energy to be deposited in the sample, in a thick-target estimation of effects.
The fluence in the experiment presented here is about 5.0 × 1015 particles cm−2, an acceptable limit in comparison with other works in the literature. Considering only the energy effectively deposited in the target, the power dissipated was about 30 μW and a dose of about 44 MGy. Taking into account a hypothetical situation in which all the beam energy was deposited in the target, power and dose values would be about 3.6 mW and 30 MGy, respectively, due to the dose dependence with the irradiated mass and therefore the particle range.69 Although the comparison between radiation effects caused by photons and charged particles is not straightforward due to the difference in energy distribution in the material, some X-ray techniques such as microXRD or microSTXM can deposit energy in the material in dose rates up to GGy s−1,70 showing that the values obtained in this work are reasonable to apply in the study of cultural heritage objects. Those total dose values can be greatly reduced by increasing the detection efficiency through the use of more detectors, reducing consequently the measurement time.
The total heat dissipated in the sample was about 314 J, considering that all the energy was deposited in the target, a concern in the case of in-vacuum analysis where heat loss is negligible. To perform cultural heritage studies, as much of the measurements are performed in-air, the heat produced by the beam interaction should not be a relevant issue. The above considerations are relative for 63,65Cu analysis, and different combinations of beam, target, current, and experiment duration should be analyzed before the measurements.
6. Conclusion
In this paper, the use of a nuclear reaction analysis combined with particle–gamma coincidence (pNRA) using a medium energy accelerator with a maximum terminal voltage 3–40 MV giving access to ion beams of energy 5–500 MeV to measure stable isotope ratios was discussed considering its advantages and limitations. In addition, the possibility to use already existent gamma-ray spectrometers to apply this technique is considered as well as the particularities to perform cultural heritage object measurements.In particular, the pNRA was tested with a modified SACI-PERERE setup with an 11.75 MeV energy proton beam to study copper isotopic concentration. The pNRA results are in accordance with the compositional analysis previously performed using RBS, which indicate that the pNRA performed using an in-vacuum experimental setup can be used to reliable determine stable isotope ratios without the destruction of the sample. However, improvements must be done to minimize the measurement time and to increase the precision of the results to detect less than 1 μg g−1 of a Cu isotope in the sample. Setup modifications, such as shielding the gamma-ray detectors to minimize the background and using faster electronics can be done to decrease the detection limit.
In the near future, experiments will be performed in-air using the same copper targets to verify the advantages and drawbacks of this other experimental possibility.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by grant 2013/19976-8, São Paulo Research Foundation (FAPESP) and by the National Council for Scientific and Technological Development (CNPq). The authors thank the LAFN and LAMFI staff for their great support to perform the experiments.References
- N. Fagel, M. Lechenault, F. Fontaine, E. Pleuger, J. Otten, M. Allan, M. Ghilardi, N. Mattielli and J. P. Goiran, Record of human activities in the Pb isotopes signatures of coastal sediments from the Roman archaeological site of Cala Francese, Cape Corsica (France), J. Archaeol. Sci. Rep., 2017, 12, 770–781 Search PubMed.
- E. Dotsika, D. E. Michael, E. Iliadis, P. Karalis and G. Diamantopoulos, Isotopic reconstruction of diet in Medieval Thebes (Greece), J. Archaeol. Sci. Rep., 2018, 22, 482–491 Search PubMed.
- P. G. C. Amaral, P. C. F. Giannini, F. Sylvestre and L. C. R. Pessenda, Paleoenvironmental reconstruction of a late quaternary lagoon system in southern Brazil (Jaguaruna region, Santa Catarina state) based on multi-proxy analysis, J. Quat. Sci., 2018, 27, 181–191 CrossRef.
- B. Toubhans, A. T. Gourlan, P. Telouk, K. Lutchman-Singh, L. W. Francis, R. S. Conlan, L. Margarit, D. Gonzalez and L. Charlet, Cu isotope ratios are meaningful in ovarian cancer diagnosis, J. Trace Elem. Med. Biol., 2020, 62, 126611 CrossRef CAS.
- S. Blotevogel, E. Schreck, S. Audry, G. D. Saldi, J. Viers, P. Courjault-Radé, J. Darrozes, L. Orgogozo and P. Oliva, Contribution of soil elemental contents and Cu and Sr isotope ratios to the understanding of pedogenetic processes and mechanisms involved in the soil-to-grape transfer (Soave vineyard, Italy), Geoderma, 2019, 343, 72–85 CrossRef CAS.
- B. L. Grimm, L. A. Stern and A. J. Lowe, Forensic utility of a nitrogen and oxygen isotope ratio time series of ammonium nitrate and its isolated ions, Talanta, 2018, 178, 94–101 CrossRef CAS.
- D. J. Huisman, J. van der Laan, G. R. Davies, B. J. H. van Os, N. Roymans, B. Fermin and M. Karwowski, Purple haze: combined geochemical and Pb-Sr isotope constraints on colourants in Celtic glass, J. Archaeol. Sci., 2017, 81, 59–78 CrossRef CAS.
- C. A. Georgiou and G. P. Danezis, Elemental and isotopic mass spectrometry, in Advanced Mass Spectrometry for Food Safety and Quality, ed. Y. Picó, Elsevier, Amsterdam, 2015, ch. 3, vol. 68, pp. 131–243 Search PubMed.
- E. Bulska and B. Wagner, Quantitative aspects of inductively coupled plasma mass spectrometry, Philos. Trans. R. Soc., A, 2016, 374, 20150369 CrossRef.
- B. E. Brumfield, N. L. LaHaye, K. C. Hartig and M. C. Phillips, Optical spectroscopy of laser-produced plasmas for standoff isotopic analysis, Appl. Phys. Rev., 2018, 5, 021301 Search PubMed.
- A. A. Bol'shakov, X. Mao, J. J. González and R. E. Russo, Laser ablation molecular isotopic spectrometry (LAMIS): current state of the art, J. Anal. At. Spectrom., 2016, 31, 119–134 RSC.
- H.-A. Synal, Developments in accelerator mass spectrometry, Int. J. Mass Spectrom., 2013, 349–350, 192–202 CrossRef CAS.
- C.-F. You, Thermal ionization mass spectrometry techniques for boron isotopic analysis: a review, in Handbook of Stable Isotope Analytical Techniques, ed. P. A. Groot, Elsevier, Amsterdam, 2004, ch. 7, vol. 1, pp. 142–152 Search PubMed.
- M. Betti, Isotope ratio measurements by secondary ion mass spectrometry (SIMS) and glow discharge mass spectrometry (GDMS), Int. J. Mass Spectrom., 2005, 242, 169–182 CrossRef CAS.
- P. J. Gale and M. L. Vestal, The Development of Time-of-Flight Mass Spectrometry, in The Encyclopedia of Mass Spectrometry, ed. M. L. Gross and R. M. Caprioli, Elsevier, Amsterdam, 2016, ch. 2, pp. 34–42 Search PubMed.
- R. R. Greenberg, P. Bode and E. A. D. N. Fernandes, Neutron activation analysis: a primary method of measurement, Spectrochim. Acta, Part B, 2011, 66, 193–241 CrossRef CAS.
- M. Kokkoris, Nuclear Reaction Analysis (NRA) and Particle-Induced Gamma-ray Emission (PIGE), in Characterization of Materials, ed. E. N. Kaufmann, Wiley, 2nd edn, 2012, vol. 3, pp. 2006–2023 Search PubMed.
- A. Zucchiatti, Ion beam analysis for the study of our cultural heritage. A short history and its milestones, Nucl. Instrum. Methods Phys. Res., Sect. B, 2019, 452, 48–54 CrossRef CAS.
- R. Acharya and P. K. Pujari, Potential of conventional and internal monostandard NAA and PGNAA and PIGE in forensic sciences: an overview, Forensic Chem., 2019, 12, 107–116 CrossRef CAS.
- M. Axiotis, A. Lagoyannis, S. Fazinić, S. Harissopulos, M. Kokkoris, K. Preketes-Sigalas and G. Provatas, A benchmarking procedure for PIGE related differential cross-sections, Nucl. Instrum. Methods Phys. Res., Sect. B, 2018, 423, 92–96 CrossRef CAS.
- P. Kristiansson and E. Swietlicki, A new technique for quantifying light elements in thin samples, Nucl. Instrum. Methods Phys. Res., Sect. B, 1990, 49, 98–105 CrossRef.
- P. Kristiansson and B. G. Martinsson, Photon-tagged nuclear reaction analysis for trace element determination, Nucl. Instrum. Methods Phys. Res., Sect. B, 1997, 136–138, 362–367 Search PubMed.
- P. Kristiansson, S. Al-Suhaili, M. Elfman, K. G. Malmqvist, J. Pallon and K. A. Sjöland, Photon-tagged nuclear reaction analysis - evaluation of the technique for a nuclear microprobe, Nucl. Instrum. Methods Phys. Res., Sect. B, 1998, 132, 159–176 CrossRef.
- M. Borysiuk, P. Kristiansson, L. Ros, N. S. Abdel, M. Elfman, C. Nilsson and J. Pallon, Preliminary results of oxygen isotope ratio measurement with a particle-gamma coincidence method, Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 348, 269–272 CrossRef CAS.
- M. Borysiuk, P. Kristiansson, L. Ros, N. Abdel, M. Elfman, E. Nilsson and J. Pallon, Evaluation of a setup for pNRA at LIBAF for applications in geosciences, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 332, 202–206 CrossRef CAS.
- A. Gurbich and IAEA, Ion Beam Analysis Nuclear Data Library (IBANDL), 2019, http://www-nds.iaea.org/ibandl/, accessed May 2020 Search PubMed.
- G. Choppin, J.-O. Liljenzin, J. Rydberg and C. Ekberg, Mechanisms and Models of Nuclear Reactions, Radiochemistry and Nuclear Chemistry, ed. G. Choppin, J.-O. Liljenzin, J. Rydberg and C. Ekberg, Academic Press, Oxford, 4th edn, 2013, ch. 11, pp. 313–338 Search PubMed.
- C. E. Souto-Oliveira, M. Babinski, D. F. Araújo, D. J. Weiss and I. R. Ruiz, Multi-isotope approach of Pb, Cu and Zn in urban aerosols and anthropogenic sources improves tracing of the atmospheric pollutant sources in megacities, Atmos. Environ., 2019, 198, 427–437 CrossRef CAS.
- D. F. Araújo, E. Ponzevera, N. Briant, J. Knoery, S. Bruzac, T. Sireau and C. Brach-Papa, Copper, zinc and lead isotope signatures of sediments from a mediterranean coastal bay impacted by naval activities and urban sources, Appl. Geochem., 2019, 111, 104440 CrossRef.
- Z. Wang, J.-W. Park, X. Wang, Z. Zou, J. Kim, P. Zhang and M. Li, Evolution of copper isotopes in arc systems: insights from lavas and molten sulfur in Niuatahi volcano, Tonga rear arc, Geochim. Cosmochim. Acta, 2019, 250, 18–33 CrossRef CAS.
- G. Othmane, S. Hull, M. Fayek, O. Rouxel, M. L. Geagea and T. K. Kyser, Hydrogen and copper isotope analysis of turquoise by SIMS: calibration and matrix effects, Chem. Geol., 2015, 395, 41–49 CrossRef CAS.
- J. M. D. Day, P. A. Sossi, C. K. Shearer and F. Moynier, Volatile distributions in and on the Moon revealed by Cu and Fe isotopes in the ‘Rusty Rock’ 66095, Geochim. Cosmochim. Acta, 2019, 266, 131–143 CrossRef CAS.
- W. Powell, R. Mathur, A. H. Bankoff, J. John, O. Chvojka, M. Tisucká, A. Bulatović and V. Filipović, Copper isotopes as a means of determining regional metallurgical practices in European prehistory: a reply to Jansen, J. Archaeol. Sci., 2018, 93, 216–221 CrossRef CAS.
- M. Lazarov and I. Horn, Matrix and energy effects during in situ determination of Cu isotope ratios by ultraviolet-femtosecond laser ablation multicollector inductively coupled plasma mass spectrometry, Spectrochim. Acta, Part B, 2015, 111, 64–73 CrossRef CAS.
- Y. Zhang, Z. Bao, N. Lv, K. Chen, C. Zong and H. Yuan, Copper Isotope Ratio Measurements of Cu-Dominated Minerals Without Column Chromatography Using MC-ICP-MS, Front. Chem., 2020, 8, 609 CrossRef CAS.
- M. Ohata and H. Hagino, Examination on simultaneous multi-element isotope ratio measurement by inductively coupled plasma time of flight mass spectrometry, Int. J. Mass Spectrom., 2018, 430, 31–36 CrossRef CAS.
- J. Lin, Y. Liu, Y. Yang and Z. Hu, Calibration and correction of LA-ICP-MS and LA-MC-ICP-MS analyses for element contents and isotopic ratios, Solid Earth Sci. Libr., 2016, 1, 5–27 CrossRef.
- H. Yuan, W. Yuan, Z. Bao, K. Chen, F. Huang and S. Liu, Development of Two New Copper Isotope Standard Solutions and their Copper Isotopic Compositions, Geostand. Geoanal. Res., 2017, 41, 77–84 CrossRef CAS.
- K. Sullivan, D. Layton-Matthews, M. Leybourne, J. Kidder, Z. Mester and L. Yang, Copper Isotopic Analysis in Geological and Biological Reference Materials by MC-ICP-MS, Geostand. Geoanal. Res., 2020, 44, 349–362 CrossRef CAS.
- J. A. Alcántara-Núñez, J. R. B. Oliveira, E. W. Cybulska, N. H. Medina, M. N. Rao, R. V. Ribas, M. A. Rizzutto, W. A. Seale, F. Falla-Sotelo, F. R. Espinoza-Quiñones and C. Tenreiro, SACI—a 4π plastic phoswich array ancillary detector system of a γ-ray spectrometer, Nucl. Instrum. Methods Phys. Res., Sect. A, 2003, 497, 429–439 CrossRef.
- C. Jeynes, N. P. Barradas and E. Szilágyi, Accurate determination of quantity of material in thin films by Rutherford backscattering spectrometry, Anal. Chem., 2012, 84, 6061–6069 CrossRef CAS.
- R. Unterumsberger, P. Hönicke, J. L. Colaux, C. Jeynes, M. Wansleben, M. Müller and B. Beckhoff, Accurate experimental determination of gallium K- and L3-shell XRF fundamental parameters, J. Anal. At. Spectrom., 2018, 33, 1003–1013 RSC.
- C. Jeynes, E. Nolot, C. Costa, C. Sabbione, W. Pessoa, F. Pierre, A. Roule, G. Navarro and M. Mantler, Quantifying nitrogen in GeSbTe:N alloys, J. Anal. At. Spectrom., 2020, 35, 701–712 RSC.
- J. R. B. Oliveira, Status and activities of the LAFN (Laboratório Aberto de Física Nuclear), J. Phys.: Conf. Ser., 2019, 1291, 012003 CrossRef CAS.
- O. Sala and G. Spalek, The nuclear structure facility at the University of São Paulo, Nucl. Instrum. Methods Phys. Res., 1974, 122, 213–225 CrossRef CAS.
- S. A. Brindhaban, P. H. Barker, M. J. Keeling and W. B. Wood, Accelerator beam energy calibration with the 27Al(p,n) and 27Al(p,γ) reactions, Nucl. Instrum. Methods Phys. Res., Sect. A, 1994, 340, 436–441 CrossRef CAS.
- R. E. Shamu, E. M. Bernstein and M. J. Parrott, Accelerator energy calibration using the 12C(α, n0)15O threshold, Nucl. Instrum. Methods, 1974, 114, 605–608 CrossRef CAS.
- P. R. P. Allegro, M. A. Rizzutto and N. H. Medina, Improvements in the PIGE technique via gamma-ray angular distribution, Microchem. J., 2016, 126, 287–295 CrossRef CAS.
- M. Harri Tabacniks, The Laboratory of Material Analysis with Ion Beams, LAMFI-USP, 2019, e-prints, arXiv:1902.08309, https://arxiv.org/abs/1902.08309.
- A. Nurmela, V. Zazubovich, J. Räisänen, E. Rauhala and R. Lappalainen, Elastic scattering cross sections of protons by copper, molybdenum, silver and tin near the Coulomb barrier, J. Appl. Phys., 1998, 84, 1796–1799 CrossRef CAS.
- T. F. Silva, C. L. Rodrigues, M. Mayer, M. V. Moro, G. F. Trindade, F. R. Aguirre, N. Added, M. A. Rizzutto and M. Tabacniks, MultiSIMNRA: a computational tool for self-consistent ion beam analysis using SIMNRA, Nucl. Instrum. Methods Phys. Res., Sect. B, 2016, 371, 86–89 CrossRef CAS.
- M. Mayer, Improved physics in SIMNRA 7, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 332, 176–180 CrossRef CAS.
- O. Tarasov and D. Bazin, Development of the program LISE: application to fusion–evaporation, Nucl. Instrum. Methods Phys. Res., Sect. B, 2003, 204, 174–178 CrossRef CAS.
- L. A. Currie, Limits for qualitative detection and quantitative determination. Application to radiochemistry, Anal. Chem., 1968, 40, 586–593 CrossRef CAS.
- N. M. A. Mohamed, Decreasing the Detection Limit of Copper for the Instrumental Neutron Activation Analysis by Measuring the Activity of 64Cu Isotope from the Annihilation Peak, Nucl. Technol., 2009, 166, 187–196 CrossRef CAS.
- E. Paredes, E. Avazeri, V. Malard, C. Vidaud, R. Ortega, A. Nonell, H. Isnard, F. Chartier and C. Bresson, A new procedure for high precision isotope ratio determinations of U, Cu and Zn at nanogram levels in cultured human cells: what are the limiting factors?, Talanta, 2018, 178, 894–904 CrossRef CAS.
- B. Erjun and H. Junde, Nuclear Data Sheets for A = 63, Nucl. Data Sheets, 2001, 92, 147–252 CrossRef CAS.
- E. Browne and J. Tuli, Nuclear Data Sheets for A = 65, Nucl. Data Sheets, 2010, 111, 2425–2553 CrossRef CAS.
- F. Pühlhofer, On the interpretation of evaporation residue mass distributions in heavy-ion induced fusion reactions, Nucl. Phys. A, 1977, 280, 267–284 CrossRef.
- W. Reisdorf, Analysis of fissionability data at high excitation energies, Z. Phys. A: At. Nucl., 1981, 300, 227–238 CrossRef CAS.
- J.-J. Gaimard and K.-H. Schmidt, A reexamination of the abrasion-ablation model for the description of the nuclear fragmentation reaction, Nucl. Phys. A, 1991, 531, 709–745 CrossRef.
- K. Hagino, N. Rowley and A. Kruppa, A program for coupled-channel calculations with all order couplings for heavy-ion fusion reactions, Comput. Phys. Commun., 1999, 123, 143–152 CrossRef CAS.
- R. J. Charity, Systematic description of evaporation spectra for light and heavy compound nuclei, Phys. Rev. C: Nucl. Phys., 2010, 82, 014610 CrossRef.
- B. Blank, G. Canchel, F. Seis and P. Delahaye, Evaluation of fusion-evaporation cross-section calculations, Nucl. Instrum. Methods Phys. Res., Sect. B, 2018, 416, 41–49 CrossRef CAS.
- V. Zagatto, J. Oliveira, P. Allegro, L. Chamon, E. Cybulska, N. Medina, R. Ribas, W. Seale, C. Silva, L. Gasques, G. Zahn, F. Genezini, J. Shorto, J. Lubian, R. Linares, D. Toufen, M. Silveira, E. Rossi and G. Nobre, γ-Particle coincidence technique for the study of nuclear reactions, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 749, 19–26 CrossRef CAS.
- T. Calligaro, V. Gonzalez and L. Pichon, PIXE analysis of historical paintings: is the gain worth the risk?, Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 363, 135–143 CrossRef CAS.
- L. Beck, P. C. Gutiérrez, S. Miro and F. Miserque, Ion beam modification of zinc white pigment characterized by ex situ and in situ μ-Raman and XPS, Nucl. Instrum. Methods Phys. Res., Sect. B, 2017, 409, 96–101 CrossRef CAS.
- A. Zucchiatti and F. Agulló-Lopez, Potential consequences of ion beam analysis on objects from our cultural heritage: an appraisal, Nucl. Instrum. Methods Phys. Res., Sect. B, 2012, 278, 106–114 CrossRef CAS.
- E. B. Podgoršak, Fundamentals of Radiation Dosimetry, in Radiation Physics for Medical Physicists, Springer, Cham, 2016, ch. 15, pp. 643–670 Search PubMed.
- L. Bertrand, S. Schöeder, D. Anglos, M. B. Breese, K. Janssens, M. Moini and A. Simon, Mitigation strategies for radiation damage in the analysis of ancient materials, TrAC, Trends Anal. Chem., 2015, 66, 128–145 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ja00283f |
| This journal is © The Royal Society of Chemistry 2021 |