Validated ensemble variable selection of laser-induced breakdown spectroscopy data for coal property analysis†
Weiran
Song
 a,
Zongyu
Hou
a,
Muhammad Sher
Afgan
a,
Zongyu
Hou
a,
Muhammad Sher
Afgan
 a,
Weilun
Gu
a,
Hui
Wang
b,
Jiacheng
Cui
a,
Zhe
Wang
a,
Weilun
Gu
a,
Hui
Wang
b,
Jiacheng
Cui
a,
Zhe
Wang
 *a and
Yun
Wang
*c
*a and
Yun
Wang
*c
aState Key Lab of Power Systems, International Joint Laboratory on Low Carbon Clean Energy Innovation, Department of Energy and Power Engineering, Tsinghua University, Beijing, 100084, China. E-mail: zhewang@tsinghua.edu.cn
bSchool of Computing and Engineering, University of West London, London, W5 5RF, UK
cRenewable Energy Resources Laboratory (RERL), Department of Mechanical and Aerospace Engineering, University of California, Irvine, CA 92697-3975, USA. E-mail: yunw@uci.edu
First published on 22nd October 2020
Abstract
Laser-induced breakdown spectroscopy (LIBS), an emerging elemental analysis technique, provides a fast and low-cost solution for coal characterization without complex sample preparation. However, LIBS spectra contain a large number of uninformative variables, resulting in reduction in the predictive ability and learning speed of a multivariate model. Variable selection based on a single criterion usually leads to a lack of diversity in the selected variables. Coupled with spectral uncertainty in LIBS measurements, this can degrade the reliability and robustness of the multivariate model when analysing spectra obtained at different times and conditions. This work proposes a validated ensemble method for variable selection which uses six base algorithms and combines the returned variable subsets based on the cross-validation results. The proposed method is tested on two sets of LIBS spectra obtained within one month under variable experimental conditions to quantify the properties of coal, including fixed carbon, volatile matter, ash, calorific value and sulphur. The results show that the multivariate model based on the proposed method outperforms those using benchmark variable selection algorithms in six out of the seven tasks by 0.3%–2% in the coefficient of determination for prediction. This study suggests that variable selection based on ensemble learning improves the predictive ability and computational efficiency of the multivariate model in coal property analysis. Moreover, it can be used as a reliable method when the user is not sure which variables to choose in LIBS application.
1. Introduction
Coal is the most abundant fossil energy on planet earth and accounts for 27% of global primary energy consumption in 2019.1 Although its share of energy consumption has fallen to its lowest level in 16 years, coal is still the main energy source in some emerging economies such as China and India. The major utilization of coal is to produce electrical energy through combustion,2 which contributes to 36.4% of global electricity generation in 2019. However, the threat of energy shortage, environmental pollution and climate change has prompted coal-fired power plants to optimize the energy system and reduce pollutant and CO2 emissions. The amount of energy and pollutants released from combustion is closely related to coal properties such as the calorific value and sulphur content. To utilize coal efficiently and cleanly, real-time and accurate coal property analyses are of great importance for the power industry.Traditional methods of measuring coal properties mainly rely on chemical processes such as liquefaction and carbonization. These methods are highly accurate but have disadvantages of being time-consuming and expensive, which cannot meet the growing demand for real-time analysis in coal-fired power plants. Current analytical technologies for rapid analysis of coal properties are X-ray fluorescence (XRF) and prompt gamma neutron activation analysis (PGNAA).3 However, XRF is not suitable for analysing low atomic number elements such as C and H, while PGNAA's neutron source poses potential health hazards. Moreover, both technologies are costly in terms of installation and maintenance and require strict regulated operations. Thus, low-cost technologies with fast, simple and safe operations are urgently needed for multi-element analysis of coal.
Laser-induced breakdown spectroscopy (LIBS) is an emerging atomic emission spectroscopic technology that determines the elemental composition and concentration based on the spectrum of laser-generated plasma. LIBS has been widely used to study coal properties due to its advantages of rapidness, minimal sample preparation and simultaneous determination of multiple elements.3,4 To determine the relationship between LIBS spectra and the investigated coal property, the simplest method is univariate analysis which manually selects one spectral line corresponding to a specific element based on theoretical or empirical knowledge.4,5 However, this method often yields unsatisfactory performance because uncontrollable fluctuations of experimental parameters and matrix effects can distort the relationship between the intensity and concentration.6 Another method is multivariate analysis which utilises the entire spectrum or a subset of variables (also called features) to extract quantitative information.7 When spectral signatures overlap due to inter-element interference,8 multivariate methods such as partial least squares (PLS) and its variants can easily outperform conventional univariate models in coal property analysis.9
LIBS data usually contain several tens of thousands of variables due to the wide wavelength range, high spectral resolution and complex sample components.10,11 A large proportion of these variables are redundant and irrelevant: (i) a variable may be highly correlated with one or more of the other variables, and (ii) a variable may not be correlated with the predictive response.7 Although the use of chemometrics and machine learning models has become an analytical routine for processing LIBS data,12,13 the large numbers of redundant and irrelevant variables can significantly reduce the predictive ability and computational efficiency of the models.14 Therefore, variable selection is generally performed prior to multivariate analysis of LIBS data. For the analysis of coal properties, recent studies have attempted using several model-based variable selection methods that identify important variables based on the result of specific algorithms. Li et al. employed a genetic algorithm (GA) and synergy interval partial least squares (siPLS) to improve the coefficient of determination (R2) and the root mean square errors (RMSE) of calorific value measurement from 0.9851 to 0.9936 and from 0.7310 MJ kg−1 to 0.4580 MJ kg−1 respectively, in prediction.15 Yan et al. applied particle swarm optimization (PSO) to select 1000–4000 variables from 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620-dimensional LIBS data, which assisted a kernel extreme learning machine (K-ELM) to achieve better results than using characteristic lines to determine the volatile matter and calorific value.16 Besides, variable selection methods such as competitive adaptive reweighted sampling (CARS) and the successive projection algorithm (SPA) were combined with PLS to quantify nitrogen and sulphur contents.17
620-dimensional LIBS data, which assisted a kernel extreme learning machine (K-ELM) to achieve better results than using characteristic lines to determine the volatile matter and calorific value.16 Besides, variable selection methods such as competitive adaptive reweighted sampling (CARS) and the successive projection algorithm (SPA) were combined with PLS to quantify nitrogen and sulphur contents.17
Variable selection provides an effective way to improve the modelling performance and learning speed without prior knowledge of the domain. Nevertheless, selecting an appropriate subset of variables remains difficult from the user perspective. Variable selection is traditionally based on a single criterion which may not deal with cases with different variances and other statistical properties equally well.18,19 When the analytical task or the composition of input data changes, using a single variable selector can yield less satisfactory results due to the lack of diversity in the selected variables.20 For example, K-ELM with PSO has better prediction performance than K-ELM based on characteristic lines for volatile matter and calorific value characterization, while the latter is more accurate than the former for quantifying the ash content.16 Furthermore, matrix effects and fluctuating experimental parameters often lead to a high degree of spectral uncertainty in long-term LIBS measurements.3,21 The intensity of spectral lines at the same wavelength can significantly change over time even for the same sample. Under such circumstances, some useful variables may be weakly related to the response according to a specific variable selection criterion. By discarding these spectral lines, the reliability and robustness of the multivariate model will be reduced when analysing new data obtained at different times and conditions.
In this work, we aim to improve the predictive capability and computational efficiency of the multivariate model for LIBS data analysis through a combination of variable selection and ensemble learning. We propose a validation-based ensemble method for variable selection which adopts six variable selection algorithms as base selectors to ensure the diversity of the selected variables. This method selects variables by aggregating the variables selected by the base selectors based on the cross-validation results of PLS regression. This method is evaluated by experiments using LIBS spectra collected within a month under fluctuating experimental parameters. A PLS regression model is constructed to quantify coal properties, including fixed carbon, volatile matter, ash, calorific value and sulphur content. The experimental result shows that the proposed method outperforms the benchmark methods in six out of the seven tasks. Thus, variable selection based on the ensemble strategy can improve the predictive ability and computational efficiency of the multivariate model in coal property analysis. Moreover, it can be used as a reliable method when the user is not sure which variable selection algorithm to use for a given task.
2. Theory and method
2.1. Variable selection
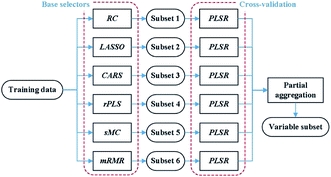
Appropriate variable selection methods can improve prediction performance, reduce computational load and provide a simple interpretation of multivariate models. Automatic selection is preferable to manual selection due to its high efficiency and capability.10 In this paper, we consider six methods as the base selectors for the proposed variable selection method, which are frequently used in the quantitative analysis of spectral data.22| y = Xβ + e | (1) |
The use of regression vector β is a straightforward method to assess the importance of each variable. Variables with RC values close to zero can be eliminated, and variables with large absolute values of RC are important. The main disadvantage of RC is that it does not consider the combination effect of variables.22
• Least absolute shrinkage and selection operator (LASSO):23 the LASSO method is a popular penalized regression approach, which minimizes the residual sum of squares and a penalty term. The LASSO estimator is defined as
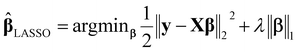 | (2) |
• Competitive adaptive reweighted sampling (CARS):26 the CARS method is an efficient variable selection method that follows the principle of “survival of the fittest”. Each set of wavelength variables will compete with each other through their own weight, the sets of large weights will remain and the rest will be removed. CARS first calculates the absolute values of PLS regression coefficients to evaluate the importance of each variable. Then N subsets from N Monte Carlo sampling runs are sequentially obtained based on the importance of each variable. A two-step variable reduction procedure (exponentially decreasing function and adaptive reweighted sampling) is employed to select important variables. Finally, by comparing the root mean square errors of cross-validation (RMSECV), the subset with the minimum RMSECV is selected. It is noted that CARS often selects a small number of variables and is unstable, which limits its use on specific types of data.27
• Recursive weighted partial least squares (rPLS):28 the rPLS method iteratively reweights the variables to magnify important variables based on the process of repeated PLS modelling. The new input data XR are updated as
| XR = XR−1 × diag(β) | (3) |
• Significance multivariate correlation (sMC):29 the sMC method statistically determines the importance of a variable by combining regression variance and residual variance from the PLS regression model. To prevent the influence of irrelevant information contained in X, the calculation is performed based on the target projection (TP) without orthogonal variance decomposition,30 which can be represented as
| X = XsMC + EsMC = tTPwTTP + EsMC | (4) |
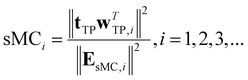 | (5) |
The main drawback of sMC is that it does not highlight the most important variables for interpreting models.31
• Minimum redundancy maximum relevance (mRMR):32 the mRMR uses mutual information to select a variable subset that has the highest relevance with the response y, subject to the constraint that selected variables are maximally dissimilar to each other.
The combination of results (subsets of variables or rankings of all variables) to obtain a final output is a crucial point in ensemble variable selection.37 The most typical way of combining subsets of variables is to calculate their intersection or union while combining the rankings of all variables includes minimum, maximum and mean calculations.20 The general evaluation of ensemble variable selection is based on the prediction performance of the final learner.
(1) Base selections: the proposed method is based on a heterogeneous ensemble, which individually adopts base selectors including RC, LASSO, CARS, rPLS, sMC and mRMR on training data.
(2) Validation: the subsets of variables returned by the six base selectors are fed to PLS regression to determine the rankings of the selectors according to the corresponding RMSECV values.
(3) Partial aggregation: based on the above rankings, we merge the subsets obtained by the first three selectors into the final variable subset.
A heterogeneous ensemble is a suitable option when the sample size of data is small or the user is not sure which available selector to use.20 Generally, the number of coal samples in many LIBS studies is small due to the high complexity and expense of conventional analysis.15,16 This, coupled with different data splitting, may lead to ranking fluctuations of different selectors. Instead of computing the intersection and the union of subsets, the proposed method partially combines subsets based on the results of 5-fold cross-validation. On one hand, it avoids an extremely small number of variables in the intersection set, which may lead to performance degradation in practice.37 On the other hand, the partial combination can significantly reduce the number of variables compared to the union of subsets. This work adopts the first three selectors to balance the prediction performance and the number of selected variables. The subset of variables determined by the proposed method is then used to construct a PLS regression model.
2.2. Multivariate analysis
PLS is a standard multivariate method for analysing high-dimensional and multi-collinear spectral data, which relies on the basic assumption that the investigated system is driven by a set of orthogonal factors,38 namely latent variables (LVs). PLS extracts LVs by projecting predictor variables X onto a subspace such that the covariance between the LVs and the response y is maximized. The PLS regression algorithm is summarized in Table 1.| Input | Predictor variables X, response y, the number of latent variables k |
| Output | T (X-score matrix), P (X-loading matrix), q (y-loading vector), regression coefficients β |
| 1 | Compute the loading weights: w = XTy |
| 2 | Normalize the weights: w = w/‖w‖ |
| 3 | Compute the score of X: t = Xw |
| 4 | Compute the loading vector of X: p = XTt/(tTt) |
| 5 | Compute the loading vector of y: q = yTt/(tTt) |
| 6 | Deflate X and y: X = X − tpT, y = y − tq |
| 7 | Store w, t, p and q in W, T, P and q respectively |
| 8 | Return to step 1 until reaching k latent variables |
| 9 | Compute the regression coefficients: β = WT(PWT)−1Q |
2.3. Model evaluation
The LIBS data were randomly split into training and test sets with a ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. This process was repeated 50 times. For a fair comparison between different variable selection methods, the same training and test sets were used in each run. Pre-processing methods including standard normal variate (SNV), 0–1 scaling and L2 normalization were tested on the acquired spectra, and the LIBS spectra were auto-scaled before variable selection and PLS regression. The PLS regression model based on the training set was optimised by 5-fold cross-validation and then used to analyse samples from the test set. The result reported is the average of the 50 different runs.
1. This process was repeated 50 times. For a fair comparison between different variable selection methods, the same training and test sets were used in each run. Pre-processing methods including standard normal variate (SNV), 0–1 scaling and L2 normalization were tested on the acquired spectra, and the LIBS spectra were auto-scaled before variable selection and PLS regression. The PLS regression model based on the training set was optimised by 5-fold cross-validation and then used to analyse samples from the test set. The result reported is the average of the 50 different runs.
The optimal number of LVs in PLS regression, RC, CARS and rPLS was searched from 1 to 10 in the case of overfitting. Since the number of Monte Carlo sampling runs in CARS does not significantly influence the prediction performance, it was adjusted to 100 for simplicity. The significance level of sMC was set to a default value of 0.01. The number of variables selected by RC and mRMR was 500 to achieve a good trade-off between prediction performance and the number of variables. Additionally, the base and proposed selectors were compared to a conventional method of processing LIBS spectra, which identifies spectral peaks, subtracts baseline and calculates the peak area.
The coefficient of determination (R2) and the RMSE of calibration, cross-validation and prediction were used to evaluate the performance of regression models:
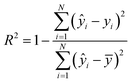 | (6) |
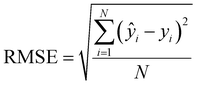 | (7) |
3. Experimental
3.1. Coal samples
Two groups of coal samples collected from different minefields and power plants of China were used in this study. Sample sizes 306 and 174 were measured within one month at the end of 2017. All samples were in the form of powders with particle size less than 200 μm and were pressed into compact and smooth pellets with a diameter of 30 mm and a thickness of 3 mm using 20 tons of pressure for around 10 seconds. Five coal properties including fixed carbon, volatile matter, ash, calorific value and sulphur were analysed by standard chemical methods. The range of coal properties is given in Table 2.| Min | Max | MEAN | STD | ||
|---|---|---|---|---|---|
| Group-1 | Carbon-1 (%) | 55.42 | 85.56 | 66.36 | 6.26 |
| Volatile matter-1 (%) | 2.63 | 32.97 | 22.21 | 6.75 | |
| Group-2 | Carbon-2 (%) | 23.97 | 53.07 | 40.01 | 4.92 |
| Volatile matter-2 (%) | 16.72 | 33.15 | 24.02 | 3.4 | |
| Ash (%) | 8.5 | 57.76 | 34.34 | 8.86 | |
| Calorific value (MJ kg−1) | 10.84 | 27.74 | 20.12 | 2.73 | |
| Sulphur (%) | 0.3 | 2.63 | 1.09 | 0.72 | |
3.2. LIBS setup
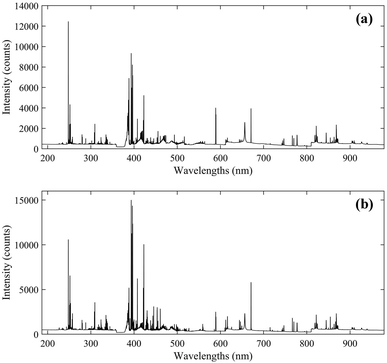
The instrumentation used in this work was an integrated LIBS system (ChemReveal, TSI, USA).39 The spectra of coal samples were induced by a Q-switched Nd:YAG laser source with a wavelength of 1064 nm. The laser energy and delay time were optimized to be 90 mJ and 0.5 μs, respectively. The plasma signal was collected through an optical fibre to a seven-channel spectrometer equipped with seven CCD detectors. The spectral wavelengths range from 186.87 nm to 979.23 nm with a resolution of around 0.09 nm. The gate width was 1 ms and cannot be changed, and the angle between the fibre and the laser beam was around 45°. The spot size was set to be 400 μm in diameter on the sample surface. For each coal pellet, 176 spectra with 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990 variables were obtained at different positions and averaged to represent a data sample. The average spectra of the two groups are displayed in Fig. 2.
990 variables were obtained at different positions and averaged to represent a data sample. The average spectra of the two groups are displayed in Fig. 2.
3.3. Software
The instrument was controlled and data were acquired using ChemReveal software.39 The data analysis was performed in MATLAB R2018b software (The MathWorks Inc., USA). The libPLS package was employed for PLS regression, RC and CARS algorithms.40 The implementation of LASSO, rPLS, sMC and mRMR algorithms was based on the MATLAB external functions.28,29,41,424. Results and discussion
4.1. Quantification performance
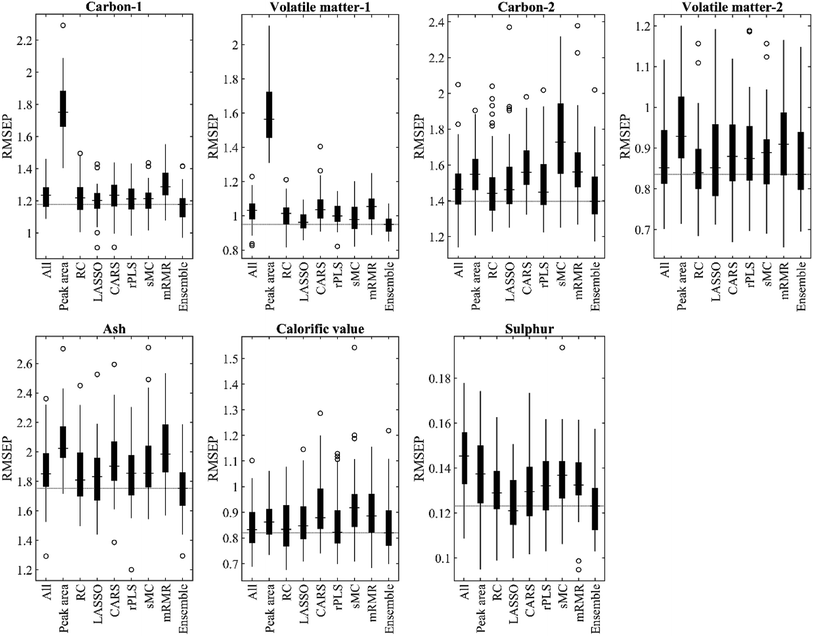
The average results of the PLS regression model on raw and normalized LIBS data are presented in Table S1 (see the ESI†). For the first group, the model based on the data normalized by SNV achieves the highest R2 in validation and prediction, which is 1.5% higher than that based on the raw data on average. The SNV normalization improves the simplicity of the PLS model, thereby reducing the optimal number of LVs. For the second group, the model combined with different normalization methods cannot improve prediction performance and model simplicity in most cases. Therefore, the raw data of the second group are directly used for variable selection and modelling.The results of PLS regression on two LIBS data with full variables and subsets of variables selected by different methods are shown in Table 3. The proposed ensemble method improves the predictive ability of PLS regression for all tasks and outperforms baseline methods except for determining volatile matter in the second group. The average RMSEP of carbon-1, volatile matter-1, carbon-2, ash, calorific value and sulphur measurements is 1.17%, 0.95%, 1.44%, 1.76%, 0.84 MJ kg−1 and 0.12%, respectively. Among all methods, the LASSO ranks the second in four out of the seven tasks followed by RC, which achieves the highest results in the volatile matter-2 task (RMSEP = 0.85%, R2P = 0.93). The PLS regression model combined with the peak area yields unsatisfactory prediction performance. The variables selected based on the peak area are intuitive for chemical interpretation; however, some important variables with low intensities may be ignored, and some of the selected variables may not be related to the response. The calibration and 5-fold cross-validation results of different methods in the seven tasks are given in Table S2.†
| Carbon-1 (%) | Volatile matter-1 (%) | Carbon-2 (%) | Volatile matter-2 (%) | |||||
|---|---|---|---|---|---|---|---|---|
| RMSEP | R 2P | RMSEP | R 2P | RMSEP | R 2P | RMSEP | R 2P | |
| All variables | 1.2332 | 0.9597 | 1.023 | 0.9766 | 1.4793 | 0.9052 | 0.871 | 0.9272 |
| Peak area | 1.7602 | 0.9179 | 1.6 | 0.9433 | 1.5659 | 0.8935 | 0.9436 | 0.915 |
| RC | 1.2181 | 0.9606 | 1.0029 | 0.9774 | 1.4945 | 0.9032 | 0.8534 | 0.9303 |
| LASSO | 1.187 | 0.9628 | 0.9698 | 0.9789 | 1.5082 | 0.9018 | 0.8742 | 0.9266 |
| CARS | 1.2301 | 0.9598 | 1.0522 | 0.9752 | 1.5943 | 0.8896 | 0.8838 | 0.925 |
| rPLS | 1.2109 | 0.9612 | 1.0047 | 0.9774 | 1.5032 | 0.9024 | 0.8871 | 0.9249 |
| sMC | 1.2072 | 0.9613 | 0.9909 | 0.9781 | 1.7488 | 0.8685 | 0.8802 | 0.9265 |
| mRMR | 1.2954 | 0.9556 | 1.0474 | 0.9756 | 1.6012 | 0.8885 | 0.9016 | 0.9218 |
| Ensemble | 1.1711 | 0.9636 | 0.9474 | 0.9799 | 1.4434 | 0.9095 | 0.8584 | 0.9295 |
| Ash (%) | Calorific value (MJ kg−1) | Sulphur (%) | ||||
|---|---|---|---|---|---|---|
| RMSEP | R 2P | RMSEP | R 2P | RMSEP | R 2P | |
| All variables | 1.8771 | 0.9547 | 0.8523 | 0.9019 | 0.1447 | 0.9572 |
| Peak area | 2.0592 | 0.9454 | 0.8682 | 0.8983 | 0.1377 | 0.961 |
| RC | 1.8513 | 0.956 | 0.8518 | 0.9011 | 0.1305 | 0.9654 |
| LASSO | 1.824 | 0.9571 | 0.8583 | 0.9003 | 0.1246 | 0.9685 |
| CARS | 1.9359 | 0.9518 | 0.9197 | 0.8852 | 0.1308 | 0.9652 |
| rPLS | 1.8488 | 0.9559 | 0.8565 | 0.9002 | 0.1322 | 0.9643 |
| sMC | 1.9176 | 0.9525 | 0.9291 | 0.8838 | 0.1372 | 0.9615 |
| mRMR | 2.0286 | 0.9471 | 0.8924 | 0.8918 | 0.1339 | 0.9634 |
| Ensemble | 1.7618 | 0.96 | 0.8436 | 0.9034 | 0.1231 | 0.9692 |
The RMSEP values of different methods are depicted in Fig. 3, where the variations in the results of the 50-run are represented by boxplots. The median RMSEP value of the proposed method is the lowest among all methods in six out of the seven tasks. Furthermore, the standard deviation of the proposed method for volatile substances-1 (0.05), ash (0.17) and sulphur (0.01) measurements are smaller than that of other methods (see Table S3†), which demonstrates the robustness of the ensemble variable selection in specific tasks.
4.2. Evaluation of the selected variables
Table 4 shows the average number of variables selected for each task by different methods. Since the highest average accuracies of cross-validation are obtained by CARS, LASSO and rPLS (see Table S2†), the proposed ensemble method will mostly merge the subsets of variables corresponding to these three methods, thereby reducing 95%–98% of the variables. The CARS and LASSO usually select the least number of variables (75–217). The LASSO selected approximately 215 and 123 variables for the first and second groups of data, respectively.| Peak area | RC | LASSO | CARS | rPLS | sMC | mRMR | Ensemble | |
|---|---|---|---|---|---|---|---|---|
| Carbon-1 | 500 | 500 | 215.88 | 217 | 594.62 | 748.74 | 500 | 699.46 |
| Volatile matter-1 | 500 | 500 | 215.32 | 147.62 | 476.14 | 1543.32 | 500 | 479.56 |
| Carbon-2 | 500 | 500 | 123.66 | 115.3 | 541.32 | 86.26 | 500 | 485.64 |
| Volatile matter-2 | 500 | 500 | 123.28 | 74.74 | 684.3 | 147.86 | 500 | 250.3 |
| Ash | 500 | 500 | 123.92 | 111.56 | 631 | 201.86 | 500 | 365.14 |
| Calorific value | 500 | 500 | 123.5 | 120.56 | 220.94 | 100.24 | 500 | 408.34 |
| Sulphur | 500 | 500 | 123.52 | 95.72 | 934.22 | 138.16 | 500 | 399.58 |
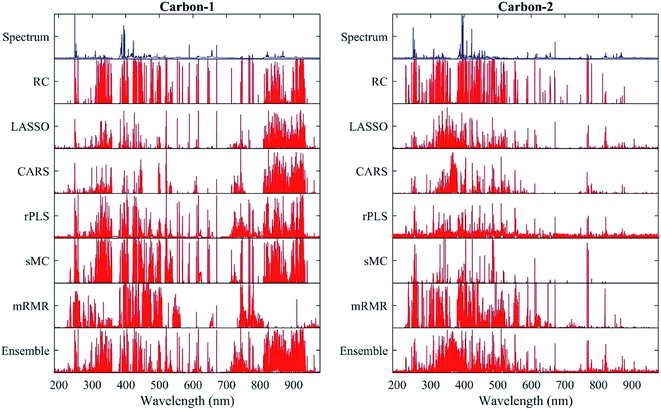
Fig. 4 displays the frequency of each wavelength selected by different methods for two sets of carbon measurement. The proposed method selects the wavelength of 247.87 nm related to C I (247.877 nm) in 42 and 17 of the 50 runs for the two sets, respectively. The wavelength of 473.67 nm and 473.6 nm has the second highest frequency (32 and 25, respectively) for the first set, corresponding to the C2 line (473.622 nm). Moreover, the wavelength of 386.06 nm which may be related to CN (386.143 nm) is selected 24 times for the second set. The frequency of the wavelengths corresponding to the other characteristic lines of carbon does not exceed 10 in most cases. The frequencies of all wavelengths for volatile matter, ash, calorific value and sulphur measurements are presented in Fig. S1.†
The wavelengths of the top frequencies determined by the proposed method is then compared with the specific wavelengths of the peak area method, as shown in Table S4.† Some of these wavelengths correspond to strong spectral peaks, while others have low intensities which are easily overlooked by using the peak area method. According to the NIST atomic spectra database, some possible wavelengths corresponding to coal properties include 247.87 nm (C I for carbon measurement), 404.79 nm (Fe I for ash measurement) and 589.00 nm (the strong Na I line overlapping with the weak S I line for the sulphur content). Besides, it is noted that many high-frequency wavelengths identified by the proposed method and the base methods are not directly related to the investigated coal properties. For example, the wavelengths of 742.38 nm (N I), 324.8 nm (Cu I) and 404.79 nm (Fe I) are also high-frequency for carbon measurement in addition to C I 247.87 nm due to the matrix effects.
5. Conclusions
In this work, an ensemble variable selection method is presented that combines the subsets of variables selected by six base algorithms. These subsets of variables are partially merged based on the cross-validation results to ensure the diversity of the selected variables and improve prediction performance. The selected variables are fed to PLS regression and tested on two sets of LIBS spectra obtained within one month under variable experimental parameters for coal property analysis, yielding an average RMSEP of 1.17% (fixed carbon-1), 0.95% (volatile matter-1), 1.44% (fixed carbon-2), 0.86% (volatile matter-2), 1.76% (ash), 0.84 MJ kg−1 (calorific value) and 0.12% (sulphur). The ensemble variable selection method outperforms the best of the benchmark methods in six out of the seven tasks, revealing that ensemble variable selection can improve the predictive ability of the multivariate model in coal property analysis. Moreover, it can serve as a reliable method for variable selection when the user is not sure which variable selection algorithm to use. Future studies will be devoted to improving the selection stability and testing the ensemble strategy on different types of LIBS data.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 51906124 and No. 61675110) and National Key Research and Development Program of China (2016YFC0302102). All the authors sincerely thank Patrick Hong for proof-reading the manuscript and helping to improve the writing quality.References
- Statistical Review of World Energy, https://www.bp.com/en/global/corporate/energy-economics/statistical-review-of-world-energy.html Search PubMed.
- J. Xu, H. Tang, S. Su, J. Liu, K. Xu, K. Qian, Y. Wang, Y. Zhou, S. Hu, A. Zhang and J. Xiang, Appl. Energy, 2018, 212, 46–56 CrossRef CAS.
- S. Sheta, M. S. Afgan, Z. Hou, S. C. Yao, L. Zhang, Z. Li and Z. Wang, J. Anal. At. Spectrom., 2019, 34, 1047–1082 RSC.
- Y. Zhao, L. Zhang, S. X. Zhao, Y. F. Li, Y. Gong, L. Dong, W. G. Ma, W. B. Yin, S. C. Yao, J. D. Lu, L. T. Xiao and S. T. Jia, Front. Phys., 2016, 11, 114211 CrossRef.
- M. Chen, T. Yuan, Z. Hou, Z. Wang and Y. Wang, Spectrochim. Acta, Part B, 2015, 112, 23–33 CrossRef CAS.
- S. M. Clegg, E. Sklute, M. D. Dyar, J. E. Barefield and R. C. Wiens, Spectrochim. Acta, Part B, 2009, 64, 79–88 CrossRef.
- S. Lu, S. Shen, J. Huang, M. Dong, J. Lu and W. Li, Spectrochim. Acta, Part B, 2018, 150, 49–58 CrossRef CAS.
- N. C. Dingari, I. Barman, A. K. Myakalwar, S. P. Tewari and M. Kumar Gundawar, Anal. Chem., 2012, 84, 2686–2694 CrossRef CAS.
- Z. Hou, Z. Wang, T. Yuan, J. Liu, Z. Li and W. Ni, J. Anal. At. Spectrom., 2016, 31, 722–736 RSC.
- F. Duan, X. Fu, J. Jiang, T. Huang, L. Ma and C. Zhang, Spectrochim. Acta, Part B, 2018, 143, 12–17 CrossRef CAS.
- Y. Wang, H. Yuan, Y. Fu and Z. Wang, Spectrochim. Acta, Part B, 2016, 126, 44–52 CrossRef CAS.
- H. Y. Kong, L. X. Sun, J. T. Hu and P. Zhang, Spectrosc. Spectral Anal., 2016, 36, 1451–1457 CAS.
- P. Zhang, L. Sun, H. Kong, H. Yu, M. Guo and P. Zeng, in AOPC 2017: Optical Spectroscopy and Imaging, 2017, vol. 1046107 Search PubMed.
- X. Fu, F. J. Duan, T. T. Huang, L. Ma, J. J. Jiang and Y. C. Li, J. Anal. At. Spectrom., 2017, 32, 1166–1176 RSC.
- W. Li, M. Dong, S. Lu, S. Li, L. Wei, J. Huang and J. Lu, Anal. Methods, 2019, 11, 4471–4480 RSC.
- C. Yan, J. Qi, J. Liang, T. Zhang and H. Li, J. Anal. At. Spectrom., 2018, 33, 2089–2097 RSC.
- F. Deng, Y. Ding, Y. Chen, S. Zhu and F. Chen, Plasma Sci. Technol., 2020, 22, 074005 CrossRef CAS.
- J. Guezenoc, L. Bassel, A. Gallet-Budynek and B. Bousquet, Spectrochim. Acta, Part B, 2017, 134, 6–10 CrossRef CAS.
- A. K. Das, S. Das and A. Ghosh, Knowl. Base Syst., 2017, 123, 116–127 CrossRef.
- B. Seijo-Pardo, I. Porto-Díaz, V. Bolón-Canedo and A. Alonso-Betanzos, Knowl. Base Syst., 2017, 118, 124–139 CrossRef.
- L. Li, Z. Wang, T. Yuan, Z. Hou, Z. Li and W. Ni, J. Anal. At. Spectrom., 2011, 26, 2274–2280 RSC.
- Y. H. Yun, H. D. Li, B. C. Deng and D. S. Cao, TrAC, Trends Anal. Chem., 2019, 113, 102–115 CrossRef CAS.
- R. Tibshirani, J. R. Stat. Soc. Series B Stat. Methodol., 1996, 58, 267–288 Search PubMed.
- H. Zou, J. Am. Stat. Assoc., 2006, 101, 1418–1429 CrossRef CAS.
- H. Zou and T. Hastie, J. R. Stat. Soc. Series B Stat. Methodol., 2005, 67, 301–320 CrossRef.
- H. Li, Y. Liang, Q. Xu and D. Cao, Anal. Chim. Acta, 2009, 648, 77–84 CrossRef CAS.
- Y. H. Yun, J. Bin, D. L. Liu, L. Xu, T. L. Yan, D. S. Cao and Q. S. Xu, Anal. Chim. Acta, 2019, 1058, 58–69 CrossRef CAS.
- Å. Rinnan, M. Andersson, C. Ridder and S. B. Engelsen, J. Chemom., 2014, 28, 439–447 CrossRef.
- T. N. Tran, N. L. Afanador, L. M. C. Buydens and L. Blanchet, Chemom. Intell. Lab. Syst., 2014, 138, 153–160 CrossRef CAS.
- T. Rajalahti, R. Arneberg, F. S. Berven, K. M. Myhr, R. J. Ulvik and O. M. Kvalheim, Chemom. Intell. Lab. Syst., 2009, 95, 35–48 CrossRef CAS.
- O. M. Kvalheim, J. Chemom., 2020, 34, 1–10 CrossRef.
- H. Peng, F. Long and C. Ding, IEEE Trans. Pattern Anal. Mach. Intell., 2005, 27, 1226–1238 Search PubMed.
- L. I. Kuncheva and C. J. Whitaker, Mach. Learn., 2003, 51, 181–207 CrossRef.
- B. Pes, N. Dessì and M. Angioni, Inf. Fusion, 2017, 35, 132–147 CrossRef.
- S. Alelyani and H. Liu, in Proceedings - 2012 11th International Conference on Machine Learning and Applications, ICMLA 2012, 2012 Search PubMed.
- B. Seijo-Pardo, V. Bolón-Canedo and A. Alonso-Betanzos, Inf. Fusion, 2019, 45, 227–245 CrossRef.
- V. Bolón-canedo and A. Alonso-betanzos, Inf. Fusion, 2019, 52, 1–12 CrossRef.
- H. Wold, in Multivariate Analysis–III, 1973, pp. 383–407 Search PubMed.
- ChemReveal LIBS Desktop Elemental Analyzer 3766, https://tsi.com/discontinued-products/chemreveal-libs-desktop-elemental-analyzer-3766/ Search PubMed.
- H. D. Li, Q. S. Xu and Y. Z. Liang, Chemom. Intell. Lab. Syst., 2018, 176, 34–43 CrossRef CAS.
- Matlab implementation of LASSO, LARS, the elastic net and SPCA, http://www2.imm.dtu.dk/pubdb/pubs/3897-full.html Search PubMed.
- H. Peng, mRMR Feature Selection Site - Hanchuan, http://home.penglab.com/proj/mRMR/ Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ja00386g |
| This journal is © The Royal Society of Chemistry 2021 |