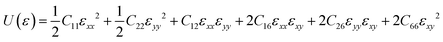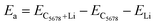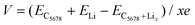Two-dimensional C₅₆₇₈: a promising carbon-based high-performance lithium-ion battery anode

Abstract

The non-hexagonal carbon rings significantly affect the electrode application of two-dimensional carbon allotropes. Many studies have been devoted to exploring novel two-dimensional carbon allotropes. However, two-dimensional carbon allotropes with a high degree of the local carbon-ring disorder are still nonexistent. Here, we design a new metallic two-dimensional planar carbon allotrope C₅₆₇₈ by using first-principles calculations. C₅₆₇₈ is composed of pentagonal, hexagonal, heptagonal, and octagonal carbon rings with a higher degree of local carbon-ring disorder. It has good dynamic, thermal, and mechanical stability. The local carbon-ring disorder results in many local electron-deficient regions and local strain regions on the basal plane of C₅₆₇₈ that can accommodate more electrons from lithium atoms and increase the adsorption sites, respectively, thus further enhancing the lithium storage capacity. It has a one-sided maximum theoretical capacity of 697 mA h g⁻¹, a lower Li diffusion barrier (<0.44 eV), and a lower average open-circuit voltage (0.33 V). These results not only propose a candidate electrode material for a lithium-ion battery but also offer insights for understanding the effect of non-hexagonal carbon rings on lithium adsorption and storage.

---

1. Introduction

Graphene, a flagship two-dimensional (2D) material with a zero bandgap and a highly stable planar honeycomb lattice, has attracted much attention due to its fascinating physical and chemical properties which are much different from those of its bulk counterpart diamond/graphite. Graphene is a promising material for lithium-ion batteries (LIBs) because its ultraflat honeycomb lattice results in a high capacity of lithium atom storage. But still there is some debate on the application of graphene as an electrode material. Some studies indicate that graphene nanosheets have a higher specific capacity of 460 mA h g⁻¹.^1,2 While others argue that under a higher lithium concentration, lithium atoms on the surface of pristine graphene tend to form clusters instead of adsorbing on the unoccupied hollow sites of graphene.^3–5

Recent studies indicate that introducing defects into pristine graphene is a good strategy to suppress the formation of lithium clusters on the surface of graphene.^4,6,7 Although the presence of structural defects such as vacancy and Stone–Wales defects destroys the perfect symmetry of graphene; it also produces many local electron-deficient regions around the defects^8–10 and many effective adsorption positions for lithium atoms on the surface of graphene. This results in a significant increase in the lithium storage capacity of graphene nanomaterials.^4,11,12 Recently, Tsai et al. theoretically confirmed that increasing the degree of local carbon-ring disorder could effectively enhance the lithium storage capacity of graphene. The local carbon-ring disorder introduces more electron-deficient regions on the basal plane of graphene. In experiments, structural defects always appear during the process of graphene growth and production. These structural defects will change the local properties of graphene around the structural defects.^13–15 For example, the bond rotation induced Stone–Wales defect¹⁶ can covert hexagonal carbon rings into non-hexagonal carbon rings (pentagons and heptagons). These non-hexagonal carbon rings create local strains on the basal plane of graphene. Recently, Li et al. proposed that applying strain on the pristine graphene can further enhance the lithium adsorption ability of graphene.¹⁷ Therefore, we could expect that the 2D carbon allotropes composed of complete or partial non-hexagonal carbon rings should have much potential to be used as electrode materials in LIBs. Recently, many 2D carbon allotropes with ordered and symmetrized non-hexagonal carbon-ring arrangements such as penta-graphene, ψ-graphene, phagraphene, biphenylene, Θ-graphene, and net-τ graphene, have been proposed by first-principles calculations. They have better lithium storage capacities, lower diffusion energy barriers, and lower open-circuit voltages.^4,18–25 However, the 2D carbon allotropes with a high degree of local carbon-ring disorder are still missing.

In this work, we predicted a new 2D carbon allotrope C₅₆₇₈ which is composed of pentagon, hexagon, heptagon, and octagon. C₅₆₇₈ is an energetically metastable carbon allotrope with respect to graphene. It has better dynamic stability. C₅₆₇₈ possesses metallicity and shows a good electrochemical performance for use in LIBs. The higher degree of the local carbon-ring disorder of C₅₆₇₈ results in a high theoretical lithium storage capacity of 697 mA h g⁻¹ (the maximum Li concentration LiC_3.2), which is larger than those of local carbon-ring ordered penta-graphene and ψ-graphene, is little smaller than that of Θ-graphene. Furthermore, the lower Li diffusion barrier (<0.44 eV) and average open-circuit voltage (0.33 V) are beneficial for practical applications of C₅₆₇₈ as a good electrode material for LIBs.

2. Methods

The calculations are performed within the density functional theory (DFT) framework, carried out within the Vienna ab initio simulation package (VASP) using the projector augmented wave method.^26,27 The 2s²2p² electrons of carbon atoms are treated as valence electrons. The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof functional for the exchange correlation was employed.²⁸ The tested plane-wave cutoff energy was taken as 500 eV. The k-points with a grid spacing of 2π × 0.03 Å⁻¹ for the integration of the electronic Brillouin zone (BZ) were used. The Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional is used to calculate the accurate electronic band structure.²⁹ An 18 Å vacuum space in the simulation cell is adopted to avoid the image interaction between neighboring layers. The weak van der Waals (vdW) interactions are omitted in current calculations because the effect of vdW is less significant for the monolayer systems.⁶ The geometries are fully optimized until the residual Hellmann–Feynman forces are less than 0.01 eV Å⁻¹. The diffusion barriers of Li atoms on the surface of C₅₆₇₈ are calculated by using the climbing-image nudged elastic band (CI-NEB) method. Theoretical phonon spectra are calculated using the supercell approach as implemented in the PHONOPY package.³⁰Ab initio molecular dynamics (AIMD) simulations under the canonical (NVT) ensemble were used to study the thermal stability of C₅₆₇₈ at high temperatures. The particle-swarm optimization (PSO) algorithm performed on the Crystal structure Analysis by Particle Swarm Optimization (CALYPSO) code was used to obtain reasonable absorption configurations for LiC_x with various concentrations.^31–33 A 2 × 1 supercell of C₅₆₇₈ was chosen as the initial substrate. Various lithium concentrations (1, 2, 4, 6, 8, and 10 lithium atoms on the basal plane) were considered. The adsorption structure search was performed for 30 generations at each concentration. Approximately 1500 candidate adsorption structures were calculated at each concentration in the global search.

3. Results and discussion

3.1 Structure and structural stability

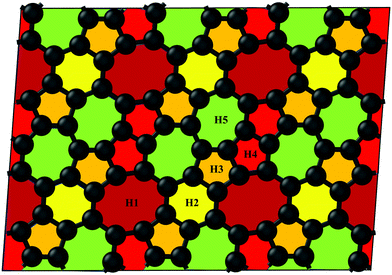
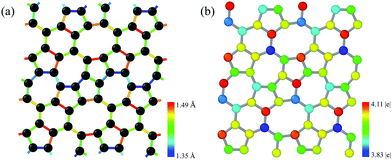
The pentagon–heptagon carbon ring alignment has good ability and is a basic structural unit of many 2D carbon allotropes such as xgraphene, ψ-graphene, and PAI-graphene.^13,21,34 Therefore, it is a good strategy to design a novel 2D carbon allotrope by using similar pentagon–heptagon alignments. Here, the double inversed pentagon–heptagon alignments (Fig. S1, ESI†) are chosen as basic units to design a novel 2D carbon allotrope. A novel 2D carbon allotrope C₅₆₇₈ which is composed of 5-6-7-8 carbon rings, is predicted as depicted in Fig. 1. The five inequivalent carbon rings are highlighted in different colors. C₅₆₇₈ is ultraflat and one-atom-thick with 16 carbon atoms in its unit cell. It has p1 plane symmetry with the optimized equilibrium lattice constants of a = 6.41 Å and b = 6.9 Å (Table S1, ESI†). Three types of non-hexagonal carbon rings pentagon, heptagon, and octagon are arranged in local disorder. The neighboring hexagons are separated by non-hexagonal carbon rings. Meanwhile, the neighboring pentagon alignments and heptagon alignments are also separated by other carbon rings. Therefore, C₅₆₇₈ has a high degree of local carbon-ring disorder that destroys the hexagonal symmetry of pristine graphene. The shortest bond length of neighboring carbon atoms in C₅₆₇₈ is 1.35 Å, as highlighted in red in Fig. 2a. The longest bond length of neighboring carbon atoms is 1.49 Å, as highlighted in blue. Other bond lengths of carbon–carbon bonds in C₅₆₇₈ are in the range of 1.35 Å to 1.49 Å, indicating that the bond lengths in C₅₆₇₈ show high local disorder. Furthermore, the charge distribution of C₅₆₇₈ also shows high local disorder. The electron charges of carbon atoms in C₅₆₇₈ are in the range of 3.83 |e| to 4.11 |e|. The disorder of local carbon rings, bond lengths, and atomic charges indicate that C₅₆₇₈ has good potential to adsorb more Li atoms on its surface.

Fig. 1 Optimized structure of C₅₆₇₈. H1–H5 are five inequivalent carbon rings.

Fig. 2 Bond length distribution and charge distribution of C₅₆₇₈.

To confirm the thermodynamic stability, we compare the total energy of C₅₆₇₈ to that of recently proposed carbon-based electrode materials including penta-graphene, h567, Θ-graphene, ψ-graphene, and phagraphene. C₅₆₇₈ has a lower total energy of −8.88 eV per atom, which is lower than those of famous penta-graphene (−8.32 eV per atom)²⁰ and C₅₆₈ (8.83 eV per atom),³⁵ much close to those of net-τ (−8.89 eV per atom),⁴ Θ-graphene (−8.98 eV per atom),²⁵ and h567 (−8.99 eV per atom),³⁶ and a little higher than those of phagraphene, ψ-graphene, and graphene (−9.03 eV per atom, −9.07 eV per atom, and −9.23 eV per atom).^21,37 These indicate that similar to penta-graphene, C₅₆₈, net-τ, Θ-graphene, etc., C₅₆₇₈ is a metastable carbon allotrope.

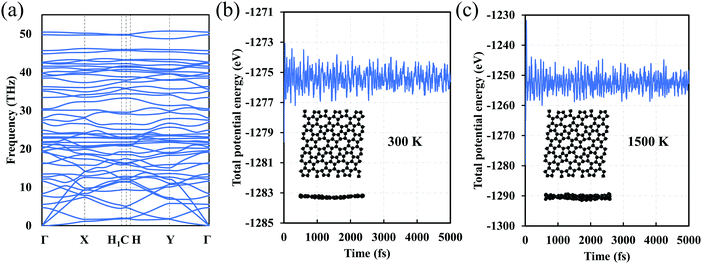
We also investigate the dynamic stability of C₅₆₇₈. The phonon dispersion of C₅₇₆₈ shows that there are no imaginary phonon modes that imply kinetic stability of C₅₆₇₈ (Fig. 3a). To finally confirm the dynamic stability, AIMD simulations for C₅₆₇₈ was performed (Fig. 3b and c). A (3 × 3) supercell of C₅₆₇₈ is used in our AIMD simulation. Two temperatures (300 K and 1500 K) are used to check the stability of C₅₆₇₈. It is found that the geometry of C₅₆₇₈ is preserved very well at temperatures of 300 and 1500 K during the AIMD simulations. Furthermore, the total potential energies of the C₅₆₇₈ supercell only fluctuate around a constant value. These calculations further confirm the dynamic stability of C₅₆₇₈.

Fig. 3 (a) Phonon dispersion of C₅₆₇₈. The variation of total potential energy as a function of the simulation time for C₅₆₇₈ at temperatures of (b) 300 and (c) 1500 K. Insets in panels b and c are snapshots of AIMD simulations at 5000 fs.

To guarantee the mechanical stability of C₅₆₇₈, the corresponding elastic constants of C₅₆₇₈ are calculated by using the following formula:

For the oblique structure, six independent elastic constants C₁₁, C₂₂, C₁₂, C₁₆, C₂₆, and C₆₆ of C₅₆₇₈ must satisfy the Born–Huang criteria:³⁸C₁₁ > 0, C₁₁C₂₂ > C₁₂², and det(C_ij) > 0. The calculated elastic constants C₁₁, C₂₂, C₁₂, C₁₆, C₂₆, and C₆₆ are 291.51, 291.60, 82.02, 7.39, 5.47, and 29.07 N m⁻¹, respectively. They satisfy the Born–Huang criteria indicating C₅₆₇₈ is a mechanically stable carbon allotrope. The calculated in-plane Young's modulus of C₅₆₇₈ is 268.4 N m⁻¹ which is smaller than that of graphene (342.2 N m⁻¹), and much close to those of penta-graphene (263.8 N m⁻¹) and h-BN monolayer (275.8 N m⁻¹), suggesting that C₅₆₇₈ has good mechanical properties. Furthermore, C₅₆₇₈ is an anisotropic two-dimensional material because its two-dimensional elastic anisotropy index (0.68) is larger than that of graphene (0) and much close to that of black phosphorene (0.65).³⁹

3.2 Electronic properties

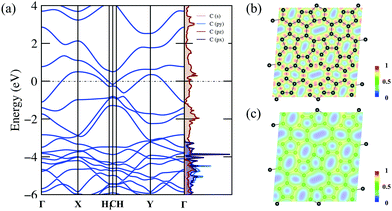
The detailed electronic structure is much important for understanding the fundamental properties of C₅₆₇₈. Therefore, we calculate the electronic band structure and projected density of states (DOS) of C₅₆₇₈ as shown in Fig. 4a. The DFT results with PBE (Fig. 4a) and HSE06 (Fig. S2, ESI†) functionals indicate that C₅₆₇₈ is a metallic material because two bands cross the Fermi level. As shown in Fig. 4a, significant overlaps between 2s, 2p_x, and 2p_y orbitals can be found that underlie strong sp² hybridization of carbon atoms in C₅₆₇₈. The projected DOS also indicates that the p_z orbitals occupy the bonding and antibonding states simultaneously and this results in the formation of π bonds between neighboring carbon atoms and the conductivity of C₅₆₇₈. To analyze the bonding features of C₅₆₇₈, the electron localization function (ELF) of C₅₆₇₈ was calculated. It is well known that the values of ELF are between 0 and 1, which corresponds to perfect localization and delocalization of electrons in a material. The ELF value of 0.5 corresponds to the state of the electron–gas-like pair. The ELF slice presented in Fig. 4b shows that the electrons localize in the middle of two neighboring carbon atoms, signaling the strong σ bonding states of the nearest neighboring carbon atoms. When the slice is moved 1 Å up from the plane of the structure (Fig. 4c), the ELF value remains nearly constant (approximately 0.5), indicating there is a delocalized electron state induced by the p_z orbitals of carbon atoms, which results in the metallicity of C₅₆₇₈. The strong structural stability and the presence of delocalized p_z orbitals are beneficial for the application of C₅₆₇₈ as an electrode material of LIBs.

Fig. 4 (a) Electronic band structure and projected density of states of C₅₆₇₈. Fermi level was set to zero. (b) ELF of C₅₆₇₈ with slices (b) crossing the structure plane and (c) 1 Å above the structure plane.

3.3 Potential application as an anode material for LIBs

Next, we calculate the adsorption energy of a single Li atom on the surface of a 2 × 2 supercell of C₅₆₇₈ to check the possibility of electrode application of C₅₆₇₈. According to previous studies, the lithium atoms preferably absorb on the hollow sites of 2D carbon allotropes. Therefore, considering the structural features of C₅₆₇₈, five possible hollow adsorption sites H1–H5 are chosen in our adsorption calculations, as shown in Fig. 1. The adsorption energy of lithium atoms is described as:
where E_a is the adsorption energy, E_C5678+Li and E_C5678 are the total energies of the system with and without lithium adsorption, respectively. E_Li is the lithium atom energy in bulk Li metal. The calculated adsorption energies of lithium atoms on H1, H2, H3, H4, and H5 sites are −0.52, −0.45, −0.50, −0.47, and −0.42 eV, respectively, comparable to that of recently predicted 2D carbon allotrope net-τ (−0.37 to −0.60 eV).⁴ The negative adsorption energies also indicate that lithium atoms tend to adsorb on the surface of C₅₆₇₈ and will not form lithium clusters. Furthermore, Bader charge analysis shows that the charge transfer from Li to the C₅₆₇₈ is ∼0.89 |e| for the H1 site, indicating that C₅₆₇₈ has the potential to accommodate more electrons from lithium atoms.

Lithium mobility is an important factor that determines the rate performance of LIBs. To investigate the lithium mobility on the surface of C₅₆₇₈, the six possible migration pathways from the H1 site to the neighbor H1 site along various directions are chosen to calculate the migration barrier (Fig. 5a). The transition states of six migration pathways are presented in Fig. 5b. It is found that the diffusion barrier along the nearest neighboring path 1 is 0.33 eV, which is close to that of graphene (0.31 eV) and ψ-graphene (0.313 eV).^21,40 The diffusion barrier along path 2 is 0.29 eV which is smaller than that of graphene. We see that the diffusion barriers of both path 3 and path 4 are 0.364 eV, while for paths 5 and 6 the diffusion barriers are 0.44 and 0.42 eV, respectively. Although the maximum diffusion barrier of C₅₆₇₈ (0.44 eV) is larger than that of graphene, it still smaller than those of Θ-graphene (0.48 eV),²⁵ xgraphene (0.49 eV),³⁴ and popgraphene (0.55 eV).²⁴ The average migration barrier of the Li atom on the surface of C₅₆₇₈ is 0.37 eV. Such a lower barrier results in a higher Li-ion mobility ability, indicating a good charge–discharge rate of C₅₆₇₈ as an anode for LIBs.

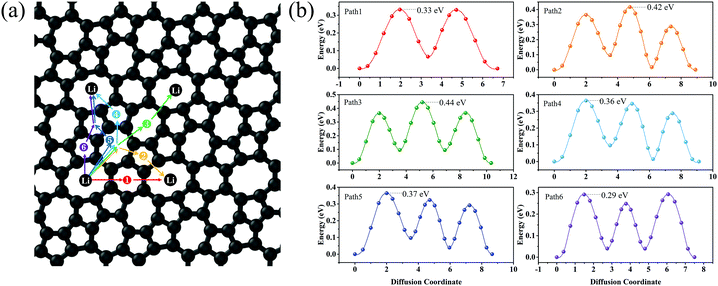Fig. 5 Six possible Li-ion migration pathways (a) and their corresponding diffusion barrier for Li on the surface of C₅₆₇₈.

In addition to the diffusion barrier, the lithium storage capacity is also an important factor for the performance of electrode materials. Therefore, the candidate adsorption configurations of lithium under various lithium concentrations are fully explored by the PSO method performed in the CALYPSO code. One side mode was used in our adsorption configuration prediction. The most stable structural configurations under various lithium atom concentrations are given in Fig. S3 (ESI†). The maximum lithium atom number is ten in Li₁₀C₃₂. The corresponding specific capacity can reach 697 mA h g⁻¹ that is larger than those of graphite and pristine graphene. Meanwhile, corresponding adsorption energy of lithium atom is −0.07 eV in Li₁₀C₃₂, which is equal to that of xgraphene (−0.07 eV). The open-circuit voltage (OCV) is another important factor for the application of a 2D carbon electrode. We use the following equation to estimate the OCV of C₅₆₇₈ with different lithium concentrations LiC_x:⁴¹

The calculated V is 0.78 V for the stoichiometry of LiC₃₂. When the lithium concentration increases to LiC_3.2, V decreases to 0.07 V. The calculated average OCV is 0.33 V, which is larger than that of graphite (0.11 V),⁴² much close to that of popgraphene (0.3 V),²⁴ and much lower than that of ψ-graphene (0.64 V).²¹ Thus, the lower average OCV shows the feasibility of C₅₆₇₈ to be a desirable electrode material in LIBs.

4. Conclusions

In summary, we predicted a novel metallic 2D carbon allotrope C₅₆₇₈ by using first-principles calculation and the CALYPSO method. C₅₆₇₈ is composed of 5-6-7-8 carbon rings with highly locally disordered carbon rings. Due to the delocalized p_z orbitals of carbon atoms in C₅₆₇₈, C₅₆₇₈ exhibits intrinsic metallization that results in good mobility of lithium on the surface of C₅₆₇₈. The local carbon-ring disorder of C₅₆₇₈ produces many electron-deficiency regions which make C₅₆₇₈ have a better ability to accommodate more electrons of lithium atoms. These make C₅₆₇₈ have a high specific capacity (697 mA h g⁻¹) and a lower diffusion energy barrier for Li-ions (<0.44 eV). It is expected that C₅₆₇₈ can be used as an electrode material for LIBs. The current study will encourage further studies on the application of 2D carbon allotropes as electrode materials.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 91745203 and 11404134). Supported by High Performance Computing Center of Jilin University, China.

References

1. G. Wang, X. Shen, J. Yao and J. Park, Carbon, 2009, 47, 2049–2053.
2. X.-Y. Shan, G. Zhou, L.-C. Yin, W.-J. Yu, F. Li and H.-M. Cheng, J. Mater. Chem. A, 2014, 2, 17808–17814.
3. S. Yu, Y.-C. Rao, S.-F. Li and X.-M. Duan, Appl. Phys. Lett., 2018, 112, 053903.
4. X. Wang, Z. Feng, J. Rong, Y. Zhang, Y. Zhong, J. Feng, X. Yu and Z. Zhan, Carbon, 2019, 142, 438–444.
5. M. Liu, A. Kutana, Y. Liu and B. I. Yakobson, J. Phys. Chem. Lett., 2014, 5, 1225–1229.
6. H. Yildirim, A. Kinaci, Z.-J. Zhao, M. K. Y. Chan and J. P. Greeley, ACS Appl. Mater. Interfaces, 2014, 6, 21141–21150.
7. E. Lee and K. A. Persson, Nano Lett., 2012, 12, 4624–4628.
8. Y.-J. Tsai and C.-L. Kuo, ACS Appl. Mater. Interfaces, 2020, 12, 22917–22929.
9. S. Chen, P. Bao, L. Xiao and G. Wang, Carbon, 2013, 64, 158–169.
10. T. Morresi, A. Pedrielli, S. A. Beccara, R. Gabbrielli, N. M. Pugno and S. Taioli, Carbon, 2020, 159, 512–526.
11. A. Hashimoto, K. Suenaga, A. Gloter, K. Urita and S. Iijima, Nature, 2004, 430, 870–873.
12. D. Datta, J. Li, N. Koratkar and V. B. Shenoy, Carbon, 2014, 80, 305–310.
13. X. Chen, A. Bouhon, L. Li, F. M. Peeters and B. Sanyal, Carbon, 2020, 170, 477–486.
14. B. Ram and H. Mizuseki, Carbon, 2018, 137, 266–273.
15. S. W. Cranford, Carbon, 2016, 96, 421–428.
16. A. J. Stone and D. J. Wales, Chem. Phys. Lett., 1986, 128, 501–503.
17. P. Li, Z. Li and J. Yang, J. Phys. Chem. Lett., 2018, 9, 4852–4856.
18. A. Rajkamal and R. Thapa, Adv. Mater. Technol., 2019, 4, 1900307.
19. S. Zhang, J. Zhou, Q. Wang, X. Chen, Y. Kawazoe and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2372–2377.
20. B. Xiao, Y.-c. Li, X.-f. Yu and J.-b. Cheng, ACS Appl. Mater. Interfaces, 2016, 8, 35342–35352.
21. X. Li, Q. Wang and P. Jena, J. Phys. Chem. Lett., 2017, 8, 3234–3241.
22. S. Thomas, E. B. Nam and S. U. Lee, ACS Appl. Mater. Interfaces, 2018, 10, 36240–36248.
23. D. Ferguson, D. J. Searles and M. Hankel, ACS Appl. Mater. Interfaces, 2017, 9, 20577–20584.
24. S. Wang, B. Yang, H. Chen and E. Ruckenstein, J. Mater. Chem. A, 2018, 6, 6815–6821.
25. S. Wang, B. Yang, H. Chen and E. Ruckenstein, Energy Storage Mater., 2019, 16, 619–624.
26. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
27. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
28. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
29. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
30. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
31. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
32. Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070.
33. Y. Wang, M. Miao, J. Lv, L. Zhu, K. Yin, H. Liu and Y. Ma, J. Chem. Phys., 2012, 137, 224108.
34. S. Wang, Y. Si, B. Yang, E. Ruckenstein and H. Chen, J. Phys. Chem. Lett., 2019, 3269–3275,  DOI:10.1021/acs.jpclett.9b00905,.
35. B. Ram and H. Mizuseki, Carbon, 2020, 158, 827–835.
36. S. Thomas, H. Jung, S. Kim, B. Jun, C. H. Lee and S. U. Lee, Carbon, 2019, 148, 344–353.
37. Z. Wang, X.-F. Zhou, X. Zhang, Q. Zhu, H. Dong, M. Zhao and A. R. Oganov, Nano Lett., 2015, 15, 6182–6186.
38. V. Wang, N. Xu, J. C. Liu, G. Tang and W.-T. Geng, 2020, arXiv:1908.08269 [cond-mat].
39. R. Li, Q. Shao, E. Gao and Z. Liu, Extreme Mech. Lett., 2020, 34, 100615.
40. G.-C. Guo, D. Wang, X.-L. Wei, Q. Zhang, H. Liu, W.-M. Lau and L.-M. Liu, J. Phys. Chem. Lett., 2015, 6, 5002–5008.
41. K. Kang, H.-S. Lee, D.-W. Han, G.-S. Kim, D. Lee, G. Lee, Y.-M. Kang and M.-H. Jo, Appl. Phys. Lett., 2010, 96, 053110.
42. Y. Jing, Z. Zhou, C. R. Cabrera and Z. Chen, J. Phys. Chem. C, 2013, 117, 25409–25413.

---

Footnote

† Electronic supplementary information (ESI) available: Data supporting this publication are provided as ESI; further data will be made available through an online repository. See DOI: 10.1039/d0ma00858c

---