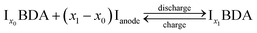Open Access Article
Open Access ArticleStructure–property relationships in organic battery anode materials: exploring redox reactions in crystalline Na- and Li-benzene diacrylate using combined crystallography and density functional theory calculations†
Rodrigo P.
Carvalho
 ab,
Cleber F. N.
Marchiori
ab,
Cleber F. N.
Marchiori
 b,
Viorica-Alina
Oltean
b,
Viorica-Alina
Oltean
 b,
Stéven
Renault
b,
Stéven
Renault
 c,
Tom
Willhammar
c,
Tom
Willhammar
 d,
Cesar
Pay Gómez
d,
Cesar
Pay Gómez
 b,
C. Moyses
Araujo
b,
C. Moyses
Araujo
 *ae and
Daniel
Brandell
*ae and
Daniel
Brandell
 *b
*b
aDepartment of Physics and Astronomy, Materials Theory Division, Uppsala University, 751 20, Uppsala, Sweden
bDepartment of Chemistry – Ångström Laboratory, Uppsala University, 751 21, Uppsala, Sweden. E-mail: daniel.brandell@kemi.uu.se
cUniversité de Nantes, CNRS, Institut des Matériaux Jean Rouxel, IMN, F-44000 Nantes, France
dDepartment of Materials and Environmental Chemistry, Stockholm University, 106 91, Stockholm, Sweden
eDepartment of Engineering and Physics, Karlstad University, 65188 Karlstad, Sweden. E-mail: Moyses.Araujo@kau.se
First published on 19th December 2020
Abstract
Organic-based materials are potential candidates for a new generation of sustainable and environmentally friendly battery technologies, but insights into the structural, kinetic and thermodynamic properties of how these compounds lithiate or sodiate are currently missing. In this regard, benzenediacrylates (BDAs) are here investigated for application as low-potential electrodes in Na-ion and Li-ion batteries. Aided by a joint effort of theoretical and experimental frameworks, we unveil the structural, electronic and electrochemical properties of the Na2BDA and Li2BDA compounds. The crystal structure of these systems in their different sodiated and lithiated phases have been predicted by an evolutionary algorithm interplayed with density functional theory calculations. Due to difficulties in obtaining useful single crystals for the BDA salts, other methods have been explored in combination with the computational approach. While the predicted structure of the pristine Na2BDA compound has been experimentally confirmed through the 3D Electron Diffraction (3DED) technique, the hydrated version of Li2BDA is analysed through single crystal X-ray diffraction. The calculated cell voltages for the sodiation (0.63 V vs. Na/Na+) and lithiation (1.12 V vs. Li/Li+) processes display excellent quantitative agreement with experimental findings. These results validate the developed theoretical methodology. Moreover, fundamental aspects of the electronic structures and their relationship with the reaction thermodynamics are discussed. The results suggest a possible disproportionation between the sodiated phases of Na2BDA, supporting a two-electron process, and also unveil major differences for the two employed cations: Na+ and Li+.
I. Introduction
During the last few decades, Li-ion batteries (LIBs) have become the technology of choice for a vast range of electrochemical energy storage (EES) devices as a consequence of the higher gravimetric and volumetric energy densities when compared to all available rechargeable battery systems.1 The current state-of-the-art technology is based on synthetic graphite and transition metal oxides, which raises concerns regarding toxicity and sustainability. The extraction of metals from ores characterizes them as non-renewable materials2 and together with the applied processing steps during the battery life-cycle (refining, electrode synthesis and possible recycling), they impose a severe environmental impact due to high CO2 emissions, which contribute to the environmental impact of electrification solutions in the energy system.3Alternatives that could replace the traditional electrodes have thereby started to gain significant attention. One of these categories involves organic electrode materials (OEMs), an option that can have low cost for production (easily synthesized from solution phase routes), good structural diversity and electrochemical performance as competitive as the inorganic counterparts.4 Some OEMs can also be extracted from abundant biomass.4–7 Several OEMs have been proposed, often based on quinones extracted from biomass through low-cost processes free of toxic solvents,8,9 but also organosulfur compounds, nitroxide radicals, and disulfides, to cite a few.10–15 Among these, conjugated carboxylates have become one of the most promising candidates due to the stability against dissolution in organic electrolytes while providing reasonable energy density. Not least have carboxylate-based molecules been explored as LIB anodes,16–20 with some of them exhibiting an impressive capacity due to the stabilization of the so-called ‘superlithiation’ phase.21–23
Despite being a very promising class of materials to be employed in environmentally friendly ESS, organic electroactive materials have some hurdles to be overcome to enable application in commercial devices. The dissolution in the electrolyte, resulting in capacity fading, and the low electronic conductivity are good examples of such problematics. To overcome these and other issues, and to move toward the development of novel materials with improved properties, a deep understanding of the electrochemical reactions taking place during the charge/discharge processes is needed, as well as an assessment of eventual structural changes that might occur during the ion de/insertion process. This is not a trivial task given the complexity of the processes and a proper investigation demands the use of sophisticated operando measurements. In this context, the use of computational tools emerges as a very powerful aid to achieve a fundamental understanding of such materials. Largely employed in the field of organic electronics, density functional theory (DFT) calculations have become appealing for the organic battery field as a mean to assess properties and processes which are not so easily reachable by experimental tools.24–34
Despite the fact that molecular level calculations can give a good insight into the materials’ electrochemical performance, some aspects can only be unveiled by considering the intrinsic environment present in the solid-state structure. Some studies have adopted to this approach by utilizing the experimental crystal structure,31 or by starting with the experimental structure for the pristine materials and evaluating the ion diffusion through nudged elastic band methods and thereafter evaluating the most probable site for ion insertion by computing the binding energy.32 Indeed, both these approaches can provide valuable insights by filling the lack of information about the crystal structure of those materials after cationic insertion. More recently, the use of an evolutionary algorithm interplayed with DFT calculation has revealed to be a very powerful methodology to resolve the crystal structure of organic electrode materials before and after ionic insertion.35–37 This strategy has enabled the assessment of important aspects of the electrochemical activity of OEMs, which are extremely challenging to resolve experimentally, e.g., the structural changes and the relation between the electronic structure and the thermodynamic aspects of the ion insertion process.36,37 In fact, a good agreement between the predicted crystal structures and those resolved experimentally has rendered this methodology useful for anticipating the properties of a novel OEM candidate to be employed as a cathode material in LIBs.38
Another issue regarding the widespread use of LIBs is the scarce resources of lithium, resulting in dramatic fluctuations of its price in the recent past. Therefore, research on Na ion batteries is facing a rapid expansion as an alternative technology. This is motivated by the significantly higher abundance and better geographical distribution of sodium resources.39,40 Inorganic sodium electrode materials have been investigated in parallel to the Li ones until the commercialization of Li-ion batteries.41–43 In the past decade, Na-based batteries have experienced a renaissance, also for OEMs.15,44,45 Most of the organic molecules that were first investigated for Li-ion batteries have also been translated to their Na-equivalents.46–50 However, their performance and behaviour are rarely similar to those of Li-based counterparts. Usually Na-ion batteries present more problematic performance, displaying slower kinetics and larger irreversible capacities due to unstable SEI layer formation.51
In this work, we investigate the crystallographic structure of two OEM compounds, disodium and dilithium benzenediacrylate (Na2BDA and Li2BDA), aiming to correlate the results with their electrochemical behaviour. However, due to large difficulties in obtaining large enough single crystals of these compounds, alternative methods were put to practice for structural determination: Single Crystal X-ray Diffraction (SCXRD) was employed for the hydrated version of the Li compound (Li2BDA· 1H2O) while 3D Electron Diffraction (3DED) was used for the Na compound. Additionally, an evolutionary algorithm interplayed with DFT calculations was employed to resolve the crystal structure for the pristine Li- and Na-benzenediacrylate, as well as their respective lithiated and sodiated phases. The predicted structure of the pristine Na2BDA, space group P21/c, displays excellent agreement with the one resolved using the RED technique. This result, along with an excellent agreement between the calculated and measured cell potentials (for both Na- and Li-based compounds), further validates the applied theoretical methodology. The latter has thereafter been employed to unveil fundamental structure–property relationships in the OEM. Thereby, a disproportionation between the sodiated phases of Na2BDA can be observed, supporting a two-electron process during the electrochemical redox activity.
II. Methodology
II.1 Computational details
First principles calculations have been carried out within the DFT framework, using the Vienna Ab initio Simulation Package (VASP),52,53 in combination with an evolutionary algorithm (EA), as implemented in the USPEX code,54,55 to resolve the crystal structures, calculate the electronic structure and assess the thermodynamics of the ionic insertion/release processes. The pristine disodium benezenediacrylate (Na2BDA), its sodiated phases and their corresponding Li-ion homologues have been investigated.The first population of the EA was composed of about 300–500 randomly generated structures, built up as follows. The molecular units were split into two components, namely either Na or Li atoms and the organic BDA moiety, which were combined to form random geometries. Here, the crystal lattice parameters are also randomized. The obtained structures were then fully optimized without any symmetry constraint. For all structures, two molecular units were added in the unit cell. By starting from the well-known organic moieties as initial guesses, the configurational space is significantly reduced and hence the discovery of the lowest energy structures accelerated.
The next generation of the EA is constructed by applying genetic transformations on the ca. 20–30 lowest energy geometries of the first population. Such transformations comprise three different types of operations: heredity, soft-mutation, and permutation. In brief, the heredity operator constructs new structures using two coherent slabs from pre-existing ones; the soft-mutation operator transforms spatial coordinates by moving atoms along the eigenvectors of the softest modes; the permutation operator exchanges different types of atoms. After applying these operators, all generated geometries are fully re-optimized as in the previous step. The subsequent generations, also composed of 20–30 individuals, are then constructed using the same approach. This procedure continues until a convergence criterion is reached, which was chosen to be the global free-energy minimum.
All aforementioned geometry optimizations were carried out using the projector-augmented wave method for DFT.53 The exchange–correlation interactions were treated at the level of the Perdew, Burke, and Ernzerhof (GGA-PBE)56 functional combined with the Grimme approach (D2) to take into account the dispersive interactions (DFT-D).57 The latter has not been added to lithium and sodium metals since the increasing amount of these atoms in the ion-inserted phases can generate an accumulated error due to fundamental limitations in DFT-D theory. The optimizations in the EA have been implemented using the following stepwise approach. The initial two steps perform a less accurate optimization of atomic positions and cell parameters, keeping the volume constant. Thereafter, two additional steps are carried out with higher accuracy and no structural constraints. For all these steps, a constant energy cut-off value of 550 eV has been selected, while increasing the reciprocal space resolution in the following order: 0.14, 0.12, 0.10 and 0.08 2π Å−1. Furthermore, the structures selected by the EA have undergone an additional optimization with a higher plane-wave cut-off energy of 600 eV and a finer 6 × 6 × 6 gamma-centered k-mesh. Additionally, a final calculation using the hybrid functional HSE06-D258 and a 4 × 4 × 4 gamma-centered k-mesh was performed in order to improve the description of the exchange–correlation interaction. This diminishes the spurious electron's self-interaction contribution present in the pure GGA scheme that tends to overestimate the electron delocalization. Furthermore, a Bader charge analysis59 has been performed for each system to understand the charge transfer in the system upon sodiation/lithiation.
The ion insertion process with reference to the metal electrode is described using the following chemical reaction:
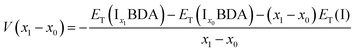 | (1) |
The formation energy of I3BDA with respect to I2BDA and I4BDA has been calculated as:
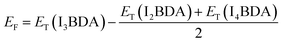 | (2) |
II.2 Experimental methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 1
water 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) solution at 50 °C, stirred for 12 hours and then dried in an oven at 100 °C.
1 (v/v) solution at 50 °C, stirred for 12 hours and then dried in an oven at 100 °C.
For the Li compound, the crystals were obtained by preparing a saturated solution of the powder compound in water (0.5 g in 10 ml) and the mixture was thereafter heated to the boiling point. A few drops of methanol were added until the solution started to precipitate. The solution was allowed to cool down and the solvent evaporated under ambient conditions to form single crystals of Li2BDA·1H2O. Drying of this compound rendered crystals too small for meaningful SCXRD experiments.
For PXRD, the samples were analysed with a Bruker D8 TwinTwin diffractometer with Cu Kα radiation (Kα1 = 1.540598 Å and Kα2 = 1.544390 Å) for collecting intensities at room temperature. The SCXRD measurements were performed on a Bruker D8 single-crystal X-ray diffractometer with Mo Kα radiation (Kα = 0.71073 Å), a graphite monochromator and an APEX II CCD area detector (6 cm × 6 cm) to collect intensities at room temperature.
III. Results and discussion
In the 3DED measurements of Na2BDA, 390 electron diffraction patterns were collected from a crystal covering a tilt range of 120.6°. The electron diffraction patterns were used for a reconstruction of the 3D reciprocal lattice of the crystal. From the reciprocal lattice, the unit cell was determined to have the parameters: a = 14.49 Å, b = 5.50 Å, c = 7.21 Å, 90.7°, 101.1° and 89.6° and systematic absence shows that the space group is P21/c. A structure solution performed in SHELXT resulted in the structure presented in Fig. 1(a). The coordination around the Na ion appears to form a trigonal prism. The same sample was also investigated by PXRD. The cell parameters then present minor differences: a = 14.53 Å, b = 5.38 Å, c = 7.11 Å, 90°, 108.84° and 90°, but the space group is still the same. For the powder data, a charge-flipping algorithm (Supper flip) was used for structure solution.63The obtained structure has also been predicted independently by employing a methodology that involves DFT and the evolutionary algorithm, as described in the method section. Both experimentally and computationally obtained geometries are shown in Fig. 1(a). An excellent agreement with the experimental findings can be found, where the computed structure possesses the same space group, P21/c, and the calculated lattice parameters being a = 13.77 Å, b = 5.34 Å, c = 6.89 Å, 90.01°, 97.31° and 89.95°. Moreover, the sodium ions also present the same trigonal prismatic coordination. To further highlight this obtained agreement, calculated XRD diffractograms of the experimentally and computationally obtained structures are displayed in Fig. 1(b). The main features are clearly present for both structures. Hereby, we are further validating the first-principles based crystal structure prediction which requires no experimental inputs. This is an important step forward for assessing the interplay between the structure and electrochemistry for such reactive organic electrode materials; a task that otherwise would require sophisticated operando techniques in purely experimental work.
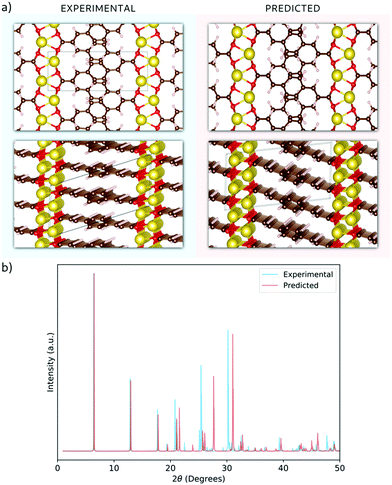
Having validated the theoretical approach, new structures have been predicted for the following sodiation process, i.e. the insertion of the reducing equivalents (Na+ + e−; Na3BDA). The results are shown in Fig. 2. It can be seen clearly that after the first sodiation step, the additionally inserted cations are incorporated into the salt layer, which in turn is expanded. Additionally, there is a clear loss of symmetry in the crystal, with the predicted space group changing to P1 with lattice parameters a = 15.02 Å, b = 5.39 Å, c = 6.72 Å, 90.01°, 78.05° and 96.09°. The new ionic interactions mainly involve the carboxylic units, with Na+ coordinated by the oxygen atoms. This scenario changes upon insertion of the second reducing equivalents, with the Na+ now inserted between the organic moieties and strongly interacting with the diacrylate molecular arms. The predicted space group for Na4BDA is P21/c with lattice parameters a = 14.03 Å, b = 5.11 Å, c = 8.09 Å, 90.05°, 76.64°, 90.05°.
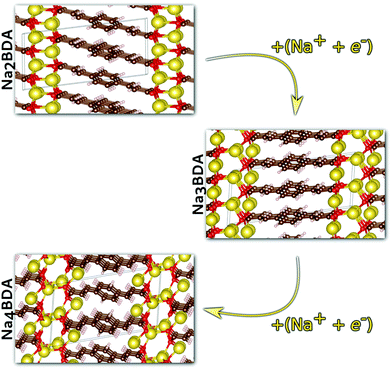 | ||
| Fig. 2 Predicted crystal structures of the disodium benzenediacrylate (Na2BDA) and its sodiated phases upon to two consecutive Na+/e− uptake. The most significant changes arise from the salt layer, where the new cation tends to be accommodated. Atom colours as in Fig. 1. | ||
All these structures are predicted in the lowest energy minima that the evolutionary algorithm can access. However, kinetic barriers and trappings in local minimum geometries could still hinder the ability to find these configurations during battery operations, where the resulting structures are often in metastable states. Therefore, additional thermodynamics calculations have been carried out to compare with the electrochemical results found experimentally when cycling Na2BDA.
Fig. 3(a) and (b) display the calculated potential profiles obtained from eqn (1). Here, two distinct functionals are used to describe the electronic exchange–correlation interaction, namely GGA-PBE-D2 and HSE06-D2. The latter is a hybrid functional that incorporates a percentage of the exact exchange calculations using the Hartree–Fock formalism64,65 and which in turn deals better with spurious self-interactions. The results show that there is a clear effect on the choice of the theory level. First, HSE06-D2 provides an average potential for the full sodiation process of 0.63 V vs. Na/Na+ that displays a better agreement with the experimental value of 0.6 V vs. Na/Na+.66 These results further validate the accuracy of the theoretical approach to describe the structures of the pristine and sodiated phases. A second, more fundamental effect is connected to the possibility of having either a stepwise one-electron or a two-electron chemical reaction. Interestingly, the GGA-PBE-D2 and HSE06-D2 results support the former and latter, respectively. As seen in Fig. 3(b), the voltage step-up indicated by HSE06-D2 reveals a thermodynamically disadvantageous process and, thus, leads to the two-electron reaction Na2BDA + 2(Na+ + e−) → Na4BDA. To further illustrate this effect, Fig. 3(c) shows the formation energy of Na3BDA with respect to Na2BDA and Na4BDA. As can be observed, Na3BDA is energetically unfavourable when the exchange–correlation is treated at the DFT/HSE06 theory level. In this case, the sodiation process would lead to a phase disproportionation, directly stabilizing Na4BDA. This corroborates recent experimental findings on related carbonyl-based organic electrodes,67–69 where two-step reactions were observed during battery cycling. As previously reported in the electrochemical analysis of the Na2BDA compound,66 a single potential plateau is indicated for the Na+ insertion process corresponding to an experimental capacity close to the theoretical one, hence endorsing the two-electron process. Thereby, the theoretical results reported here are primarily based on the DFT/HSE06-D2 framework which better corresponds to the experimentally observed data, unless explicitly stated otherwise.
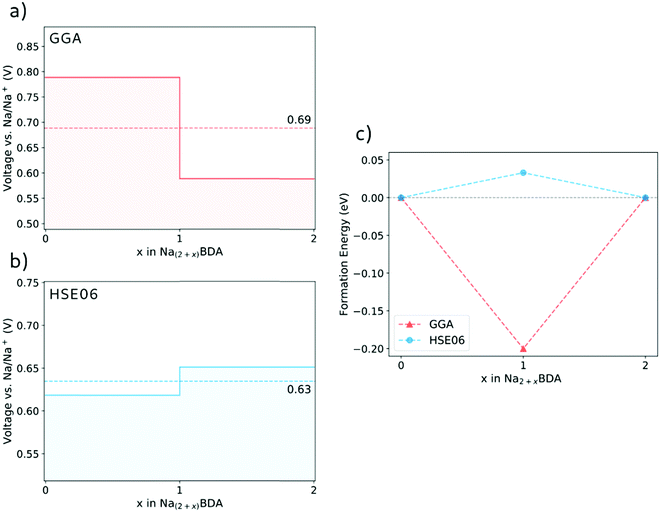 | ||
| Fig. 3 The voltage profile for the sodiation process of Na2BDA as obtained with the GGA-PBE-D2 (a) and HSE06-D2 (b) functionals. (c) Formation energy of Na3BDA with respect to Na2BDA and Na4BDA. | ||
To further unveil the underlying property–structure relationship for Na2BDA and its sodiated counterparts, Fig. 4(a)–(f) show the total and fragment-projected density of states as well as the charge density distributions of the additional electron received upon sodiation for the pristine and sodiated phases. Starting with Fig. 4(a), the first unoccupied band has contributions from the aromatic ring, the acrylate arm and the carboxylic unit of the BDA molecule. This band is redox active and will be populated by the additional electrons inserted electrochemically. From this, it can already be anticipated that those electrons will be distributed over the entire organic moiety, which works as the electron reservoir. Such charge delocalization is often associated with anodic characteristics.70 Thus, this initial electronic structure analysis also suggests a possible low potential electrode. As a reference, the crystal structure of the pristine materials is shown in Fig. 4(b). In Fig. 4(c), the DOS for the first sodiated phase is shown. It can then be seen that the redox active band starts to be populated followed by a significant narrowing of the band gap. Here, the system becomes more semi-metallic. In Fig. 4(d), we show the spatial distribution of this additional electron. To a certain degree, the whole molecule is populated but with higher electron density along some of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds. Finally, in Fig. 4(e) we show the DOS for Na4BDA where the redox active band is fully populated. The different contributions of the molecular components for the populated band are very similar to the ones in the first unoccupied band seen in Fig. 4(a). The compound thereby becomes semiconductive again, but with a narrower band gap as compared to the pristine state. Fig. 4(f) finally presents the spatial distributions of the two inserted electrons, and it can be seen that the entire molecular unit is populated. Combining these theoretical results contributes to enlighten the issue if the first sodiated phase (Na3BDA) is favourable or not. There is indeed a distinct contrast between the energetics observed for Na3BDA and those corresponding to Na2/Na4BDA, especially when considering the harsh changes in the electronic structure and the (HSE06-D2) formation energy of the former. This corresponds poorly to the rather uniform electrochemical behaviour, and is therefore less likely to appear.
C double bonds. Finally, in Fig. 4(e) we show the DOS for Na4BDA where the redox active band is fully populated. The different contributions of the molecular components for the populated band are very similar to the ones in the first unoccupied band seen in Fig. 4(a). The compound thereby becomes semiconductive again, but with a narrower band gap as compared to the pristine state. Fig. 4(f) finally presents the spatial distributions of the two inserted electrons, and it can be seen that the entire molecular unit is populated. Combining these theoretical results contributes to enlighten the issue if the first sodiated phase (Na3BDA) is favourable or not. There is indeed a distinct contrast between the energetics observed for Na3BDA and those corresponding to Na2/Na4BDA, especially when considering the harsh changes in the electronic structure and the (HSE06-D2) formation energy of the former. This corresponds poorly to the rather uniform electrochemical behaviour, and is therefore less likely to appear.
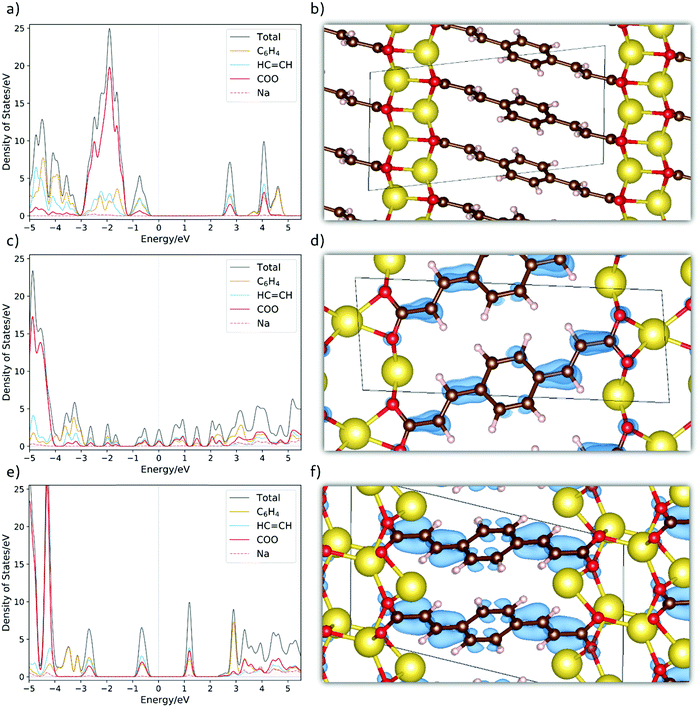 | ||
| Fig. 4 The fragment-projected Density of States (DOS) and the charge density iso-surfaces (iso value of 0.003) for (a and b) Na2BDA, (c and d) Na3BDA and (e and f) Na4BDA, respectively. The charge density is considered only for the new electron received upon sodiation. Atom colours as in Fig. 1. | ||
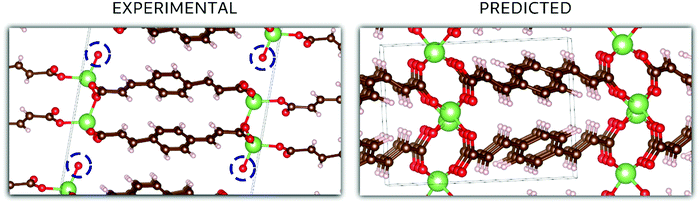
In the case of Li2BDA, the atomic structure of the compound has been determined from SCXRD data and is presented in Fig. 5. From the reciprocal lattice, the unit cell was determined to have the parameters: 13.75 Å, 5.21 Å, 16.40 Å, 90°, 95.5°, 90° and the space group P21/c (Table S1, ESI†). The coordination around the Li ion appears to form a tetrahedron. As expected, the Li and Na compounds possess the same space group but different unit cell parameters. The crystal data for Li2BDA were collected from a twin crystal at room temperature, and may hence be less optimal, but nevertheless display the main structural features. There exists a strong contrast in coordination around the different ions in the Li and Na compounds, where it is tetrahedral around Li ions and trigonal prismatic for Na ions. This can lead to different types of structural changes during the ion insertion process. A summary of the experimental and theoretical results regarding the crystal structure of both compounds can be found in Tables S1–S3 (ESI†).
In Fig. 5, the crystal structures are displayed for Li2BDA obtained experimentally and predicted computationally, following the same methodology employed for Na2BDA. Regarding the experimental structure, it must be emphasized that the system is hydrated, which is highlighted in the figure (the experimentally determined compound is Li2BDA·1H2O). As explained above, the hydrated compound was employed as a strategy to allow the use of SCXRD. Despite the presence of water, the coordination of Li ions is in good agreement between experimental and theoretical structures, showing a tetrahedron coordination shell. The computationally predicted space group for the Li2BDA compound is P21/c with lattice parameters a = 11.11 Å, b = 5.36 Å, c = 8.28 Å, 89.97°, 90.05° and 87.15°, which is generally in good agreement with the experimentally determined structure. Along the c-axis, however, the experimental unit cell is roughly doubled with twice the number of molecules when compared with the computationally predicted counterpart. Hence, c = 16.40 Å (crystallographically estimated) and c = 8.28 Å (computationally predicted) are also largely in accordance.
During the first lithiation, Li2BDA displays a similar loss of symmetry as presented for the sodium case, in which instance the initial symmetry of Na2BDA is regained after the second sodiation reaction which generates the Na4BDA phase. For the lithium compound, however, the symmetry is not recovered after the second lithiation reaction, with the predicted space group for Li3BDA being P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with lattice parameters a = 13.03 Å, b = 5.13 Å, c = 7.57 Å, 86.84°, 100.15°, 86.80° and Li4BDA being also P
with lattice parameters a = 13.03 Å, b = 5.13 Å, c = 7.57 Å, 86.84°, 100.15°, 86.80° and Li4BDA being also P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and lattice parameters a = 13.33 Å, b = 5.28 Å, c = 7.59 Å, 86.40°, 107.03° and 101.05°. In the ESI,† the crystal structures for the lithiated phases Li3BDA and Li4BDA are presented in Fig. S1. An expansion of the salt layer can also be observed when additional Li ions are incorporated. Moreover, the unit cell volume undergoes an expansion process, increasing by 1.95% after the second lithiation reaction. By comparison, the cell volume of the sodiated equivalent (Na4BDA) shows an increase of 10.78% relative to the pristine desodiated phase. The sensible difference in volume expansion between the two cases may be associated with the respective cation size, which is significantly larger for sodium ions and thereby do not allow an efficient packing. In addition, the Li compound does not only display a more compact salt layer after lithiation, but it can also be seen that the inserted lithium ions tend to interact more strongly with the carbonyl oxygens and less with the C
and lattice parameters a = 13.33 Å, b = 5.28 Å, c = 7.59 Å, 86.40°, 107.03° and 101.05°. In the ESI,† the crystal structures for the lithiated phases Li3BDA and Li4BDA are presented in Fig. S1. An expansion of the salt layer can also be observed when additional Li ions are incorporated. Moreover, the unit cell volume undergoes an expansion process, increasing by 1.95% after the second lithiation reaction. By comparison, the cell volume of the sodiated equivalent (Na4BDA) shows an increase of 10.78% relative to the pristine desodiated phase. The sensible difference in volume expansion between the two cases may be associated with the respective cation size, which is significantly larger for sodium ions and thereby do not allow an efficient packing. In addition, the Li compound does not only display a more compact salt layer after lithiation, but it can also be seen that the inserted lithium ions tend to interact more strongly with the carbonyl oxygens and less with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C acrylate arm (Fig. S1 in the ESI†), in contrast with the Na+ ions. In Fig. 6(a), the total and the fragment-projected density of states are shown. Once again, the first unoccupied band displays a fair composition of all fragments and, thus, a delocalization of the added electron over the entire molecular unit can be expected upon lithiation. This is further illustrated in Fig. 6(b), in which the charge density for the two extra electrons in the Li4BDA phase is shown. Furthermore, Fig. 6(c) presents the formation energy of the Li3BDA compound with respect to Li2BDA and Li4BDA. Similarly as for the sodium case, the HSE06-D2 result suggests a two-electron process for the lithiation reaction with Li3BDA being energetically unfavourable. Similarly to the Na analogue, this agrees with the experimentally observed electrochemical performance presented in the literature,61,71 which does not indicate any intermediate phases, and thereby reinforce the necessity to use the applied hybrid functional for estimating the electronic description of this category of materials. Therefore, considering the non-observance of the I3BDA phase (I = Li, Na), the loss of symmetry for the lithium case can be explained, with the pristine structure changing from P21/c to P
C acrylate arm (Fig. S1 in the ESI†), in contrast with the Na+ ions. In Fig. 6(a), the total and the fragment-projected density of states are shown. Once again, the first unoccupied band displays a fair composition of all fragments and, thus, a delocalization of the added electron over the entire molecular unit can be expected upon lithiation. This is further illustrated in Fig. 6(b), in which the charge density for the two extra electrons in the Li4BDA phase is shown. Furthermore, Fig. 6(c) presents the formation energy of the Li3BDA compound with respect to Li2BDA and Li4BDA. Similarly as for the sodium case, the HSE06-D2 result suggests a two-electron process for the lithiation reaction with Li3BDA being energetically unfavourable. Similarly to the Na analogue, this agrees with the experimentally observed electrochemical performance presented in the literature,61,71 which does not indicate any intermediate phases, and thereby reinforce the necessity to use the applied hybrid functional for estimating the electronic description of this category of materials. Therefore, considering the non-observance of the I3BDA phase (I = Li, Na), the loss of symmetry for the lithium case can be explained, with the pristine structure changing from P21/c to P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) when lithiated while keeping the initial symmetry (P21/c) when sodiated.
when lithiated while keeping the initial symmetry (P21/c) when sodiated.
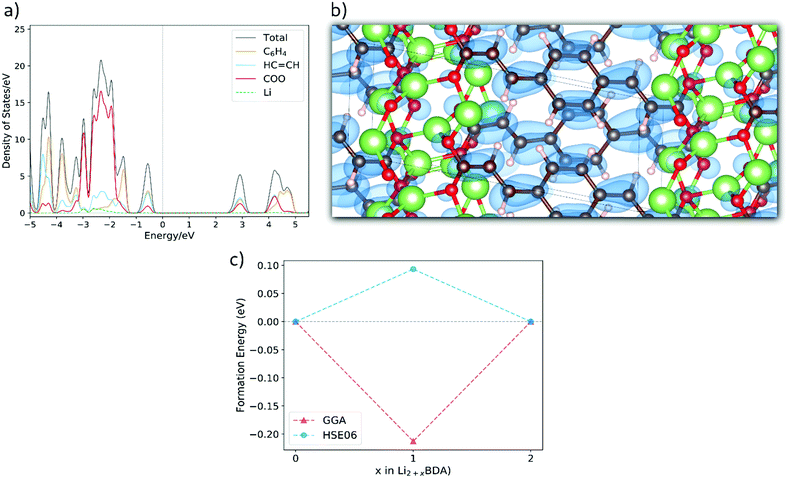 | ||
| Fig. 6 (a) Fragment-projected Density of States (DOS) for Li2BDA and (b) the charge density isosurface (value of 0.003) of the two electrons received upon lithiation reaction of Li2BDA to Li4BDA. (c) Formation energy of Li3BDA with respect to Li2BDA and Li4BDA. Atom colours as in Fig. 5. | ||
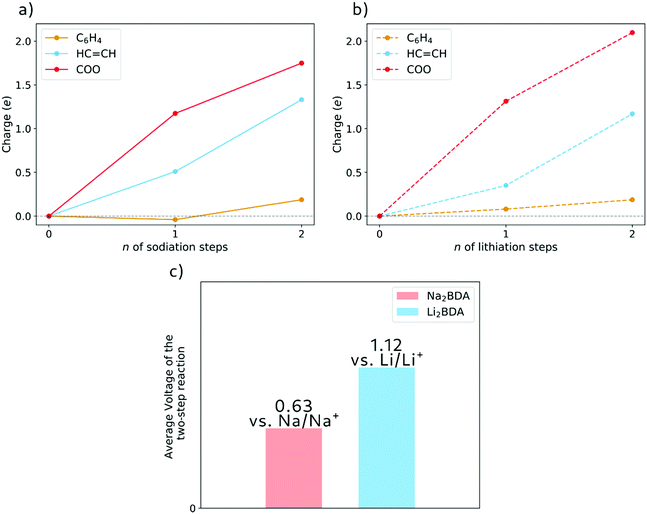
The molecular fragment charge, obtained from Bader analysis, is displayed in Fig. 7, following the variation upon sodiation/lithiation for different organic moieties in Na2BDA (a) and Li2BDA (b). In both cases, there is a tendency for the charge being consistently distributed over the acrylate unit with contributions of the organic ring appearing just after the second reduction reaction. Nevertheless, Na2BDA seems to contribute with comparatively more charge within the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C unit than in the carbonyl part of the acrylate unit as compared to the Li2BDA counterpart. This agrees with the aforementioned observation that the inserted Na+ ions appear to localize more closely to the acrylate arm than the Li+ ones. In Fig. 7(c), the predicted average voltage for the two-step reaction is shown to be 0.63 V vs. Na/Na+ (sodiation) and 1.12 V vs. Li/Li+ (lithiation), with the latter being experimentally reported to be 1.2 V vs. Li/Li+.61 Both potentials are thereby in good agreement with the experimental findings.
C unit than in the carbonyl part of the acrylate unit as compared to the Li2BDA counterpart. This agrees with the aforementioned observation that the inserted Na+ ions appear to localize more closely to the acrylate arm than the Li+ ones. In Fig. 7(c), the predicted average voltage for the two-step reaction is shown to be 0.63 V vs. Na/Na+ (sodiation) and 1.12 V vs. Li/Li+ (lithiation), with the latter being experimentally reported to be 1.2 V vs. Li/Li+.61 Both potentials are thereby in good agreement with the experimental findings.
The difference in electrochemical performance between the two systems, however, is a challenging issue to address since it is a result of the combinations of different factors. One first aspect could be a consequence of the distinct reference electrode, Na and Li, adopted for Na2BDA and Li2BDA, respectively. The larger atomic radius of the sodium ions could also be a hindrance, especially in terms of kinetics. In the same sense, the major volumetric changes that Na2BDA needs to undergo upon sodiation could further constitute an obstacle, thereby generating a lower voltage as compared to Li2BDA. Finally, the different structures formed after lithiation/sodiation could well provide different kinetics and stability.
IV. Conclusions
A combined computational–experimental framework has been used to explore some fundamental structural aspects during electrochemical reactions of the two organic redox-active disodium and dilithium benzenediacrylate (Na2BDA and Li2BDA) battery materials. Their crystal structures have been experimentally resolved and also theoretically predicted through a joint approach involving evolutionary algorithm and density functional theory calculations. It is then found that the computational methodology can successfully predict the crystal structure of the pristine compounds, presenting the same space groups, ionic coordination and lattice parameters as the experimentally derived structures of Na2BDA and Li2BDA. Following these results, the sodiated/lithiated phases have also been predicted, thereby enabling the assessment of the thermodynamics for the ion insertion process. The obtained average potentials of 0.63 V vs. Na/Na+ for the sodiation of Na2BDA and 1.12 V vs. Li/Li+ for the lithiation of Li2BDA display excellent concordance with the experimental findings, thus supporting the atomistic insights into how the ion insertion processes occur. This assessment also suggests that the sodiation (lithiation) of Na2BDA (Li2BDA) takes place through a two-electron process. From fragment-projected density of states and Bader charge analysis, it can also be seen that the Na2BDA compound stabilizes more charges around the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C arm of the acrylate than its Li equivalent, corresponding to the Na ions being more localized around this molecular moiety. These findings can explain some of the differences found in the electrochemical performance of these compounds, where the lithiation process seems kinetically and thermodynamically more favourable as the sodiation, providing less tension in the obtained structures.
C arm of the acrylate than its Li equivalent, corresponding to the Na ions being more localized around this molecular moiety. These findings can explain some of the differences found in the electrochemical performance of these compounds, where the lithiation process seems kinetically and thermodynamically more favourable as the sodiation, providing less tension in the obtained structures.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We acknowledge support from the Swedish Research Council (Grant number: 2018-04506, 349-2014-3946 and 2019-05465), the Swedish Energy Agency (Grant number: 45420-1), Formas (Grant number: 2016-00838) and STandUP for Energy. The computational infrastructure has been provided by the Swedish National Infrastructure for Computing (SNIC) at the PDC Center for High Performance Computing and National Supercomputer Centre (NSC) at Linköping University.References
- J. M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS.
- D. Larcher and J.-M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS.
- M. Romare and L. Dahllöf, The Life Cycle Energy Consumption and Greenhouse Gas Emissions from Lithium-Ion Batteries, 2017 Search PubMed.
- P. Poizot and F. Dolhem, Energy Environ. Sci., 2011, 4, 2003 RSC.
- M. Miroshnikov, K. Mahankali, N. K. Thangavel, S. Satapathy, L. M. R. Arava, P. M. Ajayan and G. John, ChemSusChem, 2020, 13, 2186–2204 CrossRef CAS.
- C. Liedel, ChemSusChem, 2020, 13, 2110–2141 CrossRef CAS.
- P. Hu, H. Wang, Y. Yang, J. Yang, J. Lin and L. Guo, Adv. Mater., 2016, 28, 3486–3492 CrossRef CAS.
- H. Chen, M. Armand, M. Courty, M. Jiang, C. P. Grey, F. Dolhem, J. M. Tarascon and P. Poizot, J. Am. Chem. Soc., 2009, 131, 8984–8988 CrossRef CAS.
- H. Chen, M. Armand, G. Demailly, F. Dolhem, P. Poizot and J. M. Tarascon, ChemSusChem, 2008, 1, 348–355 CrossRef CAS.
- B. Haeupler, A. Wild and U. S. Schubert, Adv. Energy Mater., 2015, 5, 1402034 CrossRef.
- P. Poizot, J. Gaubicher, S. Renault, L. Dubois, Y. Liang and Y. Yao, Chem. Rev., 2020, 120, 6490–6557 CrossRef CAS.
- M. E. Bhosale, S. Chae, J. M. Kim and J.-Y. Choi, J. Mater. Chem. A, 2018, 6, 19885–19911 RSC.
- P. Poizot, F. Dolhem and J. Gaubicher, Curr. Opin. Electrochem., 2018, 9, 70–80 CrossRef CAS.
- H. Wang and X. Zhang, Chem. – Eur. J., 2018, 24, 18235–18245 CrossRef CAS.
- Q. Zhao, Y. Lu and J. Chen, Adv. Energy Mater., 2017, 7, 1601792 CrossRef.
- L. Fédèle, F. Sauvage, S. Gottis, C. Davoisne, E. Salager, J.-N. Chotard and M. Becuwe, Chem. Mater., 2017, 29, 546–554 CrossRef.
- V. Medabalmi, G. Wang, V. K. Ramani and K. Ramanujam, Appl. Surf. Sci., 2017, 418, 9–16 CrossRef CAS.
- L. Fédèle, O. Ouari, F. Sauvage, A. Thiam and M. Becuwe, ChemSusChem, 2020, 13, 2321–2327 CrossRef.
- H. Zhang, Y. Lin, L. Chen, D. Wang, H. Hu and C. Shen, ChemElectroChem, 2020, 7, 306–313 CrossRef CAS.
- A. Iordache, D. Bresser, S. Solan, M. Retegan, M. Bardet, J. Skrzypski, L. Picard, L. Dubois and T. Gutel, Adv. Sustainable Syst., 2017, 1, 1600032 CrossRef.
- H. H. Lee, Y. Park, K. H. Shin, K. T. Lee and S. Y. Hong, ACS Appl. Mater. Interfaces, 2014, 6, 19118–19126 CrossRef CAS.
- S. Renault, V. A. Oltean, C. M. Araujo, A. Grigoriev, K. Edström and D. Brandell, Chem. Mater., 2016, 28, 1920–1926 CrossRef CAS.
- S.-H. Kim, H. H. Lee, J.-M. Kim, S. Y. Hong and S.-Y. Lee, Energy Storage Mater., 2019, 19, 130–136 CrossRef.
- Y. Chen and S. Manzhos, Phys. Chem. Chem. Phys., 2016, 18, 1470–1477 RSC.
- R. B. Araujo, A. Banerjee, P. Panigrahi, L. Yang, M. Sjödin, M. Strømme, C. M. Araujo and R. Ahuja, Phys. Chem. Chem. Phys., 2017, 19, 3307–3314 RSC.
- G. Ramos-Sanchez, A. Callejas-Tovar, L. G. Scanlon and P. B. Balbuena, Phys. Chem. Chem. Phys., 2014, 16, 743–752 RSC.
- S. Sun, Y. Chen and J. Yu, J. Phys. Chem. C, 2015, 119, 25770–25777 CrossRef CAS.
- J. E. Bachman, L. A. Curtiss and R. S. Assary, J. Phys. Chem. A, 2014, 118, 8852–8860 CrossRef CAS.
- K. C. Kim, T. Liu, S. W. Lee and S. S. Jang, J. Am. Chem. Soc., 2016, 138, 2374–2382 CrossRef CAS.
- R. B. Araujo, A. Banerjee, P. Panigrahi, L. Yang, M. Strømme, M. Sjödin, C. M. Araujo and R. Ahuja, J. Mater. Chem. A, 2017, 5, 4430–4454 RSC.
- K. Hernández-Burgos, S. E. Burkhardt, G. G. Rodríguez-Calero, R. G. Hennig and H. D. Abruña, J. Phys. Chem. C, 2014, 118, 6046–6051 CrossRef.
- R. B. Araujo, A. Banerjee and R. Ahuja, J. Phys. Chem. C, 2017, 121, 14027–14036 CrossRef CAS.
- M. A. Sk and S. Manzhos, J. Power Sources, 2016, 324, 572–581 CrossRef CAS.
- C. Frayret, E. I. Izgorodina, D. R. MacFarlane, A. Villesuzanne, A.-L. Barrès, O. Politano, D. Rebeix and P. Poizot, Phys. Chem. Chem. Phys., 2012, 14, 11398 RSC.
- T. Yamashita, H. Momida and T. Oguchi, Electrochim. Acta, 2016, 195, 1–8 CrossRef CAS.
- A. Banerjee, R. B. Araujo, M. Sjödin and R. Ahuja, Nano Energy, 2018, 47, 301–308 CrossRef CAS.
- C. F. N. Marchiori, D. Brandell and C. M. Araujo, J. Phys. Chem. C, 2019, 123, 4691–4700 CrossRef CAS.
- R. P. Carvalho, C. F. N. Marchiori, D. Brandell and C. M. Araujo, ChemSusChem, 2020, 13, 2402–2409 CrossRef CAS.
- M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Adv. Funct. Mater., 2013, 23, 947–958 CrossRef CAS.
- J.-Y. Hwang, S.-T. Myung and Y.-K. Sun, Chem. Soc. Rev., 2017, 46, 3529–3614 RSC.
- M. S. Whittingham, Prog. Solid State Chem., 1978, 12, 41–99 CrossRef CAS.
- P. Braconnier, J. J. Delmas, C. Fouassier and C. Hagenmuller, Mater. Res. Bull., 1980, 15, 1797–1804 CrossRef.
- C. Delmas, C. Fouassier and P. Hagenmuller, Physica B+C, 1980, 99, 81–85 CrossRef CAS.
- Y. Xu, M. Zhou and Y. Lei, Mater. Today, 2018, 21, 60–78 CrossRef CAS.
- X. Yin, S. Sarkar, S. Shi, Q. Huang, H. Zhao, L. Yan, Y. Zhao and J. Zhang, Adv. Funct. Mater., 2020, 30, 1908445 CrossRef CAS.
- L. Zhao, J. Zhao, Y.-S. Hu, H. Li, Z. Zhou, M. Armand and L. Chen, Adv. Energy Mater., 2012, 2, 962–965 CrossRef CAS.
- Y. Park, D.-S. Shin, S. H. Woo, N. S. Choi, K. H. Shin, S. M. Oh, K. T. Lee and S. Y. Hong, Adv. Mater., 2012, 24, 3562–3567 CrossRef CAS.
- A. Abouimrane, W. Weng, H. Eltayeb, Y. Cui, J. Niklas, O. Poluektov and K. Amine, Energy Environ. Sci., 2012, 5, 9632 RSC.
- K. Chihara, N. Chujo, A. Kitajou and S. Okada, Electrochim. Acta, 2013, 110, 240–246 CrossRef CAS.
- M. Lee, J. Hong, J. Lopez, Y. Sun, D. Feng, K. Lim, W. C. Chueh, M. F. Toney, Y. Cui and Z. Bao, Nat. Energy, 2017, 2, 861–868 CrossRef CAS.
- E. Matios, H. Wang, C. Wang and W. Li, Ind. Eng. Chem. Res., 2019, 58, 9758–9780 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704 CrossRef.
- C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713–720 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS.
- Y. S. Meng and M. E. Arroyo-De Dompablo, Energy Environ. Sci., 2009, 2, 589–609 RSC.
- S. Renault, D. Brandell, T. Gustafsson and K. Edström, Chem. Commun., 2013, 49, 1945–1947 RSC.
- T. Willhammar, Y. Yun and X. Zou, Adv. Funct. Mater., 2014, 24, 182–199 CrossRef CAS.
- L. Palatinus and G. Chapuis, J. Appl. Crystallogr., 2007, 40, 786–790 CrossRef CAS.
- J. C. Slater, Phys. Rev., 1928, 32, 339–348 CrossRef.
- C. J. Cramer, Essentials of computational chemistry: theories and models, John Wiley & Sons, New York, 2002 Search PubMed.
- V. A. Mihali, S. Renault, L. Nyholm and D. Brandell, RSC Adv., 2014, 4, 38004–38011 RSC.
- L. Zhu, G. Ding, L. Xie, X. Cao, J. Liu, X. Lei and J. Ma, Chem. Mater., 2019, 31, 8582–8612 CrossRef CAS.
- A. Iordache, V. Maurel, J. M. Mouesca, J. Pécaut, L. Dubois and T. Gutel, J. Power Sources, 2014, 267, 553–559 CrossRef CAS.
- B. Tian, J. Zheng, C. Zhao, C. Liu, C. Su, W. Tang, X. Li and G. H. Ning, J. Mater. Chem. A, 2019, 7, 9997–10003 RSC.
- M. Saubanère, J.-S. Filhol and M.-L. Doublet, Physical Multiscale Modeling and Numerical Simulation of Electrochemical Devices for Energy Conversion and Storage, Springer, London, 2016, pp. 1–36 Search PubMed.
- M. Armand, S. Grugeon, H. Vezin, S. Laruelle, P. Ribière, P. Poizot and J. M. Tarascon, Nat. Mater., 2009, 8, 120–125 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ma00900h |
| This journal is © The Royal Society of Chemistry 2021 |