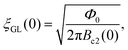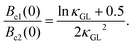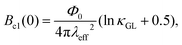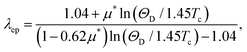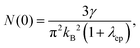DOI:
10.1039/D1MA00154J
(Paper)
Mater. Adv., 2021,
2, 3328-3335
Synthesis and superconductivity of new TiNiSi-type equiatomic germanide ThIrGe
Received
22nd February 2021
, Accepted 10th April 2021
First published on 12th April 2021
Abstract
A new germanide ThIrGe has been synthesized and characterized by X-ray diffraction, transmission electron microscopy, electrical resistivity, magnetic susceptibility and thermodynamic measurements. The structural refinement shows that, in contrast to tetragonal ThIrSi, ThIrGe crystallizes in the TiNiSi-type orthorhombic structure with the Pnma space group (a = 7.2321(2) Å, b = 4.3802(1) Å, and c = 7.7107(2) Å), which is the first Th-based ternary equiatomic intermetallic compound of this structural type. Below Tc = 5.25 K, ThIrGe becomes a weak-coupling type-II superconductor with a fully isotropic superconducting gap. The Sommerfield coefficient, upper critical field, and Ginzburg–Laudau parameter are determined to be 11.8 mJ mol−1 K−2, 2.9 T, and 19.9, respectively. First-principles calculations indicate that the density of states at the Fermi level are dominated by a hybridized contribution from the orbitals of Th, Ir and Ge, and are enhanced by the spin–orbit coupling. In addition, we demonstrate that the structural difference between ThIrGe and ThIrSi can be understood in terms of the Gibbs formation energy.
1 Introduction
Ternary equiatomic intermetallic compounds are a large family of materials and have been studied extensively over the past few decades.1–6 These compounds have the general formula MM′X, where M can be an early transition-metal, a rare-earth or an actinide element, M′ is a late transition-metal element, and X is Si, Ge or P. Depending on the constituent elements, the MM′X compounds crystallize in a variety of structures, including hexagonal ZrNiAl-type,7 orthorhombic TiNiSi-type,8 and tetragonal LaPtSi-type9 (see Fig. 1). Both the ZrNiAl-type and TiNiSi-type structures can be viewed as two-dimensional homologues based on the AlB2-type structure, in which the key structural component is the tricapped trigonal prisms with metal atoms at the corners and non-metal atoms in the center.10 The ZrNiAl-type structure contains six-membered rings enclosing an isolated prism, while the TiNiSi-type one consists of zigzag sheets of corner-sharing trigonal prisms.11 By contrast, the LaPtSi-type structure is noncentrosymmetric and an ordered variant of the α-ThSi2 structure.12 In addition to this structural diversity, these ternary compounds exhibit a range of interesting physical properties, such as complex magnetic ordering,9,13–15 heavy fermion behavior16,17 and superconductivity.18–24
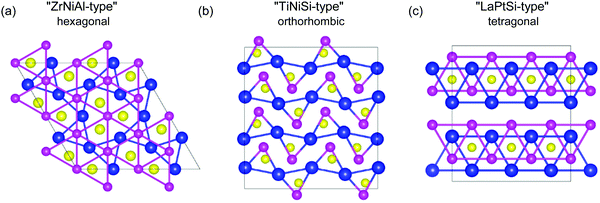 |
| | Fig. 1 Schematic structure of (a) hexagonal ZrNiAl-type, (b) orthorhombic TiNiSi-type and (c) tetragonal LaPtSi-type ternary equiatomic intermetallic compounds. The blue, pink, and yellow atoms correspond to M, M′, and X, respectively. | |
Among the TiNiSi-type MM′X compounds, the U-based UTGe (T = Co, Rh and Ir) has received considerable attention. UCoGe19,25 and URhGe20 show coexistence of ferromagnetism and superconductivity at ambient pressure. While the underlying mechanism remains unclear, both superconductivity and magnetic order are believed to be due to the U 5f electrons. In comparison, UIrGe orders antiferromagnetically and exhibits no superconductivity.17,26 Except for 5f electrons, Th has the same electronic configuration as U. It is thus of interest to investigate the Th-based isostructural counterparts, which serve as nonmagnetic references to UTGe. However, for the ThTGe series, only ThCoGe has been known to exist and it has an AlB2-type structure.27 Moreover, while all of ThTSi members can be synthesized and are found to be superconducting, they adopt the noncentrosymmetric LaPtSi-type structure.28 Actually, to our knowledge, no Th-based ternary equiatomic compound with the TiNiSi-type structure has been reported to date.
In this paper, we report the synthesis, crystal structure and physical properties of ThIrGe, a new ternary phase in the Th–Ir–Ge system. It is found that this compound possesses the orthorhombic TiNiSi-type structure and exhibits bulk type-II superconductivity below 5.25 K, which is the highest among ternary equiatomic germanides. Various superconducting parameters such as electron–phonon coupling constant, critical fields, coherence length and penetration depth, are obtained. Theoretical calculations reveal a significant hybridization between the Th, Ir and Ge orbitals at the Fermi level and nonnegligible effects of spin–orbit coupling (SOC). In addition, a comparison is made between the Gibbs formation energies of ThIrGe and ThIrSi in both the TiNiSi-type and LaPtSi-type structures.
2 Materials and methods
Polycrystalline ThIrGe sample was prepared by the arc-melting method. Stoichiometric amounts of high purity Th (99.5%), Ir (99.9%) and Ge (99.99%) elements were mixed and pressured into a pellet in an argon-filled glove box. The pellet was melted in an arc furnace under high-purity argon atmosphere for several times to ensure homogeneity, followed by rapid cooling on a water-chilled copper plate. The as-cast ingot was sealed into an evacuated quartz tube, annealed at 1000 °C for 7 days, and then quenched to room temperature. The phase purity was checked by powder X-ray diffraction (XRD) at room temperature using a Bruker D8 Advance diffractometer with Cu Kα radiation. The crystal structure refinement was carried out using the Rietveld method with the GSAS software.29 The chemical composition was measured by the Octane Plus Detector (AMETEX EDAX) coupled to a field-emitting scanning electron microscope (SEM; Hitachi S-4800). The microstructure was examined in a FEI Tecnai G2 F20 S-TWIN transmission electron microscope (TEM) operated at an accelerating voltage of 200 kV. Electrical resistivity and specific heat data were measured in a Quantum Design Physical Property Measurement System (PPMS-9 Dynacool). The dc magnetization measurements were performed in a Quantum Design Magnetic Property Measurement System (MPMS3).
First-principles calculations were carried out in the Vienna Ab initio Simulation Package (VASP)30 based on density functional theory. The Perdew–Burke–Ernzerhof (PBE)31 exchange–correlation functional was used and the convergence threshold of Hellmann–Feynman force is 0.01 eV Å−1. The energy convergence criterion was set to 10−6 eV for structural optimization and 10−8 eV for other purposes. In both structural optimization and self-consistent calculations, the wavefunction cutoff energy was fixed to 450 eV and the Γ-centered k mesh was set to 5 × 8 × 4. The latter was increased to 10 × 16 × 8 for density-of-state (DOS) calculations.
3 Results and discussion
3.1 Crystal structure and chemical composition
Fig. 2 shows XRD patterns of ThIrGe together with its structural refinement profile, and the refined results are listed in Table 1. Except for a few small ones, the diffraction peaks can be well indexed on an orthorhombic lattice with the Pnma space group. This indicates that the main phase of the sample has a TiNiSi-type structure, which is used for the structural refinement. There is a satisfactory agreement between the calculated and observed patterns (Rwp = 6.5%, Rp = 4.9%, χ2 = 2.45) and a minor impurity phase of ThIr (∼8%) is also identified. The refined lattice parameters are a = 7.2321(2) Å, b = 4.3802(1) Å, c = 7.7107(2) Å, which yields a unit-cell volume of 244.26(2) Å3. In the lattice of ThIrGe, all of Th, Ir and Ge atoms occupy the (0.0098, 0.25, 0.7024), (0.2864, 0.25, 0.4121) and (0.1864, 0.25, 0.0816), respectively, all of which are locally non-centrosymmetric. As shown in the inset of Fig. 2, the nearest neighbour Th atoms form zigzag chains running along the a-axis with an interatomic distance of 3.689 Å, which is slightly larger than that (3.60 Å) of the sum of thorium atomic radii. A set of selected interatomic distances in ThIrGe structure is given in Table 2. One can note that the nearest neighbour distance between the Th and Ir atom is only 3.002 Å. Actually, this Th-Ir distance is even shorter than those of in the cubic Lave phase superconductor ThIr2 (3.176 Å)32 and noncentrosymmetric superconductor ThIrSi (3.138 Å).28 This, together with the short nearest neighbour Th–Ir (3.002 Å), and Ir–Ge (2.557 Å) distances, suggests a hybridization of Th, Ir and Ge orbitals at the Fermi level, which is consistent with the theoretical calculation results shown below.
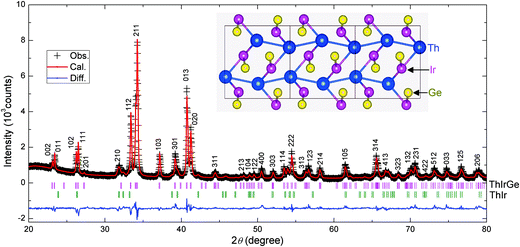 |
| | Fig. 2 Powder X-ray diffraction pattern at room temperature together with its structural refinement profile for the ThIrGe sample. The black crosses are the observed patterns and indexed on an orthorhombic unit-cell. The red and blue lines are the calculated pattern and difference plot, respectively. The peak positions for ThIrGe and ThIr are indicated by the ticks. The inset shows a schematic structure of ThIrGe, and the bonds between nearest-neighbour Th–Th, Th–Ir and Ir–Ge atoms are highlighted. | |
Table 1 Structural refinement results for ThIrGe
| ThIrGe |
| Space group |
Pnma
|
|
a (Å) |
7.2321(2) |
|
b (Å) |
4.3802(1) |
|
c (Å) |
7.7107(2) |
|
V (Å3) |
244.26(2) |
|
R
wp
|
6.5% |
|
R
p
|
4.9% |
|
χ
2
|
2.45 |
| Atoms |
X
|
y
|
z
|
Occ. |
U
iso
|
| Th |
0.0098(5) |
0.25 |
0.7024(1) |
1 |
0.0064(6) |
| Ir |
0.2864(4) |
0.25 |
0.4121(3) |
1 |
0.0075(1) |
| Ge |
0.1864(7) |
0.25 |
0.0816(7) |
1 |
0.021(2) |
Table 2 Selected interatomic distances for ThIrGe
| Interaction |
Distance (Å) |
Interaction |
Distance (Å) |
| Th–Ge (×2) |
3.238(5) |
Th–Th (×2) |
3.816(2) |
| Th–Ge (×2) |
3.096(5) |
Th–Th (×2) |
3.689(1) |
| Th–Ge (×1) |
3.190(6) |
Th–Ir (×1) |
3.002(4) |
| Th–Ge (×1) |
3.205(6) |
Th–Ir (×1) |
3.382(4) |
| Ir–Ge (×1) |
2.649(5) |
Th–Ir (×2) |
3.189(3) |
| Ir–Ge (×1) |
2.894(5) |
Th–Ir (×2) |
3.095(3) |
| Ir–Ge (×2) |
2.557(2) |
|
|
This crystal structure of ThIrGe is further confirmed by high-resolution TEM (HRTEM) measurements on single-crystalline grains, typical results of which are displayed in Fig. 3(a) and (b). As can be seen in Fig. 3(a), the selected-area electron diffraction (SAED) taken along [−2 1 1] zone axis exhibits a well-defined spot pattern, and the spots near the center can be indexed to the (102), (111) and (213) planes of the TiNiSi-type structure. Moreover, from the HRTEM image of the same area shown in Fig. 3(b), two lattice spacings of 0.327 nm and 0.340 nm can be resolved, which correspond well to the (111) and (102) planes, respectively. Note that the angle between these planes is 53°, which is quite as expected in the TiNiSi-type structure. On the other hand, the EDX measurements show that the ThIrGe sample is chemically homogeneous with an average composition of Th0.9(1)IrGe1.1(1). This demonstrates that ThIrGe is stoichiometric within the experimental error, in agreement with the refined occupancies.
 |
| | Fig. 3 (a) Selected-area electron diffraction pattern taken along the [−2 1 1] zone axis of a single-crystalline grain of the ThIrGe sample. (b) The corresponding high resolution TEM image. The distance and angel between the planes are indicated. | |
3.2 Normal-state and superconducting properties
The temperature dependence of resistivity ρ under zero field for the ThIrGe sample is shown in Fig. 4(a). With decreasing temperature, ρ decreases smoothly and exhibits a metallic behavior. The residual resistivity ρ0 and residual resistivity ratio RRR = ρ(300 K)/ρ0 are ∼75 μΩ cm and ∼3.3, respectively. Nevertheless, since our sample has a polycrystalline nature, these values depend largely on the contribution of grain boundaries and hence are not a good indicator of the sample quality. On cooling below 5.5 K, ρ drops abruptly and becomes zero at ∼5 K. As shown in Fig. 4(b), the resistive transition is gradually suppressed to lower temperature with increasing the magnetic field. This clearly indicates that the ρ drop is due to a superconducting transition. Here Tc is defined as the midpoint of ρ drop and found to be 5.25 K at zero field. While this value is close to that of ThIr2 (5.58 K),32 no corresponding phase is detected in XRD and SEM analysis. In addition, although ThIr impurity is present, its reported Tc is only 0.37 K.33 Thus the observed superconductivity is undoubtedly ascribed to ThIrGe. To our knowledge, this Tc of 5.25 K is higher than any previously known ternary equiatomic germanides.34 Following the same criterion at zero field, the Tc values at various fields are obtained and summarized in the upper critical field (Bc2) versus temperature phase diagram displayed in Fig. 4(c), in which the horizontal error bars denote the transition width. Notably, the Bc2 data show deviation from the Werthamer–Helfand–Hohenberg curve35 at low temperature but follow nicely the Ginzburg–Landau (GL) relationship| | 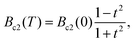 | (1) |
where t = T/Tc. An extrapolation of the data to 0 K gives the zero-temperature upper critical field Bc2(0) = 2.9 T. This value is far below the Pauli limiting field BP(0) = 1.86Tc ≈ 9.7 T,36 suggesting that Bc2 of ThIrGe is limited by the orbital effect.
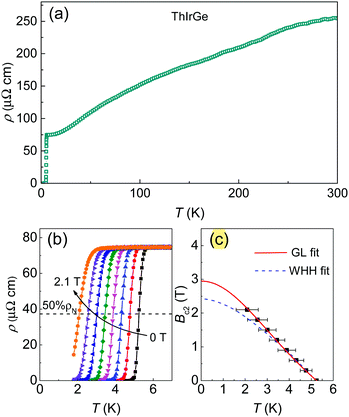 |
| | Fig. 4 (a) Temperature dependence of resistivity for the ThIrGe sample. (b) Low temperature resistivity data under various fields from 0 up to 2.1 T. (c) Temperature dependence of the upper critical field with the horizontal error bars denoting the transition width. The red solid line and blue dashed line are GL and WHH fits to the data, respectively. | |
The occurrence of superconductivity in ThIrGe is corroborated by the magnetic susceptibility (χ) measurements under a magnetic field of 1 mT in both the zero-field cooling (ZFC) and field cooling (FC) modes, whose results are shown in Fig. 5(a). A strong diamagnetic transition is observed in both the ZFC and FC data, and its onset temperature of 5.22 K agrees well with the Tc determined from the resistivity measurement. Below the transition, a bifurcation develops between the two curves, which is characteristic of a type-II superconducting behavior. At 1.8 K, the χZFC and χFC values correspond to shielding and Meissner fractions of 151.5% and 19.5%, respectively, without considering the demagnetization factor. Fig. 5(b) shows the isothermal magnetization curves at various temperatures between 1.8 and 4.6 K. In the low-field region, the M(B) data decrease linearly with increasing field due to the Meissner state. At each temperature, the effective lower critical field 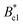 is determined as the field at which M(B) deviates from its initial linearity. The resulting temperature dependence of
is determined as the field at which M(B) deviates from its initial linearity. The resulting temperature dependence of 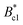 is displayed in Fig. 5(c) and can be well fitted by the mean-field equation:32
is displayed in Fig. 5(c) and can be well fitted by the mean-field equation:32
| | 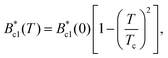 | (2) |
where
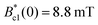
is the effective zero-temperature lower critical field. Since the demagnetization factor
Nd is related to the slope of initial magnetization curve through the relation
| | 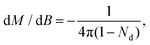 | (3) |
which gives
Nd = 0.31. Then the zero-temperature lower critical field
Bc1(0) is calculated to be
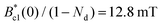
. In addition, the shielding and Meissner fractions after demagnetization correction are 104.5% and 13.5%, respectively, suggesting that superconductivity occurs in almost the whole sample volume.
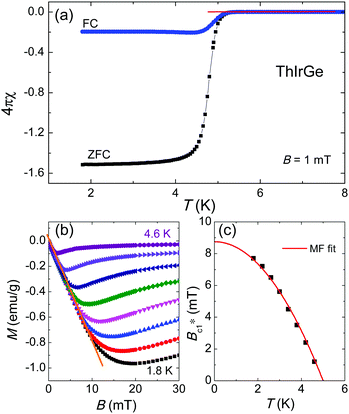 |
| | Fig. 5 (a) Low temperature magnetic susceptibility measured on the ThIrGe sample under an applied field of 1 mT. (b) Isothermal magnetization curves for the sample at various temperatures between 1.8 and 4.6 K. The solid line denotes the initial linear behavior. (c) Temperature dependence of the effective lower critical field. The solid line is a mean-field fit to the data (see text). | |
With the values of Bc1(0) and Bc2(0), various superconducting parameters can be determined. First, the Ginzburg-Landau coherence length ξGL(0) is calculated to be 107 Å using the formula
| | 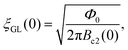 | (4) |
where
Φ0 = 2.07 × 10
−15 Wb is the flux quantum. Second, the GL parameter
κGL can be derived from the equation
37| | 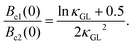 | (5) |
This gives
κGL value of 19.9, confirming that ThIrGe is a moderate type-II superconductor. Third, the penetration depth
λeff is obtained from the formula
| | 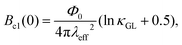 | (6) |
which yields
λeff = 2120 Å.
The bulk nature of superconductivity in ThIrGe is confirmed by the specific heat measurements. Fig. 6(a) shows the low-temperature specific heat (Cp) results at zero field and 9 T plotted as Cp/T versus T2. The zero-filed Cp data shows a distinct jump below 5.20 K, which is very close to Tc. This anomaly is suppressed completely under 9 T, which allows us to analysis the normal-state data by the Debye model
where
γ is the Sommerfield coefficient and
β(
δ) is the phonon specific-heat coefficient. The best fit yields
γ = 11.8 mJ mol
−1 K
−2,
β = 0.29 mJ mol
−1 K
−4, and
δ = 0.0027 mJ mol
−1 K
−6. Then the Debye temperature
ΘD is calculated to be 275 K using the equation
where
N = 3 is the number of atoms in the formula and
R = 8.314 J mol
−1 K
−1 is the molar gas constant. Once
ΘD is known, the electron–phonon coupling strength
λep is estimated to 0.65 based on the inverted McMillan formula
38| | 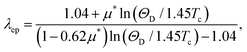 | (9) |
where
μ* = 0.13 is the Coulomb repulsion pseudopotential. Using the formula
| | 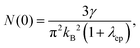 | (10) |
the bare density of states at the Fermi level
N(0) is found to be 3.04 states eV
−1 f.u.
−1. After subtraction of the phonon contribution, the normalized electronic specific heat
Cel/
γT is shown in
Fig. 6(b). The entropy conversing construction of the
Cp anomaly (blue dashed line) yields Δ
C/
γT = 1.37, close to the BCS value of 1.43.
39 Indeed, The temperature dependence of
Cel/
γT below the peak is well reproduced by the BCS theory with a zero-temperature gap value Δ(0) = 0.73 meV (red solid line). This, together with the magnitude of
λep, implies that ThIrGe is a fully gapped
s-wave superconductor in the weak coupling regime. The obtained normal-state and superconducting parameters are listed in
Table 3.
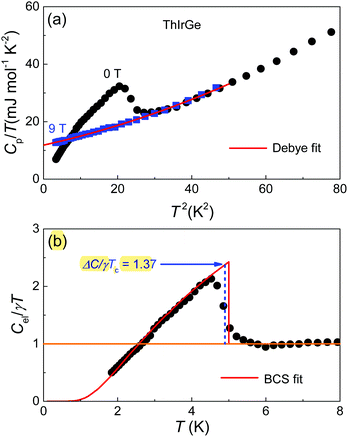 |
| | Fig. 6 (a) Low-temperature Cp/T data measured under 0 and 9 T plotted as a function of T2 for the ThIrGe sample. The red solid line is a Debye fit to the data. (b) Temperature dependence of normalized electronic specific heat at 0 T. The red solid line is the theoretical curve from the weak coupling BCS theory. The blue dashed line and arrow demonstrate the specific heat jump ΔC/γTc value based on entropy conserving construction. | |
Table 3 Normal-state and superconducting parameters of ThIrGe
| Parameter |
Unit |
ThIrGe |
|
T
c
|
K |
5.25 |
|
B
c1(0) |
mT |
12.8 |
|
B
c2(0) |
T |
2.9 |
|
ξ
GL(0) |
Å |
107 |
|
λ
GL
|
Å |
2120 |
|
κ
GL
|
— |
19.9 |
|
γ
|
mJ mol−1 K−2 |
11.8 |
|
β
|
mJ mol−1 K−4 |
0.29 |
|
Θ
D
|
K |
275 |
| ΔC/γTc |
— |
1.37 |
|
λ
ep
|
— |
0.65 |
3.3 Electronic band structure
Fig. 7(a) shows the electronic band structure for ThIrGe based on first-principles calculations both without and with SOC. In the absence of SOC, there are multiple bands crossing the Fermi level (EF), consistent with the metallic nature of this material. Turning on the SOC results in a significant change in the band dispersion near EF. In particular, the SOC splitting reaches about 0.16 eV, and 0.17 eV along Γ–Z and Z–U lines, respectively. As a consequence, the theoretical N(0) increases from 2.91 states eV−1 f.u.−1 without SOC to 3.22 states eV−1 f.u.−1 after switching on SOC, as seen in Fig. 7(b). While the N(0) from Cp measurement lies between these two values, it is obviously larger than the one without SOC, suggesting that the DOS at EF is indeed enhanced by the SOC. The projected DOS on atomic orbitals without and with SOC are displayed in Fig. 7(c) and (d), respectively. In both cases, the DOS for E − EF between −4 and −1 eV are dominated by the 5d orbital of Ir atoms. Nevertheless, as E moves closer to EF, the hybridization between the orbitals of Th, Ir and Ge becomes significant. At EF, the contribution of Th orbitals is nearly equal to that of Ir orbitals and twice that of the Ge orbitals. In the E range of 0.5 to 2 eV above EF, the contribution form Th orbitals dominates over that from Ir orbitals while the contribution from Ge orbitals is diminished. These results clearly indicate that ThIrGe is a multiorbital system with nonnegligile spin–orbit interaction.
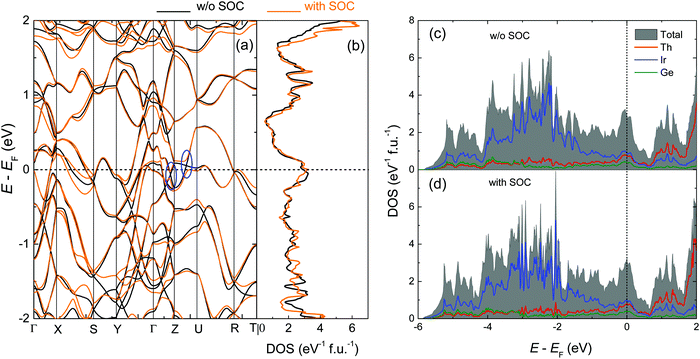 |
| | Fig. 7 (a) The electronic band structure of ThIrGe without (black) and with (orange) SOC. (b) Corresponding total density of states plotted as a function of energy. The horizontal dashed line indicates the position of Fermi level. (c and d) The projected density of states for ThIrGe without and with SOC, respectively. The vertical dashed line indicates the position of Fermi level. | |
3.4 Comparison between the Gibbs formation energies of ThIrGe and ThIrSi
From the above results, it is clear that while ThIrGe is isoelectronic to ThIrSi, their crystal structures are very different. To gain insight into this issue, we examine the Gibbs formation energy ΔGform of these compounds in both the TiNiSi-type and LaPtSi-type structures according to the following reaction:| | | Th(s) + Ir(s) + Si(Ge)(s) → ThIrSi(Ge)(s). | (11) |
Here ΔGform is obtained by evaluating the free-energy differences between the subsystems involved in the reaction, which is expressed as40| | | ΔGform = G[ThIrSi(Ge)] − G[Th] − G[Ir] − G[Si(Ge)], | (12) |
where G is the free energy of each subsystem. Since we deal with bulk samples, the entropy and zero-point energy effects are neglected41 and G can be estimated from first principles calculations. The obtained ΔGform values are summarized in Fig. 8 for better elucidation. As can be seen, ΔGform = −308.3 kJ mol−1 for ThIrSi in the LaPtSi-type structure, which is lower than that of −294.8 kJ mol−1 in TiNiSi-type structure. The situation is opposite for ThIrGe, where ΔGform is lower in the TiNiSi-type structure (−275.6 kJ mol−1) than in the LaPtSi-type structure (−267.8 kJ mol−1). These results indicate that ThIrSi and ThIrGe are energetically more stable in the LaPtSi-type and TiNiSi-type structures, respectively, in excellent agreement with the experimental observation. In this respect, it is of future interest to see whether ΔGform can be generally applicable to predict the crystal structure of MM′X compounds.
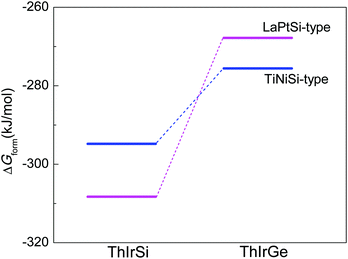 |
| | Fig. 8 The Gibbs formation energies for ThIrSi and ThIrGe in both the TiNiSi-type and LaPtSi-type structures. The two dashed lines are a guide to the eyes. | |
4 Conclusions
In summary, we have synthesized and characterized a new intermetallic germanide ThIrGe. Structural analyses indicate that this compound adopts the orthorhombic TiNiSi-type structure, which is the first example of this structural type for Th-based ternary equiatomic intermetallics. Furthermore, ThIrGe is discovered to be a bulk type-II superconductor below 5.25 K with a BCS-like superconducting gap. Theoretical calculations reveal that a notable hybridization between the Th, Ir and Ge orbitals is present at the Fermi level and the corresponding density of states are enhanced by the spin–orbit interaction. In addition, we show that the structural difference between ThIrGe and ThIrSi is consistent with comparison between the Gibbs formation energy of these materials in both structures. Our results not only provide an isostructural nonmagnetic reference to UIrGe, but also help to better understand both the structural and superconducting behavior in the family of ternary equiatomic compounds.
Conflicts of interest
The authors declare no competing interests.
Acknowledgements
We acknowledge financial support by the foundation of Westlake University. The work at Zhejiang University is supported by National Key Research Development Program of China (No. 2017YFA0303002).
Notes and references
- V. Johnson and W. Jeitschko, Ternary equiatomic transition metal silicides and germanides, J. Solid State Chem., 1972, 4, 123–130 CrossRef CAS.
- E. Hovestreydt, N. Engel, K. Klepp, B. Chabot and E. Parthe, Equiatomic ternary rare earth-transition metal silicides, germanides and gallides, J. Less-Common Met., 1982, 85, 247–274 CrossRef CAS.
- R. Muller, R. Shelton, J. Richardson Jr and R. Jacobson, Superconductivity and crystal structure of a new class of ternary transition metal phosphides TT/t′P (T = V, Zr, Nb, Ta and T/t′ = V, Ru, Rh), J. Less-Common Met., 1983, 92, 177–183 CrossRef.
- G. S. Rao, K. Wagner, G. Balakrishnan, J. Janaki, W. Paulus, R. Schollhorn, V. Subramanian and U. Poppe, Structure and superconductivity studies on ternary equiatomic silicides, MM′Si, Mater. Sci. Bull., 1985, 7, 215–228 CrossRef CAS.
- F. Canepa, P. Manfrinetti, M. Pani and A. Palenzona, Structural and transport properties of some UTX compounds where T = Fe, Co, Ni and X = Si, Ge, J. Alloys Compd., 1996, 234, 225–230 CrossRef CAS.
- P. R. Zhang, H. Q. Yuan and C. Cao, Electron-phonon coupling and nontrivial band topology in noncentrosymmetric superconductors LaNiSi, LaPtSi, and LaPtGe, Phys. Rev. B, 2020, 101, 245145 CrossRef CAS.
- L. Havela, M. Divis, V. Sechovsky, A. Andreev, F. Honda, G. Oomi, Y. Meresse and S. Heathman, U ternaries with ZrNiAl structure-Lattice properties, J. Alloys Compd., 2001, 322, 7–13 CrossRef CAS.
- G. A. Landrum, R. Hoffmann, J. Evers and H. Boysen, The TiNiSi family of compounds: structure and bonding, Inorg. Chem., 1998, 37, 5754–5763 CrossRef CAS.
- S. Ramakrishnan, K. Ghosh, A. D. Chinchure, V. Marathe and G. Chandra, Magnetism and superconductivity in RPtSi (R = La, Ce, Nd, and Sm), Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 6784 CrossRef CAS PubMed.
- A. O. Oliynyk, L. A. Adutwum, B. W. Rudyk, H. Pisavadia, S. Lotfi, V. Hlukhyy, J. J. Harynuk, A. Mar and J. Brgoch, Disentangling structural confusion through machine learning: structure prediction and polymorphism of equiatomic ternary phases ABC, J. Am. Chem. Soc., 2017, 139, 17870–17881 CrossRef CAS PubMed.
- G. J. Miller and J. Cheng, Ternary Metal-Rich Phosphides: Structure, Bonding, and Site Preferences in ZrNbP and Hf1+xMo1−xP, Inorg. Chem., 1995, 34, 2962–2968 CrossRef CAS.
- K. Klepp and E. Parthe, RPtSi phases (R = La, Ce, Pr, Nd, Sm and Gd) with an ordered ThSi2 derivative structure, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 38, 1105–1108 CrossRef.
- R. Troc and V. Tran, Magnetic properties of UT(Si,Ge) series, J. Magn. Magn. Mater., 1988, 73, 389–397 CrossRef CAS.
- T. Ueda, D. Honda, T. Shiromoto, N. Metoki, F. Honda, K. Kaneko, Y. Haga, T. D. Matsuda, T. Takeuchi, A. Thamizhavel, K. Sugiyama, K. Kindo, R. Settai and Y. Onuki, Magnetic property and pressure effect of a single crystal CeRhGe, J. Phys. Soc. Jpn., 2005, 74, 2836–2842 CrossRef CAS.
- F. Kneidinger, I. Zeiringer, A. Siderenko, E. Bauer, H. Michor, P. Rogl and J. Sereni, Physical properties of CeIrSi with trillium-lattice frustrated magnetism, Phys. Rev. B, 2019, 100, 134442 CrossRef CAS.
- W. Lee and R. Shelton, CePtSi: a new heavy-fermion compound, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 5369 CrossRef CAS PubMed.
- A. Ramirez, B. Batlogg and E. Bucher, Magnetothermal properties of UIrGe and systematic trends in magnetic heavy fermion compounds, J. Appl. Phys., 1987, 61, 3189–3190 CrossRef CAS.
- W. Lee, F. Yang, C. Shih and H. Yang, Crystal structure and superconductivity in the Ni-based ternary compound LaNiSi, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 6523 CrossRef PubMed.
- N. Huy, A. Gasparini, D. De Nijs, Y. Huang, J. Klaasse, T. Gortenmulder, A. de Visser, A. Hamann, T. Gorlach and H. V. Lohneysen, Superconductivity on the border of weak itinerant ferromagnetism in UCoGe, Phys. Rev. Lett., 2007, 99, 067006 CrossRef CAS PubMed.
- D. Aoki, A. Huxley, E. Ressouche, D. Braithwaite, J. Flouquet, J.-P. Brison, E. Lhotel and C. Paulsen, Coexistence of superconductivity and ferromagnetism in URhGe, Nature, 2001, 413, 613–616 CrossRef CAS PubMed.
- Y. P. Qi, J. G. Guo, H. C. Lei, Z. W. Xiao, T. Kamiya and H. Hosono, Superconductivity in noncentrosymmetric ternary equiatomic pnictides LaMP (M = Ir and Rh; P = P and As), Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 024517 CrossRef.
- Y. Okamoto, T. Inohara, Y. Yamakawa, A. Yamakage and K. Takenaka, Superconductivity in the hexagonal ternary phosphide ScIrP, J. Phys. Soc. Jpn., 2016, 85, 013704 CrossRef.
- K. Domieracki and D. Kaczorowski, Superconductivity in a non-centrosymmetric compound ThCoSi, J. Alloys Compd., 2016, 688, 206–210 CrossRef CAS.
- D. Singh, P. Biswas, A. Hillier and R. Singh,
et al., Superconducting properties of the noncentrosymmetric superconductor LaPtGe, Phys. Rev. B, 2018, 98, 214505 CrossRef.
- T. Hattori, Y. Ihara, Y. Nakai, K. Ishida, Y. Tada, S. Fujimoto, N. Kawakami, E. Osaki, K. Deguchi, N. Sato and I. Satoh, Superconductivity induced by longitudinal ferromagnetic fluctuations in UCoGe, Phys. Rev. Lett., 2012, 108, 066403 CrossRef CAS PubMed.
- B. Chevalier, B. Lloret, P. Gravereau, B. Buffat and J. Etourneau, Kondo fluctuations and magnetism in the new equiatomic ternary compounds UIrSi and UIrGe, J. Magn. Magn. Mater., 1988, 75, 13–18 CrossRef CAS.
- P. Manfrinetti, A. Palenzona, S. Dhar and C. Mitra, Structure and properties of some new Th compounds, Intermetallics, 1999, 7, 1291–1294 CrossRef CAS.
- A. Ptok, K. Domieracki, K. Kapcia, J. Lazewski, P. Jochym, M. Sternik, P. Piekarz and D. Kaczorowski, Electronic and lattice properties of noncentrosymmetric superconductors ThTSi (T = Co, Ir, Ni, and Pt), Phys. Rev. B, 2019, 100, 165130 CrossRef CAS.
- B. H. Toby, EXPGUI, a graphical user interface for GSAS, J. Appl. Crystallogr., 2001, 34, 210–213 CrossRef CAS.
- G. Kresse and J. Furthmuller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- G. R. Xiao, S. Q. Wu, B. Z. Li, B. Liu, J. F. Wu, Y. W. Cui, Q. Q. Zhu, G. H. Cao and Z. Ren, Normal-state and superconducting properties of the cubic Laves phase ThIr2, Intermetallics, 2021, 128, 106993 CrossRef CAS.
- T. Geballe, B. Matthias, V. Compton, E. Corenzwit, G. Hull Jr and L. D. Longinotti, Superconductivity in binary alloy systems of the rare earths and of thorium with Pt-group metals, Phys. Rev., 1965, 137, A119 CrossRef.
- X. Wang, C. B. J. Etourneau and P. Hagenmuller, Crystal structure and superconductivity of new ternary MTGe germanides (M = Ti, Zr, Hf and T = Ru, Os, Rh, Ir), Mater. Res. Bull., 1987, 22, 331 CrossRef CAS.
- N. Werthamer, E. Helfand and P. Hohenberg, Temperature and purity dependence of the superconducting critical field, Hc2. III. Electron spin and spin-orbit effects, Phys. Rev., 1966, 147, 295 CrossRef CAS.
- A. M. Clogston, Upper limit for the critical field in hard superconductors, Phys. Rev. Lett., 1962, 9, 266 CrossRef.
- C.-R. Hu, Numerical constants for isolated vortices in superconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 6, 1756 CrossRef.
- W. McMillan, Transition temperature of strong-coupled superconductors, Phys. Rev., 1968, 167, 331 CrossRef CAS.
- J. Bardeen, L. N. Cooper and J. R. Schrieffer, Therory of Superconductivity, Phys. Rev., 1957, 108, 1175 CrossRef CAS.
- J. I. Martinez, H. A. Hansen, J. Rossmeisl and J. K. Norskov, Formation energies of rutile metal dioxides using density functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 045120 CrossRef.
- M. Bollinger, K. W. Jacobsen and J. K. Norskov, Atomic and electronic structure of MoS2 nanoparticles, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 085410 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *bc
*bc
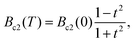
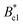 is determined as the field at which M(B) deviates from its initial linearity. The resulting temperature dependence of
is determined as the field at which M(B) deviates from its initial linearity. The resulting temperature dependence of 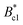 is displayed in Fig. 5(c) and can be well fitted by the mean-field equation:32
is displayed in Fig. 5(c) and can be well fitted by the mean-field equation:32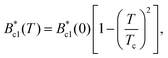
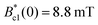 is the effective zero-temperature lower critical field. Since the demagnetization factor Nd is related to the slope of initial magnetization curve through the relation
is the effective zero-temperature lower critical field. Since the demagnetization factor Nd is related to the slope of initial magnetization curve through the relation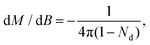
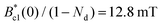 . In addition, the shielding and Meissner fractions after demagnetization correction are 104.5% and 13.5%, respectively, suggesting that superconductivity occurs in almost the whole sample volume.
. In addition, the shielding and Meissner fractions after demagnetization correction are 104.5% and 13.5%, respectively, suggesting that superconductivity occurs in almost the whole sample volume.