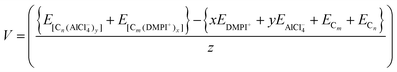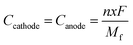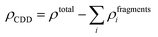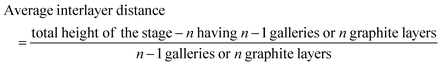DOI:
10.1039/D1MA00351H
(Paper)
Mater. Adv., 2021,
2, 5213-5223
Organic cation (DMPI) intercalated graphite anode for high voltage next generation dual-ion batteries†
Received
16th April 2021
, Accepted 24th June 2021
First published on 24th June 2021
Abstract
Developing advanced energy storage systems to address the intermittency of renewable energy sources is crucial for meeting ever-increasing energy demands. Among post lithium-ion battery systems, dual-ion batteries (DIBs) have shown bright prospects in developing low-cost and safe batteries with good electrochemical performance. Herein we have modelled, for the first time, organic cation intercalated graphite systems. Imidazolium based ionic liquid 2,3-dimethyl-1-propyl imidazolium chloride (DMPI-Cl) with the AlCl3 salt has been implemented as an electrolyte. Using first principles calculations, we have performed DMPI cation intercalation into the graphite anode based on different plausible staging mechanisms. The intercalation energy characteristics indicate favourable intercalation of DMPI into graphite following the staging mechanism, which has been further confirmed by a simulated X-ray diffraction study. A higher cell voltage (3.7–4.6 V range) comparable to lithium-ion batteries along with a maximum capacity of 62 mA h g−1 has been achieved. Charge transfer analysis presents +0.87 |e| charge transfer from DMPI to graphite, indicating DMPI cation intercalation into graphite during the charging process. Moreover, the metallic character of the DMPI cation intercalated graphite system and diffusion barrier as low as 0.2 eV suggest a constant electronic conductivity and better rate performance, respectively. Furthermore, we have explained the reason behind the inapplicability of the 1-ethyl-3-methyl imidazolium (EMI) cation as an organic cation for dual-graphite batteries and hence highlight the need to explore alternative ionic liquids. These results provide clear understanding of DMPI cation intercalation into graphite anodes and could be helpful in fabricating dual graphite electrode-based DIBs with better electrochemical performance compared to conventional DIBs using metal anodes.
1. Introduction
Increasing utilization of renewable energy sources, like wind, hydroelectric and solar power, is essential today for a sustainable economy. Due to the volatility, randomness, and intermittency in such energy sources, they cannot be directly deployed for uninterrupted power supply. As a result, development of highly efficient energy storage and conversion systems is required to assist with the widespread usage of portable electronic devices in daily life.1 Various types of rechargeable metal-ion batteries have been developed in the recent past such as Li-ion,2–4 Na-ion,5–7 Mg-ion,8,9 Zn-ion10,11 and Al-ion12,13 batteries. Among them, lithium-ion batteries (LIBs) have profoundly dominated the energy storage market due to their high output voltage and gravimetric capacity.2,4 However, using expensive transition metal oxides as cathode materials and less abundant Li metal as the anode may not be sustainable for large-scale application of LIBs in future.14,15 Moreover, the safety issues and thermal runaway events are major concerns that have not been completely resolved.16 Altogether, the high cost and the safety issues related with LIBs make them a less suitable choice for green energy storage. Hence, new materials like graphite are being explored to develop better performance low-cost batteries. Owing to its redox-amphoteric nature and layered structure, graphite can be reduced as well as oxidized by electrochemical reactions with proper cation/anion uptake and release. Thus, dual graphite batteries can be conceptualized, also called dual-ion batteries (DIBs), where both a graphite anode and cathode are involved in intercalation/deintercalation of cations and anions, respectively, during the charge/discharge cycle of a battery.17–20 In 1989, McCullough et al. first reported a DIB using graphite as both the cathode and anode along with the nonaqueous electrolyte of ClO4−.21 Graphite-based DIBs are considered as promising alternative rechargeable batteries because they have a high working voltage (4.5 V), better safety and lower cost compared to the conventional LIBs.22–25 In DIBs, the working principle is different from the rocking chair mechanism as in LIBs. Here, the cations and anions are both reversibly intercalated in the graphite anode and cathode simultaneously in the charging process, while the ions are deintercalated from graphite back to the electrolyte during the discharging process.26,27 Commonly used DIBs have lithium salts (like LiPF6 and LiTFSI) with organic solvents (ethylene carbonate and ethyl methyl carbonate) as an electrolyte, which faces several fatal problems like (i) electrolyte decomposition at a high working voltage (>4.5 V),28 (ii) graphite exfoliation due to solvent co-intercalation along with ion intercalation,28 and (iii) active battery material loss due to solid–electrolyte interphase (SEI) formation.29 Hence, compatible electrolytes and electrodes are required to reduce the exfoliation of graphite and replace lithium metal. Carlin et al. have presented room temperature ionic liquids (RTILs) as a better alternative to replace conventional volatile organic solvents.30
Ionic liquids (ILs) are low melting point salts and have emerged as an important part in electrochemistry to design new classes of electrolytes. ILs show several encouraging properties for electrochemical applications such as low vapour pressure, a broad electrochemical window, and higher ionic conductivity.31–33 A special feature of using ILs as electrolytes is that the electrochemical reaction is mainly driven due to their high oxidative and reductive stability and thus they possess a large electrochemical stability window.34–36 Several recent studies have considered DIBs involving IL electrolytes and revealed that the organic cations of ILs such as the 1-ethyl-3-methyl imidazolium cation (EMI+) and N-butyl-N-methyl pyrrolidinium (BMP+) can be intercalated into the graphite anode.37–39 The broad electrochemical stability window of ILs allows for a high cut-off charging voltage (4.0–5.0 V).37–39 Carlin and co-workers have also studied ILs composed of cations like 1-ethyl-3-methyl imidazolium (EMI+) and 2,3-dimethyl-1-propyl imidazolium (DMPI+) and anions such as CF3SO3−, AlCl4−, C6H5CO2−, PF6− and BF4− as electrolytes in dual ion batteries.25,30 Our previous reports have shown that the AlCl4 anion along with different IL based organic cations (imidazolium and pyrrolidinium) can be used as electrolytes in Al DIBs.33,40 Using organic cations as charge carriers has the added advantage of preventing unwanted co-intercalation of solvents into the graphite anode (as in the case of LiPF6) as well as diminished chances of solvent decomposition at high charging voltage.
Consequently, apart from the intercalation mechanism, there is a lack of clear molecular level understanding of the intercalation capacity and intercalated species for organic cation intercalation in graphite-like anodes. In this study, we have computationally modelled, for the first time, an organic cation intercalated graphite anode system successfully. We have chosen imidazolium-based IL 2,3-dimethyl-1-propyl imidazolium chloride (DMPI-Cl) with AlCl3 at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio as the electrolyte. We have investigated the intercalation mechanism by considering the staging manner of DMPI cation intercalation into the graphite anode. First principles calculations are performed for a systematic study of the structure, stability, electronic properties, and theoretical capacity along with the average voltage of the DMPI cation intercalated graphite electrode. Furthermore, we have also investigated the diffusion pathways of DMPI cations in the graphite system. Along with this, we have also explained why EMI+ cannot be used as an organic cation for dual-graphite battery research, although EMI based IL electrolytes are extensively used in battery technology.12,41,42 On the basis of the obtained theoretical insights, we believe that organic cation intercalated graphitic anodes could be utilised in DIBs to achieve better electrochemical features compared to DIBs using metal anodes, and our study would motivate further developments in cheaper dual graphite battery technology.
1 molar ratio as the electrolyte. We have investigated the intercalation mechanism by considering the staging manner of DMPI cation intercalation into the graphite anode. First principles calculations are performed for a systematic study of the structure, stability, electronic properties, and theoretical capacity along with the average voltage of the DMPI cation intercalated graphite electrode. Furthermore, we have also investigated the diffusion pathways of DMPI cations in the graphite system. Along with this, we have also explained why EMI+ cannot be used as an organic cation for dual-graphite battery research, although EMI based IL electrolytes are extensively used in battery technology.12,41,42 On the basis of the obtained theoretical insights, we believe that organic cation intercalated graphitic anodes could be utilised in DIBs to achieve better electrochemical features compared to DIBs using metal anodes, and our study would motivate further developments in cheaper dual graphite battery technology.
2. Computational details
First principles calculations have been performed using the Vienna Ab initio Simulation Package (VASP).43,44 All geometry optimizations and respective calculations have been performed using the generalized gradient approximation of the Perdew–Burke–Ernzerhof (GGA-PBE) functional.45 The projected augmented wave (PAW) method is used for treating the interaction between the ion core and valence electrons.46 An energy cut off of 470 eV has been implemented. During structural optimization, the Brillouin zone has been sampled with a Γ centered k-point grid of 11 × 11 × 5 for the unit cell and 2 × 2 × 1 for the considered supercells. All structures have been optimized with an energy criterion of 10−5 eV Å−1 and force criterion of ≤0.01 eV Å−1 for all the atoms to obtain full relaxation between the atomic and lattice positions. The DFT-D3 approach has also been considered for van der Waals corrections in our calculations.47 We have modelled four different stages for both the DMPI cation and AlCl4 anion intercalation process, where a 6 × 6 × 2 supercell of graphite containing 288 carbon atoms for the stage-1, stage-2 and stage-4 systems and a 6 × 6 × 3 supercell containing 432 carbon atoms for the stage-3 calculation have been chosen with the same concentration of both cations and anions. Density of states (DOS) calculations have been performed for a 4 × 4 × 1 supercell with a Γ centered k-point mesh of 9 × 9 × 1. Bader charge analysis has been performed using the Henkelman program to determine the quantitative charge transfer upon intercalation of the DMPI cation into graphite layers.48–50Ab Initio Molecular Dynamics (AIMD) simulations have been performed with the NVT ensemble for a broad temperature range of 300–600 K for a 5 picosecond (ps) timescale. The Nosé–Hoover thermostat51 with a Nosé mass parameter of 0.01 has been implemented to control the temperature fluctuations. The activation barriers for the DMPI cation diffusion pathways have been calculated using the climbing image nudged elastic band method (Cl-NEB).52 The minimum energy paths (MEPs) are initialized by considering six image structures between the fully optimized initial and final geometries with an energy convergence criterion of 10−3 eV. During the charging process, the net electrons obtained from the external circuit (with a very small time lag) induce the intercalation of DMPI cations, which subsequently transfer their charge, thereby reducing graphite. The reverse phenomenon is occurring for the AlCl4 anion transferring charge to consequently oxidise the graphite cathode. This time lag is very short compared to the time required to reach thermodynamic equilibrium of the DMPI–graphite system. Hence, in our DFT study we have considered a neutral system of both DMPI–graphite and AlCl4–graphite as we carry out our calculations in equilibrium conditions. Such consideration of neutral systems has yielded electrochemical performance results comparable to experimental reports in the past.27,54 Zero-point energy (ZPE) corrections have also been included for the diffusion barrier calculation using the formula 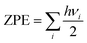 , where h is Planck's constant and vi is the vibrational frequency. The ZPE is calculated by considering the degrees of freedom of intercalated DMPI into the graphite system.
, where h is Planck's constant and vi is the vibrational frequency. The ZPE is calculated by considering the degrees of freedom of intercalated DMPI into the graphite system.
3. Results and discussion
3.1. Structural changes and stable binding sites
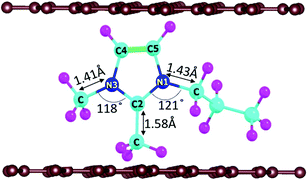
In DIBs, the cations (DMPI in our case, Scheme 1) and anions are reversibly intercalated/deintercalated from the cathode and anode in the charging/discharging process, respectively. Hence, it is important to study the structural changes upon intercalation. We have chosen two possibilities of DMPI cation intercalation in the graphite layer, where one is oriented perpendicular to the graphite layers and the other is parallel to the graphite layers (Fig. 1a and b).
 |
| | Scheme 1 Considered intercalant cation, 2,3-dimethyl-1-propyl imidazolium (DMPI), with labelled atoms. Here, the blue, cyan, magenta, and brown colours indicate N, C, H, and graphite layer carbon atoms, respectively. | |
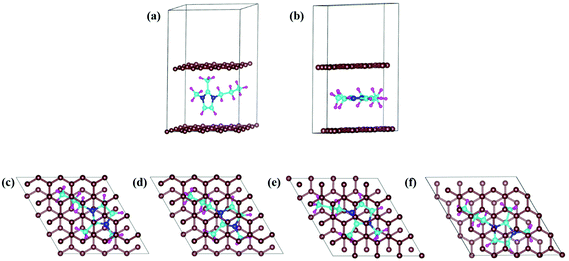 |
| | Fig. 1 DMPI intercalated structures: (a) perpendicular orientation, and (b) parallel orientation. Optimized structures of the DMPI intercalated system; (c) S1 (Top), (d) S2 (Bridge 1), (e) S3 (Bridge 2), and (f) S4 (Hollow). Here, the brown, blue, cyan, and magenta colours represent the graphite layer, and N, C, and H of the DMPI cation, respectively. | |
Owing to the strong van der Waals interaction between the imidazolium ring and graphite layers, the parallel orientation of the DMPI cation into the graphite layer is found to be stable. The perpendicular orientation shifts to parallel upon relaxation with the dispersion correction. However, without the vdW correction the perpendicular orientation is retained, which proves that the extensive interactions between π-stacked graphite and the parallel orientation (imidazole ring) of DMPI are responsible for this configuration being more stable. We have further investigated the structural distortions such as changes in bond lengths and bond angles obtained due to the anisotropic van der Waals interaction between layered graphite and the DMPI cation. Upon intercalation of DMPI, the ∠C2–N3–C bond angle decreases from 124° to 118°, and ∠C2–N1–C decreases from 126° to 121°. Similarly, bond length changes are also observed in intercalated DMPI, where the bond lengths of N1–C, N3–C and C2–C change to 1.43, 1.41 and 1.58 Å from 1.47, 1.34 and 1.48 Å in free DMPI, respectively. The alkyl group variance between DMPI and EMI is that extra methyl and propyl groups are present in the C2 and N1 positions for DMPI, respectively, compared to EMI. In our earlier report we have studied the effect of alkyl group variation in the N1 position of the imidazolium ring.33 But a fundamental understanding is required on the effect of addition of a methyl group in the C2 position of the imidazolium ring. So, with respect to the C2 position of DMPI, we have arranged four possible sites of binding in graphite layers, (i) S1 (Top), (ii) S2 (Bridge 1), (iii) S3 (Bridge 2) and (iv) S4 (Hollow), as shown in Fig. 1c–f. In the S1 (Top) site, C2 of DMPI occupies the top position of a C atom of graphite. In the S2 (Bridge 1) site, C2 occupies the bridging position between two non-bonded carbon atoms, whereas in the S3 site (Bridge 2) it occupies the bridging position of the C–C bond. Similarly, for the S4 (Hollow) site C2 occupies the centre of hexagons (C6) of the graphite layer. Our relative energy calculations in Table S1 (ESI†) show that the hollow site with respect to the C2 position is most stable for DMPI cation binding into the graphite layers. Particularly, the hollow and top site have a very small (0.009 eV) relative energy difference. Hence, there is a high possibility of the equilibrium existence of both hollow and top sites. We have carried out AIMD simulations to verify the thermal stability of the DMPI cation intercalated graphite system as well as the equilibrium existence of both hollow and top binding sites. Upon AIMD simulation at 300 K for 5 ps, we have observed that, while the AB stacking of graphite layers is unaltered, the intercalated DMPI cation shifts from the most stable site (Hollow) to the second most stable (Top) site of binding as shown in Fig. S1 (ESI†). Owing to the very small energy difference (∼0.009 eV), these structures can change the adsorption sites at the expense of thermal energy (3/2 kBT = 0.03 eV, where kB and T are Boltzmann's constant and temperature, respectively). As the calculated relative energies are less than the DFT intrinsic error, therefore all binding sites are equally accessible and DMPI can keep on changing binding sites. This has also been observed during the AIMD simulation as shown in Fig. S2 (ESI†). For sites B1 and B2, the relative energies are 0.04 and 0.05 eV, respectively, which are higher than the thermal energy (0.03 eV). Upon further simulation of DMPI bonded at the most stable hollow site of graphene at 300–600 K, the system was found to be stable (Fig. S3, ESI†). The bond lengths and bond angles of the DMPI cation do not change significantly, although the position and orientation of DMPI do fluctuate a little. Hence, from the simulation study we could confirm that these two sites (Hollow and Top) are equally stable, and we have considered the hollow site for our further studies.
3.2. Model system
In DIBs, graphite intercalation compounds (GICs) are formed between the graphite layer and intercalant species.53 The formation of GICs follows a systematic staging mechanism of intercalant insertion based on various competing interactions among the intercalate and intercalant. The van der Waals interaction between the parallelly stacked graphite layers needs to be overcome by the incoming DMPI cations. Again, the intercalated DMPI cations may experience intermolecular repulsive forces among themselves. Hence, the intercalation phenomena can proceed by maintaining a balance among these competing forces.54–57 Consequently, different stages of intercalation can be considered to occur during the charging/discharging process, which has been observed experimentally,55,58 as well as theoretically.54,56 The staging features can be represented by the stage index, which stands for the number of unintercalated graphene layers present between the intercalated layers. The stage-n system refers to the “n” number of graphene sheets or “n − 1” empty host galleries present between two intercalated layers. For instance, stage-1 GICs correspond to intercalation happening after every graphene layer, while in stage-2 intercalation will happen after a gap of two empty layers. In this manner, different stages are expected in DIBs during intercalation of DMPI cations into graphite. Hence, we have chosen the four most favourable intercalation stages for the same DMPI cation concentration. For that we have modelled a 6 × 6 × 2 supercell of graphite containing 288 carbon atoms for the stage-1, stage-2 and stage-4 systems and their corresponding relative energies have been compared as shown in Fig. 2. The stage-2 configuration is observed to be the most stable for DMPI cation intercalation, followed by stage-4 and stage-1 for the same concentration of DMPI cations. The energy required to overcome the repulsive forces between intercalant species is less than the energy required to overcome the van der Waals forces between graphite layers required for gallery height opening for intercalation. Hence, DMPI intercalation favours stage-2 rather than stage-1. Stage-4 is less stable than stage-2, which may be due to the van der Waals repulsion among the long carbon chains of four DMPI cations intercalated into a single graphene layer rather than two DMPI intercalated in two separate layers as in stage-2. Upon increasing the number of DMPI cations intercalating to 8, the relative energy difference between stage-1 and stage-2 intercalation decreases (Fig. S4, ESI†), thus indicating that stage-1 would be more stable compared to the other stages for higher concentrations of the DMPI cation. Owing to the different supercell size of stage-3, the result is not comparable to the other stages. However, the DMPI intercalation mechanism is followed during charging, and the same deintercalation mechanism is followed at the time of the discharging process. Overall, from the theoretical stability calculation, we could describe the formation of different DMPI cation intercalated stages.
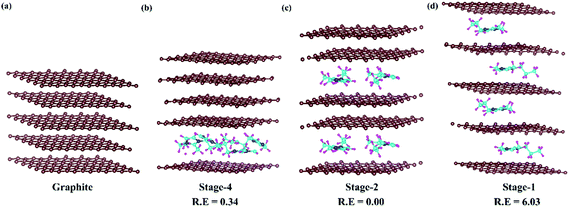 |
| | Fig. 2 Systematic representation of (a) pristine graphite and the staging mechanism of DMPI cation intercalation, (b) stage-4, (c) stage-2 and (d) stage-1. R. E is in eV units. Here, the brown, blue, cyan and magenta colours represent the graphite layer, and N, C, and H of the DMPI cation, respectively. | |
Furthermore, we have considered the maximum possible intercalation in our supercells for each stage. A 6 × 6 × 3 supercell containing 432 carbon atoms has been chosen for the stage-3 calculation. In the case of stage-1, a 288 carbon containing graphite system can intercalate a maximum of 16 DMPI cations to give a stable GIC, which can be represented by the formula unit [C288(DMPI)16]. Other lower stoichiometry of DMPI has been chosen such as 4, 8 and 12 per 288 carbon atoms of graphite, maintaining the criteria of stage-1 characteristics. Thus, the generalised formula unit would be [C288(DMPI)n] where the n values are 4, 8, 12, and 16 for stage-1. Similarly, for the other stages formula units have been considered such as n = 2, 4, 6, and 8 for stage-2; and n = 1, 2, 3, and 4 for stage-4. For stage-3, the formula unit would be [C432(DMPI)n] where n = 2, 4, 6, and 8 DMPI. All optimised structures have been provided in the ESI† (Fig. S5–S8). Overall, from the different considered stoichiometries, we have tried to get an idea about the maximum storage capacity of these systems and compared our results with experimental reports to investigate more about the staging mechanism followed by DMPI cation intercalation in graphite, Fig. 3.25
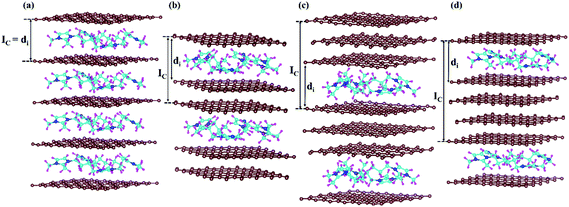 |
| | Fig. 3 Schematic representation of all optimised structures of the four different DMPI cation intercalated systems, (a) stage-1, (b) stage-2, (c) stage-3 and (d) stage-4, where Ic and di are the periodic repeating distance and intercalant gallery height, respectively, and the brown, blue, cyan, and magenta colours represent the graphite layer, and N, C, and H of the DMPI cation, respectively. | |
3.3. Binding energy
The binding energy is a good criterion to investigate the stability of intercalated graphite systems. We have calculated the binding energy for various numbers of DMPI intercalation into graphite following different staging mechanisms, using the following equation| |  | (1) |
where x is the number of DMPI cations, and E[(DMPI)xCm], ECm and EDMPI are the total energies of the DMPI intercalated graphite system, the bulk graphite system and a single DMPI cation, respectively. Hence, a more negative binding energy value indicates the more feasible intercalation of the DMPI cation into the graphite system as shown in Table 1. At a low concentration of DMPI cations (4 DMPI), intercalation into graphite is less favourable for every stage with lower binding energy (∼2.5 eV) compared to intercalation at higher concentrations. This low binding energy may be due to the activation barrier which needs to be overcome during gallery height opening against the interplanar van der Waals interactions among graphite layers. Further DMPI cation intercalation into the already opened galleries becomes more feasible in the case of each stage with higher calculated binding energies. This phenomenon is also reported in several experimental studies on DIBs, where the experimental coulombic efficiency is very poor in the first few cycles.25,27 Moreover, the binding energy (∼−3.5 eV) of DMPI cation intercalation is found to be higher than anion (AlCl4−: −1.5 eV; PF6−: −2.9 eV) binding in graphite, which is possibly due to the π–π interaction between the DMPI imidazolium ring and the graphite layers.54,55 However, upon approaching maximum DMPI cation intercalation the binding energy again decreases for each stage, which could be due to the electrostatic repulsion between neighbouring DMPI cations in the same gallery. As the binding energy value is still negative, the effective repulsive forces between cations must be less than the attractive forces due to intercalation. In an experimental report by Lv et al., a higher cut-off working voltage has been considered to maintain better coulombic efficiency, which could be due to our calculated high binding energies (2.4–4.5 eV) for DMPI cation intercalation in the graphite anode for all the possible stages.25 Additionally, we have also tried to address the advantage of using DMPI rather than EMI for intercalation into the graphitic anode for dual graphite batteries. We have calculated the binding energy of EMI cation intercalated graphite layers. Our calculated low binding energy (+0.007 eV for stage-1) for EMI cation intercalation validates the infeasibility of using EMI with graphite anodes, which has been reported experimentally.59 Hence, very poor electrochemical performance is observed which can be ascribed to the lack of alkyl substituents in the C2 position of the imidazolium ring of the EMI cation. The imidazolium cations with protons in the C2 position are less stable inside the graphite layers. This observation can be explained by applying natural bond orbital (NBO) charge calculations,60 where the C2 carbon of DMPI has almost double the charge (0.493 |e|) of the C2 carbon (0.288 |e|) of EMI (Fig. S9, ESI†). So, the resultant interaction of DMPI–graphite is more compared to EMI–graphite. This is also reflected in the experimental XRD studies, where any characteristic peak is absent for the EMI–graphite system.59 Overall, from the binding energy calculations, we can conclude that the DMPI cation has fair binding strength, which is essential in DIBs, and graphite can be used as a potential anode.
Table 1 Binding energy per DMPI cation (eV) and interlayer distance (Å) for all the stages with different concentrations
| Stages |
No. of DMPI cations |
Binding energy (eV) |
Interlayer distance (Å) |
| 1 |
4 |
−2.48 |
6.92 |
| 8 |
−3.58 |
7.14 |
| 12 |
−3.90 |
7.16 |
| 16 |
−3.59 |
7.54 |
| 2 |
2 |
−2.51 |
5.23 |
| 4 |
−3.99 |
5.30 |
| 6 |
−4.01 |
5.39 |
| 8 |
−3.80 |
5.53 |
| 3 |
2 |
−2.45 |
4.64 |
| 4 |
−4.04 |
4.61 |
| 6 |
−4.26 |
4.71 |
| 8 |
−3.76 |
5.03 |
| 4 |
1 |
−2.64 |
4.37 |
| 2 |
−4.17 |
4.39 |
| 3 |
−4.54 |
4.38 |
| 4 |
−3.90 |
4.47 |
3.4. Staging mechanism and XRD analysis
To determine the staging mechanism actually occurring during DMPI intercalation into graphite, we have simulated XRD patterns for our optimised intercalated systems. We have compared our simulated XRD patterns with the experimental results.25 We notice that the graphite structure gets deformed upon intercalation of the DMPI cations along with an increase in the interlayer spacing. As the gallery height (3.35 Å) of graphite is less than the DMPI cation size (4.6 Å),61 the graphite interlayer spacing increases in the very first intercalation step. After the intercalation of DMPI cations, the average gallery height expansion in graphite is found to be 115%, which is comparable to reports of various anion intercalation in graphite.54,55 The average interlayer distance can be calculated by the formula,
The average interlayer distance for all the stages has been included in Table 1. The distance between two layers of DMPI intercalated graphite i.e., the intercalant gallery height (di) remains similar (∼7.1–7.6 Å) for all the stages, which is comparable with the experimental report (7.16 Å) for DMPI intercalation.59 Our simulated XRD pattern of the DMPI intercalated system for all the stages (n = 1–4), as shown in Fig. 4, helps to understand the structural changes in the graphite system. The XRD patterns suggest the structural changes in graphite upon intercalation with characteristic shifting of the (002) peak of graphite. To index the stage number (n) of the GICs, two characteristic peaks are observed, the (00n + 1) and (00n + 2) planes along the stacking direction, in the XRD analysis. d00n+1 represents the spacing between adjacent layers. The intercalant gallery height (di), gallery expansion (Δd) and periodic repeating distance (Ic) of a particular stage index ‘n’ are calculated using the d-spacing values as 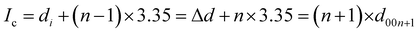 , and similarly for d00n+2, Ic = (n + 2) × d00n+2, where Δd = di − 3.35 and 3.35 Å is the interlayer distance between two consecutive graphite layers.62 In the case of pristine graphite an intense peak is found at 2θ = 26.5° belonging to its (002) plane generally.12 For our simulated XRD pattern, we can identify such a peak at 26.16° for the pristine system which shifts to 25.88°, 25.18°, 25.75° and 24.96° for stage-1, stage-2, stage-3 and stage-4 intercalation, respectively, as shown in Fig. 4. As the distortion and lateral displacement in the graphite layer stacking increase with an increase in the DMPI intercalation, other intense peaks belonging to various planes can also be identified at lower ranges of 2θ in the XRD plot as presented in Fig. S10 (ESI†). In the previous report of experimental DMPI intercalation by Lv et al., the (002) peak of the system was found to shift from 2θ = 26.4° for pristine graphite to 2θ = 26.0° for the GIC.25 Consequently, from our XRD plots we can suggest that stage-1 intercalation (2θ = 25.88°) of the DMPI cation in graphite occurs predominantly (Fig. S4, ESI†), which also agrees with an experimental study by Sutto et al.59
, and similarly for d00n+2, Ic = (n + 2) × d00n+2, where Δd = di − 3.35 and 3.35 Å is the interlayer distance between two consecutive graphite layers.62 In the case of pristine graphite an intense peak is found at 2θ = 26.5° belonging to its (002) plane generally.12 For our simulated XRD pattern, we can identify such a peak at 26.16° for the pristine system which shifts to 25.88°, 25.18°, 25.75° and 24.96° for stage-1, stage-2, stage-3 and stage-4 intercalation, respectively, as shown in Fig. 4. As the distortion and lateral displacement in the graphite layer stacking increase with an increase in the DMPI intercalation, other intense peaks belonging to various planes can also be identified at lower ranges of 2θ in the XRD plot as presented in Fig. S10 (ESI†). In the previous report of experimental DMPI intercalation by Lv et al., the (002) peak of the system was found to shift from 2θ = 26.4° for pristine graphite to 2θ = 26.0° for the GIC.25 Consequently, from our XRD plots we can suggest that stage-1 intercalation (2θ = 25.88°) of the DMPI cation in graphite occurs predominantly (Fig. S4, ESI†), which also agrees with an experimental study by Sutto et al.59
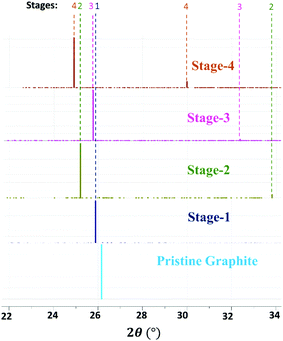 |
| | Fig. 4 Schematic diagram of the simulated XRD pattern of pristine graphite and different stages of DMPI intercalated systems where 2θ ranges from 22 to 34°. | |
3.5. Electrochemical properties
In this section, we have discussed the electrochemical performance of a DIB with dual-graphite electrodes, where DMPI cations are paired with AlCl4 anions. Upon charging, the DMPI cations and AlCl4 anions are expected to undergo intercalation into the graphite anode and cathode, respectively, while during discharging both the ions are expected to diffuse back to the electrolyte. Hence, to investigate the electrochemical properties of DMPI with the graphite anode, it is necessary to also include the AlCl4 anion intercalation into the graphite cathode.
3.5.1. AlCl4 intercalation into the graphite cathode.
The anion intercalation phenomenon for layered structures like graphite electrodes has been well studied both theoretically and experimentally.12,54 Our previous study has also established the exact staging mechanism pathway for AlCl4 anion intercalation into the graphite cathode.54 Motivated by those studies, we have modelled four stages (n = 1–4) for AlCl4 anion intercalation keeping the concentration of AlCl4 anions fixed. From our relative energy calculations, we could confirm that in the initial period of the charging process stage-4 AlCl4 intercalation is more favourable (Fig. S11, ESI†). From our simulated XRD data, we could identify the (005) and (006) planes at 2θ = 23.32° and 28.07° with a d-spacing of 3.81 and 3.17 Å, respectively. For the experimental diffraction patterns, 2θ values are obtained at 23.7° and 28.5° with a d-spacing of 3.77 and 3.15 Å, which are comparable with our simulated patterns.12
3.5.2. Voltage calculations.
The open circuit voltage (OCV) is one of the most important parameters in deciding on a suitable battery, which stands for the output voltage of a battery at full intercalation capacity or at full charge in other words. In the DIB system, the IL electrolytes (DMPI–AlCl4) behave not only as a charge carrier but also as an active material towards electrochemical activity. The OCV depends upon both the cathode and anode reactions of the DIB system. The discharge voltage can be calculated from the following cathodic and anodic reactions,| | | Cathode reaction: Cn (AlCl4)y + e− ↔ Cn + yAlCl4− | (2) |
| | | Anode reaction: Cm (DMPI)x ↔ Cm + xDMPI+ + e− | (3) |
| | | Overall: Cm (DMPI)x + Cn (AlCl4)y ↔ xDMPI+ + yAlCl4− + Cm + Cn | (4) |
where x and y are the number of DMPI cations and AlCl4 anions, respectively. Cm and Cn are the graphite anode and graphite cathode, respectively. From the above reaction it is evident that the reaction mechanism of the DIB also includes a contribution from the electrolyte medium.
The cell voltage (V) can be calculated from the Nernst equation, 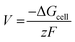 , where z and F are the number of electrons transferred and the Faraday constant, respectively, while ΔGcell is the change in Gibbs free energy during the chemical reactions.
, where z and F are the number of electrons transferred and the Faraday constant, respectively, while ΔGcell is the change in Gibbs free energy during the chemical reactions.
| ΔGcell = ΔHcell − TΔScell; ΔGcell = ΔEcell + PΔVcell − TΔScell |
As our calculations are performed at a 0 K temperature, so the changes in volume (Δ
Vcell) and entropy (Δ
Scell) of the reactions are negligible. Thus, the Gibbs free energy change only depends upon the change of internal energy (Δ
Ecell).
Therefore, the internal energy change of the overall reaction would be,
| | | ΔEcell = {xEDMPI+ + yEAlCl4− + ECm + ECn} − {E[Cn(AlCl4−)y] + E[Cm(DMPI+)x]} | (5) |
where
E[Cn(AlCl4−)y],
E[Cm(DMPI+)x],
EAlCl4− and
EDMPI+ are the total energy of the AlCl
4 intercalated graphite system and DMPI intercalated graphite system, and the AlCl
4 and DMPI fragments, respectively.
ECm and
ECn are the total energy of the graphite system.
EAlCl4− and
EDMPI+ are calculated by optimizing the AlCl
4 anions and DMPI cations as a molecular species due to the nonavailability of their crystal structure.
Then the average voltage would be,
| | 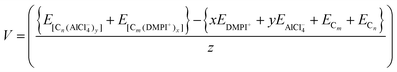 | (6) |
To understand the exact mechanism of intercalation in a DMPI–AlCl
4 DIB, we have considered the different staging intercalation behaviour of both cations and anions at the initial and final periods of the charging process. Therefore, based on our model we have considered all combinations of staging behaviour possible upon intercalating four cations and anions into the graphite anode and cathode to replicate the initial charging environment, which is presented in
Table 2. The highest calculated voltage is 5.25 V, which is obtained from the combination stage-2 DMPI–stage-4 AlCl
4 intercalated system. Experimental evidence suggests that the voltage plateaus range within 3.1–4.3 V with the cut-off charging voltage at 4.4 V
25 indicating that the discharging voltage would remain lower than 4.4 V. However, our observation and literature suggest that stage-4 intercalation in the case of AlCl
4 is more feasible compared to the other stages during the initial charging process. The combinations of stage-3 DMPI–stage-4 AlCl
4 and stage-4 DMPI–stage-4 AlCl
4 yield voltages of 5.23 and 5.16 V, respectively, which are also higher than the considered cut-off voltage in the experimental report. Interestingly, the combination of stage-1 DMPI–stage-4 AlCl
4 gives an output voltage of 3.74 V, which matches with the experimental voltage range 3.1–4.3 V. In addition, our calculated results and experimental evidence support that stage-1 formation of DMPI is more feasible than the other stages.
25,59 Thus we propose that, during the initial charging process, stage-1 DMPI–stage-4 AlCl
4 intercalation occurs. However, when the charging process approaches completion, both DMPI and AlCl
4 ions are expected to follow a stage-1 type of intercalation into the graphite system. Considering the combination of stage-1 DMPI–stage-1 AlCl
4 results in an OCV of 4.6 V for maximum intercalation (16 cations and anions) at both the electrodes, which is comparable with the upper limit of the reported experimental voltage.
25
Table 2 Calculated theoretical voltage (V) with different stages of DMPI cations and AlCl4 anions
| AlCl4 |
DMPI |
| Stage-1 |
Stage-2 |
Stage-3 |
Stage-4 |
| Stage-1 |
1.61 |
3.12 |
3.17 |
3.03 |
| Stage-2 |
2.10 |
3.61 |
3.66 |
3.52 |
| Stage-3 |
3.25 |
4.76 |
4.80 |
4.67 |
| Stage-4 |
3.74 |
5.25 |
5.23 |
5.16 |
Furthermore, we have calculated the gravimetric capacity (C) for our considered DIB system. The gravimetric capacity of both the cathode and anode can be calculated using the following equation,54
| | 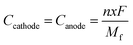 | (7) |
where
n is the number of electrons transferred per formula unit,
x is the number of ions intercalated,
F is the Faraday constant,
Mf is the mass of the formula unit, and
Ccathode and
Canode are the capacity of the cathode and anode, respectively. The total cell capacity (
Ctotal) can be expressed as a combination of the individual capacity of both the cathode and anode
63| | 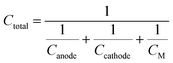 | (8) |
where 1/
CM is the specific mass of the other cell components such as the electrolyte, separator, and current collector. 1/
CM varies significantly with the cell to cell design process, so the contribution of 1/
CM in the total theoretical cell capacity is neglected. Therefore the theoretical cell capacity can be given by,
| |  | (9) |
Our calculated gravimetric capacity for the early stage of the charging process (four intercalated ions) is 15 mA h g
−1, which reaches a maximum capacity of 62 mA h g
−1 upon full intercalation (sixteen ions). In the experimentally produced DMPI–AlCl
4 DIB, the initial gravimetric capacity was reported to be 27 mA h g
−1, which could further be increased up to 82 mA h g
−1 at higher current density with subsequent loss in the coulombic efficiency of the cell.
25 During the initial charging process by considering four ion intercalation, as the DMPI cations follow stage-1 and AlCl
4 anions follow stage-4 intercalation, a partial gravimetric capacity of 15 mA h g
−1 is calculated. In a fully charged system considering sixteen ion intercalation, both DMPI and AlCl
4 ions follow stage-1 intercalation, resulting in a maximum capacity of 62 mA h g
−1. Based on our theoretical insights and available experimental observations, we believe that graphite-like layered materials can be further explored as anode materials for intercalating large size organic cations in order to achieve higher output voltages (∼4.6 V) compared to batteries based on intercalation of AlCl
4− ions only (∼2.0 V).
12,54 Moreover, we have calculated the volume expansion for DMPI intercalation in graphite to be ∼115%. So, the expansion due to DMPI intercalation is less compared to AlCl
4 intercalation in the graphite system (150–160%).
54 However, the reported cycle life values (1000 cycles) are less for the DMPI–graphite system, which could be due to the strong interaction between DMPI and graphite, hindering repeated intercalation/deintercalation cycles. Along with this, we have also tried to provide rationale for the experimentally observed self-discharge nature of the DMPI–AlCl
4 DIB with the help of a free energy calculation of the cell reactions. The cathodic reaction for AlCl
4 intercalation into the graphite cathode (reaction 2) is well established in DIB studies and AlCl
4 anions are not known to actively participate in the self-discharge process. The anodic reaction of DMPI intercalation into graphite is calculated to have a reaction free energy of +0.08 eV, which is much lower than that of the cathodic reaction (+5.6 eV). Thus, in a bias free discharging environment, DMPI deintercalation is expected to occur much spontaneously compared to AlCl
4 deintercalation. This partiality in spontaneity of the individual cell reactions may be the reason for the DMPI–AlCl
4 battery experiencing a self-discharge process, which needs to be further investigated.
3.6. Electronic properties
We have studied the electronic structure of the DMPI cation intercalated graphite system to understand the nature of the interaction between the DMPI cation and graphite host, as organic cation intercalation is less common compared to anion intercalation into the layered graphitic structure. During charging, electrons flow from the cathode to the anode through the external circuit, which allows the adsorption/intercalation of cations and anions into the anode and cathode material, respectively. Similarly, during discharge, the reverse phenomenon happens as electrons flow from the anode to the cathode, thus providing electricity. Hence, constant electronic conductivity of the electrodes during the charge/discharge cycle is essential in a battery. The electronic conductivity can be interpreted from the DOS plots on the basis of the nature of the Fermi region. Fig. 5a presents the total DOS (TDOS) and projected DOS (PDOS) for the DMPI intercalated graphite system. Graphite is known to show good in-plane electronic conductivity because of the presence of the pz electronic states at the Fermi level and no interplane conductivity as the s, px and py electronic states are far from the Fermi level. In comparison with the DOS plot of the well-known pristine graphite system, in our DOS plot of cation intercalated graphite, the Fermi level is shifted towards the conduction band due to the charge transfer from DMPI to graphite. Hence, the electronic conductivity is maintained as shown by the presence of electronic states at the Fermi level in Fig. 5a. The DMPI–graphite system is found to be metallic in nature due to overlap between the 2p orbital of the imidazolium ring of the cation containing C and N atoms and the 2p orbitals of graphite C atoms. The shifting of the Fermi level towards the conduction band indicates the reduction of graphite layers, which satisfies the criteria for selection of a suitable DIB anode material.
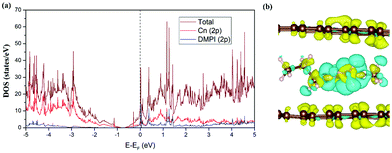 |
| | Fig. 5 (a) TDOS and PDOS of the DMPI cation intercalated graphite. The Fermi level is set to zero. (b) Isosurface (0.0008 |e| Å−3) for the CDD plot of the DMPI intercalated system, where the yellow colour indicates electron density accumulation and the cyan colour indicates electron density depletion. | |
The qualitative charge transfer between the DMPI cation and graphite layers can be illustrated by plotting the charge density difference (CDD) of the systems before and after intercalation. Thus, the CDD can be calculated from the following equation,
| | 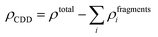 | (10) |
where
ρtotal is the total charge density of the DMPI–graphite system and
ρfragments is the charge density of the individual fragments. The CDD plot has been shown in
Fig. 5b, where the yellow colour represents charge density accumulation and the cyan colour represents charge density depletion. From the CDD plot, we can infer that charge from the loosely bound π-electron cloud of the DMPI imidazolium ring is transferred to the graphite layers. Furthermore, the C2 containing methyl group of DMPI also transfers a lesser amount of charge to the graphite layers. The charge transferred from the propyl chain of the DMPI cation is less because of the tightly bound σ-electrons of the C–C and C–H bonds. Overall, net charge is gained by the graphite layers and lost by the DMPI cation, thus indicating a partial ionic interaction between them. To justify this qualitative explanation, we have determined the quantitative charge transfer using Bader charge analysis. Quantitatively, 0.87 |
e| charge transfer is found to occur from DMPI to the graphite layer, which signifies the electrochemical reduction of graphite and DMPI being cationic, during the charging process. Overall from the DOS and CDD study, we can conclude that graphite can also be used as an anode material for DMPI cation intercalation as well as a cathode material for AlCl
4 anion intercalation, thus behaving as an amphoteric electrode material for dual graphite battery technology.
17,19,20
3.7. Diffusion pathway of DMPI cations
The fast charge/discharge rate of the DIB can be explained by the diffusion barriers of DMPI cations in the graphite layers. The diffusion barrier has a high impact on the battery performance, where the charging/discharging rate can be determined by the mobility of DMPI cations on the AB stacked plane of the graphite layers. Hence, trouble-free diffusion and high mobility of DMPI cations are a prerequisite for developing a dual graphite battery with a fast charge/discharge rate. To determine the diffusion barriers of the DMPI cation within the graphite lattice using the CI-NEB method, we have considered four minimum energy pathways (MEPs) of diffusion initiating from the most stable site (Hollow) of the DMPI cation to the next most stable binding site (Hollow) on the AB stacked graphite in Fig. 6a.52 The MEPs have been shown in Fig. 6b and the structural energy profile diagram has been displayed in Fig. S12 (ESI†). For diffusion of DMPI cations along path-1, a minimum energy barrier of 0.2 eV is obtained. Similarly, for path-2, path-3, and path-4 the diffusion barrier is calculated to be 0.35, 0.36, and 0.44 eV, respectively.
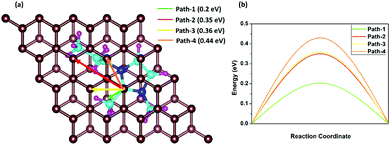 |
| | Fig. 6 Schematic representation of the four diffusion pathways, (a) nearest possible most stable hollow site in AB stacking, where the green, red, yellow and orange colour arrows indicate path-1, path-2, path-3 and path-4, respectively. (b) Energy profile diagram of the four diffusion processes, where the path-1, path-2, path-3 and path-4 energy barriers are 0.2 eV, 0.35 eV, 0.36 eV and 0.44 eV, respectively. | |
Our calculated diffusion energy barrier values are very much comparable with the various reported alkali metal cation intercalated graphite systems such as for Li or Na (0.2–0.4 eV).64,65 Therefore, our diffusion studies indicate that the organic DMPI cation intercalated anode can be used for high performance DIBs with a high discharge voltage, low diffusion barrier, and high electronic conductivity.
4. Conclusion and outlook
In this work, we have carried out a systematic computational investigation of organic cation (DMPI) intercalation into the graphite anode for the first time. Based on dispersion-corrected density functional theory calculations, we have investigated the staging mechanism of DMPI cation intercalation, the charge transfer mechanism from the graphite anode, the diffusion barrier, and electrochemical properties like the voltage and specific capacity. Here, we have modelled four different stages (stage-1, stage-2, stage-3, and stage-4) of the DMPI cation intercalated graphite system to investigate the staging mechanism and electrochemical properties. To verify the stability, we have calculated the binding energy of the DMPI cation intercalated graphite system, where the DMPI cation prefers to intercalate in the parallel over the perpendicular orientation into the AB stacked graphite plane due to π–π interactions of the aromatic imidazolium cation with the graphite hexagonal rings. Further, we have validated the thermal stability of DMPI cation intercalation at the stable hollow site of AB stacked graphite using AIMD simulations. We also report the existence of a thermal equilibrium between all the possible sites of DMPI intercalation. Upon intercalation of DMPI cations, the interlayer spacing of graphite is found to increase from 3.34 Å to 7.2 Å, which facilitates trouble-free diffusion of DMPI cations through the graphite layers. Our calculated diffusion barriers support this fact, and we observe a quite small barrier of 0.2 eV for DMPI cation diffusion inside graphite. Our calculated total energy values for different stages of DMPI cation intercalation follow the stability trend as: stage-2 < stage-4 < stage-1 during the initial charging process. However, the later stages of DMPI intercalation into graphite are expected to follow a stage-1 type intercalation mechanism as is evident by the decrease in the relative energy of stage-1 compared to the other stages with an increase in the concentration of DMPI cations. Our simulated XRD patterns for the stage-1 DMPI cation intercalation process and stage-4 AlCl4 anion intercalation process match with the experimental XRD patterns of the electrodes during the charging process, thus validating the staging mechanism proposed by us. Our calculated average voltages for the early and later periods of intercalation (3.7 V and 4.6 V) are in good agreement with the experimental range (3.1–4.3 V). These results signify the importance of using graphite anodes for organic cation intercalation along with AlCl4 anion intercalation in cathodes to achieve better electrochemical performance compared to DIBs using metal anodes along with AlCl4 intercalated graphitic cathodes. The metallic character of graphite before and after DMPI cation intercalation obtained from the DOS plots confirms the constant electronic conductivity of the graphite anode. The CDD and quantitative Bader charge analysis suggest 0.87 |e| charge transfer occurring from the DMPI cation imidazolium ring to the host graphite carbon atoms, thus indicating the electrochemical reduction of graphite during the charging process. Additionally, we have addressed the reason behind the self-discharge nature of DMPI–AlCl4 graphite DIBs. Some of the shortcomings of dual-ion batteries are electrolyte decomposition and exfoliation of the electrode materials. There is minimal scope of electrolyte decomposition occurring at our calculated output voltage of 3.7 V as it is lower than the experimentally determined cut-off voltage (4.4 V). Exfoliation can result in the loss of crystallinity of the electrode. Exfoliation can occur due to (1) a lack of proper synchronization of volume expansion and contraction of the electrode upon the charging and discharging process, and (2) all ions not being fully deintercalated in the discharge process. As the volume expansion is limited for the DMPI intercalated graphite system, hence exfoliation can occur from the presence of DMPI cations inside the graphite layer in the discharge process due to the high binding energy between DMPI cations and graphite. However, experimental data showing the presence of DMPI cations inside graphite in the discharge state is not available and hence further experimental investigation is required. Overall, this article provides an in-depth understanding of the interaction between DMPI cations and graphite and helps in explaining the different staging mechanisms for both cations and anions to obtain precise electrochemical properties such as the voltage and storage capacity for DMPI–AlCl4 graphite DIBs. We believe that these findings will motivate further exploration of various organic cations which can be suitably intercalated into anodes and coupled with AlCl4 intercalated graphite cathodes to design high performance dual ion batteries on a par with lithium-ion battery technology.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We thank IIT Indore for the lab and computing facilities. This work is supported by DST-SERB (Project Number CRG/2018/001131), and SPARC (Project Number SPARC/2018-2019/P116/SL) New Delhi. S. S. M. and S. D. thank CSIR and A. D. thanks MHRD for research fellowships.
References
- B. Dunn, H. Kamath and J. M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS PubMed.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- J. B. Goodenough and K. S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- B. L. Ellis, K. T. Lee and L. F. Nazar, Chem. Mater., 2010, 22, 691–714 CrossRef CAS.
- L. P. Wang, L. Yu, M. Srinivasan, Z. J. Xu and X. Wang, J. Mater. Chem. A, 2015, 3, 9353–9378 RSC.
- S.-W. Kim, D.-H. Seo, X. Ma, G. Ceder and K. Kang, Adv. Energy Mater., 2012, 2, 710–721 CrossRef CAS.
- V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. Carretero-González and T. Rojo, Energy Environ. Sci., 2012, 5, 5884–5901 RSC.
- M. M. Huie, D. C. Bock, E. S. Takeuchi, A. C. Marschilok and K. J. Takeuchi, Coord. Chem. Rev., 2015, 287, 15–27 CrossRef CAS.
- F. Liu, T. Wang, X. Liu and L. Fan, Adv. Energy Mater., 2021, 11, 2000787 CrossRef CAS.
- C. Xu, B. Li, H. Du and F. Kang, Angew. Chem., Int. Ed., 2012, 51, 933–935 CrossRef CAS PubMed.
- B. Lee, H. R. Lee, H. Kim, K. Y. Chung, B. W. Cho and S. H. Oh, Chem. Commun., 2015, 51, 9265–9268 RSC.
- M. C. Lin, M. Gong, B. Lu, Y. Wu, D. Y. Wang, M. Guan, M. Angell, C. Chen, J. Yang, B. J. Hwang and H. Dai, Nature, 2015, 520, 325–328 CrossRef PubMed.
- P. Bhauriyal, G. Bhattacharyya, K. S. Rawat and B. Pathak, J. Phys. Chem. C, 2019, 123, 3959–3967 CrossRef CAS.
- J. M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS PubMed.
- S. Hy, H. Liu, M. Zhang, D. Qian, B. J. Hwang and Y. S. Meng, Energy Environ. Sci., 2016, 9, 1931–1954 RSC.
- J. Wen, Y. Yu and C. Chen, Mater. Express, 2012, 2, 197–212 CrossRef CAS.
-
F. P. McCullough, C. A. Levine and R. V. Snelgrove, US Pat., 4865931A, 1989 Search PubMed.
- T. Placke, O. Fromm, S. F. Lux, P. Bieker, S. Rothermel, H.-W. Meyer, S. Passerini and M. Winter, J. Electrochem. Soc., 2012, 159, A1755–A1765 CrossRef CAS.
- I. A. Rodríguez-Pérez and X. Ji, ACS Energy Lett., 2017, 2, 1762–1770 CrossRef.
- J. A. Read, A. V. Cresce, M. H. Ervin and K. Xu, Energy Environ. Sci., 2014, 7, 617–620 RSC.
-
P. F. McCullough, C. A. Levine and R. V. Snelgrove, US Pat., 4830938A, 1989 Search PubMed.
- X. Zhou, Q. Liu, C. Jiang, B. Ji, X. L. Ji, Y. Tang and H. M. Cheng, Angew. Chem., Int. Ed., 2020, 59, 3802–3832 CrossRef CAS PubMed.
- Y. Sui, C. Liu, R. C. Masse, Z. G. Neale, M. Atif, M. AlSalhi and G. Cao, Energy Storage Mater., 2020, 25, 1–32 CrossRef.
- K. Beltrop, S. Beuker, A. Heckmann, M. Winter and T. Placke, Energy Environ. Sci., 2017, 10, 2090–2094 RSC.
- Z. Lv, M. Han, J. Sun, L. Hou, H. Chen, Y. Li and M. C. Lin, J. Power Sources, 2019, 418, 233–240 CrossRef CAS.
- T. Placke, A. Heckmann, R. Schmuch, P. Meister, K. Beltrop and M. Winter, Joule, 2018, 2, 2528–2550 CrossRef CAS.
- K. V. Kravchyk, P. Bhauriyal, L. Piveteau, C. P. Guntlin, B. Pathak and M. V. Kovalenko, Nat. Commun., 2018, 9, 1–9 CrossRef CAS PubMed.
- W. Märkle, N. Tran, D. Goers, M. E. Spahr and P. Novák, Carbon, 2009, 47, 2727–2732 CrossRef.
- S. Das, P. Bhauriyal and B. Pathak, J. Phys. Chem. C, 2020, 124, 7634–7643 CrossRef CAS.
- R. T. Carlin, H. C. De Long, J. Fuller and P. C. Trulove, J. Electrochem. Soc., 1994, 141, L73–L76 CrossRef CAS.
- M. Galiński, A. Lewandowski and I. Stepniak, Electrochim. Acta, 2006, 51, 5567–5580 CrossRef.
- E. W. Castner and J. F. Wishart, J. Chem. Phys., 2010, 132, 120901 CrossRef PubMed.
- S. S. Manna, P. Bhauriyal and B. Pathak, Mater. Adv., 2020, 1, 1354–1363 RSC.
- E. Knipping, C. Aucher, G. Guirado and L. Aubouy, New J. Chem., 2018, 42, 4693–4699 RSC.
- S. Rothermel, P. Meister, G. Schmuelling, O. Fromm, H. W. Meyer, S. Nowak, M. Winter and T. Placke, Energy Environ. Sci., 2014, 7, 3412–3423 RSC.
- F. Endres, S. Zein, E. Abedin, A. Y. Saad, E. M. Moustafa, N. Borissenko, W. E. Price, G. G. Wallace, D. R. Macfarlane, P. J. Newman and A. Bund, Phys. Chem. Chem. Phys., 2008, 10, 2189–2199 RSC.
- A. Wang, W. Yuan, J. Fan and L. Li, Energy Technol., 2018, 6, 2172–2178 CrossRef CAS.
- Z. Li, J. Liu, J. Li, F. Kang and F. Gao, Carbon, 2018, 138, 52–60 CrossRef CAS.
- J. Fan, Z. Zhang, Y. Liu, A. Wang, L. Li and W. Yuan, Chem. Commun., 2017, 53, 6891–6894 RSC.
- S. Das, S. S. Manna and B. Pathak, ACS Omega, 2021, 6, 1043–1053 CrossRef CAS PubMed.
- J. Vatsala Rani, V. Kanakaiah, T. Dadmal, M. Srinivasa Rao and S. Bhavanarushi, J. Electrochem. Soc., 2013, 10, 160 Search PubMed.
- N. Jayaprakash, S. K. Das and L. A. Archer, Chem. Commun., 2011, 47, 12610–12612 RSC.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- Y. Chen, F. Peng, Y. Yan, Z. Wang, C. Sun and Y. Ma, J. Phys. Chem. C, 2013, 117, 13879–13886 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 71, 035109 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 24103 CrossRef PubMed.
- G. Henkelman, A. Arnaldsson and H. Jó Nsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069–4074 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- M. S. Dresselhaus and G. Dresselhaus, Adv. Phys., 2002, 51, 1–186 CrossRef CAS.
- P. Bhauriyal, A. Mahata and B. Pathak, Phys. Chem. Chem. Phys., 2017, 19, 7980–7989 RSC.
- S. Kumar, P. Bhauriyal and B. Pathak, J. Phys. Chem. C, 2019, 123, 23863–23871 CrossRef CAS.
- T. Placke, G. Schmuelling, R. Kloepsch, P. Meister, O. Fromm, P. Hilbig, H.-W. Meyer and M. Winter, Z. Anorg. Allg. Chem., 2014, 640, 1996–2006 CrossRef CAS.
- P. Bhauriyal, A. Mahata and B. Pathak, J. Phys. Chem. C, 2017, 121, 9748–9756 CrossRef CAS.
- T. Ohzuku, Y. Iwakoshi and K. Sawai, J. Electrochem. Soc., 1993, 140, 2490–2498 CrossRef CAS.
- T. Sutto, T. Duncan and T. Wong, Electrochim. Acta, 2009, 54, 5648–5655 CrossRef CAS.
- F. Weinhold and C. R. Landis, Chem. Educ.: Res. Pract. Eur., 2001, 2, 91–104 CAS.
- S. Takahashi, N. Koura, S. Kohara, M.-L. Saboungi and L. A. Curtiss, Plasmas Ions, 1999, 2, 91–105 CrossRef CAS.
- J. A. Read, J. Phys. Chem. C, 2015, 119, 8438–8446 CrossRef CAS.
- U. Kasavajjula, C. Wang and A. J. Appleby, J. Power Sources, 2007, 163, 1003–1039 CrossRef CAS.
- K. Persson, Y. Hinuma, Y. S. Meng, A. Van Der Ven and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 125416 CrossRef.
- K. Nobuhara, H. Nakayama, M. Nose, S. Nakanishi and H. Iba, J. Power Sources, 2013, 243, 585–587 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Relative energies of the different binding sites, details of molecular dynamics analysis at different temperatures, comparative study of stage-1 and stage-2 with varying DMPI ions, pictorial representation of all four stages, NBO charge analysis of DMPI and EMI cations, XRD pattern of the DMPI intercalated graphite anode, stability study of different stages of the AlCl4 intercalated graphite cathode, and NEB diffusion barriers. See DOI: 10.1039/d1ma00351h |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Sandeep
Das
,
Sandeep
Das
 ,
Arunendu
Das
,
Arunendu
Das
 and
Biswarup
Pathak
and
Biswarup
Pathak
 *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio as the electrolyte. We have investigated the intercalation mechanism by considering the staging manner of DMPI cation intercalation into the graphite anode. First principles calculations are performed for a systematic study of the structure, stability, electronic properties, and theoretical capacity along with the average voltage of the DMPI cation intercalated graphite electrode. Furthermore, we have also investigated the diffusion pathways of DMPI cations in the graphite system. Along with this, we have also explained why EMI+ cannot be used as an organic cation for dual-graphite battery research, although EMI based IL electrolytes are extensively used in battery technology.12,41,42 On the basis of the obtained theoretical insights, we believe that organic cation intercalated graphitic anodes could be utilised in DIBs to achieve better electrochemical features compared to DIBs using metal anodes, and our study would motivate further developments in cheaper dual graphite battery technology.
1 molar ratio as the electrolyte. We have investigated the intercalation mechanism by considering the staging manner of DMPI cation intercalation into the graphite anode. First principles calculations are performed for a systematic study of the structure, stability, electronic properties, and theoretical capacity along with the average voltage of the DMPI cation intercalated graphite electrode. Furthermore, we have also investigated the diffusion pathways of DMPI cations in the graphite system. Along with this, we have also explained why EMI+ cannot be used as an organic cation for dual-graphite battery research, although EMI based IL electrolytes are extensively used in battery technology.12,41,42 On the basis of the obtained theoretical insights, we believe that organic cation intercalated graphitic anodes could be utilised in DIBs to achieve better electrochemical features compared to DIBs using metal anodes, and our study would motivate further developments in cheaper dual graphite battery technology.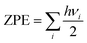 , where h is Planck's constant and vi is the vibrational frequency. The ZPE is calculated by considering the degrees of freedom of intercalated DMPI into the graphite system.
, where h is Planck's constant and vi is the vibrational frequency. The ZPE is calculated by considering the degrees of freedom of intercalated DMPI into the graphite system.

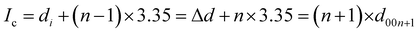 , and similarly for d00n+2, Ic = (n + 2) × d00n+2, where Δd = di − 3.35 and 3.35 Å is the interlayer distance between two consecutive graphite layers.62 In the case of pristine graphite an intense peak is found at 2θ = 26.5° belonging to its (002) plane generally.12 For our simulated XRD pattern, we can identify such a peak at 26.16° for the pristine system which shifts to 25.88°, 25.18°, 25.75° and 24.96° for stage-1, stage-2, stage-3 and stage-4 intercalation, respectively, as shown in Fig. 4. As the distortion and lateral displacement in the graphite layer stacking increase with an increase in the DMPI intercalation, other intense peaks belonging to various planes can also be identified at lower ranges of 2θ in the XRD plot as presented in Fig. S10 (ESI†). In the previous report of experimental DMPI intercalation by Lv et al., the (002) peak of the system was found to shift from 2θ = 26.4° for pristine graphite to 2θ = 26.0° for the GIC.25 Consequently, from our XRD plots we can suggest that stage-1 intercalation (2θ = 25.88°) of the DMPI cation in graphite occurs predominantly (Fig. S4, ESI†), which also agrees with an experimental study by Sutto et al.59
, and similarly for d00n+2, Ic = (n + 2) × d00n+2, where Δd = di − 3.35 and 3.35 Å is the interlayer distance between two consecutive graphite layers.62 In the case of pristine graphite an intense peak is found at 2θ = 26.5° belonging to its (002) plane generally.12 For our simulated XRD pattern, we can identify such a peak at 26.16° for the pristine system which shifts to 25.88°, 25.18°, 25.75° and 24.96° for stage-1, stage-2, stage-3 and stage-4 intercalation, respectively, as shown in Fig. 4. As the distortion and lateral displacement in the graphite layer stacking increase with an increase in the DMPI intercalation, other intense peaks belonging to various planes can also be identified at lower ranges of 2θ in the XRD plot as presented in Fig. S10 (ESI†). In the previous report of experimental DMPI intercalation by Lv et al., the (002) peak of the system was found to shift from 2θ = 26.4° for pristine graphite to 2θ = 26.0° for the GIC.25 Consequently, from our XRD plots we can suggest that stage-1 intercalation (2θ = 25.88°) of the DMPI cation in graphite occurs predominantly (Fig. S4, ESI†), which also agrees with an experimental study by Sutto et al.59

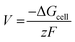 , where z and F are the number of electrons transferred and the Faraday constant, respectively, while ΔGcell is the change in Gibbs free energy during the chemical reactions.
, where z and F are the number of electrons transferred and the Faraday constant, respectively, while ΔGcell is the change in Gibbs free energy during the chemical reactions.