Selective kinetic growth and role of local coordination in forming Al₂TiO₅-based coatings at lower temperatures

Abstract

Negative thermal expansion is an elusive property found among certain materials, whose potential applications have remained limited due to the many challenges faced in their synthesis. Herein, we report the successful formation of aluminium titanate-based coatings (Al₂TiO₅), a material renowned for its low-to-negative thermal expansion, by the co-deposition of aluminium-isopropoxide and titanium-isopropoxide in a hot-wall chemical vapour deposition instrument. While coatings grown at 450 °C were amorphous as-deposited, a short-range order into the Al₂TiO₅-phase was found and analysed by using Raman spectroscopy. Upon subsequent annealing at 700 °C for 3 hours, crystalline coatings were achieved without forming any binary phases. The selective synthesis of the Al₂TiO₅ phase is ascribed to the precursors' inherent chemical similarities, resulting in a kinetic targeting of this phase and a short-range homogeneity, entailing its preferred crystallisation. The role of local coordination is expressed by demonstrating the formation of intergrowth phases ascribed to lower coordinating interstices in the compound. Both the formation and crystallisation temperatures reported herein, as well as the timescales needed for the synthesises, are considerably lower than any conventional adopted solid-state techniques used so far to attain the Al₂TiO₅ phase.

---

1. Introduction

Transition metal oxides carry unique sets of properties seldom found among other material groups. Beyond their capabilities of showing extraordinary features in the realms of magnetism,^1,2 ferroelectricity,³ photocatalysis,^4,5 electrochromism^6,7 and superconductivities,^8–10 they may also exhibit unusual thermal properties, like contracting rather than expanding upon heating. Such paradoxical behaviour is exclusively found among a rare group of compounds possessing a negative thermal expansion coefficient (NTE),¹¹ a feature commonly ascribed to the presence of differential and directional bonding characters in coordinating (and distorted) oxygen polyhedrons.^12–16 Besides common ice,¹⁷ NTE is typically observed among more intricate forms of multi-component oxide phases in the subgroups of tungstates,^18,19 molybdates,²⁰ vanadates,²¹ and titanates,^22–24 including combinations thereof.²⁵ Because of their multidisciplinary properties, these phases have increasingly started to attract interest for applications in energy harvesting,^26,27 electronics,^28,29 optics,³⁰ catalyses,^31,32 refractory³³ and metallurgy,³⁴ to name a few. This has also surged a need to find more efficient methods to synthesise these compounds, constituting this study's overall theme.

Traditionally, solid-state syntheses have been widely used to obtain many functional metal-oxides, which remains a conventionally adopted approach. Whereas these methods have successfully discovered many binary oxides, they remain inadequate in the pursuit of novel multi-component phases, having potentially improved properties, given their elaborate stoichiometries and general metastable characters.^35–38 Since solid-state techniques are heavily reliant on diffusion and thermodynamic equilibrium,^36–38 they are restricted from entering the metastable domain, lying energetically above those of the most thermodynamically stable phases,^37–39 and accurately targeting these.

As alternatives to solid-state synthesis methods, many solvent-based and “soft-chemical”⁴⁰ routes have been developed.^36,41 Besides sol–gel,⁴² solvothermal,⁴³ hydrothermal,^44,45 ion-exchange,^40,46 and various intercalation/deintercalation techniques,^47,48 they also include low-temperature chemical vapour-deposition (CVD) processes.^49,50 Rather than relying solely on the diffusion of the elements, these techniques may carry an extra degree of freedom by allowing atomic-scale control of the synthesised material through a series of step-wise polycondensations,^42,51 targeted metatheses,^37,38 and ligand reactions.⁴⁴ This added flexibility enables the adaption of functional inorganic materials not merely from their elemental compositions but also through their local short-range features,^52,53 such as coordination environments,⁵⁴ bonding characteristics and presence of (ordered) vacancies.^55,56

These features characterise many transition metal oxides, showing extensive polymorphism in the metastable domain.^44,53,54 For example, a shared elemental composition may exhibit vastly different properties depending on how the comprising metal–oxygen polyhedral units are aligned through tiltings, rotations, and distortions.^37,57 Such subtle yet essential nuances are notoriously difficult to isolate from conventional solid-state synthesis processings,^53,57 offering limited control of the reaction pathway and its corresponding kinetics.^36,41,58 Hence, a selective targeting of the metastable phases rather than any thermodynamically stable ones are rarely achieved.^37,53

Alternatively, solvent-based and “soft-chemical” techniques can readily offer such selectivity by facilitating the controlled formation and kinetic trapping of metastable compounds.^36,41,44,55 This is particularly realised from metal–organic CVD processes (MOCVD), which combines the flexibilities of strategic precursor designs to a wide range of tactical and adaptable process parameters. Additionally, mixing precursors in their gaseous states allows a facile pathway to target the stoichiometry of multi-component phases while simultaneously circumventing any significant binary constituent formation.

This study expresses these hallmarks by demonstrating the formation of aluminium-titanate-based coatings (Al₂TiO₅) at lower processing temperatures and shorter timescales than any solid-state technique. Using two reactants simultaneously, a selective kinetic growth and targeting of this phase are achieved instead of its stable binary constituents. The role of local coordination is emphasised by the suggested growth mechanism given in the discussion section. Furthermore, detailed examinations of the short-range features using Raman spectroscopy unveiled new phases beyond that of Al₂TiO₅. These phases, known as intergrowths, have previously been suggested by earlier authors in the field.⁵⁹ This study confirms these phases' existence and extends their descriptions by providing a plausible cause of their formation, relating to local changes in Al₂TiO₅'s cationic arrangements.

1.1. Al₂TiO₅ – properties and applications

Al₂TiO₅ is an oxide compound renowned for its thermal properties, such as a high melting point (1860 °C),⁶⁰ high thermal shock resistance (1544 W m⁻¹),⁶¹ low thermal conductivity (1.5 W m⁻¹ K⁻¹),⁶¹ and a low-to-negative thermal expansion coefficient.^62,63 Along with insufficient wetting towards non-ferrous metals,⁶⁴ corrosion resistance^64,65 and a remarkable self-healing ability of cracks at elevated temperatures,^66,67 the compound stands as an ideal candidate for many refractory- and metallurgical applications. Recent studies have also revealed an excellent photocatalytic potential of this material, owing to a moderate band gap (2.88 eV),⁶⁸ which has found practical use to improve solid-oxide fuel cells' performances.⁶⁹

Still, the challenges concerning the synthesis of this material have restricted its widespread applicability. Solid-state synthesis methods, like sintering, are widely adopted to obtain the Al₂TiO₅ phase by mixing and heating equimolar ratios of Al₂O₃ and TiO₂ powders. Because of these binary phases' stabilities, their mutual solubility remains relatively poor,^70,71 resulting in a low net Gibbs free energy change to drive this reaction, which is less than 600 J mol⁻¹ below 1600 K.⁷² Accordingly, elevated sintering temperatures and prolonged reactions times – occasionally lasting for several days⁷³ – are required to yield sufficiently high phase purity of this material. Even so, the formation of Al₂TiO₅ without the remaining residues of parent phases remains hard to accomplish. For that reason, Al₂TiO₅ is readily claimed to be thermally unstable, and alleged to decompose spontaneously below its formation temperature at 1280 °C through a eutectoid reaction.^62,74 Thermogravimetric analyses have supported this general view,⁶⁰ showing an endothermic reaction and positive formation enthalpy to this compound when being sintered.⁷⁵ As such, Al₂TiO₅ is commonly referred to as an “entropy-stabilised” compound owing to its positive configurational entropy term (15 J mol⁻¹ K⁻¹).^76–78

The entropy-stabilisation of this material correlate strongly with its structural features. Al₂TiO₅ is isomorphous to a group of compounds known as pseudobrookites, having general formula A₂³⁺B⁴⁺O₅,⁷⁷ which Linus Pauling first studied in 1930.⁷⁹ It crystallises in the orthorhombic system with space group Cmcm⁶² (or as Bbmm within older literature).^63,77,79 For clarity in this context, the Cmcm setting is adopted throughout this study.

The cations in Al₂TiO₅ may occupy two octahedrally coordinated crystallographic sites with different symmetries, represented by Wycoff notation as 4c (M1); 8f (M2).^62,63,77 These sites form double-chained polyhedrons running parallel with the c-axis and are connected from apex-sharing bridging oxygens across the perpendicular a-axis. Along the b-direction, the chains are linked through edge-sharing of polyhedral oxygen units. Accordingly, different bonding characteristics are present along the crystallographic axes, giving rise to a marked anisotropic behaviour of this material, particularly its thermal expansion.⁶⁷ Upon heating, Al₂TiO₅ tends to contract in the direction of its stronger bonding apex-sharing oxygens,⁶³i.e. the a-axis,⁶² meaning a negative thermal expansion in this direction.

Earlier investigations from neutron scattering,⁶² X-ray diffraction,^63,78 and high-resolution TEM investigations⁸⁰ have shown that Al₂TiO₅ readily displays cationic disorder, in the sense that the metal atoms can interchangeably reside in the two available metal interstices. The cationic mixing on both sites cause local distortions to the oxygen octahedrons⁸¹ and, conceivably, contributes to this compound's sizeable configurational entropy term.⁷⁸

Few studies have so far investigated the formation of Al₂TiO₅ as coatings, which would extend the material's applicability in harsh thermal environments as a potential thermal barrier- and corrosion-resistant coating. Principal studies using CVD as a method includes the work made by D. Leinen et al.⁸² In their study, a combined ion-beam and CVD set-up was used to deposit amorphous coatings of Al_xTi_yO_z, which reportedly transformed into a sole crystalline TiO₂ phase upon subsequent annealing. Similarly, P. Innocenzi et al. were among the first to report crystalline Al₂TiO₅ thin film formation at lower temperatures, using sol–gel as the method and the two precursors aluminium-sec-butoxide and titanium-butoxide.⁸³ However, as noted by these authors, the obtained coatings were only partially crystalline and showed a residual amorphous phase that transformed into TiO₂ on further annealing.

More recent attempts to deposit coatings of Al₂TiO₅ have encountered similar challenges with co-formation of binary constituents. D. Hau-Kuo et al. made attempts to use a combination of aluminium-sec butoxide, titanium tetrachloride, CO₂ and H₂ to deposit coatings of Al₂TiO₅ by CVD.^84,85 They referred to Al₂TiO₅ as Al₂O₃–TiO₂ interchangeably throughout their articles, implying difficulties in attaining the correct phase stoichiometry. These issues have also been noted within other deposition techniques, such as physical vapour deposition (PVD) and thermal-spraying.^86,87

Hitherto, A. Ito et al. are the only ones to have reported the formation of Al₂TiO₅ coatings without secondary binary phases formation. They used a laser CVD apparatus to deposit porous feather-like structures of Al₂TiO₅, which was investigated with TEM.⁸⁸

2. Experimental section

2.1. CVD system

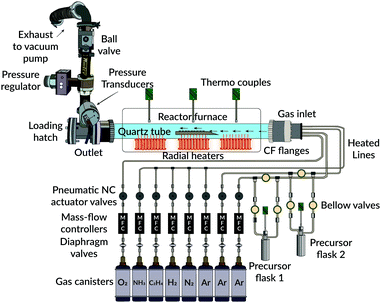
Depositions were made using an in-house built 3-zone hot-wall CVD reactor, consisting of a horizontally aligned fused quartz tube (outer diam. 600 mm, inner diam. 580 mm, 1600 mm long). A schematic illustration of the reactor is given in Fig. 1. Radial heaters were used for the deposition zones, and the temperature within the reactor was monitored using several Pt/Rh type K thermocouple units (Pentronic 8102000). All pipelines to the reactor were also heated from glass-fibre liner heating tapes kept constant at 190 °C, to avoid condensations of the precursors in the main gas-supply lines. Additionally, for uniform heating of the precursor flasks, specially designed tube-fitting heating jackets were used together with separately mounted thermocouple units inside each flask container. Multiple connected PID-controller units (Eurotherm 3216) monitored all heating.

Fig. 1 Schematic overview of in-house-built CVD equipment, marking all major components.

Highly pure (99.999% Alphagaz™, Air Liquide) argon acted as a carrier gas for all experiments. Tylan 2900-series mass-flow units, connected to PR4000B controllers (MKS), regulated the flow rates from these gases. Moreover, an automatic butterfly check valve, positioned by the outlet, monitored the reactor's total pressure during each deposition run. This check valve was regulated by a separately connected MKS 651C controller and two 10/100 torr pressure transducer units (MKS). For pumping the system to vacuum, a single oil-sealed roughing pump was used (Edwards). The operating pressure for all experiments was below 2 torr.

2.2. Substrates

Depositions were made on 1 × 1 cm Si P(100) non-etched wafer pieces. Before each deposition attempt, these pieces were carefully cleaned in an ultrasonic bath for 30 min in acetone, followed by an ethanol solution for the same duration of time. Substrates were then dried in a stream of argon gas before being immediately placed on top of a system-designed graphite sample holder.

2.3. Precursors

The used precursors for all experiments were as-received and commercially available aluminium isopropoxide (98+%, STREM chemicals) and titanium(IV) isopropoxide (≥97%, Sigma-Aldrich), abbreviated henceforth as AIP and TIP, respectively. Due to their air- and moisture sensitivity, the precursors were transferred to their respective flask under an inert argon atmosphere using a glove box. Both precursors were kept in a heating cabinet overnight at 200 °C before getting filled. For the first use, the AIP precursor was melted overnight in its container at 140 °C to achieve adequate gas-phase volatility on subsequent deposition runs.

2.4. Deposition experiments

Table 1 summarises the main parameters used for all depositions throughout this study. A constant temperature for the AIP flask was always used, set to 110 °C. For the corresponding TIP flask, the container's temperature was varied within the temperature interval of 50–70 °C. Each precursor's vapour pressure was allowed to stabilise around its set point for about 1 hour before deposition. A stream of carrier gas (25 sccm) was bubbled through each solution's container. This flow was accompanied by a separate bulk flow (850 sccm) through the main reactor chamber. Thus, during each experiment, the total flow rate of the carrier gas was fixed at 900 sccm.

Table 1 List of used deposition parameters

Pressure range	1–2 torr
Deposition temperature	450 °C
Total carrier gas flow rates	900 sccm
Deposition time	1 h
Evaporator temperature, TIP	50–70 °C (varied)
Evaporator temperature, AIP	110 °C (fixed)

---

Depositions were initialised by opening both outlet bellow valves simultaneously. The duration of each run was always 1 hour.

2.5. Annealing of samples

Annealing of the as-deposited coatings was made in incremental steps of 50 °C using a vacuum furnace. The operating base pressure of the furnace was below 5.5 × 10⁻⁸ torr. Samples were placed in an alumina crucible, and the chamber was pumped out for 8 hours before heating was started. The heating and cooling rates were fixed at 10 °C min⁻¹ and the calcination time was 3 hours.

2.6. X-ray diffraction

Offset coupled Cu Kα θ/2θ scans were made on a Bruker D8 Advance X-ray diffractometer in Bragg–Brentano configuration, equipped with an air scattering screen and a Lynxeye XE-T solid-state strip detector. The divergence for the incident beam optics was 0.6°. Measurements were made in the 2θ angular range of 10–60°, using a step size of 0.059° and a collection time of 10 s per step. To avoid scattering from the Si(100) substrate, a 1° ω detector offset was used. All conducted XRD measurements were performed at ambient room conditions. Whole pattern analyses of the annealed diffractograms were made using a Pawley refinement and the software Topas (Bruker AXS).

2.7. Raman spectroscopy

Raman spectra were recorded at ambient conditions using a micro-Raman spectrometer (Renishaw inVia Qontor) equipped with a 30 mW 405 nm (blue) laser and a long-pass edge filter, allowing analysis of in-elastically scattered light from 114 cm⁻¹ by the incident laser line. All spectra were collected using a 20× objective (Olympus, N plan, NA = 0.40) with cosmic ray removal enabled. The instrument was calibrated before measuring from a reference Si P(100) sample to ensure that its characteristic Raman mode was positioned at 520.5 cm⁻¹. The spectral resolution was ±1 cm⁻¹. Data acquisitions were performed using neutral density filters to decrease the laser's intensity to 10% and collect 50 scans in total for the range 100–2400 cm⁻¹. Measurements using lower intensities were also performed to validate that no heating effects from the laser had affected the 10% laser intensity measurements. Moreover, data acquisitions were made on several different positions on the sample surface to ensure that the Raman data was representative of the whole coating. Deconvolution and curve fitting of the obtained bands in the spectra was done in the software Fityk using a pseudo-Voigt peak profile after a baseline correction (cubic spline interpolation).

2.8. Electron microscopy

Cross-sectional and top-surface imaging of the coatings were made using a Schottky FEG Zeiss Merlin™ instrument equipped with an X-max 80 mm² silicon drift EDS detector (Oxford Instruments). For all secondary-electron and in-lens imaging, an EHT voltage of 1 kV was used together with a probe current of 100 pA. For BSE imaging, EDS mapping, and EDS line-scans, an EHT voltage of 10 kV was used along with a probe current of 1 nA. Analyses were made using the software AZtec™ (Oxford Instruments).

Additional analyses of the samples' cross-sections were made using transmission electron microscopy (TEM) via an FEI Titan 80-300 instrument operated at 300 kV. An FEI Versa 3D focused ion beam/scanning electron microscope (FIB-SEM) was used to prepare the TEM lift-out samples.

3. Results

3.1. As-deposited samples

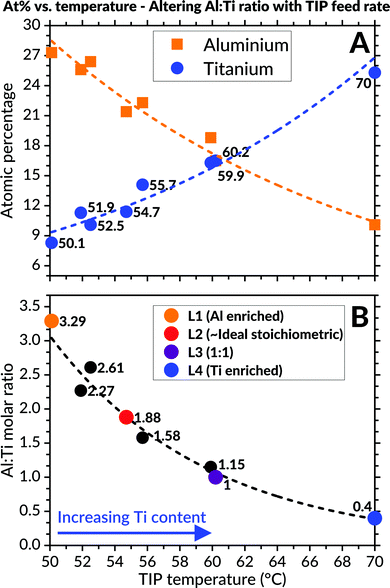
EDS analyses of the as-deposited coatings (Fig. 2) revealed variations to the cationic atomic percentages from altering the TIP precursor's evaporation temperature. A close-to-ideal stoichiometry of the Al : Ti molar ratio (1.88) was obtained when the TIP flask container's temperature was set to 54.7 °C. In order to study the effect of varying molar ratio, four different compositions were selected for further investigations. These were designated as L1 (Al-enriched), L2 (∼ideal), L3 (1 : 1) and L4 (Ti-enriched), respectively.

Fig. 2 Compilation of EDS data, showing in (A) the variation of aluminium and titanium content and in (B) the corresponding Al : Ti molar ratio. Both graphs plotted as function of heating temperature for TIP. Dashed exponential lines added for guidance of trend.

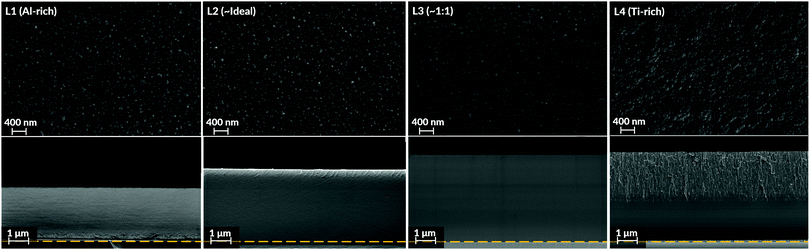
SEM top view images (Fig. 3) demonstrated morphologies consisting of nano-sized globular domains. This feature was seen in all batches regardless of Al : Ti molar ratio. The only deviance to this trend was observed for the Ti-enriched batch (L4), showing slightly smoother and larger domains on their top surfaces. For the samples' cross-sections, their intrinsic appearances were similar as well. As seen in Fig. 3, all coatings possessed a dense homogenous appearance with few distinguishing features.

Fig. 3 Plan view (top surface) and cross-sectional SEM imaging of the as deposited coatings having various Al : Ti molar ratios. Yellow dashed line marks the interface to the underlying silicon substrate.

XRD in θ–2θ geometry (Fig. 4) was conducted to study the samples' phase contents. These measurements indicated an amorphous phase by revealing an asymmetric hump in intensity at lower 2θ angles for all coatings. A few very weak peaks were seen within the L4 (Ti-enriched) sample, which was identifiable as peaks belonging to anatase. A sharp narrow peak with low intensity could also be seen at 27° in the L2 (∼ideal stoichiometric) batch. This peak, and the possible diffuse low-intense peak at 55° for this sample, could be assigned to a rutile secondary phase. However, the presence of binary phases in L2 was not further supported by either Raman spectroscopy or TEM evaluations, as described below.

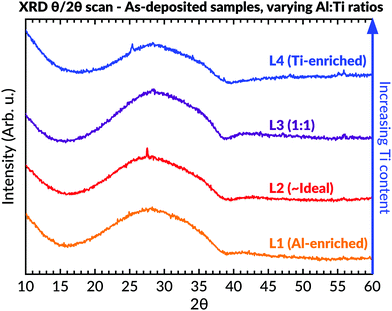Fig. 4 Diffractograms of as-deposited samples having different Al : Ti molar ratios. An amorphous background can be seen in all samples between 15–40°.

TEM analyses were adopted to cross-evaluate the structural and phase-related similarities observed from SEM. As seen in Fig. 5, (a) and (b) are bright-field (BF) micrographs of the cross-sections belonging to the L1 (Al-enriched) and L2 (∼ideal) batches, respectively. The absence of any pronounced diffraction contrast in these micrographs indicates no crystalline phase in the as-deposited coatings. This notion is also accentuated by the conducted selected area electron diffraction (SAED), as shown in (c) and (d) in Fig. 5. Accordingly, based on SEM, XRD and TEM examinations, all coatings were essentially amorphous as-deposited regardless of their inherent Al : Ti molar ratios.

Fig. 5 TEM of the L1 (Al-enriched) and the L2 (∼ideal stoichiometric) as-deposited samples. (a) and (b) are TEM BF micrographs of the L1 and the L2 samples, respectively. (c) and (d) are electron diffraction patterns collected from the L1 and the L2 samples, respectively.

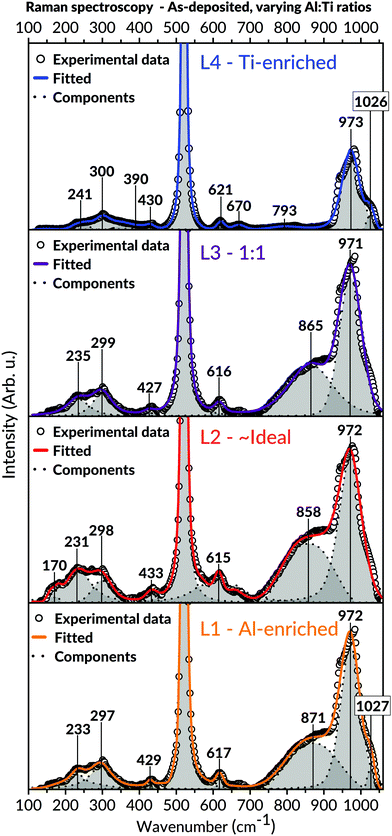
Raman spectroscopic measurements (Fig. 6) were carried out to attain additional information on the samples' short-range order. With exception to the two intense Raman bands at 520 and 970 cm⁻¹ (including the possible shoulder at 1030 cm⁻¹) originating from the Si-substrate, all coatings revealed bands positioned at values around 170; 230–300; 390–433; 615–670 and 793–871 cm⁻¹. These bands' coherent positions correspond to the Al₂TiO₅ phase and are in excellent agreement with the literature.^89,90 Interestingly, no other phases were found in the spectra of L1 and L2, including possible TiO₂ and Al₂O₃ binary phases. For instance, the ordinarily intense E_g vibrational mode of anatase, positioned around 140 cm⁻¹, was never observed in these batches.

Fig. 6 Raman spectra of as-deposited samples having different Al : Ti molar ratios. Modes assigned to Al₂TiO₅ can be found in all samples. The intense bands at 520.5 and 970 cm⁻¹ (including the possible shoulder around 1030 cm⁻¹) originates from the underlying Si-substrate. Certain modes are boxed for enhanced visualisation.

In conclusion, the combined results from XRD, EDS, TEM and Raman spectroscopy revealed many inherent similarities of the as-deposited samples regardless of their varying Al : Ti molar ratios. EDS analyses combined with TEM and XRD showed that all coatings possessed a homogenous elemental distribution and were essentially amorphous as-deposited. Few distinguishable microscopic features could be discerned from top- and cross-sectional imaging using SEM. Upon inspections with Raman spectroscopy, clear indications of a short-range order corresponding to the Al₂TiO₅ phase was seen for all samples.

3.2. Annealing of amorphous Al₂TiO₅ coatings

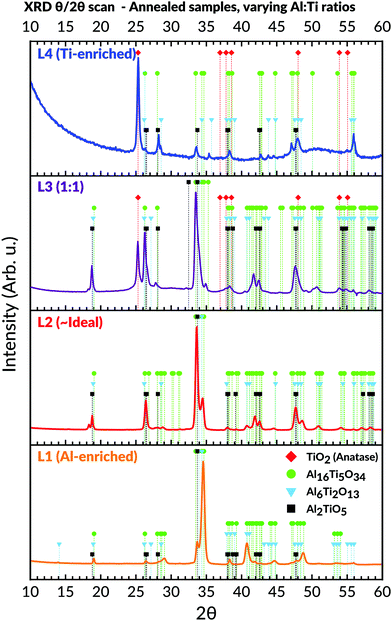
Annealing of samples showed an amorphous-to-crystalline phase transition occurring collectively for the L1, L2, and L3 sample batches at 700 °C for 3 hours. This was evident from the obtained diffractograms (Fig. 7), which matched the Al₂TiO₅ phase.⁶² Subsequent attempts also confirmed that the transition occurred for samples lacking any prior heating history, i.e. samples being directly heated from room temperature up to 700 °C and then calcinated for 3 hours.

Fig. 7 Diffractograms of annealed samples having different Al : Ti molar ratios. Peaks belonging to Al₂TiO₅ and intergrowth phases are evident in all samples. Presence of anatase can be viewed from the L3 and L4 batches in the Ti-enriched domain.

The samples belonging to L1 (Al-enriched) and L2 (∼ideal stoichiometric) were found for being primarily comprised of the Al₂TiO₅ phase even after annealing. The presence of peaks identifiable to any titania or alumina phases were absent in their corresponding diffractograms. On the contrary, peaks belonging to the anatase phase, particularly the (101) reflection at 25.3°, started to appear after annealing for the samples with Al : Ti molar ratio towards the more Ti-enriched side (i.e. L3 and L4). These anatase peaks were noticeable already after exposure to 550 °C for 3 hours (not shown). On further annealing of L3 and L4, weak peaks belonging to the Al₂TiO₅ phase started to appear for these two batches as well, which then coexisted with the anatase peaks.

Although most peaks matched accurately to either Al₂TiO₅ or anatase, some remaining peaks could not be assigned to any expected phases in the Al–Ti–O system. This observation mainly concerned the peaks appearing at 2θ values around 19°; 29°; 34.5°; 40.8°; 44.6° and 48.7° in the recorded diffractograms (Fig. 7). These peaks were particularly prominent in the L1 (Al-enriched) and L2 (∼ideal stoichiometries) sample batches, yet they could also be observed in L3 and L4. Similar observations of such peaks were initially made by Hoffman et al., who assigned these to the formation of unconventional phases present in the Al₂O₃–TiO₂ pseudo-binary phase diagram.⁵⁹ The phases existed at higher Al : Ti molar ratios and had much larger unit cells than Al₂TiO₅. The larger unit cells stem from a reduction in point symmetries, leading to an elongation of the c-axis while keeping the a- and b-axis more or less unchanged. Thus, these intergrowth phases' stoichiometries are dissimilar from Al₂TiO₅ and proposed to be Al₆Ti₂O₁₃ and Al₁₆Ti₅O₃₄, respectively.⁵⁹ Their presence is particularly marked from the intense peak seen around 34.5° in the corresponding diffractograms.⁵⁹ This intense peak could also be noticed in this study's diffractograms, particularly for the annealed Al-enriched L1 and the L2 batches. By matching the previously unassigned peaks to Hoffman et al.'s XRD data, excellent agreements to the presence of these intergrowth phases could be made.^59,91

To further elucidate the presence of these phases, whole-pattern refinements of the diffractograms belonging to L1 and L2 was carried out. These refinements confirmed that the diffractograms could solely be described based on the presence of Al₂TiO₅ and the two suggested intergrowths phases. The calculated unit cell parameters of each phase are given in Table 2, whereas the refined diffractograms and structural reports for L1 and L2 are provided in the ESI.† The values align with those given by the references, although our calculated data shows a slightly larger cell volume to the Al₁₆Ti₅O₃₄ phase in particular.

Table 2 Calculated unit cell parameters for the three phases Al₂TiO₅, Al₆Ti₂O₁₃ and Al₁₆Ti₅O₃₄, represented for the two batches L1 (Al-enriched) and L2 (∼ideal composition)

L1 – Al-enriched						L2 – ∼ideal composition
Phase	a (Å)	b (Å)	c (Å)	c/a	V (Å^3)	Phase	a (Å)	b (Å)	c (Å)	c/a	V (Å^3)
Al2TiO5	3.605(6)	9.106(14)	9.493(7)	2.63	311.6(7)	Al2TIO5	3.6003(18)	9.4292(17)	9.6809(11)	2.69	328.65(18)
Al6Ti2O13	3.709(3)	9.30(2)	12.519(16)	3.38	432.0(12)	Al6Ti2O13	3.6727(14)	9.331(3)	12.555(3)	3.42	430.3(2)
Al16Ti5O34	3.658(2)	9.287(10)	65.36(4)	17.87	2220(3)	Al16Ti5O34	3.6723(8)	9.2883(18)	65.494(10)	17.83	2234.0(7)

---

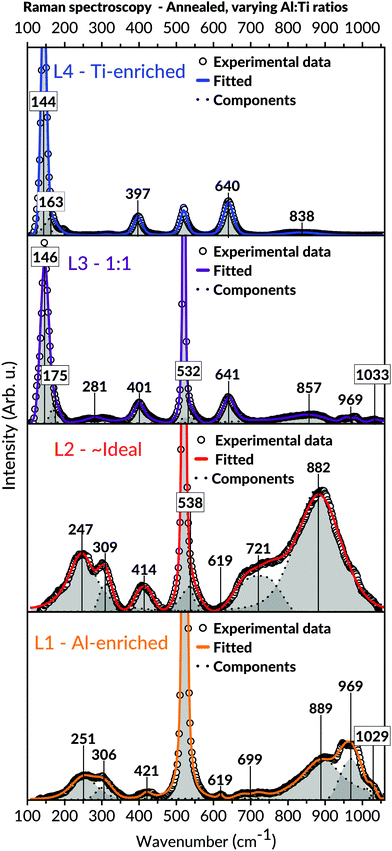
Raman spectroscopic measurements of the annealed samples, viewed in Fig. 8, were coherent with the XRD observations. Compared to the as-deposited states, the results demonstrated more refined appearances of the bands belonging to the Al₂TiO₅ phase for the L1 and L2 batch. Also, detailed analyses of the spectroscopic features in these spectra, including shifts of bands to higher wavenumbers, unveiled structural changes related to the presence of the intergrowth phases. These features are further expounded in the discussion, Section 4.3. Analogous to those observations made in L1 and L2's as-deposited states, no secondary phases such as anatase could be detected in these batches' spectra. Contrastingly, bands belonging to anatase became visible for the Ti-enriched batches after annealing, particularly for the most Ti-containing L4 batch. The modes assigned to the Al₂TiO₅ phase, initially observed in L4's as-deposited state, wholly disappeared after the annealing of this batch.

Fig. 8 Raman spectra of annealed samples with different Al : Ti molar ratios. Modes assigned to Al₂TiO₅ can be found in L1, L2, and L3, with more refined appearances than their as-deposited states. In L4, the Ti-enriched batch, only modes belonging to anatase can be distinguished. The two bands at 520.5 and 970 cm⁻¹ (including the possible shoulder around 1030 cm⁻¹) originates from the underlying Si-substrate. Certain modes are boxed for enhanced visualisation.

Microscopical characterisations of the annealed samples were made by using TEM, whose results are compiled in Fig. 9. (a) and (b) are TEM bright-field imaging for the L1 and L2 batches, respectively. Unlike the images for the as-deposited states, these demonstrated clear diffraction contrast showing a polycrystalline microstructure for both samples. Thus, the TEM results support the view that a polycrystalline transition from the initial as-deposited amorphous coatings has occurred due to the annealing of the samples.

Fig. 9 Compiled results from TEM of annealed coatings belonging to L1 (Al-enriched) and L2 (∼ideal). (a) and (b) represent bright-field (BF) micrographs for L1 and L2, respectively, showing several grains in the coating structure. In (c) and (d) BF and dark-field imaging of single grains belonging to L1 and L2 are respectively visualised, and their corresponding SAED patterns are given in (e) and (f). Indexing of the pattern in (f) matches to Al₂TiO₅ for L2, while the pattern in (e) matches to Al₆Ti₂O₁₃. Orange circled area represent the SAED aperture. Projected zone-axis is given in the lower right corner of (e) and (f).

Additional TEM evaluations by using SAED was carried out to evaluate the phases formed in the grains. (c) and (d) in Fig. 9 represent bright-field and dark-field imaging of a single grain in L1 and L2, respectively, whereas (e) and (f) represent the corresponding electron diffraction patterns. Clear diffraction spots emerged from both imaged grains, which were positively indexed to Al₂TiO₅ for L2 (∼ideal) and the larger Al₆Ti₂O₁₃ for L1 (Al-enriched). The presence of the Al₁₆Ti₅O₃₄ phase was not corroborated from these evaluations, which can be ascribed to the different probing volumes and projection depths between XRD, Raman and TEM.

In summary, the annealing procedure demonstrated an amorphous-to-crystalline phase transition for the main Al₂TiO₅ phase at 700 °C for 3 hours in a vacuum. The transformation occurred collectively for all samples regardless of their Al : Ti molar ratios and yielded polycrystalline coatings. Also, experimental data supported the simultaneous development of intergrowth phases, consistent with previous authors descriptions.⁵⁹ These were particularly prominent for the Al-enriched L1 and ∼ideal stoichiometric L2 sample batches. On the other hand, the two Ti-enriched batches (L3 and L4) demonstrated anatase formation as a second phase after the annealing. Altogether, these findings were evident from XRD, Raman spectroscopy and TEM.

4. Discussion

4.1. Selective kinetic growth and formation of the Al₂TiO₅ phase

The present study shows a new synthesis method to obtain coatings of Al₂TiO₅ from the co-deposition of aluminium isopropoxide and titanium isopropoxide at lower temperatures. In this regard, the Al : Ti molar ratio could be fine-tuned by altering the TIP precursor's partial vapour pressure. The possible range where the Al : Ti molar ratio can be adjusted is extensive despite the relatively small TIP precursor's varied heating interval. This finding is best illustrated in Fig. 2, where a significant reduction in the coatings' aluminium content occurs when the TIP flask's heating temperature and corresponding vapour pressure increases accordingly (and vice versa).

This relationship emphasises a strong and direct influence of the gas-phase mixture on the coatings' growth behaviour and final stoichiometry. Also, by evaluating the variations in coating thicknesses for the as-deposited coatings, seen in Fig. 3, the Ti-enriched batches (L3 and L4) show that an increased flux from the TIP precursor does not correspondingly increase the coatings' thicknesses. Even if the TIP precursor's vapour pressure increases within the reactor, the growth rate stagnates for higher TIP concentrations, thus becoming ostensibly independent of this parameter. Altogether, these features indicate a deposition process not limited by the supply of gaseous precursors but rather from the chemical reactions on the surface. Therefore, the presented MOCVD process seems to operate in a kinetically controlled regime, which will have implications on the growth and formation of the Al₂TiO₅ phase in competition with other possible phases.

In order to achieve the ternary Al₂TiO₅ phase rather than any binary constituents, it is argued that the rate-determining steps for the involved precursors should be essentially akin to one another. Otherwise, the fastest reaction will likely dominate, leading to inhomogeneities and loss in stoichiometric growth control. In essence, this inference implies that the involved precursors should share common chemical features, decompose similarly, operate under the same kind of growth mechanisms and, above all, possess overlapping and analogous process windows.

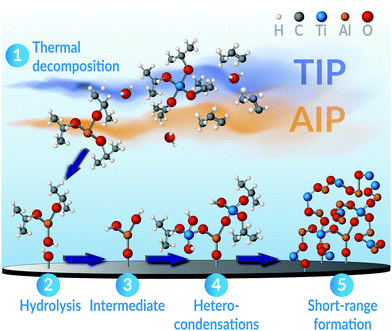
These prerequisites are met by the metal-alkoxides used within this study. In particular, previous studies on the formation of binary oxides from these precursors have revealed that both AIP and TIP independently may share a common rate-determining step. Namely, the hydrolysis of the precursors near the substrate surface.^92–94 Although deviations may exist covering the possible variations in used process parameters, as H. Vergnes et al. have noted,⁹⁵ the surface-limiting reaction step has been ascribed to a second-order mechanism for both AIP and TIP, individually.^93,94,96 More so, the activation energies of this process is practically equal between these precursors, reported as 87 ± 7 kJ mol⁻¹ for TIP⁹³ and 76–98 kJ mol⁻¹ for AIP.⁹⁷ Thus, the similarity in these precursors' rate-determining step and joint growth mechanisms infers that a kinetic selectivity^98,99 to obtain the ternary Al₂TiO₅ phase (rather than any binary ones) can be realised if these precursors are simultaneously combined. For example, in an MOCVD process as illustrated in this study and schematically shown in Fig. 10.

Fig. 10 Schematic description of the reaction steps deemed involved for the growth of the Al₂TiO₅ phase, listing five main steps. In (1) the gaseous precursors of TIP and AIP decompose thermally to yield a hydroxylated compound through the release of propene groups. At (2) the hydroxylated compound chemisorbs to the surface, where two hydroxyl groups may react by condensation reactions to form an oxy-bridge with elimination of water in the process. Hydroxylation and subsequent condensation of these groups may occur for all attached ligands (as illustrated from the intermediate in step (3). In (4), hetero-condensation occurs by attachment of a hydroxylated TIP complex to an already chemisorbed AIP molecule (or vice versa). Finally, at (5), multiple polycondensation reactions involving recurring condensation reactions of AIP and TIP lead to the formation of heterometallic Al–O–Ti bonds, resulting in a short-range order but a lack of long-range ditto, especially in the formed oxygen lattice.

Given similar process conditions for the precursors, the decomposition of AIP and TIP in our CVD process will primarily occur by thermal activation through pyrolysis.^100–102 The process may principally take two different reaction paths: (1) cyclic elimination¹⁰⁰ and (2) β-hydride elimination.^{94,96,103,104} These mechanisms are similar to those occurring in sol–gel processes,¹⁰⁰ where the precursors' successive end-transformation to their metal oxide counterparts occur via a condensation pathway.^94,100 In the process, oxy-bridges are readily formed by condensing hydroxyl groups, leading to the formation of metal–oxygen bonds and the elimination of water as a by-product.^100,105 If the rates of this process are different enough for the used reactants, the faster one will be dominating, leading primarily to homo-condensation and the principal formation of M–O–M bonds.^100,106 In such a scenario, the nucleation and growth of the multi-component phase will be impeded, and the formation of binary phases will take precedence.¹⁰⁰ On the other hand, if the condensation rates are similar between the involved reacting precursors, such as being evident for AIP and TIP, hetero-condensation is favoured instead. In this scenario, the formation of M–O–M* bonds will dominate.^100,106 The multi-component phase's growth, e.g. Al₂TiO₅, will then be significantly advantaged rather than any binary constituents.

When all involved precursors' formation rates are alike, it also becomes more feasible to adjust the coatings' final stoichiometry through varying precursor feed ratios. Supposedly, this feature is facilitated for pseudobrookite compounds like Al₂TiO₅, since these may display a nearly complete random site preference of their cations.^63,107 Hence, few limitations exist that may restrict the condensation reactions of either AIP or TIP to occur. This allows for a random mixing of the cations as the coating grows, led by an ample formation of linking oxy-bridges.¹⁰⁰ The structure of these oxy-bridges entail a high degree of Al–O–Ti order on the short-range molecular scale,¹⁰⁰ but may not necessarily create any long-range order in the evolving oxide framework. The latter notion is particularly emphasised by knowing that each gaseous AIP and TIP molecule arriving at the surface, having three or four bonded isopropyl ligands, may theoretically offer up to seven sites where these oxy-bridges can start to grow and propagate from.

Since the hetero-metallic bonds are needed to form the ternary Al₂TiO₅ phase, their preferential creation would be marked by a high level of phase purity and a short-range homogeneity.¹⁰⁶ This image conforms to the general observations made in this study's results, as seen by the SEM and TEM imaging for the as-deposited coatings (Fig. 3 and 5). Also, Raman spectroscopy (Fig. 6), enabling probing of the samples' short-range features, indicates modes belonging to Al₂TiO₅ for all inspected batches regardless of their Al : Ti molar ratios. Likewise, XRD and TEM (Fig. 4 and 5) demonstrate a complete lack of long-range order for the samples, showing that all coatings are, in essence, amorphous as-deposited.

4.2. The crystallisation of the Al₂TiO₅ phase

Upon annealing at 700 °C for 3 hours, a crystalline phase transition occurred for the Al₂TiO₅ phase in all inspected coatings regardless of their inherent Al : Ti ratio (Fig. 7). The transition is mainly observable in the L1 (Al-rich) and L2 (∼ideal) batches, where the combined results showed no other crystalline phases present. On the other hand, the L3 and L4 batches demonstrated secondary phase formation by forming anatase after annealing.

The phase transition for all samples occurring at 700 °C is interesting from a couple of aspects. Firstly, the change occurs at much lower temperatures than those used in conventional solid-state synthesis. Secondly, the heating time (3 hours) reflects a significant reduction in synthesis time. Therefore, the crystallisation of the Al₂TiO₅ phase seems to be favoured if it originates from an intermediate state characterised by a high intrinsic phase homogeneity on the molecular, short-range scale.^83,105

Such homogeneity is readily achieved by using MOCVD as a synthesis method. During growth, the step-wise atomic arrangement enables the Al₂TiO₅-phase to become stabilised in an amorphous state, held together by its oxide framework acting as a backbone for its coordinating cations. While being amorphous, the state is characterised by a high degree of hetero-metallic Al–O–Ti bonding and short-range phase homogeneity. Consequently, the ordinarily energetic and kinetically demanding steps of arranging the short-range order, a challenge seen among many conventional solid-state approaches,¹⁰⁵ are absent and already predominantly fulfilled. In such cases, only a slight readjustment, presumably mainly from the disordered oxygen framework, are required for the phase to commence its nucleation and subsequent crystallisation.^99,108 If the stoichiometry of the amorphous homogenous solid is close to the ternary phase, its crystalline formation will be significantly favoured instead of any binary phases.^98–100,105 This notion is both ascribed to a reduced nucleation barrier for the multi-component phase – stimulating its crystallisation at lower temperatures^98,99 – and insufficient diffusion at these temperatures to redistribute the cationic interior to yield any binary constituents.^100,108 From a thermodynamic perspective, the crystallisation of binary phases from such homogenous mixtures should also be at a significant disadvantage, as this would require both disproportionation and considerable diffusion lengths to occur.⁹⁹

Nevertheless, the formation of secondary phases may still arise if the stoichiometry of the amorphous phase deviates from its ideal ternary counterpart, that is, being off-stoichiometric.^100,105 In such cases, the high level of short-range homogeneity is lost in terms of the essential Al–O–Ti bonds. As shown in Fig. 7 and 8, this tendency is evident from the annealing outcome of the samples in the Ti-enriched domain (L3 and L4), where anatase readily appears as a secondary phase.

4.3. Formation of Al₆Ti₂O₁₃/Al₁₆Ti₅O₃₄ intergrowth phases

The recorded diffractograms for the annealed samples (Fig. 7) presented several features that could not be assigned to the main Al₂TiO₅ phase. These features included peak shifting and splitting effects traced to the formation of so-called intergrowth phases.⁹¹ The appearance of these intergrowth phases has earlier been associated with a high degree of stacking faults, evident by the systematic shift of specific reflections in these phases diffractograms.⁵⁹ Concurring observations to these findings are also apparent within this study, particularly for the L1 and L2 batches found in the Al-richer domain. The peak splitting features seen in the diffractograms of these batches imply a reduction in the diffracting crystals' long-range symmetry and, compatibly, the formation of the suggested intergrowth phases.

However, besides the presented XRD findings, additional information on the formation of these intergrowth phases can be extracted from the Raman spectroscopy used in this study. These investigations provide further details about the amorphous intermediates and the local short-range features in the crystalline states, both of which cannot be deduced from any diffraction measurements. Principally, these results reveal a rearrangement of the cations in the Al₂TiO₅-based structure by observing shifts in bond vibrational features in our Raman spectra. We correlate these features to structural changes of the M1 (4c) octahedral site, which is proposed to give rise to these intergrowth phases. The adjustment became more noticeable upon annealing and is characterised by a cohesive alteration of M–O bond angles and distances for this interstice, consistent with other authors' studies.⁶² As a result, an overall reduction in the distortion of the M1 cationic site occurs by changing the interstice into having a preferred four- or five-coordinating environment instead of six (for a regularly shaped octahedron). Moreover, due to this local symmetry breaking, a change of the Al₂TiO₅-based structure's long-range symmetry occurs, necessitating an enlarged unit cell to describe the arisen structure adequately. Such local symmetry breaking would be more prominent in the Al₁₆Ti₅O₃₄ intergrowth phase, where Hoffman et al. explained its structure from a repeating assemblage of M₂O₃ units possessing five-and-six coordinated cations.⁵⁹

The features leading to these deductions are particularly noticeable in the Raman spectra of the annealed L1 and L2 batches, respectively (Fig. 8). A collective shift of Raman modes to higher wavenumbers can be seen in both batches' spectra upon annealing, particularly for the bands appearing in the lower and higher spectral domain. Such features typically arise from weakening bond strength, implying an overall reduced symmetry of the local short-range environment.¹⁰⁹ Apart from the changes in the M–O bond strengths for an under-coordinated octahedron, the difference in local symmetry may also be derived from the loss of vibrational degeneracy. That is, splitting features such as doublets¹⁰⁹ and triplets seen in the lower band region of the Raman spectra. These features are mainly observed in the annealed samples and can be ascribed to local changes in symmetry bond coordination with possible contributions from vacancies and stacking faults.¹⁰⁹ Hoffman et al. indeed reported observation of stacking faults among these phases.⁵⁹

Utilising the mass difference between aluminium (∼27 u) and titanium (∼48 u), a quantitative difference in their respective M–O frequencies can be extracted assuming similar force constants. Recalling that the zone-centred maximum frequency, w_max, is given as

w_max = (2γ/μ)^1/2 (1)

where γ is the force constant and μ is the reduced mass in a linear chain model with alternating metal–oxygen bonds – a less heavy element would translate to a higher frequency shift for a situation with unchanged bond strength. Since Raman spectroscopy is exceptionally sensitive to such changes, it is possible to deduce that the lower band region in the recorded spectra relates to the heavier titanium atoms' vibrations with its surrounding coordinating atoms, i.e. oxygen. Thus, the symmetry-breaking elements and splitting effects seen for the Raman bands at lower wavenumbers primarily relate to the interstices incorporating titanium as a cation.

Before using this information to analyse the local coordination further, it is instructive to review previously reported findings. Although Al₂TiO₅ is commonly claimed to possess a complete cationic disorder, evidence has shown that the occupancy ratio between its two metal sites may vary significantly with ambient conditions, such as the phase's exposed temperature.⁷⁸ While earliest observations from Navrotsky et al. showed a general preference for Ti to occupy the M2 (8f) site within pseudobrookite compounds,⁷⁷ recent findings involving Al₂TiO₅ have instead demonstrated a moderate tendency for Ti to occupy the larger M1 (4c) site, particularly at room temperature.^62,78,110 Because Raman spectroscopy has been made at ambient room conditions in this study, it is inferred that the observed symmetry breaking relates to positional changes predominantly occurring on the M1 (4c) site. This view adds to the findings made by R. D. Skala et al., who demonstrated by neutron diffraction that a structural transition of the M1 (4c) site mainly occurred for Al₂TiO₅ after annealing.⁶² Interestingly, similar structural changes have been shown to occur for other pseudobrookite compounds, such as MgTi₂O₅.^111–114 The transition has been linked to a shift in symmetry, causing a reduction in the distortion of the M1 site.^{62,63,78,111,112} Skala et al. mentioned that this transition resulted in an increased unit-cell of Al₂TiO₅ after annealing.⁶² Likewise, Navrotsky et al. suggested a possible local ordering of cations in these pseudobrookite compounds giving rise to a denoted superstructure.⁷⁷ Nonetheless, neither of these authors recognised or ascribed these features to the formation of any new phases in the Al–O–Ti system, which Hoffman et al. initially did,⁵⁹ and which we further expound on here.

The structural transition to the M1 site is due to a synchronised transformation of the six M–O bonds constituting the disordered octahedron, which give rise to the features seen in our Raman spectra. In the study of Skala et al., the transition of the M1 site involved a lengthening of four M1–O1/M1–O3 bonds and a shortening of two M1–O2 upon increasing temperatures.⁶² Although not explicitly mentioned by these authors, such rearrangement would transpose the once distorted octahedron to a tetragonal bipyramid. This geometry is marked by its lower coordination, such as four- or five, which essentially makes up the designated intergrowth phases.^59,91 Similar occurrences of pseudo-tetrahedral units have also been found in the comparable MgTi₂O₅ pseudobrookite compound.¹¹² All the more so, Morosin & Lynch made early claims that such geometry may arise in Al₂TiO₅ by cleaving planes perpendicular to the a-axis (here referring to the Bbmm space group as used within their study).⁶³

Due to the structural transition of M1, where the site may offer a lower coordinating environment to house its cation, Skala et al. also described an increased aluminium occupancy to this site.⁶² That is, aluminium seemed to prefer the altered M1 (4c) site having lower, tetrahedral coordination, leading to increased mixing of cations between the two sites once this site had transformed.

The Raman spectra within this study can help understand the aforementioned suggestions of local structural changes not only to Al₂TiO₅ but also possibly to other relatable pseudobrookite phases. For instance, the broadening of bands seen in the annealed samples of L1 and L2 (Fig. 8) – compared to their as-deposited conditions – correlate to an increased isotropic displacement factor, implying a higher uncertainty and an increased level of cationic mixing. Similar notions have been made within comparable material systems.^109,111,113 In addition, an increased level of lower coordinating cationic sites, indicating the presence of intergrowth phases rather than Al₂TiO₅, is derived from the intense, symmetric Raman band around 850–900 cm⁻¹ in Fig. 8. This band is particularly evident in the annealed samples of L1 and L2. Typically, vibrational modes lying in this frequency region signify a tetragonal environment for aluminates and similar systems.^115–117 Likewise, their presence has been assigned to the symmetric stretching of tetragonal Al–O bonds.¹¹⁸ Hence, the combined features discernible in the Raman spectra of the annealed samples (Fig. 8) – such as vibrational shifts, splitting effects, broadenings, and significant growth of intensity for specific bands in the higher spectral domain – may all be collectively invoked to explain the presence of lower coordinating environments in our samples upon annealing.

Even if much attention has been brought to the annealed coatings, the presence of five- or even four-coordinated M1 sites in their as-deposited states cannot be entirely ruled out. That is because of AIP's known ability to stabilise itself in its vapour phase both as a trimeric and tetrameric form.¹¹⁹ The two species' ratio seems to depend on the AIP precursor's thermal prehistory, which accounts for its ability to self-oligomerise with time in its stored melted, supercooled state.¹¹⁹ Markedly, the stabilisation of five-coordinated aluminium is a known feature from using AIP as a sole precursor.¹²⁰ Therefore, if AIP's trimeric configuration attaches to an already chemisorbed tetrameric TIP molecule on the surface (or vice versa), it may efficiently encapsulate the aluminium ion into having a lower coordination environment. Such would then lead to a local symmetry breaking already during the actual growth of the coating and not necessarily from the subsequent annealing step. Seemingly, this may explain the apparent connection between the band splitting features found in the spectra's lower frequency region (Fig. 6 and 8) – indicating a lower symmetry – to the bands lying at 850–900 cm⁻¹ area – marking a tetrahedral symmetric stretching. This relation is most noticeable in the as-deposited Raman spectra of L1 and L2, yet surprisingly, it could also be viewed in the as-deposited L3 (1 : 1) batch. The observation of these features already in the as-deposited state of L3 (1 : 1) – being at higher Ti-contents – implies that the formation of the intergrowth phases, as initially explained by Hoffman et al.,⁵⁹ may not necessarily arise from an Al-enriched environment only. Instead, it emphasises the role of local coordination. This view is further supported from XRD (Fig. 7) since peaks associated with the intergrowth phases are not only visible in the Al-enriched L1 batch after annealing but in the ∼ideal stoichiometric L2 and Ti-enriched L3 (1 : 1) batches as well.

Consequently, our results suggest that the formation of the intergrowth phases is primarily dependent on the M1 (4c) site's role and local coordination rather than the strict compositional role of aluminium. In other words, the appearance of these intergrowth phases seems primarily correlated to the structural integrity, size, and function of this M1 (4c) site. Aluminium's increased possession of this site could then possibly be regarded as an effect – not a principal cause – of this transformation by offering a more suitable location to house this particular cation. It remains nonetheless to be understood why aluminium may prefer this lower coordinating site and how this, in turn, may influence the intergrowth phases' general properties on a larger, macroscopic scale.

In conclusion, the intergrowth phases' formation appears not to be compositional driven, at least not for the MOCVD process presented herein. Instead – and perhaps even more importantly – it seems that the inherent local short-range features of the M1 (4c) site found in the Al₂TiO₅-structure, and also within other similar pseudobrookite compounds, are the key and original determinants for the formation of these intergrowth phases.

5. Summary & conclusions

Solid-state techniques have long sought an efficient way to synthesise Al₂TiO₅ with good phase purity without any binary oxides co-formation. In its bulk form, the Al₂TiO₅ phase is renowned for its low-to-negative thermal expansion coefficient, making it an excellent potential candidate for many refractory and metallurgical applications. However, its synthesis has remained challenging, both in terms of solid-state processings and in the form of coatings. Herein, we have presented a co-deposition MOCVD method to obtain this phase using two analogous metal alkoxide-based precursors at lower temperatures: aluminium-isopropoxide and titanium-isopropoxide. By varying the titanium precursor's feed rate, it became possible to alter the Al : Ti molar ratio in the finalised coatings to a high degree. As a result, the grown coatings possessed a short-range homogeneity and were essentially amorphous as-deposited. Upon annealing at 700 °C for 3 hours, crystalline Al₂TiO₅ coatings were achieved without any binary phases' formation. Besides Al₂TiO₅, unconventional intergrowth phases based on Al₂TiO₅ could also be detected within the samples, especially after annealing. The appearance of the ternary Al₂TiO₅ phase instead of any binary constituents is ascribed to the shared chemical features between the used precursors, resulting in a selective kinetic growth and targeting of this phase. Moreover, the presented MOCVD process enables the step-wise atomic arrangements to yield the Al₂TiO₅-phase that, upon heating, readily crystallises at lower temperatures and shorter timescales than with any solid-state techniques presented thus far.

Raman spectroscopy was utilised to probe the local short-range features in the samples before and after annealing. These findings indicate lower coordinating domains in the samples whose presence is a characterising feature to the described intergrowth phases. Furthermore, the results show that these lower coordinating domains correlate to a transformation of the interstices found in Al₂TiO₅, mainly the M1 (4c) site. This rearrangement allows the formation of these intergrowth phases to occur in the Al₂TiO₅-structure, emphasising the role of local coordination for this compound and its role for phase evolution and final structure in potentially other pseudobrookite compounds as well.

Author contributions

Sebastian Öhman – conceptualisation, syntheses, formal analyses EDS, XRD, SEM, Raman spectroscopy, visualisation, writing – original draft except for TEM part. Ren Qiu – formal analyses TEM, writing TEM part original draft. Tomas Edvinsson – formal analyses Raman spectroscopy, supervision & guidance of Raman spectroscopic measurements, review and editing. Olof Bäcke – formal analyses TEM. Tobias Törndahl – supervision, review & editing. Mats Boman – funding acquisition, project administration, supervision, review and editing.

Conflicts of interest

The authors declare no conflict of interest (COI).

Acknowledgements

The Swedish Foundation for Strategic Research (SSF), contract RMA15-0048, and the Swedish Research Council (VR), contracts 2019-05591 and 2015-03814, are acknowledged for their financial support. All TEM characterisation experiments were carried out at the Chalmers Materials Analysis Laboratory (CMAL).

References

1. Z. Fang and K. Terakura, J. Phys.: Condens. Matter, 2002, 14(11), 3001–3014,  DOI:10.1088/0953-8984/14/11/312.
2. J. Chakhalian, J. W. Freeland, G. Srajer, J. Strempfer, G. Khaliullin and J. C. Cezar, et al. , Nat. Phys., 2006, 2(4), 244–248,  DOI:10.1038/nphys272.
3. B. Keimer, Nat. Mater., 2006, 5(12), 933–934,  DOI:10.1038/nmat1783.
4. M. Batzill, Energy Environ. Sci., 2011, 4, 3275–3286,  10.1039/c1ee01577j.
5. J. Yu and X. Yu, Environ. Sci. Technol., 2008, 42(13), 4902–4907,  DOI:10.1021/es800036n.
6. R. J. Colton, A. M. Guzman and J. W. Rabalais, Acc. Chem. Res., 1978, 11(4), 170–176,  DOI:10.1021/ar50124a008.
7. S. Green, J. Backholm, P. Georén, C. G. Granqvist and G. A. Niklasson, Sol. Energy Mater. Sol. Cells, 2009, 93(12), 2050–2055,  DOI:10.1016/j.solmat.2009.05.009.
8. M. T. Weller and C. S. Knee, J. Mater. Chem., 2001, 11, 701–712,  10.1039/b009457i.
9. Y. Kamihara, H. Hiramatsu, M. Hirano, R. Kawamura, H. Yanagi and T. Kamiya, et al. , J. Am. Chem. Soc., 2006, 128(31), 10012–10013,  DOI:10.1021/ja063355c.
10. J. G. Bednorz and K. A. Müller, Z. Phys. B: Condens. Matter, 1986, 64(2), 189–193,  DOI:10.1007/BF01303701.
11. K. Takenaka, Sci. Technol. Adv. Mater., 2012, 13(1), 013001,  DOI:10.1088/1468-6996/13/1/013001.
12. N. Shi, A. Sanson, Q. Gao, Q. Sun, Y. Ren and Q. Huang, et al. , J. Am. Chem. Soc., 2020, 142(6), 3088–3093,  DOI:10.1021/jacs.9b12442.
13. Y. Gao, C. Wang, Q. Gao, J. Guo, M. Chao and Y. Jia, et al. , Inorg. Chem., 2020, 59(24), 18427–18431,  DOI:10.1021/acs.inorgchem.0c03046.
14. J. S. O. Evans, T. A. Mary, T. Vogt, M. A. Subramanian and A. W. Sleight, Chem. Mater., 1996, 8(12), 2809–2823,  DOI:10.1021/cm9602959.
15. J. Chen, L. Hu, J. Deng and X. Xing, Chem. Soc. Rev., 2015, 44, 3522–3567,  10.1039/c4cs00461b.
16. B. A. Marinkovic, M. Ari, R. R. De Avillez, F. Rizzo, F. F. Ferreira and K. J. Miller, et al. , Chem. Mater., 2009, 21(13), 2886–2894,  DOI:10.1021/cm900650c.
17. K. Röttger, A. Endriss, J. Ihringer, S. Doyle and W. F. Kuhs, Acta Crystallogr., Sect. B: Struct. Sci., 1994, 50(6), 644–648,  DOI:10.1107/S0108768194004933.
18. J. S. O. Evans, T. A. Mary and A. W. Sleight, J. Solid State Chem., 1997, 133(2), 580–583,  DOI:10.1006/jssc.1997.7605.
19. F. R. Drymiotis, H. Ledbetter, J. B. Betts, T. Kimura, J. C. Lashley and A. Migliori, et al. , Phys. Rev. Lett., 2004, 93(2), 1–4,  DOI:10.1103/PhysRevLett.93.025502.
20. T. A. Mary and A. W. Sleight, J. Mater. Res., 1999, 14(3), 912–915,  DOI:10.1557/JMR.1999.0122.
21. V. Korthuis, N. Khosrovani, A. W. Sleight, N. Roberts, R. Dupree and W. W. Warren, Chem. Mater., 1995, 7(2), 412–417,  DOI:10.1021/cm00050a028.
22. M. A. Violini, M. F. Hernández, M. Gauna, G. Suarez, M. S. Conconi and N. M. Rendtorff, Ceram. Int., 2018, 44(17), 21470–21477,  DOI:10.1016/j.ceramint.2018.08.208.
23. X. Xing, J. Chen, J. Deng and G. Liu, J. Alloys Compd., 2003, 360(1–2), 286–289,  DOI:10.1016/S0925-8388(03)00345-1.
24. Y. He, Thermochim. Acta, 2004, 419(1–2), 135–141,  DOI:10.1016/j.tca.2004.02.008.
25. X. Chen, F. Guo, X. Deng, J. Tao, H. Ma and X. Zhao, J. Alloys Compd., 2012, 537, 227–231,  DOI:10.1016/j.jallcom.2012.04.106.
26. J. Matsuno, J. Fujioka, T. Okuda, K. Ueno, T. Mizokawa and T. Katsufuji, Sci. Technol. Adv. Mater., 2018, 19(1), 899–908,  DOI:10.1080/14686996.2018.1529524.
27. C. R. Bowen, H. A. Kim, P. M. Weaver and S. Dunn, Energy Environ. Sci., 2014, 7(1), 25–44,  10.1039/c3ee42454e.
28. Y. Sun, P. Guan, Y. Liu, H. Xu, S. Li and D. Chu, Crit. Rev. Solid State Mater. Sci., 2019, 44(4), 265–282,  DOI:10.1080/10408436.2018.1485551.
29. F. Diao and Y. Wang, J. Mater. Sci., 2018, 53(6), 4334–4359,  DOI:10.1007/s10853-017-1862-3.
30. C. Lin, A. Posadas, M. Choi and A. A. Demkov, J. Appl. Phys., 2015, 117(3), 17–20,  DOI:10.1063/1.4905738.
31. K. A. Zemski, D. R. Justes and A. W. Castleman, J. Phys. Chem. B, 2002, 106(24), 6136–6148,  DOI:10.1021/jp0142334.
32. F. Haque, T. Daeneke, K. Kalantar-zadeh and J. Z. Ou, Nano-Micro Lett., 2018, 10(2), 1–27,  DOI:10.1007/s40820-017-0176-y.
33. X. Q. Cao, R. Vassen and D. Stoever, J. Eur. Ceram. Soc., 2004, 24(1), 1–10,  DOI:10.1016/S0955-2219(03)00129-8.
34. E. Lalli, N. M. D. Vitorino, C. A. M. Portugal, J. G. Crespo, C. Boi and J. R. Frade, et al. , Mater. Des., 2017, 131, 92–101,  DOI:10.1016/j.matdes.2017.06.010.
35. A. Stein, S. W. Keller and T. E. Mallouk, Science, 1993, 259(5101), 1558–1564,  DOI:10.1126/science.259.5101.1558.
36. J. Gopalakrishnan, N. S. P. Bhuvanesh and K. K. Rangan, Curr. Opin. Solid State Mater. Sci., 1996, 1(2), 285–294,  DOI:10.1016/S1359-0286(96)80096-9.
37. A. J. Martinolich and J. R. Neilson, Chem. Mater., 2017, 29(2), 479–489,  DOI:10.1021/acs.chemmater.6b04861.
38. A. J. Martinolich, J. A. Kurzman and J. R. Neilson, J. Am. Chem. Soc., 2016, 138(34), 11031–11037,  DOI:10.1021/jacs.6b06367.
39. W. Sun, S. T. Dacek, S. P. Ong, G. Hautier, A. Jain and W. D. Richards, et al. , Sci. Adv., 2016, 2(11), e1600225,  DOI:10.1126/sciadv.1600225.
40. R. Uppuluri, A. Sen Gupta, A. S. Rosas and T. E. Mallouk, Chem. Soc. Rev., 2018, 47(7), 2401–2430,  10.1039/c7cs00290d.
41. A. J. Martinolich, J. A. Kurzman and J. R. Neilson, J. Am. Chem. Soc., 2015, 137(11), 3827–3833,  DOI:10.1021/ja512520z.
42. A. E. Danks, S. R. Hall and Z. Schnepp, Mater. Horiz., 2016, 3(2), 91–112,  10.1039/c5mh00260e.
43. Z. Jiang, S. Tian, S. Lai, R. D. McAuliffe, S. P. Rogers and M. Shim, et al. , Chem. Mater., 2016, 28(9), 3080–3089,  DOI:10.1021/acs.chemmater.6b00421.
44. S. Park, M. Peddigari, J. H. Kim, E. Kim, G. T. Hwang and J. W. Kim, et al. , Inorg. Chem., 2020, 59(5), 3042–3052,  DOI:10.1021/acs.inorgchem.9b03385.
45. B. R. Chen, W. Sun, D. A. Kitchaev, J. S. Mangum, V. Thampy and L. M. Garten, et al. , Nat. Commun., 2018, 9(1), 2553–2562,  DOI:10.1038/s41467-018-04917-y.
46. A. J. Jacobson, J. W. Johnson and J. T. Lewandowski, Inorg. Chem., 1985, 24(23), 3727–3729,  DOI:10.1021/ic00217a006.
47. V. Pralong, Prog. Solid State Chem., 2009, 37(4), 262–277,  DOI:10.1016/j.progsolidstchem.2010.08.002.
48. J. C. Grenier, A. Wattiaux, J. P. Doumerc, P. Dordor, L. Fournes and J. P. Chaminade, et al. , J. Solid State Chem., 1992, 96(1), 20–30,  DOI:10.1016/S0022-4596(05)80293-2.
49. H. Holleck, Surf. Coat. Technol., 1988, 36(1–2), 151–159,  DOI:10.1016/0257-8972(88)90145-4.
50. H. Nishinaka and M. Yoshimoto, Cryst. Growth Des., 2018, 18(7), 4022–4028,  DOI:10.1021/acs.cgd.8b00387.
51. R. Hofman, R. W. J. Morssinkhof, T. Fransen, J. G. F. Westheim and P. J. Gellings, Mater. Manuf. Process., 1993, 8(3), 315–329,  DOI:10.1080/10426919308934836.
52. J. K. Harada, N. Charles, K. R. Poeppelmeier and J. M. Rondinelli, Adv. Mater., 2019, 31(19), 1805295,  DOI:10.1002/adma.201805295.
53. J. L. Fenton, B. C. Steimle and R. E. Schaak, Inorg. Chem., 2019, 58(1), 672–678,  DOI:10.1021/acs.inorgchem.8b02880.
54. T. Lüdtke, D. Weber, A. Schmidt, A. Müller, C. Reimann and N. Becker, et al. , Z. Kristallogr. – Cryst. Mater., 2017, 232(1–3), 3–14,  DOI:10.1515/zkri-2016-1961.
55. P. K. Todd, A. Wustrow, R. D. McAuliffe, M. J. McDermott, G. T. Tran and B. C. McBride, et al. , Inorg. Chem., 2020, 59(18), 13639–13650,  DOI:10.1021/acs.inorgchem.0c02023.
56. E. C. Ethridge, S. C. Erwin and W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52(12), R8589–R8593,  DOI:10.1103/physrevb.52.r8589.
57. W. Hu, L. Li, G. Li, Y. Liu and R. L. Withers, Sci. Rep., 2014, 4, 1–9,  DOI:10.1038/srep06582.
58. P. K. Todd and J. R. Neilson, J. Am. Chem. Soc., 2019, 141(3), 1191–1195,  DOI:10.1021/jacs.8b10123.
59. S. Hoffmann, S. T. Norberg and M. Yoshimura, J. Solid State Chem., 2005, 178(9), 2897–2906,  DOI:10.1016/j.jssc.2005.07.001.
60. M. Nagano, S. Nagashima, H. Maeda and A. Kato, Ceram. Int., 1999, 25(8), 681–687,  DOI:10.1016/S0272-8842(98)00083-2.
61. I. J. Kim and H. S. Kwak, Can. Metall. Q., 2000, 39(4), 387–396,  DOI:10.1179/cmq.2000.39.4.387.
62. R. D. Skala, D. Li and I. M. Low, J. Eur. Ceram. Soc., 2009, 29(1), 67–75,  DOI:10.1016/j.jeurceramsoc.2008.05.037.
63. B. Morosin and R. W. Lynch, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28(4), 1040–1046,  DOI:10.1107/s0567740872003681.
64. M. Soofi, L. Binz and W. M. Anderson, US Pat., 10233335B2, 2019.
65. S. Tian, K. Sun, H. Cui, X. Xie, X. Wang and N. Wei, et al. , Thin Solid Films, 2019, 692, 137640,  DOI:10.1016/j.tsf.2019.137640.
66. I. M. Low and Z. Oo, J. Am. Ceram. Soc., 2008, 91(3), 1027–1029,  DOI:10.1111/j.1551-2916.2007.02199.x.
67. H. C. Kim, K. S. Lee, O. S. Kweon, C. G. Aneziris and I. J. Kim, J. Eur. Ceram. Soc., 2007, 27(2–3), 1431–1434,  DOI:10.1016/j.jeurceramsoc.2006.04.024.
68. A. Azarniya, M. Soltaninejad, M. Zekavat, F. Bakhshandeh, H. R. Madaah Hosseini and C. Amutha, et al. , Mater. Chem. Phys., 2020, 256, 123740,  DOI:10.1016/j.matchemphys.2020.123740.
69. M. M. Welander, M. S. Zachariasen, S. W. Sofie and R. A. Walker, J. Phys. Chem. C, 2019, 123(18), 11406–11413,  DOI:10.1021/acs.jpcc.9b00964.
70. W. Dean McKee and E. Aleshin, J. Am. Ceram. Soc., 1963, 46(1), 54–58,  DOI:10.1111/j.1151-2916.1963.tb13771.x.
71. S. K. Roy and R. L. Coble, J. Am. Ceram. Soc., 1968, 51(1), 1–6,  DOI:10.1111/j.1151-2916.1966.tb13316.x-i1.
72. B. Freudenberg and A. Mocellin, J. Mater. Sci., 1990, 25(8), 3701–3708,  DOI:10.1007/BF00575408.
73. M. Ilatovskaia, G. Savinykh and O. Fabrichnaya, J. Phase Equilib. Diffus., 2017, 38(3), 175–184,  DOI:10.1007/s11669-016-0509-4.
74. M. Ishitsuka, T. Sato, T. Endo and M. Shimada, J. Am. Ceram. Soc., 1987, 70(2), 69–71,  DOI:10.1111/j.1151-2916.1987.tb04931.x.
75. V. Buscaglia, G. Battilana, M. Leoni and P. Nanni, J. Mater. Sci., 1996, 31(19), 5009–5016,  DOI:10.1007/BF00355899.
76. D. M. Xirouchakis, Lithos, 2007, 95(1–2), 1–9,  DOI:10.1016/j.lithos.2006.07.009.
77. A. Navrotsky, Am. Mineral., 1975, 60(3–4), 249–256.
78. Y. Ohya, Y. Kawauchi and T. Ban, J. Ceram. Soc. Jpn., 2017, 125(9), 695–700,  DOI:10.2109/jcersj2.17086.
79. L. Pauling, Z. Kristallogr. – Cryst. Mater., 1930, 73(1), 97–112,  DOI:10.1524/zkri.1930.73.1.97.
80. T. Epicier, G. Thomas, H. Wohlfromm and J. S. Moya, J. Mater. Res., 1991, 6(1), 138–145,  DOI:10.1557/JMR.1991.0138.
81. M. Dondi, T. S. Lyubenova, J. B. Carda and M. Ocaña, J. Am. Ceram. Soc., 2009, 92(9), 1972–1980,  DOI:10.1111/j.1551-2916.2009.03172.x.
82. D. Leinen, G. Lassaletta, A. Fernández, A. Caballero, A. R. González-Elipe and J. M. Martín, et al. , J. Vac. Sci. Technol., A, 1996, 14(5), 2842–2848,  DOI:10.1116/1.580233.
83. P. Innocenzi, A. Martucci, L. Armelao, S. Licoccia, M. L. Di Vona and E. Traversa, Chem. Mater., 2000, 12(2), 517–524,  DOI:10.1021/cm991134i.
84. D.-H. Kuo, B.-Y. Cheung and R.-J. Wu, Thin Solid Films, 2001, 398–399, 35–40,  DOI:10.1016/S0040-6090(01)01300-1.
85. D.-H. Kuo and C.-N. Shueh, Thin Solid Films, 2005, 478(1–2), 109–115,  DOI:10.1016/j.tsf.2004.10.021.
86. M. A. Omari, R. S. Sorbello and C. R. Aita, J. Vac. Sci. Technol., A, 2006, 24(2), 317–323,  DOI:10.1116/1.2171710.
87. A. Richter, L. M. Berger, S. Conze, Y. J. Sohn and R. Vaßen, IOP Conf. Ser.: Mater. Sci. Eng., 2019, 480(1), 012007,  DOI:10.1088/1757-899X/480/1/012007.
88. A. Ito, S. Nishigaki and T. Goto, J. Eur. Ceram. Soc., 2015, 35(7), 2195–2199,  DOI:10.1016/j.jeurceramsoc.2015.01.027.
89. S. Webb, N. M. Alford, S. Penn, A. Templeton and X. Wang, Nondestr. Test. Eval., 2001, 17(4–5), 205–212,  DOI:10.1080/10589750108953111.
90. L. Bonhomme-Coury, N. Lequeux, S. Mussotte and P. Boch, J. Sol-Gel Sci. Technol., 1994, 2(1–3), 371–375,  DOI:10.1007/BF00486273.
91. S. T. Norberg, S. Hoffmann, M. Yoshimura and N. Ishizawa, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2005, 61(3), i35–i38,  DOI:10.1107/S0108270105002532.
92. V. Gourinchas Courtecuisse, K. Chhor, J.-F. Bocquet and C. Pommier, Ind. Eng. Chem. Res., 1996, 35(8), 2539–2545,  DOI:10.1021/ie950584r.
93. M. Reinke, Y. Kuzminykh and P. Hoffmann, J. Phys. Chem. C, 2015, 119(50), 27965–27971,  DOI:10.1021/acs.jpcc.5b07177.
94. R. Hofman, R. W. J. Morssinkhof, T. Fransen, J. G. F. Westheim and P. J. Gellings, Mater. Manuf. Process., 1993, 8(3), 315–329,  DOI:10.1080/10426919308934836.
95. H. Vergnes, D. Samélor, A. N. Gleizes, C. Vahlas and B. Caussat, Chem. Vap. Deposition, 2011, 17(7–9), 181–185,  DOI:10.1002/cvde.201004301.
96. V. A. C. Haanappel, H. D. van Corbach, R. Hofman, R. W. J. Morssinkhof, T. Fransen and P. J. Gellings, High Temp. Mater. Processes, 1996, 15(4), 245–262,  DOI:10.1515/HTMP.1996.15.4.245.
97. B. W. Schmidt, W. J. Sweet, E. J. Bierschenk, C. K. Gren, T. P. Hanusa and B. R. Rogers, J. Vac. Sci. Technol., A, 2010, 28(2), 238–243,  DOI:10.1116/1.3294718.
98. T. Novet and D. C. Johnson, J. Am. Chem. Soc., 1991, 113(9), 3398–3403,  DOI:10.1021/ja00009a027.
99. L. Fister, R. Brown and D. C. Johnson, J. Am. Chem. Soc., 1994, 116(2), 629–633,  DOI:10.1021/ja00081a025.
100. A. Vioux, Chem. Mater., 1997, 9(11), 2292–2299,  DOI:10.1021/cm970322a.
101. S. Acosta, R. J. P. Corriu, D. Leclercq, P. Lefèvre, P. H. Mutin and A. Vioux, J. Non-Cryst. Solids, 1994, 170(3), 234–242,  DOI:10.1016/0022-3093(94)90052-3.
102. C. J. Taylor, D. C. Gilmer, D. G. Colombo, G. D. Wilk, S. A. Campbell and J. Roberts, et al. , J. Am. Chem. Soc., 1999, 121(22), 5220–5229,  DOI:10.1021/ja984446f.
103. S. S. Lee, E. S. Lee, S. H. Kim, B. K. Lee, S. J. Jeong and J. H. Hwang, et al. , Bull. Korean Chem. Soc., 2012, 33(7), 2207–2212,  DOI:10.5012/bkcs.2012.33.7.2207.
104. R. Hofman, J. G. F. Westheim, V. A. C. Haanappel, T. Fransen and P. J. Gellings, Thermochim. Acta, 1993, 215(C), 329–335,  DOI:10.1016/0040-6031(93)80109-N.
105. P. Barboux, P. Griesmar, F. Ribot and L. Mazerolles, J. Solid State Chem., 1995, 117(2), 343–350,  DOI:10.1006/jssc.1995.1283.
106. M. Andrianainarivelo, R. J. P. Corriu, D. Leclercq, P. H. Mutin and A. Vioux, Chem. Mater., 1997, 9(5), 1098–1102,  DOI:10.1021/cm960405b.
107. A. Feltz and F. Schmidt, J. Eur. Ceram. Soc., 1990, 6(2), 107–110,  DOI:10.1016/0955-2219(90)90043-F.
108. F. F. Lange, M. L. Balmer and C. G. Levi, J. Sol-Gel Sci. Technol., 1994, 2(1–3), 317–321,  DOI:10.1007/BF00486263.
109. T. H. Nguyen, T. M. H. Nguyen, B. Kang, B. Cho, M. Han and H. J. Choi, et al. , J. Raman Spectrosc., 2019, 50(11), 1661–1671,  DOI:10.1002/jrs.5709.
110. S. T. Norberg, N. Ishizawa, S. Hoffmann and M. Yoshimura, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, 61(8), i160–i162,  DOI:10.1107/S1600536805021331.
111. H. Yang and R. M. Hazen, J. Solid State Chem., 1998, 138(2), 238–244,  DOI:10.1006/jssc.1998.7775.
112. A. R. Lennie, K. S. Knight and M. B. Henderson, Am. Mineral., 2007, 92(7), 1165–1180,  DOI:10.2138/am.2007.2322.
113. M. He, B. Winkler, J. D. Bauer, L. Bayarjargal, J. Ruiz-Fuertes and I. Alencar, et al. , J. Alloys Compd., 2017, 699, 16–24,  DOI:10.1016/j.jallcom.2016.12.217.
114. H. P. Liermann, R. T. Downs and H. Yang, Am. Mineral., 2006, 91(5–6), 790–793,  DOI:10.2138/am.2006.2027.
115. P. McMillan, B. Piriou and A. Navrotsky, Geochim. Cosmochim. Acta, 1982, 46(11), 2021–2037,  DOI:10.1016/0016-7037(82)90182-X.
116. P. McMillan and B. Piriou, Bull. Mineral., 1983, 106(1–2), 57–75,  DOI:10.3406/bulmi.1983.7668.
117. A. N. Novikov, D. R. Neuville, L. Hennet, Y. Gueguen, D. Thiaudière and T. Charpentier, et al. , Chem. Geol., 2017, 461, 115–127,  DOI:10.1016/j.chemgeo.2016.11.023.
118. B. O. Mysen, D. Virgo and I. Kushiro, Am. Mineral., 1981, 66(7–8), 678–701.
119. M.-M. Sovar, D. Samélor, A. N. Gleizes and C. Vahlas, Surf. Coat. Technol., 2007, 201(22–23), 9159–9162,  DOI:10.1016/j.surfcoat.2007.04.063.
120. V. Sarou-Kanian, A. N. Gleizes, P. Florian, D. Samélor, D. Massiot and C. Vahlas, J. Phys. Chem. C, 2013, 117(42), 21965–21971,  DOI:10.1021/jp4077504.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00428j

---