Open Access Article
Open Access ArticleRemarkable electrochemical and ion-transport characteristics of magnesium-fluorinated alkoxyaluminate–diglyme electrolytes for magnesium batteries†
Toshihiko
Mandai
 *,
Yong
Youn
*,
Yong
Youn
 and
Yoshitaka
Tateyama
and
Yoshitaka
Tateyama

Center for Green Research on Energy and Environmental Materials, National Institute for Materials Science (NIMS), 1-1 Namiki, Tsukuba, Ibaraki 305-0044, Japan. E-mail: MANDAI.Toshihiko@nims.go.jp
First published on 23rd July 2021
Abstract
Magnesium batteries (MBs) are fascinating options for large-scale energy-storage devices because the properties of magnesium metal anodes are more advantageous than those of their lithium or sodium counterparts. Moreover, the recent rapid progress in electrolyte materials will surely benefit MB research and development. Magnesium salts incorporating fluorinated alkoxyborate or alkoxyaluminate anions are an emerging class of potential MB electrolyte materials owing to their outstanding characteristics, such as favorable anodic stability and excellent compatibility with magnesium metal. Despite the growing number of reports on such electrolytes, the optimal electrolyte compositions remain unclear and, hence, must be investigated for practical application to MBs. Therefore, we comprehensively compared the bulk physicochemical properties, electrochemical characteristics, and ion-transport behaviors of ethereal solutions of magnesium-fluorinated alkoxyborate and alkoxyaluminate. By systematically characterizing the composition–property relationships, we found that the magnesium-fluorinated alkoxyaluminate Mg[Al(HFIP)4]2 (HFIP = hexafluoro-iso-propoxyl group) and diglyme (G2) salt–solvent combination exhibited outstanding electrochemical activity. The optimal electrolyte allowed highly stable and efficient magnesium deposition/dissolution cycling for over 250 cycles with a coulombic efficiency of 99.4% under an exceptionally low polarization <±60 mV despite the absence of strong Lewis acidic agents. As evidenced by the Vogel–Tammann–Fulcher fitting analysis, impedance spectroscopy results, and ab initio molecular dynamics calculations, the well-balanced solvation/desolvation of G2 toward Mg2+ ions and the remarkable ion-transport and interfacial characteristics and sufficient reduction stability of the [Al(HFIP)4]− were the reasons for the outstanding electrochemical performance.
Introduction
Transforming social infrastructure with the development of highly efficient energy-harvesting and -storage technologies is a very important pillar for improving societal wellbeing and achieving sustainable development worldwide. Among the various prospective technologies, large-scale stationary electrical energy-storage systems must be developed to expand the use of sustainable energy such as solar and wind power and to effectively utilize surplus nighttime electricity generated by power plants. Owing to the high natural abundance, low cost, and high specific/volumetric capacities of magnesium metal, magnesium batteries (MBs) are promising candidates for meeting such energy requirements.1 By combining high-voltage intercalation or high-capacity conversion cathodes with magnesium metal anodes, the energy densities of MBs can reach 500 Wh kg−1 or greater.2–5 The long cycle-life MBs having comparable energy densities to present lithium ion batteries have also emerged by combining well-designed nanomaterials.6–8 To manufacture such outperforming batteries, various electrode and electrolyte materials have been developed, especially in the last decade.Although the intrinsic physicochemical properties of cathode and anode materials determine the resulting battery performance (i.e., theoretical capacity and energy density) in principle, electrolytes are also striking components in battery operation as they support the mass transport of active species (directly related to power density) and facilitate interfacial reactions at both the cathode and anode. In stark contrast to lithium- and sodium-based batteries, MBs can only employ a very limited range of salt–solvent combinations, whereas conventional electrolyte solutions applicable to lithium-ion batteries do not support fundamental interfacial reactions, especially at magnesium anodes.9–11 Halide-containing ethereal solutions consisting of different magnesium sources and strong Lewis acids such as AlCl3, AlCl2(C2H5), BPh3 [Ph = phenyl group], and B(HFIP)3 [HFIP = hexafluoro-iso-propoxyl group] support reversible magnesium deposition/dissolution with excellent energy and coulombic efficiencies.10,12–20 However, these electrolytes also exhibit severe drawbacks such as insufficient anodic stability, high corrosivity, incompatibility with typical transition-metal-oxide cathodes, and moisture sensitivity—all of which extremely hinder practical battery materialization. To overcome these drawbacks, many attempts have been made to develop highly efficient magnesium-ion conductive electrolytes. For example, ethereal solutions of Mg[TFSA]2 (TFSA = trifluoromethanesulfonyl group) support reversible magnesium deposition/dissolution and, thus, have been studied extensively as potential electrolytes.21–24 However, the interfacial instability of [TFSA]− moderates cycling efficiency and causes high interfacial resistance with magnesium anodes.25,26 In contrast, weakly coordinated anion-based electrolytes incorporating boron-cluster, fluorinated alkoxyborate, and fluorinated alkoxyaluminate anions are a promising option for fulfilling the MB operation requirements.27–35 Owing to their favorable electrochemical properties and structures those are easily modified by simple synthesis methods, fluorinated alkoxyborate and alkoxyaluminate electrolytes have attracted the attention and fascination of many researchers, and various related materials including calcium and zinc salts have also been developed.36–38
The first application of a fluorinated alkoxyaluminate electrolyte to MBs was magnesium tetrakis(hexafluoro-iso-propoxy)aluminate (hereafter denoted as Mg[Al(HFIP)4]2) in 2016.30 Its ethereal solutions support magnesium deposition/dissolution with near-unity cycling efficiency despite the absence of halide compounds in the electrolyte solution. By introducing electron-withdrawing fluorinated alkoxide groups to the anion coordination center, the interactions between Mg2+ and the anions are relaxed; thus, the salt dissociates well in the electrolyte solution. Moreover, isolating the anions from the divalent-Mg2+ coordination sphere prevents anion reduction. The high dissociativity and sufficient reduction resistance of such electrolytes jointly contribute to the remarkable electrochemical characteristics of the electrolytes. The borate-based analogue, which spontaneously generated upon cycling the electrolytes containing MgF2 and B(HFIP)3, was also found as an effective electrolyte component for MBs.31 Inspired by these pioneering works, some groups have also developed fluorinated-alkoxyborate- and -alkoxyaluminate-based MB electrolytes32–35 in which even minor structural modifications such as changes in the anion coordination centers or chemical structures of the alkoxides strongly impacted the physicochemical and electrochemical properties of the resulting electrolytes. However, because all these studies were conducted by different research groups, comparative studies have not yet been conducted. Therefore, the structure–property relationships of the structurally analogous fluorinated alkoxyborate and alkoxyaluminate families remain unclear.
Herein, we comprehensively compare the bulk physicochemical properties, basic electrochemical characteristics, and ion-transport mechanisms of ethereal solutions of Mg[B(HFIP)4]2 and Mg[Al(HFIP)4]2 (Scheme 1). Through systematic investigations, we discovered a specific salt–solvent combination that exhibits excellent electrochemical magnesium deposition/dissolution. The Vogel–Tammann–Fulcher (VTF) fitting analysis of the temperature-dependent ionic conductivities and viscosities and the ab initio simulations revealed the remarkable ion conduction characteristics of the electrolyte.
Experimental
Materials
Di-n-butylmagnesium (Mg(Bu)2; 1.0 mol dm−3 heptane solution) was purchased from Sigma-Aldrich and was used as received without further purification. Trimethylaluminum (Al(CH3)3; 15% in toluene, ca. 1.8 mol dm−3) was obtained from Tokyo Chemical Industries, Co., Ltd. In addition, 1,1,1,3,3,3-hexafluoro-iso-propanol (HFIP-H), borane–tetrahydrofuran (BH3–THF), and silver nitrate were purchased from FUJIFILM Wako Chemicals. The HFIP-H was distilled over calcium oxide and stored in an Ar-filled glovebox with 3 Å molecular sieves. Anhydrous toluene, monoglyme (G1), diglyme (G2), and triglyme (G3) were obtained from Kanto Chemical Co., Inc. and were used without further purification. Tetraglyme (G4) and battery-grade magnesium bis(trifluoromethanesulfonyl)amide (Mg[TFSA]2) were purchased from Kishida Chemical Co., Ltd. The G4 was purified by vacuum distillation over sodium metal prior to use. The Mg[TFSA]2 was dried under vacuum at 120 °C for several days and then stored in an Ar-filled glovebox. The Mg[B(HFIP)4]2 was synthesized according to a procedure reported elsewhere,39 while the Mg[Al(HFIP)4]2 was synthesized according to a procedure modified from the ones reported in the literature30,40 because Al(HFIP)3 is extremely fragile and therefore, difficult to isolate. A commercial toluene solution of Al(CH3)3 (2.02 equiv. vs. Mg) was diluted further with anhydrous toluene to ca. 0.5 mol dm−3 and was slowly mixed very well with the G1–toluene (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) solution containing the as-synthesized Mg(HFIP)2. Excess HFIP-H (3.5 equiv. vs. Al) was added dropwise for over 1 h at ca. 0 °C to convert the Al(CH3)3 into Al(HFIP)3 and transmetalate the HFIP units between Mg(HFIP)2 and Al(HFIP)3. After the HFIP-H was completely added, the resulting solution was vigorously stirred at ca. 25 °C for 1 d, and the solvents and excess HFIP-H were evaporated under vacuum at 45 °C for ca. 8 h, yielding the crude sample. The as-synthesized salts were recrystallized by slowly condensing the concentrated G1 solutions in an Ar-filled glove box and subsequently drying the residues under vacuum at 45 °C for at least 12 h. The chemical structures of the purified salts were characterized by 1H nuclear magnetic resonance (NMR; JNM-ECA 400, JEOL, 1H resonance frequency = 400 MHz) spectroscopy, and the spectra are displayed in Fig. S1 (ESI†). The 1H NMR analysis of the isolated salts indicated the formation of adducts such as Mg[B(HFIP)4]2·3G1 and Mg[Al(HFIP)4]2·4G1. Because it was difficult to completely remove all the solvated and/or cocrystallized G1 without decomposing any of the undesired salts, the adducts were directly adopted as electrolyte-supporting salts and are hereafter denoted simply as Mg[B(HFIP)4]2 and Mg[Al(HFIP)4]2, respectively. The electrolyte solutions were prepared by mixing predetermined amounts of Mg[B(HFIP)4]2 or Mg[Al(HFIP)4]2 in Gn, and the solutions were vigorously stirred at 30 °C overnight in a glovebox (< 1 ppm H2O and O2). The water content of the prepared electrolytes was measured at < 30 ppm by Karl Fischer titration.
1) solution containing the as-synthesized Mg(HFIP)2. Excess HFIP-H (3.5 equiv. vs. Al) was added dropwise for over 1 h at ca. 0 °C to convert the Al(CH3)3 into Al(HFIP)3 and transmetalate the HFIP units between Mg(HFIP)2 and Al(HFIP)3. After the HFIP-H was completely added, the resulting solution was vigorously stirred at ca. 25 °C for 1 d, and the solvents and excess HFIP-H were evaporated under vacuum at 45 °C for ca. 8 h, yielding the crude sample. The as-synthesized salts were recrystallized by slowly condensing the concentrated G1 solutions in an Ar-filled glove box and subsequently drying the residues under vacuum at 45 °C for at least 12 h. The chemical structures of the purified salts were characterized by 1H nuclear magnetic resonance (NMR; JNM-ECA 400, JEOL, 1H resonance frequency = 400 MHz) spectroscopy, and the spectra are displayed in Fig. S1 (ESI†). The 1H NMR analysis of the isolated salts indicated the formation of adducts such as Mg[B(HFIP)4]2·3G1 and Mg[Al(HFIP)4]2·4G1. Because it was difficult to completely remove all the solvated and/or cocrystallized G1 without decomposing any of the undesired salts, the adducts were directly adopted as electrolyte-supporting salts and are hereafter denoted simply as Mg[B(HFIP)4]2 and Mg[Al(HFIP)4]2, respectively. The electrolyte solutions were prepared by mixing predetermined amounts of Mg[B(HFIP)4]2 or Mg[Al(HFIP)4]2 in Gn, and the solutions were vigorously stirred at 30 °C overnight in a glovebox (< 1 ppm H2O and O2). The water content of the prepared electrolytes was measured at < 30 ppm by Karl Fischer titration.
Measurements
The bulk physicochemical properties including ionic conductivity, liquid density, and viscosity were evaluated for a series of electrolytes. The ionic conductivities were measured using the complex impedance method and an impedance analyzer (VMP3, Biologic) operating in the range 500 kHz–1 Hz for a sinusoidally alternating voltage amplitude of 10 mV root-mean-square. A commercial cell equipped with two platinized platinum electrodes (CT-57101B, TOA DKK Corporation) was used for the impedance measurements. The cell was placed in a temperature-controlled chamber and held at the predetermined temperature for 1 h to equilibrate the temperature, after which the conductivity was measured at each desired temperature. The liquid densities and viscosities were measured using a U-tube oscillation densitometer and a falling-ball viscometer (DMA4500M/Lovis2000, Anton Paar GmbH). To measure the physicochemical properties, an appropriate solvent-volatility-dependent temperature range was adopted to prevent changing the solution composition. All the standard deviations in the experimental values were within ±2% of the average.Typical magnesium deposition–dissolution cycling tests were conducted using cyclic voltammetry (CV) with a three-electrode beaker cell. A Pt disk (∅ 3 mm, BAS) and a magnesium ribbon (FUJIFILM Wako Chemicals) were used as the working and counter electrodes, respectively. An Ag+/Ag reference electrode was fabricated according to a procedure described elsewhere.41 The potential of the reference electrode was calibrated as −2.49 V vs. the reference for 0 V vs. Mg2+/Mg0.39,42 The CV measurements were conducted using an electrochemical analyzer HSV-110 (Hokuto-Denko Corporation) in a glovebox. Electrochemical impedance spectroscopy (EIS) was performed to evaluate the interfacial behavior of a series of electrolytes. A symmetric Mg–Mg cell was fabricated in an Ar-filled glovebox and then precycled twice at 0.5 mA cm−2 for 30 min to remove the native passivation film. The current frequency of the precycled cells was scanned from 1 MHz to 10 mHz with a sinusoidally alternating voltage amplitude of 50 mV root-mean-square. A galvanostatic magnesium deposition/dissolution cycling test was performed on the two-electrode cells. Cu foil and homemade Mg metal plates served as the working and counter electrodes, respectively, and GA200 (t = 0.74 mm, ADVANTEC) was used as a separator. A galvanostatic cycling test was performed using an automatic charge/discharge instrument (HJ0610SD8Y, Hokuto-Denko Corporation) operating at 0.5 mA cm−2 for 30 min at 30 °C for each deposition and dissolution (0.25 mAh cm−2). Magnesium metal used in the electrochemical studies was polished mechanically by SiC abrasive papers #240, #2400, and #4000, then washed with anhydrous THF immediately prior to use. All the electrochemical cells were assembled in a glove box.
The surfaces of the electrodeposited magnesium metal were observed using scanning electron microscopy (SEM; JSM-7800F, JEOL) and subsequently characterized by energy dispersive X-ray (EDX) spectroscopy and X-ray photoelectron spectroscopy (XPS; VersaProbe II, ULVAC-PHI). Carbon fiber substrates were employed as a working electrode for the electrodeposition and subsequent SEM-EDX observations and XPS measurements to prevent the deposits from falling off the electrode surface during cell disassembly because the deposits had poorly adhered to the flat metal electrodes (Fig. S2, ESI†). All the samples were washed with anhydrous THF to remove any residual electrolyte, dried under high vacuum at ambient temperature, placed in an airtight chamber, and transferred for SEM-EDX analysis or XPS measurements without any exposure to air. XPS measurements were performed with an Al Kα X-ray source under a base pressure of 6.7 × 10−8 Pa. The binding energy of the obtained spectra was calibrated using the C 1s peak from sp2-hybridized carbon at 284.5 eV as a reference.
Ab initio cluster calculations were performed to estimate the electron affinities of the anions immersed in the electrolyte solutions. Gaussian16 calculations43 adopting M06 hybrid functional with 6-311++G(d,p) basis sets and the integral equation formalism polarizable continuum model (IEFPCM) for G2 (ε = 7.23) and G3 (ε = 7.62) were applied to obtain the electronic states of isolated [Z(HFIP)4]− (Z = B, Al) taking the solvation effects into account. Ab initio Car–Parrinello molecular dynamics (CPMD) simulations44 were carried out using the Perdew–Burke–Ernzerhof (PBE)-D2 functional45 and Goedecker–Teter–Hutter (GTH) pseudopotentials46 to obtain the equilibrium solvation structures and the diffusion properties of the Mg[Z(HFIP)4]2/Gn solutions (Z = B or Al; n = 2 or 3). The supercell size of each electrolyte was set to correspond to ca. 0.3 mol dm−3 solution involving one Mg2+ ion, considering the experimental density. The radial distribution function (RDF) profiles were obtained from the equilibrium solvation and solution structures. The diffusion coefficients were estimated via the mean-square displacements of individual species (e.g., Mg2+ ions, anions, Gn solvents) in the canonical NVT ensemble. The temperature 350 K was used to accelerate the MD sampling and the reasonable sampling time was adopted to evaluate the equilibrated diffusion coefficients.
Results and discussion
Bulk physicochemical properties
The diffusivity of the charge carriers responsible for redox reactions at each electrode is a critical parameter for determining the battery performance. In principle, the ionic conductivity qualifies the ion mobility or diffusivity; thus, it is an essential physical parameter for elucidating electrolyte characteristics. Also, clarifying the composition of electrolytes possessing the highest ionic conductivities is particularly important as ionic conductivities are directly related to the battery performance. Fig. 1 summarizes the ionic conductivity of Mg[Z(HFIP)4]2/Gn (Z = B or Al; n = 1–3) plotted as functions of salt concentration. Consistent with the findings of a previous report on Mg[B(HFIP)4]2/G1 electrolytes,3 the concentration-dependent ionic conductivities of all the systems showed a typical volcano-type profile with a local maximum at approximately 0.3 mol dm−3, regardless of the anion coordination center and glyme choices (Fig. 1). However, the G2 and G3 solutions potentially contained coordinated and/or cocrystallized G1. Because the solutions contained substantially more G2 and G3 (the main solvents) than G1 (only a trace), the effects of the residual G1 on the solution state and diffusivity were assumed to be the same level for all the solutions. The electrolyte solutions incorporating structurally analogous magnesium salts, Mg[Al(PFTB)4]2 (PFTB = perfluoro-tert-butoxy), also showed a local maximum ionic conductivity in a comparable concentration range despite the salt inherently being coordinated by seven THF molecules.34 This conductivity–concentration relationship is a common feature of such weakly coordinated anion-based magnesium electrolytes. Notably, the local maxima appear at ca. 1.0 mol dm−3 for conventional electrolyte solutions containing typical monovalent salts. In contrast, the maxima for electrolyte solutions incorporating bulky borate anions paired with monovalent ions reportedly appear at lower concentrations, ca. 0.8 mol dm−3.47 For lithium salts consisting of highly bulky fluorinated alkoxy- or arylaluminate anions such as Al(HFIP)4 and Al(HFTB)4 (HFTB = hexafluoro-tert-butoxy), the G1-solution maxima reportedly appeared in the range ca. 0.5–0.6 mol dm−3.48 For typical divalent salts such as Mg(TFSA)2, the concentration where the conductivity maxima shift lower, ca. 0.5 mol dm−3, is certainly due to the divalent-Mg2+-induced ion association.21,23,49 For the current salt–solvent electrolytes, the local maxima appeared at even lower concentrations than those observed for typical divalent systems, as indicated by the difference between the monovalent simple and bulky anions. Clearly, the remarkably low diffusivity of the highly bulky anion (vide infra) and the divalent-Mg2+-induced ion association had affected the overall conductivity.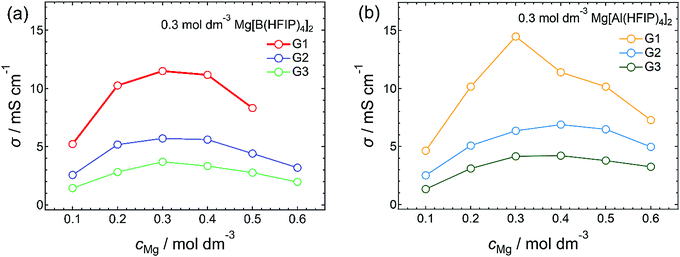 | ||
| Fig. 1 Ionic conductivities of (a) Mg[B(HFIP)4]2/Gn and (b) Mg[Al(HFIP)4]2/Gn (n = 1–3) measured at 30 °C. | ||
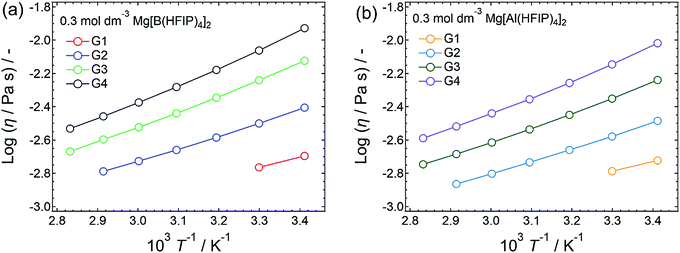
In addition to salt concentration, temperature is also a dominant factor affecting transport properties because the temperature of the medium directly affects the dynamics of ions and molecules therein. Therefore, the appropriate solvent-volatility-dependent temperature range was adopted based on the liquid-density–temperature profiles (Fig. S3, ESI†) obtained under the following experimental conditions: G1, 20–30 °C; G2, 20–70 °C; G3 and G4, 20–80 °C. The temperature–concentration–conductivity profiles obtained for Mg[Z(HFIP)4]2/Gn (Z = B or Al; n = 2 or 3) are summarized in Fig. S4 and S5 (ESI†), respectively, and a distinct anion-coordination-center-dependent result was obtained. For the Mg[Al(HFIP)4]2 electrolytes, the concentrations at which the local ionic-conductivity maxima observed were indeed temperature dependent. The ionic conductivity decreased at higher concentrations owing to the tradeoff between the mobility and the number of charged species. The solution viscosity decreased while the number of charge carriers increased with increasing salt concentration. The charge-carrier mobility, on the other hand, increased while the solution (medium) viscosity decreased with increasing temperature. The enhanced mobility counteracted the tradeoff and consequently shifted the local ionic-conductivity maxima to higher concentrations. In contrast, the concentration maxima unexpectedly always remained at 0.3 mol dm−3 regardless of the temperature measured for the Mg[B(HFIP)4]2-based counterparts, suggesting that the ion-conduction mechanism for the latter electrolytes was somewhat different from that for the former. The VTF fitting analysis of the temperature-dependent ionic conductivities and viscosities indeed demonstrated a decoupling of the ion conduction from the viscosity limitations for the latter electrolytes, while suggesting a typical vehicle conduction mechanism with a relatively low activation-energy barrier for the former (vide infra).
For the same electrolyte concentration at moderate temperatures, the ionic conductivities of the Mg[Al(HFIP)4]2-based electrolytes were always higher than those of their Mg[B(HFIP)4]2-based counterparts, regardless of the glyme length (Fig. 2). In particular, the ionic conductivities of the former G1 solutions were much higher than those of the latter ones, despite their comparable viscosities. Because the number of charge carriers in both systems was identical, the superior ionic conductivity of the former indicates that the former exhibited greater ion diffusivity and/or dissociation than the latter. The molecular dynamics (MD) simulation of the ion diffusivity suggests that the former exhibited a higher charged-species diffusion coefficient (vide infra), and the difference between the ion associativities of both structurally analogous anions may be the reason. Meanwhile, the electrolyte-solution ionic conductivities decreased with increasing glyme length, regardless of the coordination center, which simply reflected the increased solution viscosity with increasing glyme length because the individual glyme-solvent viscosities increased with increasing glyme length as follows: 0.42, 0.98, 1.96, and 3.40 for G1, G2, G3, and G4, respectively, at 20 °C.50,51
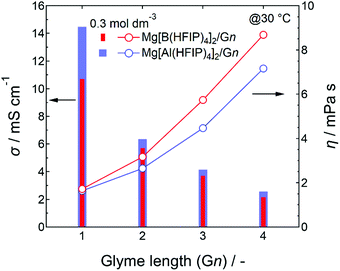 | ||
| Fig. 2 Ionic conductivities and viscosities of 0.3 mol dm−3 Mg[Z(HFIP)4]2/Gn (Z = B or Al; n = 1–4) measured at 30 °C. | ||
Electrochemical characteristics
The basic magnesium deposition/dissolution electrochemical activities of the 0.3 mol dm−3 Mg[Z(HFIP)4]2/Gn electrolytes were assessed by cyclic voltammetry, and the resulting voltammograms are shown in Fig. 3. All the electrolytes showed reversible magnesium deposition/dissolution despite the absence of strong Lewis acidic reagents, regardless of the anion coordination center and glyme length. The current densities measured for magnesium deposition at the same potential, for example, −0.5 V vs. Mg2+/Mg, were higher for the Mg[Al(HFIP)4]2-containing electrolytes than the Mg[B(HFIP)4]2-containing ones. Moreover, the magnesium deposition/dissolution current densities measured for the Mg[Al(HFIP)4]2/glyme electrolytes seemed less sensitive to changes in the glyme length than their Mg[B(HFIP)4]2-based counterparts because the magnitude of the decreased current densities with increasing glyme length was modest for the former electrolytes. The superior transport properties of the Mg[Al(HFIP)4]2-based electrolytes compared to those of their Mg[B(HFIP)4]2-based counterparts at the measured temperature were certainly responsible for this finding (vide infra).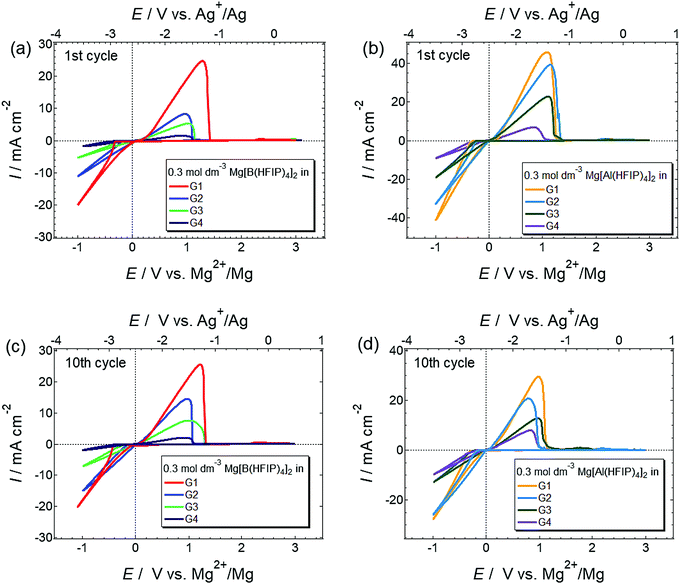 | ||
| Fig. 3 1st and 10th cyclic voltammograms scanned at 10 mV s−1 for Pt electrode immersed in 0.3 mol dm−3 (a and c) Mg[B(HFIP)4]2/Gn and (b and d) Mg[Al(HFIP)4]2/Gn (n = 1–4) at 30 °C. | ||
The magnesium-deposition (nucleation) overpotential is glyme-length dependent, and the lowest overpotential was surprisingly observed for the G2 solutions among all those incorporating the same supporting salts. The magnesium-nucleation onset potentials for the 1st cycles were 400, 310, 350, and 380 mV for 0.3 mol dm−3 Mg[B(HFIP)4]2/G1, G2, G3, and G4, respectively, and 310, 220, 250, and 230 mV for their 0.3 mol dm−3 Mg[Al(HFIP)4]2-based counterparts, respectively. A similar order was preserved for the subsequent cycles, e.g. 10th cycle, suggesting that the onset potentials are inherently electrolyte dependent. The desolvation energy barrier (i.e., the number of coordination sites in a single molecule) usually increases with increasing chelating ability at the [electrode | electrolyte] interface.52 Because the current results conflicted with the established order of the solvent coordination ability, other factors influencing interfacial processes should be considered. For example, Liao et al. recently reported that owing to the formation of an anion-derived effective solid–electrolyte interphase (SEI) layer, magnesium nucleation on a Pt working electrode immersed in a relatively concentrated Mg[Al(PFTB)4]2/G3 electrolyte exhibited a lower overpotential than the same electrode immersed in the same diluted electrolyte.34 Such anion-derived SEI formation would lead to poor coulombic efficiency. However, we did not find any evidence of increased anion decomposition in the G2-based electrolytes compared to the others because the Coulombic efficiencies measured for galvanostatic magnesium deposition/dissolution were higher for the G2-based electrolytes than the G1-based ones (vide infra). In addition, the difference between the coulombic efficiencies measured for the G1- and G2-based electrolytes was extremely small, and only <1% efficiency was obtained for the latter; hence, it would be unreasonable to attribute the SEI formation to the improved nucleation overpotential of the G2-based solutions. G2, on the other hand, is an effective chelating agent and a less-viscous solvent and often provides a unique coordination environment by forming six-fold octahedral metal-complex salts owing to its tridentate molecular structure.53–56 Because Mg2+ exhibits six-fold coordination, it indeed prefers forming a stable complex cation with G2 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio.27,33,57 In contrast, owing to the relatively low coordinating ability of bidentate G1, ligands are frequently exchanged assisted by anion coordination (i.e., tentative cation–anion association) in G1-based electrolyte solutions.58 The attractive Coulombic interactions between cations and anions would make the charged species sterically bulky and hinder the approach of the relevant species to the working electrode. Consequently, magnesium nucleation may exhibit high polarization in G1 electrolytes. For longer-glyme electrolytes, strong chelate coordination (cation–solvent interaction) can hinder the desolvation of such longer glymes from the complex cation at the [electrolyte | electrode] interface, thus requiring high polarization for desolvation and subsequent nucleation. The EIS measurements for the magnesium electrodes immersed in different electrolytes also support the CV results. Fig. 4 displays the Nyquist plots measured for the magnesium electrodes immersed in 0.3 mol dm−3 Mg[Z(HFIP)4]2/Gn. Regardless of the coordination center, an exceptionally high interfacial resistance was observed for the G1-based electrolytes. For the longer-glyme electrolytes, the interfacial resistance increased with increasing glyme length; that is, the G2-based electrolytes exhibited the lowest interfacial resistance. The cation–anion Coulombic interactions and cation–solvent induced dipole interactions (coordination-desolvation) will both affect interfacial behavior. Furthermore, the MD simulations for the G2- and G3-based electrolytes suggested a remarkably higher charge-carrier diffusivity for the former (vide infra). Taking all the interfacial and bulk properties and the mutually correlated cation–anion–solvent interactions into account, the well-balanced coulombic interaction and the coordination–desolvation effect combined with the enhanced mass transfer of the relevant species are responsible for Mg[Z(HFIP)4]2/G2 exhibited the lowest nucleation overpotential.
2 ratio.27,33,57 In contrast, owing to the relatively low coordinating ability of bidentate G1, ligands are frequently exchanged assisted by anion coordination (i.e., tentative cation–anion association) in G1-based electrolyte solutions.58 The attractive Coulombic interactions between cations and anions would make the charged species sterically bulky and hinder the approach of the relevant species to the working electrode. Consequently, magnesium nucleation may exhibit high polarization in G1 electrolytes. For longer-glyme electrolytes, strong chelate coordination (cation–solvent interaction) can hinder the desolvation of such longer glymes from the complex cation at the [electrolyte | electrode] interface, thus requiring high polarization for desolvation and subsequent nucleation. The EIS measurements for the magnesium electrodes immersed in different electrolytes also support the CV results. Fig. 4 displays the Nyquist plots measured for the magnesium electrodes immersed in 0.3 mol dm−3 Mg[Z(HFIP)4]2/Gn. Regardless of the coordination center, an exceptionally high interfacial resistance was observed for the G1-based electrolytes. For the longer-glyme electrolytes, the interfacial resistance increased with increasing glyme length; that is, the G2-based electrolytes exhibited the lowest interfacial resistance. The cation–anion Coulombic interactions and cation–solvent induced dipole interactions (coordination-desolvation) will both affect interfacial behavior. Furthermore, the MD simulations for the G2- and G3-based electrolytes suggested a remarkably higher charge-carrier diffusivity for the former (vide infra). Taking all the interfacial and bulk properties and the mutually correlated cation–anion–solvent interactions into account, the well-balanced coulombic interaction and the coordination–desolvation effect combined with the enhanced mass transfer of the relevant species are responsible for Mg[Z(HFIP)4]2/G2 exhibited the lowest nucleation overpotential.
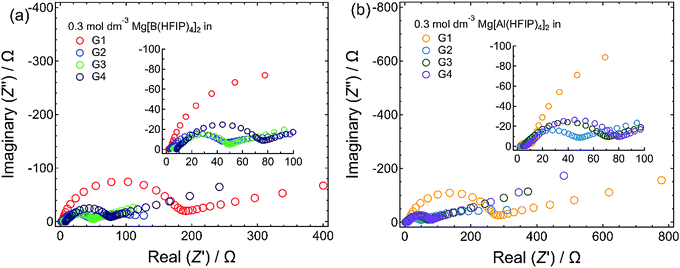 | ||
| Fig. 4 Nyquist plots measured for magnesium electrodes immersed in 0.3 mol dm−3 (a) Mg[B(HFIP)4]2/Gn and (b) Mg[Al(HFIP)4]2/Gn (n = 1–4) at 30 °C. | ||
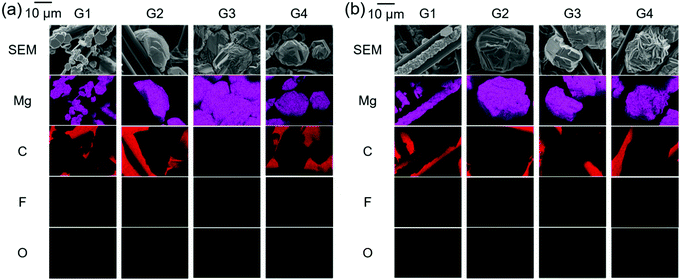
For electrolytes prepared using the same solvents, the corresponding onset potential of the Mg[Al(HFIP)4]2-based electrolytes is always lower than that of their Mg[B(HFIP)4]2-based counterparts, suggesting a relatively facile magnesium nucleation in the former electrolytes. Notably, the lower nucleation overpotential of the former electrolytes seems to be universal regardless of the working electrodes and cell fabrications used because the galvanostatic profiles also exhibited a lower overpotential for magnesium deposition on carbon-fiber and Cu electrodes in the former electrolytes (Fig. 6 and S6, ESI†). Moreover, as evidenced by the EDX mappings of the deposits (Fig. 5), relatively pure magnesium can be deposited in the former electrolyte, while magnesium deposition is sometimes associated with slight anionic decomposition in the latter one. The calculated electron affinities, often regarded as a measure of the target-species reduction resistance, of [B(HFIP)4]− and [Al(HFIP)4]− were −0.73 and −0.78 eV vs. vacuum (which approximately correspond to −1.38 and −1.33 V vs. Mg2+/Mg), respectively, implying that both anions were sufficiently stable with magnesium metal. Although a recent study demonstrated the anion–solvent interaction between certain fluorinated alkoxyaluminates and ethers by crystallography,35 such specific interactions have not yet been experimentally confirmed for the structurally analogous borates.33 The radial distribution functions (RDF profiles) of the B and Al surroundings calculated for 0.3 mol dm−3 Mg[Z(HFIP)4]2/G3 indeed suggest penetration of the solvents between HFIP ligands for [Al(HFIP)4]− (Fig. S7, ESI†). Rather prominent fluctuations between the anion coordination center and the solvents are observed for the Mg[Al(HFIP)4]2 electrolytes from ca. 3 Å while corresponding fluctuations emerge from ca. 4 Å for the Mg[B(HFIP)4]2 counterparts, suggesting the Al–solvent interactions. Such specific interactions would affect ion transport behavior (or simply further facilitate the dissociation of the Mg[Al(HFIP)4]2 salt), leading to the higher ionic conductivity of the Mg[Al(HFIP)4]2-based electrolytes (Fig. 2). Anion–solvent interactions can also weaken the influence of the Mg2+-induced electric field on the anion, thereby possibly rendering the anion reduction resistant because of increasing the distance between Mg2+and the anion. The suppressed anion decomposition in the Mg[Al(HFIP)4]2-based electrolytes during the magnesium deposition was evidenced by the EDX mapping and XPS spectra (Fig. 5 and Fig. S8, ESI†). The XPS spectra for the magnesium metals deposited from the different electrolytes showed similar spectral features irrespective of the salts. The relative intensities possibly assignable to the (decomposition) reaction products are however strong for the deposits from the borate electrolytes. In Mg 2p spectra, the intense peaks assignable to both metallic Mg0 (49.8 eV) and Mg2+ (ca. 51.5 eV) were clearly observed for both electrolytes. Although the O 1s and F 1s spectra also showed some contributions of MgO (ca. 531 eV) and CF-based compounds (ca. 686–687 eV) in addition to the residual electrolytes observed at ca. 533–534 eV (B–O or Al–O) and ca. 690 eV (C–CF3) for both deposits, rather apparent contributions of MgO and CF-compounds were observed for the deposits from the Mg[B(HFIP)4]2 electrolyte. These results strongly suggest that anion decomposition is effectively suppressed in the Mg[Al(HFIP)4]2-electrolyte during magnesium deposition process despite of the similar interfacial chemical compositions, and further support that not SEI formation but the enhanced mass-transfer kinetics and suppressed anion decomposition of the Mg[Al(HFIP)4]2-based electrolytes were responsible for the magnesium nucleation exhibiting lower overpotential. It should be noted here that the interfacial stability of the Mg[B(HFIP)4]2-based electrolytes can be modified by artificial SEI formation upon incorporation of the corresponding lithium salt as a co-salt.59 The lithium-containing SEI may be effective to suppress the electrolyte decomposition though such interphase can simultaneously impart interfacial resistance.
The onset potential (in the range 10–70 mV) for magnesium dissolution is also somewhat solvent sensitive. Nevertheless, the lowest dissolution overpotential was observed for the Mg[Al(HFIP)4]2/G2 solution, indicating a certain solution state suitable for both magnesium deposition and dissolution achievable by a special combination of [Al(HFIP)4]− and G2.
As shown in Fig. 5, the morphology of the deposits obtained under certain galvanostatic conditions strongly depends on the electrolyte composition. By employing the G1 solvent, hexagonal crystalline deposits were obtained regardless of the anion coordination center. In contrast, the longer-glyme electrolytes exhibited larger granular deposits, possibly due to the agglomeration or growth of small (hexagonal) crystals during deposition. It is widely accepted that deposition potential is a dominant factor for crystal nucleation and subsequent growth and that nucleation preferentially proceeds under a higher overpotential.60,61 Indeed, as shown in Fig. S6 (ESI†), the overpotential for magnesium deposition in the G1 electrolytes was more negative than that for magnesium deposition in the other ones. Because charge transfer is a rate-determining process under a high overpotential, the surface diffusion accelerates; hence, the deposit morphology would be the most stable hexagon required to minimize the surface energy. Furthermore, the remarkable mass-transfer characteristics of the G1 electrolytes support nucleation-driven deposition. In contrast, crystallite growth proceeded preferentially, especially in the G2 electrolytes, because larger crystallites were deposited on the substrates (Fig. 5). Although understanding the detailed crystal growth mechanism is beyond the scope of this study, the deposit morphology (or crystallinity) could be related to the subsequent dissolution and the deposition/dissolution cycling efficiencies.
The salt concentration also affected the nucleation overpotential. With increasing salt concentration, the overpotential reached 70 and 190 mV for 0.5 mol dm−3 Mg[B(HFIP)4]2/G2 and Mg[Al(HFIP)4]2/G2, respectively (Fig. S9, ESI†). Moreover, the magnitude of the decreased overpotential was low for the latter electrolytes. The elemental analysis of the deposits and the galvanostatic magnesium deposition/dissolution cycling suggested that anionic decomposition increased with increasing salt concentration, which is consistent with the findings of a previous study on Mg[Al(PFTB)4]2/G3.34 The deposits obtained from 0.5 mol dm−3 Mg[Z(HFIP)4]2/G2 (Z = B or Al) exhibited substantially more F atoms, whereas those obtained from the lower-concentration salt electrolytes exhibited fewer, indicating anion-decomposition-associated magnesium deposition in the concentrated electrolytes (Fig. 5 and Fig. S10, ESI†). The coulombic efficiencies measured for the galvanostatic magnesium deposition/dissolution cycling also implied that magnesium deposition was associated with both increasing anion decomposition and salt concentration because the concentrated electrolyte exhibited relatively lower efficiency (Fig. S11, ESI†). In lithium batteries, such anion-derived fluorine-rich SEIs effectively suppresses subsequent anion decomposition and promote interfacial kinetics.62,63 Although relatively poor efficiency was retained during prolonged cycling in the concentrated magnesium electrolyte (and, thus, the decomposition products could not suppress subsequent undesired side reactions), the products may promote interfacial kinetics. Indeed, the overpotentials measured for both nucleation and dissolution did decrease with increasing salt concentration, as evidenced by both CV and galvanostatic cycling shown in Fig. S9 and S11 (ESI†), respectively. Further studies are necessary to clarify the chemical compositions, roles, and detailed functions of the decomposition products. Taken together, the ionic conductivity and magnesium deposition–dissolution activity and efficiency suggest that a moderate salt concentration (approximately 0.3 mol dm−3) was suitable for practically applying such electrolytes to MBs.
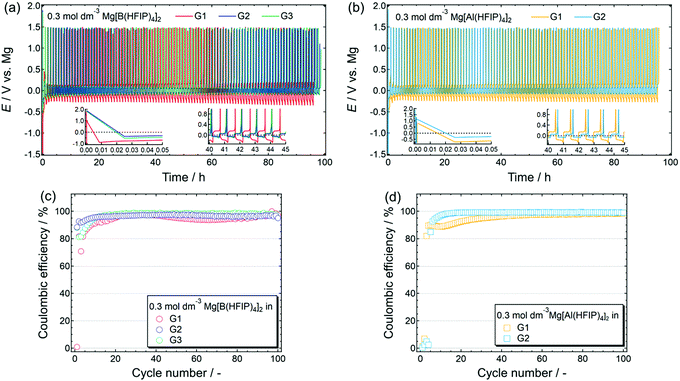
The reversible magnesium deposition–dissolution of a series of [B(HFIP)4]−- and [Al(HFIP)4]−-based electrolytes was further assessed by galvanostatic cycling measurements. Fig. 6 displays the deposition–dissolution cycling profiles measured for [Mg||Cu] cells cycled at 0.5 mA cm−2 and the corresponding coulombic efficiencies for the 0.3 mol dm−3 Mg[Z(HFIP)4]2/Gn (n = 1–3) electrolytes. Although reversible cycling was possible in the Mg[B(HFIP)4]2-based electrolytes regardless of the glyme, cycling unexpectedly failed in the Mg[Al(HFIP)4]2/G3 electrolyte. The reason for this is unclear; however, because CV cycling was possible for the other salt–solvent combinations and even Mg[Al(HFIP)4]2/G3 (Fig. 3b) in a beaker cell, the trace impurities in the commercial G3 may have reacted with the supporting salt, and the resulting compounds would have further reacted with the cell components, thereby possibly deactivating the cell.
As shown in Fig. 6a and b, all the prepared [Mg||Cu] cells required several precycles, as is often required in MB studies and is attributed to the activation of the metallic magnesium anode.42,64 Even after the electrode had been mechanically polished in an inert atmosphere, the so-called “native SEI” oxide film remained on the electrode surface.39,42,65 The native SEI strongly impedes interfacial electrochemical reactions because it is an insulator; hence, it must be chemically or electrochemically removed to facilitate interfacial reactions. Meanwhile, magnesium deposition and dissolution are glyme-length sensitive, and an exceptionally high overpotential was observed for both deposition and dissolution in the G1 solutions, regardless of the anion coordination center. In addition, the G2 solutions imparted a lower overpotential than the other solutions. Furthermore, compared with the [B(HFIP)4]2-based electrolytes, the corresponding [Al(HFIP)4]-based counterparts showed a lower overpotential and higher coulombic efficiencies during the entire cycling period. The well-suppressed decomposition of [Al(HFIP)4]-based electrolytes during magnesium deposition/dissolution processes, as evidenced by EDX (Fig. 5) and XPS (Fig. S8, ESI†), is certainly responsible of these observations.
The long-term cycling stability of the Mg[Z(HFIP)4]2/G2 electrolytes further corroborated the special combination of Mg[Al(HFIP)4]2 and G2 for reversible magnesium deposition/dissolution cycling. Indeed, after several activation precycles, that electrolyte solution exhibited particularly stable cycling with a very low overpotential (<±60 mV) and excellent coulombic efficiency (99.4%) over 250 cycles (Fig. 7). To the best of our knowledge, this is the highest performance ever achieved for reagent-free halide-based electrolytes. The high ionic conductivity and sufficient cathodic stability combined with favorable interfacial and translational kinetics all contributed to the exceptionally remarkable electrochemical characteristics of the Mg[Al(HFIP)4]2/G2 electrolyte.
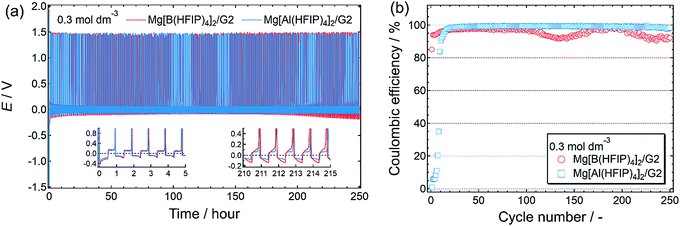 | ||
| Fig. 7 (a) Long-term cycling stability and (b) corresponding coulombic efficiency measured for [Mg||Cu] cells fabricated using 0.3 mol dm−3 Mg[Z(HFIP)4]2/G2 electrolytes. Same experimental conditions as described in Fig. 5 were adopted. (a) Insets display magnified profiles for selected periods. | ||
The anodic stability of a series of electrolytes was investigated by linear sweep voltammetry (LSV) for Pt electrodes immersed in the electrolytes, and the LSV profiles are displayed in Fig. 8. Regardless of the coordination center and glyme, all the currents increased at approximately 3.5 V vs. Mg2+/Mg. Typical hydrocarbon-based ethers including glymes are oxidized at ca. 4–4.2 V vs. Li+/Li,66 which corresponds to 3.3–3.5 V vs. Mg2+/Mg. The HOMO energy levels of [B(HFIP)4]− and [Al(HFIP)4]− are calculated to be −7.84 and −8.23 eV vs. vacuum (which approximately correspond to +5.79 and +6.18 V vs. Mg2+/Mg), respectively. Because the anions exhibited substantially high oxidation resistance, the current was attributed to the oxidative decomposition of the solvent glymes. Among the solutions prepared using the same anion, the G1 solutions were the least stable. The oxidation resistance of electrolyte solvents is enhanced by metal-ion complexation through the electric field effect. Briefly, the strong electric field produced by metal ions highly polarizes the electronic state of the surrounding solvent molecules, thereby increasing the ionization potential. In extreme equimolar Mg–glyme complexes, wherein all the glyme solvents are coordinated with Mg2+ ions, the electrolyte solvents do indeed exhibit excellent oxidation resistance (>4.0 V vs. Mg2+/Mg) owing to the strong electric field produced by small, divalent Mg2+ ions.25,67 In contrast, the solvent molecules that do not participate in coordination and ligand exchange should decompose at relatively low potentials. Because the salt–solvent ratio decreases with increasing glyme length from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 to 1
22 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 (salt
10 (salt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent) for G1 to G4 at the same salt concentration, substantially more nonpolarized or less-polarized solvent molecules are in the G1 solutions than in the others. This balanced salt–solvent ratio is possibly why the G1 solutions showed relatively poor anodic stabilities.
solvent) for G1 to G4 at the same salt concentration, substantially more nonpolarized or less-polarized solvent molecules are in the G1 solutions than in the others. This balanced salt–solvent ratio is possibly why the G1 solutions showed relatively poor anodic stabilities.
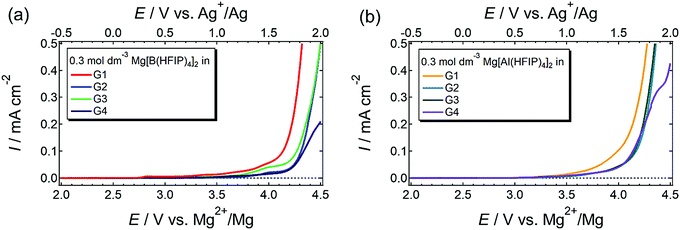 | ||
| Fig. 8 LSV profiles scanned at 1 mV s−1 for Pt electrode immersed in 0.3 mol dm−3 (a) Mg[B(HFIP)4]2/Gn and (b) Mg[Al(HFIP)4]2/Gn (n = 1–4) at 30 °C. | ||
Overall, the Mg[Al(HFIP)4]2-based electrolytes showed favorable electrochemical characteristics compared to their Mg[B(HFIP)4]2-based counterparts owing to the superior cathodic stability during magnesium deposition and the higher ionic conductivity of the former. By employing G2 as an electrolyte solvent, the resulting Mg[Al(HFIP)4]2/G2 electrolyte showed remarkable characteristics, especially the nucleation/dissolution overpotential and Coulombic efficiency measured for reversible magnesium deposition/dissolution, which corroborated the enhanced ion transport and favorable interfacial kinetics achieved by combining Mg[Al(HFIP)4]2 and G2.
Ion-transport behavior—experimental analysis and ab initio MD simulation
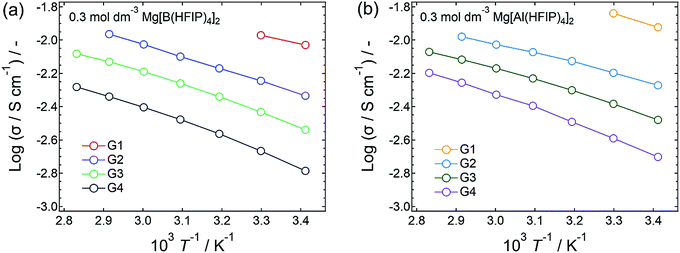
To elucidate the ion-transport mechanism of Mg[Z(HFIP)4]2-based electrolytes, the temperature dependences of the ionic conductivities and viscosities were investigated. The Arrhenius plots of the ionic conductivities and viscosities of 0.3 mol dm−3 Mg[Z(HFIP)4]2/Gn (Z = B or Al; n = 1–4) are displayed in Fig. 9 and 10 and exhibit typical convex and concave profiles, respectively, as described by the VTF equations as follows: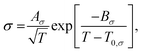 | (1) |
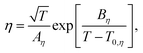 | (2) |
| Salt/solvent | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Aσ Aσ |
B σ /K | T 0,σ/K | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Aη Aη |
B η /K | T 0,η/K |
|---|---|---|---|---|---|---|
| Mg[B(HFIP)4]2/G2 | 7.61 | 408 | 168 | 4.37 | 294 | 192 |
| Mg[B(HFIP)4]2/G3 | 7.46 | 445 | 168 | 4.08 | 283 | 208 |
| Mg[B(HFIP)4]2/G4 | 7.21 | 484 | 168 | 3.91 | 308 | 207 |
| Mg[Al(HFIP)4]2/G2 | 7.15 | 330 | 168 | 4.73 | 346 | 181 |
| Mg[Al(HFIP)4]2/G3 | 7.24 | 400 | 168 | 4.61 | 383 | 185 |
| Mg[Al(HFIP)4]2/G4 | 7.41 | 488 | 168 | 4.37 | 391 | 191 |
Among the various electrolytes, 0.3 mol dm−3 Mg[Al(HFIP)4]2/G2 exhibited an exceptionally low Bσ, strongly implying that this electrolyte also exhibited particularly favorable ion transport, even at lower temperatures. Such ion-transport characteristics could explain why excellent electrochemical magnesium deposition/dissolution was achieved using this salt–solvent combination (Fig. 6 and 7).
Ionic conductivity involves contributions from the total-charged-species conduction, while only the conduction of the relevant ions is responsible for targeting electrochemical processes. Therefore, the transference number of the relevant species (Mg2+) should be estimated to further elucidate the effective Mg2+ transport abilities of each electrolyte. Owing to the unexpectedly high interfacial resistance of the magnesium electrodes (even after mechanical polishing), the complex alternating current/direct current (AC/DC) polarization method could not be applied to the electrodes in the present study. Instead, the diffusivities of the electrolyte components were investigated by ab initio MD simulation. The calculated diffusion coefficients (Ds) of Mg2+, [Z(HFIP)4]− (anion), and the center of mass of the corresponding solvent (solvent) are summarized in Table 2. The tMg2+ values calculated using DMg2+ and Danion [tMg2+ = DMg2+/(DMg2+ + Danion)] are also included. Notably, the effect of G1 on the parent-salt diffusivities was not considered in the simulations.
| Electrolytea | D/10−6 m2 s−1 | t Mg2+ | ||
|---|---|---|---|---|
| D Mg2+ | D anion | D solvent | ||
| a Salt concentration was fixed at ca. 0.3 mol dm−3 for entire series of electrolytes. b Diffusion coefficients were estimated from ab initio MD simulations. c Transference number (tMg2+) was calculated as follows: tMg2+ = DMg2+/(DMg2+ + Danion). | ||||
| Mg[B(HFIP)4]2/G3 | 0.64 | 1.09 | 5.07 | 0.370 |
| Mg[Al(HFIP)4]2/G3 | 2.79 | 3.65 | 4.88 | 0.433 |
| Mg[Al(HFIP)4]2/G2 | 6.23 | 3.10 | 13.60 | 0.668 |
As shown in Table 2, the solvents diffused faster than the other components. By comparing the D values of the electrolytes incorporating the same solvent (G3), the D values of the ionic species were higher for the [Al(HFIP)4]− electrolyte than for the [B(HFIP)4]− counterpart, while the solvent diffusivities seemed comparable, which partly corroborated the superior ionic conductivity and somewhat lower viscosity of the former electrolyte. For the electrochemical characteristics of conventional lithium-based electrolyte solutions, tLi+ usually lies in the range 0.1–0.3. However, the tMg2+ values were unexpectedly high for the present electrolytes. Because of the weak coordination ability of [Z(HFIP)4]− and the number of sites capable of coordinating with metal ions in single G2 and G3 molecules (3 and 4, respectively), at least two solvent molecules should participate in the coordination of a single Mg2+ ion in the solutions because the preferential coordination number of Mg2+ in ethereal solutions is 6 or 7.23,49,56,58 The van der Waals volumes estimated for the resulting solvated Mg2+, [Mg(G2)2]2+ (310 Å3), and [Mg(G3)2]2+ (372 Å3) ions were smaller or comparable to that of [Z(HFIP)4]− (387 and 394 Å3 for [B(HFIP)4]− and [Al(HFIP)4]−, respectively). The smaller or comparable volumes of the solvated cations against bulky anions is partly why the tMg2+ values became substantially high. Meanwhile, a somewhat high tMg2+ and a slightly lower Dsolvent for Mg[Al(HFIP)4]2/G3 compared to those for Mg[B(HFIP)4]2/G3 also suggested anion–solvent interactions.35
The ab initio MD simulations corroborated the remarkable electrochemical characteristics of the Mg[Al(HFIP)4]2/G2 electrolyte. The large difference between the Dsolvent values for Mg[Al(HFIP)4]2/G2 and Mg[Al(HFIP)4]2/G3 indicated better overall diffusivity of the former electrolyte, which is consistent with their respective viscosities. Although DMg2+ and Danion for Mg[Al(HFIP)4]2/G3 exhibited a relationship like that for Mg[B(HFIP)4]2/G3, Mg2+ diffused faster than the anion in Mg[Al(HFIP)4]2/G2. Surprisingly, Danion was lower for Mg[Al(HFIP)4]2/G2 than for Mg[Al(HFIP)4]2/G3. This characteristic ion-diffusion behavior suggested unique Mg2+ and anion environments and consequent conduction possibly induced by mutual cation–anion and anion–solvent interactions, especially in the Mg[Al(HFIP)4]2/G2 electrolyte. As previously described, [Al(HFIP)4]− can interact with surrounding solvent molecules owing to the relatively large Al–O separation.35 Such anion–solvent interactions may be stronger in G2 because of its relatively small molecular structure compared to G3; hence, the hydrodynamic volume of the resulting anion–solvent complex, that is, [Al(HFIP)4·(G2)n]−, would increase, thereby leading to modest diffusivity. Detailed theoretical studies on a series of alkoxyaluminate- and alkoxyborate-based electrolytes will be reported in a separate paper. Notably, the diffusion coefficients and transference number of the components were simply estimated based on ab initio MD simulations for the translational diffusion of the corresponding species. Very recently, the inconsistency between the simple translational diffusion model and the relevant battery performance has been highlighted.68 The data obtained by conducting a well-designed experiment and calculating the ion-conduction mechanism suggested that the contribution of the ion–ion dynamics to the electrochemical characteristics was significantly correlated to the observed diffusivity. Thus, the diffusion data must be carefully considered to elucidate and interpret the ion-transport kinetics observed during electrochemical processes. The observed characteristics of the Mg[Al(HFIP)4]2/G2 electrolyte correlated well with the calculated diffusivities in this study. Therefore, the remarkably favorable electrochemical characteristics of the Mg[Al(HFIP)4]2/G2 compared to the other salt–solvent combinations must have arisen from the superior Mg2+ diffusivity in the electrolyte solutions and the remarkably favorable interfacial kinetics.
Conclusion
Ethereal solutions incorporating magnesium-fluorinated alkoxyborate or alkoxyaluminate salts are promising electrolyte candidates for practical application to MBs. To optimize the compositions of such electrolytes, the bulk physicochemical properties, electrochemical characteristics, and ion-transport behaviors were systematically and comprehensively studied for a series of Mg[Z(HFIP)4]2/Gn (Z = B or Al; n = 1–4). The concentration dependence of the ionic conductivities exhibited typical volcano-type profiles, and the conductivity maxima were observed at a salt concentration of 0.3 mol dm−3 at 30 °C, regardless of the anion coordination center (Z). However, the temperature–concentration–conductivity profiles were distinct depending on the anions, suggesting different ion-transport mechanisms, especially at higher temperatures. At the same concentration and ambient temperature, the Mg[Al(HFIP)4]2-based electrolytes always exhibited higher ionic conductivities than their Mg[B(HFIP)4]2-based counterparts, regardless of the glyme length. This superior ionic conductivity arising from higher charge-carrier diffusivity was responsible for the remarkable magnesium deposition/dissolution electrochemical activity of the former electrolytes.The comprehensive investigation of the electrochemical magnesium deposition/dissolution and ion-transport characteristics unexpectedly found a special salt–solvent combination, Mg[Al(HFIP)4]2/G2. Such an optimal electrolyte allowed remarkably stable and efficient magnesium deposition/dissolution cycling for over 250 cycles and an excellent coulombic efficiency of 99.4% under an exceptionally low polarization of <±60 mV. The ab initio MD simulation also suggested that the optimal electrolyte exhibited an exceptionally high translational Mg2+ diffusivity. As evidenced by impedance spectroscopy, the VTF fitting analysis, and ab initio MD simulations, the well-balanced mutual cation–anion–solvent interactions and sufficient reduction resistance of the anion combined with the remarkable ion transport and interfacial characteristics may be responsible to the exceptional electrochemical activity of the electrolytes. Although research into practical cathode and anode materials is still in the early stages (and, thus, such materials compatible with the present electrolytes must be developed for application to high-performance MBs), this work demonstrates that Mg[Al(HFIP)4]2/G2 can be the primary electrolyte for application to future MBs. Further in-depth studies on the interfacial characteristics of this electrolyte at both the magnesium anode and cathode are underway and will be reported in a forthcoming paper.
Author contributions
Toshihiko Mandai: conceptualization, data curation, formal analysis, funding acquisition, investigation, project administration, resources, validation, writing – original draft and review & editing. Yong Youn: data curation, formal analysis, writing –review & editing. Yoshitaka Tateyama: data curation, formal analysis, writing –review & editing.Conflicts of interest
There is no conflict of interests to declare.Acknowledgements
This work was financially supported by the Advanced Low-Carbon Technology-Specially Promoted Research for Innovative Next Generation Batteries Program (ALCA-SPRING, Grant Number JPMJAL1301) and the NEXT Center of Innovation Program (COI-NEXT, Grant Number JPMJPF2016) of the Japan Science and Technology Agency (JST). It was also supported in part by MEXT as “Program for Promoting Researches on the Supercomputer Fugaku” (Fugaku Battery & Fuel Cell Project), Grant Number JPMXP1020200301. The authors are grateful for the kind support provided by Ms Oshida for SEM and EDX observations at the NIMS Battery Research Platform. TM is also thankful for support from Dr Sodeyama for the viscosity and density measurements and a research grant for specially promoted research subjects established by NIMS. This research used the computational resources of supercomputers at NIMS and Fugaku through the HPCI System Research Project (project ID: hp200131).References
- J. Muldoon, C. B. Bucur and T. Gregory, Angew. Chem., Int. Ed., 2017, 56, 12064–12084 CrossRef CAS PubMed.
- H. Tang, N. Xu, C. Pei, F. Xiong, S. Tan, W. Luo, Q. An and L. Mai, ACS Appl. Mater. Interfaces, 2017, 9, 28667–28673 CrossRef CAS PubMed.
- Z. Z. Karger, R. Liu, W. Dai, Z. Li, T. Diemant, B. P. Vinayan, C. B. Minella, X. Yu, A. Manthiram, R. J. Behm, M. Ruben and M. Fichtner, ACS Energy Lett., 2018, 3, 2005–2013 CrossRef.
- M. Mao, T. Gao, S. Hou, F. Wang, J. Chen, Z. Wei, X. Fan, X. Ji, J. Ma and C. Wang, Nano Lett., 2019, 19, 6665–6672 CrossRef CAS PubMed.
- Z. Z. Karger and M. Fichtner, Front. Chem., 2019, 6, 656 CrossRef PubMed.
- Y. Wang, Z. Liu, C. Wang, X. Yi, R. Chen, L. Ma, Y. Hu, G. Zhu, T. Chen, Z. Tie, J. Ma, J. Liu and Z. Jin, Adv. Mater., 2018, 30, 1802563 CrossRef PubMed.
- X. Xue, R. Chen, C. Yan, P. Zhao, Y. Hu, W. Kong, H. Lin, L. Wang and Z. Jin, Adv. Energy Mater., 2019, 9, 1900145 CrossRef.
- Y. Wang, Z. Liu, C. Wang, Y. Hu, H. Lina, W. Kong, J. Ma and Z. Jin, Energy Storage Mater., 2020, 26, 494–502 CrossRef.
- Z. Lu, A. Schechter, M. Moshkovich and D. Aurbach, J. Electroanal. Chem., 1999, 466, 203–217 CrossRef CAS.
- D. Aurbach and N. Pour, J. Electrochem. Soc., 1990, 137, 775–780 CrossRef.
- L. P. Lossius and F. Emmenegger, Electrochim. Acta, 1996, 41, 445–447 CrossRef CAS.
- D. Aurbach, H. Gizbar, A. Schechter, O. Chusid, H. E. Gottlieb, Y. Gofer and I. Goldberg, J. Electrochem. Soc., 2002, 149, A115–A121 CrossRef CAS.
- D. Aurbach, G. S. Suresh, E. Levi, A. Mitelman, O. Mizrahi, O. Chusid and M. Brunelli, Adv. Mater., 2007, 19, 4260–4267 CrossRef CAS.
- F. Wang, Y. Guo, J. Yang, Y. Nuli and S. Hirano, Chem. Commun., 2012, 48, 10763–10765 RSC.
- Y. Cheng, R. M. Stolley, K. S. Han, Y. Shao, B. W. Arey, N. M. Washton, K. T. Mueller, M. L. Helm, V. L. Sprenkle, J. Liu and G. Li, Phys. Chem. Chem. Phys., 2015, 17, 13307–13314 RSC.
- Y. Yang, W. Wang, Y. Nuli, J. Yang and J. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 9062–9072 CrossRef CAS.
- J. T. Herb, C. A. N. Lund and C. B. Arnold, J. Mater. Chem. A, 2017, 5, 7801–7805 RSC.
- I. Shterenberg, M. Salama, Y. Gofer and D. Aurbach, Langmuir, 2017, 33, 9472–9478 CrossRef CAS PubMed.
- Y. Yang, Y. Qiu, Y. NuLi, W. Wang, J. Yang and J. Wang, J. Mater. Chem. A, 2019, 7, 18295–18303 RSC.
- A. Du, Z. Zhang, H. Qu, Z. Cui, L. Qiao, L. Wang, J. Chai, T. Lu, S. Dong, T. Dong, H. Xu, X. Zhou and G. Cui, Energy Environ. Sci., 2017, 10, 2616–2625 RSC.
- S. Y. Ha, Y.-W. Lee, S. W. Woo, B. Koo, J. S. Kim, J. Cho, K. T. Lee and N.-S. Choi, ACS Appl. Mater. Interfaces, 2014, 6, 4063–4073 CrossRef CAS.
- T. Fukutsuka, K. Asaka, A. Inoo, R. Yasui, K. Miyazaki, T. Abe, K. Nishio and Y. Uchimoto, Chem. Lett., 2014, 43, 1788–1790 CrossRef.
- S. Terada, T. Mandai, S. Suzuki, S. Tsuzuki, K. Watanabe, Y. Kamei, K. Ueno, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2016, 120, 1353–1365 CrossRef CAS.
- Z. Ma, M. Kar, C. Xiao, M. Forsyth and D. R. MacFarlane, Electrochem. Commun., 2017, 78, 29–32 CrossRef CAS.
- T. Mandai, K. Tatesaka, K. Soh, H. Masu, A. Choudhary, Y. Tateyama, R. Ise, H. Imai, T. Takeguchi and K. Kanamura, Phys. Chem. Chem. Phys., 2020, 21, 12100–12111 RSC.
- F. Tuerxun, K. Yamamoto, M. Hattori, T. Mandai, K. Nakanishi, A. Choudhary, Y. Tateyama, K. Sodeyama, A. Nakao, T. Uchiyama, M. Matsui, K. Tsuruta, Y. Tamenori, K. Kanamura and Y. Uchimoto, ACS Appl. Mater. Interfaces, 2020, 12, 25775–25785 CrossRef CAS PubMed.
- O. Tutusaus, R. Mohtadi, T. S. Arthur, F. Mizuno, E. G. Nelson and Y. V. Sevryugina, Angew. Chem., Int. Ed., 2015, 54, 7900–7904 CrossRef CAS PubMed.
- N. T. Hahn, T. J. Seguin, K.-C. Lau, C. Liao, B. J. Ingram, K. A. Persson and K. R. Zavadil, J. Am. Chem. Soc., 2018, 140, 11076–11084 CrossRef CAS PubMed.
- M. Watanabe, J. Kanazawa, T. Hamamura, T. Shimokawa, K. Miyamoto, M. Hibino, K. Nakura, Y. Inatomi, Y. Kitazawa and M. Uchiyama, Mater. Adv., 2021, 2, 937–941 RSC.
- J. T. Herb, C. A. N. Lund and C. B. Arnold, ACS Energy Lett., 2016, 1, 1227–1232 CrossRef CAS.
- Z. Zhang, Z. Cui, L. Qiao, J. Guan, H. Xu, X. Wang, P. Hu, H. Du, S. Li, X. Zhou, S. Dong, Z. Liu, G. Cui and L. Chen, Adv. Energy Mater., 2017, 1602055 CrossRef.
- Z. Z. Karger, M. E. G. Bardaji, O. Fuhr and M. Fichtner, J. Mater. Chem. A, 2017, 5, 10815–10820 RSC.
- J. Luo, Y. Bi, L. Zhang, X. Zhang and T. L. Liu, Angew. Chem., Int. Ed., 2019, 58, 6967–6971 CrossRef CAS.
- K.-C. Lau, T. J. Seguin, E. V. Carino, N. T. Hahn, J. G. Connell, B. J. Ingram, K. A. Persson, K. R. Zavadil and C. Liao, J. Electrochem. Soc., 2019, 166, A1510–A1519 CrossRef CAS.
- K. Tang, A. Du, X. Du, S. Dong, C. Lu, Z. Cui, L. Li, G. Ding, F. Chen, X. Zhou and G. Cui, Small, 2020, 16, 2005424 CrossRef CAS PubMed.
- A. Shyamsunder, L. E. Blanc, A. Assoud and L. F. Nazar, ACS Energy Lett., 2019, 4, 2271–2276 CrossRef CAS.
- Z. Li, O. Fuhr, M. Fichtner and Z. Z. Karger, Energy Environ. Sci., 2019, 12, 3496–3501 RSC.
- M. Yang, D. M. Driscoll, M. Balasubramanian and C. Liao, J. Electrochem. Soc., 2020, 167, 160529 CrossRef CAS.
- T. Mandai, ACS Appl. Mater. Interfaces, 2020, 12, 39135–39144 CrossRef CAS PubMed.
- A. Kraft, N. Trapp, D. Himmel, H. Böhrer, P. Schlüter, H. Scherer and I. Krossing, Chem. – Eur. J., 2012, 18, 9371–9380 CrossRef CAS PubMed.
- T. Mandai, Y. Akita, S. Yagi, M. Egashira, H. Munakata and K. Kanamura, J. Mater. Chem. A, 2017, 5, 3152–3156 RSC.
- T. Mandai and H. Somekawa, Chem. Commun., 2020, 56, 12122–12125 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. W. Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 (Revision A.03), Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS.
- M. Rohde, P. Eiden, V. Leppert, M. Schmidt, A. Garsuch, G. Semrau and I. Krossing, ChemPhysChem, 2015, 16, 666–675 CrossRef CAS PubMed.
- S. Tsujioka, B. G. Nolan, H. Takase, B. P. Fauber and S. H. Strauss, J. Electrochem. Soc., 2004, 151, A1418–A1423 CrossRef CAS.
- T. Kimura, K. Fujii, Y. Sato, M. Morita and N. Yoshimoto, J. Phys. Chem. C, 2015, 119, 18911–18917 CrossRef CAS.
- H.-C. Ku and C.-H. Tu, J. Chem. Eng. Data, 2000, 45, 391–394 CrossRef CAS.
- D. Kodama, M. Kanakubo, M. Kokubo, S. Hashimoto, H. Nanjo and M. Kato, Fluid Phase Equilib., 2011, 302, 103–108 CrossRef CAS.
- S. Tsuzuki, T. Mandai, S. Suzuki, W. Shinoda, T. Nakamura, T. Morishita, K. Ueno, S. Seki, Y. Umebayashi, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2017, 19, 18262–18272 RSC.
- W. A. Henderson, N. R. Brooks, W. W. Brennessel and V. G. Young, Jr., J. Phys. Chem. A, 2004, 108, 225–229 CrossRef CAS.
- W. A. Henderson, J. Phys. Chem. B, 2006, 110, 13177–13183 CrossRef CAS.
- K. Westman, R. Dugas, P. Jankowski, W. Wieczorek, G. Gachot, M. Morcrette, E. Irisarri, A. Ponrouch, M. R. Palacín, J.-M. Tarascon and P. Johansson, ACS Appl. Energy Mater., 2018, 1, 2671–2680 CrossRef CAS.
- T. Mandai, K. Dokko and M. Watanabe, Chem. Rec., 2019, 19, 708–722 CrossRef CAS.
- K. Fujii, M. Sogawa, N. Yoshimoto and M. Morita, J. Phys. Chem. B, 2018, 122, 8712–8717 CrossRef CAS PubMed.
- C. Zhang, K. Ueno, A. Yamazaki, K. Yoshida, H. Moon, T. Mandai, Y. Umebayashi, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2014, 118, 5144–5153 CrossRef CAS.
- K. Tang, A. Du, S. Dong, Z. Cui, X. Liu, C. Lu, J. Zhao, X. Zhou and G. Cui, Adv. Mater., 2020, 32, 1904987 CrossRef CAS.
- J. J. D. Yoreo and P. G. Vekilov, Rev. Mineral. Geochem., 2003, 54, 57–93 CrossRef.
- M. V. Mirkin and A. P. Nilov, J. Electroanal. Chem. Interfacial Electrochem., 1990, 283, 35–51 CrossRef CAS.
- Z. Peng, N. Zhao, Z. Zhang, H. Wan, H. Lin, M. Liu, C. Shen, H. He, X. Guo, J.-G. Zhang and D. Wang, Nano Energy, 2017, 39, 662–672 CrossRef CAS.
- X. Fan, L. Chen, X. Ji, T. Deng, S. Hou, J. Chen, J. Zheng, F. Wang, J. Jiang, K. Xu and C. Wang, Chem, 2018, 4, 174–185 CAS.
- T. Yim, S.-G. Woo, S.-H. Lim, J.-Y. Yoo, W. Cho, M.-S. Park, Y.-K. Han, Y.-J. Kim and J. Yu, ACS Sustainable Chem. Eng., 2017, 5, 5733–5739 CrossRef CAS.
- H. Kuwata, M. Matsui and N. Imanishi, J. Electrochem. Soc., 2017, 164, A3229–A3236 CrossRef CAS.
- T. Mandai, K. Yoshida, S. Tsuzuki, R. Nozawa, H. Masu, K. Ueno, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2015, 119, 1523–1534 CrossRef CAS PubMed.
- K. Hashimoto, S. Suzuki, M. L. Thomas, T. Mandai, S. Tsuzuki, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2018, 20, 7998–8007 RSC.
- K. Shigenobu, K. Dokko, M. Watanabe and K. Ueno, Phys. Chem. Chem. Phys., 2020, 22, 15214–15221 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00448d |
| This journal is © The Royal Society of Chemistry 2021 |