Open Access Article
Open Access ArticleTowards the understanding of halogenation in peptide hydrogels: a quantum chemical approach†
Tom
Bettens
 a,
Valentin
Lacanau
b,
Ruben
Van Lommel
ac,
Tess
De Maeseneer
d,
Wouter
Vandeplassche
b,
Jolien
Bertouille
b,
Joost
Brancart
a,
Valentin
Lacanau
b,
Ruben
Van Lommel
ac,
Tess
De Maeseneer
d,
Wouter
Vandeplassche
b,
Jolien
Bertouille
b,
Joost
Brancart
 e,
Thomas M. A.
Barlow
b,
Tatiana
Woller
a,
Niko
Van den Brande
e,
Paula
Moldenaers
d,
Frank
De Proft
a,
Annemieke
Madder
e,
Thomas M. A.
Barlow
b,
Tatiana
Woller
a,
Niko
Van den Brande
e,
Paula
Moldenaers
d,
Frank
De Proft
a,
Annemieke
Madder
 f,
Richard
Hoogenboom
f,
Richard
Hoogenboom
 g,
Charlotte
Martin
b,
Steven
Ballet
g,
Charlotte
Martin
b,
Steven
Ballet
 *b and
Mercedes
Alonso
*b and
Mercedes
Alonso
 *a
*a
aDepartment of General Chemistry (ALGC), Faculty of Science and Bio-engineering Sciences, Vrije Universiteit Brussel (VUB), Pleinlaan 2, 1050 Brussels, Belgium. E-mail: mercedes.alonso.giner@vub.be
bResearch Group of Organic Chemistry (ORGC), Faculty of Science and Bio-engineering Sciences, Vrije Universiteit Brussel (VUB), Pleinlaan 2, 1050 Brussels, Belgium. E-mail: Steven.Ballet@vub.be
cDepartment of Chemistry, Molecular Design and Synthesis, KU Leuven, Celestijnenlaan 200F, Leuven Chem&Tech, Box 2404, 3001 Leuven, Belgium
dSmart Matter, Rheology, and Technology, Department of Chemical Engineering, KU Leuven, Celestijnenlaan 200J, P.B. 2424, 3001 Leuven, Belgium
ePhysical Chemistry and Polymer Science (FYSC), Vrije Universiteit Brussel (VUB), Pleinlaan 2, 1050 Brussels, Belgium
fDepartment of Organic and Macromolecular Chemistry, Organic and Biomimetic Chemistry Research Group (OBCR), Ghent University, Krijgslaan 281 S4, 9000 Ghent, Belgium
gDepartment of Organic and Macromolecular Chemistry, Supramolecular Chemistry Group, Centre of Macromolecular Chemistry (CMaC), Ghent University, Krijgslaan 281 S4, 9000 Ghent, Belgium
First published on 18th June 2021
Abstract
Non-covalent interactions involving aromatic rings play a central role in many areas of modern chemistry. In medicinal and bioorganic chemistry, the intermolecular interactions between the aromatic side chains of amino acids, such as phenylalanine and tyrosine, are of great interest. To enhance the affinity between such aromatic side chains, halogenation is a promising modification strategy. In the current work, the nature and strength of halogenated π–π stacked phenylalanine (Phe) dimers have been investigated using density functional theory, energy decomposition analyses and the non-covalent interaction (NCI) method. Our analysis shows that increasing the degree of halogenation enhances the strength of the stacking interactions and, moreover, the heavier halides (Cl, Br and I) lead to stronger interactions compared to the lighter F. This effect was traced back to local secondary interactions of the halide with the aliphatic C–H bonds of the phenylalanine side chain. Based on the computational findings, a set of peptide hydrogelators was synthesized, and the resulting hydrogel properties were further investigated via dynamic rheometry. Experimental observations can be correlated to the trends found in the theoretical analysis, suggesting that local interactions indeed play a noticeable role in enhancing peptide-based hydrogel strength.
Introduction
Experimental and computational studies have shown the considerable impact of substituents on non-covalent interactions involving aromatic rings.1,2 In contrast to conventional models relying on substituent-induced changes in the aryl π-system,3 Wheeler and Houk demonstrated the local nature of substituent effects in stacking interactions.4 For a broad variety of stacked dimers, substituent effects were explained in terms of direct interactions between substituents and the nearby vertex of the other arene.5 As a consequence, substituent effects in stacking interactions are additive, transferable and dependent on the relative position of the substituents. The additivity of substituent effects in aromatic stacking interactions was validated experimentally by Hwang et al.6 The formation of aromatic stacking interactions and the ability to electrostatically influence the interaction energies through the introduction of substituents were confirmed by NMR spectroscopy, X-ray crystallography and linear Hammett plots for monosubstituted systems. Accordingly, simple additivity models were shown to accurately predict substituent effects. Very recently, Wheeler and co-workers proposed a predictive model for the stacking energy between several heterocycles and the side chains of aromatic amino acids (Phe, Tyr and Trp).7 In the gas phase, this model includes the heavy-atom count of both the amino acid and heterocycle, as well as electrostatic potential characteristics of the heterocycle. In the solution phase model, the heavy atom count of the heterocycle was replaced by its polarizability. These earlier reports indicate that the strength of stacking interactions can be fine-tuned by changing the number and distribution of heteroatoms within the heterocycle.Peptide-based hydrogels are underpinned by different non-covalent interactions, including hydrogen bonding, ionic, and van der Waals interactions between amide, aromatic and aliphatic moieties, rendering them reversible and adaptive in nature. In such systems, specific amino acid derivatives and peptides can self-assemble into fibers, a process followed by fiber entanglement, which eventually leads to the formation of the physical hydrogel network. To improve the self-assembly process leading to hydrogel formation, it is important to identify optimal amino acid side chains and substitution patterns within these side chains, strengthening non-covalent interactions in such peptide-based hydrogels, while avoiding peptide precipitation. A target amino acid for this goal is the Phe aromatic side chain. This aromatic moiety proved to be crucial in the self-assembly process of previously reported hexapeptide hydrogelator 1 (Fig. 1 with three phenylalanine amino acids).8 It was anticipated that halogenation of the aromatic side chains in positions 1, 3 and 5 of the peptide sequence would lead to altered hydrogel properties by modulating the complex interplay of non-covalent interactions within and between the assembled fibers. Such chemical modifications could eventually influence the in vivo behavior of injected hydrogels, for instance in the context of controlled drug delivery and regenerative medicine.9
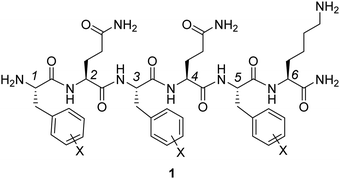 | ||
| Fig. 1 Representation of hexapeptide [H-FQFQFK-NH2] 1, which is a hydrogelator that will be further investigated here by substitution of the phenylalanine units with halogen atoms. | ||
Previous studies exploited the use of Fmoc-Phe-OH 2 and related molecules as self-assembling hydrogelators (Fig. 2).10 It was demonstrated that the assembly of these molecules can be profoundly enhanced by the incorporation of various substituents, including halogenation of the side chains.11 Nilsson and co-workers showed that introducing a single halogen substituent on the phenyl ring increases the rigidity of the Fmoc-Phe-OH 2 based hydrogels.12 They stated that the steric and electronic character of the amino acid derivative dictates hydrogel rigidity, and the gel stiffness increased in the order of Br < Cl < F. More recently, it was suggested by Pizzi that the occurrence of halogen bonding can result in hydrogels with stronger mechanical properties than their non-halogenated counterparts. In fact, the hydrogel rigidity could be ranked according to halogen atom polarizability, which are opposite findings compared to those reported by Nilsson.13 Similarly, the amyloid mimicking peptide H-DFNKF-OH 3 and the peptide hydrogelator H-KLVFF-OH 4 were modified through insertion of halogens in para-position of both phenylalanines.14,15 The reported data showed that di-halogenation could further improve peptide hydrogel strength in specific cases.
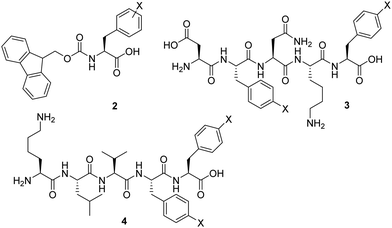 | ||
| Fig. 2 Representation of previously studied halogenated peptide hydrogelators: Fmoc-Phe(X)-OH (2); H-DF(X)NKF(X)-OH (3) and H-KLVF(X)F(X)-OH (4). | ||
Overall, these previous results emphasize that halogen substitution serves as a viable strategy for tuning rheological properties of peptide hydrogels; however, no unified framework to describe the halogenation effect exists. Hence, a detailed analysis of stacking interactions involving halogenated moieties is needed for identifying the factors governing their strength.
In this paper, the strength and origin of side chain interactions of natural and halogenated Phe units have been characterized using density functional theory (DFT) calculations,16 energy decomposition analysis (EDA)17 and the non-covalent interaction (NCI) method.18 By using this integrated approach, some of the authors recently provided a fundamental understanding of non-covalent interactions involving aromatic and aliphatic groups.19 Subsequently, this knowledge was exploited in the rational design of polymer/graphene nanocomposites.20
Additionally, we have shown that the NCI method can be effectively applied to proteins as a fast and efficient hydrogen bond detector, outperforming conventional geometrical methods.21 Besides the NCI method, the EDA analysis provides a quantitative framework to identify the dominant factor in the interaction energies of halogenated dimers. In this study, we set out to elucidate how halogen substituents can tune the strength of non-covalent interactions, which strongly influences the fiber formation within peptide hydrogel networks and, hence, impacts the resulting hydrogel properties.12–15 These calculations provide insights into the most appropriate choice of halogen substitution in phenylalanine aromatic cores in terms of halogen type and position. The most optimal substitution patterns were identified and used in the synthesis of a set of hexapeptide hydrogelators and the bulk rheological properties of the corresponding hydrogels were determined experimentally.
Results and discussion
Effect of halogenation on interaction strength involving π–π stacked Phe⋯Phe residues
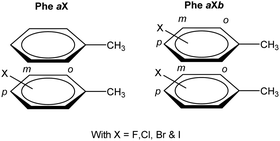
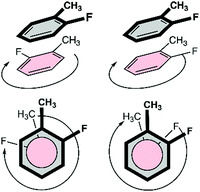
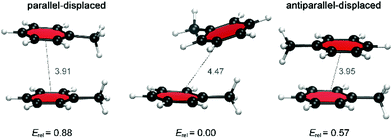
At first, an interaction library was constructed encompassing different stacked dimers representative for natural and halogenated Phe⋯Phe pairs. The phenylalanine side chain was modeled by toluene rather than benzene. Due to the additional methyl group, toluene constitutes a more accurate model than benzene to rationalize orientational preferences in π–π interactions in phenylalanine-containing peptides and proteins.22 By truncating the amino acid side chain between the Cβ and Cα atoms, the role of steric and ancillary interactions on the orientational preferences of phenyl rings can be optimally described.23 In the toluene dimer, the stacked configurations (Fig. 3) were predicted to be energetically more favorable than the T-shaped motif.22The halogenation pattern of the phenyl rings (ortho, meta, para) and its concomitant influence on the relative orientation of the two rings was investigated in detail for X = F. For each pair of a fluorinated toluene and parent toluene (i.e. the Phe aF dimers), the relative orientation – characterized by a rotation of the parallel rings in the case of π–π stacking (Fig. 4) – was varied in steps of 30°, resulting in a total of 12 Phe⋯Phe input structures for each dimer. Additionally, we investigated the influence of adding the same halogen on the other toluene moiety on the stability of the dimers (Phe aFb dimers). This resulted in 24 additional Phe⋯Phe dimers to consider and was carried out for the fluorine substituent on all possible combinations of substitution patterns (oXo, oXm, oXp, mXm, mXp, pXp). For comparative purposes, the parent toluene–toluene dimer was also included.
Because multiple rotamers are possible for each dimer, we first performed a systematic study on all the ortho/meta/para fluorophenylalanine combinations in order to find the most stable rotamer (Fig. 4). This conformational search at the M06/cc-pVTZ level revealed three rotamers for the parent toluene–toluene dimer (Fig. 5), four rotamers for the pF dimer, six stacked configurations for the oF, mF, oFp, mFp and pFp dimers and twelve different rotamers for the oFo, oFm and mFm dimers. The reason behind the smaller number of configurations in the set of dimers containing a para-substituted unit is the presence of a C2 symmetry axis in para-substituted toluene. Subsequently, single-point energy calculations using the larger aug-cc-pVTZ basis set including the Counterpoise correction were performed on the three most stable conformations for each halogenated Phe⋯Phe dimer to obtain more accurate energies (Table S2, ESI†). Based on these energies, the most stable conformation was identified, and this conformation was selected for our investigation of the heavier halogens.
 | ||
| Fig. 5 Relative BSSE-corrected energies (in kcal mol−1) and center-to-center phenyl ring distances (in Å) for different stacked dimer configurations for the parent toluene dimer. | ||
For the toluene–toluene dimer, changes in the relative orientation of the aromatic rings led to small energy differences around 0.6 kcal mol−1 (Fig. 5). The preferred orientation corresponds to the tilted parallel-displaced (PD) configuration, which is only 0.6–0.9 kcal mol−1 more stable than the antiparallel- and parallel-displaced configuration, respectively. Larger energy differences were calculated for the dimers in which one toluene unit is fluorinated; a trend that is continued when both toluene units are fluorinated, already suggesting a critical influence of the halogen on the interaction strength. For the Phe aF dimers (i.e. the systems bearing one fluorine on one of the two rings), the relative energies for stacked dimers vary up to 1.5 kcal mol−1, whereas a maximum energy difference of 2.0 kcal mol−1 was found for Phe aFb dimers (i.e. systems with one fluorine on each of the aromatics; Table S2, ESI†).
Fig. 6 displays the most stable configurations of the fluorinated Phe⋯Phe dimers. In all cases, the energy minima correspond to the PD geometry with the halogen atom(s) oriented away from the phenyl π-cloud. However, the preferred relative orientation of the halogen and methyl groups changes as a function of the halogen substitution pattern. For the oF dimers, the preferred stacked configuration involves a direct C–H⋯X interaction between the halogen atom and the hydrogen atoms of the methyl group of the other ring. For the mF and pF systems, the most stable stacking geometry favors the dispersion interactions between the methyl groups. The same orientational differences are even more pronounced for the Phe aFb dimers. Whereas the antiparallel-displaced configuration is preferred for mFm, mFp and pFp dimers due to C–H⋯X interactions, the parallel-displaced configuration with interacting methyl groups is favored in the oFo, oFm and oFp dimers.
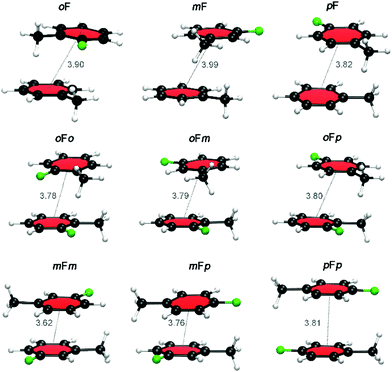 | ||
| Fig. 6 Lowest energy conformations of the fluorinated Phe⋯Phe dimers. The center-to-center distances (in Å) are indicated. | ||
The counterpoise-corrected interaction energies (ECPint) computed at the M06/aug-cc-pVTZ(-PP) level of theory for the aX dimers are listed in Table 1. Although the energy differences are small, the interaction energies become larger upon halogen substitution, except for mF, and the stabilizing effect increases for heavier halogens in the order F < Cl < Br < I; in line with the larger polarizability. This trend confirms previous experimental and theoretical studies.13,25,26 Note that fluorine substitution leads to similar or lower interaction energies compared to the toluene dimer. Regarding the halogenation pattern, we observe that para-substitution stabilizes the dimers to a larger extent than ortho-substitution and the energy differences are larger for heavier halides I and Br (Fig. 7). Accordingly, pI exhibits the largest interaction energy (−4.52 kcal mol−1), representing an increase of around 1 kcal mol−1 with respect to the energetically most stable parent toluene dimer H.
| System | E CPint | R | V NCI | System | E CPint | R | V NCI |
|---|---|---|---|---|---|---|---|
| a Interaction energies were computed at the M06/aug-cc-pVTZ(-PP) level of theory. b Integrations were not performed for dimers containing I, owing to the inability of the NCIPLOT program to handle effective core potentials. | |||||||
| H | −3.63 | 4.47 | 51.83 | mClm | −6.52 | 3.34 | 72.37 |
| oF | −3.60 | 3.90 | 58.83 | mClp | −5.21 | 3.74 | 67.21 |
| mF | −3.48 | 3.99 | 56.43 | mClo | −4.82 | 3.89 | 56.85 |
| pF | −3.60 | 3.82 | 59.83 | oClo | −4.51 | 3.81 | 60.93 |
| oCl | −3.94 | 3.85 | 54.24 | oClp | −4.92 | 3.88 | 58.00 |
| mCl | −3.95 | 3.80 | 62.87 | pClp | −4.56 | 3.91 | 59.49 |
| pCl | −4.11 | 3.82 | 66.44 | mBrm | −6.21 | 3.62 | 74.68 |
| oBr | −4.08 | 3.85 | 54.22 | mBrp | −5.59 | 3.75 | 69.06 |
| mBr | −4.21 | 3.79 | 64.09 | mBro | −5.18 | 3.92 | 58.65 |
| pBr | −4.27 | 3.80 | 68.79 | oBro | −4.57 | 3.87 | 64.43 |
| oI | −4.15 | 4.00 | —b | oBrp | −5.34 | 3.80 | 58.17 |
| mI | −4.33 | 3.81 | —b | pBrp | −4.75 | 3.93 | 61.89 |
| pI | −4.52 | 3.82 | —b | mIm | −6.55 | 3.64 | —b |
| mFm | −4.36 | 3.62 | 58.68 | mIp | −5.85 | 3.79 | —b |
| mFp | −4.12 | 3.76 | 54.93 | mIo | −6.15 | 3.73 | —b |
| mFo | −3.99 | 3.79 | 54.79 | oIo | −5.36 | 3.84 | —b |
| oFo | −3.65 | 3.78 | 57.04 | oIp | −5.72 | 4.06 | —b |
| oFp | −3.86 | 3.80 | 56.15 | pIp | −5.42 | 4.02 | —b |
| pFp | −3.65 | 3.81 | 54.23 | ||||
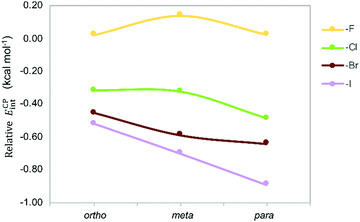 | ||
| Fig. 7 Stabilizing effect in Phe aX dimers with respect to parent toluene dimer H as a function of the halide and the halogenation pattern. | ||
Next, the stacking of the Phe aXb dimers with each phenyl ring containing one halogen was investigated following the same computational procedure (Table 1). Similar to the Phe aX dimers, the stacking interaction becomes stronger as the size of the halogen increases. The largest variation in the interaction energies is observed when going from fluorine to chlorine. Regardless of the halogen, the mXm substitution induces the largest stabilization as compared to the parent toluene dimer H. Such stabilization is quite substantial for heavier halogens, being 2 to 3 kcal mol−1 for both bromine and iodine. The largest interaction energies of mXm dimers correlate with the considerable shortening of center-to-center distances (Fig. 6). For the stacking of halobenzenes, the substitution pattern has a large influence on the interaction energies, as shown in Fig. 8.
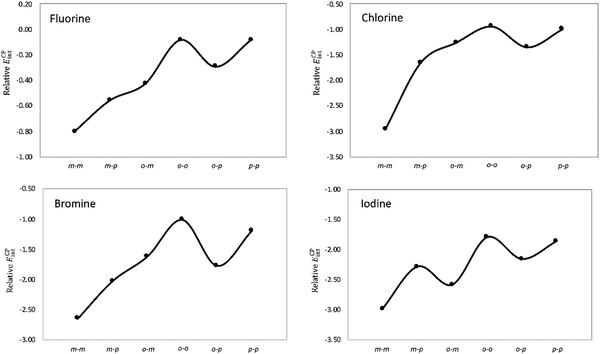 | ||
| Fig. 8 Stabilizing effect (in kcal mol−1) in Phe aXb dimers relative to the toluene dimer as a function of the halogenation pattern. | ||
A graphical visualization of the evolution of the interaction energies in the Phe aX and Phe aXb dimers is given in Fig. 9. From this graph, it is clear that Phe⋯Phe dimers become more stabilized when substituted with heavier halogen atoms. Regarding the substitution pattern, meta-halogenation on both rings and para-halogenation on one ring have the strongest stabilizing effect.
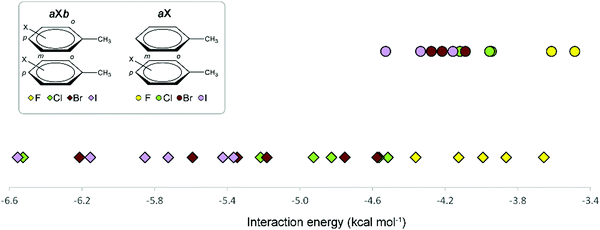 | ||
| Fig. 9 Overview of the interaction energies of Phe aX (●) and Phe aXb (✦) dimers as a function of the halogen atom. | ||
Towards insight into the nature of the stacking interactions in halogenated Phe⋯Phe dimers
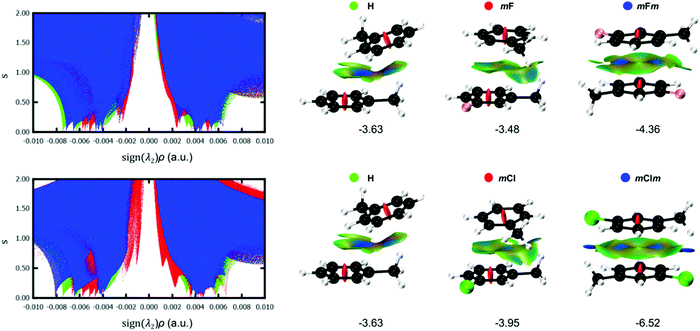
To obtain further insight into the effect of halogenation on the stacking interactions, the NCI index was computed for selected Phe⋯Phe dimers. An important advantage is the modest dependence of NCI on the computational method,27 in contrast to the interaction energies which are highly dependent on the exchange–correlation functional.28 In addition, the visualization of the non-covalent interactions in real space is very advantageous to reveal the substituent effect on stacking interactions. Fig. 10 shows the s(ρ) diagrams and gradient isosurfaces of the toluene dimer H, aX dimers (mF and mCl) and aXb dimers (mFm and mClm). From these graphs, the effect of the type and number of halogens can be clearly visualized. Regarding the type of halogen, the strengthening of the stacking interaction when going from fluorine to chlorine is evidenced by the shift of the characteristic NCI peaks toward larger density values in the attractive region [sign(λ2) < 0]. Such stabilizing effect is particularly visible for the mXm dimers, in which two non-classical hydrogen bonds (C–H⋯X) are strengthened significantly when changing fluorine by chlorine, as demonstrated by the blue isosurfaces in the mClm dimer in Fig. 10. The C–H⋯F interactions are considerably weaker in mFm, corresponding to green isosurfaces. The NCI plots also explain why mXm are the most stable dimers since the methyl group and the halogen from opposite rings have a suitable orientation to undergo C–H⋯X interactions, while maintaining a favourable π–π stacking (Fig. 10). The 3D isosurfaces support the local nature of the halogen substitution effect in stacking interactions.2,5A more quantitative analysis can be performed based on the integrated volumes within the NCI region (VNCI in Table 1). The integration of NCI quantities within the interacting region were shown to mimic the potential energy curves of conventional hydrogen bonds.29 Based on the integrated volumes, the stacking interactions of the meta-halogenated dimers weaken in the following order: mBrm > mClm > mBr > mCl > mFm > mF. The interaction energies more or less follow the same trend, with a correlation coefficient of R2 = 0.85 for this set of derivatives (Fig. S2, ESI†). In contrast, the correlation between the interaction energies and the centroid–centroid distance (R) is much worse for the same set of dimers (R2 = 0.55). These results support the deficiency of geometrical criteria to quantify the strength of stacking interactions, in line with previous findings.21
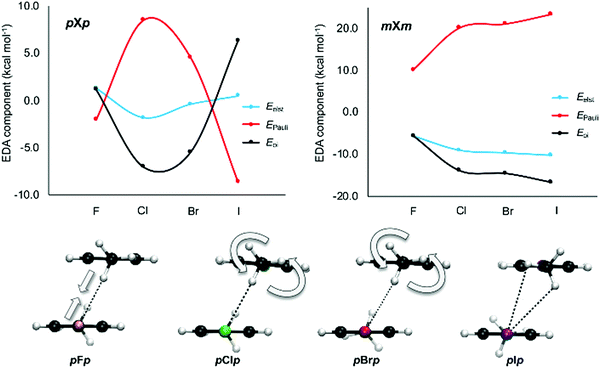
To gain additional insight into the interactions between the aromatic dimers, an energy decomposition analysis (EDA) was performed for all halogenated dimers as well as the most stable stacked configuration of the parent toluene–toluene dimer. The results show that the strength of the interaction is the outcome of a delicate balance between attractive electrostatic and orbital interactions and repulsive Pauli interaction. From the NCI plots in Fig. 10, it seems that the large chlorine is involved in a stronger CH⋯X interaction than the smaller fluorine. All halogenated dimers display such interaction, except for mX and pX (Fig. 6). Overall, the largest variation in the energy components is observed when going from F to Cl, in line with the interaction energies. From the EDA analysis in Table S3 (ESI†), it is clear that the electrostatic interaction becomes stronger upon substitution of F by Cl, but the electrostatic advantage is compensated by stronger Pauli repulsion (the only exception being oXm). Therefore, it is the orbital interaction term that appears to be decisive for the more stabilizing interaction energies in chlorinated dimers relative to the fluorinated analogues.
This is particularly clear for structures where two CH⋯X interactions are present, such as the mXm or pXp set of dimers (Fig. 11). When comparing the mFm dimer to the other mXm dimers, an absolute increase is observed for both attractive electrostatic and orbital interactions as well as Pauli repulsion. This is rationalized by the local CH⋯X interactions becoming strengthened when larger halides are involved. For the pXp dimers, the same trend is observed when comparing pFp with pClp. However, for the heavier halide substituted dimers, pBrp and pIp, a different trend is found as now electrostatics, Pauli repulsion and the orbital interaction become smaller in absolute value with increasing halogen size. This can be explained by looking at the CH⋯X interaction. As the halide becomes bigger, the Pauli repulsion increases to the extent where the nature of this interaction changes to lower the repulsion. This is accomplished by a gradual rotation of the methyl group of the opposing aromatic ring (Fig. 11). Consequently, the CH⋯X interaction has a bifurcated character in the pIp dimer. This analysis underlines again the local effect of halogen substitution on π–π interactions.
Overall, this in-depth theoretical study provides insight into the effect of halogenation on π–π stacking interactions. On one side, the interaction energies at the DFT-level suggest that the stacking interaction becomes stronger as the size and number of halogen atoms increases. On the other side, the halogenation pattern of the phenyl rings further influences the interaction strength, with mXm dimers exhibiting the largest stabilizing effect regardless of the halogen. The presence of local C–H⋯X hydrogen bonds contributes to the strengthening of the stacking interactions, as revealed by the NCI and EDA analysis. These theoretical results support that halogenation may indeed be a viable strategy for tuning the rheological properties of peptide-based hydrogels. Accordingly, in the next step, the most interesting substitution patterns were incorporated in the self-assembling phenylalanine-containing hexapeptide hydrogelator sequences (Fig. 1).
Connection to experimental data on peptide hydrogels
As mentioned above, we reported earlier on a new family of short amphipathic peptide-based hydrogels, which form thixotropic injectable hydrogels upon dissolution in aqueous solutions.8,30 The ‘parent’ lead structure in this effort is the sequence H-FQFQFK-NH2 (Fig. 1, with X = H), which proved to efficiently form a controlled drug delivery hydrogel.8,31 Based on the theoretical analysis performed on the halogenated dimers, we postulate that halogenated phenylalanines would provide peptide-based hydrogels with improved mechanical properties.To verify whether halogen substitution would impact the material properties of the peptide hydrogel, a library of halogenated phenylalanine-containing peptides (compounds 5 to 36) was synthesized via solid phase peptide synthesis (SPPS) using standard Fmoc-chemistry. All peptides were synthesized in good yields (see ESI†) and gelation in phosphate buffer solution (PBS) was checked at a concentration of 2 weight percentage (wt%). An initial qualitative analysis by means of the vial inversion test revealed that most of the prepared peptide hydrogelators indeed allow the formation of hydrogels, whereby their physical appearance indicated that the halogenated phenylalanines had a substantial impact on the rigidity of the resulting hydrogels. Subsequently, quantitative data were obtained to validate the material properties of the halogenated peptide hydrogels by dynamic rheology confirming that strong hydrogels were formed as the storage modulus (G′) was higher than the loss modulus (G′′) at the applied frequency (all raw measurement data are included in the ESI†). Furthermore, the physical nature of the hydrogels was confirmed by their shear-thinning behaviour, a key property for their injectability. Viscosity measurements further confirmed that the halogenated peptide hydrogels display in many cases a higher rigidity, in comparison to the corresponding non-halogenated peptide 1. At 2 wt% in phosphate buffer, the hydrogel composed of the lead sequence 1 had a G′ value of 63 ± 8 kPa, whereas the library of halogenated phenylalanine-based peptides gave G′ values up to 314 ± 63 kPa, which is up to a five-fold increase in rigidity (Table 2).
| No. | Sequence | G′ (kPa) at 10 rad s−1 | |
|---|---|---|---|
| Amino acid position number of the amino in superscript. | |||
| 1 | H | H-F1QF3QF5K-NH2 | 63 ± 8 |
| 5 | I | H-F(p-I)QFQFK-NH2 | 150 ± 17 |
| 6 | H-FQF(p-I)QFK-NH2 | 24 ± 5 | |
| 7 | H-FQFQF(p-I)K-NH2 | 314 ± 63 | |
| 8 | H-F(m-I)QFQFK-NH2 | 108 ± 30 | |
| 9 | H-FQF(m-I)QFK-NH2 | 132 ± 21 | |
| 10 | H-FQFQF(m-I)K-NH2 | Not a gel | |
| 11 | H-F(o-I)QFQFK-NH2 | 69 ± 12 | |
| 12 | H-FQF(o-I)QFK-NH2 | 20 ± 4 | |
| 13 | H-FQFQF(o-I)K-NH2 | 11 ± 3 | |
| 14 | H-F(p-I)QFQF(p-I)K-NH2 | Not a gel | |
| 15 | H-F(m-I)QFQF(m-I)K-NH2 | 69 ± 8 | |
| 16 | H-F(o-I)QFQF(o-I)K-NH2 | Not a gel | |
| 17 | H-F(p-I)QF(p-I)QF(p-I)K-NH2 | Not soluble | |
| 18 | H-F(m-I)QF(m-I)QF(m-I)K-NH2 | 81 ± 2 | |
| 19 | Br | H-FQFQF(p-Br)K-NH2 | 59 ± 8 |
| 20 | H-F(m-Br)QFQFK-NH2 | 93 ± 25 | |
| 21 | H-FQF(m-Br)QFK-NH2 | 260 ± 62 | |
| 22 | H-FQFQF(m-Br)K-NH2 | 120 ± 4 | |
| 23 | H-F(p-Br)QFQF(p-Br)K-NH2 | Not soluble | |
| 24 | H-F(m-Br)QFQF(m-Br)K-NH2 | 265 ± 88 | |
| 25 | H-F(p-Br)QF(p-Br)QF(p-Br)K-NH2 | Not a gel | |
| 26 | H-F(m-Br)QF(m-Br)QF(m-Br)K-NH2 | 180 ± 43 | |
| 27 | Cl | H-FQFQF(p-Cl)K-NH2 | 86 ± 13 |
| 28 | H-F(m-Cl)QFQFK-NH2 | 60 ± 8 | |
| 29 | H-FQF(m-Cl)QFK-NH2 | 17 ± 2 | |
| 30 | H-FQFQF(m-Cl)K-NH2 | 208 ± 19 | |
| 31 | H-F(m-Cl)QFQF(m-Cl)K-NH2 | 233 ± 26 | |
| 32 | H-F(p-Cl)QF(p-Cl)QF(p-Cl)K-NH2 | Not a gel | |
| 33 | F | H-F(m-F)QFQFK-NH2 | 50 ± 14 |
| 34 | H-FQF(m-F)QFK-NH2 | 123 ± 33 | |
| 35 | H-FQFQF(m-F)K-NH2 | 117 ± 13 | |
| 36 | H-F(m-F)QFQF(m-F)K-NH2 | 79 ± 11 | |
It is noteworthy to mention that while the theoretical results were performed on simplified Phe⋯Phe dimer models, the physical hydrogels under investigation are much more complex systems since they contain three Phe residues, namely Phe1, Phe3 and Phe5 (with the numbering starting from the N-terminus to the C-terminus of the sequence: H-F1QF3QF5K-NH2 in Table 2). Consequently, a series of halogenated hydrogelators were prepared to allow investigating the influence of the type and position of the halide on the phenyl ring, but also the location of the halogenated phenylalanine within the peptide sequence. Notwithstanding the complexity of the hydrogel systems, it was possible to establish qualitative correlations between the experimentally obtained data and the theoretical calculations.
Since iodination and bromination resulted in the strongest intermolecular interactions for mono-halogenated dimers (aX model, vide supra), an extended collection of the iodinated and brominated peptide hydrogelators was analyzed first. More specifically, pI substitution appears to exhibit the largest interaction energy (Fig. 7), and hence is expected to significantly increase the stiffness of the resulting gels. Accordingly, we first prepared mono-iodinated sequences, by inserting pI Phe residues in position 1, 3 or 5 to afford hydrogelators 5, 6 and 7 respectively. Interestingly, while the insertion of pI in position 1 and 5 (5, 7) significantly increases the G′ value by two- or five-fold, respectively, substitution on the Phe3 (6) induces the opposite effect by lowering the G′ to 24 ± 5 kPa. These first results highlight that the position of the mono-halogenated Phe residue strongly impacts the mechanical properties of the hydrogel. Importantly, hydrogelator 7, containing pI Phe5, was characterized as the strongest gel with a G′ value of 314 ± 63 kPa, which is in line with the theoretical calculations. In a systematic approach, we then evaluated the importance of the position of the mono-iodinated Phe in the peptide sequence for the other halogenation patterns (mI and oI). While mI substituted Phe (8–10) gave rise to stiffer gels when inserted in positions 1 and 3, oI substitutions never improved the mechanical properties of the hydrogels (11–13), and even lowered G′, in comparison to the parent peptide 1, which is potentially indicative of unfavorable steric interactions within the peptide assembly. Overall, the G′ values determined by rheology demonstrate a stabilizing effect of halogenation, according to a pattern pI > mI > oI, which is in line with the calculated interaction energies (Table 2 and Fig. 7).
Next, the insertion of two or three halogenated Phe residues was considered, since the theoretical calculations also delivered evidence of the stabilizing effect of aXb dimers and in particular mXm dimers (Fig. 8–10). The benefit of mXm dimers was also validated experimentally with the sequences 14–18, amongst which only meta-substituted iodoPhe containing peptides were able to form hydrogels (15 and 18) with similar or slightly improved G′, whereas oIo and pIp patterns seem to perturb efficient self-assembly and hence prevent the gelation of the corresponding sequences 14, 16 and 17. This might be explained by the altered dispositions of the aromatics when the halogenated residues are located in peptide sequence and form supramolecular assemblies, as compared to the ideal geometries applied in the isolated dimer models.
Subsequently, the most interesting modifications were also explored for bromine, chlorine and fluorine derivatives. Similarly to what was observed for the iodo-substituted hydrogelators, the position of the halogenated Phe residues in the sequence drastically influences the mechanical properties of the gels. Despite the fact that no general rules could be derived from this experimental set of mono-substituted peptides, preferred substitution patterns can be established per halide. While mono-substituted (pI and mI) sequences appear to be more suited for iodine sequences; in case of bromine and chlorine, mono-halogenation (mX) in positions 3 and 5 respectively, as well as halogenation (mXm) in both positions 1 and 5 of the sequence seems the most promising substitution pattern to access strong hydrogels. Altogether, and for both aX and aXb models, the theoretical calculations show a stabilizing effect along an increased size of the halogen atom. Such a tendency was in casu verified experimentally for mX substituted Phe1 residues (33 < 28 < 20 < 8). In line with the calculations (Fig. 7), fluorine insertion provided the lowest stabilization when applied to this specific hexapeptide hydrogelator type (cf.33 to 36).
Overall, we can conclude that halogenation represents a promising modification strategy to enhance peptide hydrogel rigidity. The description and understanding of the more complex interplay between multiple halogenated Phe units on the hexapeptides and the influence thereof on formation of fibers and eventually hydrogels remains beyond the capacity of the current calculation strategy. Nevertheless, we have clearly demonstrated that, despite the large jump in complexity between the developed theoretical model and the designed hydrogel systems, theoretical calculations are an important tool to support the design of halogenated hydrogels with improved mechanical properties.
Conclusion
In summary, the effects of halogenation on π–π stacking interactions between aromatic side chains of phenylalanine were investigated through DFT calculations, energy decomposition analysis and the NCI method. The role of the number, position and nature of halogen atoms has been elucidated for toluene dimers (toluene representing the phenylalanine side chain), in which one or both rings are substituted with a halogen atom, in order to model Phe⋯Phe stacking in peptides. The lowest energy configuration was identified through a systematic search on all the ortho/meta/para fluorophenylalanine combinations. In all cases, the lowest energy structure corresponds to an (anti)parallel-displaced geometry where the halogen atom(s) are directed away from the phenyl π-cloud of the stacking partner. Overall, the interaction energies become more stabilizing upon halogenation and the stabilizing effect increases for heavier halogens in the order F < Cl < Br < I. Regardless of the halogen, the meta–meta substitution induces the largest stabilization as compared to the unsubstituted dimer. The stabilization, owing to the introduction of heavy halogen atoms (Br and I), is around 3 kcal mol−1. In such meta–meta dimers, the methyl group and halogen from opposite rings adopt a suitable orientation to undergo C–H⋯X interactions, while maintaining a favourable π–π stacking. NCI and EDA analyses support the local effect of halogen substitution on π–π interactions and a complex interplay between electronic and steric effects. Subsequently, this knowledge was exploited in the synthesis of a library of halogenated hexapeptides and their mechanical properties were tested using dynamic rheometry. Heavier halides resulted in stiffer gels. Halogen type, ring position as well as the position of the halogenated Phe in the peptide sequence, strongly influence the hydrogelation propensity of halogenated peptides. Experimentally, the iodinated hexapeptide 7 [H-FQFQF(p-I)K-NH2] forms the strongest hydrogel, having a G′ value of 314 ± 63 kPa, hence significantly improving the mechanical properties of the non-halogenated parent hydrogelator 1 (G′ = 63 ± 8 Pa) Therefore, it can be concluded that theoretical analysis, next to providing insight into the strength of the phenylalanine side chain interactions, qualitatively supports the effect of halogenation substitution on the hydrogel strength. A quantitative relationship between the calculated interactions and the rheological measurements is admittedly still out of reach as an exact model of the self-assembled supramolecular system has yet to be determined. The formation of a supramolecular structure is a multiscale process, for which an exact theoretical model covering the full scale does not exist to date. Nevertheless, the calculations described in the current paper do provide insights which are not only of value for the field of soft materials but are also highly valuable to (bio-)molecular design in general.Computational details
Density functional theory calculations were carried out with Gaussian 09 software package32 using the M06 functional33 in combination with the Dunning's correlation consistent basis sets.34 The M06 hybrid functional has been proven to perform very well for a variety of non-covalent interactions involving π systems.35 The B97D functional provides an excellent accuracy for π–π stacking interactions in line with other studies,5,19 but overestimates cation–π interactions.29,35 Benchmark calculations of non-covalent interactions of halogenated molecules recently show that DFT interaction energies are close to the reference CCSD(T)/CBS level.26 In addition, benchmark CCSD(T)-F12b interaction energies36 were computed for selected systems with Molpro.2012.1 software37 in combination with the standard aug-cc-pVDZ basis set. The performance of the M06 functional on the interaction energies of the toluene and several mono-halogenated dimers has been assessed with respect to the explicitly correlated CCSD(T)-F12b method (Table S1, ESI†). Explicitly correlated approaches have been developed to account for the basis set incompleteness on the electron correlation energy.24 Accordingly, they dramatically decrease the basis set error of wave function methods, yielding very accurate energies at a lower computational cost. Overall, a good agreement between the M06 and CCSD(T)-F12b energies is found with a correlation coefficient R2 of 0.91 (see ESI†). We observed that the hybrid M06 systematically underestimates the stacking interactions with a mean absolute error (MAE) of 1.5 kcal mol−1. However, such MAE is still lower than the MAE computed for CCSD-F12 without triple excitations (2.04 kcal mol−1) (Fig. S1, ESI†). Geometries of the dimers and associated monomers were fully optimized and characterized by harmonic vibrational frequencies using at the M06/cc-pVTZ level of theory. Subsequent single point calculations were performed at the M06/aug-cc-pVTZ level of theory. An ultrafine grid was employed in all the calculations to minimize the integration grid errors, especially important for the Minnesota functionals.38 Basis set superposition error (BSSE)39 of all the dimers were computed with the counterpoise method.40 The counterpoise correction on the DFT calculations appears to be important, with BSSE values ranging from 0.53 kcal mol−1 to 1.17 kcal mol−1. For the iodine atom, the cc-pVDZ-PP and aug-cc-pVTZ-PP basis sets were used, which includes small-core pseudopotentials accounting also for relativistic effects.Non covalent interactions were further analyzed with the non covalent interaction (NCI) index using the NCIPLOT program41 starting from the M06 wavefunctions of the optimized geometries. NCI detects covalent and non-covalent interactions in real space according to the reduced density gradient (s):17
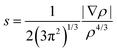 | (1) |
Density properties can be integrated within the NCI region to obtain the volume (VNCI) of the isosurface enclosed within it.45 To perform such integrations, it is necessary to establish a unique definition of the NCI region. To identify this region, the s(ρ) plot of the monomers was computed. The lower edge of the reference s(ρ) curve is splined and all the points of the dimer s(ρ) plot lying below the splined curve are localized in real space. In practice, these integrations are performed numerically, by summation over a cubic grid with 0.1 a.u. increments. It is also possible to separate the attractive and repulsive contributions depending on the sign of the second eigenvalue (λ2) at each point.
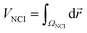 | (2) |
| Eint = EPauli + Eelst + Eoi | (3) |
Author contributions
T. B., R. V. L. and T. W. were in charge of carrying out all theoretical calculations. V. L., T. D. M., J. B., T. B. and W. V. have performed all peptide syntheses and collected all rheological data. J. B., N. V. D. B. and P. M. have supervised the rheology measurements. C. M. and S. B. supervised the peptide synthesis. F. D. P., A. M., R. H., C. M., S. B. and M. A. have conceptualized the study. All authors contributed to the manuscript writing and S. B. and M. A. coordinated the program.Conflicts of interest
There are no conflicts to declare.Acknowledgements
F. D. P. wishes to acknowledge the Vrije Universiteit Brussel (VUB) for a Strategic Research Program and the Francqui foundation for a position as Francqui research professor. S. B. is grateful for VUB funding associated with the Strategic Research Program Exploit-PeptIT and the IRP9 program. M. A. thanks the FWO for a postdoctoral fellowship (12F4416N) and the VUB for financial support. R. V. L. acknowledges the FWO for a PhD fellowship (1185219N). W. V., A. M., C. M., R. H. and S. B. also thank the FWO for funding (G054119N). Computational resources and services were provided by the Shared ICT Services Centre funded by the VUB, the Flemish Supercomputer Center (VSC) and FWO.References
- (a) C. J. Pace and J. Gao, Acc. Chem. Res., 2013, 46, 907–915 CrossRef CAS PubMed; (b) H.-J. Schneider, Acc. Chem. Res., 2013, 46, 1010–1019 CrossRef CAS PubMed; (c) K. Madhusudan Makwana and R. Mahalakshmi, Protein Sci., 2015, 24, 1920–1933 CrossRef CAS; (d) L.-J. Riwar, N. Trapp, B. Kuhn and F. Diederich, Angew. Chem., Int. Ed., 2017, 56, 11252–11257 CrossRef CAS PubMed.
- (a) S. E. Wheeler, Acc. Chem. Res., 2013, 46, 1029–1038 CrossRef CAS PubMed; (b) R. K. Raju, J. W. G. Bloom, Y. An and S. E. Wheeler, ChemPhysChem, 2011, 12, 3116–3130 CrossRef CAS; (c) R. M. Parrish and C. D. Sherrill, J. Am. Chem. Soc., 2014, 136, 17386–17389 CrossRef CAS PubMed.
- (a) C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534 CrossRef CAS; (b) S. L. Cockroft, C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, J. Am. Chem. Soc., 2005, 127, 8594–8595 CrossRef CAS PubMed; (c) S. L. Cockroft, J. Perkins, C. Zonta, H. Adams, S. E. Spey, C. M. R. Low, J. G. Vinter, K. R. Lawson, C. J. Urch and C. A. Hunter, Org. Biomol. Chem., 2007, 5, 1062–1080 RSC.
- (a) S. E. Wheeler and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10854–10855 CrossRef CAS PubMed; (b) S. E. Wheeler and J. W. G. Bloom, J. Phys. Chem. A, 2014, 118, 6133–6147 CrossRef CAS PubMed.
- S. E. Wheeler, J. Am. Chem. Soc., 2011, 133, 10262–10274 CrossRef CAS PubMed.
- J. Hwang, P. Li, W. R. Carroll, M. D. Smith, P. J. Pellechia and K. D. Shimizu, J. Am. Chem. Soc., 2014, 136, 14060–14067 CrossRef CAS PubMed.
- A. N. Bootsma, A. C. Doney and S. E. Wheeler, J. Am. Chem. Soc., 2019, 141, 11027–11035 CrossRef CAS PubMed.
- (a) C. Martin, E. Oyen, J. Mangelschots, M. Bibian, T. B. Haddou, J. Andrade, J. Gardiner, B. Van Mele, A. Madder, R. Hoogenboom and S. Ballet, MedChemComm, 2016, 7, 542–549 RSC; (b) C. Martin, E. Oyen, Y. Van Wanseele, T. B. Haddou, H. Schmidhammer, J. Andrade, L. Waddington, A. Van Eeckhaut, B. Van Mele, J. Gardiner and S. Ballet, Mater. Today Chem., 2017, 3, 49–59 CrossRef.
- (a) H. Hosseinkhani, Chem. Rev., 2013, 113(7), 4837–4861 CrossRef CAS PubMed; (b) S. Koutsopoulos, Peptide Applications in Biomedicine, Biotechnology and Bioengineering, Woodhead Publishing, 2018, pp. 387–408 Search PubMed.
- (a) D. M. Ryan, S. B. Anderson, F. T. Senguen, R. E. Youngman and B. L. Nilsson, Soft Matter, 2010, 6, 475–479 RSC; (b) D. M. Ryan, T. M. Doran, S. B. Anderson and B. L. Nilsson, Langmuir, 2011, 27(7), 4029–4039 CrossRef CAS PubMed.
- W. Liyanage and B. L. Nilsson, Langmuir, 2016, 32, 787–799 CrossRef CAS.
- D. M. Ryan, S. B. Anderson and B. L. Nilsson, Soft Matter, 2010, 6, 3220–3231 RSC.
- A. Pizzi, L. Lascialfari, N. Demitri, A. Bertolani, D. Maiolo, E. Carretti and P. Metrangolo, CrystEngComm, 2017, 19, 1870–1874 RSC.
- A. Bertolani, L. Pirrie, L. Stefan, N. Houbenov, J. S. Haataja, L. Catalano, G. Terraneo, G. Giancane, L. Valli and R. Milani, Nat. Commun., 2015, 6, 7574 CrossRef PubMed.
- A. Pizzi, C. Pigliacelli, A. Gori, O. Ikkala, N. Demitri, G. Terraneo, V. Castelletto, I. W. Hamley, F. B. Bombelli and P. Metrangolo, Nanoscale, 2017, 9, 9805–9810 RSC.
- (a) S. Ehrlich, J. Moellmann and S. Grimme, Acc. Chem. Res., 2013, 46, 916–926 CrossRef CAS; (b) S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CAS; (c) N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS; (d) S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- (a) T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1755–1759 CrossRef CAS; (b) F. M. Bickelhaupt and E. J. Baerends, Rev. Comput. Chem., 2000, 15, 1–86 CAS; (c) I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953–4967 RSC.
- (a) E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed; (b) J. R. Lane, J. Contreras-García, J.-P. Piquemal, B. J. Miller and H. G. Kjaergaard, J. Chem. Theory Comput., 2013, 9, 3263–3266 CrossRef CAS PubMed; (c) N. Mandal and A. Datta, J. Org. Chem., 2020, 85, 13228–13238 CrossRef CAS PubMed; (d) T. K. Mandal, S. Samanta, S. Chakraborty and A. Datta, ChemPhysChem, 2013, 14, 1149–1154 CrossRef CAS.
- M. Alonso, T. Woller, F. J. Martín-Martínez, J. Contreras-García, P. Geerlings and F. De Proft, Chem. – Eur. J., 2014, 20, 4931–4941 CrossRef CAS PubMed.
- S. Güryel, M. Alonso, B. Hajgató, Y. Dauphin, G. Van Lier, P. Geerlings and F. De Proft, J. Mol. Model., 2017, 23, 43 CrossRef.
- L. A. H. van Bergen, M. Alonso, A. Palló, L. Nilsson, F. De Proft and J. Messens, Sci. Rep., 2016, 6, 30369 CrossRef CAS.
- (a) C. Chipot, R. Jaffe, B. Maigret, D. A. Pearlman and P. A. Kollman, J. Am. Chem. Soc., 1996, 118, 11217–11224 CrossRef CAS; (b) R. Chelli, F. L. Gervasio, P. Procacci and V. Schettino, J. Am. Chem. Soc., 2002, 124, 6133–6143 CrossRef CAS PubMed.
- (a) K. Berka, R. Laskowski, K. E. Riley, P. Hobza and J. Vondrášek, J. Chem. Theory Comput., 2009, 5, 982–992 CrossRef CAS PubMed; (b) K. L. Copeland, J. A. Anderson, A. R. Farley, J. R. Cox and G. S. Tschumper, J. Phys. Chem. B, 2008, 112, 14291–14295 CrossRef CAS PubMed.
- (a) C. Hättig, W. Klopper, A. Köhn and D. P. Tew, Chem. Rev., 2012, 112, 4–74 CrossRef PubMed; (b) L. Kong, F. A. Bischoff and E. F. Valeev, Chem. Rev., 2012, 112, 75–107 CrossRef CAS.
- (a) J. Řezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2012, 8, 4285–4292 CrossRef; (b) M. H. Kolář and P. Hobza, Chem. Rev., 2016, 116, 5155–5187 CrossRef PubMed.
- C. D. Tatko and M. L. Waters, Org. Lett., 2004, 6, 3969–3972 CrossRef CAS PubMed.
- J. Contreras-García, R. A. Boto, F. Izquierdo-Ruiz, I. Reva, T. Woller and M. Alonso, Theor. Chem. Acc., 2016, 135, 242 Search PubMed.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS.
- J. Contreras-García, W. Yang and E. R. Johnson, J. Phys. Chem. A, 2011, 115, 12983–12990 CrossRef PubMed.
- M. Bibian, J. Mangelschots, J. Gardiner, L. Waddington, M. M. D. Acevedo, B. G. De Geest, B. Van Mele, A. Madder, R. Hoogenboom and S. Ballet, J. Mater. Chem. B, 2015, 3, 759–765 RSC.
- C. Martin, M. Dumitrascuta, M. Mannes, A. Lantero, D. Bucher, K. Walker, Y. Van Wanseele, E. Oyen, S. Hernot, A. Van Eeckhaut and S. Ballet, J. Med. Chem., 2018, 61, 9784–9789 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian Inc., Wallingford CT, 2010 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- (a) T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS; (b) D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- (a) R. Neves, P. A. Fernandes and M. J. Ramos, J. Chem. Theory Comput., 2011, 7, 2059–2067 CrossRef PubMed; (b) M. R. Davis and D. A. Dougherty, Phys. Chem. Chem. Phys., 2015, 17, 29262–29270 RSC.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schetz, P. Celani, W. Gyçrffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Kçppl, S. J. R. Lee, Y. Liu, A. W. Lloyd, Q. Ma, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklaß, D. P. O’Neill, P. Palmieri, D. Peng, K. Pfleger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and M. Welborn, MOLPRO Version 2012.1, 2012, https://www.molpro.net Search PubMed.
- S. E. Wheeler and K. N. Houk, J. Chem. Theory Comput., 2010, 6, 395–404 CrossRef CAS PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- F. B. van Duijneveldt, J. G. C. M. van Duijneveldt-van de Rijdt and J. H. van Lenthe, Chem. Rev., 1994, 94, 1873–1885 CrossRef CAS.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- R. A. Boto, J. Contreras-García, J. Tierny and J.-P. Piquemal, Mol. Phys., 2016, 114, 1406–1414 CrossRef CAS.
- J. R. Lane, J. Contreras-García, J.-P. Piquemal, B. J. Miller and H. G. Kjaergaard, J. Chem. Theory Comput., 2013, 9, 3263–3266 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- J. Contreras-García, W. Yang and E. R. Johnson, J. Phys. Chem. A, 2011, 115, 12983–12990 CrossRef.
- (a) T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1755–1759 CrossRef CAS; (b) F. M. Bickelhaupt and E. J. Baerends, Rev. Comput. Chem., 2000, 15, 1–86 CAS; (c) L. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1345 Search PubMed.
- (a) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS; (b) ADF, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2016, http://www.scm.com.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00455g |
| This journal is © The Royal Society of Chemistry 2021 |