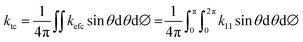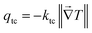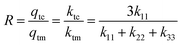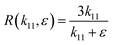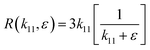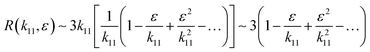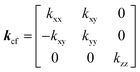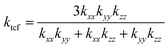DOI:
10.1039/D1MA00496D
(Paper)
Mater. Adv., 2021,
2, 5942-5954
A novel enhanced performance thermal rectifier based on NPG functionalized carbon fibers
Received
7th June 2021
, Accepted 12th July 2021
First published on 30th July 2021
Abstract
Theoretically, a thermal rectifier is a one-way heat transfer solid state device. If these components become a reality, they will significantly impact on thermal energy recycling and management. In this work, by grafting neopentylglycol (NPG) molecules to carboxylic acid functional groups (–COOH) on the surface of a carbon fiber (CF), a novel two-segmented thermal rectifier has been implemented to efficiently enhance the rectification factor. The device controls the heat by way of the existing first order phase transition in NPG, which triggers rotational molecular reorientations at a prescribed temperature. Thermal measurements of the diode show that the device is able to conduct almost three-fold more heat in the forward bias than in the reverse one. Furthermore, for the restricted class of symmetries established by NPG, and by using anisotropic heat conduction theory in solids, we demonstrate that the experimental (2.95) and predicted (3) rectification factors match quite well. Thereby, such systems possess a significantly enhanced rectification factor which depends on the principal thermal conductivity tensor components present in each phase. Hence, partially functionalized carbon fibers with NPG are newfangled candidate materials which can provide avenues to achieve high performance thermal diodes via surface chemical functionalization.
1. Introduction
Major global energy losses can be identified as waste heat; estimations reveal that 80% of the global primary energy consumption is lost after conversion processes giving rise to the dominating root cause of current global warming and carbon footprint.1–3 Therefore, even reclaiming a small portion of such waste heat would itself nearly satisfy the electricity needs of the planet.4 Nowadays, the main promising way to recover waste heat is via thermoelectric devices. Thermoelectricity enabling direct conversion of heat into electricity using thermoelectric converters is a promising energy technology, which is under intense research to provide a solution to thermal energy recovery and management. The performance of a thermoelectric material is evaluated by the dimensionless figure of merit, ZT, which is defined as ZT = S2σT/k, where σ and k are the electrical and thermal conductivity respectively, S is the Seebeck coefficient and T is the absolute temperature.
The enhancement of ZT is not an easy task because these physical parameters are interdependent, and an improvement in one of these properties affects adversely another one. Hence, the development of high-performance thermoelectric materials is very challenging. Recently, materials’ nanostructuring was used to increase the thermoelectric performance; theoretically Dresselhaus et al.5 have shown that quantum wires as well as superlattices6 have the potential to achieve a significant increase in ZT compared with bulk materials. In this sense, carbon nanostructures and carbon based composites such as carbon nanotubes (CNTs), graphene as well as polymer-based carbon composites have experienced rapid development as TE materials because of their intrinsic ultrahigh electrical conductivity and light weight which have led to high TE performance and superior flexibility.7–9 However, by using only such current thermoelectric conventional strategies it is a challenge to recycle wide-scale waste heat and reuse it for further purposes. Hence, an alternative solution to the waste heat problem would be the development of solid state thermal devices which could help to recover it.
In a thermal domain, the thermal diode is an analogue to the renowned electrical diode, a device where heat current q preferentially flows in the forward than in the reverse direction, qf > qr. Hence, such thermal rectifiers could have a huge impact not only as thermal energy harvesting devices but also as heat control solid state devices.10,11
The performance of a thermal rectifier is evaluated by the rectification factor R, which is defined as R = qf/qr. In practice, a value of R ≥ 10 is a required limit to deem the effect useful for actual applications. Nevertheless, the primary limit for the application of this technology is the relatively low thermal rectification factor accomplished by current materials. In this sense, in bulk materials thermal rectification has mainly been achieved via the temperature dependence of the thermal conductivity, and the acoustic impedance mismatch between the constituent materials;12–19 whereas in nanomaterials, the dominant mechanisms for thermal rectification are phonon spectral overlap, phonon spectral mismatch, and phonon spatial confinement.20–27 Evidently, in spite of the several strategies proposed, neither bulk nor molecular mechanisms have evidenced that the rectification factor can reach one order of magnitude. For instance, by using the aforementioned strategies, the best reported rectification factor at the bulk scale is R ∼ 2 for a thermal diode based on icosahedral quasicrystals placed between two heat reservoirs kept at 900 K and 300 K28 respectively. On the other hand, at the nanoscale, an amazing value of R ∼ 3.3 was achieved with inorganic nanolayers via interfacial thermal boundary resistance.29 The problem with nanostructured rectifiers is that they are too thin to establish appreciable temperature gradients and to withstand large heat fluxes, not to mention that most of the proposed architectures30–33 require coupling and layout between individual atoms, which are very difficult to accomplish in practice. Hence, too much work remains to be done in order to achieve a practical thermal rectifier at room temperature. At the beginning of this decade, an alternative strategy to accomplish enhanced performance thermal rectifiers using solid-state junctions based on phase-change materials showed great potential, and rectification factors of ∼1.1434 at 55 K, as well as ∼1.5,35 and ∼1.736 at room temperature were achieved via first and second order phase transitions respectively. Such results demonstrated that PCMs are promising next-generation thermal rectifying materials. Lately, following the potential of PCMs for obtaining enhanced performance thermal rectifiers at room temperature, an R ∼ 2 was achieved in a heterojunction diode based on organic PCMs.37 Although most of the thermal diodes based on PCMs reported so far present relatively low thermal rectification factors,34–43 theoretical analysis has shown their potential to maximize their rectification factor by giving some criteria.44,45 In this sense, a value of R ∼ 2.6 was reported in a dual phase change organic thermal diode constituted by the junction of an octadecane-impregnated polystyrene foam (PFH-O) and poly(N-isopropylacrylamide) (PNIPAM) under ambient conditions.46 Besides, recently, an R ∼ 2.7 was accomplished in a thermal diode consisting of two slabs of Ag chalcogenides.47Fig. 1 shows an evolution map for experimental thermal diodes based on PCMs. Thus, motivated by the promising results obtained in the former PCM based thermal diodes, in the present research through the development of novel diode architecture, an enhanced performance thermal rectifier with R ∼ 2.95 has been used at room temperature. The device is based on a partially functionalized carbon fiber with NPG molecules which manipulates the heat via molecular transformations above the transition temperature.
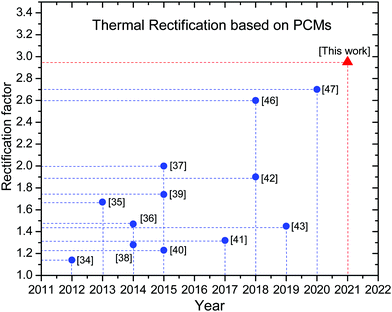 |
| | Fig. 1 Experimental thermal rectification map based on solid–solid phase change materials. | |
2. Thermal diode concept
Fig. 2a depicts the proposed architecture for a thermal diode based on a partially functionalized carbon fiber which gives rise to a two-segment material. One of the ends is the segment with the carboxylic acid functional groups on the surface of the carbon fiber, and the second one is the NPG functionalized end.
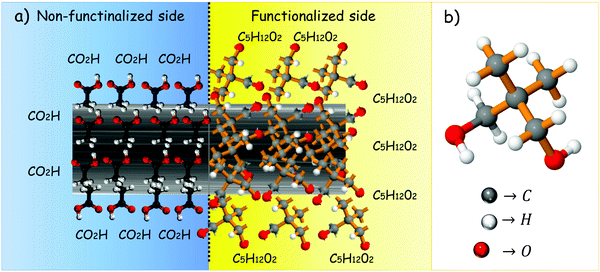 |
| | Fig. 2 (a) Proposed thermal diode architecture based on an NPG functionalized carbon fiber, and (b) molecular configuration of NPG. | |
The molecular configuration of NPG is shown in Fig. 2b. Five carbon atoms consist of the centered tetrahedron, where two are attached to hydrogen atoms in the methyl group (–CH3), while another two form the hydroxymethyl group (–CH2–OH). Basically, NPG presents a lattice transition occurring at a temperature of Tt ∼ 320 K, which is confirmed by differential scanning calorimetry (DSC), as shown later.
Below this transition temperature, NPG molecules have a layered structure ordered on a monoclinic lattice or α-phase with space group P21/C, where hydroxyl groups within the same layer form hydrogen bonds between O and H atoms. At just a few Kelvin degrees above Tt, this ordered α-phase transforms into a disordered isotropic cubic FCC lattice or γ-phase with intermolecular hydrogen bond rotation, as shown in Fig. 3a.48
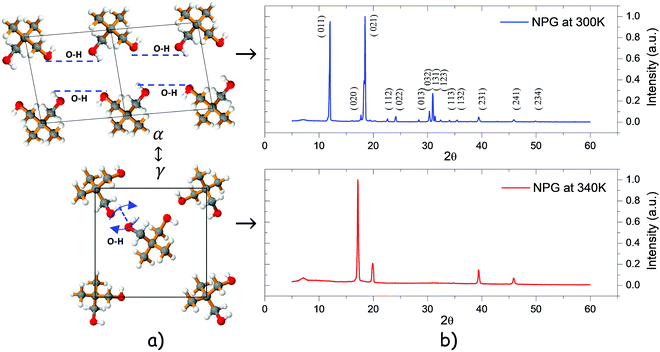 |
| | Fig. 3 (a) Crystallographic plane of the monoclinic(α) and cubic phase(γ) of NPG before and after transition, and (b) XRD patterns corresponding to the monoclinic(α) and cubic phase(γ). | |
This crystalline structure changing from a monoclinic configuration to a face centered cubic form is confirmed via XRD patterns where the (011) Bragg peak disappears from the low temperature phase to a high temperature phase, as evidenced by the XRD patterns shown in Fig. 3b at 300 K and 340 K, respectively. Explicit dynamic aspects of NPG transformation can be found in the literature.48–52 In the low temperature α phase NPG exists in an associated state because the intermolecular hydrogen bonds come into being; when the temperature is going up at Tt, the intermolecular hydrogen bonds will weaken. This action causes the corresponding hydroxyl bond to strengthen gradually prompting the –OH absorption band to move to a higher wave number.
In Fig. 4a, the infrared spectra portions of the NPG at 300 K and 340 K show a strong absorption centered at about 3300 cm−1 and 3400 cm−1 respectively. A wave number shift of k ∼ 100 cm−1 is identified with the –OH stretching band. Since the –OH groups are most directly involved in bonding of the NPG, this absorption band can sense the changes in the crystalline structure occurring during the solid–solid transformation. Such a wave number shift is especially increased above of the phase transition temperature. Hence, changes in the vibrational frequency of NPG molecules will be followed by changes in the vibrational frequency of phonons causing a drastic change in the behavior of the thermal conductivity of NPG, as shown in Fig. 4b. Therefore, by analyzing Fig. 4b, below Tt, the thermal conductivity increases rapidly with decreasing T due to the increasing order of the system; above Tt, in the γ-phase, one has instead complete disorder; thus, an increase in the thermal conductivity is observed as T increases. Besides, DSC analysis of NPG is shown in Fig. 4c. Clearly, at ∼320 K a transition is present under heating that corresponds with the minimum thermal conductivity, i.e. below Tt, k increases rapidly with decreasing T due to the increasing order of the system (dk/dT < 0); whereas above Tt, in the cubic phase one has instead a complete disorder (dk/dT > 0) and k increases rapidly with increasing T. Based on this behavior, Fig. 5 presents a qualitative concept of the proposed thermal diode.
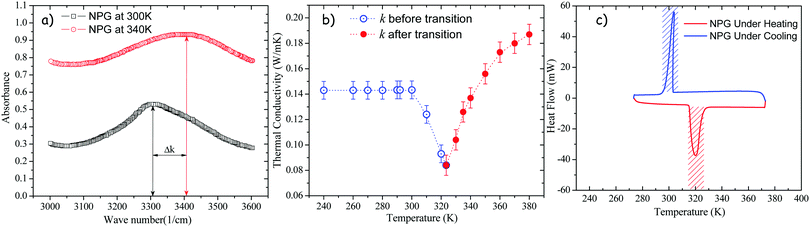 |
| | Fig. 4 (a) Infrared absorption spectra of NPG at 300 K and 340 K. (b) Temperature dependent thermal conductivity of NPG, and (c) DSC of NPG. | |
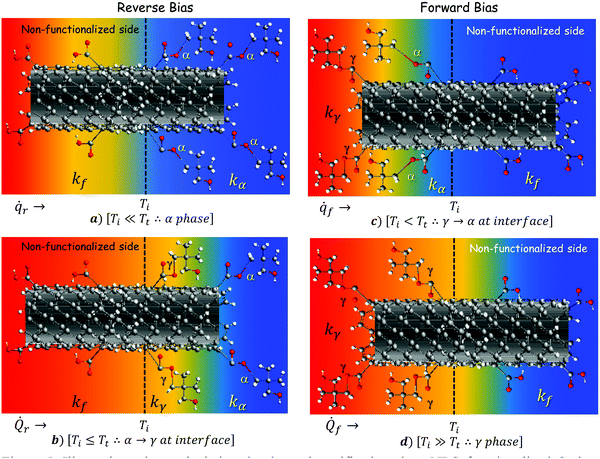 |
| | Fig. 5 Illustrative scheme depicting the thermal rectifier based on NPG functionalized carbon fiber. Thermal diode under (a) partial and (b) total reverse thermal bias, as well as under (c) partial, and (d) total forward thermal bias. | |
Fig. 5a and b represent the thermal diode under reverse thermal bias, and Fig. 5c and d show it under forward thermal bias. Specifically, Fig. 5a shows the situation when an arbitrary heat flux ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) r is applied directly to the non-functionalized segment. If we consider that
r is applied directly to the non-functionalized segment. If we consider that ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) r is not enough heat to increase the interface temperature Ti beyond Tt (Ti < Tt), the NPG functionalized segment will remain in the α-phase. As a result, the effective thermal conductivity of the system will depend on the thermal conductivity of the fiber kf and the thermal conductivity kα of the NPG functionalized segment in the α-phase. However, if heat flux is increased from
r is not enough heat to increase the interface temperature Ti beyond Tt (Ti < Tt), the NPG functionalized segment will remain in the α-phase. As a result, the effective thermal conductivity of the system will depend on the thermal conductivity of the fiber kf and the thermal conductivity kα of the NPG functionalized segment in the α-phase. However, if heat flux is increased from ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) r to
r to ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) r, then the interface temperature will achieve or even overcome the transition temperature Ti ≥ Tt, as shown in Fig. 5b. In this case, the NPG functionalized segment will be partially transformed into the γ-phase, and the effective thermal conductivity of the system will depend on kf, kα and kγ, but with a small influence of kγ because the non-functionalized segment causes thermal resistance delaying the whole transition of the NPG functionalized segment. Conversely, Fig. 5c shows the situation when an arbitrary heat flux
r, then the interface temperature will achieve or even overcome the transition temperature Ti ≥ Tt, as shown in Fig. 5b. In this case, the NPG functionalized segment will be partially transformed into the γ-phase, and the effective thermal conductivity of the system will depend on kf, kα and kγ, but with a small influence of kγ because the non-functionalized segment causes thermal resistance delaying the whole transition of the NPG functionalized segment. Conversely, Fig. 5c shows the situation when an arbitrary heat flux ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) f is applied directly to the NPG functionalized segment, i.e. in the forward thermal bias. In this case, if we consider that
f is applied directly to the NPG functionalized segment, i.e. in the forward thermal bias. In this case, if we consider that ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) f is not enough heat to increase the interface temperature Ti beyond Tt (Ti < Tt), the NPG functionalized segment will remain partially transformed in the γ-phase. As a result, the effective thermal conductivity of the system will depend on kf, kα and kγ, but in this case with a small influence of kα. However, if heat flux is increased from
f is not enough heat to increase the interface temperature Ti beyond Tt (Ti < Tt), the NPG functionalized segment will remain partially transformed in the γ-phase. As a result, the effective thermal conductivity of the system will depend on kf, kα and kγ, but in this case with a small influence of kα. However, if heat flux is increased from ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) f to
f to ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) f, then the interface temperature will match or even overcome the transition temperature Ti ≥ Tt, as shown in Fig. 5d. Under this situation, the NPG functionalized segment will be entirely transformed into the γ-phase, thus the effective thermal conductivity of the system will depend only on kf and kγ. Evidently, different behaviors in the effective thermal conductivities will be present in the system depending on the direction and level of the applied heat flux. Therefore, because of the phase transition present in NPG, thermal rectification can be expected in the partially functionalized carbon fiber depicted in Fig. 2a. Furthermore, it is worth mentioning that if the applied heat flux continues increasing in either forward or reverse bias, then the NPG functionalized segment will be wholly transformed into the γ-phase at a certain moment. Nevertheless, in the forward bias mode the NPG functionalized segment will accomplish quicker the γ-phase transition than in the reverse bias mode. This is because, in the forward bias mode, the NPG functionalized segment is in contact directly with the heat source, whereas in the reverse bias mode it is not, which delays the phase transition. Therefore, once the γ-phase transition is achieved in either reverse or forward bias, the thermal diode will start with a sudden rise in the heat flux at certain prescribed temperatures, named the breakdown temperature and forward temperature respectively. Such temperatures will control the on-state and breakdown-state of the device, similar to the forward voltage and breakdown voltage in electronic diodes. Evidently, an important content of NPG molecules attached along the functionalized segment must be accomplished to ensure an intra- and inter-molecular heat transfer along the NPG segment. In this sense, the amount of grafted NPG molecules will depend on the amount of COOH molecules attached to the carbon fiber surface, as the content of COOH increases, NPG molecule content will also increase and vice versa. Thereby, it is crucial to achieve a great deal of grafted NPG molecules because NPG is directly related to the rectification effect, and a lack in the content of NPG will blur the rectification effect in the device. However, it is well known that chemical functionalization of surfaces has been demonstrated to be an important strategy to modify energy carrier transport mechanisms in carbonaceous materials.53 Thereby, a substantial content of COOH organic molecules covalently attached to the surface gives rise to the formation of localized defect sites, which will act as surficial scattering centers for electrons and phonons. Undoubtedly, it will affect the device performance by altering the thermal conductance of the device, which will delay or hasten the transition of the NPG segment.
f, then the interface temperature will match or even overcome the transition temperature Ti ≥ Tt, as shown in Fig. 5d. Under this situation, the NPG functionalized segment will be entirely transformed into the γ-phase, thus the effective thermal conductivity of the system will depend only on kf and kγ. Evidently, different behaviors in the effective thermal conductivities will be present in the system depending on the direction and level of the applied heat flux. Therefore, because of the phase transition present in NPG, thermal rectification can be expected in the partially functionalized carbon fiber depicted in Fig. 2a. Furthermore, it is worth mentioning that if the applied heat flux continues increasing in either forward or reverse bias, then the NPG functionalized segment will be wholly transformed into the γ-phase at a certain moment. Nevertheless, in the forward bias mode the NPG functionalized segment will accomplish quicker the γ-phase transition than in the reverse bias mode. This is because, in the forward bias mode, the NPG functionalized segment is in contact directly with the heat source, whereas in the reverse bias mode it is not, which delays the phase transition. Therefore, once the γ-phase transition is achieved in either reverse or forward bias, the thermal diode will start with a sudden rise in the heat flux at certain prescribed temperatures, named the breakdown temperature and forward temperature respectively. Such temperatures will control the on-state and breakdown-state of the device, similar to the forward voltage and breakdown voltage in electronic diodes. Evidently, an important content of NPG molecules attached along the functionalized segment must be accomplished to ensure an intra- and inter-molecular heat transfer along the NPG segment. In this sense, the amount of grafted NPG molecules will depend on the amount of COOH molecules attached to the carbon fiber surface, as the content of COOH increases, NPG molecule content will also increase and vice versa. Thereby, it is crucial to achieve a great deal of grafted NPG molecules because NPG is directly related to the rectification effect, and a lack in the content of NPG will blur the rectification effect in the device. However, it is well known that chemical functionalization of surfaces has been demonstrated to be an important strategy to modify energy carrier transport mechanisms in carbonaceous materials.53 Thereby, a substantial content of COOH organic molecules covalently attached to the surface gives rise to the formation of localized defect sites, which will act as surficial scattering centers for electrons and phonons. Undoubtedly, it will affect the device performance by altering the thermal conductance of the device, which will delay or hasten the transition of the NPG segment.
3. Experimental procedure
Materials and NPG functionalization of carbon fibers
First, the polyacrylonitrile (PAN)-based carbon fibers (CFs) from Toray Industries were cleaned by reflux with acetone (Certified ACS ≥ 99.5%, Fisher Chemical) for 24 hours. Then, these CF were ultrasonically cleaned with ethanol (absolute, ACS, Fermont), methanol (Optima™, LC/MS, Fisher Chemical) and Deionized Water (of 18.2 MW cm−1 resistivity), each for 30 minutes. The carboxylic functionalization of the CFs was done by a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) mixture of concentrated sulfuric acid (H2SO4, 95–98% ACS, FCC, VWR Chemicals BDH and Nitric acid (HNO3, 68–70%, ARISTAR, ACS, VWR Chemicals BDH) for 2 hours at 80 °C. For the neutralization of acid residues by carboxylic functionalization, the CFs have been subjected to hydrogen peroxide (H2O2, 30%, BAKER ANALYZED, ACS, J.T. Baker) immersion for 12 hours. After this treatment, one end of the CFs was covered by one solution at 10 wt% of polymethyl methacrylate (PMMA, average Mw ∼ 996
1 (v/v) mixture of concentrated sulfuric acid (H2SO4, 95–98% ACS, FCC, VWR Chemicals BDH and Nitric acid (HNO3, 68–70%, ARISTAR, ACS, VWR Chemicals BDH) for 2 hours at 80 °C. For the neutralization of acid residues by carboxylic functionalization, the CFs have been subjected to hydrogen peroxide (H2O2, 30%, BAKER ANALYZED, ACS, J.T. Baker) immersion for 12 hours. After this treatment, one end of the CFs was covered by one solution at 10 wt% of polymethyl methacrylate (PMMA, average Mw ∼ 996![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 by GPC, powder, Sigma-Aldrich) in anisole (anhydrous, 99.7%, Sigma-Aldrich). Another free end of the CFs was refluxed by one aqueous solution at 15 wt% and 5 M of 2,2-dimethyl-1,3-propanediol (neopentyl glycol, 99%, Alfa Aesar) in H2SO4 (95–98% ACS, FCC, VWR Chemicals BDH), respectively. To etch the section of the covered CFs by PMMA, this was immersed in an aqueous solution of 1M sodium hydroxide (NaOH, BAKER ANALYZED, A.C.S. Reagent, J.T. Baker). Next, this same section treated with NaOH was placed in concentrated glacial acetic acid (99.96%, CTR) for 24 hours to remove the PMMA completely. Subsequently, the two sections of the CFs were cleaned with a methanol solution: water (1
000 by GPC, powder, Sigma-Aldrich) in anisole (anhydrous, 99.7%, Sigma-Aldrich). Another free end of the CFs was refluxed by one aqueous solution at 15 wt% and 5 M of 2,2-dimethyl-1,3-propanediol (neopentyl glycol, 99%, Alfa Aesar) in H2SO4 (95–98% ACS, FCC, VWR Chemicals BDH), respectively. To etch the section of the covered CFs by PMMA, this was immersed in an aqueous solution of 1M sodium hydroxide (NaOH, BAKER ANALYZED, A.C.S. Reagent, J.T. Baker). Next, this same section treated with NaOH was placed in concentrated glacial acetic acid (99.96%, CTR) for 24 hours to remove the PMMA completely. Subsequently, the two sections of the CFs were cleaned with a methanol solution: water (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume) to dissolve the PMMA residues and to remove any organic impurity formed during the process.
1 by volume) to dissolve the PMMA residues and to remove any organic impurity formed during the process.
Characterization
NPG crystalline structure transformation from a monoclinic configuration to face centered cubic form was confirmed by DRX patterns using a Panalytical Empyream diffractometer with an Anton Paar HTK 16N high temperature chamber using a Cu-Kα radiation X-ray source. Furthermore, crystalline phase identification was carried out via the crystallographic software X'Pert High Score Plus based on the International Centre for Diffraction Data (ICDD). NPG transition temperatures are provided in DSC analysis, and they were measured by the TA Instruments Q200 DSC equipped with a refrigerated cooling system based on liquid nitrogen. The sample was cooled down to 0 °C at 5 °C per min, followed by heating from 0 to 100 °C at 5 °C per min and then cooled down to 0 °C at 5 °C per min. Besides, NPG FTIR spectra were measured on a Thermo-Nicolet spectrophotometer model 6700. Likewise, the functionalization process leads to an inclusion of NPG chemical moieties on the carbon fiber surface, which was verified by X-ray photoelectron spectroscopy (XPS) via the analysis of the high resolution C1s spectra of the functionalized and non-functionalized carbon fiber segments through a Thermo-Fisher Scientific ESCALAB 250Xi XPS system with an Al-Kα radiation X-ray source.
Bulk NPG temperature dependent thermal conductivities were measured from 240 K to 380 K by a Hot Disk M1 system combined with a closed cycle cryostat from ARS Systems. NPG samples 1 cm in thickness and 4 cm diameter were situated on either side of the Kapton 8563 sensor with an input power of 100 mW for 10 s.
NPG functionalized carbon fiber diode dimensions
A thermal rectifier consists of a total length of 10 cm, of which approximately 5 cm length corresponds to the functionalized side, and the remaining 5 cm to the non-functionalized segment. Each end of the segments was attached to each of the suspended heaters with a heat conductive epoxy.
Q–ΔT transfer characteristics of the thermal diode
To supply heat in reverse and forward bias mode, a DC electrical current sweep with regular increments of the order of mA is applied to the ∼100 Ω Pt thin film resistive heater by using the Keithley 6221 AC/DC power supply; the thin planar Pt heater is placed on the surface of the pyrolytic graphite plate, and it has dimensions of 3 mm in width and 4 mm in length. By waiting long enough at each current increment, this action gives rise to several steady state temperature rises ΔT on the thermal diode at both modes.
Temperature rises are detected via the data acquisition card model NI-9210 C Series Temperature Input Module from national instruments. In this way, a set of ΔT and their corresponding heat fluxes Q are obtained, then finally the transfer curve Q–ΔT can be plotted. To ensure measurement repeatability, each measurement was performed at least 10 times, and the results shown in Fig. 9 are the average of the whole set of measurements. It is worth mentioning that the sample was suspended during the measurements so as to avoid significant lateral heat flow leaks which could affect significantly the measurements due to convective and conduction effects. Measurement details are shown in Section 4.2.
4. Results: experiment and theory
Chemical functionalization of surfaces is an important strategy to engineer functional materials by tailoring the properties of the base structure. In this sense, in the present research a novel two-segment thermal diode based on a partially functionalized carbon fiber is successfully developed. One of the segments of the carbon fiber is functionalized with NPG as the PCM material, whereas the second one is the segment with the carboxylic acid functional groups. Because of the NPG functionalized section, the thermal diode is characterized by presenting opposing thermal conductivity trends at a prescribed temperature leading to a thermal rectification factor as high as 2.95; which, to the best of our knowledge, is the highest thermal rectification factor demonstrated by a PCM thermal diode material to date.
4.1. Thermal rectifier making: grafting of the NPG functionalities onto the carbon fiber surface
Before surface functionalization, the as-received carbon fibers were subjected to a cleaning process to remove sizing agent, and then they were washed using deionized water followed by a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 acid treatment of concentrated H2SO4
1 acid treatment of concentrated H2SO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HNO3 at 80 °C for 2 h, and dried at 70 °C for 24 h to obtain COOH-carbon fibers. After acid treatment, carbon fibers with a carboxylic acid group were partially further functionalized in a solution of H2O/NPG/H2SO4 under ultrasonic vibration for 48 h which afforded NPG-carbon fiber. Surface functionalization process details are shown in the Experimental procedure section.
HNO3 at 80 °C for 2 h, and dried at 70 °C for 24 h to obtain COOH-carbon fibers. After acid treatment, carbon fibers with a carboxylic acid group were partially further functionalized in a solution of H2O/NPG/H2SO4 under ultrasonic vibration for 48 h which afforded NPG-carbon fiber. Surface functionalization process details are shown in the Experimental procedure section.
To confirm the presence of NPG onto the carbon fibers surface, XPS spectra were carried out. Fig. 6 shows the high resolution C1s spectra of the COOH-carbon fiber segment (red solid line), and that of the NPG functionalized carbon fiber segment (black solid line). By comparing both spectra, a broadening of the peak located at 284.7 eV of the NPG functionalized segment is evident. Such broadening is related to the existence of the NPG functionalities and represents an increment in the relative component areas of around 10% with regard to the COOH-carbon fiber segment. Although the presence of hydrogen cannot be quantified by XPS, the broadening of the main peak indicates the increase of sp3 hybridized carbon atoms, which is mainly attributed to the incorporation of hydrogen,54 in this case from NPG. As shown in Fig. 7a and b, each spectrum is decomposed into five components, specifically C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (284.7 eV-sp2), C–C (285.4 eV-sp3), C–OH (286.5 eV), C
C (284.7 eV-sp2), C–C (285.4 eV-sp3), C–OH (286.5 eV), C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (287.5 eV) and COOH (289.0 eV) as labeled in both figures. By inspecting carefully the C1s peak, both COOH-carbon fiber and NPG-carbon fiber reveals the presence of hydroxyl and carboxyl groups as indicated by the well-pronounced peaks around 286.5 and 289.1 eV respectively. The ratios of the area under the respective Gaussian curve (for C–OH and COOH curves) were calculated and the percentages are shown in Table 1, from which we found that the NPG-functionalization treatment caused an increase in the ratio of adsorbed oxygen (27.84% + 11.56% = 39.4%) in the carbon fiber compared to the initial carbon fiber (17.90 + 11.52 = 29.42%). These results clearly indicate that the functionalization procedure increases hydroxyl content due to the NPG chains.
O (287.5 eV) and COOH (289.0 eV) as labeled in both figures. By inspecting carefully the C1s peak, both COOH-carbon fiber and NPG-carbon fiber reveals the presence of hydroxyl and carboxyl groups as indicated by the well-pronounced peaks around 286.5 and 289.1 eV respectively. The ratios of the area under the respective Gaussian curve (for C–OH and COOH curves) were calculated and the percentages are shown in Table 1, from which we found that the NPG-functionalization treatment caused an increase in the ratio of adsorbed oxygen (27.84% + 11.56% = 39.4%) in the carbon fiber compared to the initial carbon fiber (17.90 + 11.52 = 29.42%). These results clearly indicate that the functionalization procedure increases hydroxyl content due to the NPG chains.
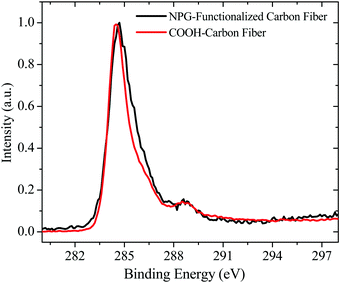 |
| | Fig. 6 Normalized XPS C1s spectra of carbon fiber with and without NPG functionalization. | |
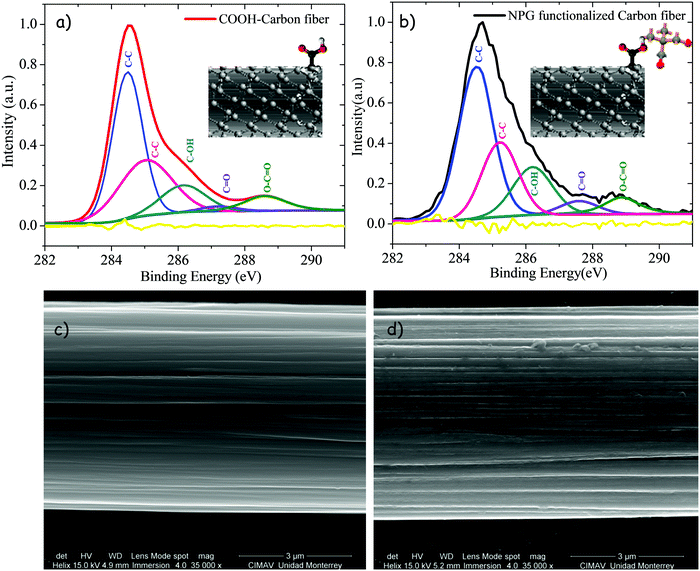 |
| | Fig. 7 High resolution C1s XPS spectra of carbon fibers (a) before and (b) after functionalization, and SEM images of carbon fibers (c) before and (d) after functionalization at 35 000X magnification. | |
Table 1 Summarized fraction of areas under the respective Gaussian curves of sp2C, sp3C, C–OH, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and COOH for carbon fibers before and after functionalization
O, and COOH for carbon fibers before and after functionalization
| Component peak |
Binding energy (eV) |
COOH-Carbon fiber (relative component areas %) |
NPG-Carbon fiber (relative component areas %) |
| C–C(sp2) |
284.7 |
31.44 |
30.41 |
| C–C(sp3) |
285.4 |
21.76 |
19.48 |
| C–OH |
286.5 |
17.90 |
27.84 |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
287.5 |
11.38 |
10.71 |
| COOH |
289.0 |
11.52 |
11.56 |
The surface morphologies for the COOH-carbon fiber, and NPG functionalized carbon fiber segments were examined by SEM. As shown in Fig. 7c, the COOH-carbon fiber segment presented a relatively soft surface constituted of narrow grooves distributed in parallel along the longitudinal direction of the fiber. Nevertheless, as shown in Fig. 7d, the NPG functionalized carbon fiber segment presented differences in the surface morphologies after grafting the NPG chains. Moreover, it can also prove that NPG chains were grafted onto the carbon fiber surface successfully.
4.2. Thermal measurements
In the present research, because of the extremely low thermal mass of the functionalized carbon fiber, as well as to avoid uncertainties due to radiation and convection heat losses, the Q–ΔT transfer characteristics of the thermal diode have been obtained through a lab custom set-up based on the absolute method.55 In this technique, a temperature difference ΔT across the sample is measured in response to an applied amount of heating power Q. Hence, the thermal conductance of the thermal rectifier in the forward and reverse bias is given by the slope of Q versus ΔT sweep at fixed base temperature. Basically, the sample is installed between two suspended thin film Pt heaters which have embedded onto their surface a type-K micro-thermocouple that works as a temperature sensor. With the aim to minimize heat loss by conduction with the surroundings, the heater/sensor system is placed onto the surface of a thin plate of pyrolytic graphite, which subsequently is suspended via magnetic levitation above the magnetic field of a neodymium permanent magnet. In this way, conduction heat leaks to the surroundings will be limited significantly, and will be subjected only to wiring. The illustrative experimental set up is shown in Fig. 8a, and it is merely a schematic and generalized picture of the implemented real system. In terms of driving heat conduction losses due to wiring, wires with a high thermal resistance are desirable. Thus, the diameter of wires must be as small as possible and possess low thermal conductivity. We have used low thermal conductivity Manganin wires with 0.003′′ in diameter for heater power wiring. Manganin is a relatively low thermal conductivity material (∼20 W mK−1), yet one that also has reasonable values of electrical resistivity (∼40 × 10−8 Ω m). Besides, type-K micro-thermocouples with 0.0025′′ in diameter were also used for temperature sensing. Heat loss through the connection wires has been calculated and it is typically less than 5% in our experimental design. Along with heat leak minimization by conduction, magnetic levitation also provides a stable position to the thermal diode by avoiding elongations and contractions that could induce significant uncertainties during measurements, this is due to the existing piezoresistivity effects in carbon fibers.56
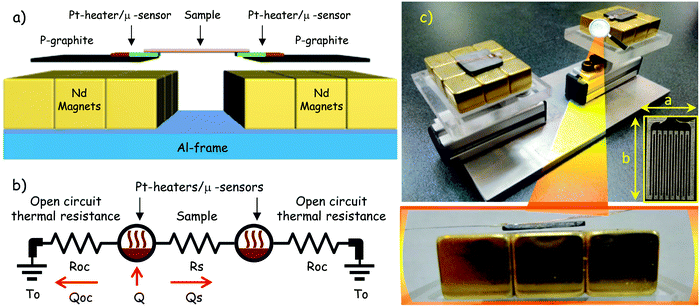 |
| | Fig. 8 (a) Illustrative scheme depicting the experimental set-up of the measurement cell, (b) equivalent thermal circuit of the measurement cell, and (c) actual measurement cell, inset shows the planar Pt heater, here a = 3 mm, and b = 4 m, and magnification shows the levitated system to avoid lateral heat losses. | |
Likewise, to avoid heat losses by convection, the best way to minimize these convection losses is to do the measurements with the sample in a moderate vacuum (10−4 to 10−5 torr); we accomplished 10−6 torr during measurements. Moreover, heat loss due to radiation effects between the surroundings and the sample can be substantial. In our actual experimental set-up, a thermally anchored radiation shield is used in order to protect the equipment from thermal fluctuations coming from the surroundings. It is worth mentioning that our measurements were performed at 300 K where the radiation uncertainties are in the order of approx. 3%, at significantly lower temperatures (e.g. 100 K) or at significantly higher temperatures (e.g. 850 K) the measurement uncertainty due to heat loss to the environment is somewhat greater and is in the order of about 7%. Fig. 8b shows the equivalent thermal circuit of the measurement device. The thermal resistances defined by Roc represent the vacuum gap between the magnet and the heater/sensor system, for this reason they can be approached as infinite thermal resistances or open circuit thermal resistances. The base temperature is represented as To, and Rs is the thermal resistance of the sample. Evenly, Q = Qoc + Qs, represent the input heating power, a portion Qoc is conducted to the surroundings via Roc, and the rest Qs is conducted into the sample. Hence, if it is assumed that Roc → ∞, then Q = Qs, and the thermal conductance of the sample can be experimentally estimated from the slope of the plot Q versus ΔT. Fig. 8c presents an optical image of the measurement cell, magnification shows one of the pyrolytic graphite plates levitating, which includes the heater and sample attached onto its surface (see the inset).
On the other hand, forward bias mode is considered when heat is applied directly to the NPG-functionalized segment, whereas in reverse bias, heat is applied directly to the non-functionalized segment. Therefore, lattice transition in the NPG-functionalized segment must be achieved quicker under forward bias than in reverse bias conditions giving rise to nonlinear heat conduction. Fig. 9a presents Q–ΔT transfer characteristics of the thermal diode at 300 K base temperature. In this figure solid lines correspond to ten consecutive measurements, whereas discrete solid symbols represent the average of ten measurements. Furthermore, for clarity during analysis, Fig. 9b shows the average values corresponding to the ten measurements. Evidently, in reverse bias mode (solid black squares) a linear behavior is observed at least in the range from −150 mW to slightly above 0 mW. Such behavior could be interpreted as if the supplied heat was not enough to increase the temperature above 320 K at the interface between the non-functionalized side and the functionalized side. Hence, the NPG-functionalized segment never starts the solid–solid transition. However, in forward bias mode asymmetric heat conduction is observed with regard to the reverse bias mode. In fact, lattice transition starts almost immediately after the heat is supplied, which is unveiled by the slope change from S1 to S2 in the plot Q–ΔT. Besides, this change from S1 to S2 could be interpreted as if only a portion along the NPG-functionalized segment had been lattice transformed (solid red circles). Once the supplied heat is enough to completely accomplish the lattice transition of the NPG-functionalized segment, a second change in the slope from S2 to S3 is unveiled in the plot of Q–ΔT (solid blue triangles). Such changes in the slope represent changes in the thermal conductance of the device, meaning that in reverse bias the device will conduct less heat than in forward bias because it presents a lower thermal conductance S1 as compared to either S2 or S3.
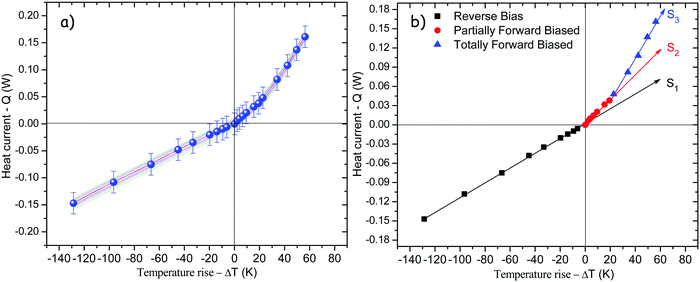 |
| | Fig. 9
Q–ΔT transfer characteristics for (a) ten consecutive measurements of the thermal diode, and (b) measurement average of the thermal rectifier at 300 K base temperature. Solid lines in both plots represent the best linear fit to experimental data, whereas the slope Si stands for thermal conductance of the device respectively. | |
Table 2 shows the experimental thermal conductance values, as well as the thermal rectification factors obtained from the ratio between the thermal conductances in the forward and reverse bias modes. Hypothetically, if thermal conductance had not presented change under forward and reverse bias, then Q–ΔT would be linear in both conditions indicating a rectification factor 1, as it is in the case of linear thermal devices better known as thermal barriers or thermal resistances.57 On the other hand, in the partially transformed condition, R ∼ 1.8, whereas R ∼ 2.95 for a totally transformed NPG-functionalized segment, meaning that the NPG-functionalized segment experiences temperatures well above 320 K giving rise to phase transition, and therefore to an increase in its thermal conductance.
Table 2 Experimental thermal conductances and the thermal rectification factors of the thermal rectifier based on NPG-functionalized carbon fiber at 300 K base temperature
|
Q–ΔT [Slope(W/K)] |
R = Si/S1 |
NPG segment |
|
S
1 = 1.14 × 10−3 |
1 |
Non-transformed |
|
S
2 = 2.05 × 10−3 |
∼1.8 |
Partially transformed |
|
S
3 = 3.36 × 10−3 |
∼2.95 |
Totally transformed |
4.3. Analytical results
To analyze and validate the findings, we have used an analytical model based on the thermal conductivity tensor theory which has been demonstrated to predict accurately the thermal rectification factor of thermal diodes based on phase change materials with lattice transitions.58 According to Duhamel's generalization of Fourier's law of heat conduction, the local heat flux under a 3D orthogonal coordinate system (x, y, z) is given by59| | 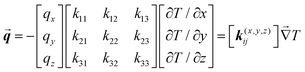 | (1) |
where k(x,y,z)ij stands for the thermal conductivity components of the anisotropic material, which relates the temperature gradient field 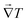 to the heat flux vector
to the heat flux vector ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0071_20d1.gif) . Here, we are concerned with the thermal conductivity tensors of the crystalline structure of NPG which changes from a monoclinic configuration to face centered cubic during transition.
. Here, we are concerned with the thermal conductivity tensors of the crystalline structure of NPG which changes from a monoclinic configuration to face centered cubic during transition.
In the monoclinic configuration, due to symmetry considerations some of the components become zero; hence, the thermal conductivity tensor is given by60
| | 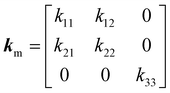 | (2) |
In the cubic configuration, in addition to some components being zero, also
k11 =
k22 =
k33; hence, the thermal conductivity tensor is given by
60| | 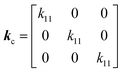 | (3) |
However, if the monoclinic-cubic transition is due to the rotational molecular reorientations caused by the temperature gradient vector applied to
k(x,y,z)ij, then
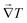
must point in the
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif)
direction given by
| | 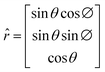 | (4) |
where
θ and ∅ angles indicate that the NPG chains could be randomly oriented over all directions.
In the case of our thermal diode, under reverse thermal bias, the NPG functionalized segment will be directly in contact with the cold end of the temperature gradient; thus, it will be in the monoclinic lattice or α-phase. Therefore, under this condition the sample will experience a heat flux defined by
| | 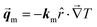 | (5) |
Conversely, under forward thermal bias, the NPG functionalized segment will be directly in contact with the hot end of the temperature gradient; thus, it will be in the cubic lattice or γ-phase. Therefore, under this condition the sample will experience a heat flux defined by
| | 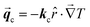 | (6) |
Besides, it is only the component of
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0071_20d1.gif)
that is aligned with
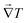
that contributes to the net heat flux. Thus we are interested in the net values of the scalars
qnm =
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0071_20d1.gif) m
m·
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif)
, and
qnc =
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0071_20d1.gif) c
c·
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif)
, here
qnm and
qnc stand for the net heat fluxes of the monoclinic and cubic phases respectively.
For the monoclinic phase, using the thermal conductivity tensor given in eqn (2), as well as combining eqn (4) and (5) yields
| | 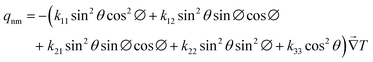 | (7) |
If we compare
eqn (7) with the isotropic form of Fourier's law of the net heat conduction,
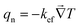
, then it can be identified by analogy the effective thermal conductivity
kefm for the monoclinic phase as
| | kefm = k11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∅ + k12 ∅ + k12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∅ ∅![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∅ + k21 ∅ + k21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∅ ∅![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∅ + k22 ∅ + k22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∅ + k33 ∅ + k33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (8) |
Finally, in order to obtain the total thermal conductivity of the monoclinic phase
ktm, it is necessary to take into account all the possible orientations of the NPG chains; thus, by averaging
eqn (8) over all directions we get:
| | 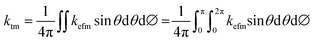 | (9) |
By combining
eqn (8) and (9), and carrying out ∅ and
θ integration, the total thermal conductivity of the monoclinic phase is given by
| | 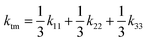 | (10) |
Likewise, the total heat flux of the monoclinic phase can be expressed as
| | 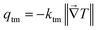 | (11) |
Following in analogy to the previously described procedure, the net heat flux of the cubic phase can be expressed as
| | 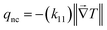 | (12) |
Again, by comparing
eqn (12) with the isotropic form of Fourier's law of the net heat conduction,
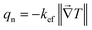
, then it can be identified by analogy of the effective thermal conductivity
kefc for the monoclinic phase as
Now, by averaging
eqn (13) over all directions
| | 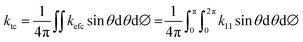 | (14) |
The total thermal conductivity of the cubic phase
ktc yields simply
Likewise, the total heat flux of the cubic phase can be expressed as
| | 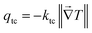 | (16) |
Conventionally, the performance of a thermal rectifier is evaluated by the rectification factor
R, which is defined as
R =
qf/
qr. In our specific case, the rectification factor is obtained by the ratio between the total heat flux of the cubic phase and the total heat flux of the monoclinic phase
R =
qtc/
qnc, which correspond to the phases presented in the device under forward and reverse thermal bias respectively. Hence, by combining
eqn (11) and (16), the rectification factor can be approached as
| | 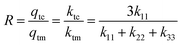 | (17) |
Evidently, according to
eqn (17), in order to estimate the rectification factor it is necessary to know the thermal conductivity tensor components of the NPG in the monoclinic and cubic phase. Besides, clearly
eqn (17) establishes a limit to
R which is related to the main axes
kij tensor components. Nevertheless, by observing the experimental total thermal conductivity of NPG shown in
Fig. 4b it can be concluded that
ktm < 1, and
ktc < 1. Therefore, the components
kij must be
kij ≪ 1, so if we assume that
k22 +
k33 ≪ 1, then
eqn (17) can be expressed as
| | 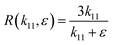 | (18) |
where
ε stands for
ε =
k22 +
k33.
The asymptotic behavior of the function R(k11,ε) with respect to ε may depend upon k11, where k11 can be seen as an independent variable; in which case we say that the expansion is non-uniform. Eqn (18) can be rewritten as
| | 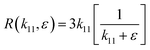 | (19) |
Clearly, always
k11 > 0, as well as
ε → 0
+, thus
R can be approached as
| | 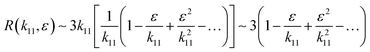 | (20) |
By analyzing
eqn (20), it can be concluded that as
ε approaches zero the value of
R ∼ 3. This is an important contribution of the present research work; in phase change materials with lattice transitions, the rectification factor seems to be limited by the ratio of their corresponding thermal conductivity tensor components. Thus, for the restricted class of symmetries of interest in this work, the ratio between the principal axes of the effective thermal conductivity tensor which defines the thermal rectification factor tends to three; amazingly the value obtained for the proposed thermal rectifier once the cubic phase is completely accomplished is
R ∼ 2.95.
Fig. 10 shows the behavior of
eqn (18) as a function of
k11, and
ε. The function
R(
k11,
ε) defines a surface given by an infinity set of (
k11,
ε) data. Evidently, for positive values of
k11, and
ε; as
ε → 0
+, quickly
R → 3 (upper red zone in the plot), whereas for values of
ε ≫ 0, and
k11 ≫ 0,
R ≪ 3 (lower green zone in the plot).
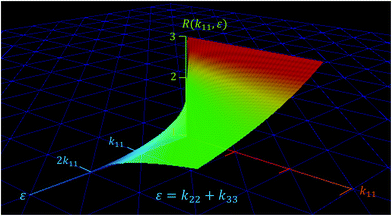 |
| | Fig. 10 Thermal rectification as a function of the main components of the thermal conductivity tensor of the NPG. | |
On the other hand, it is well known that carbon fibers are comprised of graphite crystallites arranged as polycrystals along the fiber axis.61,62 Therefore, reflecting the orientation distribution of graphite crystallites, carbon fibers exhibit anisotropic thermal properties presenting a hexagonal symmetry with five components in the thermal conductivity tensor,54 which are defined by
| | 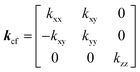 | (21) |
where
kcf represents the thermal conductivity tensor of the carbon fiber, and
kxx =
kyy; this restriction holds in the special case of a single-phase system as long as the constituent material has the required hexagonal, tetragonal, or trigonal symmetry, such as polycrystalline graphite.
If we now consider the carbon fiber as a polycrystalline wire one grain in diameter and many grains long, then by applying a similar procedure to that previously described, the total thermal conductivity of the carbon fiber can be expressed as
| | 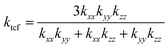 | (22) |
Moreover, because of the NPG anisotropy, the temperature isotherms are no longer necessarily parallel to the heat flux adiabats. Therefore, taking into consideration such anisotropic effects, the effective thermal conductivity of the thermal diode can be approached as
| |  | (23) |
where
kti stands for
ktc, and
ktm;
i.e. i = c, m depending on the NPG phase present in the thermal diode. Evidently, thermal conductivity of the carbon fiber is bigger than the thermal conductivity of NPG; thus, by assuming this consideration as valid,
eqn (23) transforms into
kTef ∼
kti. Hence, because of the relatively high thermal conductivity of carbon fiber, the total effective thermal conductivity in the forward and reverse thermal bias can entirely be defined by
ktc, and
ktm respectively. For this reason, in the present research the limit in the rectification factor has been approached through
eqn (17). Equally, this kind of rectification factor is both measured and analyzed with our analytical theory, and these values match quite well.
Conclusions
In the present research, we have developed and theoretically analyzed a novel thermal rectifier architecture that consists of a PAN-carbon fiber partially functionalized with NPG, which is a phase change material. This promising architecture shows an enhanced performance as compared to the previously reported thermal diodes based on phase change materials. A maximum thermal rectification ratio of ∼2.95 has been estimated from the experimental results, which, to the best of our knowledge, is the highest thermal rectification ratio demonstrated by a thermal diode based on a phase change material to date. Furthermore, such a result has theoretically been confirmed by using the thermal conductivity tensor theory for anisotropic heat conduction of solids, and these values match quite well. In this sense, guided by our analytical theory, we might infer that in lattice transition phase change materials, the rectification factor seems to be limited by the ratio of the principal thermal conductivity tensor components present in each phase, which is an important contribution of the present research. Hence, the obtained results are paramount to the development of enhanced performance thermal diodes for thermal energy harvesting, and management.
Author contributions
J. A. Q. developed and supervised the conceptualization and methodology of the project, and wrote the original draft, and funding acquisition. M. A. C. C. synthesized materials and samples, as well as carried out chemical, structural and morphological analysis. J. A. L. G. implemented the experimental procedure for thermal characterization of materials and devices. All authors contributed equally to data examination and discussion.
Conflicts of interest
The authors declare no conflict of interest.
Acknowledgements
This work was supported by the National Council for Science and Technology, Conacyt Mexico, through the grant for fundamental research No. 1358 under the national issues framework. Thanks to our research collaborators at the GENES group. J. A. L. G. and M. A. C. C. acknowledge Conacyt for the research fellowship.
References
- C. Forman, Renew. and Sust. Ener. Rev., 2016, 57, 1568–1579 CrossRef.
- Q. Bian, Environ. Syst. Res., 2020, 9(8), 1–11 Search PubMed.
- Q. Bian, Int. J. Environ. Clim. Change, 2019, 9(12), 801–822 CrossRef.
- E. Pop, Nano Res., 2010, 3, 147–169 CrossRef CAS.
- L. D. Hicks and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 16631–16634 CrossRef CAS PubMed.
- L. D. Hicks and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 12727–12731 CrossRef CAS PubMed.
- Y. Zhang, Q. Zhang and G. Cheng, Carbon Energy, 2020, 2(3), 408–436 CrossRef CAS.
- J. Wu, Y. Sun, W.-B. Pei, L. Huang, W. Xu and Q. Zhang, Synth. Met., 2014, 196, 173–177 CrossRef CAS.
- C.-J. Yao, H.-L. Zhang and Q. Zhang, Polymers, 2019, 11(107), 1–19 Search PubMed.
- B. Li, Appl. Phys. Lett., 2006, 88, 143501 CrossRef.
- L. Wang and B. Li, Phys. Rev. Lett., 2007, 99, 177208 CrossRef PubMed.
- C. Starr, The Copper Oxide Rectifier, Physics (College Park Md), 1936, 7, 15–19 CAS.
- A. Majumdar and P. Reddy, Appl. Phys. Lett., 2004, 84, 4768–4770 CrossRef CAS.
-
R. R. Somers II, L. Fletcher and R. D. Flack, 1987, 22nd Aerospace Sciences Meeting, 398.
- J. R. Barber and K. Wright, Int. J. Mech. Sci., 1967, 9, 811–815 CrossRef.
- M. Peyrard, Europhys. Lett., 2006, 76, 49 CrossRef CAS.
- W. Kobayashi, Y. Teraoka and I. Terasaki, Appl. Phys. Lett., 2009, 95, 171905 CrossRef.
- C. Dames, J. Heat Transfer, 2009, 131, 61301–61307 CrossRef.
- B. Li, J. Lan and L. Wang, Phys. Rev. Lett., 2005, 95, 104302 CrossRef PubMed.
- H. Sadat and V. Le Dez, Appl. Therm. Eng., 2016, 107, 1248–1252 CrossRef.
- Y. Wang, A. Vallabhaneni, J. Hu, B. Qiu, Y. P. Chen and X. Ruan, Nano Lett., 2014, 14, 592–596 CrossRef CAS PubMed.
- N. Yang, G. Zhang and B. Li, Appl. Phys. Lett., 2009, 95, 33107 CrossRef.
- T. Ouyang, Y. Chen, Y. Xie, X. L. Wei, K. Yang, P. Yang and J. Zhong, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 245403 CrossRef.
- J. Lee, V. Varshney, A. K. Roy, J. B. Ferguson and B. L. Farmer, Nano Lett., 2012, 12, 3491–3496 CrossRef CAS PubMed.
- J. W. Jiang, J. S. Wang and B. Li, Europhys. Lett., 2010, 89, 46005 CrossRef.
- J. Hu, X. Ruan and Y. P. Chen, Nano Lett., 2009, 9, 2730–2735 CrossRef CAS PubMed.
- N. Yang, G. Zhang and B. Li, Appl. Phys. Lett., 2008, 93, 243111 CrossRef.
- T. Takeuchi, Sci. Technol. Adv. Mater., 2014, 15, 064801 CrossRef PubMed.
- M. Tovar-Padilla, L. Licea-Jimenez, S. A. Pérez-Garcia and J. Alvarez-Quintana, Appl. Phys. Lett., 2015, 107, 084103 CrossRef.
- Z. Zhang, Y. Chen, Y. Xie and S. Zhang, Appl. Therm. Eng., 2006, 102, 1075–1080 CrossRef.
- B. Hu and L. Yang, Chaos: An Interdiscip J. Nonlinear. Sci., 2005, 15, 15119 CrossRef PubMed.
- J. Lan, W. Lei and B. Li, Int. J. Mod. Phys. B, 2007, 21, 4013–4016 CrossRef.
- G. Casati, Nat. Nanotechnol., 2007, 2, 23 CrossRef CAS PubMed.
- W. Kobayashi, D. Sawaki, T. Omura, T. Katsufuji, Y. Moritomo and I. Terasaki, Appl. Phys. Express, 2012, 5(2), 027302 CrossRef.
- J. J. Martínez-Flores, L. Licea-Jimenez, S. A. Pérez Garcia and J. Alvarez-Quintana, J. Appl. Phys., 2013, 114, 104904 CrossRef.
- K. I. Garcia-Garcia and J. Alvarez-Quintana, Int. J. Therm. Sci., 2014, 81, 76–83 CrossRef.
- E. Pallecchi, Z. Chen, G. E. Fernandes, Y. Wan, J. H. Kim and J. Xu, Mater. Horiz., 2015, 2, 125 RSC.
- J. Zhu, K. Hippalgaonkar, S. Shen, K. Wang, Y. Abate, S. Lee, J. Wu, X. Yin, A. Majumdar and X. Zhang, Nano Lett., 2014, 14(8), 4867–4872 CrossRef CAS PubMed.
- Z. Teng and L. Tengfei, Small, 2015, 11, 4657–4665 CrossRef PubMed.
- R. Chen, Y. Cui, H. Tian, R. Yao, Z. Liu, Y. Shu, C. Li, Y. Yang, T. Ren, G. Zhang and R. Zou, Sci. Rep., 2015, 5, 8884 CrossRef CAS PubMed.
- S. Wang, A. L. Cottrill, Y. Kunai, A. R. Toland, P. Liu, W.-J. Wang and M. S. Strano, Phys. Chem. Chem. Phys., 2017, 19(20), 13172–13181 RSC.
- J. J. Martinez-Flores, Dinesh Varshney and J. Alvarez-Quintana, Appl. Phys. Lett., 2018, 113, 264102 CrossRef.
- J. A. Leon-Gil, J. J. Martinez-Flores and J. Alvarez-Quintana, J. Mater. Sci., 2019, 54, 3211–3221 CrossRef CAS.
- A. L. Cottrill and M. S. Strano, Adv. Energy Mater., 2015, 5, 1500921 CrossRef.
- H. Kang, F. Yang and J. J. Urban, Phys. Rev. Appl., 2018, 10(2), 024034 CrossRef CAS.
- A. L. Cottrill, S. Wang, A. T. Liu, W.-J. Wang and M. S. Strano., Adv. Energy Mater., 2018, 1702692 CrossRef.
- K. Hirata, T. Matsunaga, S. Singh, M. Matsunami and T. Takeuchi, J. Electron. Mater., 2020, 49, 2895–2901 CrossRef CAS.
- H. Singh, A. Talekar, W.-M. Chien, R. Shi, D. Chandra, A. Mishra, M. R. Tirumala and D. J. Nelson, Energy, 2015, 91, 334–349 CrossRef CAS.
- B. Li, Y. Kawakita, S. Ohira-Kawamura, T. Sugahara, H. Wang, J. Wang, Y. Chen, S. I. Kawaguchi, S. Kawaguchi, K. Ohara, K. Li, D. Yu, R. Mole, T. Hattori, T. Kikuchi, Shin-ichiro Yano, Z. Zhang, Z. Zhang, W. Ren, S. Lin, O. Sakata, K. Nakajima and Z. Zhang, Nature, 2019, 567, 506–510 CrossRef CAS PubMed.
- P. Lloveras, A. Aznar, M. Barrio, P. H. Negrier, C. Popescu, A. Planes, L. Mañosa, E. Stern-Taulats, A. Avramenko, N. D. Mathur, X. Moya and J.-L. Tamarit, Nat. Commun., 2019, 10, 1803 CrossRef CAS PubMed.
- J. Salud, M. Barrio, D. O. López, J. L. L. Tamarita and X. Alcobe, J. Appl. Crystallogr., 1998, 31, 748–757 CrossRef CAS.
- D. Chandra, C. S. Day and C. S. Barrett, Powder Diffr., 1993, 8(2), 109–117 CrossRef CAS.
- H. Park, J. Zhao and J. P. Lu, Nano Lett., 2006, 6(5), 916–919 CrossRef CAS PubMed.
- G. J. Ehlert, Y. Lin and H. A. Sodano, Carbon, 2011, 49, 4246–4255 CrossRef CAS.
-
Thermal conductivity: theory, properties, and applications. ed. T. M. Tritt. Kluwer Academic/Plenum Publishers, New York, 2004, pp. 188–192 Search PubMed.
- S. Blazewicz, B. Patalita and P. H. Touzain, Carbon, 1997, 35(10–11), 1613–1618 CrossRef CAS.
- G. Wehmeyer, T. Yabuki, C. Monachon, J. Wu and C. Dames, Appl. Phys. Rev., 2017, 4, 041304 Search PubMed.
- J. Alvarez-Quintana, J. Phys. D: Appl. Phys., 2021, 54, 185301 CrossRef CAS.
- F. Erchiqui and Z. Annasabi, Int. J. Heat Mass Transfer, 2019, 136, 1250–1264 CrossRef.
-
M. Necati Ozisik, Heat Conduction, 2nd edn Wiley, New York, 1993, ch. 15, pp. 617–652 Search PubMed.
-
O. Paris and H. Peterlik, Handbook of Textile Fibre Structure, 1st edn, Woodhead Publishing, 2009, vol. 2, ch. 10, pp. 353–377 Search PubMed.
- R. Perret and W. Ruland, J. Appl. Crystallogr., 1970, 3, 525–532 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *cd
*cd



![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) r is applied directly to the non-functionalized segment. If we consider that
r is applied directly to the non-functionalized segment. If we consider that ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) r is not enough heat to increase the interface temperature Ti beyond Tt (Ti < Tt), the NPG functionalized segment will remain in the α-phase. As a result, the effective thermal conductivity of the system will depend on the thermal conductivity of the fiber kf and the thermal conductivity kα of the NPG functionalized segment in the α-phase. However, if heat flux is increased from
r is not enough heat to increase the interface temperature Ti beyond Tt (Ti < Tt), the NPG functionalized segment will remain in the α-phase. As a result, the effective thermal conductivity of the system will depend on the thermal conductivity of the fiber kf and the thermal conductivity kα of the NPG functionalized segment in the α-phase. However, if heat flux is increased from ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) r to
r to ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) r, then the interface temperature will achieve or even overcome the transition temperature Ti ≥ Tt, as shown in Fig. 5b. In this case, the NPG functionalized segment will be partially transformed into the γ-phase, and the effective thermal conductivity of the system will depend on kf, kα and kγ, but with a small influence of kγ because the non-functionalized segment causes thermal resistance delaying the whole transition of the NPG functionalized segment. Conversely, Fig. 5c shows the situation when an arbitrary heat flux
r, then the interface temperature will achieve or even overcome the transition temperature Ti ≥ Tt, as shown in Fig. 5b. In this case, the NPG functionalized segment will be partially transformed into the γ-phase, and the effective thermal conductivity of the system will depend on kf, kα and kγ, but with a small influence of kγ because the non-functionalized segment causes thermal resistance delaying the whole transition of the NPG functionalized segment. Conversely, Fig. 5c shows the situation when an arbitrary heat flux ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) f is applied directly to the NPG functionalized segment, i.e. in the forward thermal bias. In this case, if we consider that
f is applied directly to the NPG functionalized segment, i.e. in the forward thermal bias. In this case, if we consider that ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) f is not enough heat to increase the interface temperature Ti beyond Tt (Ti < Tt), the NPG functionalized segment will remain partially transformed in the γ-phase. As a result, the effective thermal conductivity of the system will depend on kf, kα and kγ, but in this case with a small influence of kα. However, if heat flux is increased from
f is not enough heat to increase the interface temperature Ti beyond Tt (Ti < Tt), the NPG functionalized segment will remain partially transformed in the γ-phase. As a result, the effective thermal conductivity of the system will depend on kf, kα and kγ, but in this case with a small influence of kα. However, if heat flux is increased from ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) f to
f to ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) f, then the interface temperature will match or even overcome the transition temperature Ti ≥ Tt, as shown in Fig. 5d. Under this situation, the NPG functionalized segment will be entirely transformed into the γ-phase, thus the effective thermal conductivity of the system will depend only on kf and kγ. Evidently, different behaviors in the effective thermal conductivities will be present in the system depending on the direction and level of the applied heat flux. Therefore, because of the phase transition present in NPG, thermal rectification can be expected in the partially functionalized carbon fiber depicted in Fig. 2a. Furthermore, it is worth mentioning that if the applied heat flux continues increasing in either forward or reverse bias, then the NPG functionalized segment will be wholly transformed into the γ-phase at a certain moment. Nevertheless, in the forward bias mode the NPG functionalized segment will accomplish quicker the γ-phase transition than in the reverse bias mode. This is because, in the forward bias mode, the NPG functionalized segment is in contact directly with the heat source, whereas in the reverse bias mode it is not, which delays the phase transition. Therefore, once the γ-phase transition is achieved in either reverse or forward bias, the thermal diode will start with a sudden rise in the heat flux at certain prescribed temperatures, named the breakdown temperature and forward temperature respectively. Such temperatures will control the on-state and breakdown-state of the device, similar to the forward voltage and breakdown voltage in electronic diodes. Evidently, an important content of NPG molecules attached along the functionalized segment must be accomplished to ensure an intra- and inter-molecular heat transfer along the NPG segment. In this sense, the amount of grafted NPG molecules will depend on the amount of COOH molecules attached to the carbon fiber surface, as the content of COOH increases, NPG molecule content will also increase and vice versa. Thereby, it is crucial to achieve a great deal of grafted NPG molecules because NPG is directly related to the rectification effect, and a lack in the content of NPG will blur the rectification effect in the device. However, it is well known that chemical functionalization of surfaces has been demonstrated to be an important strategy to modify energy carrier transport mechanisms in carbonaceous materials.53 Thereby, a substantial content of COOH organic molecules covalently attached to the surface gives rise to the formation of localized defect sites, which will act as surficial scattering centers for electrons and phonons. Undoubtedly, it will affect the device performance by altering the thermal conductance of the device, which will delay or hasten the transition of the NPG segment.
f, then the interface temperature will match or even overcome the transition temperature Ti ≥ Tt, as shown in Fig. 5d. Under this situation, the NPG functionalized segment will be entirely transformed into the γ-phase, thus the effective thermal conductivity of the system will depend only on kf and kγ. Evidently, different behaviors in the effective thermal conductivities will be present in the system depending on the direction and level of the applied heat flux. Therefore, because of the phase transition present in NPG, thermal rectification can be expected in the partially functionalized carbon fiber depicted in Fig. 2a. Furthermore, it is worth mentioning that if the applied heat flux continues increasing in either forward or reverse bias, then the NPG functionalized segment will be wholly transformed into the γ-phase at a certain moment. Nevertheless, in the forward bias mode the NPG functionalized segment will accomplish quicker the γ-phase transition than in the reverse bias mode. This is because, in the forward bias mode, the NPG functionalized segment is in contact directly with the heat source, whereas in the reverse bias mode it is not, which delays the phase transition. Therefore, once the γ-phase transition is achieved in either reverse or forward bias, the thermal diode will start with a sudden rise in the heat flux at certain prescribed temperatures, named the breakdown temperature and forward temperature respectively. Such temperatures will control the on-state and breakdown-state of the device, similar to the forward voltage and breakdown voltage in electronic diodes. Evidently, an important content of NPG molecules attached along the functionalized segment must be accomplished to ensure an intra- and inter-molecular heat transfer along the NPG segment. In this sense, the amount of grafted NPG molecules will depend on the amount of COOH molecules attached to the carbon fiber surface, as the content of COOH increases, NPG molecule content will also increase and vice versa. Thereby, it is crucial to achieve a great deal of grafted NPG molecules because NPG is directly related to the rectification effect, and a lack in the content of NPG will blur the rectification effect in the device. However, it is well known that chemical functionalization of surfaces has been demonstrated to be an important strategy to modify energy carrier transport mechanisms in carbonaceous materials.53 Thereby, a substantial content of COOH organic molecules covalently attached to the surface gives rise to the formation of localized defect sites, which will act as surficial scattering centers for electrons and phonons. Undoubtedly, it will affect the device performance by altering the thermal conductance of the device, which will delay or hasten the transition of the NPG segment.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) mixture of concentrated sulfuric acid (H2SO4, 95–98% ACS, FCC, VWR Chemicals BDH and Nitric acid (HNO3, 68–70%, ARISTAR, ACS, VWR Chemicals BDH) for 2 hours at 80 °C. For the neutralization of acid residues by carboxylic functionalization, the CFs have been subjected to hydrogen peroxide (H2O2, 30%, BAKER ANALYZED, ACS, J.T. Baker) immersion for 12 hours. After this treatment, one end of the CFs was covered by one solution at 10 wt% of polymethyl methacrylate (PMMA, average Mw ∼ 996
1 (v/v) mixture of concentrated sulfuric acid (H2SO4, 95–98% ACS, FCC, VWR Chemicals BDH and Nitric acid (HNO3, 68–70%, ARISTAR, ACS, VWR Chemicals BDH) for 2 hours at 80 °C. For the neutralization of acid residues by carboxylic functionalization, the CFs have been subjected to hydrogen peroxide (H2O2, 30%, BAKER ANALYZED, ACS, J.T. Baker) immersion for 12 hours. After this treatment, one end of the CFs was covered by one solution at 10 wt% of polymethyl methacrylate (PMMA, average Mw ∼ 996![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 by GPC, powder, Sigma-Aldrich) in anisole (anhydrous, 99.7%, Sigma-Aldrich). Another free end of the CFs was refluxed by one aqueous solution at 15 wt% and 5 M of 2,2-dimethyl-1,3-propanediol (neopentyl glycol, 99%, Alfa Aesar) in H2SO4 (95–98% ACS, FCC, VWR Chemicals BDH), respectively. To etch the section of the covered CFs by PMMA, this was immersed in an aqueous solution of 1M sodium hydroxide (NaOH, BAKER ANALYZED, A.C.S. Reagent, J.T. Baker). Next, this same section treated with NaOH was placed in concentrated glacial acetic acid (99.96%, CTR) for 24 hours to remove the PMMA completely. Subsequently, the two sections of the CFs were cleaned with a methanol solution: water (1
000 by GPC, powder, Sigma-Aldrich) in anisole (anhydrous, 99.7%, Sigma-Aldrich). Another free end of the CFs was refluxed by one aqueous solution at 15 wt% and 5 M of 2,2-dimethyl-1,3-propanediol (neopentyl glycol, 99%, Alfa Aesar) in H2SO4 (95–98% ACS, FCC, VWR Chemicals BDH), respectively. To etch the section of the covered CFs by PMMA, this was immersed in an aqueous solution of 1M sodium hydroxide (NaOH, BAKER ANALYZED, A.C.S. Reagent, J.T. Baker). Next, this same section treated with NaOH was placed in concentrated glacial acetic acid (99.96%, CTR) for 24 hours to remove the PMMA completely. Subsequently, the two sections of the CFs were cleaned with a methanol solution: water (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume) to dissolve the PMMA residues and to remove any organic impurity formed during the process.
1 by volume) to dissolve the PMMA residues and to remove any organic impurity formed during the process.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 acid treatment of concentrated H2SO4
1 acid treatment of concentrated H2SO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HNO3 at 80 °C for 2 h, and dried at 70 °C for 24 h to obtain COOH-carbon fibers. After acid treatment, carbon fibers with a carboxylic acid group were partially further functionalized in a solution of H2O/NPG/H2SO4 under ultrasonic vibration for 48 h which afforded NPG-carbon fiber. Surface functionalization process details are shown in the Experimental procedure section.
HNO3 at 80 °C for 2 h, and dried at 70 °C for 24 h to obtain COOH-carbon fibers. After acid treatment, carbon fibers with a carboxylic acid group were partially further functionalized in a solution of H2O/NPG/H2SO4 under ultrasonic vibration for 48 h which afforded NPG-carbon fiber. Surface functionalization process details are shown in the Experimental procedure section.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (284.7 eV-sp2), C–C (285.4 eV-sp3), C–OH (286.5 eV), C
C (284.7 eV-sp2), C–C (285.4 eV-sp3), C–OH (286.5 eV), C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (287.5 eV) and COOH (289.0 eV) as labeled in both figures. By inspecting carefully the C1s peak, both COOH-carbon fiber and NPG-carbon fiber reveals the presence of hydroxyl and carboxyl groups as indicated by the well-pronounced peaks around 286.5 and 289.1 eV respectively. The ratios of the area under the respective Gaussian curve (for C–OH and COOH curves) were calculated and the percentages are shown in Table 1, from which we found that the NPG-functionalization treatment caused an increase in the ratio of adsorbed oxygen (27.84% + 11.56% = 39.4%) in the carbon fiber compared to the initial carbon fiber (17.90 + 11.52 = 29.42%). These results clearly indicate that the functionalization procedure increases hydroxyl content due to the NPG chains.
O (287.5 eV) and COOH (289.0 eV) as labeled in both figures. By inspecting carefully the C1s peak, both COOH-carbon fiber and NPG-carbon fiber reveals the presence of hydroxyl and carboxyl groups as indicated by the well-pronounced peaks around 286.5 and 289.1 eV respectively. The ratios of the area under the respective Gaussian curve (for C–OH and COOH curves) were calculated and the percentages are shown in Table 1, from which we found that the NPG-functionalization treatment caused an increase in the ratio of adsorbed oxygen (27.84% + 11.56% = 39.4%) in the carbon fiber compared to the initial carbon fiber (17.90 + 11.52 = 29.42%). These results clearly indicate that the functionalization procedure increases hydroxyl content due to the NPG chains.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and COOH for carbon fibers before and after functionalization
O, and COOH for carbon fibers before and after functionalization
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O
O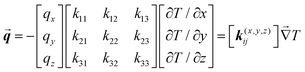
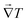 to the heat flux vector
to the heat flux vector ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0071_20d1.gif) . Here, we are concerned with the thermal conductivity tensors of the crystalline structure of NPG which changes from a monoclinic configuration to face centered cubic during transition.
. Here, we are concerned with the thermal conductivity tensors of the crystalline structure of NPG which changes from a monoclinic configuration to face centered cubic during transition.
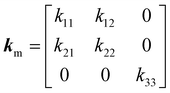
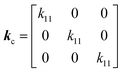
 must point in the
must point in the ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) direction given by
direction given by
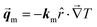
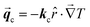
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0071_20d1.gif) that is aligned with
that is aligned with  that contributes to the net heat flux. Thus we are interested in the net values of the scalars qnm =
that contributes to the net heat flux. Thus we are interested in the net values of the scalars qnm = ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0071_20d1.gif) m·
m·![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) , and qnc =
, and qnc = ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0071_20d1.gif) c·
c·![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) , here qnm and qnc stand for the net heat fluxes of the monoclinic and cubic phases respectively.
, here qnm and qnc stand for the net heat fluxes of the monoclinic and cubic phases respectively.
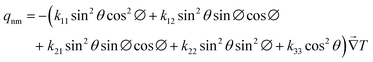
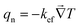 , then it can be identified by analogy the effective thermal conductivity kefm for the monoclinic phase as
, then it can be identified by analogy the effective thermal conductivity kefm for the monoclinic phase as![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∅ + k12
∅ + k12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∅
∅![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∅ + k21
∅ + k21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∅
∅![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∅ + k22
∅ + k22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∅ + k33
∅ + k33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ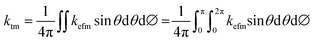
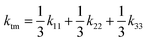
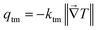
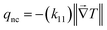
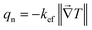 , then it can be identified by analogy of the effective thermal conductivity kefc for the monoclinic phase as
, then it can be identified by analogy of the effective thermal conductivity kefc for the monoclinic phase as