DOI:
10.1039/D1MA00510C
(Paper)
Mater. Adv., 2021,
2, 5955-5966
Electronic properties and high-pressure behavior of wolframite-type CoWO4†
Received
11th June 2021
, Accepted 27th July 2021
First published on 29th July 2021
Abstract
In this work we characterize wolframite-type CoWO4 under ambient conditions and under compression up to 10 GPa, with emphasis on its electronic structure. X-Ray diffraction and vibrational experiments, supported by ab initio calculations, show that CoWO4 is stable under high-pressure conditions, as no structural changes are detected in the studied pressure range. Interesting findings come from optical absorption spectroscopy. On the one hand, CoWO4 is confirmed to have one of the lowest band gaps among similar wolframites, around 2.25 eV. This makes CoWO4 suitable for use in applications such as the photocatalysis of organic pollutants and water splitting. Additionally, a monotonic decrease of the band gap is found upon compression. This phenomenon is seldom observed in AWO4 wolframites and is attributed to the open character of the d shell of Co2+. Our results are supported by theoretical ab initio simulations and are discussed with reference to other wolframites.
1. Introduction
AWO4 wolframites, where A is a divalent metallic cation, are crystalline compounds mainly studied for their optical properties. Depending upon the divalent cation, they may crystalize in a tetragonal structure known as scheelite or in a monoclinic structure known as wolframite.1 Many of these compounds have multiple technological applications. They are, in fact, luminescent and scintillating materials, and are employed in high-energy physics for the detection of γ and X photons, in fluorescent devices, as dielectric ceramics in microwave applications and fiber optics.2–5 AWO4 wolframites have also been proposed for use in sensors for gases or nitric acid6,7 and some of them, among which ZnWO4 and CoWO4, have shown promising performances in the photodegradation of organic pollutants.8,9 CoWO4 has also interesting magnetic properties.10 Monoclinic wolframite-type compounds share the same crystal structure (space group P2/c) and generally are semiconductors with energy gaps, Eg, covering from the near-ultraviolet to the visible.11
Among wolframites, CoWO4 has been one of the less studied compounds, even if it has recently started to get attention mainly because of its low band gap (2.3–2.7 eV), which makes it a good candidate for green technologies, in particular as a photocatalyst for degradation of pollutants present in water or for the production of hydrogen fuel by means of water splitting.12–17 For these environmentally friendly applications, an accurate knowledge of the electronic properties of CoWO4 is important. In particular, the band-gap energy of CoWO4 has not yet been measured by optical-absorption spectroscopy. Some applications of CoWO4 involve extreme environments, in particular at high pressure, and it is thus important to accurately characterize the influence of high pressure on the structural, vibrational, and optical properties of CoWO4.
In this work, we focus our attention on wolframite-type CoWO4. Characterizing it under ambient and high-pressure conditions, we have determined the structural stability of CoWO4 up to at least 10 GPa, as all relevant physical magnitudes are found to vary smoothly in the studied pressure range. Structural and vibrational properties of CoWO4, such as its bulk modulus and its anisotropic compressibility, are found to be compatible with those of analogue wolframites, along with its Raman phonons and their evolution under compression. On the other hand, interesting results come from the analysis of the optical absorption spectra. In fact, we could state that CoWO4 is among the wolframites with the lowest band gap, Eg = 2.25(1) eV. Additionally, the band gap is shown to steeply decrease under compression, something unusual for AWO4 wolframites and that has been reported only for MnWO4 so far. We discuss these results on the basis of theoretical simulations and by comparison with MnWO4 (Eg = 2.37 eV).18 We have found that the contribution of unfilled Co2+ 4d states to both the top of the valence band and the bottom of the conduction band is responsible for the low band gap of CoWO4 and its negative dependence on pressure. These findings are important from the point of view of the potential application of CoWO4, as tunable low band-gap compounds may be useful in photodegradation appliances. Also, they are likely to stimulate new research in the field of the electronic structure of AWO4 wolframites, as significant trends are expected to be established linking the electron configuration of the A atom and the behavior of the band gap of these compounds.
2. Experimental details
Na2WO4 and anhydrous CoCl2 obtained from Alfa Aesar (purity > 99%) were used as precursors for the preparation of CoWO4. Stoichiometric quantities of the reactants were weighed, and the mixture was ground in an agate mortar with the addition of ethanol. The product was washed with distilled water to remove sodium chloride. Subsequently, it was heated at 500 °C. XRD measurements at ambient pressure were taken with the sample in the powder form using Cu Kα radiation (λ = 1.5406 Å), confirming that the obtained product was CoWO4, with no detectable minority phases or impurities. High-Pressure (HP) XRD experiments, of up to around 10 GPa, were performed at the MSPD beamline of ALBA Synchrotron19 using a Diamond Anvil Cell (DAC) loaded with CoWO4 in the powder form. The culets of the diamond had a diameter of 500 μm The sample was deposited in the hole of a pre-indented stainless-steel gasket (diameter 200 μm), together with ruby chips for the determination of the pressure through the ruby-fluorescence method20 and a methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol
ethanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water (MEW) mixture in the 16
water (MEW) mixture in the 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio as the pressure-transmitting medium (PTM). 2D diffraction images were taken on a Rayonix CCD detector, using a wavelength λ = 0.4246 Å and transformed to intensity-2θ patterns using DIOPTAS.21 Rietveld and Le Bail fits were performed using POWDER CELL.22 The Equation of State (EOS) of CoWO4 was calculated by fitting a 2nd order Birch–Murnaghan EOS to the pressure–volume data obtained from the HP experiments. Structure drawing and bond length measurements were performed with VESTA.23
1 volume ratio as the pressure-transmitting medium (PTM). 2D diffraction images were taken on a Rayonix CCD detector, using a wavelength λ = 0.4246 Å and transformed to intensity-2θ patterns using DIOPTAS.21 Rietveld and Le Bail fits were performed using POWDER CELL.22 The Equation of State (EOS) of CoWO4 was calculated by fitting a 2nd order Birch–Murnaghan EOS to the pressure–volume data obtained from the HP experiments. Structure drawing and bond length measurements were performed with VESTA.23
HP optical absorption experiments in the UV-vis range were performed on a pre-compressed pellet of CoWO4 loaded in a DAC (similarly to what was done for HP XRD). Two light sources, an UV and a deuterium lamp were used. Absorption spectra were measured by comparing, at each pressure point, the spectrum of the light source through the pressure transmitting medium and through the sample (“sample-in, sample-out method”).
Raman spectroscopy was performed with a powder sample in a DAC, loaded similarly to the DACs used for HP XRD and UV-vis spectroscopy. Raman spectra were collected in the backscattering geometry using a He–Ne laser (λ = 632.8 nm), a JOBIN-YVON TRH1000 spectrophotometer, an edge filter, and a thermoelectrically cooled multichannel CCD (HORIBA SYNAPSE) as the detector.
3. Theoretical simulations
The simulations of the structural, electronic, dynamical, and elastic properties were carried out using density functional theory (DFT)24 and the VASP (Vienna Ab initio Simulation Package) package.25,26 We use the pseudopotential method with the projector augmented wave (PAW) scheme,27 using a plane-wave cutoff of 540 eV to ensure high accurate convergence. The k-point integration in the Brillouin zone (BZ) was done using a big sampling of 6 × 6 × 6 grid for the primitive unit cell. Generalized Gradient Approximation, GGA with the Perdew, Burke, and Ernzerhof for solids, PBEsol prescription for the exchange–correlation energy.28 Besides, we perform our simulations with the DFT+U scheme of Dudarev et al.29 to treat the strongly correlated states of Co and W atoms by means of a single effective parameter, Ueff = U − J, where U and J are the screened Coulomb and exchange parameters. The selected values of Ueff were 3.32 and 6.2 eV, for the Co and W atoms, respectively.30 The antiferromagnetic configuration was found to have the lowest energy. The cell parameters and the atomic positions are relaxed to obtain the optimized configurations for a given volume, where the atomic forces were less than 0.004 eV Å−1, and the stress tensor is diagonal with an accuracy of less than 0.1 GPa. This procedure allows us to obtain a set of volume, energy, and pressure data from our simulations.
Phonopy package31 was used to perform lattice-dynamics calculations. The frequencies, and the eigenvectors of the normal vibration modes were determined at Γ point. The elastic properties were computed employing the method implemented in the VASP code.32,33 These elastic constants are obtained for the fully optimized structures by small deformations, which produce small strains in different directions taking into account the structure symmetry.33 The electronic band structure along the high symmetry directions of the first BZ were obtained using the relaxed theoretical structures at different pressures.
4. Results and discussion
XRD experiments
As described above, wolframite-type CoWO4 crystallizes naturally in a monoclinic structure belonging to the P2/c space group (S.G. 13, Z = 2). The ambient-pressure XRD pattern for CoWO4, together with the Rietveld fit, is shown in Fig. 1. All the XRD peaks are correctly indexed in the P2/c space group. Atomic positions, as calculated by us through theoretical simulations, are compatible with the values given in the literature34 (see comparison in Table 1) and have been not refined in our fits. Cell parameters as obtained by XRD in open air are a = 4.670(5) Å, b = 5.687(6) Å, c = 4.951(5) Å, β = 90.08(9)° (volume V = 131.5(2) Å3), in good agreement with those measured using neutron diffraction (ref. 34) and those obtained by ab initio simulations (Table S1, ESI†). According to these data, the structure of wolframite-type CoWO4 can be described as a distorted hexagonal packing of O atoms in which Co and W both are 6-fold coordinated with oxygens. The coordination octahedral units CoO6 and WO6 share two edges with neighboring polyhedra of the same type, forming alternating chains of identical octahedra along the [001] axis (Fig. 2a and b). Besides, these polyhedra are slightly irregular, as the bond lengths Co–O and W–O are not all equal (Table 2).
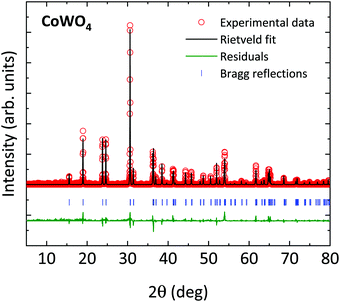 |
| | Fig. 1 Ambient-pressure XRD pattern for CoWO4, as obtained by a powder sample in open air (λ = 1. 1.5406 Å) and Rietveld fit. Red circles: experimental data; black line: Rietveld fit; green line: residuals; blue ticks: Bragg reflections. | |
Table 1 Atomic positions for wolframite-type CoWO4, from ref. 34, and comparison with theoretical values from ab initio simulations (in parentheses)
| Atom |
Wyckoff |
x/a
|
y/b
|
z/c
|
| Co |
2f |
1/2 |
0.6712(8) (0.65955) |
1/4 |
| W |
2e |
0 |
0.1773(4) (0.17883) |
1/4 |
| O1 |
4g |
0.2176(3) (0.22012) |
0.1080(4) (0.10863) |
0.9321(3) (0.92811) |
| O2 |
4g |
0.2540(3) (0.26102) |
0.3757(4) (0.38128) |
0.3939(3) (0.40212) |
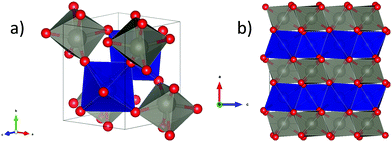 |
| | Fig. 2 (a) Ambient-pressure structure of wolframite-type CoWO4. Red, blue, and grey spheres are respectively oxygen, cobalt, and tungsten atoms. The coordination polyhedra of tungsten and cobalt are shown in blue and grey, respectively; (b) projection of wolframite-type CoWO4 unit cell onto the (010) plane, showing the alternate chains of CoO6 and WO6 octahedra along [001]. | |
Table 2 Bond distances d in the CoO6 WO6 octahedra of CoWO4 and their volume V at ambient pressure
| Bond |
Multiplicity |
d (Å) |
V (Å3) |
| Co–O1 |
2 |
2.033(4) |
12.1456 |
| Co–O2 |
2 |
2.1198(18) |
| Co–O2 |
2 |
2.157(5) |
| W–O1 |
2 |
2.1164(4) |
9.3647 |
| W–O1 |
2 |
1.916(3) |
| W–O2 |
2 |
1.785(3) |
The evolution of the XRD patterns of CoWO4 under compression in nearly hydrostatic conditions35 is summarized in Fig. 3. As shown, all the patterns up to 9.5 GPa can be indexed in the same P2/c space group. The shrinking of the unit cell is pointed out by the progressive shifting of the Bragg reflections towards higher values of 2θ. Apart from this, the only notable change in the patterns is the splitting of some peaks, which is more evident in the 8–10° angular range. These splitting are due to the variation of the β angle of the monoclinic structure, which is initially very close to 90° and increases with a positive pressure coefficient of ∂β/∂P = 0.088(4) deg GPa−1 (Table 3 and Fig. 4). At ambient pressure, the most intense diffraction peak is an overlap of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11) and (111) reflections (at 8.34° and 8.35°, respectively); these appear clearly separated at 9.5 GPa. Similarly, the (002) and (021) peaks (9.84° and 9.88° at ambient pressure), which are strictly convoluted at low pressure, greatly increase their separation at higher pressure (see Fig. 3). In short, despite a steady increase of the monoclinic β angle, no phase transitions are detected in the studied pressure range. As we will see in the following, this conclusion is corroborated by Raman spectroscopy and theoretical simulations.
11) and (111) reflections (at 8.34° and 8.35°, respectively); these appear clearly separated at 9.5 GPa. Similarly, the (002) and (021) peaks (9.84° and 9.88° at ambient pressure), which are strictly convoluted at low pressure, greatly increase their separation at higher pressure (see Fig. 3). In short, despite a steady increase of the monoclinic β angle, no phase transitions are detected in the studied pressure range. As we will see in the following, this conclusion is corroborated by Raman spectroscopy and theoretical simulations.
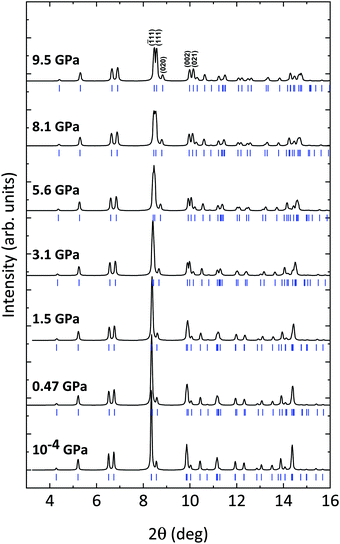 |
| | Fig. 3 Powder XRD patterns of CoWO4 at selected pressures. Blue ticks indicate the positions of the Bragg reflections. Reflections for which the splitting at high pressure is more evident have been indicated. | |
Table 3 Linear functions describing the pressure dependence of unit-cell parameters of CoWO4. Intercept and slope are referred to the linear fits of the values of cell parameters vs. pressure
| Parameter |
Intercept |
Slope |
k
i
(10−3 GPa−1) |
|
a
|
4.669(2) Å |
−0.0091(4) Å GPa−1 |
1.95(9) × 10−3 GPa−1 |
|
b
|
5.683(3) Å |
−0.0182(7) Å GPa−1 |
3.2(1) × 10−3 GPa−1 |
|
c
|
4.949(1) Å |
−0.0073(2) Å GPa−1 |
1.48(4) × 10−3 GPa−1 |
|
β
|
90.12(2) deg |
0.089(4) deg GPa−1 |
— |
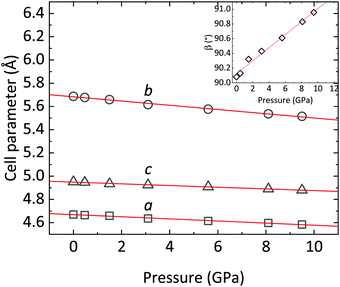 |
| | Fig. 4 CoWO4 unit-cell parameters a, b and c as a function of pressure. The trend of the monoclinic β angle is shown in the inset. Red lines are linear fits of the data. | |
In the following, the compressibility of CoWO4 is analyzed from the powder XRD data. Fig. 4 summarizes the variation of the cell parameters as a function of pressure. As anticipated, a, b, and c smoothly decrease upon increasing pressure.
The axial compressibility of CoWO4, (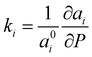 , for the aiaxis, a0i being the cell parameter at ambient pressure) can be studied from the linear fits of the cell parameters vs. pressure. The values in Table 3 show that the compressibility along the b axis is much higher than along the a and c axes. This anisotropic behavior, and the increase of the monoclinic angle, is commonly observed in wolframites, and has been reported previously for MgWO4, CdWO4 and MnWO4, among others.36–38
, for the aiaxis, a0i being the cell parameter at ambient pressure) can be studied from the linear fits of the cell parameters vs. pressure. The values in Table 3 show that the compressibility along the b axis is much higher than along the a and c axes. This anisotropic behavior, and the increase of the monoclinic angle, is commonly observed in wolframites, and has been reported previously for MgWO4, CdWO4 and MnWO4, among others.36–38
A more rigorous insight on the axial compressibility of CoWO4 comes from the analysis of its compressibility tensor. For monoclinic structures, the tensor is symmetric and has only four non-zero components, whose values can be calculated using the analytical expressions given by Knight.39 These components for CoWO4 are summarized in Table 4, in which also the eigenvalues and eigenvectors of the compressibility tensor are shown. One of the eigenvectors is parallel to the unique crystallographic b-axis, while the other two define a plane perpendicular to it. Compressibility is clearly anisotropic, as it varies between 9.0252 × 10−4 and 3.2095 × 10−3 GPa−1 and the axis with the maximum compressibility is the unique b-axis (β22 component). On the other hand, the direction of minimum compressibility lies in the ac plane, forming an angle of 53.65° with the c axis (from c to a), corresponding to the crystallographic direction [![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ,0,4].39 To first order, the isothermal compressibility of CoWO4 is given by the trace of the compressibility tensor,
,0,4].39 To first order, the isothermal compressibility of CoWO4 is given by the trace of the compressibility tensor, 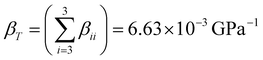 ,39 corresponding to an approximate value of the bulk modulus B0 = 150.76 GPa. For completeness, we also show the compressibility indicatrix, calculated using PASCal, in Fig. S1 (ESI†).40
,39 corresponding to an approximate value of the bulk modulus B0 = 150.76 GPa. For completeness, we also show the compressibility indicatrix, calculated using PASCal, in Fig. S1 (ESI†).40
Table 4 Isothermal compressibility tensor coefficients, βij, their eigenvalues, λi, and eigenvectors, evi, and angle of minimum direction of compression, ψ, for CoWO4
|
β
11 (GPa−1) |
1.952 × 10−3 |
|
β
22 (GPa−1) |
3.209 × 10−3 |
|
β
33 (GPa−1) |
1.471 × 10−3 |
|
β
13 = β31 (GPa−1) |
7.726 × 10−4 |
|
λ
1 (GPa−1) |
2.5209 × 10−3 |
| ev1 |
(0.80540, 0, 0.59273) |
|
λ
2 (GPa−1) |
3.2095 × 10−3 |
| ev2 |
(0, 1, 0) |
|
λ
3 (GPa−1) |
9.02527 × 10−4 |
| ev3 |
(−0.59273, 0, 0.8054) |
|
ψ (deg) |
53.65 |
An alternative estimate of the bulk modulus B0 is obtained by fitting the experimental pressure–volume data to a 2nd-order Birch–Murnaghan EOS (Fig. 5), which gives a comparable result of B0 = 131(3) (V0 = 131.43(10) Å3) GPa. These values are in line with the bulk moduli of other wolframites such as MgWO4, MnWO4, and ZnWO4 (see Table 5 for a comparison).36,41,42Ab initio simulations of the volume at ambient pressure agree within a 1% with the experimental values. Also, fitting a 2nd-order Birch–Murnaghan EOS on the theoretical pressure–volume data, as shown in Fig. S2 (ESI†), gives a compatible, although slightly overestimated, value of B0 (Table 5). It is interesting to notice that the experimental value of B0 is very close to the one expected from the phenomenological rule proposed by Ruiz-Fuertes et al. (B0 = 137 GPa), which relates the bulk modulus with the inverse of A–O distance in AWO4 wolframites (A being a divalent element).41 It is noteworthy that our ab initio simulations predict that atomic positions are nearly constant across the studied pressure range, with a maximum variation around 0.3% over an increase of 1 GPa in pressure for an oxygen atom. This value is comparable with the experimental uncertainty on the atomic positions in CoWO4 (see Table 1). Hence, in the following we will assume that atomic positions are constant in the entire pressure range. Therefore, the CoO6 and WO6 octahedra will have the same bulk modulus of the CoWO4 unit cell, given that their volume varies accordingly to the volume of the whole unit cell in the absence of atomic displacements. In turn, this implies that CoO6 and WO6 octahedra are equally compressible and contribute equally to the volume reduction of the unit cell under compression, unlike that observed in other AWO4 wolframites.36
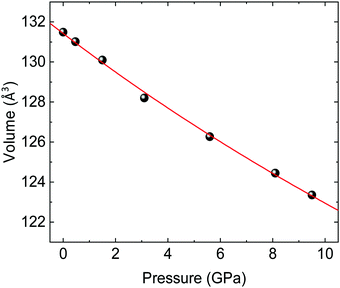 |
| | Fig. 5 Pressure–volume data for wolframite-type CoWO4 (black spheres) and fit with a 2nd-order Birch–Murnaghan EOS (red line). Errors are comparable to symbol size. | |
Table 5 Values of the bulk modulus (B0), its derivative (B0′) and the volume at ambient pressure (V0) for CoWO4 and analogue wolframites. The experimental value of B0 in parenthesis for CoWO4 has been estimated as the inverse of the trace of the compressibility tensor. The theoretical value of B0 in parentheses for CoWO4 has been obtained directly by ab initio simulations
| Compound |
V
0 (Å3) |
B
0 (GPa) |
B
0′ |
Ref. |
| CoWO4 |
| Experiment |
131.43(10) |
131(3) (150.76) |
4 |
This work |
| Theory |
129.114(13) |
164.3(5) (161.15) |
4 |
This work |
| MgWO4 |
| Experiment |
131.1(3) |
160(13) |
4.5(3) |
41
|
| Experiment |
— |
144(3) |
|
36
|
| MnWO4 |
| Experiment |
— |
131(2) |
4 |
36
|
| Experiment |
138.8(2) |
145(3) |
4.3(2) |
42
|
| ZnWO4 |
| Experiment |
132.9(5) |
145(6) |
6.6(9) |
41
|
Vibrational spectroscopy
The Raman spectrum of monoclinic-type CoWO4 at ambient pressure, together with its evolution up to 10 GPa, is shown in Fig. 6. Group theory predicts a total of 18 Raman active modes for monoclinic-type CoWO4, with a mechanical representation at the Γ point given by Γ = 8Ag + 10Bg.43 All of the predicted modes have been detected in our experiments (Fig. 6 and Table 6), including one at 244 cm−1 which, to the best of our knowledge, had not been reported before. For AWO4 wolframites, active Raman modes can be classified into internal, high-frequency stretching modes of the WO6 octahedron, and external modes, originated by the motion of the A cation and the WO6 octahedron as a unit.38 The distribution of the modes in CoWO4 is the archetypical one for similar tungstates (4 modes above 600 cm−1, 2 isolated modes in the 500–550 cm−1 range, and 12 modes below 405 cm−1).41 Nonetheless, for CoWO4, the frequency of some of the modes differs significantly between previous experimental reports.38,44–47 These discrepancies are mostly observed in the low-frequency range, i.e. mostly external modes are affected. It is thus reasonable to argue that these differences may arise from different preparation methods, which may impact sample purity and cell parameters.
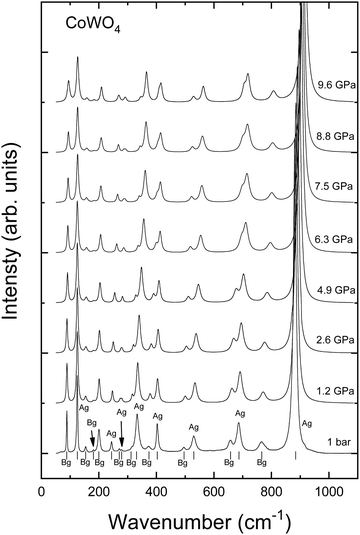 |
| | Fig. 6 Raman spectra of wolframite-type CoWO4 at ambient conditions (bottom) and at selected pressures. The symmetry and position of each peak are shown for the spectrum at ambient pressure (ticks). | |
Table 6 Symmetry, frequency under ambient conditions (ω0), linear pressure coefficient and the Grüneisen parameter (dP/dω and γ, respectively) of the Raman active phonons for CoWO4, as obtained from experiments and ab initio simulations. The asterisk indicates a phonon which had not been experimentally reported before
| Mode |
Experiment |
Theory |
| Exp |
ω
0 (cm−1) |
dω/dP (cm−1 GPa−1) |
γ
|
ω
0 (cm−1) |
dω/dP (cm−1 GPa−1) |
γ
|
| Bg |
88(1) |
0.66(4) |
0.89(7) |
92.83 |
0.79 |
1.11 |
| Ag |
125(1) |
0.12(3) |
0.12(3) |
128.42 |
0.74 |
0.75 |
| Bg |
154(1) |
0.45(4) |
0.35(4) |
157.27 |
1.03 |
0.86 |
| Bg |
181(1) |
0.27(3) |
0.18(2) |
183.66 |
0.60 |
0.43 |
| Bg |
200(1) |
0.93(3) |
0.56(4) |
189.19 |
0.54 |
0.37 |
| Ag |
244(1)* |
2.74(10) |
1.34(9) |
222.88 |
2.70 |
1.59 |
| Bg |
271(1) |
2.24(13) |
0.99(8) |
277.89 |
2.61 |
1.23 |
| Ag |
278(1) |
1.26(13) |
0.54(6) |
294.77 |
0.70 |
0.31 |
| Bg |
316(1) |
3.44(18) |
1.31(10) |
309.94 |
1.77 |
0.75 |
| Ag |
333(1) |
3.67(16) |
1.32(10) |
338.56 |
3.50 |
1.35 |
| Bg |
373(1) |
3.80(17) |
1.22(9) |
358.51 |
3.95 |
1.44 |
| Ag |
403(1) |
1.45(7) |
0.43(3) |
399.97 |
1.17 |
0.38 |
| Bg |
495(1) |
3.45(8) |
0.83(5) |
494.23 |
2.96 |
0.78 |
| Ag |
529(1) |
3.60(14) |
0.82(6) |
523.69 |
3.06 |
0.77 |
| Bg |
657(1) |
5.2(4) |
0.94(9) |
629.86 |
3.83 |
0.80 |
| Ag |
686(1) |
3.52(15) |
0.61(4) |
677.89 |
2.64 |
0.51 |
| Bg |
766(1) |
4.49(19) |
0.70(5) |
756.31 |
4.07 |
0.70 |
| Ag |
881(1) |
3.37(8) |
0.46(3) |
853.38 |
2.66 |
0.41 |
All in all, the frequencies as obtained in our experiments and those calculated by ab initio simulations are in good agreement, and the same can be said for the Grüneisen parameters, defined as 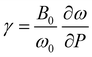 (Table 6). Minor discrepancies between theory and experiments are not unusual for wolframite-type compounds.38 For CoWO4, the phonons which appear to be more sensitive to pressure are the one at 244 cm−1 and the three in the range from 316 to 373 cm−1, with a value of γ well above 1 (Table 6). A similar situation is found in wolframite-type MgWO4, for which the highest Grüneisen parameters are low-frequency external modes within similar ranges.41 The data in Fig. 6 support the stability of wolframite-type CoWO4, as no qualitative differences are detectable among the Raman spectra at different pressure. Given that all phonons’ linear pressure coefficients are positive (Table 6), no vanishing or splitting phonons are found in the studied pressure range, confirming the absence of structural transitions. As shown in Fig. 7, all Raman modes consistently blueshift upon compression.
(Table 6). Minor discrepancies between theory and experiments are not unusual for wolframite-type compounds.38 For CoWO4, the phonons which appear to be more sensitive to pressure are the one at 244 cm−1 and the three in the range from 316 to 373 cm−1, with a value of γ well above 1 (Table 6). A similar situation is found in wolframite-type MgWO4, for which the highest Grüneisen parameters are low-frequency external modes within similar ranges.41 The data in Fig. 6 support the stability of wolframite-type CoWO4, as no qualitative differences are detectable among the Raman spectra at different pressure. Given that all phonons’ linear pressure coefficients are positive (Table 6), no vanishing or splitting phonons are found in the studied pressure range, confirming the absence of structural transitions. As shown in Fig. 7, all Raman modes consistently blueshift upon compression.
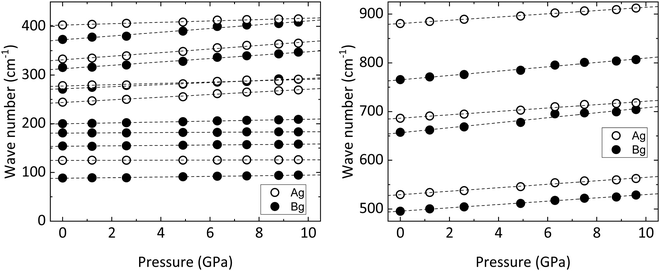 |
| | Fig. 7 Frequency of Raman modes vs. pressure for wolframite-type CoWO4 (circles). Dashed lines are the linear fits used for the calculation of the pressure coefficients and Grüneisen parameters. | |
Our ab initio simulations support the experimental results. As shown in Fig. S3 (ESI†), theoretical calculations correctly predict all phonons hardening under high pressure conditions. Therefore, no phonons become imaginary at any pressure point, ruling out the presence of phase transitions.
Wolframite-type CoWO4 also has 15 IR active phonons, whose mechanical representation at the Γ point is Γ = 7Au + 8Bu (excluding acoustic modes).43 Although experimental IR spectroscopy data for CoWO4 are not available by us at the moment, we have calculated the IR phonons and their evolution under pressure (see Fig. S4 and Table S2, ESI†). The distribution of calculated IR modes is in good agreement with previous results.46 Similarly to the Raman modes, IR phonons generally harden with pressure. Only one Bu mode around 247 cm−1 appears to have a small negative pressure coefficient. However, this cannot be interpreted as a sign of dynamical instability, as in the studied pressure range, all modes keep their real (positive) character.
The volumetric thermal expansion coefficient α of an oxide like CoWO4 can be obtained using a statistical thermodynamic approach by assuming that all the energy of a crystal resides in its vibrations.48,49 This has been successfully done in the past for BaWO4 using Raman and IR frequencies.49 Using this approach and the calculated frequencies and pressure dependences for different modes, we have estimated the thermal expansion for CoWO4 at ambient pressure and as a function of pressure. This information is relevant for the use of CoWO4 as an oxidation protection layer of ferritic stainless steel.50 We found that at ambient pressure α = 11 × 10−6 K−1, in agreement with results reported from recent high-temperature XRD studies.50 Under compression, we have determined that the thermal expansion coefficient α of CoWO4 linearly decreases with pressure at a rate of −2 × 10−7 K−1 GPa−1, α = 9 × 10−6 K−1 at 10 GPa. This behavior is similar to that reported for BaWO4.49
Elastic properties
In the following we will discuss the elastic behavior of CoWO4. The monoclinic structure of CoWO4 only allows 13 independent non-zero components for the symmetric 6 × 6 elasticity matrix C, i.e. the diagonal Cii components (i = 1,…,6) plus C12, C13, C15, C23, C25, C35, C46.51 The values of these coefficients are shown in Table 7.
Table 7 Elastic constants Cij (in GPa) at 1 bar for of wolframite-type CoWO4
|
C
11
|
C
22
|
C
33
|
C
44
|
C
55
|
C
66
|
C
12
|
C
13
|
C
23
|
C
15
|
C
25
|
C
35
|
C
46
|
| 222 |
252 |
307 |
77 |
83 |
71 |
125 |
116 |
116 |
11 |
3 |
29 |
−9 |
The Cij parameters of CoWO4 in Table 7 are roughly similar to those reported previously for CdWO4 and ZnWO4 and may be thus considered typical for AWO4 compounds52,53 even when they are calculated using an orthorhombic approximation for the structure of these compounds.54
The eigenvalues λ1 (i = 1,…,6) of the C matrix, as shown in Table 8, are all positive under ambient conditions, thus satisfying one of the four equivalent formulations of the Born elastic stability criterion. The positivity of all eigenvalues in fact, states a necessary and sufficient condition for the stability of the wolframite structure under ambient conditions.55
Table 8 Eigenvalues λ1 (in GPa, i = 1,…,6) of the elasticity matrix C of wolframite-type CoWO4
|
λ
1
|
64.5 |
|
λ
2
|
77.9 |
|
λ
3
|
83.5 |
|
λ
4
|
110.5 |
|
λ
5
|
172.8 |
|
λ
6
|
502.8 |
Under hydrostatic compression, the magnitudes which describe the elastic properties of a crystal are the components Bij of the elastic stiffness tensor B. These are related to the Cij coefficients by the following relationships:
| Bii = Cii − P (i = 1,…,6); |
| B12 = C12 + P, B13 = C13 + P, B23 = C23 + P; |
| B15 = C15, B25 = C25, B35 = C35, B46 = C46, |
where
P is the pressure.
56 Under simulated hydrostatic compression, all of the
Bij stiffness coefficients increase steadily, except for
B46 which presents a moderate decrease. On the other hand,
B44 and
B25 reach a maximum around 3 and 4 GPa, respectively, before decreasing slowly (
Fig. 8a).
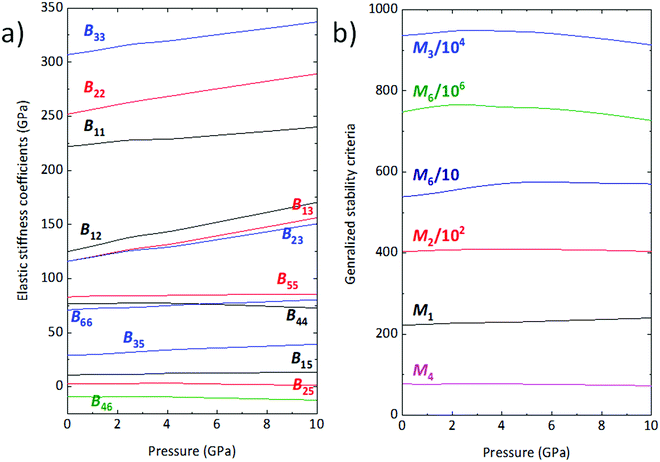 |
| | Fig. 8 (a) Elastic stiffness coefficients Bij as a function of pressure; (b) generalized stability criteria for wolframite-type CoWO4. | |
In the presence of an external load, such as non-zero hydrostatic compression, the equilibrium conditions for a crystal structure are given by the Born generalized criterion, which implies that the B matrix must be definitely positive.56,57 This is equivalent to saying that the following six inequalities must be fulfilled:
| M3 = (B22B33 − B232)B11 − B33B122 + 2B23B12B13 − B22B132 > 0 |
| M5 = B122B352 − B33B55B122 + 2B55B12B13B23 − 2B12B13B25B35 |
| −2B12B15B23B35 + 2B33B12B15B25 + B132B252 − B22B55B132 |
| −2B13B15B23B25 + 2B22B13B15B35 + B152B232 − B22B33B152 |
| −B11B55B232 + 2B11B23B25B35 − B11B33B252 − B11B22B352 + B11B22B33B55 > 0 |
As shown in Fig. 8b, Mi values are all positive across the entire pressure range and, plausibly, also well above 10 GPa. The wolframite structure of CoWO4 is thus expected to be stable even at pressures greater than 10 GPa. This result is compatible with our vibrational analysis, whose extrapolation excludes the appearance of phonons with negative frequency, and thus of dynamic instabilities, in the range immediately above 10 GPa.
Knowing the C matrix and its inverse S = C−1 (compliance tensor), elastic parameters such as the bulk modulus, B0, the shear modulus, G, the Young's modulus E, and the Poisson ratio, ν, can be calculated at ambient pressure, using the expression reported by Zhao et al.,58 in both the Voigt and the Reuss approximations. These parameters are summarized in Table 9 for CoWO4 and all of them are in line with those already reported for CdWO4 and ZnWO4.52–54
Table 9 Bulk modulus, B, shear modulus, G, the Young's modulus, E, and the Poisson's ratio, ν, of wolframite-type CoWO4 at ambient pressure. The B/G ratio is also shown
|
|
Voight |
Reuss |
Average |
|
B
0 (GPa) |
166 |
162 |
164 |
|
G (GPa) |
75 |
71 |
73 |
|
E (GPa) |
194 |
186 |
190 |
|
ν
|
0.305 |
0.308 |
0.307 |
|
B
0/G ratio |
2.232 |
2.27 |
2.251 |
The average bulk modulus B0 = 164 GPa calculated using the C matrix is slightly overestimated with respect to the experimental value, even if such discrepancies are not uncommon for wolframites.38,53 Nonetheless, the bulk modulus calculated using the elastic matrix is in perfect agreement with theoretical values shown in Table 5. Finally, the high B0/G ratio (>2) indicates that CoWO4 is a malleable material. Elastic parameters as a function of pressure are resumed in Fig. S5 (ESI†). While the bulk modulus increases uniformly under compression, the shear modulus slightly decreases, probably in connection with the increase of the monoclinic β angle observed experimentally, which may also be the reason behind the decrease of the Young's modulus above 4 GPa (Fig. S5a–c, ESI†). Although increasing with pressure, the Poisson ratio has a value ν < 0.5 across the studied pressure range (Fig. S5d, ESI†), thus reflecting both the slightly anisotropic compressibility of wolframite-type CoWO4 (see results in the XRD section) and an increasing ionic character of the chemical bond.59,60 Finally, the bulk/shear ratio also increases under compression, indicating the high ductility of CoWO4 (Fig. S5d, ESI†).
Given the scarcity of studies regarding the elastic properties of AWO4 wolframites, these results represent a valuable addition to the knowledge of those compounds, and we hope that they may stimulate more research on this subject, as significant trends may be thus established between the elastic properties of AWO4 materials and composition/external conditions (pressure/temperature).
Electronic properties
According to our calculations, wolframite CoWO4 is predicted to have two electronic gaps around 2.3 eV under ambient conditions, which are very close in energy: a direct gap at the Γ point and an indirect Γ → Z gap (Fig. 9a). On the other hand, when (αhv)1/2 is plotted versus hν (where α is the absorbance and hν the energy of the incident light), a linear trend is found for energies above 2.3 eV (Tauc plot, Fig. 10), meaning that the fundamental gap in wolframite CoWO4 is of an indirect nature. This is not surprising, as AWO4 wolframites whose A2+ cation has unfilled d subshells have been shown to have indirect gaps.18,61
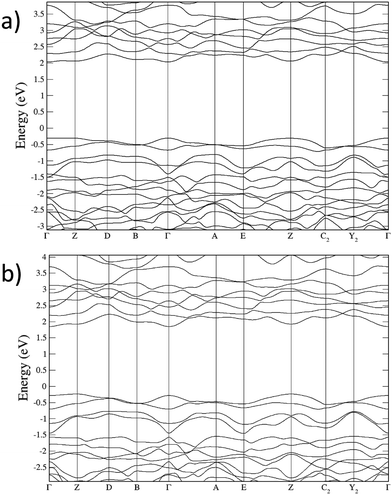 |
| | Fig. 9 Electronic band structure of wolframite CoWO4; (a) under ambient conditions, and (b) at 10 GPa. | |
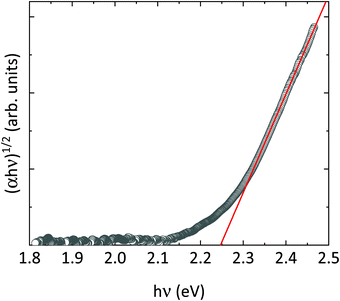 |
| | Fig. 10 Tauc plot of the absorbance spectrum of wolframite CoWO4 at ambient pressure. The fit of the linear region is shown in red. | |
The band gap energy Eg of CoWO4, as extracted from the data in Fig. 10, is Eg = 2.25(1) eV, in full agreement with theoretical calculations (Eg = 2.33 eV). These values suggest that the previous studies slightly overestimate Eg.12,62 This can be understood considering that these values were determined either from indirect electrical measurements or from diffuse reflectance measurements in nanoparticles, two techniques that are less accurate that optical absorption. The value here determined for the band gap is also lower than those of analogue orthotungstates, which have gaps in the range of 2.37–4.06 eV (Table 10), CoWO4 being the wolframites with the lowest band gap so far.11,18 Interestingly, our result is in line with the predictions of Lacomba-Perales et al., which highlight a correlation between the band gap and the cationic radii in AWO4 wolframites.11 The value we determined for the band gap of CoWO4 (2.25(1) eV), makes it an excellent candidate as a semiconductor electrode for efficient visible light photolysis of water.63
Table 10 Band gap Eg of wolframite-type CoWO4 with pressure coefficient as measured in this work and comparison with analogue wolframites (from ref. 18)
| Compound |
Theory Eg (eV) |
Experiments Eg (eV) |
Experiments dEg/dP (meV GPa−1) |
| MgWO4 |
3.22 |
4.06 |
13.9 |
| ZnWO4 |
2.79 |
3.98 |
12.7 |
| CdWO4 |
2.91 |
4.02 |
12.0 |
| MnWO4 |
1.83 |
2.37 |
−22.2 |
| CoWO4 |
2.33 |
2.25(1) |
−28.1(4) |
The small band gap of CoWO4 can be understood by analyzing the electronic contributions to its density of states (DOS). In AWO4 wolframites with large energy gaps, such as MgWO4, ZnWO4 and CdWO4, the bottom of the conduction band is dominated by W 5d states hybridized with the O 2p state, while the upper part of the valence band is dominated by O 2p states slightly hybridized with 5d states of W. The contribution of the A2+ cation to both bands is negligible. On the other hand, for MnWO4, which has a narrower band gap, 2d states of Mn2+ contribute to both the valence and the conduction bands.18 Given the similar electronic configuration of Mn and Co, it is thus fair to assume that for wolframite CoWO4, the Co2+ 3d states are the reason behind the reduced band gap. Indeed, our calculations (Fig. 11a) show that under ambient conditions, the top of the valence band is contributed predominantly by 3d states of CO2+ which still give a significant contribution to the bottom part of the conduction band along with W 5d states and, to a lesser extent, O 2p states. Other AWO4 wolframites, with an A+2 having unfilled d states, such as FeWO4 and NiWO4, are also expected to exhibit a comparatively small band gap.11,61,64 This strengthens the hypothesis regarding the fundamental contribution of the open d states to the band gap of these compounds.
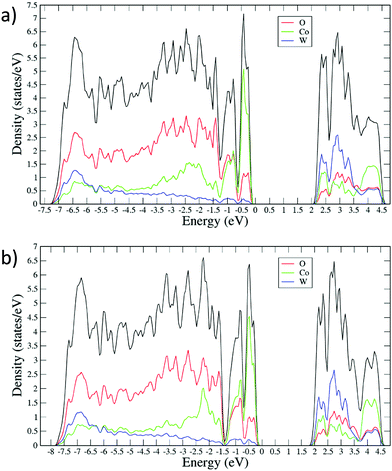 |
| | Fig. 11 Partial density of state of CoWO4 (a) under ambient conditions and (b) at a pressure of 10 GPa. | |
In the following, we will discuss the behavior of the band gap of CoWO4 under high pressure conditions. Fig. 12 shows the (αhv)1/2vs. hν Tauc plot of the absorption tail of CoWO4 at selected pressures. Same as in Fig. 10, all plots present a linear region above a certain energy hν of the incident light, meaning that the band gap of wolframite CoWO4 retains its indirect character in this pressure range. This can be explained by the limited changes in the topology of the band structure of CoWO4 under compression (see Fig. 9a and b). On the other hand, it is evident how, unlike analogue wolframites, the band gap of CoWO4 closes with pressure (Fig. 13). Again, the absence of structural phase transitions in the studied pressure range is reflected in the smooth decrease of the band gap, without any discontinuous collapse. The decrease is linear, with a large negative pressure coefficient dEg/dP = −28.1(4) meV GPa−1, a dependence on pressure even larger than that of wolframite MnWO4 (−22.2 meV GPa−1). The experimental result is in perfect agreement with ab initio calculations, which give a similar value of −24.9(3) meV GPa−1 for the pressure coefficient. The relative contribution of Co, W and O states to the DOS of CoWO4 remains unaffected in the studied pressure range, as shown in Fig. 11b. Nonetheless, features such as the two-peak shape structure in the −1.5 to 0 eV range become more evident at high pressure. An analogous behavior is seen, again, in MnWO4, in which a similar feature is available in the DOS.18 The unfilled Mn2+ 3d states are split by the octahedral crystal field into twofold eg and threefold tg states, which give place to a two-peaks feature in the DOS of around −0.75 eV The splitting is enhanced by the pressure due to the shortening of the Mn–O bonds.18,36 Again, it is reasonable to expect a similar reason behind the behavior of the peak-like feature of the DOS of CoWO4 at the top of the valence band.
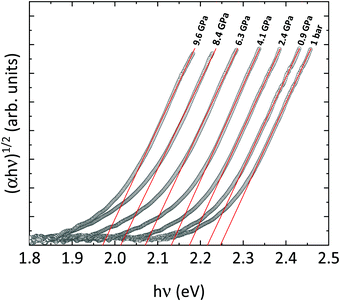 |
| | Fig. 12 Tauc plot of the absorbance spectrum of wolframite CoWO4 at selected pressures (shown above each curve). The fits of the linear regions are shown in red. | |
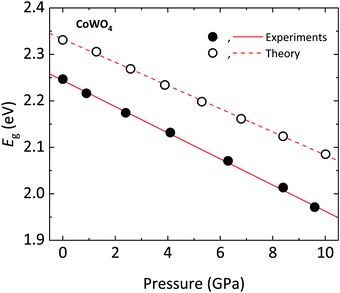 |
| | Fig. 13 Band gap Eg of wolframite CoWO4 as a function of pressure (circles) with corresponding linear fits (lines). Closed (open) symbols and solid (dashed) lines correspond to experimental (theoretical) results. | |
As mentioned, the decrease of the band gap with pressure is unusual for AWO4 wolframites. Akin to what was observed for MnWO4, in CoWO4 the unfilled 3d states of Co contribute to the bottom of the conduction band. These d states are pushed down in energy by pressure, contrary to what happens for wolframites with filled d states such as MgWO4, ZnWO4, and CdWO4.18,37 On the other hand, for all of the mentioned compounds, the top of the valence band is unaffected by pressure. The net result is a decrease (resp. increase) of the band gap with pressure for AWO4 wolframites with an open (resp. closed) d shell.
On the basis of our findings and previous results, a trend may thus be established, by which AWO4 wolframites with an A2+ cation with open d shell are expected to exhibit a comparatively small band gap, which further decreases under high-pressure conditions. Further experimental studies are required to confirm this hypothesis.
To conclude the discussion of the electronic properties of CoWO4, we will comment on the effective mass of electrons and holes (me and mh, respectively), which we have obtained from DFT calculations. This parameter is related to the carrier mobility, which directly affects the separation and diffusion rate of photo-induced charge carriers, one of the most important factors determining being the photocatalytic activity of a semiconductor. The effective mass of holes and electrons has been calculated from the second derivative of the energy with the wave vector. Due to the monoclinic structure of wolframite, the effective masses of carriers will be also anisotropic, being described by a non-diagonal tensor.65 For instance, it can be seen in Fig. 8 that the top valence band in the band structure of CoWO4 is more dispersive along G–A and G–B than along G–Z and G–Y2. A similar anisotropy is observed in the bottom conduction band of the band structure around the Z point (the minimum of the conduction band). For practical purposes, an average effective mass can be defined as 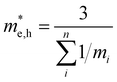 [a], where mi are the eigenvalues of the effective mass tensor. By following this procedure, we have determined that at ambient pressure
[a], where mi are the eigenvalues of the effective mass tensor. By following this procedure, we have determined that at ambient pressure 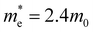 and
and 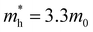 . The first value is very high in comparison with the typical electron-mobility of semiconductors suggesting that CoWO4 has a low performance as an n-type semiconductor. In contrast, the second value is comparable to the hole-mobility of the best p-type semiconductors.66 These observations are consistent with the experimental observation that un-doped CoWO4 is a p-type semiconductor.62 On the other hand, it is known that the relative ratio of effective mass determines the recombination rate of carriers.67 In our case
. The first value is very high in comparison with the typical electron-mobility of semiconductors suggesting that CoWO4 has a low performance as an n-type semiconductor. In contrast, the second value is comparable to the hole-mobility of the best p-type semiconductors.66 These observations are consistent with the experimental observation that un-doped CoWO4 is a p-type semiconductor.62 On the other hand, it is known that the relative ratio of effective mass determines the recombination rate of carriers.67 In our case 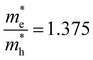 , which means that electrons and holes should easily recombine and show short lifetimes. Therefore, our study indicates that CoWO4 as the ideal band-gap energy to be used as a photocatalytic electrode; but also has the same limitations regarding photocurrent that a typical photocatalytic material as BiVO4 or TiO2 has.68,69
, which means that electrons and holes should easily recombine and show short lifetimes. Therefore, our study indicates that CoWO4 as the ideal band-gap energy to be used as a photocatalytic electrode; but also has the same limitations regarding photocurrent that a typical photocatalytic material as BiVO4 or TiO2 has.68,69
5. Conclusions
A multifaceted characterization was performed on wolframite-type CoWO4 under room conditions and at high pressures, of up to 10 GPa, by means of XRD, Raman spectroscopy, optical absorption spectroscopy, and ab initio simulations. All these techniques agree in that CoWO4 is stable in the studied pressure range, as no signs of phase transitions could be detected. The bulk modulus of CoWO4 has been found to be in line with the values of other AWO4 wolframites, and its compressibility is equally anisotropic. The elastic constants of CoWO4 have been calculated and are found to be in line with those of analogue wolframites. For completeness, we have also discussed the elastic properties of CoWO4 under compression, as the characterization of the elastic behavior of wolframite is often neglected in the study of these compounds. The most intriguing experimental results are those regarding the electronic structure of CoWO4, which has been found to be an indirect semiconductor with a reduced band gap, of around 2.25 eV, when other wolframites such as CdWO4, MgWO4 and ZnWO4 have large direct gaps, with values around 4 eV. In addition, the band gap redshifts upon compression, something which may be beneficial for photocatalytic applications, and that has been seldom observed in AWO4 wolframites. These results are attributed to the open character of the d shell of Co2+, which contribute to both the bottom of the conduction band as well as to the top of the valence band. These allow us to draw broad conclusions as, by comparison with previous results, the electronic structure of wolframite AWO4 appears to be strongly influenced by the open or closed character of the d shell of the A2+ cation. As such, other wolframites, such as FeWO4 and NiWO4, are expected to behave similarly to CoWO4. In this respect, new studies and experiments are required to confirm significant trends in analogue compounds.
Author contributions
The manuscript was written through the contributions of all authors. All authors have approved the final version of the manuscript.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
This research was supported by the Spanish Ministerio de Ciencia, Innovación y Universidades, the Spanish Research Agency, and the European Fund for Regional Development under Grant No. PID2019-106383GB-C41/43, FIS2017-83295-P and RED2018-102612-T and by Generalitat Valenciana under Grant Prometeo/2018/123 (EFIMAT). E. B would like to thank the University of Valencia for his “Attracció de Talent” postdoctoral contract (UV-INV_POSTDOC19-1026935). Powder X-ray diffraction experiments were performed at the Materials Science and Powder Diffraction beamline of ALBA Synchrotron (experiment no. 2016081784).
References
- D. Errandonea and F. J. Manjón, Prog. Mater. Sci., 2008, 53, 711–773 CrossRef CAS.
- V. B. Mikhailik and H. Kraus, Phys. Status Solidi, 2010, 247, 1583–1599 CrossRef CAS.
- T. T. Monajemi, D. Tu, B. G. Fallone and S. Rathee, Med. Phys., 2006, 33, 1090–1100 CrossRef CAS PubMed.
- M. Mai and C. Feldmann, J. Mater. Sci., 2012, 47, 1427–1435 CrossRef CAS.
- R. C. Pullar, S. Farrah and N. M. Alford, J. Eur. Ceram. Soc., 2007, 27, 1059–1063 CrossRef CAS.
- V. Dusastre and D. E. Williams, J. Mater. Chem., 1999, 965–971 RSC.
- C. M. Gonzalez, X. Du, J. L. Dunford and M. L. Post, Sens. Actuators, B, 2012, 173, 169–176 CrossRef CAS.
- K. Jothivenkatachalam, S. Prabhu, A. Nithya, S. Chandra Mohan and K. Jeganathan, Desalin. Water Treat., 2015, 54, 3134–3145 CrossRef CAS.
- H. Fu, C. Pan, L. Zhang and Y. Zhu, Mater. Res. Bull., 2007, 42, 696–706 CrossRef CAS.
- N. Hollmann, Z. Hu, T. Willers, L. Bohatý, P. Becker, A. Tanaka, H. H. Hsieh, H. J. Lin, C. T. Chen and L. H. Tjeng, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 1–6 CrossRef.
- R. Lacomba-Perales, J. Ruiz-Fuertes, D. Errandonea, D. Martínez-García and A. Segura, EPL, 2008, 83, 3 Search PubMed.
- G. V. Geetha, R. Sivakumar, Y. Kuroki, C. Gopalakrishnan and C. Sanjeeviraja, AIP Conf. Proc., 2020, 2265, 030094 CrossRef CAS.
- C. Ling, L. Q. Zhou and H. Jia, RSC Adv., 2014, 4, 24692 RSC.
- S. M. AlShehri, J. Ahmed, T. Ahamad, P. Arunachalam, T. Ahmad and A. Khan, RSC Adv., 2017, 7, 45615–45623 RSC.
- K. Hoang, M. Oh and Y. Choi, RSC Adv., 2018, 8, 4191–4196 RSC.
- H. Cui, B. Li, Y. Zhang, X. Zheng, X. Li, Z. Li and S. Xu, Int. J. Hydrogen Energy, 2018, 43, 18242–18252 CrossRef CAS.
- M. I. Ahmed, A. Adam, A. Khan, A. U. Rehman, M. Qamaruddin, M. N. Siddiqui and M. Qamar, Mater. Lett., 2016, 183, 281–284 CrossRef CAS.
- J. Ruiz-Fuertes, S. López-Moreno, J. López-Solano, D. Errandonea, A. Segura, R. Lacomba-Perales, A. Muñoz, S. Radescu, P. Rodríguez-Hernández, M. Gospodinov, L. L. Nagornaya and C. Y. Tu, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 1–9 CrossRef.
- F. Fauth, I. Peral, C. Popescu and M. Knapp, Powder Diffr., 2013, 28, S360–S370 CrossRef CAS.
- H. K. Mao, P. M. Bell, J. W. Shaner and D. J. Steinberg, J. Appl. Phys., 1978, 49, 3276–3283 CrossRef CAS.
- C. Prescher and V. B. Prakapenka, High Pressure Res., 2015, 35, 223–230 CrossRef CAS.
- W. Kraus and G. Nolze, J. Appl. Crystallogr., 1996, 29, 301–303 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
-
P. Kristine, Materials Data on CoWO4, https://materialsproject.org/materials/mp-19092/.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- N. Chetty, A. Muoz and R. M. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 11934–11936 CrossRef CAS PubMed.
- Y. Le, Page and P. Saxe, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104104 CrossRef.
- H. Weitzel, Z. Kristallogr. – New Cryst. Struct., 1976, 144, 238–258 Search PubMed.
- S. Klotz, J.-C. Chervin, P. Munsch and G. Le Marchand, J. Phys. D: Appl. Phys., 2009, 42, 075413 CrossRef.
- J. Macavei and H. Schulz, Z. Kristallogr. - Cryst. Mater., 1993, 207, 193–208 CrossRef CAS.
- D. Errandonea and J. Ruiz-Fuertes, Crystals, 2018, 8, 1–19 CrossRef.
- J. Ruiz-Fuertes, D. Errandonea, S. López-Moreno, J. González, O. Gomis, R. Vilaplana, F. J. Manjón, A. Muñoz, P. Rodríguez-Hernández, A. Friedrich, I. A. Tupitsyna and L. L. Nagornaya, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 1–11 CrossRef.
- K. S. Knight, Phys. Chem. Miner., 2010, 37, 529–533 CrossRef CAS.
- M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329 CrossRef CAS.
- J. Ruiz-Fuertes, S. López-Moreno, D. Errandonea, J. Pellicer-Porres, R. Lacomba-Perales, A. Segura, P. Rodríguez-Hernández, A. Muoz, A. H. Romero and J. González, J. Appl. Phys., 2010, 107, 0–10 CrossRef CAS.
- J. Ruiz-Fuertes, A. Friedrich, O. Gomis, D. Errandonea, W. Morgenroth, J. A. Sans and D. Santamaría-Pérez, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 1–7 Search PubMed.
- E. Kroumova, M. I. Aroyo, J. M. Perez-Mato, A. Kirov, C. Capillas, S. Ivantchev and H. Wondratschek, Phase Transitions, 2003, 76, 155–170 CrossRef CAS.
- H. V. S. B. Azevêdo, R. A. Raimundo, L. S. Ferreira, M. M. S. Silva, M. A. Morales, D. A. Macedo, U. U. Gomes and D. G. L. Cavalcante, Mater. Chem. Phys., 2020, 242 CrossRef.
- R. L. Moreira, R. M. Almeida, K. P. F. Siqueira, C. G. Abreu and A. Dias, J. Phys. D: Appl. Phys., 2015, 49, 45305 CrossRef.
- E. C. Xiao, M. Liu, Q. Ren, Z. Cao, M. Guo, G. Dou, Z. M. Qi and F. Shi, Ceram. Int., 2020, 46, 15705–15708 CrossRef CAS.
- M. Salamanca, Y. E. Licea, A. Echavarría, A. C. Faro and L. A. Palacio, Phys. Chem. Chem. Phys., 2009, 11, 9583–9591 RSC.
- A. Chopelas, Phys. Earth Planet. Inter., 1996, 98, 3–15 CrossRef CAS.
- R. Lacomba-Perales, D. Martinez-Garciá, D. Errandonea, Y. Le Godec, J. Philippe and G. Morard, High Pressure Res., 2009, 29, 76–82 CrossRef CAS.
- L. Gan, T. Nishimura, S. A. Sheikh, I. Saeki and H. Murakami, Corros. Sci., 2020, 176, 109037 CrossRef CAS.
-
J. F. Nye, Physical properties of crystals. Their representation by tensors and matrices, Oxford University Press, Oxford, UK, 1985 Search PubMed.
- D. L. Shruthi, A. Jagannatha Reddy, G. N. Anil Kumar, C. K. Jayasankar and R. Hari Krishna, Mater. Res. Express, 2019, 6, 12 Search PubMed.
- M. G. Brik, V. Nagirnyi and M. Kirm, Mater. Chem. Phys., 2013, 137, 977–983 CrossRef CAS.
- Y. V. Pisarevskii, I. M. Silvestrova, R. Voszka, Péter, I. Földvári and J. Janszky, Phys. Status Solidi, 1988, 107, 161–164 CrossRef CAS.
- F. Mouhat and F. X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 4–7 CrossRef.
- G. Grimvall, B. Magyari-Köpe, V. Ozoliņš and K. A. Persson, Rev. Mod. Phys., 2012, 84, 945–986 CrossRef CAS.
- D. C. Wallace, Phys. Rev., 1967, 162, 776–789 CrossRef CAS.
- X. S. Zhao, S. L. Shang, Z. K. Liu and J. Y. Shen, J. Nucl. Mater., 2011, 415, 13–17 CrossRef CAS.
- G. N. Greaves, A. L. Greer, R. S. Lakes and T. Rouxel, Nat. Mater., 2011, 10, 823–837 CrossRef CAS PubMed.
- A. Muñoz and P. Rodríguez-Hernández, Crystals, 2018, 8, 10–12 CrossRef.
- S. Rajagopal, V. L. Bekenev, D. Nataraj, D. Mangalaraj and O. Y. Khyzhun, J. Alloys Compd., 2010, 496, 61–68 CrossRef CAS.
- R. Bharati, R. A. Singh and B. M. Wanklyn, J. Mater. Sci., 1981, 16, 775–779 CrossRef CAS.
- S. A. Razek, M. R. Popeil, L. Wangoh, J. Rana, N. Suwandaratne, J. L. Andrews, D. F. Watson, S. Banerjee and L. F. J. Piper, Electron. Struct., 2020, 2, 023001 CrossRef.
- M. A. P. Almeida, L. S. Cavalcante, C. Morilla-Santos, P. N. L. Filho, A. Beltrán, J. Andrés, L. Gracia and E. Longo, Mater. Charact., 2012, 73, 124–129 CrossRef CAS.
- D. J. Moss, E. Ghahramani, J. E. Sipe and H. M. van Driel, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1542–1560 CrossRef CAS PubMed.
- G. Hautier, A. Miglio, G. Ceder, G.-M. Rignanese and X. Gonze, Nat. Commun., 2013, 4, 2292 CrossRef PubMed.
- H. Zhang, L. Liu and Z. Zhou, Phys. Chem. Chem. Phys., 2012, 14, 1286–1292 RSC.
- Y. Yamada and Y. Kanemitsu, Appl. Phys. Lett., 2012, 101, 133907 CrossRef.
- K. Ding, B. Chen, Y. Li, Y. Zhang and Z. Chen, J. Mater. Chem. A, 2014, 2, 8294–8303 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00510c |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Plácida
Rodríguez-Hernández
*a,
Plácida
Rodríguez-Hernández
 b,
Alfonso
Muñoz
b,
Alfonso
Muñoz
 b,
Manuel Bajo
Buenestado
b,
Manuel Bajo
Buenestado
 a,
Catalin
Popescu
a,
Catalin
Popescu
 c and
Daniel
Errandonea
c and
Daniel
Errandonea
 a
a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol
ethanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water (MEW) mixture in the 16
water (MEW) mixture in the 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio as the pressure-transmitting medium (PTM). 2D diffraction images were taken on a Rayonix CCD detector, using a wavelength λ = 0.4246 Å and transformed to intensity-2θ patterns using DIOPTAS.21 Rietveld and Le Bail fits were performed using POWDER CELL.22 The Equation of State (EOS) of CoWO4 was calculated by fitting a 2nd order Birch–Murnaghan EOS to the pressure–volume data obtained from the HP experiments. Structure drawing and bond length measurements were performed with VESTA.23
1 volume ratio as the pressure-transmitting medium (PTM). 2D diffraction images were taken on a Rayonix CCD detector, using a wavelength λ = 0.4246 Å and transformed to intensity-2θ patterns using DIOPTAS.21 Rietveld and Le Bail fits were performed using POWDER CELL.22 The Equation of State (EOS) of CoWO4 was calculated by fitting a 2nd order Birch–Murnaghan EOS to the pressure–volume data obtained from the HP experiments. Structure drawing and bond length measurements were performed with VESTA.23
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11) and (111) reflections (at 8.34° and 8.35°, respectively); these appear clearly separated at 9.5 GPa. Similarly, the (002) and (021) peaks (9.84° and 9.88° at ambient pressure), which are strictly convoluted at low pressure, greatly increase their separation at higher pressure (see Fig. 3). In short, despite a steady increase of the monoclinic β angle, no phase transitions are detected in the studied pressure range. As we will see in the following, this conclusion is corroborated by Raman spectroscopy and theoretical simulations.
11) and (111) reflections (at 8.34° and 8.35°, respectively); these appear clearly separated at 9.5 GPa. Similarly, the (002) and (021) peaks (9.84° and 9.88° at ambient pressure), which are strictly convoluted at low pressure, greatly increase their separation at higher pressure (see Fig. 3). In short, despite a steady increase of the monoclinic β angle, no phase transitions are detected in the studied pressure range. As we will see in the following, this conclusion is corroborated by Raman spectroscopy and theoretical simulations.
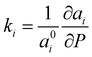 , for the aiaxis, a0i being the cell parameter at ambient pressure) can be studied from the linear fits of the cell parameters vs. pressure. The values in Table 3 show that the compressibility along the b axis is much higher than along the a and c axes. This anisotropic behavior, and the increase of the monoclinic angle, is commonly observed in wolframites, and has been reported previously for MgWO4, CdWO4 and MnWO4, among others.36–38
, for the aiaxis, a0i being the cell parameter at ambient pressure) can be studied from the linear fits of the cell parameters vs. pressure. The values in Table 3 show that the compressibility along the b axis is much higher than along the a and c axes. This anisotropic behavior, and the increase of the monoclinic angle, is commonly observed in wolframites, and has been reported previously for MgWO4, CdWO4 and MnWO4, among others.36–38![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ,0,4].39 To first order, the isothermal compressibility of CoWO4 is given by the trace of the compressibility tensor,
,0,4].39 To first order, the isothermal compressibility of CoWO4 is given by the trace of the compressibility tensor, 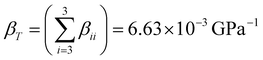 ,39 corresponding to an approximate value of the bulk modulus B0 = 150.76 GPa. For completeness, we also show the compressibility indicatrix, calculated using PASCal, in Fig. S1 (ESI†).40
,39 corresponding to an approximate value of the bulk modulus B0 = 150.76 GPa. For completeness, we also show the compressibility indicatrix, calculated using PASCal, in Fig. S1 (ESI†).40

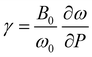 (Table 6). Minor discrepancies between theory and experiments are not unusual for wolframite-type compounds.38 For CoWO4, the phonons which appear to be more sensitive to pressure are the one at 244 cm−1 and the three in the range from 316 to 373 cm−1, with a value of γ well above 1 (Table 6). A similar situation is found in wolframite-type MgWO4, for which the highest Grüneisen parameters are low-frequency external modes within similar ranges.41 The data in Fig. 6 support the stability of wolframite-type CoWO4, as no qualitative differences are detectable among the Raman spectra at different pressure. Given that all phonons’ linear pressure coefficients are positive (Table 6), no vanishing or splitting phonons are found in the studied pressure range, confirming the absence of structural transitions. As shown in Fig. 7, all Raman modes consistently blueshift upon compression.
(Table 6). Minor discrepancies between theory and experiments are not unusual for wolframite-type compounds.38 For CoWO4, the phonons which appear to be more sensitive to pressure are the one at 244 cm−1 and the three in the range from 316 to 373 cm−1, with a value of γ well above 1 (Table 6). A similar situation is found in wolframite-type MgWO4, for which the highest Grüneisen parameters are low-frequency external modes within similar ranges.41 The data in Fig. 6 support the stability of wolframite-type CoWO4, as no qualitative differences are detectable among the Raman spectra at different pressure. Given that all phonons’ linear pressure coefficients are positive (Table 6), no vanishing or splitting phonons are found in the studied pressure range, confirming the absence of structural transitions. As shown in Fig. 7, all Raman modes consistently blueshift upon compression.





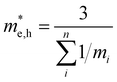 [a], where mi are the eigenvalues of the effective mass tensor. By following this procedure, we have determined that at ambient pressure
[a], where mi are the eigenvalues of the effective mass tensor. By following this procedure, we have determined that at ambient pressure 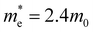 and
and 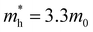 . The first value is very high in comparison with the typical electron-mobility of semiconductors suggesting that CoWO4 has a low performance as an n-type semiconductor. In contrast, the second value is comparable to the hole-mobility of the best p-type semiconductors.66 These observations are consistent with the experimental observation that un-doped CoWO4 is a p-type semiconductor.62 On the other hand, it is known that the relative ratio of effective mass determines the recombination rate of carriers.67 In our case
. The first value is very high in comparison with the typical electron-mobility of semiconductors suggesting that CoWO4 has a low performance as an n-type semiconductor. In contrast, the second value is comparable to the hole-mobility of the best p-type semiconductors.66 These observations are consistent with the experimental observation that un-doped CoWO4 is a p-type semiconductor.62 On the other hand, it is known that the relative ratio of effective mass determines the recombination rate of carriers.67 In our case 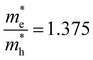 , which means that electrons and holes should easily recombine and show short lifetimes. Therefore, our study indicates that CoWO4 as the ideal band-gap energy to be used as a photocatalytic electrode; but also has the same limitations regarding photocurrent that a typical photocatalytic material as BiVO4 or TiO2 has.68,69
, which means that electrons and holes should easily recombine and show short lifetimes. Therefore, our study indicates that CoWO4 as the ideal band-gap energy to be used as a photocatalytic electrode; but also has the same limitations regarding photocurrent that a typical photocatalytic material as BiVO4 or TiO2 has.68,69



