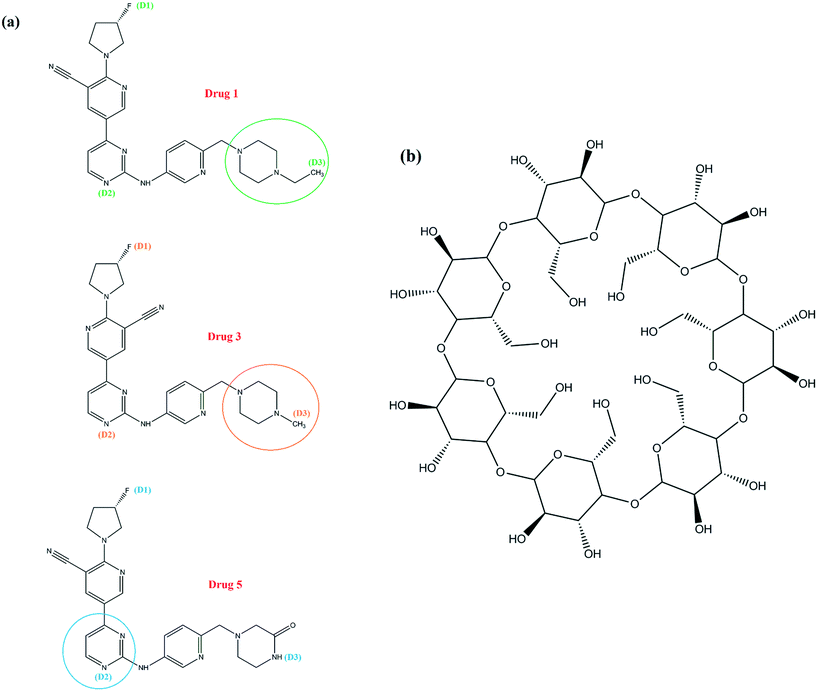
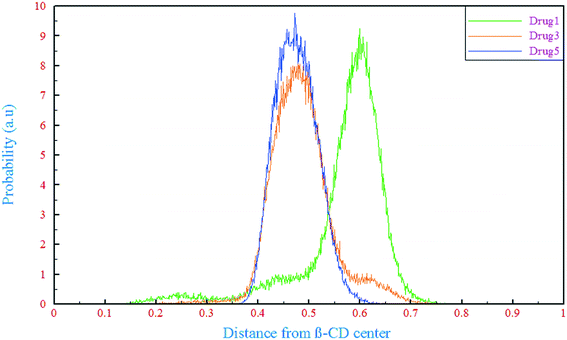
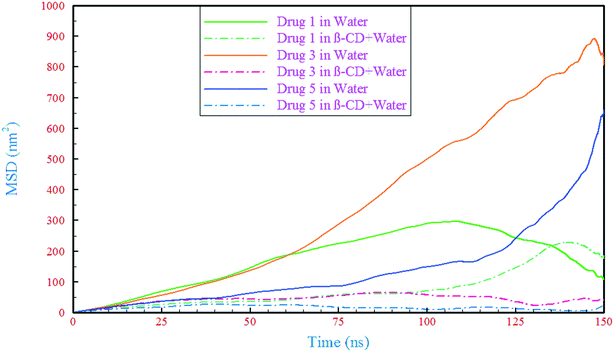
A detailed computational study on binding of kinase inhibitors into β-cyclodextrin: inclusion complex formation

Abstract

It is well known that the limited aqueous solubility of some drugs often reduces their bioavailability to targets. Inclusion complex formation of drugs with β-cyclodextrin is one of the best approaches for drug delivery improvement. Extensive microscopic molecular dynamics simulations were performed to study the interactions between β-cyclodextrin and a class of kinase inhibitor drugs. Solvation free energy calculations demonstrated that these drugs are insoluble in water and reinforced the need for a carrier to increase the solubility. The binding of these drugs into β-cyclodextrin was assessed by calculating the binding free energy, and it was found that all drugs tended to be bound thermodynamically. Examination of the dynamic properties showed that the drugs were loaded into β-cyclodextrin, so due to the loading of drugs into the β-cyclodextrin, the mean square displacement (MSD) of all the drugs drastically decreased. The loading of drugs was accompanied by pushing of water out of the center of the β-cyclodextrin cavity. The drugs showed different orientations and mechanisms for loading into β-cyclodextrin. By studying the root mean square fluctuation (RMSF), it was revealed that the drugs were flexible in interaction with β-cyclodextrin; in contrast, β-cyclodextrin retained its rigidity in all simulated systems.

---

Design, System, Application

In this work, the potential of theoretical approaches to study, build, and design a new inclusion complex based on β-cyclodextrin as a carrier and kinase inhibitors (three anti-cancer drugs as a guest) was investigated. This study introduces β-CD as an adequate carrier in the design of drug-delivery systems for these new kinase inhibitors, and examples can be found in the main text of the article. A new drug-delivery system is designed for this class of drugs, and dynamic and thermodynamic studies justify its efficacy and effectiveness. In brief, using theoretical tools, new “host–guest” supramolecular complexes were built and studied. This new design consists of an integrated system of drugs (guest) and a carrier (host) that can be used for drug-delivery of this category of drugs.

1. Introduction

The natural α-, β- and γ-cyclodextrins (CDs) are cyclic oligosaccharides that attracted considerable scientific attention because of their potential to improve the physicochemical stability, solubility, dissolution rate, and bioavailability of drugs. Because of the presence of CH₂ groups, there is a unique hydrophobic cavity in the core of their structures while the outer layer is mostly hydrophilic due to the primary and secondary hydroxyl groups.¹ Hence, CDs have a well-proven ability to trap or encapsulate other molecules which makes them a great choice to form “host–guest” supramolecular complexes.^2,3 CDs have been widely used to enhance the aqueous solubility of drugs, and ensure higher bioavailability and shelf-life of drugs as well as protecting susceptible drugs against hydrolysis, oxidation, and photodecomposition.^4–6 A drug delivery system is expected to deliver the required amount of drug to the targeted site for the necessary period of time, both efficiently and precisely. Different carrier materials are being constantly developed to overcome the undesirable properties of drug molecules. In this regard, CDs have been found as potential candidates because of the mentioned abilities.⁷ For example, it is well known that 18β-glycyrrhetinic acid (derived from licorice) has anti-inflammatory effects. The use of a complex of 18β-glycyrrhetinic acid and hydroxypropyl γ-cyclodextrin, to improve oral bioavailability, significantly increased the 18β-glycyrrhetinic acid concentration in the plasma of indomethacin treated mice, which in turn ameliorated the small intestinal injury caused by indomethacin administration.⁸

Various factors such as the chemical structures as well as physicochemical properties of both the drug and the CD, solvents, thermodynamic interactions between the CD, guest molecule and solvent, method of preparation, additives, temperature, etc. affected the inclusion complex formation. It has been proven that the structure of drug moieties has a key role in the formation of drug–CD complexes and should have certain characteristics such as a skeleton with more than 5 atoms (C, P, S, N) and less than 5 condensed rings, a melting point <250 °C and a structure with a key functional group (hydrophilic moiety) that causes drugs to be placed in the hydrophobic CD cavity.^9,10 Among the CDs, the extended use of β-CD and its derivatives as drug carriers is due to its cavity size and relative ease of chemical modification. β-CD has a relatively low solubility in water, compared with α- and γ-CDs that are nine and eleven times more soluble, respectively.^11,12

Over the past few years, structural and thermodynamics considering of drug–CD interactions in both experimental and theoretical studies have grown.^13–18 One of the most important classes of drugs are kinase inhibitors.^19,20 Kinases are enzymes that add phosphate groups (PO₄³⁻) to other molecules. A large protein complex mediates the phosphorylation of the inhibitor of kB (IκB), which results in the activation of nuclear factor κB (NF-κB). Two subunits of this complex, IκB kinase alpha (IKKα) and IκB kinase beta (IKKβ) that are serine kinases, are required for NF-κB activation.²¹ In addition, two protein kinases that exhibit structural similarity to IKKα and IKKβ are IKKε and TBK1 (TANK-binding kinase), which activate the critical interferon response factor 3 (IRF3) and IRF7.^22,23 There are multiple disease states that are mediated by IKKε, TBK1, and/or SIK2 mechanisms, and inhibition of these may have an impact on the treatment of various diseases like breast cancer, ovarian cancer, obesity, asthma, psoriasis, Crohn's disease, and septic shock.

Kinase inhibitors can be important treatments for human diseases and the field of kinase inhibitor chemistry is swiftly expanding, with the increase of innovation in preclinical target validation and medicinal chemistry, and supporting experimental and computational technologies emerging.²⁴ Kargbo²⁵ introduced six prominent compounds based on the 5-(pyrimidin-4-yl)-2-(pyrrolidin-1-yl)nicotinonitrile structure as inhibitors, which can affect IKKε, TBK1, and/or SIK2 activity and lead to the mentioned disease process, and reported their impact on the enzyme potency of the IKKε, TBK1 and/or SIK2 kinases including inhibition values, volume of distribution (V_D), and biological half-life (t_1/2). The results showed that these compounds can play a role in inhibition of the IKKε, TBK1 and SIK2 kinases.

Molecular dynamics (MD) simulations enable us to get a very detailed picture of molecular events and are powerful and precise tools that provide valuable complementary information about details of interactions between drug molecules and membranes, proteins, and CDs for experimental studies.^26–30 In this research, to get a detailed understanding based on molecular mechanisms, a theoretical study of the interactions between β-CD (as a carrier) and Kargbo's kinase inhibitors has been done.

2. Computational details

2.1 Molecular dynamics simulations

2.1.1 Simulation details. The molecular structures of the selected drugs and β-CD are shown in Fig. 1. The setup details of simulated systems, and the main skeleton of drugs are given (Fig. S2) in the ESI.† The selection of the drugs was based on quantum calculations, which is discussed in the ESI† as well. All molecular dynamics (MD) simulations were performed in the NPT ensemble using the GROMACS 5.1.1 package.³¹ The topology and coordinate files based on the GROMOS 54a7 force field^32,33 were used to describe the neutral form of both drug molecules and β-CD, and validation tests for structural parameters were performed in order to use this force field (Table S1†). All of the systems were hydrated by 4000 water molecules and with periodic boundary conditions in all three dimensions. For water molecules, the extended simple point charge model (SPC/E) was used.³⁴ In all systems, steepest descent energy minimization was used to remove undesirable atomic contacts and calm down the water molecules within the systems.³⁵ At first, the positions of drugs and β-CD were restrained and equilibration was conducted in the NVT ensemble for 1 ns and then followed by equilibration in the NPT ensemble for 9 ns. After the equilibration steps, all simulations were run for 150 ns from the starting conditions and coordinates of the atoms. All the bond lengths were constrained with the LINCS algorithm.³⁶ The temperature was set at 300 K by means of the V-rescale coupling method^37,38 with a time constant of 0.1 ps. The pressure was held constant at 1 bar using a compressibility of 4.5 × 10⁻⁵ bar⁻¹ and by coupling the simulation cell to a Parrinello–Rahman barostat, with a coupling time constant of 2 ps.³⁹ To integrate Newton's equations of motion, the leap-frog algorithm with a time step of 2 fs was applied.⁴⁰ The long-range Coulomb interaction was taken into account by means of the particle mesh Ewald (PME)⁴¹ technique and the cut-off distances for Coulomb interactions and van der Waals (vdW) interactions were both set to be 1 nm.

Fig. 1 Molecular structure of the three kinds of drugs (a) and β-CD (b).

2.1.2 Free energy computation details. The free energy differences between Hamiltonians at different values of λ were computed by using the Bennett acceptance ratio method (BAR),⁴² and a thermodynamic cycle based on alchemical free energy calculations⁴³ was used for calculation of binding free energy. We computed the free energy caused by the induction between the drug and its environment. The potential energy of interaction between the drug molecules and their environment is therefore slowly turned off using a λ parameter that goes from 0 to 1. Therefore, 21 λ points were employed for each ΔG_solv calculation. In order to prevent the unstable electrostatic interactions that cause unstable configurations and unreliable energies, electrostatic solute–solvent interactions were turned off with a larger λ at the beginning, compared to the vdW terms.⁴⁴ Hence, an even Δλ = 0.05 from 0 to 1 was used for vdW interactions, while for electrostatic interactions, at first Δλ = 0.1 was selected for decoupling. For the free energy calculations, the final configuration of each simulated system was used as the initial computing file (Fig. 2). To prevent the overlapping of solute–solvent atoms for low λ values, the soft-core potentials with α = 0.5, σ = 0.3, and p = 1 were employed. Each of these simulations were 5 ns long and the last 1 ns was used for extracting the free energy.

Fig. 2 Snapshots of the initial and final configurations of the drugs and β-CD.

2.2 Quantum details

All geometries were optimized using density functional theory (DFT) based on B3LYP and the standard 6-31+G(d) basis set.^45–47 The conductor-like polarizable continuum model (CPCM) was used to apply solvent effects of water.^48,49 To investigate the reactive sites of the structures for electrophilic and nucleophilic reactions, the molecular electrostatic potential (MEP) was studied using 6-31+G (d).^50,51 All calculations were performed using the Gaussian 03 program package.⁵²

3. Results and discussion

3.1 Inclusion complex formation: dynamic properties

3.1.1 Distance and orientation of drugs to β-CD. One of the important aspects of the dynamics of drug molecules in β-CD is their penetration through the middle of β-CD. The center of mass (COM) motion of the drug molecules relative to β-CD was observed and analyzed for this purpose, as shown in Fig. 3. In all of the β-CD/drug containing systems, the drug distances from the β-CD center were less than 6 Å where the averages for drugs 1, 3, and 5 were 5.68, 4.85, and 4.75 Å all the time, respectively. The distance of drug 5 is less than those of the two other drugs and it can be explained by the preferential orientation and entry angle of this drug into β-CD. As can be seen from Fig. 1, all the drugs have an L-shaped structure, but only drug 5 has entered from the apex (from the middle of the molecular structure which represents almost the center of mass) into β-CD, so it is expected that this drug has the lowest distance compared to the other ones. By considering the trajectories and final configurations of the β-CD/drug complexes, it was revealed that 21 atoms of drug 1 and 18 and 8 atoms of drug 3 and drug 5, respectively, entered into the β-CD cavity, as shown by the circles in Fig. 1. In order to study the flexibility of these drugs in interaction with β-CD, an angle was assigned between three atoms (D1, D2, and D3) of each drug and the average values during the simulation time in the β-CD/drug containing systems were compared with those in the drug-only containing systems, which are summarized in Table 1. As seen, the fluorine part of drug 1 and drug 3 interacts with the exterior wall of β-CD and loading occurs from the opposite side. Hence, due to the fact that the drugs are loaded into β-CD from one end of the drug, compared to the system including just the drug, the drug's flexibility has decreased for drugs1 and 3 in the presence of β-CD, so decrements from 60.44 to 53.36 and 67.14 to 65.53 were seen for drug 1 and drug 3, respectively. Meanwhile, the entry into β-CD for drug 5 occurs from the center of the molecular structure, and the two ends of the molecule are located outside of β-CD and allow interaction with the bulk water, which is therefore more flexible. So, an increase in the internal angle of the drug molecule is seen in the β-CD/drug5 containing system, compared to the drug 5-only containing system.

Fig. 3 Probability distribution of the distance between the drugs and the β-CD center.

Table 1 The average values of the inner angle for each drug molecule

Drugs	Drug 1	Drug 3	Drug 5
Systems
Drug + β-CD + water	53.36° (±0.65)	65.53° (±1.89)	86.93° (±3.49)
Drug + water	60.44° (±1.16)	67.14° (±1.16)	65.64° (±0.92)

---

3.1.2 Mean square displacement. To investigate the dynamic properties of drug influence on β-CD, we calculated the mean square displacement (MSD) of the drugs and β-CD. In order to obtain the diffusion coefficient of β-CD in the reference system (containing just β-CD/water), the time interval of 5–123 ns, where the MSD curve shows the closest behavior to being linear (Fig. S3†), was used for the slope fitting. Our result (0.294 × 10⁻⁹ m² s⁻¹) was of the same magnitude as the experimental data⁵³ and also in good agreement with the result of previous simulations.⁵⁴ The displacement of drugs in the water containing system has been compared with that of the complex (β-CD/drug) containing systems, Fig. 4. As can be seen, in all cases, the drugs exhibit a drastic reduction in their displacement after about 30 ns, which could be due to the drug loading into β-CD and represents the formation of a β-CD/drug complex. The lowest decrease in drug mobility is for drug 1 and the highest is for drug 5. It seems that in the formation of the complex, strong interaction between the drug and β-CD has led to an increase in the dynamic resistance of both the drug and β-CD, thus preventing the movement of both species. These observations are compatible with the formation of H-bonds (discussed in section 3.2.1). By comparing the results of Table 2 and Fig. 4, the reduction in the movement of the drugs is proportional to the number of H-bonds between the drugs and β-CD, as well as between the drugs and water molecules in the β-CD cavity. Therefore, the formation of more hydrogen bonds can be considered as one of the reasons for the lower mobility of drug 5 in the drug 5 containing system.

Fig. 4 The mean square displacement of the drugs in the simulated systems.

Table 2 Average number of different hydrogen bonds in the simulated systems

Systems	Number of H-bonds between β-CD and drug	Number of H-bonds between water and special part of drug	Number of H-bonds between water and drug
β-CD + drug 1 + water	0.390 (±0.030)	0.014 (±0.005)	1.990 (±0.028)
Drug 1 + water	—	0.081 (±0.006)	2.361 (±0.029)
β-CD + drug 3 + water	0.460 (±0.030)	0.021 (±0.003)	1.970 (±0.132)
Drug 3 + water	—	0.093 (±0.007)	1.226 (±0.018)
β-CD + drug 5 + water	0.847 (±0.090)	0.540 (±0.007)	2.660 (±0.029)
Drug 5 + water	—	0.917 (±0.019)	3.860 (±0.035)

---

3.1.3 Structural deviations. A comparison of the structural drift of β-CD and the drugs in the simulations provides information regarding the conformational stability and overall conformational motion on the timescale of the simulations. The structural drift was evaluated by calculating the root mean square deviation (RMSD) of β-CD and the drugs from the initiation of simulation (t = 0), as shown in Fig. 5. The average RMSD value for β-CD in the reference system was ∼0.11 nm, which is in agreement with a previous MD simulation study.⁵⁵ In all of the simulated systems, after a few nanoseconds from the beginning of simulations, small fluctuations in the RMSD of β-CD show that the simulations have reached well on the way to equilibration. The β-CD structure does not seem to differ significantly in all of the simulated systems and a similarity between all of the β-CD structures is seen. To get more details, the root-mean-square fluctuation (RMSF) was evaluated, as shown in Fig. 6. By considering all atoms, it is revealed that the flexibility of β-CD does not change significantly with the addition of different drugs (Fig. 6a). Checking the heavy atoms (Fig. S4†) showed that the carbon atom connected to the primary hydroxyl group (C6) and the oxygen atoms of all the OH groups (O2, O3, and O6) clearly exhibit larger RMSF values than the atoms of the inside of the rings, as shown in Fig. 6. Qualitatively, this observation is consistent with empirical findings.⁵⁶ Overall, it can be concluded that β-CD has a relative rigidity facing the drugs.

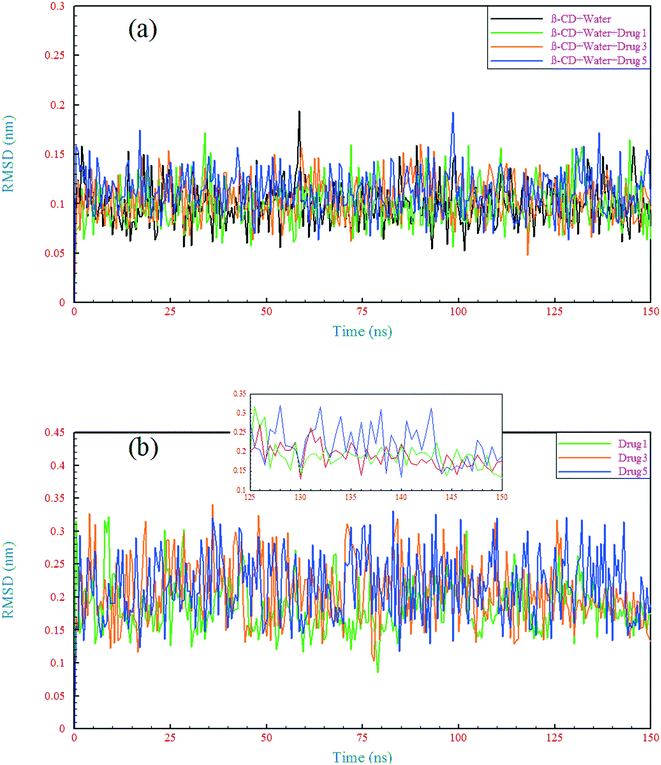Fig. 5 Root mean square deviation of the β-CD structure (a) and drugs (b) in different simulated systems as a function of time.

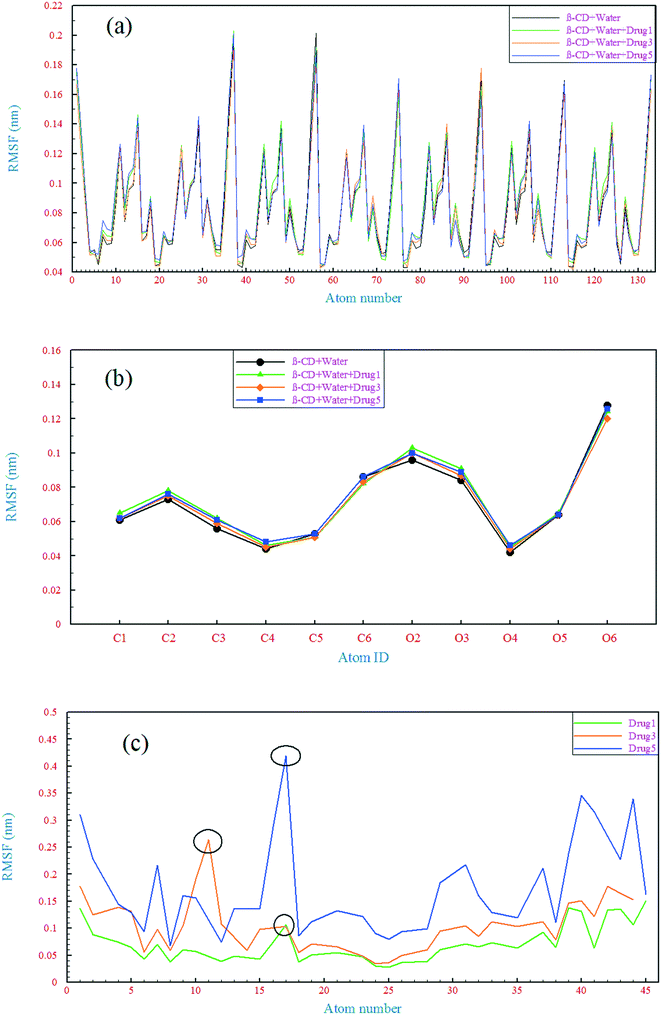Fig. 6 Root mean square fluctuation of all the β-CD atoms (a), heavy atoms of β-CD (b), and heavy atoms of the drugs (c).

The RMSD behavior of the drugs, however, is somewhat different; all the drugs have a relatively high RMSD until near the end of simulation (especially drug 5). As seen in Fig. 5b, in the last 6 ns of each simulation, the dynamic behavior of the drugs has stabilized and shows a small fluctuation around 0.18 nm, which can be regarded as a reason for the appropriate and final loading of the drug. Analyzing the RMSF of heavy atoms of the drugs showed that the highest RMSF, and therefore the highest flexibility among the drugs, is ascribed to drug 5. The highest RMSFs are seen in the atoms at the last two ends of the molecular structures. In the case of drug 5, these two ends have high values, which is in agreement with the results obtained from examining the internal angle of this drug in section 3.1.1, and evidence for this claim was discussed. Interestingly, the highest peak in the RMSF for drugs 3 and 5 is ascribed to nitrogen with a triple bond and of course one of the highest peaks for drug 1 belongs to this atom, as shown by the circles in Fig. 6c.

3.1.4 Solvent accessible surface area (SASA). The extent to which a drug interacts with its environment and solvent is naturally proportional to the degree to which it is exposed to these environments. In this regard, the solvent-accessible surface area (SASA) is an indicator of the accessibility of the surrounding solvent to a molecule.⁵⁷ In this study, the SASA for the complexes (β-CD/drug) was calculated in two different ways. In the first form, in the β-CD/drug containing system, the SASA was calculated for the complex and mentioned as “REAL” in Fig. 7. In the other form, the SASA of the drug in the drug-only containing system was calculated, and its value was added to the SASA value of β-CD in the reference system and was expressed as an expected assessment of the complex SASA, mentioned as “EXPECTED” in Fig. 7. Initial evaluation for all SASAs shows that the expected values are higher than the obtained values. It seems that the value of SASA in all systems has decreased due to the loading of the drugs inside the β-CD cavity and also due to the excretion of water molecules from the β-CD center. By examining the interaction energies between the components (Table 4), it was found that the contribution of vdW repulsion between water/drug and water/β-CD in the complex containing system significantly increased compared to that in the drug-only containing systems and reference system. Hence, the SASA for the complex in all complex containing systems is significantly lower than those expected.

Fig. 7 Time evolution of the SASA for the complex (β-CD/drug) in β-CD/drug containing systems (REAL) and expected SASA obtained from the sum of the related values in separate systems (EXPECTED).

3.2 Inclusion complex formation: thermodynamic properties

3.2.1 Hydrogen bonds and penetration of water. Regarding the hydrogen bonding formation ability of both the drugs and polar groups of β-CD, a competition between these molecules for hydrogen bonding formation with water molecules is inevitable. Therefore, the formation of different kinds of hydrogen bonds (H-bonds) between the drugs and β-CD, and the drugs and water molecules has been studied. In the present study, H-bonds are determined by a maximum distance of 3.5 Å between the acceptor and hydrogen and also a maximum angle of 30° between the acceptor-hydrogen and hydrogen-donor vectors.⁵⁸ The results of various kinds of H-bonds in the simulated systems are collected in Table 2. It seems that due to the presence of an oxygen atom in the structure of drug 5, more H-bonds have been formed between β-CD and the drug in the drug 5 containing system than those for drugs 1 and 3. One can see that there is a bit more hydrogen bonding between β-CD and the drug in the drug 3 containing system than in the drug 1 containing system which can be attributed to the lower distance (greater diffusion) of this drug from β-CD as shown in the previous section. The parts of the drugs that loaded into the β-CD cavity (indicated by the circles in Fig. 1) still have the ability to form H-bonds with water. Therefore, the presence of water molecules within the β-CD cavity can be deduced and these parts of the drugs revealed different numbers of hydrogen bonds. In drug 5, this part has the highest electronegativity compared to the other ones; hence, more hydrogen bonding is observed (0.54). Analysis of water molecules within the β-CD cavity was done by counting the number of water molecules in different spheres defined as a function of the distance to the COM of β-CD, as summarized in Table 3. The number of water molecules in the β-CD cavity is nearly the same as the experimental results (which is ∼11)⁵⁹ and the total number of water molecules is in excellent agreement with the results from previous simulations.⁶⁰ The results showed that the presence of drugs molecules caused a strong outflow of water molecules, in comparison with the reference system, in the innermost layer of the β-CD center (0–0.5 nm). The number of water molecules in the β-CD cavity center (0–0.5 nm) is in accordance with the loading and penetration of the drugs. As seen in the previous section, the penetration of 21 atoms of drug1 drives the highest number of water molecules out of the β-CD cavity center. But, due to the penetration of only 8 atoms of drug 5, the lowest number of water molecules is pushed out. In the next layer (0.5–0.8 nm), the lowest number of water molecules is ascribed to the drug 5 containing system. In this region, the middle part of the drug 5 molecular structure, that contains a ring, is located and it makes less space dynamically accessible to water molecules. These results are supported by radial distribution functions (RDFs) of water oxygen around β-CD, as shown in Fig. 8. For the reference system, the RDF is in excellent agreement with previous simulations,⁵⁵ with the maximum peak at around 0.2 nm. Herein, by adding each of the drugs, this peak disappeared, so it can be concluded that evacuation of water molecules from the center of the β-CD cavity occurred in all simulated systems. Although the presence of water molecules in the center of β-CD is still palpable, no other peaks can be seen up to a distance of about 1 nm. The value of RDF in the range of 0–0.5 nm is still higher for the drug 5 containing system than those for the two other systems. For the drug 3 containing system, it is also slightly higher than that for the drug 1 containing system, which is in agreement with the previous finding. In the range of 0.9–1 nm, which is outside β-CD, the first peak of RDF with values slightly lower than the reference system is observed for all simulated systems.

Table 3 Number of water molecules in different spheres inside β-CD

Distance	0–0.5 nm	0.5–0.8 nm	.8–0.9 nm	0.9–1.0 nm	0–1.0 nm (total)
Systems
β-CD + water (reference)	9.75 (±0.06)	20.59 (±0.07)	22.85 (±0.09)	46.84 (±0.11)	100.03 (±0.12)
β-CD + Drug 1 + water	0.77 (±0.03)	16.90 (±0.09)	21.17 (±0.10)	43.61 (±0.14)	82.45 (±0.15)
β-CD + Drug 3 + water	1.02 (±0.08)	16.55 (±1.08)	21.49 (±1.54)	44.43 (±1.33)	83.48 (±1.34)
β-CD + Drug 5 + water	1.97 (±0.05)	14.60 (±0.11)	21.04 (±0.10)	43.32 (±0.16)	80.93 (±0.17)

---

Fig. 8 Radial distribution function (RDF) of oxygen of water around β-CD in different simulated systems.

3.2.2 Chemical reactivity. Molecular electrostatic potential (MEP) maps are one of the best ways to describe the chemical reactivity of compounds. The different values of the electrostatic potential are symbolized by different colors at the MEP surface: red, blue and green represent the regions of most negative (electrophilic reactivity), most positive (nucleophilic reactivity) and zero electrostatic potential, respectively. The potential decreases in the order blue > green > yellow > orange > red.^61,62 Hence, MEP maps have been plotted for predicting the molecule reactivity towards the positively or negatively charged parts of β-CD, as depicted in Fig. 9. According to the MEP maps, because of the higher polarity at the fluorine part of the drugs and the secondary face (wide open) of β-CD, one can rather expect loading of the drugs into the secondary face (wide open) of β-CD to occur from the fluorine side of the drugs, while loading of the drugs into β-CD happened from a different side, as already seen. By examining the interaction energies between β-CD and the drugs (Table 4), it was found that the vdW contribution is much higher than that of electrostatics. Therefore, in drug loading, it was the vdW interactions that determine the direction and entry of the drug into the secondary face of β-CD. Hence, loading of the drugs occurred from the green parts, which are the most neutral regions in the MEPs.

Fig. 9 Molecular electrostatic potential (MEP) maps formed by mapping of total density over electrostatic potential for β-CD from the secondary face (wide open) (a), drug 1 (b), drug 3 (c), and drug 5 (d).

Table 4 Analysis of energies in the different simulated systems

Energies (kJ mol^−1)	Coulombic between water and drug	vdW between water and drug	Coulombic between water and β-CD	vdW between water and β-CD	Coulombic between drug and β-CD	vdW between drug and β-CD	Free energy of solvation	Free energy of binding
Systems
β-CD + drug 1 + water	−35.57 (±0.22)	−107.07 (±0.13)	−204.18 (±1.50)	−211.89 (±0.25)	−9.18 (±0.25)	−136.52 (±0.58)	—	−72.10 (±1.12)
Drug 1 + water	−48.52 (±0.44)	−162.32 (±2.30)	—	—	—	—	42.64 (±0.56)	—
β-CD + drug 3 + water	−35.70 (±0.89)	−103.59 (±1.90)	−204.41 (±1.30)	−217.31 (±0.45)	−7.83 (±0.26)	−128.46 (±1.10)	—	−62.41 (±1.56)
Drug 3 + water	−29.00 (±0.12)	−141.12 (±0.83)	—	—	—	—	43.05 (±0.99)	—
β-CD + drug 5 + water	−52.58 (±0.57)	−100.00 (±0.66)	−204.63 (±1.10)	−220.69 (±0.59)	−9.53 (±0.17)	−120.34 (±0.61)	—	−49.08 (±1.69)
Drug 5 + water	−76.50 (±0.41)	−153.24 (±1.10)	—	—	—	—	20.04 (±0.34)	—
β-CD + water	—	—	−253.17 (±1.20)	−292.04 (±0.45)	—	—	—	—

---

3.2.3 Solvation and binding free energy. The solvation free energy (ΔG_solv) values of the drugs were calculated using the BAR method, as described above, and are summarized in Table 4. Since the drugs have multiple aromatic rings and a hydrophobic structure, the ΔG_solv values of all of them are positive. The main skeletons of all the drugs are similar, with the only difference being at the end of the structure and the presence of an oxygen atom in drug 5 instead of hydrophobic ethyl and methyl groups in drugs 1 and 3, respectively. Compared to drugs 1 and 3, drug 5 is more polar due to this oxygen atom, and this is reflected in its H-bonds. So, the number of H-bonds between drug 5 and water in the drug-only containing system (∼3.86) is significantly higher than that in the other two, as seen in Table 2. Therefore, the ΔG_solv of drug 5 in water solvent is remarkably less positive (∼20.04 kJ mol⁻¹). Another key factor can be total interaction energy between drug 5 and water (∼−229.74 kJ mol⁻¹), in which those for drug 1 (∼−210.84 kJ mol⁻¹) and drug 3 (∼−170.12 kJ mol⁻¹) are less negative. This relatively makes drug 5 thermodynamically more favorable to dissolving in the water phase. A similar discussion can be made to compare the difference between ΔG_solv in drugs 1 and 3. Drug 1 provides a few more H-bonds with water (∼1.99 with less error), and also its total interaction energy with water is more negative in value compared to that of drug 3. So, the ΔG_solv of drug 1 is quite similar to that of drug 3, but still is a bit more positive. It has been reported that enhancing lipophilicity can increase the volume of distribution (V_D),⁶³ because drugs with a high lipid solubility have lower plasma protein binding capabilities and higher V_D.⁶⁴ Besides, acids mostly show low V_D.⁶³ Electronegativity can be related to the acidity of molecules. Small values of electronegativity characterize bases (Lewis base), and large values represent acids (Lewis acid).⁶⁵ The electronegativity values obtained by quantum calculations are 3.867, 3.877, and 4.019 for drug 1, drug 3, and drug 5 respectively. Drug 5 with the highest electronegativity value can act as a Lewis acid and has the highest solubility in water as a Lewis base; hence, it can dissolve in water more easier than the other drugs. In addition, the MEP images for the mentioned drugs mostly demonstrate green and blue colors with neutral charges and positive charges which represent the hydrophobicity of the structures, and their low tendency to dissolve in water. However, because of the existing oxygen atom (red color) in drug 5, it has a more negative charge distribution than drug 1 and drug 3 that shows its highest electronegativity, highest solubility in water, and lowest V_D. Also, there is a direct connection between V_D and biological half-life (t_1/2), in fact, the greater V_D caused the longer t_1/2, because of lower plasma protein binding.⁶⁶ Accordingly, both the V_D and t_1/2 values from the experimental results match with the electronegativity and MEP images.

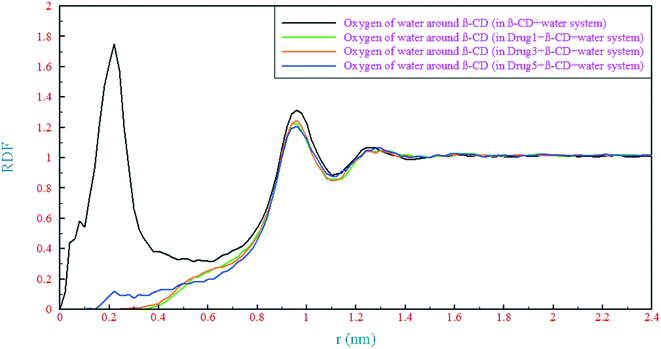
Moreover, the findings about the solvation free energies in water are in good agreement with the experimental observations related to the V_D and t_1/2 of the drugs, so it is determined that among the three drugs, the highest V_D and t_1/2 are ascribed to drug 3 and the lowest ones are ascribed to drug 5.²⁵ In fact, drug 3 tends to dissolve in fat more than the other two drugs. The study of free energy can be an approach to assess the metabolism and excretion of these drugs, so a suitable carrier can increase or decrease their dissolution in adipose tissue. From the results of this section, it can be seen that the formation of drug/β-CD complexes is highly thermodynamically desirable and therefore the formation of these complexes can increase the concentration of these drugs in plasma and reduce their metabolism and excretion.

The ability of a drug molecule to bind into β-CD in aqueous solution is expected to be related to its binding free energy (ΔG_bind). Results show that the ΔG_bind for drug 1 (∼−72.10 kJ mol⁻¹) is more negative than those for drugs 3 and 5 (∼−62.41 and −49.08 kJ mol⁻¹, respectively). As discussed before, all the drugs are hydrophobic and the same goes for the cavity of β-CD. Thus, all three drugs tend to be loaded inside the cavity. Compared to drugs 3 and 5, drug 1 has an ethyl chain in its structure which makes it more favorable for inclusion into the β-CD cavity. Drug 3 has a methyl group that makes it less polar than drug 5. Finally, the most positive value of ΔG_bind is associated with drug 5, which has higher polarity resulting from the oxygen atom in its structure. Another important parameter that affected the loading of drugs is the total interaction energy between drug 5 and β-CD, as seen in Table 4. Thermodynamically, the greatest tendency to bind to β-CD is ascribed to drug 1 and the total interaction energy value between drug 1 and β-CD (∼−145.7 kJ mol⁻¹) is higher than those for drugs 3 and 5 (∼−136.29 and −129.87 kJ mol⁻¹, respectively). Finally, a supplementary discussion based on molecular structure and charge distributions from a quantum point of view is presented to describe the free energy behavior of the simulated systems (section 6 in the ESI†).

4. Conclusion

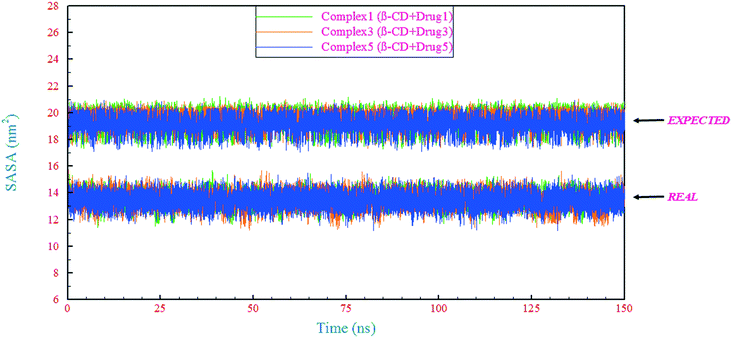
A theoretical study of inclusion complexes of β-cyclodextrin with kinase inhibitors was done. According to the results, the drugs showed different mechanisms of loading into β-cyclodextrin, in which drugs 1 and 3 were loaded from the end of the opposite side of the fluorine, while drug 5 was loaded from the middle of the molecular structure. The outflow of water molecules from the center of the β-CD cavity was proportional to the amount of penetration of each drug. In comparison to those in the drug-only containing systems, the drugs' RMSDs in all of the complex containing systems were reduced and these reductions in mobility of the drugs are related to the formation of H-bonds between the drugs and β-CD, and also between the drugs and water molecules in the β-CD cavity. Considering the RMSDs as well as RMSFs for the β-CD structure in the different simulated systems revealed that the β-CD structure was almost inflexible in interaction with the drugs. Analyzing the RMSF of heavy atoms of the drugs showed that the highest flexibility was ascribed to drug 5, and in all drugs, the nitrogen atom with a triple bond had great flexibility. By calculation of SASA, it was found that the vdW repulsions between water/drug and water/β-CD in the different kinds of systems can cause a reduction in SASA of the complex.

Solvation free energy analysis showed that all three drugs were hydrophobic and they need a carrier, with drug 3 (43.05 kJ mol⁻¹) being the most hydrophobic, and drug 5 (20.04 kJ mol⁻¹) having the greatest tendency to dissolve in water. However, due to the presence of an ethyl group at the end of the molecular structure of drug 1 and an oxygen atom at the end of drug 5's molecular structure, drug 1 and drug 5 showed the most negative (−72.10 kJ mol⁻¹) and the least negative (−49.08 kJ mol⁻¹) binding free energy, respectively. These results are supported by the same trend in total interaction energies.

5. Conflicts of interest

There are no conflicts to declare.

References

1. M. I. Sancho, S. Andujar, R. D. Porasso and R. D. Enriz, Theoretical and experimental study of inclusion complexes of β-cyclodextrins with chalcone and 2′, 4′-dihydroxychalcone, J. Phys. Chem. B, 2016, 120, 3000–3011.
2. G. Crini, A history of cyclodextrins, Chem. Rev., 2014, 114, 10940–10975.
3. H. Shelley and R. J. Babu, Role of cyclodextrins in nanoparticle-based drug delivery systems, J. Pharm. Sci., 2018, 107, 1741–1753.
4. F. Hirayama and K. Uekama, Cyclodextrin-based controlled drug release system, Adv. Drug Delivery Rev., 1999, 36, 125–141.
5. A. L. Laza-Knoerr, R. Gref and P. Couvreur, Cyclodextrins for drug delivery, J. Drug Targeting, 2010, 18, 645–656.
6. V. J. Stella and R. A. Rajewski, Cyclodextrins: their future in drug formulation and delivery, Pharm. Res., 1997, 14, 556–567.
7. G. Tiwari, R. Tiwari and A. K. Rai, Cyclodextrins in delivery systems: Applications, J. Pharm. BioAllied Sci., 2010, 2, 72.
8. T. Ishida, I. Miki, T. Tanahashi, S. Yagi, Y. Kondo, J. Inoue, S. Kawauchi, S. Nishiumi, M. Yoshida and H. Maeda, Effect of 18β-glycyrrhetinic acid and hydroxypropyl γcyclodextrin complex on indomethacin-induced small intestinal injury in mice, Eur. J. Pharmacol., 2013, 714, 125–131.
9. T. Loftsson, H. H. Sigurđsson, M. Másson and N. Schipper, Preparation of solid drug/cyclodextrin complexes of acidic and basic drugs, Die Pharmazie - An International Journal of Pharmaceutical Sciences, 2004, 59, 25–29.
10. S. Jacob and A. B. Nair, Cyclodextrin complexes: Perspective from drug delivery and formulation, Drug Dev. Res., 2018, 79, 201–217.
11. R. Estrada III and G. Vigh, Comparison of charge state distribution in commercially available sulfated cyclodextrins used as chiral resolving agents in capillary electrophoresis, J. Chromatogr. A, 2012, 1226, 24–30.
12. K. J. Naidoo, J. Y.-J. Chen, J. L. M. Jansson, G. Widmalm and A. Maliniak, Molecular properties related to the anomalous solubility of β-cyclodextrin, J. Phys. Chem. B, 2004, 108, 4236–4238.
13. M. R. Caira, S. A. Bourne, H. Samsodien and V. J. Smith, Inclusion complexes of 2-methoxyestradiol with dimethylated and permethylated β-cyclodextrins: models for cyclodextrin–steroid interaction, Beilstein J. Org. Chem., 2015, 11, 2616–2630.
14. A. Semalty, Y. S. Tanwar and M. Semalty, Preparation and characterization of cyclodextrin inclusion complex of naringenin and critical comparison with phospholipid complexation for improving solubility and dissolution, J. Therm. Anal. Calorim., 2014, 115, 2471–2478.
15. S. K. Upadhyay and S. M. Ali, Solution structure of loperamide and β-cyclodextrin inclusion complexes using NMR spectroscopy, J. Chem. Sci., 2009, 121, 521–527.
16. W. Sangpheak, W. Khuntawee, P. Wolschann, P. Pongsawasdi and T. Rungrotmongkol, Enhanced stability of a naringenin/2, 6-dimethyl β-cyclodextrin inclusion complex: Molecular dynamics and free energy calculations based on MM-and QM-PBSA/GBSA, J. Mol. Graphics Modell., 2014, 50, 10–15.
17. B. Nutho, W. Khuntawee, C. Rungnim, P. Pongsawasdi, P. Wolschann, A. Karpfen, N. Kungwan and T. Rungrotmongkol, Binding mode and free energy prediction of fisetin/β-cyclodextrin inclusion complexes, Beilstein J. Org. Chem., 2014, 10, 2789–2799.
18. C. Rungnim, S. Phunpee, M. Kunaseth, S. Namuangruk, K. Rungsardthong, T. Rungrotmongkol and U. Ruktanonchai, Co-solvation effect on the binding mode of the α-mangostin/β-cyclodextrin inclusion complex, Beilstein J. Org. Chem., 2015, 11, 2306–2317.
19. W. W. Feng and M. Kurokawa, Lipid metabolic reprogramming as an emerging mechanism of resistance to kinase inhibitors in breast cancer, Cancer Drug Resist., 2019, 1–17.
20. P. Wu, T. E. Nielsen and M. H. Clausen, Small-molecule kinase inhibitors: an analysis of FDA-approved drugs, Drug Discovery Today, 2016, 21, 5–10.
21. M. J. Bloom, S. D. Saksena, G. P. Swain, M. S. Behar, T. E. Yankeelov and A. G. Sorace, The effects of IKK-beta inhibition on early NF-kappa-B activation and transcription of downstream genes, Cell. Signalling, 2019, 55, 17–25.
22. K.-J. Han, X. Su, L.-G. Xu, L.-H. Bin, J. Zhang and H.-B. Shu, Mechanisms of the TRIF-induced interferon-stimulated response element and NF-κB activation and apoptosis pathways, J. Biol. Chem., 2004, 279, 15652–15661.
23. S. Ning, J. S. Pagano and G. N. Barber, IRF7: activation, regulation, modification and function, Genes Immun., 2011, 12, 399–414.
24. F. M. Ferguson and N. S. Gray, Kinase inhibitors: the road ahead, Nat. Rev. Drug Discovery, 2018, 17, 353.
25. R. B. Kargbo, Kinase Inhibitors for Treatment of Cancer and Inflammation, 2018.
26. M. Fermeglia, M. Ferrone, A. Lodi and S. Pricl, Host–guest inclusion complexes between anticancer drugs and β-cyclodextrin: computational studies, Carbohydr. Polym., 2003, 53, 15–44.
27. K. Azizi and M. Ganjali Koli, Molecular dynamics simulations of Oxprenolol and Propranolol in a DPPC lipid bilayer, J. Mol. Graphics Modell., 2016, 64, 153–164.
28. M. Ganjali Koli and K. Azizi, The partition and transport behavior of cytotoxic ionic liquids (ILs) through the DPPC bilayer: insights from molecular dynamics simulation, Mol. Membr. Biol., 2017, 33, 64–75,  DOI:10.1080/09687688.2017.1384859.
29. M. G. Koli and K. Azizi, Investigation of benzodiazepines (BZDs) in a DPPC lipid bilayer: Insights from molecular dynamics simulation and DFT calculations, J. Mol. Graphics Modell., 2019, 90, 171–179.
30. H. Aghazadeh, M. Ganjali Koli, R. Ranjbar and K. Pooshang Bagheri, Interactions of GF-17 derived from LL-37 antimicrobial peptide with bacterial membranes: a molecular dynamics simulation study, J. Comput.-Aided Mol. Des., 2020, 34, 1261–1273.
31. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1, 19–25.
32. A. K. Malde, L. Zuo, M. Breeze, M. Stroet, D. Poger, P. C. Nair, C. Oostenbrink and A. E. Mark, An automated force field topology builder (ATB) and repository: version 1.0, J. Chem. Theory Comput., 2011, 7, 4026–4037.
33. M. Stroet, B. Caron, K. M. Visscher, D. P. Geerke, A. K. Malde and A. E. Mark, Automated topology builder version 3.0: prediction of solvation free enthalpies in water and hexane, J. Chem. Theory Comput., 2018, 14, 5834–5845.
34. H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91, 6269–6271.
35. J. Snyman, Practical mathematical optimization: an introduction to basic optimization theory and classical and new gradient-based algorithms, Springer Science & Business Media, 2005.
36. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, LINCS: a linear constraint solver for molecular simulations, J. Comput. Chem., 1997, 18, 1463–1472.
37. A. Baumketner, Removing systematic errors in interionic potentials of mean force computed in molecular simulations using reaction-field-based electrostatics, J. Chem. Phys., 2009, 130, 104106.
38. G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126, 14101.
39. M. Parrinello and A. Rahman, Crystal structure and pair potentials: A molecular-dynamics study, Phys. Rev. Lett., 1980, 45, 1196.
40. R. W. Hockney, S. P. Goel and J. W. Eastwood, Quiet high-resolution computer models of a plasma, J. Comput. Phys., 1974, 14, 148–158.
41. T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An N· log (N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092.
42. C. H. Bennett, Efficient estimation of free energy differences from Monte Carlo data, J. Comput. Phys., 1976, 22, 245–268.
43. D. L. Mobley, J. D. Chodera and K. A. Dill, On the use of orientational restraints and symmetry corrections in alchemical free energy calculations, J. Chem. Phys., 2006, 125, 84902.
44. A. Rizzi, T. Jensen, D. R. Slochower, M. Aldeghi, V. Gapsys, D. Ntekoumes, S. Bosisio, M. Papadourakis, N. M. Henriksen and B. L. De Groot, The SAMPL6 SAMPLing challenge: Assessing the reliability and efficiency of binding free energy calculations, J. Comput.-Aided Mol. Des., 2020, 1–33.
45. P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136, B864.
46. B. Miehlich, A. Savin, H. Stoll and H. Preuss, Results obtained with the correlation energy density functionals of Becke and Lee, Yang and Parr, Chem. Phys. Lett., 1989, 157, 200–206.
47. R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford Univ Press, New York, 1989.
48. M. Cossi, V. Barone, B. Mennucci and J. Tomasi, Ab initio study of ionic solutions by a polarizable continuum dielectric model, Chem. Phys. Lett., 1998, 286, 253–260.
49. M. Cossi, N. Rega, G. Scalmani and V. Barone, Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model, J. Comput. Chem., 2003, 24, 669–681.
50. T. Lu, Multiwfn. Version 3.2.1, A multifunctional wavefunction analyzer, 2013, (n.d.).
51. T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
52. M. J. Frisch and A. B. Nielsen, Gaussian 03 Programmer's Reference, Gaussian, 2003.
53. A. C. F. Ribeiro, D. G. Leaist, M. A. Esteso, V. M. M. Lobo, A. J. M. Valente, C. I. A. V. Santos, A. M. Cabral and F. J. B. Veiga, Binary mutual diffusion coefficients of aqueous solutions of β-cyclodextrin at temperatures from 298.15 to 312.15 K, J. Chem. Eng. Data, 2006, 51, 1368–1371.
54. W. Khuntawee, P. Wolschann, T. Rungrotmongkol, J. Wong-Ekkabut and S. Hannongbua, Molecular dynamics simulations of the interaction of beta cyclodextrin with a lipid bilayer, J. Chem. Inf. Model., 2015, 55, 1894–1902.
55. C. Cézard, X. Trivelli, F. Aubry, F. Djedaïni-Pilard and F.-Y. Dupradeau, Molecular dynamics studies of native and substituted cyclodextrins in different media: 1. Charge derivation and force field performances, Phys. Chem. Chem. Phys., 2011, 13, 15103–15121.
56. J. E. H. Koehler, W. Saenger and W. F. Van Gunsteren, Molecular dynamics simulation of crystalline β-cyclodextrin dodecahydrate at 293 K and 120 K, Eur. Biophys. J., 1987, 15, 211–224.
57. T. Ooi, M. Oobatake, G. Nemethy and H. A. Scheraga, Accessible surface areas as a measure of the thermodynamic parameters of hydration of peptides, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 3086–3090.
58. D. van der Spoel, P. J. van Maaren, P. Larsson and N. Timneanu, Thermodynamics of hydrogen bonding in hydrophilic and hydrophobic media, J. Phys. Chem. B, 2006, 110, 4393–4398.
59. G. Crini, S. Fourmentinn and E. Lichtfouse, Cyclodextrin Fundamentals, Reactivity and Analysis, 2018, p. 262,  DOI:10.1007/978-3-319-76159-6.
60. E. Mixcoha, J. Campos-Terán and A. Piñeiro, Surface adsorption and bulk aggregation of cyclodextrins by computational molecular dynamics simulations as a function of temperature: α-CD vs β-CD, J. Phys. Chem. B, 2014, 118, 6999–7011.
61. E. Khan, A. Shukla, A. Srivastava and P. Tandon, Molecular structure, spectral analysis and hydrogen bonding analysis of ampicillin trihydrate: a combined DFT and AIM approach, New J. Chem., 2015, 39, 9800–9812.
62. S. Shahab, M. Sheikhi, L. Filippovich, R. Alnajjar, Z. Ihnatovich, K. Laznev, A. Strogova, M. Atroshko and M. Drachilovskaya, Quantum-chemical modeling, spectroscopic (FT-IR, excited states, UV/Vis, polarization, and Dichroism) studies of two new benzo [d] oxazole derivatives, J. Mol. Struct., 2020, 1202, 127352.
63. D. A. Smith, K. Beaumont, T. S. Maurer and L. Di, Volume of distribution in drug design: Miniperspective, J. Med. Chem., 2015, 58, 5691–5698.
64. J. E. Hall, Guyton and Hall textbook of medical physiology e-Book, Elsevier Health Sciences, 2015.
65. R. G. Pearson, Absolute electronegativity and hardness correlated with molecular orbital theory, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 8440–8441.
66. S. Kirshblum and V. W. Lin, Spinal cord medicine, Springer Publishing Company, 2018.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0me00140f

---