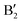Valley polarization caused by crystalline symmetry breaking†
Yuanyuan
Wang
,
Wei
Wei
 *,
Fengping
Li
,
Xingshuai
Lv
,
Baibiao
Huang
*,
Fengping
Li
,
Xingshuai
Lv
,
Baibiao
Huang
 and
Ying
Dai
and
Ying
Dai
 *
*
School of Physics, State Key Laboratory of Crystal Materials, Shandong University, Jinan 250100, China. E-mail: weiw@sdu.edu.cn; daiy60@sdu.edu.cn
First published on 29th October 2020
Abstract
In two-dimensional (2D) hexagonal lattices with inversion asymmetry, time-reversal (T) connected valleys are at the center of current valleytronic research. In order to trigger valley polarization, dynamical processes and/or magnetism have been considered. In this work, we propose a new mechanism, valley-contrasting sublattice polarization (VCSP), to polarize valleys by reducing the crystalline symmetry that connects the valleys. In our mechanism, significant valley polarization could be readily generated without magnetism, an electric field, or an optical process. Based on tight-binding model analysis and first-principle calculations, the control of valley polarization via crystalline symmetry can be successfully realized in concrete LaOBiS2 polytypes with Peierls-like structure distortion. Our results provide an unprecedented possibility for exploring valley-contrasting physics.
New conceptsBased on our proposed valley-contrasting sublattice polarization mechanism, we report for the first time the role played by crystallographic symmetry, rather than time-reversal asymmetry, in introducing valley polarization. Using this new mechanism, evident valley polarization could be readily generated without magnetism, electric fields, or optical processes. Tight-binding model analysis and first-principles calculations confirm that LaOBiS2 is a concrete and ideal carrier to translate the new valley polarization paradigm to practical applications, suggesting high experimental possibility. Therefore, we believe that these intriguing findings will spark great attention in the field of valleytronics. |
Introduction
In addition to the charge and spin degrees of freedom, valleys, i.e., the multiple energy extrema of the conduction and valence bands in momentum space, represent an emergent degree of freedom with which low-energy electrons can also be endowed. Valleytronics is analogous to spintronics, which utilizes the spin degree of freedom, as the valley degree of freedom can also be manipulated to encode, process and store information.1–7 In recent years, the study of valleytronics has flourished with the accessibility of group-VI transition metal dichalcogenides (TMDCs, such as MoS2, WS2, and WSe2)1,8–12 in which two inequivalent valleys, K and K′, are connected by time-reversal symmetry (T).In two-dimensional (2D) hexagonal lattices with inversion symmetry breaking, the functions of the K and K′ valleys are odd under T, and, therefore, opposite Berry curvatures and orbital magnetic moments are assigned to them.13 Thus, in order to use the valley index as an information carrier, several strategies have been proposed, such as dynamical processes,12,14–19 magnetic fields, magnetic doping and the magnetic proximity effect.20–28 From a device applications point of view, static methods are preferred over dynamical processes, and magnetic regulation usually weakens the device performance due to the unavailability of a large external magnetic field, clustering effect, and impurity scattering. In this respect, 2D ferrovalley materials with spontaneous valley polarization due to the intrinsic magnetism caused by T breaking have been proposed to overcome these challenges.29–31 However, the few existing materials still suffer from many drawbacks, including insufficient valley polarization,29,30 and the ferromagnetic ground state of 2D structures is still controversial.31
Compared to magnetic and optical control, the use of fully electric field control with existing semiconductor technology to achieve valley polarization is more promising. However, it is evident that under the existing spin–valley coupling paradigm, an electric field cannot couple to valleys since it cannot break the T. In order to realize electric control of valley polarization, a so-called valley-layer coupling (VLC) mechanism was proposed, in which direct interactions between valleys and external gate electric fields were introduced.32 In this case, crystalline symmetry, instead of T, connects the inequivalent valleys. The application of a gate electric field for external regulation still presents the problem of power consumption, and adequate materials are scarce. The electric control of valley polarization thus remains greatly challenging, and it is still highly desirable to search for an unpresented way to realize valley polarization in easily accessible materials.
In this work, we propose a tantalizing design principle for valley polarization deprecating the use of an external field, magnetism, or circularly polarized light to tackle these challenges. A new coupling mechanism, which we refer to as valley-contrasting sublattice polarization (VCSP), is proposed. In the paradigm in which valleys are connected by crystalline symmetry instead of T, p4mm (LG 55) can be added to the set of layer groups that meet the requirements, and model analysis confirms the feasibility of our VCSP mechanism to achieve valley polarization. In accordance with the symmetry requirement for our VCSP mechanism, specific materials were used to prove our idea via model analysis and first-principles calculations (calculation details can be found in the ESI†). The results shown that robust valley polarization can be achieved by VCSP, and our results thus enrich the significant new arena of symmetry-controlled valley-contrasting physics.
Results and discussion
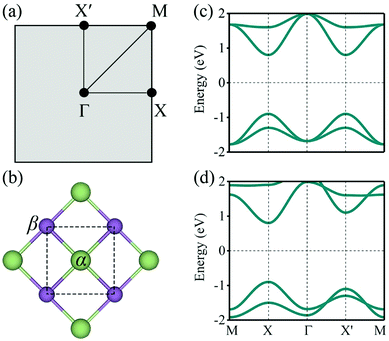
In order to gain deep insight into the symmetry requirements for systems with symmetry-controlled valley polarization, it is necessary to clarify the difference between the patterns of valleys connected by T and by crystalline symmetry. In the 2D hexagonal Brillouin zone of nonmagnetic TMDCs with D3h symmetry, for example, band edges are located at the K and K′ points. In the light of the C3 symmetry operation of D3h, the time-reversal point of K (i.e., −K) is equivalent to K′. The T and inversion asymmetry guarantee opposite Berry curvature and energy degeneracy between the K and K′ points. In this case, valley polarization can be achieved by T breaking. On the other hand, in order to remove the energy degeneracy of two inequivalent valleys by reducing the crystalline symmetry rather than T breaking, two inequivalent valleys must be located at the same time-reversal invariant momentum (TRIM) point, Fig. 1(a). In this situation, the crystalline symmetry operation U guarantees that they are degenerate in energy. As shown in Fig. 1(b), we find that 2D materials with a square lattice consisting of two sublattices can meet the basic symmetry requirements, provided that X and X′ occur at the requested TRIM point.32 It is evident that 2D materials with the layer group p4mm would be a rational choice, where X and X′ are connected by {C4z|000} or {m1–10|000}, rather than T.Based on the above analysis, an effective model was developed to discuss our new design principle to realize valley polarization. As Fig. 1(b) shows, a single-layer checkerboard lattice with p4mm symmetry was considered as a prototype structure. Here, it is assumed that low-energy physics occurs at the point X (X′) with little group C2v, with the conduction band minimum (CBM) and valence band maximum (VBM) corresponding to the one-dimensional representation B1 or B2, respectively. Therefore, the px (py) orbitals of the different sublattices (α and β) contribute to the CBM and VBM at the point X (X′), and the basis states are chosen to be |μ,pi,k〉, where μ ∈ {α,β} and i ∈ {x,y} represent the different sublattices and atomic orbitals, respectively. By considering the orbital interaction without spin–orbit coupling (SOC), the Hamiltonian can be written as
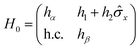 | (1) |
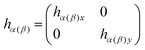 | (2) |
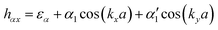 | (3) |
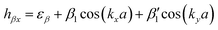 | (4) |
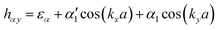 | (5) |
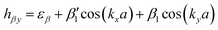 | (6) |
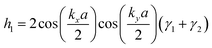 | (7) |
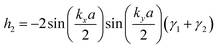 | (8) |
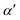 , β1,
, β1, 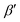 , γ1 and γ2 are material-dependent parameters.
, γ1 and γ2 are material-dependent parameters. ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) represents the Pauli matrices for the sublattice index. As shown in Fig. 1(c), this model gives rise to a pair of valleys with energy degeneracy at the points X and X′. The two inequivalent valleys are connected by {C4z|000} and {m1–10|000}. For valley polarization to occur, a perturbation H′ = Δ(I2×2⊗
represents the Pauli matrices for the sublattice index. As shown in Fig. 1(c), this model gives rise to a pair of valleys with energy degeneracy at the points X and X′. The two inequivalent valleys are connected by {C4z|000} and {m1–10|000}. For valley polarization to occur, a perturbation H′ = Δ(I2×2⊗![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) z) is necessary to break these symmetries and lift the energy degeneracy, as indicated in Fig. 1(d). In materials with heavy elements, the large band splitting caused by SOC should be considered. In the ESI,† the Hamiltonian with SOC is shown, and the relevant band structures are presented in Fig. S1 (ESI†). As a consequence of the time-reversal-invariant momenta (TRIM), however, the Kramer degeneracy of the point X (X′) cannot be broken. As a result, SOC introduces mainly Rashba-type band splitting, and the two-fold degeneracy at the point X (X′) is still present. Without loss of generality, the influence of SOC at the point X (X′) will not be discussed in the main text.
z) is necessary to break these symmetries and lift the energy degeneracy, as indicated in Fig. 1(d). In materials with heavy elements, the large band splitting caused by SOC should be considered. In the ESI,† the Hamiltonian with SOC is shown, and the relevant band structures are presented in Fig. S1 (ESI†). As a consequence of the time-reversal-invariant momenta (TRIM), however, the Kramer degeneracy of the point X (X′) cannot be broken. As a result, SOC introduces mainly Rashba-type band splitting, and the two-fold degeneracy at the point X (X′) is still present. Without loss of generality, the influence of SOC at the point X (X′) will not be discussed in the main text.
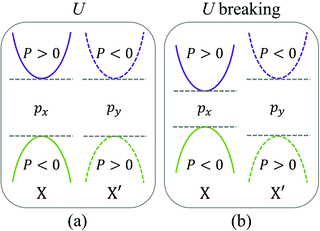
In order to better understand the physics of valley polarization, we proposed the VCSP mechanism for the material lattices shown in Fig. 1(b). The sublattice polarization is defined as Pn(k)
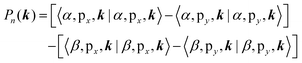 | (9) |
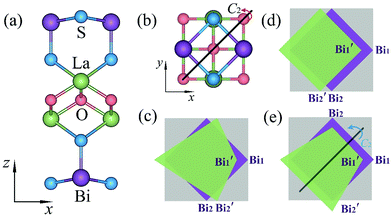
After demonstrating that the crystalline symmetry can control valley polarization, we now focus on material development. In the past few years, layered LaOBiS2 has been widely studied due to its novel properties such as charge density instability,33,34 hidden spin polarization,35,36 electrically tunable Rashba effect, and quantum anomalous Hall effect.37,38 However, the valleytronic properties of LaOBiS2 and similar structures (ZrCuSiAs-type) have not been explored so far. As illustrated in Fig. 3(a) and (b), LaOBiS2 adopts a square lattice with the layer group p4/nmm, and its unit cell consists of a triple-layer (TL) structure with the La2O2 layer sandwiched between two BiS2 layers. The Bi (S) atom in the upper layer is vertically aligned with the S (Bi) atom in the lower layer, and the two BiS2 layers are related by the glide operation ĝz = {![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) z|τ}, which consists of a reflection in the x–y plane, followed by a non-primitive translation
z|τ}, which consists of a reflection in the x–y plane, followed by a non-primitive translation 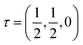 . In Fig. 4a–c, the electronic properties of TL LaOBiS2 are presented. In the absence of SOC, the energy dispersion relation shows a semiconductor nature with direct band gaps located at the points X and X′. By projecting the bands onto different atomic orbitals, we find that the low-energy spectra near the Fermi level originate mainly from the BiS2 layers, with the CBM and VBM near X (X′) points being dominated by the px (py) orbitals of Bi and S atoms, respectively. This indicates that the La2O2 layer acts as a barrier to prevent the interactions between the upper and lower BiS2 layers, and, therefore, the electric properties of the checkerboard lattice can be well preserved. TL LaOBiS2 thus satisfies the requirements that we put forward in the model analysis.
. In Fig. 4a–c, the electronic properties of TL LaOBiS2 are presented. In the absence of SOC, the energy dispersion relation shows a semiconductor nature with direct band gaps located at the points X and X′. By projecting the bands onto different atomic orbitals, we find that the low-energy spectra near the Fermi level originate mainly from the BiS2 layers, with the CBM and VBM near X (X′) points being dominated by the px (py) orbitals of Bi and S atoms, respectively. This indicates that the La2O2 layer acts as a barrier to prevent the interactions between the upper and lower BiS2 layers, and, therefore, the electric properties of the checkerboard lattice can be well preserved. TL LaOBiS2 thus satisfies the requirements that we put forward in the model analysis.
To realize valley polarization, an out-of-plane external electric field is usually applied to break the symmetry. In the case of TL LaOBiS2, as expected, an out-of-plane electric field breaks the {S4z|000} and 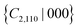 symmetries, which connect the X and X′ valleys. As Fig. 4(d) shows, however, the intervalley energy degeneracy cannot be lifted by a vertical field, but intravalley band splitting occurs due to the asymmetric potential. This is a consequence of the still-extant
symmetries, which connect the X and X′ valleys. As Fig. 4(d) shows, however, the intervalley energy degeneracy cannot be lifted by a vertical field, but intravalley band splitting occurs due to the asymmetric potential. This is a consequence of the still-extant 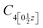 symmetry little group at the point X (X′), which protects the intervalley energy degeneracy. In other words, the equivalence between px and py has not been removed. In addition, the heavy atom (Bi) will cause a large SOC; the energy dispersion taking the SOC into account is shown in Fig. S2(f) (ESI†). It can be found that the SOC breaks the two-fold degeneracy (except at the TRIM), but the band dispersion is still symmetric around the Γ point because of the Kramer degeneracy. In the absence of structural distortion, therefore, SOC cannot remove the intervalley energy degeneracy, and the sublattice polarization is not influenced.
symmetry little group at the point X (X′), which protects the intervalley energy degeneracy. In other words, the equivalence between px and py has not been removed. In addition, the heavy atom (Bi) will cause a large SOC; the energy dispersion taking the SOC into account is shown in Fig. S2(f) (ESI†). It can be found that the SOC breaks the two-fold degeneracy (except at the TRIM), but the band dispersion is still symmetric around the Γ point because of the Kramer degeneracy. In the absence of structural distortion, therefore, SOC cannot remove the intervalley energy degeneracy, and the sublattice polarization is not influenced.
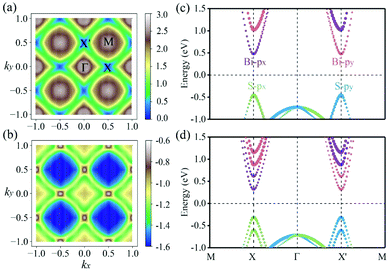
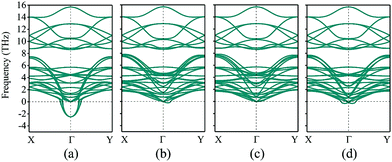
In the phonon spectrum of pristine TL LaOBiS2 (DS0) in Fig. 5(a), it is of interest that the branches of the optical vibrational modes drop around the Γ point with a negative frequency, which is an indication of a potential structural phase transition. The two doubly degenerate Eu and Eg phonon modes at the Γ point indicate that the Bi and S atoms in each BiS2 layer tend to move oppositely in x–y plane, thus forming three polytypes of LaOBiS2. In this first case, the initial displacements were imposed on the Bi atoms in the top (Bi1) and bottom (Bi2) of BiS2 layers along the −x and +x directions, respectively, as shown in Fig. 3(c). In Fig. 5(b), the phonon dispersion confirms the dynamic stability of the distorted structure (DS1); this distortion is similar to the Peierls-like structural distortion. As shown in Fig. 6(a) and Fig. S2(b) (ESI†), it is greatly significant that the energy degeneracy of the X and X′ valleys is lifted because of the breaking of the {S4z|000}, 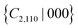 and
and 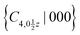 symmetries. In particular, the intervalley energy splittings for the CBM and VBM are 175.1 and 31.8 meV, respectively. These energy values are greater than the thermal energy at room temperature, suggesting potential applications in room-temperature valleytronic devices. In the second case, a low-energy distorted structure in which both the Bi1 and Bi2 atoms moved slightly along the −x direction (DS2) was obtained, and is dynamically stable (see Fig. 3(d) and 5(c)). If the three symmetry operations are removed, symmetry analysis finds that valley polarization may occur. As shown in Fig. 6(b) and Fig. S2(c) (ESI†), as expected, DS2 lifts the intervalley energy degeneracy, and the energy splittings are 135.8 and 26.7 meV for the CBM and VBM, respectively. As the two BiS2 layers show C4z rotation symmetry, the atom distortions in the x and y directions are equivalent; thus, the displacement of both the Bi1 and Bi2 atoms along the y direction gives rise to similar results to that in the x direction.
symmetries. In particular, the intervalley energy splittings for the CBM and VBM are 175.1 and 31.8 meV, respectively. These energy values are greater than the thermal energy at room temperature, suggesting potential applications in room-temperature valleytronic devices. In the second case, a low-energy distorted structure in which both the Bi1 and Bi2 atoms moved slightly along the −x direction (DS2) was obtained, and is dynamically stable (see Fig. 3(d) and 5(c)). If the three symmetry operations are removed, symmetry analysis finds that valley polarization may occur. As shown in Fig. 6(b) and Fig. S2(c) (ESI†), as expected, DS2 lifts the intervalley energy degeneracy, and the energy splittings are 135.8 and 26.7 meV for the CBM and VBM, respectively. As the two BiS2 layers show C4z rotation symmetry, the atom distortions in the x and y directions are equivalent; thus, the displacement of both the Bi1 and Bi2 atoms along the y direction gives rise to similar results to that in the x direction.
If the Bi1 atom of the top BiS2 layer deforms along the −x direction while the Bi2 atom of the bottom layer moves toward the −y direction, we obtain the third energetically favorable distorted structure (DS3, Fig. 3(e)); its dynamic stability is confirmed by the phonon spectrum in Fig. 5(d). As shown in Fig. 6(c) and Fig. S2(d) (ESI†), DS3 retains the energy degeneracy of the X and X′ valleys due to the preserved 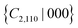 symmetry. In order to prove our analysis, an out-of-plane external electric field of 0.1 V Å−1 (achievable with current experimental techniques39) was applied to DS3 to break the
symmetry. In order to prove our analysis, an out-of-plane external electric field of 0.1 V Å−1 (achievable with current experimental techniques39) was applied to DS3 to break the 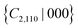 symmetry. From Fig. 6(d) and Fig. S2(e) (ESI†), we can see that the field can induce a valley energy splitting of 131.2 and 28.4 meV for the CBM and VBM, respectively. Both the CBM and VBM move upward in the X′ valley and down in the X valley, successfully generating valley polarization in good agreement with our analysis. As listed in Table S1 (ESI†), the polytypes DS1, DS2 and DS3 are likely to coexist due to the relatively small energy difference among them (0.005 meV per atom), and are about −2.2 meV per atom lower in energy than DS0. In addition, the relevant structural parameters are also summarized in Table S1 (ESI†). It should be emphasized that, for DS1 and DS2, valley polarization can be achieved spontaneously due to the breakage of the {S4z|000},
symmetry. From Fig. 6(d) and Fig. S2(e) (ESI†), we can see that the field can induce a valley energy splitting of 131.2 and 28.4 meV for the CBM and VBM, respectively. Both the CBM and VBM move upward in the X′ valley and down in the X valley, successfully generating valley polarization in good agreement with our analysis. As listed in Table S1 (ESI†), the polytypes DS1, DS2 and DS3 are likely to coexist due to the relatively small energy difference among them (0.005 meV per atom), and are about −2.2 meV per atom lower in energy than DS0. In addition, the relevant structural parameters are also summarized in Table S1 (ESI†). It should be emphasized that, for DS1 and DS2, valley polarization can be achieved spontaneously due to the breakage of the {S4z|000}, 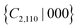 and
and 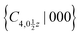 symmetries by spontaneous structural distortion, and such structural distortion occurs without the need for an out-of-plane external electric field. In case of DS3, however, spontaneous structure distortion still preserves the
symmetries by spontaneous structural distortion, and such structural distortion occurs without the need for an out-of-plane external electric field. In case of DS3, however, spontaneous structure distortion still preserves the 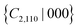 symmetry, which protects the intervalley energy degeneracy. In order to break the
symmetry, which protects the intervalley energy degeneracy. In order to break the 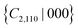 symmetry, approaches such as an experimentally achievable out-of-plane electric field could be employed, and our results confirm that the energy degeneracy between X and X′ can be lifted after removing the
symmetry, approaches such as an experimentally achievable out-of-plane electric field could be employed, and our results confirm that the energy degeneracy between X and X′ can be lifted after removing the 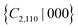 symmetry.
symmetry.
As shown in Fig. S1 and S2 (ESI†), the model analysis and first-principle calculation results indicate that the valley polarization is retained in the distorted structures when the SOC is considered. In addition, for the CBM in DS1, DS2 and DS3 the energy splitting is consistently larger than that of the VBM, which can be attributed to the structural distortion. In particular, for DS1, DS2 and DS3 the distortion mainly changes the interaction strength between the py orbitals of neighboring Bi atoms rather than S atoms. It has been demonstrated that subtle electronic markers of the different polytypes of the layered compound LaOBiS2 can be distinguished by ARPES;40 therefore, valley polarization is observable due to the large energy difference between X and X′ in TL LaOBiS2. As a result of the C2v little group, the VBM at the valley centers X and X′ corresponds to the 1D representations B1 and B2, respectively; thus, the VBM and additional CB couple only to the B1 (B2) state at X (X′) by x-linearly (y-linearly) polarized light excitation. This is analogous to the 2D rectangular-lattice group-IV monochalcogenides SnS and GeSe41,42 and the 2D square-lattice TiSiCO.32 TL LaOBiS2 polytypes could be potential candidates for polarizers by using special linearly polarized light to selectively excite electrons from the valence to the conduction band for individual valleys. Additionally, polarization switching could also be detected optically by combining a polarized light detector.43 It should be pointed out that the middle La2O2 layer produces a strong polar field, which causes Rashba splitting for the BiS2 layer at X and X′ points when SOC is considered. As a result, coupling between valley and helical Rashba spin polarization could introduce other fascinating properties, which require further study in future works.
Conclusions
In conclusion, we proposed a new design principle, i.e., valley-contrasting sublattice polarization, to realize the symmetry control of valley polarization. The feasibility of this principle was confirmed via effective model analysis. Remarkably, this new mechanism for valley polarization is applicable to ZrCuSiAs-type structures, particularly layered LaOBiS2 polytypes. The large intervalley energy splitting indicates great promise for device applications, and we look forward to experimental confirmation of our results.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 51872170), Young Scholars Program of Shandong University (YSPSDU), Shandong Provincial Key Research and Development Program (Major Scientific and Technological Innovation Project) (No. 2019JZZY010302), Natural Science Foundation of Shandong Province (No. ZR2019MEM013), and Taishan Scholar Program of Shandong Province.References
- A. Rycerz, J. Tworzydlo and C. Beenakker, Nat. Phys., 2007, 3, 172–175 Search PubMed
.
- O. Gunawan, Y. P. Shkolnikov, K. Vakili, T. Gokmen, E. P. De Poortere and M. Shayegan, Phys. Rev. Lett., 2006, 97, 186404 CrossRef CAS
.
- D. Xiao, W. Yao and Q. Niu, Phys. Rev. Lett., 2007, 99, 236809 CrossRef
.
- W. Yao, D. Xiao and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235406 CrossRef
.
- D. Xiao, G.-B. Liu, W. Feng, X. Xu and W. Yao, Phys. Rev. Lett., 2012, 108, 196802 CrossRef
.
- Z. Zhu, A. Collaudin, B. Fauqué, W. Kang and K. Behnia, Nat. Phys., 2012, 8, 89–94 Search PubMed
.
- T. Cai, S. A. Yang, X. Li, F. Zhang, J. Shi, W. Yao and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 115140 CrossRef
.
- X. Xu, W. Yao, D. Xiao and T. F. Heinz, Nat. Phys., 2014, 10, 343–350 Search PubMed
.
- G. B. Liu, D. Xiao, Y. Yao, X. Xu and W. Yao, Chem. Soc. Rev., 2015, 44, 2643–2663 RSC
.
- J. R. Schaibley, H. Yu, G. Clark, P. Rivera, J. S. Ross, K. L. Seyler, W. Yao and X. Xu, Nat. Rev. Mater., 2016, 1, 16055 CrossRef CAS
.
- H. Guan, N. Tang, H. Huang, X. Zhang, M. Su, X. Liu, L. Liao, W. Ge and B. Shen, ACS Nano, 2019, 13, 9325–9331 CrossRef CAS
.
- Y. Ominato, J. Fujimoto and M. Matsuo, Phys. Rev. Lett., 2020, 124, 166803 CrossRef CAS
.
- D. Xiao, M.-C. Chang and Q. Niu, Rev. Mod. Phys., 2010, 82, 1959–2007 CrossRef CAS
.
- X. Chen, T. Yan, B. Zhu, S. Yang and X. Cui, ACS Nano, 2017, 11, 1581–1587 CrossRef CAS
.
- H. Zeng, J. Dai, W. Yao, D. Xiao and X. Cui, Nat. Nanotechnol., 2012, 7, 490–493 CrossRef CAS
.
- T. Cao, G. Wang, W. Han, H. Ye, C. Zhu, J. Shi, Q. Niu, P. Tan, E. Wang, B. Liu and J. Feng, Nat. Commun., 2012, 3, 887 CrossRef
.
- W.-T. Hsu, Y.-L. Chen, C.-H. Chen, P.-S. Liu, T.-H. Hou, L.-J. Li and W.-H. Chang, Nat. Commun., 2015, 6, 8963 CrossRef CAS
.
- C. J. Ciccarino, T. Christensen, R. Sundararaman and P. Narang, Nano Lett., 2019, 18, 5709–5715 CrossRef
.
- K. F. Mak, K. He, J. Shan and T. F. Heinz, Nat. Nanotechnol., 2012, 7, 494–498 CrossRef CAS
.
- Y. Ye, J. Xiao, H. Wang, Z. Ye, H. Zhu, M. Zhao, Y. Wang, J. Zhao, X. Yin and X. Zhang, Nat. Nanotechnol., 2016, 11, 598–602 CrossRef CAS
.
- Y. Li, J. Ludwig, T. Low, A. Chernikov, X. Cui, G. Arefe, Y. D. Kim, A. M. van der Zande, A. Rigosi, H. M. Hill, S. H. Kim, J. Hone, Z. Li, D. Smirnov and T. F. Heinz, Phys. Rev. Lett., 2014, 113, 266804 CrossRef
.
- G. Aivazian, Z. Gong, A. M. Jones, R.-L. Chu, J. Yan, D. G. Mandrus, C. Zhang, D. Cobden, W. Yao and X. Xu, Nat. Phys., 2015, 11, 148–152 Search PubMed
.
- C. Jiang, F. Liu, J. Cuadra, Z. Huang, K. Li, A. Rasmita, A. Srivastava, Z. Liu and W.-B. Gao, Nat. Commun., 2017, 8, 802 Search PubMed
.
- C. Ke, Y. Wu, W. Yang, Z. Wu, C. Zhang, X. Li and J. Kang, Phys. Rev. B, 2019, 100, 195435 CrossRef CAS
.
- J. Qi, X. Li, Q. Niu and J. Feng, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 121403 CrossRef
.
- L. Xu, M. Yang, L. Shen, J. Zhou, T. Zhu and Y. P. Feng, Phys. Rev. B, 2018, 97, 041405 CrossRef CAS
.
- G. Plechinger, P. Nagler, A. Arora, A. G. del Águila, M. V. Ballottin, T. Frank, P. Steinleitner, M. Gmitra, J. Fabian, P. C. M. Christianen, R. Bratschitsch, C. Schüller and T. Korn, Nano Lett., 2016, 16, 7899–7904 CrossRef CAS
.
- X.-X. Zhang, T. Cao, Z. Lu, Y.-C. Lin, F. Zhang, Y. Wang, Z. Li, J. C. Hone, J. A. Robinson, D. Smirnov, S. G. Louie and T. F. Heinz, Nat. Nanotechnol., 2017, 12, 883–888 CrossRef CAS
.
- W.-Y. Tong, S.-J. Gong, X. Wan and C.-G. Duan, Nat. Commun., 2016, 7, 13612 CrossRef CAS
.
- X. Li, T. Cao, Q. Niu, J. Shi and J. Feng, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3738–3742 CrossRef CAS
.
- C. Zhang, Y. Nie, S. Sanvito and A. Du, Nano Lett., 2019, 19, 1366–1370 CrossRef
.
- Z.-M. Yu, S. Guan, X.-L. Sheng, W. Gao and S. A. Yang, Phys. Rev. Lett., 2020, 124, 037701 CrossRef CAS
.
- Q. Liu, X. Zhang and A. Zunger, Phys. Rev. B, 2016, 93, 174119 CrossRef
.
- T. Yildirim, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 020506 CrossRef
.
- X. Zhang, Q. Liu, J.-W. Luo, A. J. Freeman and A. Zunger, Nat. Phys., 2014, 10, 387–393 Search PubMed
.
- Q. Liu, X. Zhang, H. Jin, K. Lam, J. Im, A. J. Freeman and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 235204 CrossRef
.
- Q. Liu, Y. Guo and A. J. Freeman, Nano Lett., 2013, 13, 5264–5270 CrossRef CAS
.
- X.-Y. Dong, J.-F. Wang, R.-X. Zhang, W.-H. Duan, B.-F. Zhu, J. O. Sofo and C.-X. Liu, Nat. Commun., 2015, 6, 8517 CrossRef CAS
.
- Y. Zhang, T.-T. Tang, C. Girit, Z. Hao, M. C. Martin, A. Zettl, M. F. Crommie, Y. R. Shen and F. Wang, Nature, 2019, 459, 820–823 CrossRef
.
- X. Zhou, Q. Liu, J. A. Waugh, H. Li, T. Nummy, X. Zhang, X. Zhu, G. Cao, A. Zunger and D. S. Dessau, Phys. Rev. B, 2017, 95, 075118 CrossRef
.
- A. S. Rodin, L. C. Gomes, A. Carvalho and A. H. Castro Neto, Phys. Rev. B, 2016, 93, 045431 CrossRef
.
- P. Z. Hanakata, A. Carvalho, D. K. Campbell and H. S. Park, Phys. Rev. B, 2016, 94, 035304 CrossRef
.
- X.-W. Shen, W.-Y. Tong, S.-J. Gong and C.-G. Duan, 2D Mater., 2018, 5, 011001 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0mh01441a |
| This journal is © The Royal Society of Chemistry 2021 |