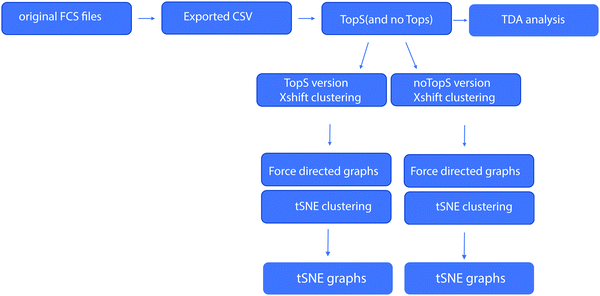
Identification of stem cells from large cell populations with topological scoring†
Mihaela E.
Sardiu‡
a,
Andrew C.
Box‡
a,
Jeffrey S.
Haug
a and
Michael P.
Washburn
 *ab
*ab
aStowers Institute for Medical Research, 1000 E. 50th St, Kansas City, MO 64110, USA. E-mail: mpw@stowers.org; Tel: +816-926-4457
bDepartment of Pathology and Laboratory Medicine, The University of Kansas Medical Center, 3901 Rainbow Boulevard, Kansas City, Kansas 66160, USA
First published on 13th August 2020
Abstract
Machine learning and topological analysis methods are becoming increasingly used on various large-scale omics datasets. Modern high dimensional flow cytometry data sets share many features with other omics datasets like genomics and proteomics. For example, genomics or proteomics datasets can be sparse and have high dimensionality, and flow cytometry datasets can also share these features. This makes flow cytometry data potentially a suitable candidate for employing machine learning and topological scoring strategies, for example, to gain novel insights into patterns within the data. We have previously developed a Topological Score (TopS) and implemented it for the analysis of quantitative protein interaction network datasets. Here we show that TopS approach for large scale data analysis is applicable to the analysis of a previously described flow cytometry sorted human hematopoietic stem cell dataset. We demonstrate that TopS is capable of effectively sorting this dataset into cell populations and identify rare cell populations. We demonstrate the utility of TopS when coupled with multiple approaches including topological data analysis, X-shift clustering, and t-Distributed Stochastic Neighbor Embedding (t-SNE). Our results suggest that TopS could be effectively used to analyze large scale flow cytometry datasets to find rare cell populations.
Introduction
Utilizing high-throughput technologies, dynamic -omics data including genomics, transcriptomics, epigenomics, proteomics, and metabolomics has produced temporal-spatial big biological datasets which generally can be analyzed using similar approaches.1,2 Statistically, -omics data is typically presented as a large data matrix where the rows correspond to variables like the expression level of a gene in genomics, the expression level of a protein in proteomics, and the expression of protein markers on a cell in flow cytometry, and the columns correspond to independent samples.3,4 Major challenges persist regarding the analysis of large scale -omic datasets. This includes challenges regarding how to handle the complexity of data and how should the data be translated to discover the underlying biology from these large and complex matrices.It is therefore necessary to use different analysis methods or scoring strategies for large scale datasets to achieve more biological understanding and generate novel hypotheses. We recently introduced a new topological score for the analysis of proteomics data named Topological Scoring (TopS).5,6 The TopS method has already been used in an analysis of biological networks and its performance has been tested against other tools for proteomics analysis.5–8 TopS uses a likelihood score on quantitative values and in principle it can use any type of quantitative data, rather than being restricted to one type of -omics data. TopS generates large and small values corresponding to strong or weak links between variables and samples relative to other samples in a matrix.5,6 In general, TopS in combination with machine learning can be used to detect subnetworks consisting of points with similar patterns in large networks.
Flow cytometry is a technology that typically generates large scale quantitative datasets for the discovery of specific rare cell populations such as bone marrow-residing hematopoietic stem cells (HSCs).9,10 The ability to detect specific cell populations that associate strongly with different cell-surface protein markers typically presents challenge to data analysis and many clustering methods have been used to study such a dataset.9,10 Here, we report the results of analyzing the Nilsson rare human hematopoietic stem cell dataset9,10 by TopS and machine learning (Fig. 1). We compared the use of TopS to original transformed data and expert gating results to test the usage of TopS for the analysis of a multi-color cytometry data set. Here we implemented three different computational approaches-based on machine learning including topological data analysis (TDA),11–14 X-shift clustering,15–17 and t-Distributed Stochastic Neighbor Embedding (t-SNE)18–20 analysis for the analysis and visualization of the flow cytometry data. TDA is one of the newer and powerful method for the analysis of large datasets.11–14 TDA is using topological and geometric approaches to infer relevant features in complex datasets. X-shift clustering has been used in the analyses of the CyTOF (cytometry by time of flight) and flow cytometry datasets and it is using weighted K-nearest neighbor density estimation (KNN-DE) to determine the clusters in a large dataset.15–17 Lastly, t-SNE is a non-linear technique for dimensionality reduction that is commonly used for the visualization of high-dimensional datasets.18–20 Unlike TDA and X-shift, t-SNE is often used with other unsupervised learning algorithms for data classification. We demonstrate that TopS is an effective approach for processing data prior to utilization of TDA, X-shit, or t-SNE and is capable of efficiently finding rare cell populations in a flow cytometry sorted human hematopoietic stem cell dataset.
Results and discussion
Clustering of human hematopoietic stem cell dataset
One of the major challenges for the study of hematopoietic stem cells (HSCs) is their identification and isolation from larger pools of cells.9,10 Thus, developing biological and computational techniques for the identification of HSCs is of great importance. Here we selected a publicly available data from experiments in immunology using flow cytometry to demonstrate the use of TopS in the analysis of flow cytometry data. The Nilsson rare data contains rare population from bone marrow cells from healthy donor with 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 number of cells, 13 cell-surface protein markers and 358 (0.8%) manually gated cells (Table S1, ESI†).9,10 Early studies showed that no single cell-surface protein marker could specifically define the HSCs and there is need of additional markers to purify HSCs to homogeneity.9,10 The Nilsson rare data consists of 13 different markers (i.e. CD10, CD110, CD11b, CD123, CD19, CD3, CD34, CD38, CD4, CD45, CD45RA, CD49fpur, CD90bio) that led to the identification of 9 different cell populations such as myeloid cells; B-lymphoid cells; CD4-T-cells; CD4+ T-cells; common lymphoid progenitors (CLPs); megakaryocyte/erythrocyte progenitors (MEPs); granulocyte/macrophage progenitors (GMPs); multipotent progenitor (MPPs); and hematopoietic stem cells (HSCs).9,10 The original data was pre-processed as described in Weber et al.10 by using an arc-sinh transformation with a standard factor of 150 (i.e. arcsinh(x/150)) (Table S1, ESI†). From here on we call this matrix original/transformed data. TopS was next used to generate topological values on this dataset (Table S2, ESI†).
140 number of cells, 13 cell-surface protein markers and 358 (0.8%) manually gated cells (Table S1, ESI†).9,10 Early studies showed that no single cell-surface protein marker could specifically define the HSCs and there is need of additional markers to purify HSCs to homogeneity.9,10 The Nilsson rare data consists of 13 different markers (i.e. CD10, CD110, CD11b, CD123, CD19, CD3, CD34, CD38, CD4, CD45, CD45RA, CD49fpur, CD90bio) that led to the identification of 9 different cell populations such as myeloid cells; B-lymphoid cells; CD4-T-cells; CD4+ T-cells; common lymphoid progenitors (CLPs); megakaryocyte/erythrocyte progenitors (MEPs); granulocyte/macrophage progenitors (GMPs); multipotent progenitor (MPPs); and hematopoietic stem cells (HSCs).9,10 The original data was pre-processed as described in Weber et al.10 by using an arc-sinh transformation with a standard factor of 150 (i.e. arcsinh(x/150)) (Table S1, ESI†). From here on we call this matrix original/transformed data. TopS was next used to generate topological values on this dataset (Table S2, ESI†).
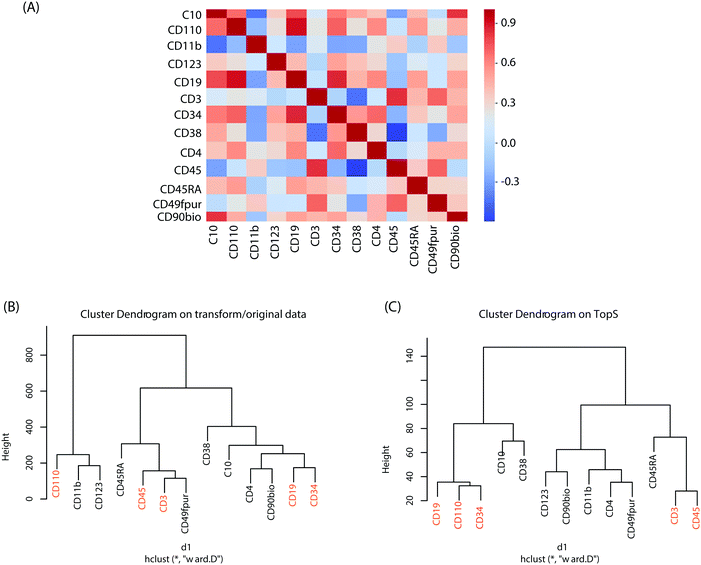
To better understand the changes in the expression of these cell-surface protein markers in the original/transformed data, we first applied a Pearson correlation (see Methods). In Fig. 2A we represented the correlations between the cell-surface protein markers using their expression in the 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 cells. Overall, the Pearson correlations show a high range of correlations, ranging from rather low to high correlation coefficients. The highest correlations were between the CD110 and CD19 with a correlation of 0.911 followed by the correlation between CD19 and CD34 with a correlation of 0.857 (Fig. 2A). This result indicates that CD19, CD34 and CD110 might form a small cluster. In contrast, the lowest correlations were observed between CD3 and CD38 with an anticorrelation of −0.44147 followed by the correlation between CD10 and CD11b markers with an anticorrelation of −0.433 (Fig. 2A). These results suggest a substantial difference between the cell-surface protein markers profiles.
140 cells. Overall, the Pearson correlations show a high range of correlations, ranging from rather low to high correlation coefficients. The highest correlations were between the CD110 and CD19 with a correlation of 0.911 followed by the correlation between CD19 and CD34 with a correlation of 0.857 (Fig. 2A). This result indicates that CD19, CD34 and CD110 might form a small cluster. In contrast, the lowest correlations were observed between CD3 and CD38 with an anticorrelation of −0.44147 followed by the correlation between CD10 and CD11b markers with an anticorrelation of −0.433 (Fig. 2A). These results suggest a substantial difference between the cell-surface protein markers profiles.
Hierarchical clustering was also performed on both the original/transformed data and the topological scores using the TopS Shiny app to further illustrate the classification of the samples according to similarities of the cell-surface protein markers profiles (Fig. 2B). Interestingly, the markers pairs with the highest correlations are separated from each other when the original/transformed data is used (Fig. 2B). On the other hand, when using TopS the markers with the highest correlations in the matrix (i.e. CD19, CD110 and CD34) were under the same tree (Fig. 2C) in agreement with the Pearson correlations reported above. In addition, all the markers with the lowest correlations were positioned in both clusters away from each other (Fig. 2C). This figure illustrates the value of additional normalization methods like TopS to better elucidate the structure of the data and better cluster the samples. Furthermore, Fig. 2 also suggested that various distance metrics must be explored when the transformed/original data is used.
Topological scoring of dataset with machine learning approaches
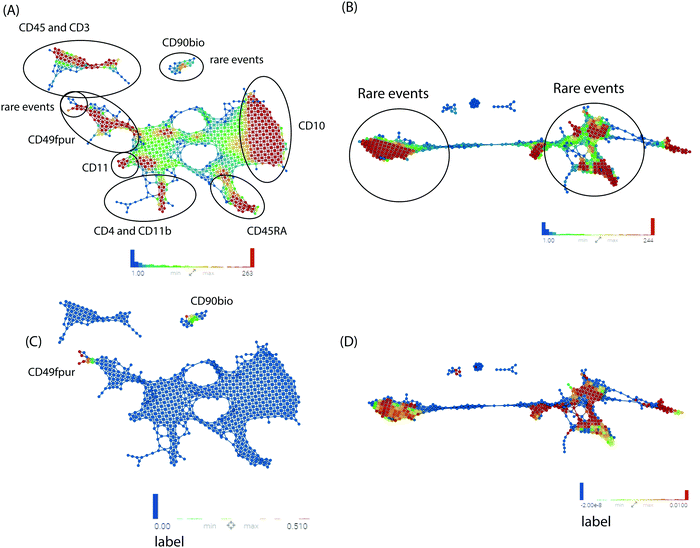
Next, we utilized multiple machine learning approaches with or without TopS to evaluate the ability of TopS to discern rare cells in the Nilsson rare human hematopoietic stem cell dataset. To begin, we investigated the utility of topological data analysis (TDA).11–14 TDA has been used for different omics data including cytometry data.21 TDA is a method that allows for the study of high dimensionality data sets by extracting shapes or patterns from the underlying data such that the researcher can gain new insights into patterns and relationships within the data.11–14 TDA also allows identification of clusters of rare events with a unique signature in a much larger data set.11–14 Because of its robustness to noise, TDA has proved effective in identifying meaningful groupings or patterns of samples and data points from a diverse set of biological data types including microarray, transcriptome data and protein–protein interaction networks.22,23Here, the input data for TDA was represented in a matrix, with each column corresponding to each cell-surface protein marker and each row corresponding to a cell. The values were transformed values or topological scores for each cell-surface protein marker in different cell types. A network of nodes with edges between them was then created using the TDA approach based on Ayasdi platform. Nodes in the network represent clusters of multiple cells, which is an important feature of the TDA network. This contrasts with other networks where nodes consist of a single cell. Nodes in Fig. 3 are colored based on the rows per node and on the label that corresponds to the gated cells (0 for major/multiple cells or 1 for HSCs cells). Our aim was to provide a global overview of this complex dataset with the focus on the detection of rare events using TDA and additionally show the benefit of using TopS with TDA for the analysis of flow cytometry data. In Fig. 3, we show the TDA analysis using (A) the topological score and (B) the original/transformed data in which the nodes are colored by the rows per node. In Fig. 3A we observed that the cells are well separated in different groups based on the expression profiles. Importantly, Fig. 3A also revealed group of cells in which the expressions of specific markers were enriched when compared with the rest of the markers, which is one of the unique features of the TopS. For example, we observed that the rare events were separated in two groups by TDA and the CD90bio and CD49fpur markers are enriched in these cells when compared with the other markers, and this agrees with the known association of CD90 and CD49f with human HSCs.24
TDA and TopS also detected other groups of cells where other markers were enriched. For example, on the right side of the Fig. 3A, we can observe that the CD10 marker was highly expressed in the group of cells colored by red. TDA also shows a substantial amount of cross-talks between different markers. In contrast, in Fig. 3B, when the original data/transformed data was used, TDA didn’t separate the data very well using the same parameters as in Fig. 3A, and the majority of the rare events were spread through the entire network. To better highlight the location of the rare events in the two networks we colored the nodes by the label that corresponds to the gated cells and we observed a more focused localization of these cells when using TopS with TDA (Fig. 3C and D).
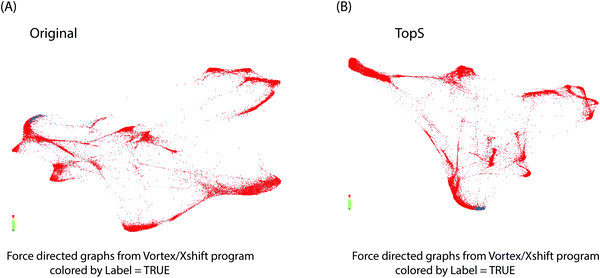
We next investigated the use of X-shift clustering15,16,25,26 on the Nilsson rare flow cytometry data. X-shift (VorteX) is a standalone application with graphical interface that uses the weighted k-means density estimation.15,16,25,26 Validation of the number of neighbors value by elbow point gives an optimal number of neighbors for density estimate of 62 for 38 clusters in the case of TopS and an optimal number of neighbors for density estimate of 62 for 30 clusters for the use of the original/transformed data (Table S3, ESI†). The results of TDA analysis using TopS data agrees with the results from the X-shift where the rare events were separated in two clusters. Similarly, X-shift produced two clusters for the rare events when the original/transformed data was used, however the overall numbers of clusters was smaller than the number of clusters obtained for TopS (Fig. 4A and B, colored in blue). It is desirable to have more clusters than few in order to avoid smaller populations merging in larger clusters.27 Fig. S1A and B (ESI†) show that TopS provides wider range of numbers than in the original/transformed data, thus the over representative values in the matrix can be identified and therefore the markers that bring the most contribution in the detection of the rare events can be easily selected.
Lastly, wet performed a t-SNE18–20 analysis on the original/transformed and TopS data sets followed by a k-means clustering approach on the two vectors generated from the t-SNE (Table S4, ESI†). The number of clusters used for the k-means were obtained from the X-shift as optimal numbers. Using k = 38 for TopS and k = 30 in the case of the original/transformed data, t-SNE produced similar results as the X-shift and the TDA. Using TopS, the rare events were separated in two clusters (Fig. S2A and B, ESI†). Like X-shift, t-SNE recovered two clusters for the rare events when original/transformed data is used (Fig. S2C and D, ESI†). The smallest cluster identified cells in which the C90bio marker was remarkably expressed when compared with the other markers, while the largest cluster identified cells in which the C49fpur and CD45 were highly enriched (Table S4, ESI†). To visualize the difference between these two clusters determined by t-SNE using TopS values we decided to represent the clusters as heat maps (Fig. S3, ESI†). The first cluster showed cells with high enrichment of several markers (Fig. S3A, ESI†) while the second cluster was an exception where cell populations has CD90bio with the highest enrichment (Fig. S3B, ESI†). These results also show that CD90bio, CD45 and CD49fpur are likely the most important markers among the 13 markers in the recovery of the HSCs cells from this dataset.9,10
Conclusions
High-dimensional flow cytometry is an important technique of choice to define and identify different population cells and detect expression levels of thousands of proteins markers.9,10 We recently developed a topological score (i.e. TopS) that generates large range of values which subsequently can be used to identify overwhelming pairs, like those between an affinity purified protein and an associated protein, in a quantitative matrix.5,6 Thus, subnetworks with highly scored pairs can be selected and visualized with TopS.5,6 Previously, TopS was used on smaller to medium matrices with thousands of rows (i.e. up to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rows) for the analysis of networks, hence our goal was to extend its usage for the larger data sets like flow cytometry data. Here we tested the TopS Shiny app for the analysis of a flow cytometry dataset described in Weber et al.10 and we showed the results for the Nilsson rare data.9,10
000 rows) for the analysis of networks, hence our goal was to extend its usage for the larger data sets like flow cytometry data. Here we tested the TopS Shiny app for the analysis of a flow cytometry dataset described in Weber et al.10 and we showed the results for the Nilsson rare data.9,10
We first demonstrated that TopS values can be used with different clustering approaches for the analysis of the flow cytometry data. Using Nilsson rare data,9,10 we applied three clustering methods with different approaches with the special focus on the identification of the rare events. Given the difficulties of identifying small clusters in a large dataset, TopS in combination with these methods identified the smallest population of rare events in a separate cluster (Fig. S2B and S4, ESI†). We demonstrated that rare populations have different patterns as they are pulled by different markers. As a result, they were separated in different clusters and not in a single cluster as one would expect. Using TopS we could identify a group of cells (Fig. S4 and Table S4, ESI†) in which the markers are having the highest expression. This data show that markers involved in T-cell and stem cells like CD11b, CD123, CD3 and CD90bio have the highest expressions in cells in this dataset. However, when focusing only on the HSCs cells, we could show that TopS values revealed that the CD90bio, CD45, and CD49fpur are the most useful markers in the recovery of these cells and that a biological basis for the separation of HSCs into two clusters likely exists. These results could be beneficial for designing further experiments for the HSCs isolation. TopS in combination with machine learning can be effective in marker reduction (i.e. from 13 markers to three/four markers) in the analysis of the bone marrow cells. Future work should focus on exploration of normalization methods and clustering approaches for a better representation of flow cytometry data. In conclusion, TopS5,6 could be an effective approach for processing flow cytometry data prior to further computational analysis with approaches like TDA,11–14 X-shift,15–17 and t-Distributed Stochastic Neighbor Embedding (t-SNE).18–20
Experimental
Data set
To evaluate the TopS method, we selected for our analysis an available data set from experiments in immunology using multicolor flow cytometry.10,25 We have used a publicly available high-dimensional data set where cell population identities are known from the expert manual gating. The data was downloaded from the FlowRepository at https://flowrepository.org/id/FR-FCM-ZZPH. The data was manually gated cell population labels as the reference populations. The Nilsson rare data contain rare population from bone marrow cells from healthy donor with 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 number of cells, 13 cell-surface markers and 358 (0.8%) manually gated cells.10,25 Data was transformed using arcsinh and TopS method as described in Sardiu et al.6 Pre-processing of the original data included the application of an arc-sinh transformation with a standard factor of 150 (i.e. arcsinh(x/150)).
140 number of cells, 13 cell-surface markers and 358 (0.8%) manually gated cells.10,25 Data was transformed using arcsinh and TopS method as described in Sardiu et al.6 Pre-processing of the original data included the application of an arc-sinh transformation with a standard factor of 150 (i.e. arcsinh(x/150)).
Overview of the TopS method
The updated TopS Shiny app together with detailed documentation is freely available on github at https://github.com/WashburnLab/TopS_updated. Here, the raw data was assembled into a matrix in which the columns represent the individual cell-surface markers and rows represented pull-down cells. The elements of the matrix were represented by the transformed expression of cell-specific protein markers. The data was next normalized on the columns, rows and total sum of the numerical values in the matrix.We used a simple model to calculate a score for each link between every cell and every marker in the matrix as follows:
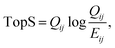 | (1) |
Pearson correlation output
Pearson correlation was used here to illustrate the similarity between the 13 cell–protein markers (Fig. 2A). Pearson correlation on the original/transformed data was calculated using phyton seaborn package corr(). The heatmap was used to illustrate the correlation between different samples using expression profiles. The heatmap shows a data matrix where coloring gives an overview of the numeric differences between cell-surface protein markers.Clustering with topological data analysis
The input data for TDA were represented in a matrix, with each column corresponding to each cell-surface protein marker and each row corresponding to a cell where the values are expression profiles. A network of nodes with edges between them was then created using the TDA approach based on the Ayasdi platform.11–14 Nodes in the network represent clusters of cells. Nodes in the figures were colored based on the metric Neighborhood lens1 and Neighborhood lens2. Two types of parameters were needed to generate a topological analysis: The first is a measurement of similarity, called metric, which measures the distance between two points in space (i.e. between rows in the data). The second are lenses, which are real valued functions on the data points. Lenses could come from statistics (mean, max, min), from geometry (centrality, curvature) and machine learning (PCA/SVD, Autoencoders, Isomap). In the next step the data was partitioned. Lenses were used to create overlapping bins in the data set, where the bins are preimages under the lens of an interval. Overlapping families of intervals were used to create overlapping bins in the data. Metrics were used with lenses to construct the network output. There were two parameters used in defining the bins. One is resolution, which determines the number of bins. Higher resolution means more bins. The second is gain, which determines the degree of overlap of the intervals. Once the bins were constructed, we performed a clustering step on each bin, using single linkage clustering with a fixed heuristic for the choice of the scale parameter. This gives a family of clusters within the data, which may overlap, and we then constructed a network with one node for each such cluster, and we connected two nodes if the corresponding clusters contain a data point in common.Clustering with X-shift via Vortex
X-shift is using graphical tool for cluster analysis of multiparametric datasets.15,16,26 The following parameters were used to run the X-shift application: transformation: none; noise threshold: yes, 1.0; feature rescaling: std; normalization: none; minimal Euclidean length: no; distance measure: angular distance; density estimate: N nearest neighbors (K) from 150 to 5, steps 30; N: determine automatically; elbow point for automatic number of clusters was determined.Data analysis with t_SNE
To spatially map the cells in the dataset we first applied a t-distributed stochastic neighbor embedding(t-SNE), a nonlinear visualization of the data.18–20 We then applied k-means clustering to this transformed matrix using the Hartigan–Wong algorithm and a maximum number of iterations set at 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. We used k = 30 for the original/transformed data and k = 38 for the TopS values to partition our data. The number of clusters were generated from the X-shift tool using elbow point. All computations were run using R environment using k-means function for the partition and daisy function to compute all the pairwise dissimilarities (Euclidean distances) between observations in the dataset for the silhouette.
000. We used k = 30 for the original/transformed data and k = 38 for the TopS values to partition our data. The number of clusters were generated from the X-shift tool using elbow point. All computations were run using R environment using k-means function for the partition and daisy function to compute all the pairwise dissimilarities (Euclidean distances) between observations in the dataset for the silhouette.
Conflicts of interest
The authors declare no competing interests.Acknowledgements
Research reported in this publication was supported by the Stowers Institute for Medical Research and the National Institute of General Medical Sciences of the National Institutes of Health under Award Number RO1GM112639 to MPW.References
- C. Wu, F. Zhou, J. Ren, X. Li, Y. Jiang and S. Ma, High-Throughput, 2019, 8(1) DOI:10.3390/ht8010004.
- Y. Li, F. X. Wu and A. Ngom, Briefings Bioinf., 2018, 19, 325–340 Search PubMed.
- Y. Hasin, M. Seldin and A. Lusis, Genome Biol., 2017, 18, 83 CrossRef.
- M. Bersanelli, E. Mosca, D. Remondini, E. Giampieri, C. Sala, G. Castellani and L. Milanesi, BMC Bioinf., 2016, 17(Suppl 2), 15 CrossRef.
- M. E. Sardiu, L. Florens and M. P. Washburn, Methods, 2019 DOI:10.1016/j.ymeth.2019.08.010.
- M. E. Sardiu, J. M. Gilmore, B. D. Groppe, A. Dutta, L. Florens and M. P. Washburn, Nat. Commun., 2019, 10, 1118 CrossRef.
- M. J. Levy, D. C. Montgomery, M. E. Sardiu, J. L. Montano, S. E. Bergholtz, K. D. Nance, A. L. Thorpe, S. D. Fox, Q. Lin, T. Andresson, L. Florens, M. P. Washburn and J. L. Meier, Cell Chem. Biol., 2020, 27(3), 322–333.e5 CrossRef CAS.
- G. Dayebgadoh, M. E. Sardiu, L. Florens and M. P. Washburn, J. Proteome Res., 2019, 18, 3479–3491 CrossRef CAS.
- A. Rundberg Nilsson, D. Bryder and C. J. Pronk, Cytometry, Part A, 2013, 83, 721–727 CrossRef.
- L. M. Weber and M. D. Robinson, Cytometry, Part A, 2016, 89, 1084–1096 CrossRef CAS.
- P. G. Camara, Current opinion in systems biology, 2017, 1, 95–101 CrossRef.
- P. G. Camara, D. I. Rosenbloom, K. J. Emmett, A. J. Levine and R. Rabadan, Cell Syst., 2016, 3, 83–94 CrossRef CAS.
- L. Li, W. Y. Cheng, B. S. Glicksberg, O. Gottesman, R. Tamler, R. Chen, E. P. Bottinger and J. T. Dudley, Sci. Transl. Med., 2015, 7, 311ra174 CrossRef.
- P. Y. Lum, G. Singh, A. Lehman, T. Ishkanov, M. Vejdemo-Johansson, M. Alagappan, J. Carlsson and G. Carlsson, Sci. Rep., 2013, 3, 1236 CrossRef CAS.
- M. Gossez, T. Rimmele, T. Andrieu, S. Debord, F. Bayle, C. Malcus, F. Poitevin-Later, G. Monneret and F. Venet, Sci. Rep., 2018, 8, 17296 CrossRef.
- N. Samusik, Z. Good, M. H. Spitzer, K. L. Davis and G. P. Nolan, Nat. Methods, 2016, 13, 493–496 CrossRef CAS.
- V. van Unen, T. Hollt, N. Pezzotti, N. Li, M. J. T. Reinders, E. Eisemann, F. Koning, A. Vilanova and B. P. F. Lelieveldt, Nat. Commun., 2017, 8, 1740 CrossRef.
- N. V. Acuff and J. Linden, J. Immunol., 2017, 198, 4539–4546 CrossRef CAS.
- A. Platzer, PLoS One, 2013, 8, e56883 CrossRef CAS.
- S. Toghi Eshghi, A. Au-Yeung, C. Takahashi, C. R. Bolen, M. N. Nyachienga, S. P. Lear, C. Green, W. R. Mathews and W. E. O'Gorman, Front. Immunol., 2019, 10, 1194 CrossRef.
- T. Lakshmikanth, A. Olin, Y. Chen, J. Mikes, E. Fredlund, M. Remberger, B. Omazic and P. Brodin, Cell Rep., 2017, 20, 2238–2250 CrossRef CAS.
- M. E. Sardiu, J. M. Gilmore, B. Groppe, L. Florens and M. P. Washburn, Sci. Rep., 2017, 7, 43845 CrossRef.
- M. E. Sardiu, J. M. Gilmore, B. D. Groppe, D. Herman, S. R. Ramisetty, Y. Cai, J. Jin, R. C. Conaway, J. W. Conaway, L. Florens and M. P. Washburn, EMBO Rep., 2015, 16, 116–126 CrossRef CAS.
- L. Lange, D. Hoffmann, A. Schwarzer, T. C. Ha, F. Philipp, D. Lenz, M. Morgan and A. Schambach, Stem Cell Rep., 2020, 14, 122–137 CrossRef CAS.
- J. Nilsson, I. Granrot, J. Mattsson, B. Omazic, M. Uhlin and S. Thunberg, Vox Sang., 2017, 112, 459–468 CrossRef CAS.
- A. K. Kimball, L. M. Oko, B. L. Bullock, R. A. Nemenoff, L. F. van Dyk and E. T. Clambey, J. Immunol., 2018, 200, 3–22 CrossRef CAS.
- G. K. Chen, E. C. Chi, J. M. Ranola and K. Lange, PLoS Comput. Biol., 2015, 11, e1004228 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0mo00039f |
| ‡ Authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |