Dual-gated mono–bilayer graphene junctions

Abstract

A lateral junction with an atomically sharp interface is extensively studied in fundamental research and plays a key role in the development of electronics, photonics and optoelectronics. Here, we demonstrate an electrically tunable lateral junction at atomically sharp interfaces between dual-gated mono- and bilayer graphene. The transport properties of the mono–bilayer graphene interface are systematically investigated with I_ds–V_ds curves and transfer curves, which are measured with bias voltage V_ds applied in opposite directions across the asymmetric mono–bilayer interface. Nearly 30% difference between the output I_ds–V_ds curves of graphene channels measured at opposite V_ds directions is observed. Furthermore, the measured transfer curves confirm that the conductance difference of graphene channels greatly depends on the doping level, which is determined by dual-gating. The V_ds direction dependent conductance difference indicates the existence of a gate tunable junction in the mono–bilayer graphene channel, due to different band structures of monolayer graphene with zero bandgap and bilayer graphene with a bandgap opened by dual-gating. Simulation of the I_ds–V_ds curves based on a new numerical model validates the gate tunable junction at the mono–bilayer graphene interface from another point of view. The dual-gated mono–bilayer graphene junction and new protocol for I_ds–V_ds curve simulation pave a possible way for functional applications of graphene in next-generation electronics.

---

Introduction

Two dimensional (2D) materials, such as graphene,¹ transition metal dichalcogenides (TMDCs)² and black phosphorus (BP),³ have been extensively investigated due to their unique physical properties. Until now, plenty of remarkable electronic and optoelectronic properties have been demonstrated in 2D materials,^4–6 such as ultrahigh carrier mobility of 200 000 cm² V⁻¹ s⁻¹ and reduced noise levels in suspended graphene,^7,8 high current on/off ratio of 1 × 10⁸ in monolayer MoS₂ transistors² and ambipolar transport in BP transistors,⁹ as well as an anisotropic photoresponse and chiral light emission in BP and WS₂ based devices.^10,11 Of particular importance, the electronic structures and physical properties of 2D materials strongly depend on the number of layers, and functional devices can be built based on this principle.^12–15 For example, mono- and bilayer graphene possess massless Dirac-like energy band and nearly parabolic dispersion, respectively.⁶ The strongly distinct band structures of mono- and bilayer graphene make it possible to construct a lateral junction with atomically sharp interface.^16–20 Furthermore, bilayer graphene under dual-gate modulation acquires an opened bandgap as large as 200 meV.^21,22 Consequently, ambipolar transport and current on/off ratio larger than 10⁴ are obtained in dual-gated bilayer graphene.^23,24

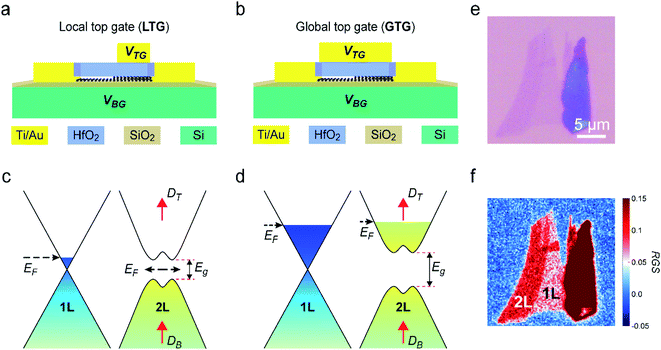
Here, we investigate the interface between dual-gated mono- and bilayer graphene, with two types of top gate electrodes deposited above the graphene channels, covering only bilayer graphene (local top gate, LTG, Fig. 1a) or the whole graphene channel (global top gate, GTG, Fig. 1b). Transfer curves and I_ds–V_ds curves of the graphene devices are systematically measured with bias voltage V_ds applied in opposite directions along the length of the channel. In addition, I_ds–V_ds curves of the devices are simulated based on a new numerical model with measured transfer curves as the only input. The results of both measurements and numerical simulation indicate that an electronic junction is successfully built at the mono–bilayer graphene interface, and this junction is considerably enhanced when the doping level of graphene is close to zero. The gate tunable mono–bilayer graphene junction is a promising candidate for the practical applications of graphene.

Fig. 1 Structure of mono–bilayer graphene junctions. (a and b) Architectures of dual-gated mono–bilayer graphene junction devices with local (a) and global (b) top gate electrodes. (c) Alignment between the Fermi level E_F of monolayer (1L) and bilayer (2L) graphene when the doping level is close to zero. (d) Alignment between E_F of mono- and bilayer graphene under heavy doping. A bandgap E_g is opened in bilayer graphene in the presence of top and bottom electrical displacement field D_T and D_B. (e) Optical microscope image of a typical mono–bilayer graphene flake. (f) RGS mapping of the flake in (e). The two areas with RGS of ∼0.06 and ∼0.12 are mono- and bilayer graphene, respectively.

Results and discussion

Architectures of the two different mono–bilayer graphene devices are demonstrated in Fig. 1a and b. The heavily doped silicon substrate works as the back gate electrode, where back gate voltage V_BG is applied to modulate both mono- and bilayer graphene in the channels. Top gate electrodes with two different coverings are assigned to the devices, to modulate the graphene channels with top gate voltage V_TG. The top gate electrode locally modulates bilayer graphene in the LTG device, while it globally modulates the entire graphene channel of the GTG device. In the presence of V_BG and V_TG, the induced bottom and top electrical displacement field D_B and D_T play a double role. Their difference D_B − D_T determines net doping of mono- and bilayer graphene, and (D_B + D_T)/2 gives rise to bandgap opening in bilayer graphene.^21,23 Therefore, a heterojunction is expected to be built between gapless monolayer graphene and bilayer graphene with an opened bandgap.

Conductance of the dual-gated mono–bilayer graphene is expected to highly depend on the Fermi level, as well as the opened bandgap in bilayer graphene. Here, we define a new parameter “effective gate voltage” (V_BG-eff and V_TG-eff correspond to back and top gate, respectively), that means, the voltage drop between gate electrodes and a point in the graphene channels. For example, when bias voltage V_ds is applied on the drain electrode and the source electrode is grounded, the “effective top gate” V_TG-eff in the channel ranges from V_TG − V_ds at the drain to V_TG − 0 at the source. V_TG-eff can be approximated uniform in the graphene channel when V_ds is remarkably smaller than V_TG, whereas it significantly changes along the length of the channel when V_ds is comparable with V_TG. As illustrated in Fig. S1,† when V_ds is applied on the electrode connected to monolayer graphene and the electrode connected to bilayer graphene is grounded, V_TG-eff in the monolayer section is lower than that in the bilayer section, and this configuration is called the “Mb” mode. Otherwise, in the opposite case when the V_ds is applied on the electrode connected to bilayer graphene, V_TG-eff in the monolayer section is higher than that in the bilayer section, and this configuration is called the “Bm” mode. Since V_TG-eff directly influences the doping level and further the conductance of graphene, the difference between V_TG-eff in Mb and Bm modes results in different conductance of the graphene channel. Meanwhile, the change of V_TG-eff results in different bandgap opened in bilayer graphene, which contributes to the conductance change of the graphene channel as well. As illustrated in Fig. 1c, when the net doping of graphene determined by D_B − D_T is close to zero, the channel conductance can be readily tuned by a small shift of gate voltage. However, when the net doping of graphene is quite heavy (Fig. 1d), the channel conductance tends to saturate and is almost independent of gate voltage. Therefore, the I_ds–V_ds curves measured with V_ds in opposite directions are expected to considerably differ from each other when the gate voltages approach the charge neutrality point (CNP).

In order to validate the principle design, mono–bilayer graphene flakes are carefully selected after mechanical exfoliation, followed by device fabrication. The optical microscope image of a typical graphene flake is shown in Fig. 1e, and its thickness is characterized by two methods. Based on the Raman spectrum shown in Fig. S2,† mono- and bilayer graphene areas in this flake can be identified according to the ratio of 2D/G and Lorentzian fitting of 2D peaks.²⁵ Additionally, the thickness of graphene could be confirmed by means of the relative green shift (RGS) based on optical microscope images.^26–28Fig. 1f demonstrates RGS results of this typical graphene flake. The two areas with RGS values of ∼0.06 and ∼0.12 are mono- and bilayer graphene. The agreement between the results of Raman and RGS proves the reliability of RGS based graphene thickness identification in our experiments. Details of Raman and RGS based characterization are explained in the Experimental section. In the following sections, the thickness of the two graphene flakes shown in Fig. S3a and b† is characterized using the RGS method. Based on the RGS results in Fig. S3c and d,† both of the two flakes are composed of distinct mono- and bilayer graphene areas. Next, LTG and GTG dual-gated graphene devices are fabricated with the two flakes through a standard microfabrication process as illustrated in Fig. S4† and described in the Experimental section, and optical microscope images of the fabrication process are shown in Fig. S5.†

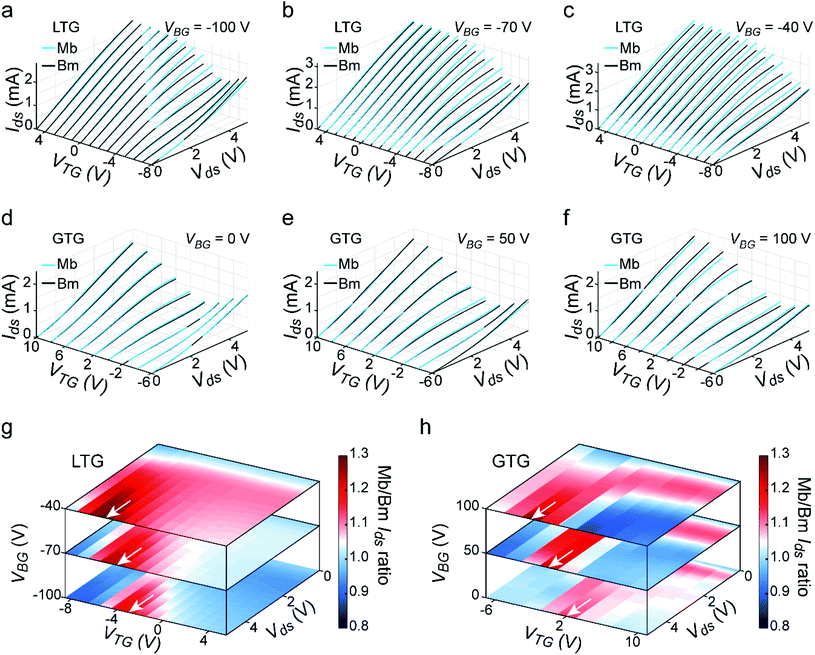
Transport properties of the graphene junction devices are firstly investigated using I_ds–V_ds curves measured in Mb and Bm modes. Fig. 2a–c demonstrate I_ds–V_ds curves of the LTG device measured at various gate voltages, showing that the I_ds of Mb measurements is different from that of Bm measurements. The significant difference between I_ds of Mb and Bm measurements is a characteristic of the electronic junction in the mono–bilayer graphene channel, because the I_ds of uniform channel measured in Mb and Bm modes should be the same. It is apparent that this I_ds difference can be greatly modulated by V_TG and V_BG, similar to the modulation of graphene conductance in transfer curves. In addition, I_ds–V_ds curves of the GTG device measured at various gate voltages are demonstrated in Fig. 2d–f, where less difference between I_ds of Mb and Bm measurements is found. In order to quantitatively compare the I_ds–V_ds curves of Mb and Bm measurements, the ratio of I_ds measured in Mb and Bm modes (Mb/Bm I_ds ratio) is calculated, and the results of LTG and GTG devices are shown in Fig. 2g and h, respectively. For both LTG and GTG devices, the Mb/Bm I_ds ratio maintains ∼1.0 when V_ds < 0.5 V, meaning that the mono–bilayer graphene works just like a uniform material. Nevertheless, this ratio greatly fluctuates around 1.0 when V_ds > 1 V, indicating that an effective electronic junction is built at the mono–bilayer graphene interface. The maximum ratio is achieved at decreased V_TG (−3 V, −4 V, and −5 V for the LTG device and 2 V, 0 V, and −2 V for the GTG device) when V_BG is increased, as indicated by the white arrows in Fig. 2g and h. The Mb/Bm I_ds ratio can be as high as roughly 1.3, in other words, the difference between I_ds of Mb and Bm measurements is around 30%. The reason behind the gate tunable Mb/Bm I_ds ratio could be explained by the transfer curves shown in the following section.

Fig. 2 I _ds–V_ds curves of mono–bilayer graphene junction devices. (a–c) I_ds–V_ds curves of the LTG device measured at V_BG = −100 V, −70 V and −40 V. (d–f) I_ds–V_ds curves of the GTG device measured at V_BG = 0 V, 50 V and 100 V. (g) Mb/Bm I_ds ratio calculated with the data of the LTG device in (a–c). (h) Mb/Bm I_ds ratio calculated with the data of the GTG device in (d–f). The maximum Mb/Bm I_ds ratios, as indicated with white arrows, are obtained at decreased V_TG when V_BG is increased.

Fig. 3a and b show the transfer curves of LTG and GTG devices measured in the Mb mode. For both LTG and GTG devices, V_TG at charge neutrality points (V_TG-CNP) is shifted approaching negative when V_BG is increased from −100 V to 100 V with 10 V steps, indicating that the doping level of graphene is jointly tuned by both V_TG and V_BG. As shown in Fig. 3a, channel resistance R_ds at charge neutrality points (R_ds-CNP) of the LTG device has a minimum value of 3.27 kΩ at V_BG = 70 V, whereas the R_ds-CNP of the GTG device monotonically decreases from 21.45 kΩ to 9.48 kΩ as V_BG is increased. V_TG-CNP values in the transfer curves of Fig. 3a and b are extracted and plotted in Fig. 3c, showing that V_BG and V_TG-CNP have a roughly linear relationship similar to the published results of dual-gated graphene devices.^21,29 The transfer curves measured in the Bm mode and corresponding V_TG-CNP, as shown in Fig. S6,† exhibit little difference from the results in Fig. 3a–c, because the V_ds of 0.1 V in transfer curves measurements leads to little difference between V_TG-eff in Mb and Bm modes. V_TG values for the maximum Mb/Bm I_ds ratio indicated with white arrows in Fig. 2g and h are present as red in Fig. 3c. In particular, V_TG-CNP of the GTG device at V_BG = 100 V, 50 V and 0 V are almost the same as V_TG where maximum Mb/Bm I_ds ratios in the GTG device are achieved. The similar V_BG dependence of V_TG-CNP and V_TG at the maximum Mb/Bm I_ds ratios suggests that the junction between dual-gated mono- and bilayer graphene heavily depends on the overall doping of graphene determined by D_B and D_T. As shown in Fig. 3d, for both the LTG and GTG devices, the maximum Mb/Bm I_ds ratio is increased when R_ds-CNP is decreased. Since the decreased R_ds-CNP mainly results from the decreased bandgap of bilayer graphene, it is reasonable to say that the gate tunable bandgap opened in bilayer graphene contributes to the generation of this directional junction as well.

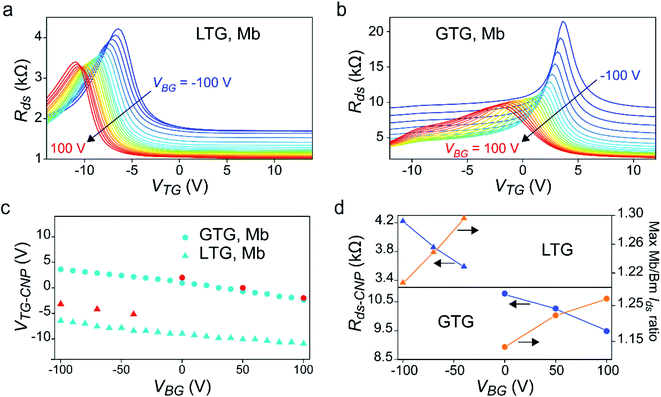Fig. 3 Transfer curves of mono–bilayer graphene junction devices measured in the Mb mode. (a and b) Transfer curves of LTG (a) and GTG (b) graphene junction devices measured at various V_BG. The V_BG ranges from −100 V to 100 V with 10 V steps in the measurements. (c) V_TG at charge neutrality point (V_TG-CNP) of the transfer curves in (a) and (b). The red markers indicate where maximum Mb/Bm I_ds ratios are obtained, as shown in Fig. 1(g) and (h). (d) Dependence of R_ds at charge neutrality point (R_ds-CNP) in the transfer curves and maximum Mb/Bm I_ds ratios in I_ds–V_ds curves on gate voltages.

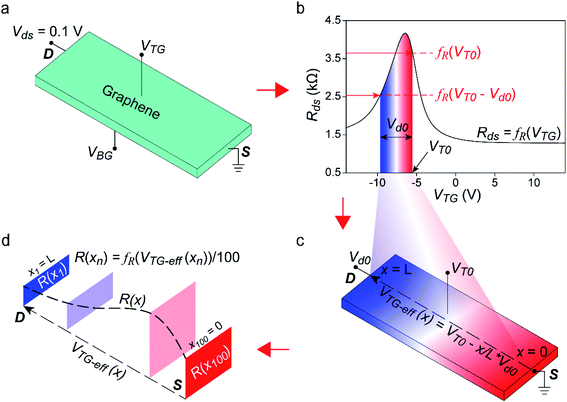
As further proof of the relation between the mono–bilayer graphene junction and gate voltages, a novel numerical model for simulating I_ds–V_ds curves based on measured transfer curves is proposed. I_ds–V_ds curves of graphene devices at high electric field when V_ds ≫ 0.1 V have been extensively studied based on both experimental measurements and theoretical simulation.^30,31 Results of the various models can perfectly explain and quantitatively fit the measured I_ds–V_ds curves. Nevertheless, there are multiple parameters (such as gate voltages at CNP, capacitance of dielectric layers, drift velocity of carriers, etc.) in these models that need to be measured or estimated initially, increasing a certain degree of difficulty and complexity. For easing the simulation process, a new numerical model is proposed to simulate output I_ds–V_ds curves with measured transfer curves as the only input, without any additional parameters needed to be measured or estimated. In the new model, every point in the I_ds–V_ds curves is determined using the formula: I_ds = V_ds/R_ds, where R_ds is simulated channel resistance based on the measured transfer curves. Taking the measurement of the LTG device at V_BG = −100 V as an example (Fig. 4a), the low bias voltage V_ds = 0.1 V in transfer curve measurements has little effect on V_TG-eff, therefore V_TG-eff is assumed to be equal to V_TG at every point in the graphene channel. The measured transfer curve describes a function: R_ds = f_R(V_TG), as illustrated in Fig. 4b. Since the steps of V_TG sweeping are quite small (0.28 V for LTG device measurements and 0.24 V for GTG device measurements), the curve between two measured points can be assumed to be linear. As illustrated in Fig. S7,† the corresponding R_ds for an arbitrary top gate V₀ can be calculated with the formula: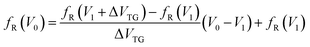, where V₁ is the lower V_TG point neighboring V₀ in the transfer curve and ΔV_TG is the sweeping step of V_TG; details of the derivation of this formula are explained in Fig. S7.† When top gate voltage V_T0 and source–drain bias voltage V_d0 are applied on the device, the electric potential in graphene channel changes from 0 V at the source (S) electrode to V_d0 at the drain (D) electrode as illustrated in Fig. 4c. Initially, the distribution of electric potential in the channel is assumed to be linear. Namely, if the positions of the source and drain are defined as x = 0 and x = L, the electric potential at position x along the channel length is x/L × V_d0 (Fig. 4c). As a result, V_TG-eff at position x in the graphene channel is V_T0 − x/L × V_d0. Therefore, V_TG-eff at different positions in the graphene channel ranges from V_T0 − V_d0 to V_T0, and total R_ds of the channel can be calculated with the transfer curve in the range of V_T0 − V_d0 to V_T0 in Fig. 4b. To calculate total R_ds, the whole graphene channel is divided into 100 sections with an identical length of L × 1/100 (Fig. 4d). Effective top gate V_TG-eff of the n-th section at x_n = L × n/100 is V_T0 − x_n/L × V_d0 = V_T0 − n/100 × V_d0, and as a result, resistance of this section is R_n = f_R(V_T0 − n/100 × V_d0) × 1/100. Finally, resistance of the whole channel is calculated as R_ds = ∑R_n = 1/100 × ∑ f_R(V_T0 − n/100 × V_d0), and the I_ds at bias voltage V_d0 in I_ds–V_ds curve is I_d0 = V_d0/R_ds. The I_ds–V_ds curves of the GTG device can be simulated in a similar manner, with its own transfer curves as input.

Fig. 4 Schematic of the model for simulating R_ds. (a) Nearly uniform distribution of electric potential in the graphene channel when V_ds = 0.1 V is applied for transfer curves measurements. (b) R_ds of graphene channel is assumed to be a function f_R of V_TG: R_ds = f_R(V_TG), which is described by the transfer curves. Total R_ds of the graphene channel measured at top gate voltage V_T0 and source–drain bias voltage V_d0 can be calculated based on the curve in the colored range. (c) When top gate voltage V_T0 and bias voltage V_d0 are applied on a graphene device, V_TG-eff at different positions in the graphene channel are assumed to linearly change from V_T0 − V_d0 at drain (D) electrode to V_T0 at source (S) electrode. (d) The whole graphene channel is divided into 100 sections along its length, and the resistance R(x_n) of a section at x_n is defined as 1/100 of f_R(V_TG-eff(x_n)), V_TG-eff(x_n) is the effective top gate at x_n.

To assess the simulation model, simulated I_ds–V_ds curves of LTG and GTG devices are compared with respect to the measured results. Fig. 5a–d present the simulated (Sim) I_ds–V_ds curves of LTG and GTG devices at the gate voltages in Fig. 2c and f, as well as the measured (Mea) results demonstrated for straightforward comparison. Apparently, the simulation accuracy seems quite acceptable at most of the (V_TG, V_ds) combinations, while the difference between simulated and measured I_ds–V_ds curves is enlarged at specific (V_TG, V_ds) combinations. This rule can be quantitatively understood with the ratio of simulated and measured I_ds (I_ds Sim/Mea ratio) shown in Fig. 5e–h, where the white dashed lines are defined by V_TG − V_ds = V_TG-CNP. The I_ds Sim/Mea ratio fluctuates between 0.9 and 1.1 at (V_ds, V_TG) combinations far from the white dashed lines, in other words, the simulation error is less than 10% when the graphene is heavily doped by dual-gating. Therefore, the dual-gated mono–bilayer graphene works like a uniform material as assumed in the simulation model, and this result could be interpreted with the transfer curves in Fig. 2a and b, indicating that R_ds tends to be independent of V_TG, when V_TG is far from CNPs. In contrast, the I_ds Sim/Mea ratio at (V_ds, V_TG) combinations close to the white lines can be lower than 0.4. In other words, the simulation error is larger than 60% when the doping level of dual-gated graphene is close to zero, where R_ds values of the devices are substantially sensitive to the shift of V_TG according to the curves in Fig. 3a and b. The I_ds Sim/Mea ratios of LTG and GTG devices under other conditions shown in Fig. S8† also confirm the dependence of simulation error on V_TG − V_ds. Since the graphene channel is assumed to be uniform in the simulation model, the considerable simulation error indicates that the graphene channel does not work as a uniform material, in other words, there is a junction built at the dual-gated mono–bilayer graphene interface. Accordingly, it is reasonable to say that the dual-gated mono–bilayer graphene works like a uniform channel at heavy doping, while like a heterojunction when the doping is close to zero. The gate dependent Mb/Bm I_ds ratios and Sim/Mea I_ds ratios suggest that a gate tunable electronic junction is successfully built in dual-gated mono–bilayer graphene, and the junction tends to be remarkable when the dual-gating induced doping is close to zero.

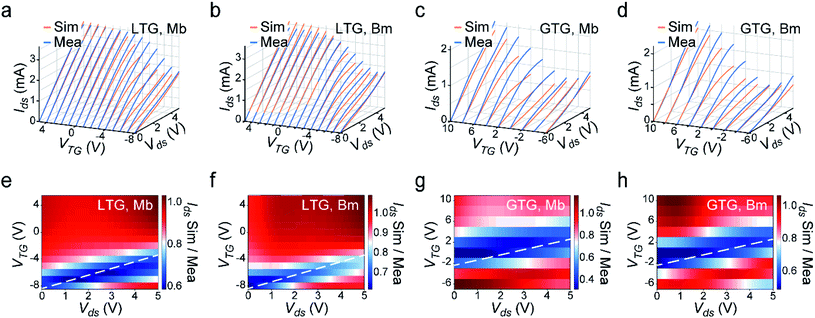Fig. 5 Comparison between simulated and measured I_ds–V_ds curves. (a–d) Measured (Mea) I_ds–V_ds curves shown in Fig. 2 and the simulated (Sim) results based on transfer curves in Fig. 3 and S6.†V_BG of LTG and GTG devices are −40 V and 100 V. (e–h) Ratio of I_ds Sim/Mea calculated with the data in (a–d). The red areas with Sim/Mea ≈ 1 correspond to high accuracy R_ds simulation, while the blue areas with Sim/Mea ≪ 1 present low simulation accuracy, because the simulated I_ds is much smaller than the measured counterpart. The white dashed lines correspond to V_TG − V_ds equals to V_TG-CNP in Fig. 3 and S6.†

Conclusion

In conclusion, directional electronic transport across a dual-gated mono–bilayer graphene interface is systematically investigated, and a new protocol for I_ds–V_ds curve simulation is proposed. The measured I_ds–V_ds curves demonstrate that the mono–bilayer graphene has different conductance under bias voltage V_ds in opposite directions (Mb and Bm modes), indicating that an electronic junction is built at the atomically sharp mono–bilayer graphene interface. Additionally, the gate dependent Mb/Bm I_ds ratio and I_ds–V_ds curve simulation indicate that this electronic junction is gate tunable, and the junction could be enhanced when the doping level of graphene is close to zero. Overall, the electrical measurements and numerical simulation prove the existence of a gate tunable junction at the dual-gated mono–bilayer graphene interface. Besides, the proposed simulation model explains I_ds–V_ds curves at a high electric field in a novel way and simplifies the prediction of output I_ds–V_ds curves with measured transfer curves. In the future, the mono–bilayer graphene junction can be enhanced by enlarging the bandgap opening of bilayer graphene with novel device structures,^23,24 thus the junction would be more functional and valuable. These results indicate that dual-gated mono–bilayer graphene junctions are promising candidates for functional electronics in the future.

Experimental section

Preparation and characterization of graphene flakes

Graphene flakes are obtained by scotch tape based mechanical exfoliation of highly oriented pyrolytic graphite (2D semiconductors), and transferred to a cleaned Si wafer with a 280 nm thick SiO₂ top layer. The thickness of graphene flakes is critical in this project, so that they are carefully characterized by two methods before device fabrication. The first method is based on the color contrast of the optical microscope (Olympus BX60) images. Green channel G₀ in the RGB value of pixels in the optical images is extracted with a custom MATLAB script, and RGS is defined as RGS = (G₀ − G_s)/G_s, where G_s is the averaged green value of bare Si/SiO₂ areas.^26–28 The areas of mono- and bilayer graphene should have RGS values of ∼0.06 and ∼0.12, respectively. The second method is the Raman spectrum. Graphene flakes are characterized using a Raman spectrometer (Horiba LabRAM HR) with a 514 nm excitation laser. According to the ratio of 2D/G and Lorentz fitting of 2D peaks, areas of mono- and bilayer graphene can be identified.²⁵ Consistency between the results of RGS and Raman characterization indicates that RGS characterization based on our equipment is reliable for identifying the graphene thickness.

Device fabrication

The graphene devices are fabricated through the process flow illustrated in Fig. S4.† Firstly, source and drain electrodes of 5 nm/100 nm Ti/Au are deposited through standard electron beam lithography (EBL, Vistec EBPG 5000), electron beam evaporation (MASA IM-9912) and lift-off process. Graphene areas between the source and drain electrodes are further patterned to a regular shape with EBL and reactive ion etching (RIE, Oxford Instruments PlasmaLab 80 Plus), to avoid the influence of interface states.¹⁶ The residues of EBL resist after RIE is removed with acetone, followed by high vacuum annealing (AML – AWB wafer bonding machine) at 200 °C for 2 hours. Right after annealing, the devices are transferred to evaporation equipment and a 2 nm thick Al layer is deposited on graphene. Subsequently, the Al layer is oxidized on a 130 °C hotplate in air for 3 min to form a Al₂O₃ seeding layer.²⁹ Above the Al₂O₃ layer, a 20 nm thick HfO₂ layer is grown by atomic layer deposition (ALD, Beneq TFS-500) at 200 °C, with TDMAH and water used as hafnium and oxidant sources. Finally, top gate electrodes are deposited through a process same to that of source and drain electrodes. The fabricated devices are connected to a printed circuit board for electrical measurements by wire bonding (Delvotec 53XX). Optical microscope images of the fabrication process are demonstrated in Fig. S5,† showing that source and drain electrodes are arranged to be parallel with the interface between mono- and bilayer graphene.

Electrical measurements

All the electrical measurements in this article are carried out with a semiconductor device parameter analyzer (Agilent B1500A) under ambient conditions. The I_ds–V_ds curves are measured by sweeping the bias voltage V_ds at various combinations of V_TG and V_BG, and transfer curves are measured by sweeping the top gate voltage at various back gate voltages. All the measurements are conducted at V_ds in opposite directions (Mb and Bm modes) along the channel length.

Numerical simulation

Values of simulated R_ds and I_ds are calculated with a custom MATLAB script based on the measured transfer curves.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

We acknowledge the provision of facilities by Aalto University at the OtaNano – Micronova Nanofabrication Centre and the OtaNano – Low Temperature Laboratory, and the funding from the Academy of Finland (276376, 295777, 312297, and 314810), Academy of Finland Flagship Programme (320167, PREIN), the European Union's Horizon 2020 research and innovation program (820423,S2QUIP), and ERC (834742).

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
2. B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147–150.
3. L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 372–377.
4. F. Bonaccorso, Z. Sun, T. Hasan and A. C. Ferrari, Nat. Photonics, 2010, 4, 611–622.
5. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162.
6. A. C. Ferrari, F. Bonaccorso, V. Fal'ko, K. S. Novoselov, S. Roche, P. Bøggild, S. Borini, F. H. L. Koppens, V. Palermo and N. Pugno, et al. , Nanoscale, 2015, 7, 4598–4810.
7. K. I. Bolotin, K. J. Sikes, Z. Jiang, M. Klima, G. Fudenberg, J. Hone, P. Kim and H. L. Stormer, Solid State Commun., 2008, 146, 351–355.
8. Z. Cheng, Q. Li, Z. Li, Q. Zhou and Y. Fang, Nano Lett., 2010, 10, 1864–1868.
9. L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 372–377.
10. H. Yuan, X. Liu, F. Afshinmanesh, W. Li, G. Xu, J. Sun, B. Lian, A. G. Curto, G. Ye and Y. Hikita, et al. , Nat. Nanotechnol., 2015, 10, 707–713.
11. Y. J. Zhang, T. Oka, R. Suzuki, J. T. Ye and Y. Iwasa, Science, 2014, 344, 725–728.
12. K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805.
13. S. Kim, G. Myeong, W. Shin, H. Lim, B. Kim, T. Jin, S. Chang, K. Watanabe, T. Taniguchi and S. Cho, Nat. Nanotechnol., 2020, 15, 203–206.
14. L. Li, J. Kim, C. Jin, G. J. Ye, D. Y. Qiu, F. H. da Jornada, Z. Shi, L. Chen, Z. Zhang and F. Yang, et al. , Nat. Nanotechnol., 2017, 12, 21–25.
15. C. Zhang, Y. Chen, J.-K. Huang, X. Wu, L.-J. Li, W. Yao, J. Tersoff and C.-K. Shih, Nat. Commun., 2016, 7, 10349.
16. C. P. Puls, N. E. Staley and Y. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 235415.
17. X. Xu, N. M. Gabor, J. S. Alden, A. M. van der Zande and P. L. McEuen, Nano Lett., 2010, 10, 562–566.
18. G. Liu, S. Rumyantsev, M. Shur and A. A. Balandin, Appl. Phys. Lett., 2012, 100, 033103.
19. X. Wang, W. Xie, J. Chen and J.-B. Xu, ACS Appl. Mater. Interfaces, 2014, 6, 3–8.
20. J. Tian, Y. Jiang, I. Childres, H. Cao, J. Hu and Y. P. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 125410.
21. Y. Zhang, T.-T. Tang, C. Girit, Z. Hao, M. C. Martin, A. Zettl, M. F. Crommie, Y. R. Shen and F. Wang, Nature, 2009, 459, 820–823.
22. K. F. Mak, C. H. Lui, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2009, 102, 256405.
23. T. Taychatanapat and P. Jarillo-Herrero, Phys. Rev. Lett., 2010, 105, 166601.
24. X. Liu, Z. Wang, K. Watanabe, T. Taniguchi, O. Vafek and J. Li, 2020, preprint, arXiv:2003.11072, https://arxiv.org/abs/2003.11072.
25. A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov and S. Roth, et al. , Phys. Rev. Lett., 2006, 97, 187401.
26. J. B. Oostinga, H. B. Heersche, X. Liu, A. F. Morpurgo and L. M. K. Vandersypen, Nat. Mater., 2008, 7, 151–157.
27. M. F. Craciun, S. Russo, M. Yamamoto, J. B. Oostinga, A. F. Morpurgo and S. Tarucha, Nat. Nanotechnol., 2009, 4, 383–388.
28. S. Russo, M. F. Craciun, M. Yamamoto, S. Tarucha and A. F. Morpurgo, New J. Phys., 2009, 11, 095018.
29. S. Kim, J. Nah, I. Jo, D. Shahrjerdi, L. Colombo, Z. Yao, E. Tutuc and S. K. Banerjee, Appl. Phys. Lett., 2009, 94, 062107.
30. B. Chakraborty, A. Das and A. K. Sood, Nanotechnology, 2009, 20, 365203.
31. I. Meric, M. Y. Han, A. F. Young, B. Ozyilmaz, P. Kim and K. L. Shepard, Nat. Nanotechnol., 2008, 3, 654–659.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0na00547a

---