Open Access Article
Open Access ArticleMachine learning methods for multi-walled carbon nanotubes (MWCNT) genotoxicity prediction†
Marianna
Kotzabasaki‡
 *,
Iason
Sotiropoulos‡
*,
Iason
Sotiropoulos‡
 ,
Costas
Charitidis
,
Costas
Charitidis
 and
Haralambos
Sarimveis
and
Haralambos
Sarimveis
 *
*
School of Chemical Engineering, National Technical University of Athens, 9 Heroon Polytechneiou Street, Zografou Campus, 15780, Athens, Greece. E-mail: mariannako@chemeng.ntua.gr; hsarimv@central.ntua.gr; Fax: +30 2107723138; Tel: +30 2107723236 Tel: +302107723237
First published on 12th April 2021
Abstract
Multi-walled carbon nanotubes (MWCNTs) are made of multiple single-walled carbon nanotubes (SWCNTs) which are nested inside one another forming concentric cylinders. These nanomaterials are widely used in industrial and biomedical applications, due to their unique physicochemical characteristics. However, previous studies have shown that exposure to MWCNTs may lead to toxicity and some of the physicochemical properties of MWCNTs can influence their toxicological profiles. In silico modelling can be applied as a faster and less costly alternative to experimental (in vivo and in vitro) testing for the hazard characterization of MWCNTs. This study aims at developing a fully validated predictive nanoinformatics model based on statistical and machine learning approaches for the accurate prediction of genotoxicity of different types of MWCNTs. Towards this goal, a number of different computational workflows were designed, combining unsupervised (Principal Component Analysis, PCA) and supervised classification techniques (Support Vectors Machine, “SVM”, Random Forest, “RF”, Logistic Regression, “LR” and Naïve Bayes, “NB”) and Bayesian optimization. The Recursive Feature Elimination (RFE) method was applied for selecting the most important variables. An RF model using only three features was selected as the most efficient for predicting the genotoxicity of MWCNTs, exhibiting 80% accuracy on external validation and high classification probabilities. The most informative features selected by the model were “Length”, “Zeta average” and “Purity”.
Introduction
Multi-walled carbon nanotubes (MWCNTs) are long, hollow cylindrical tubes with outer diameters in the range 3–30 nm and lengths that can reach the order of cm. MWCNTs have large length-to-diameter ratio, varying between 10 and ten million, while their wall thickness is quite constant along the axis, thus the inner channel is straight.1MWCNTs were discovered by Sumio Iijima in 1991,2 as soot-like products in the Krätschmer–Huffman arc discharge synthesis reactor used for the formation of fullerene (C60).3 Later, single-walled carbon nanotubes (SWCNTs) were discovered.4 SWCNTs are assembled into coaxial Russian-doll structures, forming MWCNTs with walls corresponding to each single-walled nanotube. The intertubular distance in MWCNTs is 0.340 nm. The main difference between SWCNTs and MWCNTs is that the former are flexible, while the latter are tough and rigid, rod-shaped structures. SWCNTs are also of smaller widths, with diameters typically in the range 1–2 nm, with curved structures rather than straight.5
Due to unique tubular structures and perfect covalent C–C bonding, MWCNTs exhibit fascinating physical and chemical properties, such as ultra-high mechanical strength, very good electrical and thermal conductivity (∼3000 W m−1 K−1, comparable to diamond), large aspect ratios, high surface area (SA), desirable chemical and environmental stability and distinct optical characteristics.6 MWCNTs are the strongest materials ever discovered. A MWCNT's highest measured tensile strength was up to 63 GPa, which is around 50 times higher than steel.5,7
The aforementioned MWCNTs' superb (and unique) characteristics give them great potential in various emerging applications in areas from biotechnology (imaging, tissue engineering, sensors and targeted drug delivery) to electronics (energy production and storage, transistors) and other fields of materials science (photonics, multi-functional coatings/films and nanocomposites).8 In the biomedical area, a number of applications of MWCNTs have been proposed including drug delivery, diagnosis and imaging, cancer diagnosis, gene therapy, photothermal therapy, etc. For instance, MWCNTs are efficiently used as carrier to deliver quantum dots (QDs) and proteins into cancer cells because QDs have photoluminescent properties, which are beneficial in bioimaging. MWCNTs may also be used for the treatment of HIV/AIDS and Neurodegenerative Diseases like Alzheimer Syndrome, while carboxylated-nanotubes may have potential as antioxidants in anti-ageing cosmetics and food preservation. Moreover, they have emerged as potential biosensors and nanorobots in diagnostics and as nanoprobes in scanning probe microscopy.9
Although MWCNTs have exceptional physicochemical properties, concerns have been raised about their safety, which are due to their small sizes and fibrous structures. MWCNTs may pose hazards, similar to asbestos.10 A number of physicochemical properties and characteristics of MWCNTs have been associated with their toxicological profiles: tube length and diameter, specific surface area, surface reactivity, metal impurities/catalysts, agglomeration state/dispersion, surface functionalization and rigidity/flexibility.11 As Poland et al. reported,12 longer MWCNTs exhibited stronger inflammation activity to mouse in the intraperitoneal administration route. Lam et al.,13 also pointed out that the content of metal used as a catalyst is very important. They concluded that the impure metals may enhance the pulmonary toxicity of carbon nanoforms. In other studies, it has been shown that contamination of amorphous carbon in the MWCNTs may affect strongly their biological activity, compared to purer MWCNTs.14,15 Additionally, it was reported that the agglomeration state of carbon nanomaterials also affected toxicity. Exposure to well-dispersed MWCNTs led to fewer granulomatous lesions in the lung, while non-dispersed nanostructures produced granulomatous inflammation.9
The investigation and study of potential hazards resulting from exposure to engineered MWCNTs is of particular interest in the nanotoxicology area. In silico predictive modelling is a computational data-driven approach that can be applied for the prediction of adverse effects of MWCNTs, in the effort to reduce animal testing. This aligns with Annex XI16 of Registration, Evaluation, Authorisation and Restriction of Chemicals (REACH) regulation (European Parliament and Council 2006), which describes alternative (non-animal) approaches such as grouping and read-across,17 Quantitative Structure–Activity Relationship (QSAR),18in vitro methods and weight of evidence, which can be used instead of in vivo tests to examine and evaluate the risks of exposure to chemicals.
Read-across methods are based on the hypothesis that similar chemical substances, follow a regular pattern, based on their chemical composition and/or physicochemical (PC) properties and may also have comparable toxicological properties. Thus, the toxicological profile of one target substance can be predicted by using data for the same endpoint from other reference substances. Grouping of MWCNTs types to read-across data for toxicological endpoints has been efficiently evaluated by Aschberger et al.,11 following the workflow proposed by the European Chemical Agency (ECHA) for grouping and reading across nanomaterials.19
Nano-QSARs, are mathematical models, which are based on the idea that the structure of a substance affects its activity and thus similar structures exhibit similar activities. Molecular descriptors (which are the physicochemical properties of MWCNTs in our case) play a fundamental role in QSAR and other in silico models, since they formally are the numerical representation of a molecular structure. For instance, Kotzabasaki et al.20 developed a robust QSAR model for predicting the nanotoxicity of superparamagnetic iron oxide nanoparticles (SPIONs) in stem-cell monitoring applications, using as molecular descriptors only the “overall particle size” and the “magnetic core chemical composition” of SPIONs. Kim21 and co-workers have successfully proposed a nano-QSAR model based on Quasi-SMILES to predict the cytotoxicity of MWCNTs to human lung cells.
In this study, we have developed a fully validated QSAR model for the prediction of genotoxicity of MWCNTs. Firstly, we selected 15 different types of MWCNTs and constructed a dataset that includes both physicochemical and toxicological data. Genotoxicity was selected as the hazard endpoint. According to REACH, genotoxicity testing is required, even at the lowest tonnage level (above 1 tonne per year per manufacturer/importer) for all substances manufactured in the EU.22 Next, we developed and fully validated a nanotoxicity classification QSAR model for predicting genotoxicity of MWCNTs using physicochemical characteristics as input features. A number of cheminformatics workflows based on machine learning algorithms, were constructed and implemented in order to produce the best performing model. The modelling workflows were designed to include the selection of the most important variables affecting the toxicity of MWCNTs and the definition of the domain of applicability (DOA)23 of the predictive model. The model was finally implemented as a ready-to-use web application in the Jaqpot computational platform (https://app.jaqpot.org/) and is available to the community through the BIORIMA virtual organisation.
Computational methodology
Predictive modeling workflow
This particular case study follows a workflow shown below in algorithm of Fig. 1.In the final step of this study, the model with the best performance was chosen and was implemented as a user-friendly web application in the Jaqpot platform.
Data collection and treatment
Fifteen high purity MWCNTs were selected, based on the richness and quality of the available physicochemical and toxicological data. Information on these MWCNTs was gathered from relevant MWCNT dossiers and from peer reviewed literature.11,26–29 According to previous studies, ten out of the fifteen MWCNTs (NRCWE040s – NRCWE-049)28,29 can be organized into three groups with respect to their physicochemical properties (thin, thick and short, group I–III, respectively). Each group included three functionalized MWCNTs which differed in the type of functionalization: a pristine, an –OH and a –COOH type. Group III also included a –NH2 type functionalized MWCNT.27 The five remaining analogues were taken from the OECD Working Party on Manufactured Nanomaterials (WPMN)30 (NM-400 – NM-403 & NRCWE-006 ‘a different batch of NM-400’). These MWCNTs were not functionalized and are called standard materials in the literature.28 Additional samples were found in the literature, but due to incomplete information, they were not included in our analysis. The full list of available characteristics (features) of MWCNTs are presented in Table 1. The “Genotoxicity” endpoint was measured in both in vivo studies for DNA strand breaks (Comet assay) and in vitro studies in mammalian cells for gene mutation (micro nucleus).11 Despite the different sources of the data, data integrity was secured since all studies were performed on the same MWCNTs.11,27,29| Features |
|---|
| Carbon purity (%)11 |
| Minimum length (nm)29 |
| Maximum length (nm)29 |
| Average length (nm)29 |
| Minimum diameter (nm)29 |
| Maximum diameter (nm)29 |
| Average diameter (nm)29 |
| Specific surface area (SSA) measured by BET (m2 g−1)29 |
| % Impurities (Fe2O3, CoO, NiO, MgO, MnO)29 |
| Concentration of endotoxins (Eu ml−1)29 |
| Combustion elemental analysis (CEA), C, H, N, O (wt%)27 |
| Surface coatings OH, COOH, NH2, (mmol g−1)27 |
| Zeta average (Zave) batch and zeta average at 12.5 and 200 μg ml−1 (nm)27 |
| Polydispersity index (PdI) batch and PdI at 12.5 and 200 μg ml−1 (ref. 27) |
| Reactive oxygen species (ROS) and respective peak concentrations (μg ml−1)27 |
The information available for each MWCNT was structured in a ready-for-modelling dataset including both physicochemical and toxicological information (Table S1 in the ESI†). The 15 MWCNTs with their partitioning into groups, the genotoxicity end-points and some key physicochemical features are presented in Table 2.
| Group | Code | Type | Length | Diameter | BET | Impurity | Purity | CEA | Endotoxinest | Genotoxicity |
|---|---|---|---|---|---|---|---|---|---|---|
| Group I | NRCWE-040 | Pristine | 518.9 | 22.1 | 150 | 0.773 | 98.60 | 96.00 | 0.18 | 0 |
| NRCWE-041 | –OH | 1005.0 | 26.9 | 152 | 0.462 | 99.20 | 97.00 | 0.22 | 0 | |
| NRCWE-042 | –COOH | 723.2 | 30.2 | 141 | 0.321 | 99.20 | 96.00 | 026 | 0 | |
| Group II | NRCWE-043 | Pristine | 771.3 | 55.6 | 82 | 1.219 | 98.50 | 96.00 | 0.25 | 0 |
| NRCWE-044 | –OH | 1330.0 | 32.7 | 74 | 1.006 | 98.60 | 97.00 | 0.27 | 1 | |
| NRCWE-045 | −COOH | 1553.0 | 30.2 | 119 | 2.782 | 96.30 | 93.00 | 0.34 | 1 | |
| Group III | NRCWE-046 | Pristine | 717.2 | 29.1 | 223 | 0.783 | 98.70 | 96.00 | 0.19 | 0 |
| NRCWE-047 | –OH | 532.5 | 22.6 | 216 | 0.781 | 98.70 | 97.00 | 0.01 | 0 | |
| NRCWE-048 | –COOH | 1604.0 | 17.9 | 185 | 0.721 | 98.80 | 96.00 | 0.03 | 0 | |
| NRCWE-049 | –NH | 731.4 | 14.9 | 199 | 0.738 | 98.80 | 97.0 | 0.05 | 0 | |
| Standard | NM-400 | Pristine | 847.0 | 11.0 | 254 | 0.368 | 90.00 | 88.00 | 0.24 | 1 |
| Materials | NM-401 | Pristine | 4048.0 | 67.0 | 18 | 0.065 | 99.19 | 98.00 | 0.42 | 0 |
| NM-402 | Pristine | 1372.0 | 11.0 | 226 | 1.313 | 92.97 | 92.00 | 0.01 | 1 | |
| NM-403 | Pristine | 1373.0 | 13.0 | 227 | 5.313 | 90.00 | 97.00 | 0.01 | 1 | |
| NRCWE-006 | Pristine | 5700.0 | 65.0 | 26 | 0.680 | 99.00 | 98.00 | 0.51 | 1 |
Data pre-processing
The data that were used in this study were mainly selected from three literature studies and are extensively presented in Table S1 of the ESI.†11,27,29 First step of the data pre-processing section was to fill the missing values of the physicochemical properties. In more details, “impurity” values, collected from the Poulsen et al. work,29 contained percentages of impurities (wt%) in different metal oxides, resulting to a dataset with many missing values. In order to bypass this issue, a new feature was created (“Impurity”), as the summation of the different types of impurities. In addition, the “Endotoxins” values of NRWCE-041 and NM-400 analogues were missing, and were filled with the mean of the “Endotoxins” values of the rest of the materials in the same group.Next step was the augmentation of the dataset. The standard deviations of “Diameter” values were used to create two new features: “Minimum Diameter” and “Maximum Diameter”. Feature “Type” indicates the type of the functional group of an observation and was originally a categorical field. This feature was encoded via the “One-Hot Encode” method resulting to 4 new binary features: “Type_Pristine”, “Type_OH”, “Type_COOH” and “Type_NH2”. For each analogue, these columns contained the value “0”, except from the column that represented the specific type of the analogue, e.g. for analogue NRCWE-041 “Type_Pristine”, “Type_COOH” and “Type_NH2” values were “0”, whereas the “Type_OH” column had the value “1”. The original “Type” column was then discarded.
The endpoint “genotoxicity” of this study was a binary column with values “1”, indicating an analogue as genotoxic, and “0” indicating an analogue as non-genotoxic. The endpoint values were taken from the Aschberger et al. study.11 Hence, according to the results of the in vitro chromosome aberration (micronucleus) analogues, NM-400, NM-402, NM-403 and NRCWE-006 were considered as toxic. In addition, results of in vivo DNA damage-comet assay indicated that NRCWE-044 and NRCWE-045 in different concentrations could result to DNA strand breaks, and these NMs were also considered as genotoxic.11
Finally, all features were scaled between values “0” and “1” (Table S2†). Scaling was performed by subtracting from each feature the lowest value and dividing it with the difference between highest and lowest values (min–max scaling).
Train–Test Split
Instead of a random split, we preferred to use the Kennard–Stone (KS) algorithm31 for partitioning the available dataset into training and test sets. The KS method provides a uniform coverage over the available data and selects analogues for the training set, which are on the boundaries of the data set, so that the produced models cover a wide DOA23 in the multi-dimensional input space. The basic idea behind the KS algorithm is that Euclidean inter-sample distances are calculated first and the most separated analogues, are selected as training data points.Machine learning/chemoinformatics methodologies
In this study we used several supervised and unsupervised chemoinformatic techniques, in order to develop the most efficient model for predicting genotoxicity of MWCNTs. These techniques were applied using python 3.6.7.32Unsupervised techniques
Principal Component Analysis (PCA) 33,34 is a technique that reduces dimensionality of the dataset and removes the noise and the redundant information. PCA produces an orthogonal transformation on a set of features (in this case MWCNTs' physicochemical properties) and creates new latent features, known as Principal Components (PCs). Each principal component is a linear combination of all primary features. PCs are orthogonal to each other.35Supervised techniques
Random Forest (RF) 34,36 combines simple tree predictors in a way that each tree depends on the values of a random vector sampled independently, while for all trees in the forest, the same distribution is applied. The RF model decides according to the leveraged Gini impurity of each tree (mean decrease in Gini) leading to predictive models that do not overfit during the training process.Support Vector Machines (SVM) 34,37 is a method that aims to represent the data as points in the multi-dimensional space, mapped in a way that the samples of each class are divided by the widest possible gap. Given a training set, SVM constructs a set of hyperplanes that discern the analogues according to their class (in this case genotoxic or non-genotoxic). Finally, the hyperplane with the largest distance to the nearest training sample of any class is chosen for the classification.
Logistic Regression (LR) 34,38 is a statistical model that uses the “logistic function” in order to predict if a sample is labeled in class “0” or in class “1”. In LR, the logit function (log-odds) is calculated as a linear combination of the features and the values of this function can vary between 0 and 1. Then, by applying the logistic function the log-odds are converted to probability of class and also vary between 0 and 1. Finally, if the probability of a sample is higher than 0.5 the sample is labeled in class “1”, else it is tagged in class “0”.39
Naive Bayes (NB) 34,39 is a probabilistic model, based on the Bayes' theorem (eqn (1)), assuming independence among the features. A Gaussian NB model (GNB) is a Naive Bayes model where the likelihood of the features is assumed to follow a Gaussian distribution (eqn (2)).
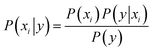 | (1) |
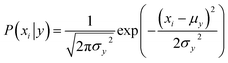 | (2) |
Bayesian optimization
Bayesian optimization40 is a technique that aims to minimize a function, f(x) on a bounded set S. In Bayesian optimization, the basic idea is to construct a probabilistic model for f(x) and use this model to decide the next point in S where the function will be evaluated. The Bayesian optimization method was applied for tuning the hyperparameters of the RF, LR and SVM methods. Table 3 presents the hyperparameters involved in the RF, SVM and LR methods, that were tuned during the training process.| Model | Hyperparameter | Description |
|---|---|---|
| RF | n_estimators | Number of trees in the forest |
| Min_samples_split | Minimum number of observations required to split a node | |
| Max_features | Maximum number of features to consider when looking for the best split of a node | |
| LR | C | Inverse of regularization strength |
| Penalty | Norm used in the penalization | |
| SVM | C | Regularization parameter |
| Gamma | Kernel coefficient | |
| Kernel | Kernel type |
Recursive feature elimination (RFE)
Recursive Feature Elimination (RFE)41 is a feature selection method. RFE removes iteratively the features with the lowest predictive importance until the specified number of features is reached. In order to apply this method, the machine learning algorithm should provide weights of the feature in the decision function of the produced model. In our analysis, the RFE method was applied to the RF36 and LR algorithms.38Leverage method for defining DOA
DOA23 is the physicochemical space on which the developed model is trained. Predictions on outliers (i.e. MWCNTs which are not inside the DOA) are not considered as reliable. DOA was defined, in this study, according to the Leverage method, which calculates a threshold depending on the number of features and the number of the training samples (eqn (3)). In the process of making prediction for a new MWCNT, the leverage value is calculated according to eqn (4), where X is the information matrix of the training set and xi is the vector containing the input features of the new MWCNT.42 Query MWCNTs with leverage higher than the defined threshold are considered to be unreliably predicted.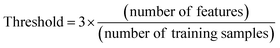 | (3) |
| hi = xTi(XTX)−1xi | (4) |
Results and discussion
In this study we developed two alternative workflows in order to select the most accurate and robust model for prediction genotoxicity of MWCNTs. The first workflow starts with the application of the PCA method, which reduces the dimension of the input space, by producing the principle components (PCs) or latent variables. The produced model still needs all the input features to calculate a prediction for a new MWCNT.In the second workflow, the aim was to eliminate the “noisy” features, i.e. features which were not highly informative for predicting the endpoint of interest. The RFE method was used for selecting the most important variables.
Predictive modelling using the reduced dataset produced by PCA
Fig. 2 presents the level of variance explained by applying the PCA method as a function of the number of PCs. Two PCs explained slightly more than 65% of the variance. In order to maintain most of the available information, we proceeded with using the first nine PCs corresponding to explaining 96% of the variance (Table S3†).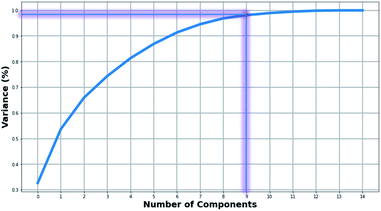 | ||
| Fig. 2 Diagram representing the percentage of the explained variance as a function of the principal components. | ||
For the selection of the testing samples, the KS algorithm31 was applied on the reduced dataset produced by the application of the PCA method. The following five analogues:
• NRCWE-040
• NRCWE-041
• NRCWE-048
• NM-401
• NM-402
were included in the test set, while the remaining 10 MWCNTs formulated the training set.
The RF, LR, SVM and NB statistical models were applied on the training set, in order to examine if the dimensional reduction process improves the prediction of genotoxicity endpoint. The hyperparameters of the RF, LR, SVM methods were optimized using the Bayesian optimization technique where the cross-validated accuracy score in the training set was the objective function that was minimised.40 The optimal parameters are presented in Table 4.
| Model | Hyperparameter | Optimal values |
|---|---|---|
| RF | n_estimators | 9 |
| Min_samples_split | 0.1025 | |
| Max_features | 0.6983 | |
| LR | C | 43.71 |
| Penalty | L2 | |
| SVM | C | 4.37 |
| Gamma | — | |
| Kernel | Linear |
The metrics of the models on the training set showed that all models were able to learn the underlying patterns of the training dataset, leading to an accuracy score of 1.0. The trained models were then used to predict the genotoxicity endpoint of the testing analogues. The performance of the produced models on the test set was examined using several classification metrics: confusion matrix, accuracy score, precision, specificity, sensitivity, F1-score and MCC metrics (eqn (S1)–(S7) of the ESI†). The accuracy score in a 4-fold cross validation test25 was used to evaluate the robustness of the models. The results are summarized in Table 5.
| RF | LR | SVM | NB | |||||
|---|---|---|---|---|---|---|---|---|
| Accuracy | 0.800 | 0.800 | 0.800 | 0.600 | ||||
| Precision | 0.000 | 0.50 | 0.500 | 0.000 | ||||
| Sensitivity | 0.000 | 1.000 | 1.000 | 0.000 | ||||
| Specificity | 1.000 | 0.750 | 0.750 | 0.750 | ||||
| F1-score | 0.000 | 0.670 | 0.667 | 0.000 | ||||
| MCC | 0.000 | 0.612 | 0.612 | −0.250 | ||||
| Cross-validation | 0.833 | 0.542 | 0.708 | 0.625 | ||||
| Confusion matrix | 4 | 0 | 3 | 1 | 3 | 1 | 3 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | |
The values of the metrics indicated that NB was unable to predict correctly two out of five testing samples. In addition, the RF model classified all the testing samples as non-genotoxic indicating a possible overfit of the model. The rest of the models had an accuracy score of 0.8 due to a misclassification of a non-genotoxic MWCNT. However, this particular MWCNT (NRCWE-048) is considered to be slightly out the domain of applicability of the models, hence in can be neglected. The low cross validation metric indicated that the LR and NB models failed the cross-validation test. The RF and SVM models' high cross-validation scores illustrated that both these models are highly robust.
Predictive modeling using feature selection
In our second approach the full dataset was considered first. The KS algorithm31 was used for splitting the scaled-dataset into training and testing subsets. The five selected testing analogues from this method were the same as in the PCA approach. The Bayesian optimization method40 was applied on the training set for selecting the optimal values of the hyperparameters of the RF, LR and SVM methods using again the cross-validated accuracy metric as the objective function to be minimized. The optimal values are presented in Table 6.| Model | Hyperparameter | Optimal values |
|---|---|---|
| RF | n_estimators | 10 |
| Min_samples_split | 0.5 | |
| Max_features | 0.1 | |
| LR | C | 43.71 |
| Penalty | L2 | |
| SVM | C | 9.98 |
| Gamma | 0.254 | |
| Kernel | Sigmoid |
The metrics of the models on the training set showed that all models were able to learn the training dataset. In more details, the RF, LR and NB models classified all training samples correctly, whereas the SVM model misclassified one non-genotoxic MWCNT, leading to a 0.9 training accuracy score and 0.82 MCC score. The produced models were validated on the test-dataset using the same classification metrics that were presented in the first approach. The results are presented in Table 7.
| RF | LR | SVM | NB | |||||
|---|---|---|---|---|---|---|---|---|
| Accuracy | 0.600 | 0.800 | 0.8000 | 0.600 | ||||
| Precision | 0.0.333 | 0.500 | 0.333 | 0.333 | ||||
| Sensitivity | 1.000 | 1.000 | 1.000 | 0.500 | ||||
| Specificity | 0.500 | 0.500 | 0.750 | 0.500 | ||||
| F1-score | 0.500 | 0.667 | 0.500 | 0.500 | ||||
| MCC | 0.666 | 0.612 | 0.612 | 0.408 | ||||
| Cross-validation | 0.708 | 0.458 | 0.917 | 0.458 | ||||
| Confusion matrix | 2 | 2 | 3 | 1 | 3 | 1 | 2 | 2 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
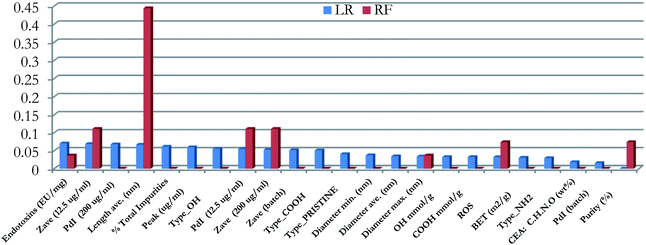
The performance of all produced models was clearly poorer compared to the models trained on the reduced PCA dataset. None of the models managed to predict correctly all the testing samples, while cross validation scores were lower, with the exception of the SVM method. The reason for this poor performance was the existence of noisy and non-informative features in the training set. Therefore, we proceeded with eliminating these variables, by applying the RFE method.41 This method was applied on the RF and LR algorithms only, because these models include attributes that distinguish the most significant features. The significances of the features in the LR model are represented by their coefficient at the exponential of the decision function, whereas the significance of the features in the RF models is indicated by the Gini criterion.36 The importance of the features in the two models is presented graphically in Fig. 3.
The RFE iterative process41 was applied to exclude the less important features, by eliminating the features with the smallest importance in each iteration. The result of this process was the development of LR and RF models, which use only four or three features accordingly, as shown in Table 8.
| Features for the LR model | Features for the RF model |
|---|---|
| Zeta average at 12.5 μg ml−1 | Zeta average at 12.5 μg ml−1 |
| Length (average) | Length (average) |
| Polydispersity index (batch) | Purity (%) |
| Purity (%) | — |
The “Purity” of MWCNTs as well as the “Zeta average” values at a 12.5 μg ml−1 dose and the “Length” were considered as significant features for both models. The two models were further optimized by applying the Bayesian optimization method. The optimal values of the hyperparameters are displayed in Table 9.
| Model | Hyperparameter | Optimal values |
|---|---|---|
| LR | C | 4.37 |
| Penalty | L2 | |
| RF | n_estimators | 19 |
| Min_samples_split | 0.116 | |
| Max_features | 0.666 |
The performance of these trained models was tested by classifying both the training and the corresponding testing analogues. Both models classified correctly all training samples, leading to an accuracy score equal to 1.0. The metric values corresponding to the test set are presented in Table 10.
| RF | LR | |||
|---|---|---|---|---|
| Accuracy | 0.800 | 0.800 | ||
| Precision | 0.500 | 0.500 | ||
| Sensitivity | 1.000 | 1.000 | ||
| Specificity | 0.750 | 0.750 | ||
| F1-score | 0.666 | 0.666 | ||
| MCC | 0.612 | 0.612 | ||
| Cross-validation | 0.917 | 1.000 | ||
| Confusion matrix | 3 | 1 | 3 | 1 |
| 0 | 1 | 0 | 1 | |
The accuracy score, precision, recall and F1-metrics and the confusion matrices all indicated that both LR and RF models were able to classify correctly the majority of the testing samples. Among the two methods, LR had a higher cross-validation score and was more robust. To further evaluate the performance of the two models, we present in Table 11 the probability distributions of all predicted outputs over the set of two classes. The probabilities were similar for the RF and the LR models and not close to 0.5, which indicating that the successful classifications are not due to chance correlations.
| RF | LR | |||
|---|---|---|---|---|
| MWCNT | Prob. of “0” class | Prob. of “1” class | Prob. of “0” class | Prob. of “1” class |
| NRWCE-040 | 0.74 | 0.26 | 0.74 | 0.26 |
| NRWCE-041 | 0.74 | 0.26 | 0.82 | 0.18 |
| NRWCE-048 | 0.68 | 0.32 | 0.73 | 0.27 |
| NM-401 | 0.31 | 0.69 | 0.36 | 0.64 |
| NM-402 | 0.00 | 1.00 | 0.31 | 0.69 |
Next step of the workflow was the calculation of DOA23,42 according to the Leverage method for the models. The thresholds were estimated to be equal to 1.2 for the LR model and 0.9 for the RF model and the values of the testing analogues are displayed below in Table 12. According to this table, all test MWCNTs were clearly within the DOA of the model, which further supported our confidence on the predictions of the model.
| Name | RF | LR | ||
|---|---|---|---|---|
| Leverage value | Reliability | Leverage value | Reliability | |
| NRCWE-040 | 0.20 | Reliable | 0.20 | Reliable |
| NRCWE-041 | 0.18 | Reliable | 0.36 | Reliable |
| NRCWE-048 | 0.33 | Reliable | 0.43 | Reliable |
| NM-401 | 0.48 | Reliable | 0.51 | Reliable |
| NM-402 | 0.13 | Reliable | 0.19 | Reliable |
Final results and model selection
In the first workflow, the application of the PCA data reduction and transformation method affected positively the performance of all models (increased precision and significantly improved the MCC metric). In the second workflow, the dimensional reduction of the dataset was achieved through the RFE method, which was applied on the RF and LR training procedures and resulted to models that use only 3 and 4 input features, accordingly, with 80% accuracy on the testing dataset. Several predictive models were produced as a result of the application of the two workflows. In order to select the best performing model, multiple criteria were taken into account:A number of models produced by the two workflows were highly successful with respect to the prediction accuracy criterion. The final LR and RF models were similar in terms of performance. The LR model's mean cross validation score is equal to 1.0 indicating that it may be considered as a slightly more robust model compared to the RF modes (mean cross validation score 0.917). However, the simplicity criterion was considered as a key parameter to select the best model to classify the genotoxicity of MWCNTs. Under this consideration, the RF that predicted the genotoxicity end point using only three input features was selected as the model that outperformed the rest with respect to all other criteria: highest cross validation score, high MCC score on the testing data, high probabilities of the predictions and use of only three features. This model was chosen as the most efficient model for predicting genotoxicity of MWCNTs. The model was finally trained on the full dataset, in order to take into account all the information in the available dataset. The final model predicted correctly the genotoxicity endpoint for all samples in the full dataset. The threshold that defines the DOA of the full model was 0.9.
Web implementation of the model
The source code for developing the model is available at: https://github.com/ntua-unit-of-control-and-informatics/MWCNTshttps://github.com/ntua-unit-of-control-and-informatics/SPIONs. The model has been implemented as a web service in the Jaqpot 5 modelling platform (https://app.jaqpot.org/) and is available in the following URL: https://app.jaqpot.org/model/THPwkjY80z7yaIFNAYJR under the BIORIMA organisation. In the overview tab, more details about the model are presented including a Predictive MarkUp Language (PMML) representation which contains the scaling coefficients and the logit function. For accessing the model, the interested user should first register in Jaqpot 5 and then become a member of the BIORIMA organisation by sending an e-mail to: E-mail: hsarimv@central.ntua.gr.Discussion and conclusions
The remarkable properties of MWCNTs and their potential use in a wide range of applications has led researchers to consider nanotubes based on carbon as one of the potential materials that may play key roles in the future of nanoscale-based applications. In this paper we have focused on developing a fully validated mathematical model for the prediction of genotoxicity of MWCNTs. Genotoxicity was selected as the toxicological endpoint, due to data completeness in literature and its relevance in risk assessment; it is a REACH requirement at the lowest tonnage level.22 Toxicological data of MWCNTs were extracted from both in vivo and in vitro studies.11 The goal was to develop the most efficient classification model for MWCNTs (geno)toxicity by designing and executing two different cheminformatics workflows employing various state-of-the-art machine learning applications. After a thorough validation of the models using multiple performance criteria, a model produced by the RF method and the RFE variable selection procedure, was selected as the model with the best performance. Another efficient model using four descriptors only, was produced by the LR method. The “percentage of pure carbon”, the “Zeta average” and the “Length” play a significant role in the prediction for both models. The LR model selected an additional physicochemical characteristic (“the polydispersity index”). These results are in agreement with the literature. “Carbon purity” and “zeta potential” have been reported by Aschberger et al.11 as important factors affecting MWCNTs genotoxic hazard potential. “Length” has also been suggested in the literature11 as a critical factor for MWCNTs in vivo toxicity. More specifically, long MWCNTs were usually considered to be more hazardous43 than short ones, in in vivo tests, causing cell death and ROS generation.44,45In conclusion, this study exhibited the value of using chemoinformatic techniques to produce a reliable model for predicting genotoxicity of MWCNTs. In future studies the predictive power of the model can be improved by considering information and data on extrinsic properties of the surrounding medium (pH, serum proteins, ionic strength).46,47
Conflicts of interest
There are no conflicts to declare.Acknowledgements
H. Sarimveis, C. Charitidis and M. Kotzabasaki acknowledge financial support by BIORIMA (Grant Agreement 760928), a project funded by the European Commission under the Horizon 2020 Programme.Notes and references
- R. Vajtai, Springer Handbook of Nanomaterials, 2013 Search PubMed.
- S. Iijima, Nature, 1991, 354, 56–58 CrossRef CAS.
- W. Krätschmer, L. D. Lamb, K. Fostiropoulos and D. R. Huffman, Nature, 1990, 347, 354–358 CrossRef.
- S. Iijima and T. Ichihashi, Nature, 1993, 363, 603–605 CrossRef CAS.
- N. Saifuddin, A. Z. Raziah and A. R. Junizah, J. Chem., 2013, 676815 Search PubMed.
- C. Liu and H. M. Cheng, Mater. Today, 2013, 16, 19–28 CrossRef CAS.
- M. F. Yu, B. S. Files, S. Arepalli and R. S. Ruoff, Phys. Rev. Lett., 2000, 84, 5552–5555 CrossRef CAS PubMed.
- A. Venkataraman, E. V. Amadi, Y. Chen and C. Papadopoulos, Nanoscale Res. Lett., 2019, 14(1), 220 CrossRef PubMed.
- P. Sharma, N. Kumar Mehra, K. Jain and N. K. Jain, Curr. Drug Delivery, 2016, 13, 796–817 CrossRef CAS PubMed.
- Y. Morimoto, M. Horie, N. Kobayashi, N. Shinohara and M. Shimada, Acc. Chem. Res., 2013, 46, 770–781 CrossRef CAS PubMed.
- K. Aschberger, D. Asturiol, L. Lamon, A. Richarz, K. Gerloff and A. Worth, Comput. Toxicol., 2019, 9, 22–35 CrossRef.
- C. A. Poland, R. Duffin, I. Kinloch, A. Maynard, W. A. H. Wallace, A. Seaton, V. Stone, S. Brown, W. MacNee and K. Donaldson, Nat. Nanotechnol., 2008, 3, 423–428 CrossRef CAS PubMed.
- C. W. Lam, J. T. James, R. McCluskey and R. L. Hunter, Toxicol. Sci., 2004, 77, 126–134 CrossRef CAS PubMed.
- D. B. Warheit, B. R. Laurence, K. L. Reed, D. H. Roach, G. A. M. Reynolds and T. R. Webb, Toxicol. Sci., 2004, 77, 117–125 CrossRef CAS PubMed.
- N. Kobayashi, M. Naya, K. Mizuno, K. Yamamoto, M. Ema and J. Nakanishi, Inhalation Toxicol., 2011, 23, 814–828 CrossRef CAS PubMed.
- European Parliament, Council, Regulation (EC) No 1223/2009 of the European Parliament and of the Council of 30 November 2009 on cosmetic products, Off. J. Eur. Union., 2009, L342, 59–209 Search PubMed.
- L. Lamon, K. Aschberger, D. Asturiol, A. Richarz and A. Worth, Nanotoxicology, 2019, 13, 100–118 CrossRef CAS PubMed.
- S. C. Peter, J. K. Dhanjal, V. Malik, N. Radhakrishnan, M. Jayakanthan and D. Sundar, Encyclopedia of Bioinformatics and Computational Biology, 2019, vol. 2, pp. 661–676 Search PubMed.
- European Chemicals Agency, Version 1.0, 2017, pp. 1–29 Search PubMed.
- M. I. Kotzabasaki, I. Sotiropoulos and H. Sarimveis, RSC Adv., 2020, 10, 5385–5391 RSC.
- T. X. Trinh, J.-S. Choi, H. Jeon, H.-G. Byun, T.-H. Yoon and J. Kim, Chem. Res. Toxicol., 2018, 31(3), 183–190 Search PubMed.
- European Parliament and Council, Regulation (Ec) No 1907/2006 of the European Parliament and of the Council of 18 December 2006 Reach, Off. J. Eur. Union., 2006, L396, 3–280 Search PubMed.
- K. Roy, S. Kar and P. Ambure, Chemom. Intell. Lab. Syst., 2015, 145, 22–29 CrossRef CAS.
- H. Abdi and L. J. Williams, Wiley Interdiscip. Rev.: Comput. Stat., 2010, 2, 433–459 CrossRef.
- T. Hastie, R. Tibshirani, J. Friedman and J. Franklin, Math. Intell, 2004, 27(2), 83–85 Search PubMed.
- T. Kato, Y. Totsuka, K. Ishino, Y. Matsumoto, Y. Tada, D. Nakae, S. Goto, S. Masuda, S. Ogo, M. Kawanishi, T. Yagi, T. Matsuda, M. Watanabe and K. Wakabayashi, Nanotoxicology, 2013, 7(4), 452–461 CrossRef CAS PubMed.
- P. Jackson, K. Kling, K. Jensen, P. Clausen, A. Madsen, H. Wallin and U. Vogel, Environ. Mol. Mutagen., 2015, 56(2), 183–203 CrossRef CAS PubMed.
- S. Poulsen, P. Jackson, K. Kling, K. Knudsen, V. Skaug, Z. Kyjovska, B. Thomsen, P. Clausen, R. Atluri, T. Berthing, S. Bengtson, H. Wolff, K. Jensen, H. Wallin and U. Vogel, Nanotoxicology, 2016, 10, 1–39 CrossRef PubMed.
- S. Poulsen, K. Knudsen, P. Jackson, I. Weydahl, A. Saber, H. Wallin and U. Vogel, PLoS One, 2017, 12(4), e0174167 CrossRef PubMed.
- K. Rasmussen, J. Mast, T. P. D. E. Verleysen, N. Waegeneers, F. Steen, J. Pizzolon, L. Temmerman, D. E. Van K. Jensen, R. Birkedal, P. Clausen, Y. Kembouche, N. Thieriet, O. Spalla, C. Guiot, D. Rousset, O. Witschger, S. Bau and C. Gaillard, Multi-walled Carbon Nanotubes, NM-400, NM-401, NM-402, NM-403: Characterization and Physico-Chemical Properties, Publications Office of the European Union, Luxembourg, 2014 Search PubMed.
- R. Kennard and L. Stone, Technometrics, 1969, 11, 137–148 CrossRef.
- G. V. Rossum and F. L. Drake, Python Reference Manual, PythonLabs, Virginia USA, 2001, http://www.python.org Search PubMed.
- P. F. Karl, London, Edinburgh Dublin Philos. Mag. J. Sci., 1901, 2(11), 559–572 CrossRef.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot, E. Duchesnay and G. Louppe, J. Mach. Learn. Res., 2012, 2825–2830 Search PubMed.
- I. Jolliffe and J. Cadima, Philos. Trans. R. Soc., A, 2016, 374, 20150202 CrossRef PubMed.
- L. Breiman, Mach. Learn., 2001, 45, 5–32 CrossRef.
- B. Boser, I. Guyon and V. Vapnik, Proceedings of the Fifth Annual ACM Workshop on Computational Learning Theory, 1996, pp. 144–152 Search PubMed.
- J. Cramer, SSRN Electron. J., 2002, 167–178 Search PubMed.
- H. Zhang, Proceedings of the Seventeenth International Florida Artificial Intelligence Research Society Conference, 2004, vol. 2 Search PubMed.
- B. Betrò, J. Glob. Optim., 1991, 1(1), 1–14 CrossRef.
- B. Darst, K. Malecki and C. Engelman, BMC Genet., 2018, 19, 65 CrossRef CAS PubMed.
- F. Sahigara, M. Kamel, D. Ballabio, A. Mauri, V. Consonni and R. Todeschini, Molecules, 2012, 17, 4791–4810 CrossRef CAS PubMed.
- F. Murphy, C. Poland, R. Duffin and K. Donaldson, Nanotoxicology, 2013, 7(6), 1157–1167 CrossRef CAS PubMed.
- H. Johnston, G. Hutchison, F. Christensen, S. Read, S. Hankin, K. Aschberger and V. Stone, Nanotoxicology, 2010, 4, 207–246 CrossRef CAS PubMed.
- G. Vietti, D. Lison and S. van den Brule, Part. Fibre Toxicol., 2016, 13, 11 CrossRef PubMed.
- J. Arts, M. Irfan, A. Keene, R. Kreiling, D. Lyon, M. Maier, K. Michel, N. Neubauer, T. Petry, U. Sauer, D. Warheit, K. Wiench, W. Wohlleben and R. Landsiedel, Regul. Toxicol. Pharmacol., 2016, 76, 234–261 CrossRef PubMed.
- A. Oomen, P. Bos, T. Fernandes, H. Kerstin, D. Borschi, H. Byrne, K. Aschberger, S. Gottardo, d. K. F. v. D. Kühnel, D. Hristozov, A. Marcomini, L. Migliore, J. Scott-Fordsmand, P. Wick and R. Landsiedel, Nanotoxicology, 2014, 8(3), 334–348 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0na00600a |
| ‡ Both authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |