Open Access Article
Open Access Article1T-CrO2 monolayer: a high-temperature Dirac half-metal for high-speed spintronics†
Shenda
He‡
a,
Pan
Zhou‡
 a,
Yi
Yang
*b,
Wei
Wang
a and
L. Z.
Sun
a,
Yi
Yang
*b,
Wei
Wang
a and
L. Z.
Sun
 *a
*a
aHunan Provincial Key Laboratory of Thin Film Materials and Devices, School of Materials Science and Engineering, Xiangtan University, Xiangtan, 411105, China. E-mail: zhoupan71234@xtu.edu.cn; lzsun@xtu.edu.cn
bSchool of Materials Science and Engineering, Xiangtan University, Xiangtan, 411105, China. E-mail: yangyi@xtu.edu.cn
First published on 31st March 2021
Abstract
Two-dimensional (2D) materials with complete spin-polarization, high-speed conduction electrons, large Curie temperatures and robust ferromagnetic ground states are desirable for spintronic applications. Based on first-principles calculations, we demonstrate that the 1T-CrO2 monolayer is an intrinsic 3d ferromagnetic Dirac half metal (DHM) with two symmetry protected Dirac cones near the Fermi level. The Fermi velocities (3.21 × 105 m s−1 and 4.85 × 105 m s−1) of the Dirac cones are in the same order as that of graphene, indicating its excellent transport properties. Its 2.48 eV half-metallic gap is large enough to prevent the spin-flip transition. Moreover, the two Dirac cones are robust against biaxial strain of up to ±4%. The robust ferromagnetism is mainly contributed by the 3d states of Cr and its Curie temperature is up to 507 K. Our results indicate that the ferromagnetic 1T-CrO2 monolayer is a promising candidate for high temperature, high efficiency spintronics applications.
1 Introduction
Spintronics, through manipulating the spin degree of freedom in electronic devices, is a promising technology for next-generation electronics due to its low power consumption, high speed carrier transfer, high integration density and nonvolatility.1 Half-metals,2 behaving as metals in one spin channel but as insulators or semiconductors in the opposite spin channel, have attracted great attention due to their direct application in spin filters, detectors and sensors for spintronics. Since the discovery and preparation of graphene,3 hundreds of researchers, both experimental and theoretical, have been pursuing new 2D Dirac materials2,4–6 due to their unique properties and tremendous potential applications, especially in nanoscale spintronics. There has been tremendous progress in searching for novel 2D materials with a broad range of electronic and optical properties,3,7,8 unfortunately, most of them in the pristine form are nonmagnetic, which significantly hinders their application in spintronics.9 Although magnetism can be introduced by dopants or defects,10,11 these may destroy the Dirac state12 and the long-range magnetic order was rarely observed. Hence, it is desirable to search for simple and intrinsic 2D materials with stoichiometric crystals which are ferromagnetic.Subsequent to the establishment of the spin gapless semiconductors (SGSs) concept in spintronics,13 Dirac half metals (DHMs) have been proposed based on a simple Kondo lattice model.14 As for DHMs, a graphene-like Dirac state exists in one spin channel and a band gap opens in the other one, preventing the spin-flip of the spin-polarized Dirac state. Massless Dirac fermions derived from the linear dispersion of the Dirac cone show a substantially different nature from ordinary electrons, such as ballistic charge transport and enormously high carrier mobilities.15,16 The coexistence of 100% spin polarization and massless Dirac fermions gives DHMs great potential for future nano-electronics, spintronics and optoelectronics. Moreover, the manipulation of both the charge and spin of the electrons only needs small external perturbations,17 which meets the requirements of next-generation spintronic and electronic devices. Since the DHM concept was introduced,14,18 several materials have been theoretically proposed to be DHMs,9,10,19,20 such as heterostructures (CrO2/TiO2),21 two-dimensional metal–organic frameworks (Mn(C6H5)3, Mn-DCA and M3C12O12),1,22,23 honeycomb-Kagome lattices (VCl3, C3Ca2 and Nb2O3)12,24,25 and MXene materials (YN2).9,26 In comparison with TM doped 2D materials, one of the most intriguing merits of DHMs is their potentially high working temperature due to the intrinsic exchange interactions. For example, the Curie temperatures of YN2 monolayers are up to 392 K, giving hope for their practical applications.26 The high working temperatures of DHMs makes them a promising platform for the emerging area of spintronics devices with high Fermi velocities. However, until now, DHMs have rarely been predicted and, consequently, the realization and observation of intrinsic DHMs in experiments are still challenging. Thus, exploring DHM materials, particularly DHMs with high Curie temperatures, is crucial to promote the development of spintronic devices.
In this work, using the first-principles method, we find that the 1T-CrO2 monolayer is an intrinsic ferromagnetic DHM with a high Curie temperature of 507 K. When spin–orbit coupling is not considered, two spin-polarized Dirac cones are located at the high symmetry point K and the high symmetry line Γ–K, which endows the monolayer with interesting properties and potential applications in spintronics. The Fermi velocities, vf, of the two Dirac cones (3.21 × 105 m s−1 and 4.85 × 105 m s−1) are in the same order as those of graphene (9.5 × 105 m s−1) and YN2 (3.74 × 105 m s−1),9,27 which reveals the great carrier mobility of the monolayer. Moreover, the Dirac cones are protected by rotation symmetry and are robust under biaxial strain of up to ±4%. When considering the SOC, a small band gap opens for the two Dirac cones, however, this can be ignored at room temperature. Our results indicate that the 1T-CrO2 monolayer is a promising DHM candidate for spintronics with a high Curie temperature.
2 Computational methods
The first-principles calculations were performed with the Vienna ab initio simulation package (VASP).28,29 The projector-augmented-wave (PAW) potential was adopted to describe the interactions between the nucleus and the electrons. The generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) was used for the exchange–correlation functional,30 and the hybrid functional HSE06 (ref. 31) was used to validate the results obtained with PBE. The spin–orbit coupling effect was also taken into account as part of our calculations.30,32 The cutoff energy was set to 520 eV, and the energetic and force convergence criteria were set as 10−6 eV and 10−2 eV, respectively. A 11 × 11 × 1 Γ-centered Monkhorst–Pack K-sampling mesh was used for integration in the Brillouin zone (BZ). The atomic positions and the lattice constants were fully optimized by the conjugate gradient algorithm. A vacuum region of 20 Å was used to avoid interactions between neighboring periodic images of the monolayer. To confirm the dynamic stability of the 1T-CrO2 monolayer, phonon spectra were obtained using the finite displacement method implemented in the CASTEP package33 in Materials Studio software. Ultrasoft pseudopotentials were used, and the energy cutoff and SCF tolerance were set at 500 eV and 5 × 10−7 eV per atom, respectively. The cutoff radius was set at 5.0 Å, which means that a 4 × 4 × 1 supercell was employed. The Monkhorst–Pack grid and separation of dispersion were set at the fine-level. To study the thermal stability of the 1T-CrO2 monolayer, ab initio molecular dynamics (AIMD) simulations at 300 K for 6 ps were performed. Furthermore, to account for the localized 3d orbitals of the TM atoms more accurately, the Hubbard U correction was employed within the rotationally invariant DFT + U approach proposed by Dudarev et al.,34 where only the Ueff = U − J value is meaningful instead of the individual U and J values. We chose a broad range of Ueff values (0 ∼ 5 eV) to allow a detailed examination of the effects of electronic correlation on the electronic structure of the system. The magnetic anisotropy energy (MAE) is defined as the difference of the energies corresponding to the in-plane axis and out-of-plane axis. To obtain the magnetic anisotropy energy (MAE), noncollinear non-self-consistent calculations with SOC were performed.3 Results and discussions
3.1 Structure and stability of the 1T-CrO2 monolayer
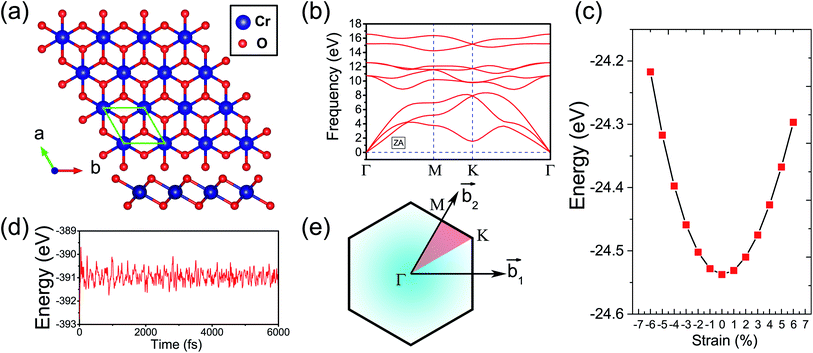
Fig. 1(a) presents the top and side views of the 1T-CrO2 monolayer, which contains one chromium (Cr) atom and two oxygen (O) atoms per unit cell, and the Cr atom is sandwiched into the two staggered O atomic layers. The space group of the monolayer is P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1(D33d, no. 164). The lattice constants of 1T-CrO2 are a = b = 2.89 Å and the bond length between neighbouring Cr and O atoms is 1.92 Å. To prove the stability of the monolayer, we calculate the energies under different strains and the results are presented in Fig. 1(c). The percentage strain is defined as ε = (a1 − a0)/a0, where a0 and a1 are the lattice constants without or with strain, respectively. We find that the pristine 1T-CrO2 is located at the energy extremum and it is stable under strain. Moreover, by distorting the 1T-CrO2 monolayer, we can obtain a stable 1Td-phase of CrO2 with a ferromagnetic magnetic ground state. However, its average energy is higher than that of 1T-CrO2. Therefore, we can conclude that the 1T phase is more stable than the 1Td phase for 2D CrO2. The charge transfer between Cr and O atoms was investigated by Bader charge population analysis.35 The results show that each O atom gets an average of 0.88e from the Cr atom, which indicates the ionic–covalent characteristic of the Cr–O bonds. To evaluate the energy stability of the 1T-CrO2 monolayer, its cohesive energy Ec(CrO2) and formation energy Ef(CrO2) were obtained with the following formulae:
m1(D33d, no. 164). The lattice constants of 1T-CrO2 are a = b = 2.89 Å and the bond length between neighbouring Cr and O atoms is 1.92 Å. To prove the stability of the monolayer, we calculate the energies under different strains and the results are presented in Fig. 1(c). The percentage strain is defined as ε = (a1 − a0)/a0, where a0 and a1 are the lattice constants without or with strain, respectively. We find that the pristine 1T-CrO2 is located at the energy extremum and it is stable under strain. Moreover, by distorting the 1T-CrO2 monolayer, we can obtain a stable 1Td-phase of CrO2 with a ferromagnetic magnetic ground state. However, its average energy is higher than that of 1T-CrO2. Therefore, we can conclude that the 1T phase is more stable than the 1Td phase for 2D CrO2. The charge transfer between Cr and O atoms was investigated by Bader charge population analysis.35 The results show that each O atom gets an average of 0.88e from the Cr atom, which indicates the ionic–covalent characteristic of the Cr–O bonds. To evaluate the energy stability of the 1T-CrO2 monolayer, its cohesive energy Ec(CrO2) and formation energy Ef(CrO2) were obtained with the following formulae: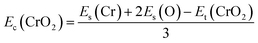 | (1) |
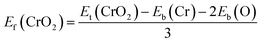 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 and 1T-HfTe2.41 To analyze the mechanical stability, we calculated the linear elastic constants and the results with Voigt notation42 are C11 = 18.69 Gpa nm, C22 = 18.53 Gpa nm, C12 = 9.25 Gpa nm and C44 = 4.59 Gpa nm. We can see that the elastic constants satisfy the Born-Huang criteria well43 (C11C22–C122 > 0 and C44 > 0), which suggests the mechanical stability of the 1T-CrO2 monolayer. Moreover, ab initio molecular dynamics (AIMD) simulations were carried out for 6 ps (with a time step of 1 fs) at 300 K and 600 K using a 4 × 4 × 1 supercell. The snapshots (the results can be found in Fig. S1 in the ESI†) and evolution of the energies as a function of time (see Fig. 1(d) and S1(c)†) reveal that 1T-CrO2 is preserved well under these temperatures.
40 and 1T-HfTe2.41 To analyze the mechanical stability, we calculated the linear elastic constants and the results with Voigt notation42 are C11 = 18.69 Gpa nm, C22 = 18.53 Gpa nm, C12 = 9.25 Gpa nm and C44 = 4.59 Gpa nm. We can see that the elastic constants satisfy the Born-Huang criteria well43 (C11C22–C122 > 0 and C44 > 0), which suggests the mechanical stability of the 1T-CrO2 monolayer. Moreover, ab initio molecular dynamics (AIMD) simulations were carried out for 6 ps (with a time step of 1 fs) at 300 K and 600 K using a 4 × 4 × 1 supercell. The snapshots (the results can be found in Fig. S1 in the ESI†) and evolution of the energies as a function of time (see Fig. 1(d) and S1(c)†) reveal that 1T-CrO2 is preserved well under these temperatures.
3.2 Magnetic ordering
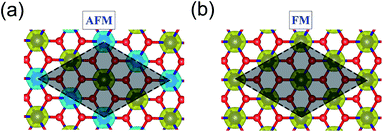
3d transition metal Cr is included in 1T-CrO2 and its preferential magnetic ground state firstly needs to be confirmed. As shown in Fig. 2, the antiferromagnetic (AFM) and ferromagnetic (FM) configurations are presented for the supercell of 2 × 2 × 1. The energy of the FM configuration is 0.144 eV per Cr atom lower than that of the AFM one, indicating the ferromagnetic ground state of the 1T-CrO2 monolayer. The integration of the spin-polarized electronic density around the Cr atoms shows that the magnetic moment of each Cr atom is 2 μB, corresponding to the d1↓3↑ spin configuration of Cr2+.The magnetic exchange of the 1T-CrO2 monolayer can be explained by the Goodenough–Kanamori–Anderson (GKA) formalism.44–46 According to the GKA formalism, the magnetic properties are determined by two distinct exchange mechanisms: the direct exchange between two Cr atoms, and the superexchange interaction of Cr–O–Cr chains. Since the angle of Cr–O–Cr is nearly 90° (97.61°), and the distance of two Cr2+ cations is 2.89 Å, as shown in Fig. 3(a), the direct AFM exchange interactions are weak and the majority exchange mechanism is the superexchange interaction. The d-orbitals of Cr can only couple with the orthogonal p-orbitals of O, making it impossible for electrons on one of the d-orbitals of Cr to hop to the d-orbital of the nearest Cr atom. Therefore, the superexchange between the nearest Cr atoms is mediated by the middle O atom that forms a bridge between the two Cr atoms. It is worth noting that the p-orbitals which mediate the hopping of the two d-orbitals of the Cr atoms are the px and py orbitals of the O atoms, as shown in Fig. 3(b). The energy of the system depends on the relative spin orientation of the d and p states. According to Hund’s rule, the O atoms tend to be triplet, namely the spin orientations of the px and py orbitals are parallel, which means that the d state hopping electrons of the two Cr atoms are also parallel to each other. In this case, the superexchange of the system produces the FM ordering for the 1T-CrO2 monolayer. The magnetic anisotropy of the 1T-CrO2 monolayer induced by SOC47 is an important property related to its magnetic stability, which keeps the long-range magnetic ordering of the monolayer and counteracts thermal fluctuations.48 We have performed noncollinear magnetic calculations to obtain the magnetic anisotropy energy (MEA) of the 1T-CrO2 monolayer, and the results indicate that the easy magnetization axis is along the in-plane [100] direction.
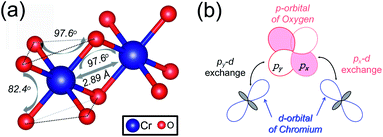 | ||
| Fig. 3 (a) The structural parameters of the 1T-CrO2 monolayer and the angle of Cr–O–Cr. (b) Illustration of the superexchange mechanism in 1T-CrO2. | ||
3.3 Electronic properties and Curie temperature
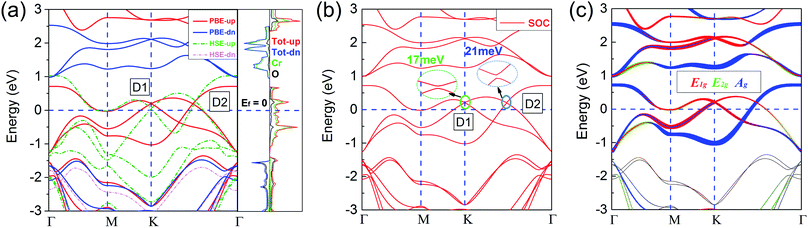
Based on the ferromagnetic ground state of the 1T-CrO2 monolayer proven above, the spin-resolved band structure without spin–orbit coupling (SOC) and the corresponding local density of states (LDOS) are shown in Fig. 4(a). The results indicate that there are two Dirac cones in the spin up channel located at the high symmetry point K (denoted as D1) and the high symmetry line Γ–K (denoted as D2). D1 is rightly located at the K point and is similar to that of graphene and 1T-Na2C.27 Therefore, we expect that this cone is protected by C3 rotation symmetry. For the cone of D2, we find that only the C2 rotation operator exists along the high symmetry line Γ–K (Fig. S2†). Further symmetry representation calculations reveal that the two crossing bands have opposite eigenvalues to the C2 operator, which indicate D2 is protected by the C2 rotation symmetry. The energy levels of the two Dirac points are 0.194 eV (D1) and 0.187 eV (D2) higher than the Fermi level. The results show that the system has half metallic behaviour and the Dirac cones are 100% spin polarized. Moreover, the insulating spin-down channel shows a band gap of 2.48 eV, making the spin-up channel, which includes the spin-polarized Dirac cones, extremely pure and steady around the Fermi level. These characteristics are favorable for spintronics due to it meaning spin-flip is avoided.According to the spin-resolved LDOS and orbital-resolved band structures shown in Fig. 4, we find that the band crossings are mainly contributed to by the d states of the Cr atoms. Furthermore, the vf of the Dirac cones are 3.21 × 105 m s−1 (D1) and 4.85 × 105 m s−1 (D2), which are in the same order as that of graphene (9.5 × 105 m s−1),27 and in particular the vf of D2 is above half of that of graphene, implying the high electron mobility in the monolayer. The large gap of the insulating channel (spin-down), in combination with the pure and high electron mobility in the other channel (spin-up) of the 1T-CrO2 monolayer, can filter the current into a single spin channel effectively. These properties can be beneficial for the application of the 1T-CrO2 monolayer in polarization optics and spintronics.13 When considering the effect of SOC, the results shown in Fig. 4(b) indicate that the Dirac cones open negligible gaps of 17 meV (D1) and 21 meV (D2). The feature of the Dirac cones is still preserved due to the tiny gap induced by the SOC which can always be ignored with the thermal perturbation under room temperature.
Additionally, the calculated 2D Young’s modulus is 140 N m−1, which is lower than that of graphene (340 N m−1)49 but higher than those of 2D MoS2 (130 N m−1)50 and 2D NiCl3 (25 N m−1).20 According to the stress–strain diagram in Fig. S6,† we find that the stress suddenly changes at a strain of 20%. This indicates that 20% is the elastic limit of 2D CrO2. That is to say that this material can keep its original stable structure when the strain is not beyond 20%. These results demonstrate that the effect of strain must be taken into consideration because it may influence the band structure of the monolayer. Therefore, we checked the stability of the DHM properties under external strain. The DHM states are still preserved under strain of up to ±4%, and the results can be found in Fig. S3 in the ESI,† indicating the robustness of the DHM properties of the 1T-CrO2 monolayer with regards to external strain.
For 3d transition metal compounds, the influence of correlation effects is significant. To estimate the correlation effects, the GGA + U method was used. Moreover, the cRPA51 method was used to evaluate the Hubbard U. The calculated Ueff = 2 eV, which indicates that the electronic correlation of element Cr in the 1T-CrO2 monolayer is weaker than that in the Cr2O3 bulk state (Ueff = 3.6 eV).52 The band structure with Hubbard Ueff = 2 eV is presented in Fig. S4(b) in the ESI.† The results indicate that the Dirac cones are well preserved. Interestingly, the Hubbard Ueff enlarges the band gap of the spin-down channel to larger than 3 eV, which is favorable for avoiding the spin flip of the spin-up channel. Furthermore, we chose a broad range of values of Ueff from 0 eV to 5 eV to examine in detail the correlation effect on the electronic structure of the system, and the results are shown in Fig. S4 in the ESI.† The results show that the influence of the Hubbard Ueff on the electronics of the system, especially the Dirac cones, is negligible. The half-metallicity is well retained and the Dirac cone D1 is close to Fermi level with the increase in the value of Ueff. Intriguingly, the band gap of the spin-down channel is enlarged with the increase in the value of Ueff. These results indicate that the DHM characteristics of the 1T-CrO2 monolayer are robust to the on site Hubbard Ueff correction.
The Curie temperature (Tc) is one of the most important parameters to guarantee the magnetic ordering stability of the 1T-CrO2 monolayer. Based on the energy difference (ΔE = 0.144 eV) of the AFM and FM orderings, we can estimate the Tc from the mean-field approximation (MFA)53via
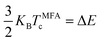 | (3) |
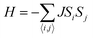 | (4) |
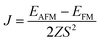 | (5) |
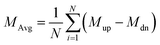 | (6) |
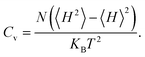 | (7) |
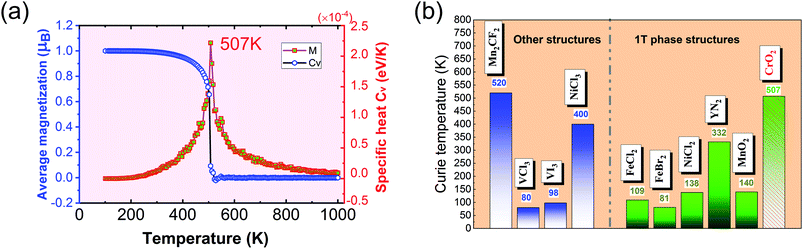
The calculated results of these at different temperatures are presented in Fig. 5. We find that the average magnetic moment suddenly decreases at around 507 K. At the same time, the specific heat Cv also reaches a sharp peak near this temperature. Both of these results reveal that the Curie temperature of CrO2 is close to 507 K. This value share similar level with that of Mn2CF2 (ref. 55) and is higher than those of other transition metal compounds.9,12,20,56,57 A detailed comparison can be found in Fig. 5(b). For a triangular system, the ratio of Curie temperatures between mean field and experiment is approximately equal to 0.61(TMFAc/Tc ≈ 0.61)53. According to our results of TMFAc = 1114 K and Tc = 507 K, the ratio of these is 2.2, which is almost three times the empirical value. The high Tc of the 1T-CrO2 monolayer demonstrates that it is a potential candidate for future room temperature spintronics.
4 Conclusions
In the present work, we find that the 1T-CrO2 monolayer is a stable DHM with a Curie temperature of 507 K. Its ferromagnetic ground state can be understood by the superexchange mechanism from the GKA rules. The large insulating gap (2.48 eV) of the opposite spin channel prevents the spin-flip transition happening between the two different channels. There are two spin-polarized Dirac cones at the high symmetry point K and along the high symmetry line K–Γ. The Fermi velocities of these two cones are in the same order as that of graphene. We expect the 1T-CrO2 monolayer to be a promising platform for future high efficiency spintronic applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors Shenda He and Pan Zhou contributed equally to this work. This work is supported by the National Natural Science Foundation of China (Grants No. 11804287 and 11574260), the Natural Science Foundation of Hunan Province, China (Grant No. 2019JJ50577), and the Scientific Research Fund of Hunan Provincial Education Department (18A051).Notes and references
- X. Wang, T. Li, Z. Cheng, X.-L. Wang and H. Chen, Appl. Phys. Rev., 2018, 5, 041103 Search PubMed.
- R. A. de Groot, F. M. Mueller, P. G. v. Engen and K. H. J. Buschow, Phys. Rev. Lett., 1983, 50, 2024–2027 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- P. Dowben, J. Phys.: Condens. Matter, 2007, 19, 310301 CrossRef PubMed.
- K. W. Lee and C. E. Lee, Adv. Mater., 2012, 24, 2019–2023 CrossRef CAS.
- I. Galanakis and E. Saslogul, Appl. Phys. Lett., 2011, 99, 052509 CrossRef.
- K. F. Mak, K. L. McGill, J. Park and P. L. McEuen, Science, 2014, 344, 1489–1492 CrossRef CAS PubMed.
- Q. Sun, Y. Dai, Y. Ma, N. Yin, W. Wei, L. Yu and B. Huang, 2D Mater., 2016, 3, 035017 CrossRef.
- Z. Liu, J. Liu and J. Zhao, Nano Res., 2017, 10, 1972–1979 CrossRef CAS.
- Y. Li, D. West, H. Huang, J. Li, S. B. Zhang and W. Duan, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 201403 CrossRef.
- J. Červenka, M. Katsnelson and C. Flipse, Nat. Phys., 2009, 5, 840–844 Search PubMed.
- J. He, S. Ma, P. Lyu and P. Nachtigall, J. Mater. Chem. C, 2016, 4, 2518–2526 RSC.
- X. L. Wang, Phys. Rev. Lett., 2008, 100, 156404 CrossRef CAS PubMed.
- H. Ishizuka and Y. Motome, Phys. Rev. Lett., 2012, 109, 237207 CrossRef PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200 CrossRef CAS PubMed.
- S. V. Morozov, K. S. Novoselov, M. I. Katsnelson, F. Schedin, D. C. Elias, J. A. Jaszczak and A. K. Geim, Phys. Rev. Lett., 2008, 100, 016602 CrossRef CAS PubMed.
- X. Wang, Natl. Sci. Rev., 2017, 4, 252–257 CrossRef CAS.
- Y. Akagi and Y. Motome, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155132 CrossRef.
- Y. Wang, S. Li, C. Zhang, S. Zhang, W. Ji, P. Li and P. Wang, J. Mater. Chem. C, 2018, 6, 10284–10291 RSC.
- J. He, X. Li, P. Lyu and P. Nachtigall, Nanoscale, 2017, 9, 2246–2252 RSC.
- T. Cai, X. Li, F. Wang, S. Ju, J. Feng and C. Gong, Nano Lett., 2015, 15, 6434–6439 CrossRef CAS PubMed.
- Y. Wang, W. Ji, C.-w. Zhang, P. Li, P. Wang, B. Kong, S. Li, S. Yan and K. Liang, Appl. Phys. Lett., 2017, 110, 233107 CrossRef.
- M. Wu, Z. Wang, J. Liu, W. Li, H. Fu, L. Sun, X. Liu, M. Pan, H. Weng and M. Dincă, 2D Mater., 2016, 4, 015015 CrossRef.
- W. Ji, B. Zhang, S. Zhang, C. Zhang, M. Ding, P. Li and P. Wang, J. Mater. Chem. C, 2017, 5, 8504–8508 RSC.
- S. Zhang, C. Zhang, S. Zhang, W. Ji, P. Li, P. Wang, S. Li and S. Yan, Phys. Rev. B, 2017, 96, 205433 CrossRef.
- X. Kong, L. Li, O. Leenaerts, W. Wang, X. Liu and F. M. Peeters, Nanoscale, 2018, 10, 8153–8161 RSC.
- W. Ji, B. Zhang, S.-F. Zhang, C. Zhang, M. Ding, P. Wang and R. Zhang, Nanoscale, 2018, 10, 13645–13651 RSC.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. Payne, Z. Kristall., 2005, 220, 567–570 CAS.
- S. Dudarev, G. Botton, S. Savrasov, C. Humphreys and A. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- Y. Han, K. C. Lai, A. Lii-Rosales, M. C. Tringides, J. W. Evans and P. A. Thiel, Surf. Sci., 2019, 685, 48–58 CrossRef CAS.
- G. Özbal, R. Senger, C. Sevik and H. Sevinçli, Phys. Rev. B, 2019, 100, 085415 CrossRef.
- L.-M. Yang, V. Bacic, I. A. Popov, A. I. Boldyrev, T. Heine, T. Frauenheim and E. Ganz, J. Am. Chem. Soc., 2015, 137, 2757–2762 CrossRef CAS PubMed.
- J. Weng and S.-P. Gao, Phys. Chem. Chem. Phys., 2018, 20, 26453–26462 RSC.
- G. Özbal, R. T. Senger, C. Sevik and H. Sevinçli, Phys. Rev. B, 2019, 100, 085415 CrossRef.
- M. L. Adam and A. A. Bala, Computational Condensed Matter, 2021, 26, e00527 CrossRef.
- R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428 CrossRef.
- M. Born and K. Huang, Dynamical theory of crystal lattices, Clarendon press, 1954 Search PubMed.
- J. B. Goodenough, Phys. Rev., 1955, 100, 564 CrossRef CAS.
- J. Kanamori, J. Appl. Phys., 1960, 31, S14–S23 CrossRef.
- P. W. Anderson, Phys. Rev., 1959, 115, 2 CrossRef CAS.
- J. L. Lado and J. Fernández-Rossier, 2D Mater., 2017, 4, 035002 CrossRef.
- N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133 CrossRef CAS.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- J. Jiang, Z. Qi, H. S. Park and T. Rabczuk, Nanotechnology, 2013, 24, 435705 CrossRef PubMed.
- B. Amadon, T. Applencourt and F. Bruneval, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 125110 CrossRef.
- S. Shi, A. L. Wysocki and K. D. Belashchenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 104404 CrossRef.
- N. W. Ashcroft, N. D. Mermin and D. Wei, Solid State Physics, Cengage Learning Asia Pte Limited, 2016 Search PubMed.
- J. Kotze, arXiv:0803.0217, 2008.
- J. He, P. Lyu and P. Nachtigall, J. Mater. Chem. C, 2016, 4, 11143–11149 RSC.
- V. V. Kulish and W. Huang, J. Mater. Chem. C, 2017, 5, 8734–8741 RSC.
- M. Kan, J. Zhou, Q. Sun, Y. Kawazoe and P. Jena, J. Phys. Chem. Lett., 2013, 4, 3382–3386 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0na00884b |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |