Tuning the band gap of M-doped titanate nanotubes (M = Fe, Co, Ni, and Cu): an experimental and theoretical study

Abstract

Herein, we report a systematic experimental and theoretical study about a wide-ranged band gap tuning of protonated titanate nanotubes H₂Ti₃O₇ (Ti-NT) by an easy ion-exchange method using a low concentration (1 wt%) of transition metal cations. To characterize and describe the effect of M doping (M = Cu²⁺, Ni²⁺, Co²⁺, and Fe³⁺) on the electronic, optical and structural properties, semiconductors were analyzed by a combination of experimental methods and density functional theory (DFT) calculations. The nanotube band gap can be modified from 1.5 to 3.3 eV, which opens the possibility to use them in several optoelectronic applications such as photocatalysts under solar light irradiation.

---

Introduction

Since Kasuga et al. reported the hydrothermal synthesis of 1D titanate nanotubes (Ti-NT),¹ this semiconductor has been attracting the scientific community’s attention for its outstanding properties: chemical stability, low-cost production, non-toxicity, wide band gap, semiconductor properties, attractive ion-exchange capacity, good proton conductivity, and high specific surface area, among others.² These features conferred the possibility of use Ti-NT in several applications as metal ions adsorbents,^3–5 in heterogeneous catalysis,^6–8 photocatalysis,^9–12 solar cells,^13–15 and battery production,¹⁶ and many others.

In particular, it has been demonstrated that Ti-NT is capable of adsorbing heavy metals (U⁴⁺, Pb²⁺, Cd²⁺, Cu²⁺, Cr²⁺, among others) from water.^3–5 Ion-exchange is considered the primary mechanism of the metal cation adsorption by exchanging the Na⁺/H⁺ ions located in the interlayers of Ti-NT for the metal cations. Although Ti-NT has been widely studied, its crystal structure controversy is still under discussion. Recently, Faccio et al.¹⁷ demonstrated using DFT calculations and XRD experiments that H₂TiO₃ is the most suitable crystal structure. This crystal structure comprises two layers of (Ti₃O₇)²⁻ with H⁺ or Na⁺ cations between them and makes possible the ion-exchange property.

The Ti-NT ion-exchange feature provides the opportunity of modifying its optoelectronic properties by introducing different metal cations into the crystal structure. It is well known that Ti-NT is a semiconductor with an indirect band gap of ∼3.3 eV.^14,18 In this regard, the influence of different metal cations on the Ti-NT optical properties has been studied previously.^9,19–22 Lee and Zaki studied the influence of cations with different valences (Mg²⁺, Ca²⁺, Zn²⁺, K⁺, Cr³⁺, Ce³⁺, Ce⁴⁺, Mo⁵⁺, and La³⁺). These results showed that the semiconductor band gaps could be modified in the range of 2.02–2.8 eV.¹⁹ Additionally, Tang et al. reported a comparative study of Ti-NT doped with various metal cations (Cu²⁺, Co²⁺, Ni²⁺, Fe²⁺, and Mn²⁺). Nevertheless, the band gap energy was only slightly modified from 3.43 (Ti-NT) to 3.18 eV (Fe–Ti-NT).⁹ Finally, Marques et al. studied the influence of rare earths (RE) ions (Pr³⁺, Er³⁺, Nd³⁺, and Yb³⁺) into the photoluminescence (PL) properties of the Ti-NT, finding that the incorporation of RE cations enhances PL emission into the Ti-NT by an ion-exchange method.²³

Herein, we present an experimental and theoretical study to comprehensively investigate the influence of doping the Ti-NT with different cations (Cu²⁺, Ni²⁺, Co²⁺, and, Fe³⁺) on the physicochemical properties. Results show that the band gap can be widely tuned between 1.5 and 3.3 eV, with only 1 wt% of the metal cation, opening the possibility to use these modified Ti-NT in several optoelectronic applications, such as photocatalysis under solar light irradiation.

Experimental section

Synthesis

Protonated titanate nanotubes (Ti-NT) were synthesized using a hydrothermal method based on the methodology reported elsewhere.²⁴ First, 5 g of TiO₂ (anatase, Sigma-Aldrich) and 80 mL of a 10 M NaOH solution were stirred and poured into a Teflon-lined stainless-steel autoclave vessel. The hydrothermal reaction was performed at 140 °C for 20 h, under autogenous pressure inside an air-circulating oven. After the synthesis, the autoclave was cooled down to room temperature naturally. Then, reaction products were washed several times with a 0.1 M HCl solution until a pH of 7 was achieved to exchange Na⁺ cations by H⁺. Finally, the Ti-NT were dried in a vacuum oven at 80 °C overnight.

Modified M/Ti-NT were prepared using 0.5 g of as-prepared titanate nanotubes. The nanotubes were dispersed in 80 mL of distilled water, stirred, and heated to 80 °C. Subsequently, the metal precursor solution (Cu(NO₃)₂·2.5H₂O, Ni(NO₃)₂·6H₂O, Co(NO₃)₂·6H₂O and, Fe(NO₃)₃·9H₂O (Sigma-Aldrich)) with the appropriate amount to get 1 wt% of metal cation was added. The solution was stirred for 3 h. The product was filtered, washed, and dried at 80 °C for 6 h.

Characterization

The crystalline structure was determined by X-ray diffraction (XRD) in a Bruker D-8 diffractometer with CuKα radiation, a Ni-0.5% Cu-Kα filter in the secondary beam, and a 1-dimensional position sensitive silicon strip detector (Bruker, Linxeye). The patterns were obtained in the range 6°–110°, with a 2θ step of 0.039° and 134.4 s per point. Rietveld refinement of XRD data was performed with the BGMN code using the graphical interface Profex.²⁵ Besides, the structure of the materials was analyzed using Raman spectroscopy in a Thermo Scientific DRX Raman Microscope with an excitation wavelength of 532 nm and a 2 cm⁻¹ resolution. All Raman spectra were recorded at ambient conditions.

The sample morphology was studied by transmission electron microscopy (TEM) in a JEM 2010 F FasTem analytical electron microscope. Specific surface area and pore size distribution of materials was determined from N₂ adsorption/desorption isotherms at −196 °C in a Quantachrome Autosorb MP-1 apparatus. The BET and BJH models were used for this purpose. Metal content was determined by energy-dispersive X-ray spectroscopy (EDS) using a Thermo Noran microanalysis system coupled to a JSM 5600 LV scanning electron microscope (SEM), working at 20 kV and magnification of 500×.

The stability of the samples was studied by thermal analysis. TGA and DSC experiments were carried out, respectively, in a Q500HR model TA Instrument thermobalance and a scanning P-DSC calorimeter, from Instrument Specialists Incorporated. The analyses were performed using a 10 °C min⁻¹ ramp from room temperature to 600 °C under an N₂ saturated atmosphere.

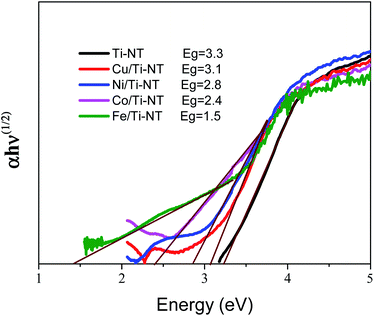
The optical properties were studied by UV-vis diffuse reflectance spectra (DRS) in a UV-vis spectrophotometer (Shimadzu 2600) equipped with an integration sphere (ISR 2600) in the interval ranging from 200 to 600 nm and using BaSO₄ as a reference blank. The spectra were converted from reflectance to absorbance by the Kubelka–Munk method. The band gap energy (E_g) was calculated by extrapolating the linear portion of the (F(R) × hυ)²versus hυ curves to F(R) = 0, considering that Ti-NT presents an indirect allowed transition.¹⁸ Finally, the photoluminescence spectra were measured in a fluorescence spectrometer (PerkinElmer LS 55) with an exciting wavelength of 315 nm.

Computational details

All calculations were performed considering periodic boundary conditions using Density Functional Theory (DFT), as implemented in the Spanish Initiative for Electronic Simulations of Thousands of Atoms (SIESTA) ab initio package²⁶ using a basis set of finite-range of numerical atomic orbitals. All geometries were previously optimized with the generalized gradient-approximation (GGA)²⁷ with the exchange–correlation functional of Perdew–Burker–Ernzerhof (PBE)^28,29 with the semi-empirical dispersion correction D2 (DFT/PBE-D2).³⁰ All calculations were optimized with spin-polarized. We used the Troullier–Martins pseudopotentials³¹ and considering a double-z basis set, including the polarization function (DZP) with an energy shift of 200 meV. The charge transfer for ion metal atoms was studied using the Hirshfeld scheme.³²

All calculations were performed with the following convergence criteria: 10⁻⁵ eV for the total energy, 10⁻⁵ e for the electron density, and the Hellmann–Feynman forces were converged to be less than 0.05 eV Å⁻¹ for the structure optimizations. The real-space mesh cut-off energy is set to 250 Ry (3400 eV). The Monkhorst and Pack grid³³ 3 × 5 × 3 k-points were used^34–36 for the Brillouin zone integration. For optical properties, the imaginary part of the dielectric function is calculated using SIESTA ab initio computational code,²⁶ which is based on the first-order dependent perturbation theory. From the optimized geometries, single-point calculations were performed using GGA + U method. The Hubbard parameter was used to gain a more realistic description. The GGA + U is implemented with a Hubbard-like³⁷ parameter to better describe the effect of electron–electron interaction in a localized atomic shell (3d) of the transition metal atoms (M). This methodology was proposed by Dudarev et al.,³⁸ which improves the description of the electronic properties concerning the experimental results. The Hubbard parameter is obtained as U_eff = U − J, between the Coulomb repulsion U and screen exchange, while J is a parameter to be specified. In the calculations of electronic structure properties, the valence electronic states of H-1s¹, O-2s², and 2p⁴, Ti-3d² and 4s², Fe-3d⁶ and 4s², Co-3d⁷ and 4s², Ni-3d⁸ and 4s², Cu-3d¹⁰ and 4s¹; were considered for all calculations.

The method used to choose the appropriate U value was to explore various U values for the ion metal atoms to obtain the experimental band gap energy of this work. The U parameter was tested in the range of 1–7 eV for transition metal atoms except for copper, for which a value up to 10 eV was tried out. According to the DFT + U method we found the following Hubbard parameter, U_eff, values: 4.5 eV for Ti atom,^39–41 4 eV for Fe atom,^18,42 1 eV for Co atom,³⁴ 6 eV for Ni atom, and 9.79 eV for Cu atom.⁴³ DFT + U calculations were performed with spin-polarized.

The effect of the doping metal atom on the photocatalytic potential was analyzed. A DFT + U calculation was carried out to theoretically predict the positions of the valence band maximum (VBM) and conduction band minimum (CBM) for all systems under study (more details of this method in ESI†). Likewise, the work function (Φ),^44,45 defined as the energy necessary to remove an electron from a solid (Fermi energy level) to a neighboring vacuum, was calculated. The Φ is calculated as Φ = V_VAC − E_F, in which V_VAC is the electrostatic potential in a vacuum region far from the M/Ti-NT slab (which was adjusted to simulate a vacuum region), and E_F is the Fermi energy of each M/Ti-NT system.

Results and discussion

Structural characterization

The crystalline structure of as-prepared materials was determined by XRD (Fig. 1). The undoped and all the M/Ti-NT samples depicted the peaks related to the H₃Ti₂O₇ phase (COD-96-433-6946)⁴⁶ and no other signals were observed. Ti-NT crystal structure was preserved after the ion-exchange process. Rietveld refinement of the diffractograms was performed using the BGMN program and the graphical interface Profex.²⁵ The fitting quality was evaluated with the weighted residual square sum (R_wp), a value between 3 and 5%, representing a good quality model (Table S1† shows the unit cell atomic position).⁴⁶ H₂Ti₃O₇ crystallizes in the monoclinic system with a space group C2/m.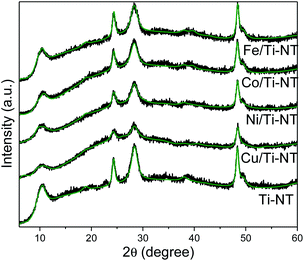

Fig. 1 Experimental XRD patterns of as-prepared Ti-NT (black spectra), and smoothed-free background XRD patterns by Rietveld refinement (green lines).

Table 1 presents the “a” lattice parameter calculated by Rietveld refinement in all the materials and the theoretical “a” lattice parameter. The lattice parameters of unmodified Ti-NT are a = 17.311 Å, b = 3.780 Å, c = 9.551 Å. After metal incorporation by the ion-exchange method, the “a” lattice parameter changes depending on the cation from 16.946 (Co²⁺) to 17.532 Å (Fe³⁺). On the contrary, “b” and “c” (Table S2†) parameters do not present a significant variation; they are like lattice parameters of unmodified titanate nanotubes (b = 3.7 Å and c = 9.55 Å). In the “a” axis, these titanate nanotubes are composed of stepped host layers of edge-sharing TiO₆ octahedrons having interlayer hydrogen cations (Fig. S1†); by ion-exchange, the protonated titanates can be easily modified into M_xH_2−xTi₃O₇, a transition-metal-doped protonated titanate.^47,48 Therefore, the substitution of hydrogen atoms for metal cations only should cause a change in the “a” lattice parameter and not in the other two parameters because the layers of (Ti₃O₇)²⁻ remain untouched. It is worth to notice that no relationship between the “a” lattice parameter and the ionic radii of the metal was found. The doping site is generated in hollow regions where H atoms were replaced; therefore, variation of the lattice constant “a” may be related to the crystal lattice strain in the (100) plane.

Table 1 Experimental and theoretical lattice “a” parameter

Material	a (Å)	a (Å)
	Experimental	Theoretical
Ti-NT	17.311	15.992
Cu/Ti-NT	17.137	16.526
Ni/Ti-NT	17.517	16.595
Co/Ti-NT	16.946	16.559
Fe/Ti-NT	17.532	16.585

---

DFT calculations were carried out to gain insight on the effect of atom doping using a pristine [H₂Ti₃O₇]₄ supercell model,⁴⁹ which contains 48 atoms. The lattice parameters of the pristine [H₂Ti₃O₇]₄ supercell model (Ti-NT) were optimized according to the DFT/PBE-D2 theory. The Ti-NT pristine structure lattice parameters are close to the monoclinic system found previously,⁴⁶a = 15.99 Å, b = 3.79 Å, and c = 9.47 Å (Fig. S2a†). Compared to Ti-NT lattice parameters found by Rietveld refinement, the theoretical lattice parameters are slightly different; nevertheless, the differences are contained in the error range, “a” (7.6%), “b” (0.29%), and “c” (0.79%).

The doped systems M/Ti-NT were obtained by replacing two H atoms in the Ti-NT supercell to represent the metal atom dopant M²⁺ oxide state. In the Fe/Ti-NT configuration, two different possible oxidation states, Fe²⁺ and Fe³⁺, were studied. It is worth noting that the experimental doping percentage (1 wt%) of the metal cation is not preserved in the computational calculations. Nevertheless, the model allowed to finely reproduce the properties observed experimentally. According to the DFT/GGA-U calculations reported by Peng et al.,⁵⁰ the electronic behavior of this kind of doped system (FeHTi₆O₁₄), is best described with an oxidation state of Fe³⁺. Therefore, the optimized lattice parameters for all doped systems M/Ti-NT (M = Fe–Cu) are reported in Fig. S2 in the ESI.† According to theoretical calculations, elongation of the pristine “a” lattice parameter (error of 5.4% for Fe, 2.24% for Co, 5.36% for Ni, and 3.56% for Cu) is evident for all the doped materials. For “b” lattice parameter, a variation of 0.1 Å (error of 0.52% for Fe, 1.05% for Co, 0.79% for Ni, and 1.6% for Cu) was observed. Additionally, the “c” lattice parameter showed a slight contraction for all doped systems (error of 2.09% for Fe, 1.89% for Co, 3.24% for Ni, and 1.97% for Cu). The “b” and “c” parameter changes are less than 0.2 Å. The calculation error is between 0.52 and 5.36%.⁵¹ This small variation is not significant for the simulation results. Therefore, the theoretical lattice parameters are in good agreement with those issued from the Rietveld refinement (Table 1), where only the “a” lattice parameter changed notably after the ion-exchange process.

To further analyze the doped titanate nanotubes structure, Raman spectroscopy was used, and Fig. S3† shows the Raman spectra of all as-prepared materials. According to previous studies, Raman peaks at 118, 160, and 189 cm⁻¹ correspond to the Ti–O–Na/H bending modes, while those located at 280, 448, 668, and 702 cm⁻¹ can be attributed to the Ti–O–Ti stretching in edge-shared TiO₆. While the one at 915 cm⁻¹ is attributed to Ti–O–Na/H vibrations in the interlayer regions of the nanotube walls (in the cited work this band is observed at 906 cm⁻¹).⁵² It is well known that the anatase TiO₂ (precursor) Raman modes are observed at 144, 192, 398, 517, and 640 cm⁻¹;¹⁰ these modes are not present in any of the as-prepared Raman spectra, confirming the absence of the precursor anatase phase. Raman modes principal differences between the pristine and the doped Ti-NT are observed in the peaks at 118, 160, 189, and 915 cm⁻¹. The incorporation of different cations slightly modifies the intensity and the position of these Raman modes. These bands are related to the Ti–O–H/Na vibrational modes, confirming that the metal cations replace hydrogen atoms. The slight modification of these bands is related to the low metal content. In all the cases, the total metal loading was 1 wt%, and as shown ahead, besides doping, deposition of metal oxide nanoparticles in the surface is also observed. Therefore, this would indicate that not all the metal cations are hosted in the crystal structure of Ti-NT.

Microstructural characterization

The microstructural, textural, and composition features of the M–Ti-NT were studied by N₂ adsorption–desorption, TEM, and EDS analysis. Fig. 2 shows a TEM micrograph of the pristine Ti-NT in which it is evident the multiwalled nanotubular morphology with an external diameter distribution between 13 and 17 nm and an inner diameter between 6 and 10 nm. The nanotubes length has a broad distribution from 25 to 150 nm.

Fig. 2 TEM image of the unmodified Ti-NT.

After the ion-exchange, the nanotubular morphology did not change, but some nanoparticles are recognized as shown in Fig. S4.† In all the cases, the size of the nanoparticles is less than 5 nm. This result suggests that not all metal cations are introduced in the crystal lattice of the Ti-NT. Unfortunately, by XRD and Raman spectroscopy, no signal to identify the crystal structure was observed, and the resolution of TEM images is not good enough to characterize them. Nevertheless, by UV-Vis spectroscopy, insight on the metal oxide composition is obtained; the results are discussed below.

Additionally, Fig. S5† shows the N₂ adsorption–desorption isotherms. All the isotherm presents a hysteresis loop characteristic of a mesoporous material (2–50 nm). The specific surface area (SSA) was calculated using the BET model. The SSA is shown in Table 2; all the as-prepared materials present values between 201 and 223 m² g⁻¹. The pore-size distribution of as-prepared materials based on the Barrett–Joyner–Halenda (BJH) method are presented in Fig. S6.† The distribution is equal in all the Ti-NT with a pore size of around 6 nm, which is in good agreement with the inner diameter of the nanotubes observed by TEM analysis. Therefore, the incorporation of metal cations does not significantly impact the textural properties of the titanate nanotubes. Finally, as-prepared nanotubes were characterized through energy-dispersive X-ray spectroscopy to assess the total metal load; results are presented in Table 2. In all the cases, the metal content is close to the nominal 1 wt%. Additionally, the sodium content was measured; the sodium values are between 4 and 7 wt% in all the samples which indicates that even when the nanotubes were washed several times, Na⁺ ions were not completely replaced by H⁺ ions in the structure. This should be the cause for the difference between the theoretical and experimental “a” lattice parameter (Table 1).

Table 2 Specific surface area, pore size distribution and metal content of all as-prepared nanotubes

Material	Specific surface area (m^2 g^−1)	Pore diameter (nm)	Metal content (wt%)
Ti-NT	223	6.3	—
Cu/Ti-NT	211	6.3	0.82
Ni/Ti-NT	201	6.1	0.72
Co/Ti-NT	212	6.1	1.05
Fe/Ti-NT	222	6.1	1.32

---

Thermal stability analysis

The thermal stability is an important characteristic of the Ti-NT compound. Increasing the temperature between 120–400 °C in Ti-NT results in dehydration accompanied by a decrease in interlayer spacing in the walls of the nanotubes; during this process, intermediate phases (H₂Ti₆O₁₃ and H₂Ti₁₂O₂₅) can be formed. A further temperature increment results in the transformation into titanium oxide (TiO₂, anatase phase).⁵³ Besides, it has shown that incorporating of a metal cation (Co²⁺) decreases the thermal stability of the titanate nanotubes producing a composite of TiO₂ and CoTiO₃ nanorods.⁶

The thermal stability of as-prepared samples was studied by thermogravimetric decomposition analysis (TGA) and differential scanning calorimetry (DSC) analysis. Fig. S7† shows the decomposition thermograms. All the samples presented two different decomposition processes. Initially, between 40 and 150 °C, all the samples show a weight loss of 10 wt%, which could be attributed to a dehydration process of water previously adsorbed. The second process was observed between 290 to 360 °C. This second process should be the crystal deprotonation process, which forms the intermediate H₂Ti₆O₁₃ and H₂Ti₁₂O₂₅ phases to produce TiO₂ finally. The crystal structure transformation to TiO₂ was evidenced by DSC experiments (Fig. S8†). All the materials present an exothermic peak at around 360 °C, which is related to the formation of TiO₂; this is in good agreement with the TGA experiments where at 360 °C the crystal deprotonation process concludes. Therefore, the thermal stability is not affected after the ion-exchange process.

Optical and electronic properties

The optical properties were studied by UV-Vis diffuse reflectance spectroscopy (DRS). The spectra of all as-prepared materials are shown in Fig. 3. The absorption edge of unmodified Ti-NT starts at ∼380 nm with maximum absorption at ∼270 nm, which indicates that Ti-NT light absorption is in the UV region. This result is in good agreement with previous reports.⁵⁴ When Ti-NT were modified by the introduction of metal transition cations (Fe, Co, Ni, and Cu), a redshift in the absorption edge was observed; Cu/Ti-NT absorption begins at 400 nm, Ni/Ti-TN at 410 nm, Co/Ti-NT at 470 nm, and Fe/Ti-NT at 600 nm. Thus, all the modified titanate nanotubes absorb light in the visible region (380–700 nm). The observed absorption redshift is attributed to the insertion of the metal 3d orbitals within the forbidden band and the subsequent charge-transfer transition between the d-electrons of the dopant and the conduction band of the Ti-NT.^34,48 In fact, it seems that there is a relationship between d-electrons of the transition metal and the light absorption properties of the materials; a lower number of d-electrons corresponds to a higher absorption redshift. Besides, other absorption edges are observed in all the M-doped Ti-NT. Cu/Ti-NT presents an absorption edge at around 600 nm, which is characteristic of CuO; Cu₂O presents an absorption edge at a lower wavelength (450 nm).⁵⁵ Ni/Ti-NT has an absorption edge between 400 and 500 nm. It has demonstrated that NiO nanoparticles have a broad adsorption edge, between 360 and 550 nm.⁵⁶ The Co/TiNT has an absorption edge at 550 nm, related to the wurtzite-type CoO nanoparticles.⁵⁷ Finally, in Fe/Ti-NT absorption spectrum, it is not easy to separate the absorption edge belonging to the nanoparticles observed by TEM because it presents a broad adsorption edge that should screen the nanoparticles absorption. For example, Fe₂O₃ nanoparticles have a broad absorption edge which begins at 600 nm.⁵⁸ The same trend of Fe/TiNT has been observed in previous reports.^59,60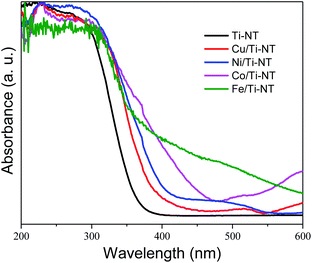

Fig. 3 UV-Vis diffuse reflectance spectra (DRS) of undoped titanate nanotube (Ti-NT) and metal-doped Ti-NT.

The theoretical optical response was analysed through the photon interaction with the electrons of these metal-doped Ti-NT complexes. The optical properties were described by the imaginary part of the dielectric function⁶¹ε(w) = ε₁(w) + iε₂(w), obtained using the first-order perturbation theory as implemented in SIESTA code.²⁶ The optical calculations were done for all possible directions which were averaged into each structure. The dielectric function and the absorption coefficient for all compounds under study are shown in Fig. 4. The imaginary part of the dielectric function ε₂(w) shows the most intense peak, which corresponds to the Ni/Ti-NT complex (∼312 nm), and the lowest intensity corresponds to the pristine Ti-NT system (∼330 nm). The wavelength amplitude at the ε₂(w) peaks for all systems is maintained in a range of 210 to 400 nm. Therefore, compared to pristine Ti-NT, a slight change in the ε₂(w) values for the M/Ti-NT (M = Fe–Cu) complexes system can be seen. Such values remain in the near UV-region. The changes in the optical properties due to doping with metal cations in the M/Ti-NT (M = Fe–Cu) complexes are evident; it is possible to appreciate it in a redshift of the adsorption spectrum edge. The optical absorption spectrum is broader when M atoms are incorporated, compared to the pristine Ti-NT model. Based on the theoretical results, the M/Ti-NT (M = Fe–Cu) complexes have a continuous absorption spectrum in the UV-visible light region due to the M (3d) electronic states contribution. This is evidenced by calculations of the total density of states (DOS) and partial density of states (PDOS), which will be further discussed.

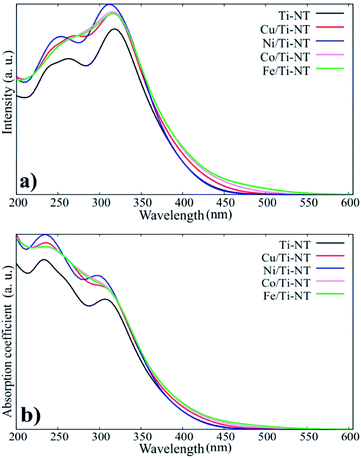Fig. 4 a) The imaginary part of the dielectric function for all system under studied. (b) The absorption coefficient for all system under studied.

The optical redshift absorption also indicates a reduction in the energy of the band gap. As Ti-NT has an indirect electronic transition,¹⁸ the optical band gap energies of the samples were calculated using the Tauc method by plotting the function (α(ν)hν)^1/2vs. hν (Tauc plot), and extrapolating the linear portion of the curve to zero absorption; h is Planck’s constant, α(ν) is the absorption coefficient, and ν is the radiation frequency. Fig. 5 shows the Tauc plots and the band gap values of all the as-prepared materials. The pristine Ti-NT presents a band gap of 3.3 eV while all the M/Ti-NT exhibit lower band gap values; 3.1 eV, 2.8 eV, 2.4 eV, and 1.5 eV, respectively, for Cu, Ni, Co, and Fe, M/Ti-NT. Therefore, after incorporating the metal cations, the materials present an active band gap under visible light irradiation.

Fig. 5 Tauc plots and band gap value of undoped titanate nanotubes (Ti-NT) and metal-doped M/Ti-NT.

To deeply understand the effect of the metal doping on the Ti-NT electronic structure, DFT calculations were carried out for all the studied systems. It is widely known that the standard DFT calculations fail to describe the correct electronic structure in transition metal oxides^41,62–66 systems due to the strong Coulomb repulsion derived from the electronic correlation on metal ions that contain partly filled d shells. DFT + U method is implemented with a Hubbard-like parameter to better describe the effect of electron–electron interaction in a localized atomic shell (3d) of the transition metal atoms (M). The U parameter was tested in the range of 1–7 eV for transition metal atoms except for copper, for which a value up to 10 eV was tried out. Thus, DFT + U method was employed to estimate the band gap energy.

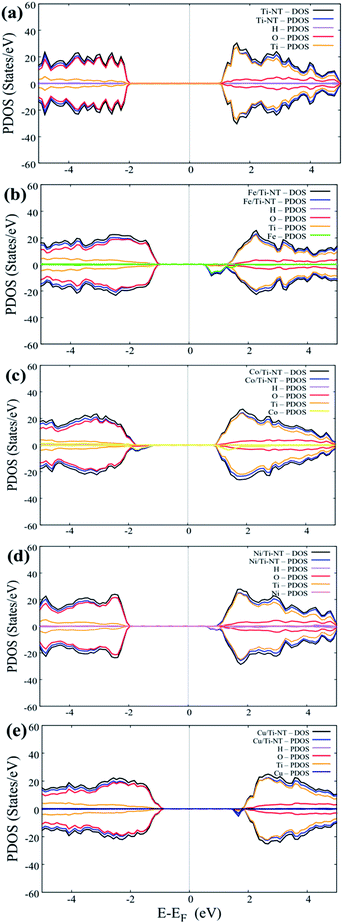
Fig. 6 shows the DOS and PDOS calculated using DFT + U. The pristine structure (Ti-NT) shows a semiconductor behavior that presents an intrinsic nature. The high contribution in the valance states is attributed to the O(2p) states, while Ti(3d) atoms dominate the conducting states. The electronic nature of this compound is predominant in other TiO₂ structures.⁶⁷ The electronic structure nature is modified when Ti-NT is doped with M cations. In the case of Fe/Ti-NT system, electronic states were within band gap and could be correlated with the hybridization between the O(2p), Ti(3d), and Fe(3d) states which influences the conduction band. When Ti-NT are doped with Co cation, similar behaviour is observed, where more electronic states are formed in the band gap. This effect is attributed to Co(3d) states, which influence the valence band. In the case of Ni-doped Ti-NT, the electronic states present high hybridization between the O(2p), Ti(3d), and Ni(3d) states. The contribution of the electronic states of Ni(3d), are shifted above to the Fermi level. Finally, the Cu/Ti-NT system presents the O(2p) and Ti(3d) states at the edge of the valence band and the Cu(3d) doping contribution is located slightly below the conduction band. This electronic behaviour is in good agreement with the results reported by Shen et al.³⁵ It must be pointed out that the contributions of the doping atoms are located at the edge of the conduction band, except in the Co/Ti-NT system where the contribution is in the valence band.

Fig. 6 Total Density of States (DOS) and Partial Density of States (PDOS) of all complexes under study: (a) pristine system (Ti-NT), (b) doped with Fe atom, (c) doped with Co atom, (d) doped with Ni atom and (e) doped with Cu atom.

Furthermore, all energy band structure was calculated to elucidate the semiconductor character of these kinds of compounds. Fig. S9 in the ESI† displays the band structures calculated along the G–F–Q–Z–G direction of the Brillouin zone.

The formation of a band gap is evident in all cases. All doped systems (M/Ti-NT) exhibited lower band gap values compared to pristine Ti–N system (3.3 eV); the band gap of Cu/Ti-NT (2.97 eV), Ni/Ti-TN (2.86 eV), Co/Ti-NT (2.40 eV), and, Fe/Ti-NT (1.78 eV). In the Cu/Ti-NT case, two possible band gap values were obtained (2.66 and 2.97 eV); the first one can be attributed to a spin-down state, as seen in Fig. 6e. Therefore, the band gap theoretical shrinking when Ti-NT are doped with metal cations presents a similar behaviour, which corroborates the experimental results where the band gap was contracted to lower values when Ti-NT are doped with metal cations.

Table 3 shows the band gap values obtained by DFT + U method and the Tauc method; it is possible to appreciate that the calculated and experimental values are similar in all the cases. These results support that the Ti-NT optical and electronic properties can be modified by the cation incorporation into the crystal structure. Similarly, it is possible to appreciate that the use of Tauc method brings a close approximation for the band gap value, obtained by theoretical approximations.

Table 3 Calculated and experimental band gap, of undoped titanate nanotubes (Ti-NT) and metal-doped M/Ti-NT

Material	Calculated band gap (eV)	Experimental band gap (eV)
Ti-NT	3.3	3.3
Cu/Ti-NT	3.1	2.97
Ni/Ti-NT	2.8	2.86
Co/Ti-NT	2.4	2.4
Fe/Ti-NT	1.5	1.78

---

In comparison, in a previous work reported by Tang et al.,⁹ where the same metal cations were used, the band gap energy was only slightly modified from 3.43 (Ti-NT) to 3.18 eV (Fe–Ti-NT). In that case, the ion-exchange was performed using an aqueous ammonia solution, which should change the solution pH, limiting the metal cation insertion into the Ti-NT crystal structure. Therefore, it is presumed that this process occurs easier when the ion-exchange is performed without changing the solution pH. The higher extent of metal cations incorporation reported in this work brings the possibility of tuning the Ti-NT optical properties, particularly the band gap, in a broad range value, opening the prospect of using these semiconductors optoelectronic applications under visible light illumination.

Photoluminescence (PL) spectroscopy was used to study the electronic properties of the photogenerated electron/hole (e⁻/h⁺) pairs in semiconductors. Photoluminescence of a semiconductor results from a photon emission produced by the recombination of an electro/hole pair.⁶⁸ Moreover intensity of PL peaks is related to the e⁻/h⁺ recombination rate.⁶⁹Fig. 7 shows the PL spectra of pristine and M-doped Ti-NT under light excitation (λ = 315 nm). All the samples were measured in the same experimental conditions; therefore, it is possible to compare the intensities qualitatively.

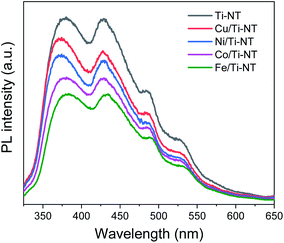Fig. 7 Photoluminescence spectra (PL) of undoped titanate nanotubes (Ti-NT) and metal-doped M/Ti-NT.

The spectrum of pristine Ti-NT presents a broad band with peaks with a maximum of 380, 429, 486, and 528 nm. A PL broad band is characteristic of multiphononic processes in which the emission takes place through several paths due to the high density of electronic states caused by defects within the band gap region. This situation allows the momentum of the electron to relax in the form of a non-radiative process before its radiative recombination. In the case of titanate nanotubes, two different oxygen defects have been related to the presence of different photoluminescence peaks; mono-ionized oxygen vacancies that are energetically close to the conduction or valence band (shallow defects) and double-ionized oxygen vacancies that are energetically closer to the Fermi level and they are classified as deep defects.⁷⁰ Additionally, surface hydroxyl groups are dominant sites for trapping electrons and act as shallow acceptor levels.⁷¹

On the other hand, the PL spectra of the metal-doped Ti-NT have the same characteristic peaks of the pristine sample indicating similar multi-phononic recombination. The main difference is the lower PL intensity compared to the pristine Ti-NT. The lower the PL intensity, the lower the electron–hole recombination rate and the larger the number of photogenerated carriers. As a result, with the M doping of Ti-NT, the separation of the electron–hole pair is improved due to the presence of higher number of vacancies and defects. An interesting trend was found; the lower the band gap (Table 2) the lower the recombination rate. As the titanate nanotubes band gap is highly modified and the recombination rate is diminished by the insertion of transition metal cations, a possible application of these semiconductors is as photocatalysts. These results suggest that the M doping can successfully enhance the photocatalytic performance of Ti-NT.

In order to verify if the semiconductors show a proper band alignment for photocatalytic reactions, a theoretical analysis of the band-edge position compared to the redox potential for the CO₂ photocatalytic conversion to hydrocarbon molecules was performed, as an example. Fig. 8 and Table 4 show the redox potentials of each semiconductor under study compared to the redox potential of CO₂ photoreduction. It is evident that most of the semiconductor show and adequate band alignment for performing this reaction; only the valence band of Fe/Ti-NT has a lower potential for reducing the CO₂ for most of the different products. Nevertheless, it could perform a selective reduction of CO₂ to CH₄. Therefore, these semiconductors could be used as photocatalysts for the CO₂ photoreduction reaction.

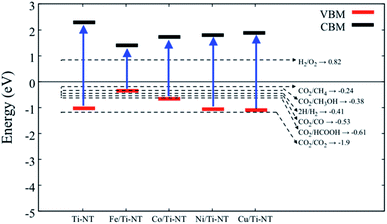Fig. 8 Redox potential of each semiconductor under study. The dotted lines represent the redox potential (eV) of CO₂ reduction into a hydrocarbon molecule.

Table 4 Energies of the VBM and CBM, obtained in accordance to eqn (S1) and (S2) of ESI

Material	VBM (eV)	CBM (eV)
Ti-NT	−1.02	2.27
Fe/Ti-NT	−0.35	1.42
Co/Ti-NT	−0.67	1.72
Ni/Ti-NT	−1.06	1.79
Cu/Ti-NT	−1.09	1.87

---

Conclusions

In conclusion, this work shows an easy ion-exchange method that modifies the Ti-NT optical and electronic properties. The incorporation of a low concentration (1 wt%) of metal cations (Cu²⁺, Ni²⁺, Co²⁺, and Fe³⁺) into the Ti-NT crystal structure produces an absorption edge redshift, a contraction of the band gap values and a reduction of the recombination rate. The band gap can be tuned in a wide range, from 1.5 (Fe/Ti-NT) to 3.3 eV (Ti-NT). Theoretical calculations corroborate the experimental results and deepen the understanding of the electronic structure and optical response of M/Ti-NT semiconductors.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work in this paper.

Acknowledgements

A. Gómez-Cortés for technical support, A. Morales for XRD diffraction patterns, C. Zorrilla for Raman spectra S. Tehuacanero-Cuapa for TEM analysis and M. Aguilar-Franco for EDS measurements. J. M. acknowledges the support given by PAPIIT-UNAM (IA102820, IN109319); Fondo Sectorial de Investigación para la Educación-CONACYT under Project no. A1-S-13294, and the Supercomputing Department of UNAM for the computing resources under Projects LANCAD-UNAM-DGTIC-310 and LANCAD-UNAM-DGTIC-370. O. A. Jaramillo-Quintero wants to acknowledge the support provided by CONACYT-México (Project A1-S-15336). Melissa Méndez-Galvan thanks the scholarship financial support of PNPC-CONACyT. Christian A. Celaya thanks the Dirección General de Asuntos del Personal Académico (DGAPA) for postdoctoral fellowship.

Notes and references

1. T. Kasuga, M. Hiramatsu, A. Hoson, T. Sekino and K. Niihara, Langmuir, 1998, 14, 3160–3163.
2. N. Ameur and R. Bachir, ChemistrySelect, 2020, 5, 1164–1185.
3. W. Liu, X. Zhao, T. Wang, D. Zhao and J. Ni, Chem. Eng. J., 2016, 286, 427–435.
4. N. Li, L. Zhang, Y. Chen, M. Fang, J. Zhang and H. Wang, Adv. Funct. Mater., 2012, 22, 835–841.
5. W. Liu, T. Wang, A. G. L. Borthwick, Y. Wang, X. Yin, X. Li and J. Ni, Sci. Total Environ., 2013, 456–457, 171–180.
6. H. A. Lara-García, J. A. Mendoza-Nieto, H. Pfeiffer and L. Torrente-Murciano, Int. J. Hydrogen Energy, 2019, 44, 30062–30074.
7. A. Sandoval, R. Zanella and T. E. Klimova, Catal. Today, 2017, 282, 140–150.
8. E. Wada, M. Kitano, K. Yamamoto, K. Nakajima, S. Hayashi and M. Hara, Catal. Sci. Technol., 2016, 6, 4832–4839.
9. Z. Tang, Y. Zhang and Y. Xu, ACS Appl. Mater. Interfaces, 2012, 4, 1512–1520.
10. J. Yang, X. Shen, J. Wei, L. Zhang, D. Zhao and B. Yao, Catal. Sci. Technol., 2016, 6, 7604–7614.
11. X. Ma and X. Lang, Sustainable Energy Fuels, 2020, 4, 1754–1763.
12. B. C. Viana, O. P. Ferreira, A. G. Souza Filho, C. M. Rodrigues, S. G. Moraes, J. M. Filho and O. L. Alves, J. Phys. Chem. C, 2009, 113, 20234–20239.
13. J. Yu, Q. Li, J. Fan and B. Cheng, Chem. Commun., 2011, 47, 9161–9163.
14. F. Pignanelli, L. Fernández-Werner, M. Romero, D. Mombrú, M. A. Tumelero, A. A. Pasa, E. Germán, R. Faccio and Á. W. Mombrú, Mater. Res. Bull., 2018, 106, 40–48.
15. P. Roy, D. Kim, K. Lee, E. Spiecker and P. Schmuki, Nanoscale, 2010, 2, 45–59.
16. J. Li, Z. Tang and Z. Zhang, Electrochem. Commun., 2005, 7, 62–67.
17. L. Fernández-Werner, F. Pignanelli, B. Montenegro, M. Romero, H. Pardo, R. Faccio and Á. W. Mombrú, J. Energy Storage, 2017, 12, 66–77.
18. X. G. Xu, X. Ding, Q. Chen and L. Peng, Phys. Rev. B, 2006, 73, 165403.
19. A. H. Zaki and M. J. Lee, ACS Omega, 2019, 4, 19623–19634.
20. N. A. M. Barakat, A. H. Zaki, E. Ahmed, A. A. Farghali and F. S. Al-Mubaddel, Int. J. Hydrogen Energy, 2018, 43, 7990–7997.
21. M. S. Mahmoud, E. Ahmed, A. A. Farghali, A. H. Zaki, E. A. M. Abdelghani and N. A. M. Barakat, Colloids Surf., A, 2018, 554, 100–109.
22. A. I. J. Joseph and S. Thiripuranthagan, RSC Adv., 2015, 5, 9792–9805.
23. T. M. F. Marques, C. Luz-Lima, M. Sacilloti, K. Fujisawa, N. Perea-Lopez, M. Terrones, E. N. Silva, O. P. Ferreira and B. C. Viana, J. Nanomater., 2017, 2017, 3809807.
24. T. Kasuga, M. Hiramatsu, A. Hoson, T. Sekino and K. Niihara, Adv. Mater., 1999, 11, 1307–1311.
25. N. Doebelin and R. Kleeberg, J. Appl. Crystallogr., 2015, 48, 1573–1580.
26. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2012, 14, 2745–2779.
27. R. G. Parr, Density Functional Theory of Atoms and Molecules, in Horizons of Quantum Chemistry, ed. K. Fukui and B. Pullman, Académie Internationale Des Sciences Moléculaires Quantiques/International Academy of Quantum Molecular Science, Springer, Dordrecht, 1980, vol. 3,  DOI:10.1007/978-94-009-9027-2_2.
28. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1998, 80, 891.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
30. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
31. N. Troullier and J. L. Martins, Phys. Rev. B, 1991, 43, 1993–2006.
32. E. R. Davidson and S. Chakravorty, Theor. Chim. Acta, 1992, 83, 319–330.
33. H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192.
34. Y. An, Z. Li, D. Wang and J. Shen, Phys. Status Solidi, 2013, 250, 1592–1598.
35. Y. An, Z. Li and J. Shen, Phys. B, 2013, 429, 127–132.
36. S. Fleischmann, Y. Sun, N. C. Osti, R. Wang, E. Mamontov, D. E. Jiang and V. Augustyn, J. Mater. Chem. A, 2020, 8, 412–421.
37. S. A. Tolba, K. M. Gameel, B. A. Ali, H. A. Almossalami and N. K. Allam, Density Functional Calculations – Recent Progresses of Theory and Application, InTech, 2018,  DOI:10.5772/intechopen.72020.
38. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B, 1998, 57, 1505.
39. E. German, R. Faccio and Á. W. Mombrú, Appl. Surf. Sci., 2017, 426, 1182–1189.
40. W. Elsayed, S. Abdalla and N. Seriani, Phys. Status Solidi, 2020, 257, 1900054.
41. Y. Jagvaral, Q. Guo, H. He and R. Pandey, Phys. Chem. Chem. Phys., 2019, 21, 9335–9341.
42. Y. Yalçin, M. Kiliç and Z. Çinar, Appl. Catal., B, 2010, 99, 469–477.
43. B. Himmetoglu, R. M. Wentzcovitch and M. Cococcioni, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 115108.
44. M. V. Mamonova and V. V. Prudnikov, Russ. Phys. J., 1998, 41, 1174–1179.
45. F. Opoku, K. K. Govender, C. G. C. E. van Sittert and P. P. Govender, Appl. Surf. Sci., 2018, 427, 487–498.
46. K. Kataoka, N. Kijima and J. Akimoto, Inorg. Chem., 2013, 52, 13861–13864.
47. P. Szirmai, E. Horváth, B. Náfrádi, Z. Micković, R. Smajda, D. M. Djokić, K. Schenk, L. Forró and A. Magrez, J. Phys. Chem. C, 2013, 117, 697–702.
48. B. Barrocas, A. J. Silvestre, A. G. Rolo and O. C. Monteiro, Phys. Chem. Chem. Phys., 2016, 18, 18081–18093.
49. Y. An, D. Wang and C. Wu, Phys. E, 2014, 60, 210–213.
50. X. G. Xu, X. Ding, Q. Chen and L. M. Peng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 035423.
51. S. Lutfalla, V. Shapovalov and A. T. Bell, J. Chem. Theory Comput., 2011, 7, 2218–2223.
52. T. M. F. Marques, O. P. Ferreira, J. A. P. Da Costa, K. Fujisawa, M. Terrones and B. C. Viana, J. Phys. Chem. Solids, 2015, 87, 213–220.
53. E. Morgado Jr, P. M. Jardim, B. A. Marinkovic, F. C. Rizzo, M. A. S. de Abreu, J. L. Zotin and A. S. Araújo, Nanotechnology, 2007, 18, 495710.
54. S. X. Lu, H. Zhong, D. M. Mo, Z. Hu, H. L. Zhou and Y. Yao, Green Chem., 2017, 19, 1371–1377.
55. M. Balık, V. Bulut and I. Y. Erdogan, Int. J. Hydrogen Energy, 2019, 44, 18744–18755.
56. J. Adhikary, P. Chakraborty, B. Das, A. Datta, S. K. Dash, S. Roy, J. W. Chen and T. Chattopadhyay, RSC Adv., 2015, 5, 35917–35928.
57. A. Lu, Y. Chen, D. Zeng, M. Li, Q. Xie, X. Zhang and D.-L. Peng, Nanotechnology, 2014, 25, 035707.
58. S. W. Cao, J. Fang, M. M. Shahjamali, Z. Wang, Z. Yin, Y. Yang, F. Y. C. Boey, J. Barber, S. C. J. Loo and C. Xue, CrystEngComm, 2012, 14, 7229–7235.
59. M. S. Mahmoud, E. Ahmed, A. A. Farghali, A. H. Zaki and N. A. M. Barakat, Mater. Chem. Phys., 2018, 217, 125–132.
60. W. Q. Han, W. Wen, D. Yi, Z. Liu, M. M. Maye, L. Lewis, J. Hanson and O. Gang, J. Phys. Chem. C, 2007, 111, 14339–14342.
61. G. Giuseppe Parravicini, Solid State Physics, Academic Press, 2nd edn, 2013.
62. B. Traore, L. Pedesseau, J.-C. C. Blancon, S. Tretiak, A. D. Mohite, J. Even, C. Katan, M. Kepenekian, A. D. Mohite, J. Even, C. Katan and M. Kepenekian, ACS Appl. Mater. Interfaces, 2020, 12, 6633–6640.
63. A. A. Araújo-Filho, F. L. R. Silva, A. Righi, M. B. da Silva, B. P. Silva, E. W. S. Caetano and V. N. Freire, J. Solid State Chem., 2017, 250, 68–74.
64. A. Vittadini, M. Schirmer, M. M. Walz, F. Vollnhals, T. Lukasczyk, H. P. Steinrück, H. Marbach, A. Riss, M. J. Elser, B. Schürer and O. Diwald, Langmuir, 2012, 28, 7851–7858.
65. B. Bukowski and N. A. Deskins, Phys. Chem. Chem. Phys., 2015, 17, 29734–29746.
66. S. A. H. Abass and N. Seriani, Phys. Status Solidi B, 2018, 255, 1700612.
67. D. Toprek, V. Koteski, J. Belošević-Čavor, V. Ivanovski and A. Umićević, Comput. Theor. Chem., 2017, 1120, 17–23.
68. H. H. Mohamed and D. W. Bahnemann, Appl. Catal., B, 2012, 128, 91–104.
69. I. Aouadi, H. Touati, J. M. Tatibouët and L. Bergaoui, J. Photochem. Photobiol., A, 2017, 346, 485–492.
70. I. M. Iani, V. Teodoro, N. L. Marana, U. Coleto, J. R. Sambrano, A. Z. Simões, M. D. Teodoro, E. Longo, L. A. Perazolli, R. A. C. Amoresi and M. Aparecida Zaghete, Appl. Surf. Sci., 2021, 538, 148137.
71. S. Mathew, A. Kumar Prasad, T. Benoy, P. P. Rakesh, M. Hari, T. M. Libish, P. Radhakrishnan, V. P. N. Nampoori and C. P. G. Vallabhan, J. Fluoresc., 2012, 22, 1563–1569.

---

Footnotes

† Electronic supplementary information (ESI) available: Characterization figures are found. See DOI: 10.1039/d0na00932f

‡ These two authors contribute equally to the work.

---