Open Access Article
Open Access ArticleInfluence of size polydispersity on magnetic field tunable structures in magnetic nanofluids containing superparamagnetic nanoparticles
Dillip Kumar
Mohapatra
a,
Philip J.
Camp
 bc and
John
Philip
bc and
John
Philip
 *a
*a
aSmart Materials Section, Corrosion Science and Technology Division, Metallurgy and Materials Group, Indira Gandhi Centre for Atomic Research, HBNI, Kalpakkam-603102, India. E-mail: philip@igcar.gov.in; mdillip@igcar.gov.in
bSchool of Chemistry, University of Edinburgh, David Brewster Road, Edinburgh EH9 3FJ, Scotland, UK. E-mail: philip.camp@ed.ac.uk
cDepartment of Theoretical and Mathematical Physics, Institute of Natural Sciences and Mathematics, Ural Federal University, 51 Lenin Avenue, Ekaterinburg 620000, Russia
First published on 24th April 2021
Abstract
We probe the influence of particle size polydispersity on field-induced structures and structural transitions in magnetic fluids (ferrofluids) using phase contrast optical microscopy, light scattering and Brownian dynamics simulations. Three different ferrofluids containing superparamagnetic nanoparticles of different polydispersity indices (PDIs) are used. In a ferrofluid with a high PDI (∼0.79), thin chains, thick chains, and sheets are formed on increasing the in-plane magnetic field, whereas isotropic bubbles, and hexagonal and lamellar/stripe structures are formed on increasing the out-of-plane magnetic field over the same range. In contrast, no field-induced aggregates are seen in the sample with low polydispersity under the above conditions. In a polydisperse sample, bubbles are formed at a very low magnetic field strength of 30 G. Insights into the structural evolution with increasing magnetic field strength are obtained by carrying out Brownian dynamics simulations. The crossovers from isotropic, through hexagonal columnar, to lamellar/stripe structures observed with increasing field strength in the high-polydispersity sample indicate the prominent roles of large, more strongly interacting particles in structural transitions in ferrofluids. Based on the observed microstructures, a phase diagram is constructed. Our work opens up new opportunities to develop optical devices and access diverse structures by tuning size polydispersity.
1. Introduction
A ferrofluid is a stable colloidal suspension containing superparamagnetic nanoparticles dispersed in a carrier fluid.1 Among various magnetic nanomaterials such as Fe3O4, γ-Fe2O3, CoFe2O4, NiFe2O4, MnFe2O4 and ZnFe2O4, magnetite (Fe3O4) nanoparticles are widely used materials in ferrofluids, owing to their high saturation magnetization, ease of synthesis, long term stability and superior bio-compatibility.1,2 Fe3O4 nanoparticles are prepared by various techniques such as coprecipitation,2 solvothermal decomposition,3 hydrothermal synthesis,4,5 sol–gel synthesis,6 microwave-assisted synthesis,7 sonochemical synthesis,8 ultrasonication,9 one-pot citrate sol–gel route,10etc. Composite Fe3O4 nanoparticles have many applications in diverse fields such as magnetic resonance imaging contrast agents, cancer therapy, optical imaging, pathogen control, corrosion control and all-in-one devices.11–15 The addition of magnetic nanomaterials is shown to modify the superconducting transition temperature and electrical behavior of materials.16Magnetic field induced structural transitions in ferrofluids have been a topic of interest from both the fundamental and practical points of view.1,17 The self-assembly of magnetic nanoparticles under an external magnetic field gives rise to interesting optical properties that are exploited in applications such as light controllable magnetic fluid based devices,18,19 optical limiters,20 biomedicine,21etc. Besides that, such magnetic nanofluids are also used in field-induced heating,22 hyperthermia therapies,23 magnetic resonance imaging,24 and thermal transport25–28 and as a model system to probe interaction forces at the nanoscale.29 The behavior of magnetic fluids under various experimental conditions depends on the equilibrium and non-equilibrium field-induced structures formed in a magnetic field.
The field-induced aggregation and structural phase transitions in ferrofluids depend on the magnetic interaction strength between the particles, the magnetic field strength, the orientation of the field with respect to the sample, the rate of change of the field, the sample thickness, polydispersity, volume fraction, the temperature, etc.30–34 Small-angle light-scattering techniques are widely used to investigate the aggregation kinetics of magnetic nanoparticles in a magnetic fluid.35–38 Similarly, other techniques such as small-angle neutron scattering39,40 and optical microscopy41,42 have also been used to characterize magnetic fluids. Several robust theoretical and numerical formalisms have been developed to understand the interparticle interactions under an external magnetic field in magnetic nanofluids under different conditions.43 Studies have been undertaken on structure formation in magnetic fluids using Brownian dynamics,44 Monte Carlo simulation,45 molecular and stochastic dynamic simulations,46,47 and models based on thermodynamic theory.48
Optical microscopy has been used to study field-induced particle aggregation in magnetic fluids, where the magnetic fluid is confined between two glass plates (Hele-Shaw cell) and undergoes structural transitions in the presence of a magnetic field, such as between a dilute ‘gas’ phase, linear chains, columns, and thin magnetic sheets due to the lateral coalescence of magnetic columns.49 A cross-sectional view shows individual columns, which appear as ‘bubbles’ in microscopy images, approaching one another to form a hexagonal close packed structure, and finally a stripe pattern (corresponding to thin magnetic sheets) with increasing out-of-plane magnetic field. Such isotropic-to-hexagonal-to-stripe transitions in the presence of an out-of-plane magnetic field are well established.50,51 The stripes at high magnetic field strengths can show long-range order and parallel alignment or be more intricate with labyrinthine structures. Bubble-to-stripe transitions have been studied in various systems such as ferrimagnetic garnet films52,53 and immiscible ferrofluid thin films (magnetic fluids confined with an immiscible non-magnetic liquid).50,54,55 The patterns in immiscible ferrofluids are formed by the interface between the magnetic and nonmagnetic phases, and their formation is explained by the competition between the magnetic and interfacial surface energy. The surface tension tends to minimize the area of the interface, whereas the interactions between the magnetic particles favor extended interfaces.31 Hexagonal structures predominate at a low particle volume fraction, and labyrinthine patterns emerge at a high volume fraction and with a high magnetic field strength.56–58 Ytreberg et al. proposed a theory to explain the transition between hexagonal and striped structures with increasing magnetic field,59 and a loss of a local minimum in the free energy of hexagonal patterns for very low and very high magnetic field intensities has been proposed.
Particle-size polydispersity is inevitable in any ferrofluid, and it plays an important role in field-induced structure formation. A polydisperse fluid can be considered as a mixture of a large number of components, where the particle size, shape, or interaction strength may vary. This not only affects the equation of state for the system, but also the phase transitions. The initial susceptibility of a polydisperse ferrofluid is found to be larger than that of a monodisperse ferrofluid,60 and in general, the magnetic properties show a very strong dependence on the volume fraction of large particles. With an increase in the volume fraction of large particles, the magnetization increases much faster at weak fields due to the strong particle–field interaction, which leads to a larger initial susceptibility. Large particles act as nucleation sites and attract nearby particles to form chains via dipolar head–tail interaction. The zippering of different chains is also more significant in polydisperse samples, and it occurs at lower field strengths as compared to more monodisperse samples.
Colloidal suspensions of superparamagnetic particles exhibit fascinating physical properties with numerous applications, and they are wonderful model systems to probe microscopic phenomena such as order–disorder structural transitions, self-assembly, aggregation, and complex dynamics. Despite the vast number of studies on the field-dependent properties of ferrofluids, most of the research until now has been confined to equilibrium or steady-state properties. In many technological applications, ferrofluids are subjected to a magnetic field but the behavior of ferrofluids depends on the properties of suspended nanoparticles. However, the exact conditions under which different structures such as thin chains, thick chains, sheets, isotropic bubbles, and hexagonal and lamellar/stripe structures are largely unknown. To the best of our knowledge, no systematic experimental study has been reported on the effect of particle-size polydispersity on field induced structures and structural transitions. In this paper, we detail the field-induced microstructures in ferrofluids with different polydispersity indices (PDIs), with either in-plane or out-of-plane fields with respect to the confining cell. Phase contrast optical microscopy, light scattering, and magnetization experiments are used to characterize the structures formed in three ferrofluids with various PDIs, and the experimental results for a high-PDI case are complemented by Brownian-dynamics simulations. This paper is organized as follows. Experimental materials and methods and simulation details are summarized in Sections 2 and 3. The results are presented and discussed in Section 4, and Section 5 concludes the paper.
2. Experimental
Three different ferrofluids containing oleic-acid stabilized magnetite (Fe3O4) nanoparticles at the same volume fraction (Φ = 0.037) were used in the present study: these three samples were named M1, M2, and M3. The particles were synthesized using the co-precipitation technique,61 and then dispersed in kerosene as the carrier fluid. The average crystallite diameters of the particles were 9.6 nm, 8.3 nm, and 10.5 nm for samples M1, M2, and M3, respectively. Transmission electron microscopy (TEM) images of the prepared particles are obtained using a JEOL JEM 2100 high resolution microscope. A Rigaku Ultima IV X-ray diffractometer (Cu-Kα radiation and wavelength λX-ray = 1.5416 Å) was used to acquire the diffraction patterns of the Fe3O4 magnetic nanoparticles in the angle range 2θ = 20–80°. The scan rate and step size were kept constant at 2° min−1 and 0.02°, respectively. The average crystallite diameter was obtained from the most intense Bragg reflection peak using Scherrer's equation. The hydrodynamic diameters and polydispersity indices were measured with dynamic light scattering (DLS) using a Malvern Zeta Nanosizer (ZEN 3600). Magnetization measurements were carried out up to ±2 T using a cryogen-free vibrating sample magnetometer (Cryogenics Ltd., UK) at both room temperature (300 K) and low temperature (4 K). Thermogravimetric analysis (TGA, 1100 LF, Mettler Toledo, Switzerland) was carried out to quantify the amount of steric stabilizer (oleic acid) on the surfaces of the magnetic nanoparticles. The samples were heated in the temperature range 30–650 °C at a heating rate of 10 °C min−1 under an inert (argon) atmosphere. A LEICA DM IRM inverted phase contrast microscope equipped with an ORCA-Flash 4.0 LT camera (Hamamatsu, Japan) was used for optical imaging.3. Simulation
To complement the experimental study and to gain additional insights into field-induced structure formation, Brownian dynamics simulations of sample M3 were carried out. This sample was selected because, as is shown in Section 4, it shows the greatest diversity of structures. The simulations were carried out with N = 12 × 36 × 36 = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 552 particles in a cuboidal cell with periodic boundary conditions, a constant z dimension (in the field direction) equal to 671 nm, and x and y cell dimensions set equal and to a value which gives the required volume fraction. A discretized particle-size distribution N(σ) was chosen to mimic the DLS results reported in Section 4; more details are given in Section 4.4. The dipole moment on a particle of diameter σ was set equal to
552 particles in a cuboidal cell with periodic boundary conditions, a constant z dimension (in the field direction) equal to 671 nm, and x and y cell dimensions set equal and to a value which gives the required volume fraction. A discretized particle-size distribution N(σ) was chosen to mimic the DLS results reported in Section 4; more details are given in Section 4.4. The dipole moment on a particle of diameter σ was set equal to 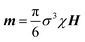 , where χ is the experimental susceptibility, and H = (0, 0, H) is the external magnetic field. The short-range interactions between two particles i and j were given by the Weeks–Chandler–Andersen (WCA) potential,62 given by uWCAij(r) = uLJij(r) − uLJij(r0), where uLJij(r) = 4ε[(σij/r)12 − (σij/r)6] is the Lennard-Jones (LJ) potential, σij = (σi + σj)/2 is the mean particle diameter,
, where χ is the experimental susceptibility, and H = (0, 0, H) is the external magnetic field. The short-range interactions between two particles i and j were given by the Weeks–Chandler–Andersen (WCA) potential,62 given by uWCAij(r) = uLJij(r) − uLJij(r0), where uLJij(r) = 4ε[(σij/r)12 − (σij/r)6] is the Lennard-Jones (LJ) potential, σij = (σi + σj)/2 is the mean particle diameter, 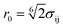 is the position of the minimum of the LJ potential, and ε = kBT is an energy parameter, assumed to be the same for all pairs of particles, and equal to the thermal energy. The WCA potential is therefore a soft, purely repulsive potential which models the short-range, non-magnetic interactions between sterically stabilized nanoparticles. The magnetic interactions were computed using the particle–particle particle-mesh Ewald summation method63 with conducting boundary conditions, to avoid any finite-size artefacts arising from demagnetization fields within the (small) simulation cell. The BD simulations were carried out at 300 K with a time step (in LJ units) of δt* = 0.00025 (this being small to take account of the dynamics of the small-particles), and for at least 106 timesteps, chosen so that the system reached a steady state. All simulations were performed using LAMMPS.64 Details of the computed observables are given in Section 4.4.
is the position of the minimum of the LJ potential, and ε = kBT is an energy parameter, assumed to be the same for all pairs of particles, and equal to the thermal energy. The WCA potential is therefore a soft, purely repulsive potential which models the short-range, non-magnetic interactions between sterically stabilized nanoparticles. The magnetic interactions were computed using the particle–particle particle-mesh Ewald summation method63 with conducting boundary conditions, to avoid any finite-size artefacts arising from demagnetization fields within the (small) simulation cell. The BD simulations were carried out at 300 K with a time step (in LJ units) of δt* = 0.00025 (this being small to take account of the dynamics of the small-particles), and for at least 106 timesteps, chosen so that the system reached a steady state. All simulations were performed using LAMMPS.64 Details of the computed observables are given in Section 4.4.
4. Results and discussion
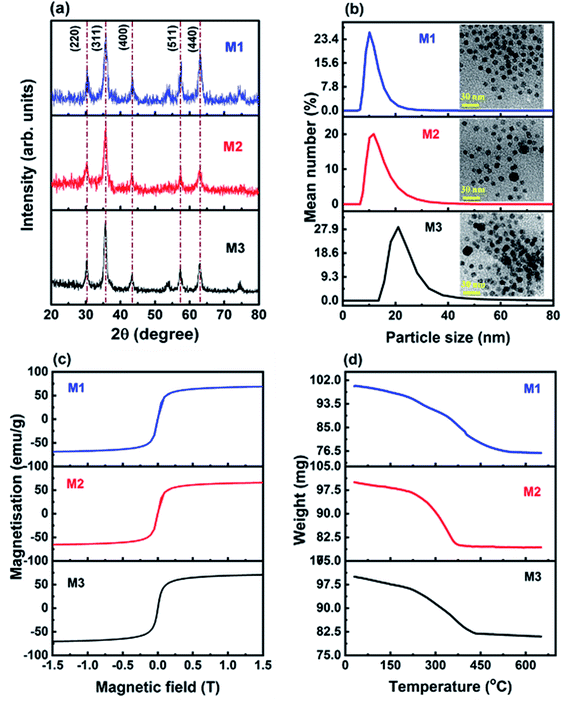
The X-ray diffraction, TEM, DLS, magnetization and thermogravimetric data of the samples M1, M2, and M3 are shown in Fig. 1(a–d).Fig. 1(a) shows the XRD pattern of oleic acid coated iron oxide nanoparticles. The Bragg diffraction peaks correspond to the (220), (311), (400), (511) and (440) planes of Fe3O4 (JCPDS file no. 19-0629). The average crystallite size was estimated to be 9.6 (±0.7), 8.3 (±0.6) and 10.5 (±0.6) nm for M1, M2 and M3, respectively. Our earlier room temperature Mössbauer studies of Fe3O4 nanoparticles showed that the hyperfine fields 48.00 and 46.00 T correspond to Fe3+ ions at tetrahedral sites and Fe2+ and Fe3+ ions at octahedral sites in Fe3O4 spinel respectively, with nearly zero quadrupole splitting.2 Therefore, the Mössbauer studies qualitatively establish the presence of Fe2+ and Fe3+ ions in the octahedral sites of the magnetite crystal.2Fig. 1(b) shows the number distribution curves of M1, M2 and M3, where the average hydrodynamic size of M1, M2 and M3 was found to be 10 (±0.6), 11.7 (±0.9) and 20.9 (±1) nm, respectively. The polydispersity index was found to be 0.22, 0.23 and 0.79 for M1, M2 and M3, respectively. The polydispersity of M3 is rather high due to the presence of larger aggregates. The insets of Fig. 1(b) show the TEM images of M1, M2 and M3 samples. The most probable sizes were ∼9, 8.8 and 11.2 nm for M1, M2 and M3, respectively. Fig. 1(c) shows the M–H curves of M1, M2, and M3. The saturation magnetization is found to be 69 (±0.6), 66 (±0.7) and 71 (±0.7) emu/g for M1, M2 and M3, respectively. Since the average size of nanoparticles was similar, there was not much difference in the saturation magnetization values. The M–H curves did not show any hysteresis at room temperature, which indicates the superparamagnetic nature of these particles.
Fig. 1(d) shows the thermogravimetric weight loss curves of the dried surfactant coated magnetite nanoparticles of M1, M2 and M3. The weight loss percentages were approximately 24, 21 and 19% for M1, M2 and M3, respectively. The weight loss percentage of surfactant adsorbed on the surface of nanoparticles, calculated using the formula assuming spherical particles having a monolayer of surfactant,65 was 19, 21.4 and 17.7% for M1, M2 and M3, respectively. On comparison, M1 showed a slightly higher surfactant content than that required for a monolayer, whereas M3 had a little less than that required to form a monolayer. The non-uniform coating would have led to larger aggregates even in the absence of a magnetic field and resulted in the higher polydispersity and hydrodynamic size of M3. For M2, an adequate amount of surfactant was present to form a monolayer. Table 1 reports the consolidated physical properties of the three samples obtained from XRD, DLS, magnetization, and TGA experiments. The polydispersity index obtained from the DLS study is defined as PDI = (sσ/μσ)2 where sσ and μσ are, respectively, the standard deviation and mean of the hydrodynamic diameter (σ) distribution. The amount of surfactant required to form a monolayer was computed and is compared with that of the experimental data (Table 1).
| Sample name | Crystallite diameter (nm) | Hydrodynamic diameter (nm) | Polydispersity index | Magnetization (emu g−1) | Surfactant weight loss (%) | Surfactant wt% required for a monolayer |
|---|---|---|---|---|---|---|
| M1 | 9.6 ± 0.7 | 10 ± 0.6 | 0.22 | 69 ± 0.6 | 24 | 19 |
| M2 | 8.3 ± 0.6 | 11.7 ± 0.9 | 0.23 | 66 ± 0.7 | 21 | 21.4 |
| M3 | 10.5 ± 0.6 | 20.9 ± 1 | 0.79 | 71 ± 0.7 | 19 | 17.7 |
4.1 Effect of polydispersity on field-induced structural transformations in ferrofluids
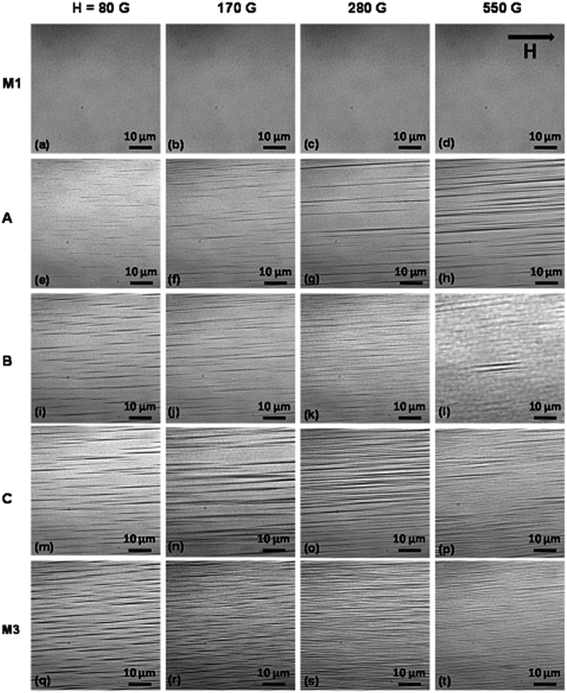
The field-induced microstructures formed at different magnetic field strengths in M1, M2, and M3 samples were studied using a phase contrast optical microscope. The external magnetic field was varied by using two permanent magnets placed in the two arms of a motorized stage, where the distance between the arms was varied using a stepper motor control. The magnets were brought closer to one another at different speeds (the ‘ramp rate’), giving different magnetic field strengths, and the resulting images were captured.The phase contrast optical microscopy images of samples M1, M2, and M3 at different magnetic field strengths of 0 G, 30 G, 80 G, 170 G, 280 G, and 550 G are shown in Fig. 2. The direction of the applied magnetic field H is shown by an arrow in Fig. 2(m). In sample M1, no aggregates are observed even at the highest field strength of 550 G, indicating that all aggregates are nano-sized (smaller than the 100 nm resolution limit of the microscope). In sample M2, above a field strength of 280 G, submicron-sized aggregates are seen. At 280 G, the microscopy images of sample M2 show several short and thin chains with an average length and width of around 12 μm and 0.9 μm, which increase to 37 and 1.6 μm, respectively as the magnetic field strength is increased to 550 G. In sample M3, very thick and long chains are observed at a field strength of 170 G, where the average length and width of the chains are 306 μm and 3.5 μm, respectively. As the field is increased to 280 G, adjacent chains coalesce to form thick sheets, which span the entire area being imaged.
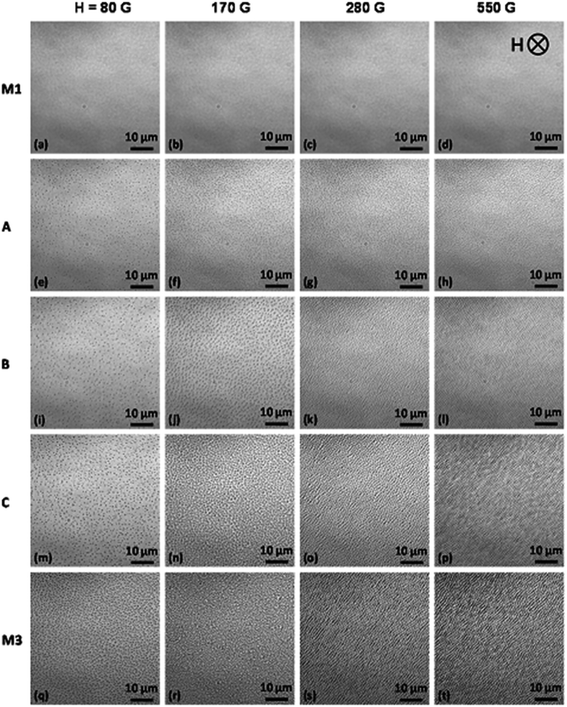
The cross-sectional views of magnetic field-induced microstructures in samples M1, M2, and M3 at different magnetic field strengths of 0 G, 30 G, 80 G, 170 G, 280 G, and 550 G are shown in Fig. 3. Here, the external magnetic field was applied perpendicular to the sample plane (out-of-plane). The cross-sectional views of columns and sheets appear as ‘bubbles’ and stripes, respectively. Similar to Fig. 2, no such bubbles are observed in sample M1 at any magnetic field strength up to 550 G, which indicates that all aggregates are less than 100 nm in size. In sample M2, only a few bubbles are seen at the highest field strengths of 280 G and 550 G. Although the polydispersity is very high in sample M3, in zero field, all particles are well dispersed in the sample, and even if there are aggregates of larger particles, their size is much less than the 100 nm resolution limit of the microscope. Hence, no structures are observed in the absence of a magnetic field, but bubbles appear even at a very low magnetic field strength of 30 G. In this case, the bubbles are randomly positioned in the plane, with an average intercolumn spacing of 3 μm. There are more columns at a field strength of 80 G, with a smaller intercolumn spacing of 1.5 μm. Hexagonal close packed columnar structures are apparent above a magnetic field strength of H = 170 G, with an even smaller intercolumn spacing of 0.6 μm. Overall, the average intercolumn spacing is found to vary inversely with the external magnetic field strength (∝H−1 with R2 ≃ 0.99) up to a field strength of 170 G, beyond which the columns coalesce and form stripe patterns. This is in agreement with an earlier report by Horng et al.66 At a field strength of 280 G, columns coalesce through lateral interactions to form stripe patterns (lamellar structures), with the stripes being extended perpendicular to the direction of the external magnetic field. The average width of a stripe at 280 G is 1.6 μm. As the field is increased further to 550 G, the number of stripes increases, the thickness of the stripes decreases, and the distance between the stripes decreases to 0.7 μm. At 280 G, the stripes are parallel to each other without significant bending. At 550 G, however, the stripes show a zig-zag modulation. This instability or undulation at 550 G can be understood as follows. As the field is increased, the width of the stripes decreases, while the length of the stripes increases (Fig. 3). In addition, since the ferrofluid is a paramagnetic substance, the local concentration of the magnetic material in the cell volume should increase with increasing field strength, with particles being supplied by the surrounding ferrofluid reservoir. Since the stripe structures are confined in the field direction (the cell thickness was approximately 21 μm), the simplest way to increase the length is through undulation. The zig-zag pattern gives rise to a larger area of interaction between the stripes, which leads to stabilization through long-range magnetic interaction between stripes.50
To sum up, in sample M3, three different structural arrangements of columns occurred in the presence of an out-of-plane field, these being isotropic, hexagonal, and stripe/lamellar structures with increasing magnetic field. These structures are shown in more detail in Fig. 4.
Fig. 4(a)–(c) show the structural progression between isotropic, hexagonal, and stripe patterns in sample M3 with magnetic field strengths of 80 G, 170 G, and 280 G. Fig. 4(d)–(f) show enlarged views, and Fig. 4(g)–(i) show the corresponding fast Fourier transform (FFT) images of the isotropic columnar distribution, hexagonal arrangement of columns, and stripe patterns. At H = 80 G, all columns are distributed randomly, and hence the FFT gives a circular pattern as shown in Fig. 4(g). At H = 170 G, the columns are closer to one another and adopt a local 2D hexagonal coordination but without long-range order. Close inspection of the FFT patterns reveals that the enlarged image [Fig. 4(e)] contains both five-fold and seven-fold coordination sites, along with the expected six-fold coordination sites. Five-fold and seven-fold coordination sites coincide with the positions of bubbles that are, respectively, smaller and larger than the bubbles that surround the six-fold coordination sites. It is known that size polydispersity creates dislocations and bubble-area mismatches, leading to size adjustment of the five-fold and seven-fold coordinated bubbles.67 Due to the misorientation of columns, a hexagonal pattern is seen in Fig. 4(h), instead of the six diffraction spots expected for a perfect hexagonal structure.68 Similar hexagonal patterns have also been seen in other systems such as a charged superparamagnetic colloid of Fe3O4 nanoparticles coated with silica,69 and a ferrofluid with magnetic holes (nonmagnetic particles dispersed in a magnetized ferrofluid solution).70 The stripe pattern [Fig. 4(i)] indicates periodic ordering of the domains along the longitudinal direction of the pattern, and the angular distribution indicates the directionality of the stripe pattern. When stripes are parallel to each other, two spots are seen in Fig. 4(i). The increased magnetic moment and decreased column separation at 280 G cause a stronger repulsion between the columns, which results in the aggregation of columns into lamellar structures in order to minimize the free energy.
The superparamagnetic nanoparticles in the dispersion are in Brownian random motion in the absence of a magnetic field, the particles are largely unmagnetized, and hence the net magnetic moment is zero. On exposure to an external magnetic field, the induced magnetic moments of the nanoparticles are aligned along the magnetic field direction. The magnetic moment of each particle is given by 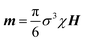 , where σ is the diameter of the particle, χ is the effective susceptibility, and H is the external magnetic field. The anisotropic interaction energy Uij between two particles i and j is given by
, where σ is the diameter of the particle, χ is the effective susceptibility, and H is the external magnetic field. The anisotropic interaction energy Uij between two particles i and j is given by
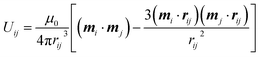 | (1) |
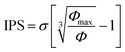 , where Φmax ≃ 0.63 is the maximum particle fraction, corresponding to random close packing. For a monodisperse sample, the strength of the magnetic dipolar interaction between the particles is quantified by the coupling constant (Λ) which is defined as the ratio between the magnetic dipolar interaction energy at contact (rij = σ) and the thermal energy,
, where Φmax ≃ 0.63 is the maximum particle fraction, corresponding to random close packing. For a monodisperse sample, the strength of the magnetic dipolar interaction between the particles is quantified by the coupling constant (Λ) which is defined as the ratio between the magnetic dipolar interaction energy at contact (rij = σ) and the thermal energy, 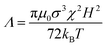 , where kB is Boltzmann's constant, and T is the temperature. The magnetic nanoparticles self-assemble to form linear aggregates in the direction of the magnetic field if Λ ≫ 1. The initial susceptibility was experimentally estimated from a linear regression analysis of the magnetization curves up to 10 mT and was found to be approximately 5.6, 6.4, and 7.4 for samples M1, M2, and M3, respectively.71 At low Φ, and at very low magnetic fields (<10 mT), the magnetization curve is mainly that of non-interacting particles (according to Table 2 at 3 mT, Λ ≪ 1 and hence the Langevin susceptibility χL = 8ΦΛ ≪ 0.296). The higher susceptibility of sample M3 is due to the larger particles, with smaller surface area-to-volume ratios and a less significant demagnetized surface layer.
, where kB is Boltzmann's constant, and T is the temperature. The magnetic nanoparticles self-assemble to form linear aggregates in the direction of the magnetic field if Λ ≫ 1. The initial susceptibility was experimentally estimated from a linear regression analysis of the magnetization curves up to 10 mT and was found to be approximately 5.6, 6.4, and 7.4 for samples M1, M2, and M3, respectively.71 At low Φ, and at very low magnetic fields (<10 mT), the magnetization curve is mainly that of non-interacting particles (according to Table 2 at 3 mT, Λ ≪ 1 and hence the Langevin susceptibility χL = 8ΦΛ ≪ 0.296). The higher susceptibility of sample M3 is due to the larger particles, with smaller surface area-to-volume ratios and a less significant demagnetized surface layer.
| Sample name | σ S (nm) | σ L (nm) | χ | H (G) | Λ LL | Λ LS | Λ SS |
|---|---|---|---|---|---|---|---|
| M1 | 9 | 16 | 5.6 | 30 | 0.009 | 0.004 | 0.002 |
| 80 | 0.07 | 0.03 | 0.01 | ||||
| 120 | 0.2 | 0.06 | 0.03 | ||||
| 170 | 0.3 | 0.1 | 0.06 | ||||
| 280 | 0.85 | 0.3 | 0.15 | ||||
| 550 | 3.3 | 1.2 | 0.58 | ||||
| M2 | 10 | 20 | 6.4 | 30 | 0.03 | 0.007 | 0.003 |
| 80 | 0.17 | 0.05 | 0.02 | ||||
| 120 | 0.4 | 0.1 | 0.05 | ||||
| 170 | 0.8 | 0.2 | 0.1 | ||||
| 280 | 2.18 | 0.6 | 0.3 | ||||
| 550 | 8.4 | 2.49 | 1.05 | ||||
| M3 | 20 | 34 | 7.4 | 30 | 0.2 | 0.07 | 0.03 |
| 80 | 1.17 | 0.48 | 0.24 | ||||
| 120 | 2.6 | 1.07 | 0.5 | ||||
| 170 | 5.3 | 2.1 | 1.1 | ||||
| 280 | 14.3 | 5.82 | 2.91 | ||||
| 550 | 55.2 | 22.4 | 11.2 |
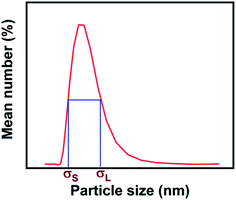
To help us to understand the effect of polydispersity on the field-induced structural transformations in magnetic colloids, a bidisperse approximation can be used.72 In a bidisperse system, two additional parameters are introduced: the particle-size ratio and the volume fraction of the larger particles. From the size distribution curve obtained by DLS, it was found that samples M1, M2, and M3 contained particles with diameters in the ranges of 7–21 nm, 7–28 nm, and 15–44 nm, respectively. Here we consider a bidisperse system composed of small particles with diameter σS, and large particles with diameter σL, defined as shown in Fig. 5. The magnetic moments of the two types of particles are referred to as mS and mL.
In such a bidisperse system, three different coupling constants can be defined: large–large (LL), large-small (LS), and small–small (SS). The magnetic field induced microstructures in such a system should somehow correspond to different values of the coupling constants 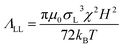 ,
, 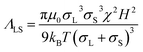 , and
, and 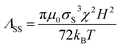 .73 These constants describe the strengths of the magnetic dipole interactions between the various components, and some illustrative values are provided in Table 2.
.73 These constants describe the strengths of the magnetic dipole interactions between the various components, and some illustrative values are provided in Table 2.
In sample M1, since the number of large-sized particles is relatively small, the average separation between the large-sized particles is much larger than the diameter of the small ones. The large number of small particles provides a magnetic background for the large ones. If the large-small particle interactions are neglected, this background field can be assumed as a continuous magnetic medium with an effective magnetic permeability μeff. The dipolar interaction energy between two large particles in such a magnetic medium is therefore μeff times smaller than that in a nonmagnetic medium.74 This weakening of the interaction energy will effectively reduce the aggregation probability of the large particles. At H = 550 G, ΛLL and ΛLS are greater than one, while ΛSS is less than one, indicating favorable conditions for the formation of aggregates through large–large and large–small particle interactions. Since ΛSS < 1, the small particles may attach to chains formed by large particles due to their dipole–dipole interaction in two possible ways: by approaching from a direction perpendicular to the chain axis, and getting trapped in a triangular arrangement by two large particles at contact; or by attaching to the ends of the chains.
The dipole–dipole interaction force is given by F = 3mimj(1 − 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/r4ij, where θ is the angle between the interparticle separation vector rij and the field H. The dipole–dipole interaction is attractive along the direction of the magnetic field and repulsive perpendicular to the direction of the magnetic field. The chains made of larger particles are assumed to be linear with all the dipole moments well aligned. The optimum attractive energy is attained when the dipole moments of the small particles are oriented parallel to the chain axis. However, this energy is not stronger than kBT in the case of transversely attaching particles. Hence, the small particles tend to attach at the ends of the chains of large particles due to relatively strong attraction. The attractive energy is not very sensitive to the chain length, due to the r−3 decay of the dipolar potential energy. If the number of small particles is high, then there is a high probability for them to be attached to the ends of the chains. When two short chains with small particles at their ends approach each other and combine into a longer chain, the smaller ones in the middle make the composite chain less stable as compared to a chain formed only from large particles, and as a result of thermal fluctuations, the composite chain may break at the location of the small particles.74 This restricts the further growth of the chains and also prevents the lateral coalescence of chains or columns, which can lead to a decrease in the chain length with an increase in the volume fraction of small particles (poisoning effect).74,75 The field-induced aggregation in sample M1 is very slow and all chains would have to be nanosized, because they are not discernible in the phase contrast optical microscopy images, even at a magnetic field strength of 550 G (Fig. 2 and 3).
θ)/r4ij, where θ is the angle between the interparticle separation vector rij and the field H. The dipole–dipole interaction is attractive along the direction of the magnetic field and repulsive perpendicular to the direction of the magnetic field. The chains made of larger particles are assumed to be linear with all the dipole moments well aligned. The optimum attractive energy is attained when the dipole moments of the small particles are oriented parallel to the chain axis. However, this energy is not stronger than kBT in the case of transversely attaching particles. Hence, the small particles tend to attach at the ends of the chains of large particles due to relatively strong attraction. The attractive energy is not very sensitive to the chain length, due to the r−3 decay of the dipolar potential energy. If the number of small particles is high, then there is a high probability for them to be attached to the ends of the chains. When two short chains with small particles at their ends approach each other and combine into a longer chain, the smaller ones in the middle make the composite chain less stable as compared to a chain formed only from large particles, and as a result of thermal fluctuations, the composite chain may break at the location of the small particles.74 This restricts the further growth of the chains and also prevents the lateral coalescence of chains or columns, which can lead to a decrease in the chain length with an increase in the volume fraction of small particles (poisoning effect).74,75 The field-induced aggregation in sample M1 is very slow and all chains would have to be nanosized, because they are not discernible in the phase contrast optical microscopy images, even at a magnetic field strength of 550 G (Fig. 2 and 3).
In sample M2, the number of large-sized particles is higher than in sample M1. Only above H = 280 G is ΛLL > 1, where larger sized particles should form aggregates in the direction of the magnetic field, and hence a few small chains appear as shown in Fig. 2(k) and 3(k). At H = 550 G, all three coupling constants are greater than or equal to one, and hence the number of chains is larger, and they are randomly distributed throughout the sample.
Sample M3 contains significantly more large-sized particles than samples M1 and M2. Larger particles have larger dipolar strength in the dispersion. The initial susceptibility and the magnetization curve of this system show a strong dependence on the number of larger particles. With an increase in the number of larger particles, the magnetization of the system increases faster in weak fields, and this leads to a larger initial susceptibility. At H = 280 G, all three interaction parameters are much larger than one. The potential energy of a dipole moment in an external magnetic field is given by UH = −μ0m⋅H, and the gradient of the magnetic field induces a magnetic packing force FH = −∇UH, which drives magnetic particles towards regions with the maximum local magnetic field strength. It has been reported that larger particles play an important role as condensation centers in the formation of nuclei.76 Once the chain length is above a critical value, it attracts the nearest small cluster (containing both large and small particles) towards it and forms a thicker column. Hence, this can be viewed as a kind of heterogeneous nucleation, where clusters of large particles act as nucleation points, and the rate is fast as compared to homogeneous nucleation. This mechanism enhances the degree of particle-size polydispersity within the columns. The introduction of small magnetic nanoparticles into a column induces a local magnetic field gradient, similar to the introduction of non-magnetic particles in a magnetic dispersion.77 The magnetic moments of the large particles and consequently those of the small particles in a column increase under a strong magnetic field, which further increases the concentration of small particles in regions with a high local magnetic field strength. Due to the increased magnetic moment, small–small particle interactions lead to the formation of chains with a smaller intercolumn separation. So, the increased magnetic moments and decreased chain separation cause stronger repulsion (i.e., due to steric hindrance) between the chains, which eventually results in the aggregation of chains into lamellar structures to minimize the free energy.77 This occurs by shifting a neighboring chain by a distance σ/2 corresponding to the radius of the nanoparticles. When the interchain repulsive forces are sufficiently strong, for example, at a high concentration of the particle chains, the system becomes thermodynamically unstable, and chains start to aggregate into sheets with zigzag and 2D labyrinthine structures to minimize the repulsive potentials.78,79 Zhang et al. showed that the transition from 1D chains to 2D labyrinths is due to the minimization of the repulsive potential under the conditions of a strong magnetic field gradient and a high volume fraction of large particles.79 It has been shown that for particle sizes in the range 5–8 nm and with a narrow size distribution (PDI < 0.017), the columns are isolated and well defined with closely packed nanoparticles inside the columns,80 and no transition is observed from a columnar to a labyrinthine pattern. In contrast, for broader size distributions (PDI > 0.017), defects at the ends and the edges of the columns, resulting from a cohesion of the nanoparticles inside the columns, favor the fusion of columns into labyrinthine structures. The formation of these patterns is explained by the minimization of free energy comprising magnetic, interfacial, and entropic contributions.57–59,81
4.2 Effect of the volume fraction of large particles on field-induced microstructures
To study the effect of the volume fraction of large particles (ΦL) on field-induced microstructures in ferrofluids, we prepared binary mixtures of samples M1 and M3 with various compositions. In total, five different samples named M1, A, B, C, and M3 were prepared. The volume fractions of small and large particles in the samples (based on the bidisperse model presented in Table 2) and the polydispersity indices are given in Table 3.| Sample name | Φ S | Φ L | Polydispersity index (PDI) |
|---|---|---|---|
| M1 | 0.017 | Nil | 0.22 |
| A | 0.008 | 0.008 | 0.47 |
| B | 0.004 | 0.012 | 0.60 |
| C | 0.00198 | 0.0148 | 0.71 |
| M3 | Nil | 0.017 | 0.79 |
The field-induced microstructures in all five samples were studied at different magnetic field strengths using a phase contrast optical microscope. The resulting images at magnetic field strengths of 80 G, 170 G, 280 G, and 550 G are shown in Fig. 6. The direction of H is shown by an arrow in Fig. 6(d). Similar to Fig. 2, no visible aggregates or chains are seen in sample M1 at any magnetic field strength. In sample A, with half of the total volume fraction containing large particles (i.e., ΦL = 0.008), chains are formed in the direction of the magnetic field even at a small field strength of 80 G, where the larger sized particles act as nucleation centers. The average length of the chains increases from 20 μm to 225 μm as the magnetic field strength increases from 80 G to 550 G. The zippering of chains is seen above a field strength of 170 G, and the progressive growth of small chains, through long chains, to zippered columns is seen on increasing the magnetic field from 80 G to 550 G. In sample B, the average length of the chains increases from 32 μm to 305 μm, as the magnetic field strength is increased from 80 G to 550 G. Similarly, in samples C and M3, with ΦL = 0.0148 and 0.017, respectively, short chains, long chains, zippered columns, and finally magnetic sheets are formed when the field strength is increased from 80 G to 550 G.
The cross-sectional (top) views of field induced structures in samples M1, A, B, C, and M3 at magnetic field strengths of 80 G (a, e, i, m, q), 170 G (b, f, j, n, r), 280 G (c, g, k, o, s), and 550 G (d, h, l, p, t) are shown in Fig. 7. Here, the orientation of the magnetic field is normal to the sample plane. In sample A, a large number of bubbles are seen at 80 G. The number of bubbles increases within the field of view, and the interbubble spacing decreases, with increasing magnetic field. The bubbles are distributed randomly in the dispersions even at 550 G. However, in samples B, C, and M3, above a certain magnetic field strength, hexagonal close packed structures and finally lamellar structures (formed by lateral aggregation of columns) are observed. The isotropic, hexagonal columnar, and lamellar/stripe patterns observed in samples B, C, and M3 indicate the prominent roles of the larger sized particles and the applied magnetic field strength in structural transitions in ferrofluids. The lamellar structures are formed only at a high volume fraction and high magnetic field strength.
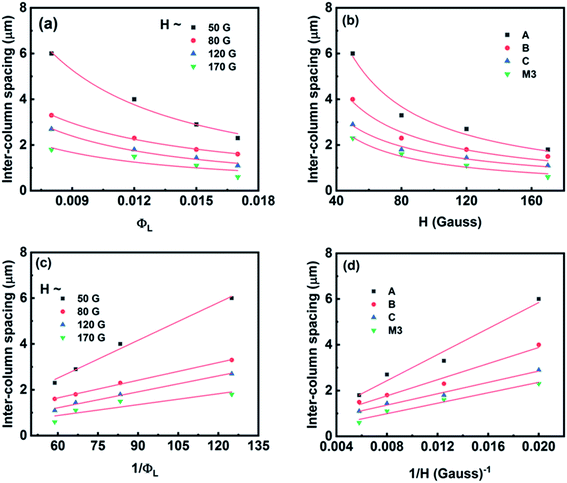
The average intercolumn spacing, determined from the microscopy images using IMAGE J software, as a function of both the volume fraction of large particles and the applied magnetic field strength, is shown in Fig. 8. The magnetic field strengths considered are below that at which stripe patterns start to form. Fig. 8(a) shows that the intercolumn spacing decreases with increasing ΦL and shows a power-law dependence (i.e., ∼ΦL−x), where the exponent x has values of 1.17 (R2 = 0.98), 0.95 (R2 = 0.99), 1.08 (R2 = 0.98), and 1.006 (R2 = 0.80) at magnetic field strengths of 50 G, 80 G, 120 G, and 170 G, respectively. Fig. 8(b) shows that the intercolumn spacing decreases and shows a power-law dependence with the magnetic field strength (∼H−y), where the exponent y is found to be 0.99 (R2 = 0.97), 0.88 (R2 = 0.96), 0.81 (R2 = 0.98), and 0.94 (R2 = 0.97) for samples A, B, C, and M3, respectively. Fig. 8(c) and (d) show the dependence of the intercolumn spacing on ΦL−1 and H−1, respectively, confirming the roughly inverse dependence of the spacing on the volume fraction and field strength.
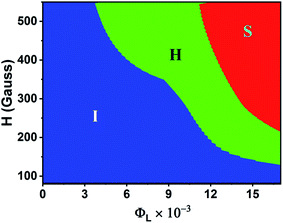
From the microscopy results, a phase diagram is constructed on the basis of the volume fraction of the larger particles and the applied magnetic field strength. The phase diagram showing the regions of isotropic (I), hexagonal (H), and stripe (S) phases is shown in Fig. 9. In the blue region of the graph, short chains and columns are randomly positioned throughout the sample, and this is called the isotropic phase. In the green and red regions, respectively, hexagonal close packed columnar structures and stripe patterns are formed. Under a high magnetic field and with a high volume fraction of large particles, a stripe/lamellar pattern is observed. At intermediate magnetic fields and a moderate volume fraction of large particles, hexagonal structures are formed. When the concentration of large particles is low, no hexagonal or stripe structures are observed, even under a strong magnetic field.
4.3 Scattered pattern and light transmission through magnetic nanofluids
The scattered light intensity patterns from samples M1, M2, and M3 at magnetic field strengths of 0 G, 80 G, 170 G, and 550 G are shown in Fig. 10. The magnetic field direction is parallel to the direction of light propagation, and the wavelength of the light is λ = 632.8 nm (He–Ne laser). In the absence of a magnetic field, there is no clustering of the magnetic nanoparticles, and since the particles are smaller than the wavelength of incident light (σ≪λ), Rayleigh scattering gives rise to one central spot on the screen. When the size of the scatterers is comparable to the wavelength of incident light, the scattering changes from the Rayleigh to the Mie regime. In the case of sample M1, the spot intensity remains unchanged with an increase of the magnetic field strength, indicating that the scatterer size remains within the Rayleigh regime. Fig. 2 shows that no micron-sized chains are visible in sample M1, even at the highest magnetic field strength of 550 G. Due to the presence of only smaller aggregates such as pairs, triplets, and other small chains, no changes in the intensity of the transmitted light spot are observed. In sample M2, there is a slight decrease in light intensity at 80 G. At 170 G, intense speckles of white spots and dark spots appear around the central spot. The speckle pattern formed when light passes though the magnetic nanofluid is due to the interference of dephased scattered waves emanating from randomly positioned particles.82 The structural transition from disorder to order in colloidal media has been studied by measuring such speckle parameters.83 The scattered waves from ordered media remain in phase rather than be dephased, which increases the probability of constructive inference of scattered waves. As the field increases, the number of single chains increases in the direction of the magnetic field. At 550 G, the system contains isolated particles, pairs, triplets, small chains, and large chains, as shown in Fig. 2. The number of speckles and the speckle contrast both increase, and the speckles are arranged in a circle indicating that linear aggregates are formed along the light-propagation direction. The increase in speckle contrast indicates a decrease in the mobility of the growing aggregates on increasing the magnetic field strength.83 In sample M3, the transmitted light spot at zero field is transformed into a circular pattern at 80 G, where the speckles are distributed on the circumference of the circle, indicating the formation of long chains and zippered columns that are distributed randomly in the sample, as shown in Fig. 2 and 3. The reason for the formation of a circular pattern can be explained on the basis of light scattered by cylindrical surfaces.84 The scattered fields are derived for an infinite right circular cylinder of diameter d when it is illuminated by a plane homogeneous wave EI(x) = E0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp
exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ikêix) propagating in the direction êi = (sin
(ikêix) propagating in the direction êi = (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ)êx − (cos
ζ)êx − (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ)êz, where k = 2π/λ, and ζ is the angle between the incident light wave and the cylindrical axis. The shape dependence of the conic section on the incident angle with respect to the cylinder axis is explained by deriving the expression of the scattered electromagnetic field from the cylindrical surface.85,86 It is inferred that the surfaces of the constant phase, or wave fronts, of the scattered waves are the points which satisfy the condition f(x, y, z) = r
ζ)êz, where k = 2π/λ, and ζ is the angle between the incident light wave and the cylindrical axis. The shape dependence of the conic section on the incident angle with respect to the cylinder axis is explained by deriving the expression of the scattered electromagnetic field from the cylindrical surface.85,86 It is inferred that the surfaces of the constant phase, or wave fronts, of the scattered waves are the points which satisfy the condition f(x, y, z) = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ − z
ζ − z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ = C, where C is a constant. The result is that the wave fronts are cones of half angle ζ with their apexes at
ζ = C, where C is a constant. The result is that the wave fronts are cones of half angle ζ with their apexes at 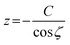 . The propagation of the scattered waves can be visualized as a cone that is sliding down the cylinder. The direction of propagation at any point on the cone or wave normal ês is ês = ∇f = (sin
. The propagation of the scattered waves can be visualized as a cone that is sliding down the cylinder. The direction of propagation at any point on the cone or wave normal ês is ês = ∇f = (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ)êr − (cos
ζ)êr − (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ)êz. The Poynting vector is therefore in the direction of ês. On placing a screen at some distance from the cylinder (parallel to the incident light), the scattering pattern forms a conic section. For ζ = 0°, the scattered pattern will be a circle as shown for sample M3 at 80 G in Fig. 10(j). The scattered pattern forms an ellipse at 0° < ζ ≤ 45° and transforms into a hyperbola at 45° ≤ ζ ≤ 90°. When the incident light is normal to the cylinder axis, a straight-line pattern is formed. In sample M3 at 170 G, six bright spots with some speckles are observed at the circumference of the circular pattern, indicating the presence of a short-range ordered hexagonal pattern. At 550 G, a straight-line pattern is observed due to the scattering of light from stripe-like structures, which is analogous to the scattering pattern form a straight line when the incident-light direction is normal to the cylinder axis.
ζ)êz. The Poynting vector is therefore in the direction of ês. On placing a screen at some distance from the cylinder (parallel to the incident light), the scattering pattern forms a conic section. For ζ = 0°, the scattered pattern will be a circle as shown for sample M3 at 80 G in Fig. 10(j). The scattered pattern forms an ellipse at 0° < ζ ≤ 45° and transforms into a hyperbola at 45° ≤ ζ ≤ 90°. When the incident light is normal to the cylinder axis, a straight-line pattern is formed. In sample M3 at 170 G, six bright spots with some speckles are observed at the circumference of the circular pattern, indicating the presence of a short-range ordered hexagonal pattern. At 550 G, a straight-line pattern is observed due to the scattering of light from stripe-like structures, which is analogous to the scattering pattern form a straight line when the incident-light direction is normal to the cylinder axis.
Fig. 11 shows the transmitted light intensity as a function of time for samples M1, M2, and M3 at magnetic field strengths of 100 G and 300 G. Here, the transmitted light intensity is the ratio of the light intensities in the presence and the absence of the magnetic field. The magnetic field was switched on at time t = 0 s and kept constant up to t = 600 s. The transmitted light intensity through samples M1 and M2 in the presence of a magnetic field remains invariant with time. However, sample M3 shows drastic changes in the transmitted intensity in the presence of a magnetic field. At 100 G, the transmitted intensity remains constant during the initial time interval (t = 0–75 s), and after that it increases linearly with time with a slope of about 0.02 s−1 (R2 = 0.99). At 300 G, the transmitted light intensity starts to increase after 35 s and ultimately shows a power-law increase with time (∼tx), where the exponent x is found to be 1.5 (R2 = 0.98). Similar trends in the temporal variation of the transmitted light intensity were observed for a ferrofluid emulsion.87 Sample M3 contains larger sized particles that act as nucleation centers, which initiate chain formation even at a low magnetic field strength. With a further increase in the magnetic field strength, the aspect ratio of the chains increases. Once the chains reach the maximum length, the lateral interaction between chains leads to zippering. As the number density of chains decreases and the spacing between the chains increases, more light is transmitted. This explains the growth in transmitted light intensity in sample M3 with a strong magnetic field. Due to the presence of nanosized aggregates with high diffusion coefficients, no changes in the transmitted light intensity as a function of time are observed for samples M1 and M2.
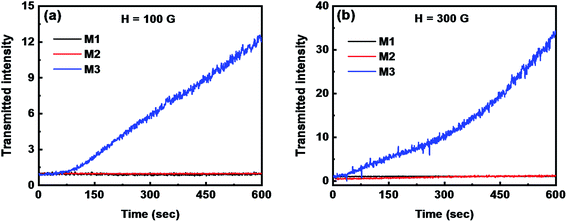 | ||
| Fig. 11 Transmitted light intensity as a function of time for samples M1, M2, and M3 at magnetic field strengths of (a) 100 G and (b) 300 G. | ||
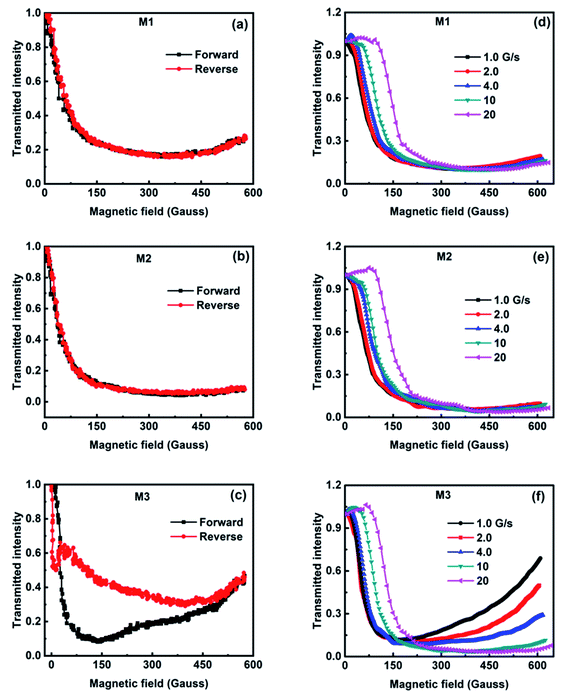
Fig. 12(a)–(c) show the variation of the transmitted light intensity as a function of magnetic field strength at a ramp rate of 2 G s−1, during both the increase and decrease, for samples M1, M2, and M3. For sample M3, a large hysteresis in the transmitted light intensity curve is observed during the increase and decrease of the magnetic field. However, for samples M1 and M2, no hysteresis is observed during the increase and decrease of the field, which indicates rapid aggregation and disaggregation processes. The significant hysteresis area observed with sample M3 indicates slow field-induced aggregation arising from the higher polydispersity. This observation shows that the polydispersity plays an important role in the aggregation and disaggregation processes. The transmitted light intensity returns to its initial value after switching off the magnetic field, indicating that the particles are redispersed after removing the applied magnetic field. Fig. 12(d)–(f) show the variation of the transmitted light intensity as a function of magnetic field at different ramp rates of 1, 2, 4, 10 and 20 G s−1 for samples M1, M2, and M3. For all ramp rates, the transmitted light intensity through samples M1 and M2 is found to decrease with increasing magnetic field and reach a plateau at a high magnetic field strength. The transmitted light intensity through sample M3 increases after reaching a minimum in the presence of the magnetic field strength for all ramp rates, except 20 G s−1, indicating the formation of long chains and columns in the direction of the magnetic field, which scatter more light in the forward direction.
4.4 Insights into chain and sheet formation from Brownian dynamics simulations
Brownian dynamics simulations are used to gain further insight into the crossover between columnar and stripe patterns in sample M3. Fig. 13(a) shows the particle-size distribution from the DLS study, along with a discretized version containing 11 fractions for use in the simulations. As explained in Section 4.1, the ferrofluid is a paramagnetic substance, and hence it is attracted to a region with high magnetic field intensity. As a result, the exact volume fraction of particles within the experimental observation region is not known and neither is the local particle-size distribution. So for the purposes of illustration, it is assumed that the particle size distribution in the observation region is the same as that for the bulk sample, and the volume fraction is scanned between 1 and 6 times the stock value, meaning Φ = 0.037–0.222. The third moment of the particle-size distribution is σ3 = 1.23 × 104 nm3, and so with N = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 552 particles and a fixed z dimension of 671 nm, the x and y dimensions of the cell ranged from 2014 nm at the lowest volume fraction to 822 nm at the highest volume fraction. Since the average particle diameter is 22 nm, the box dimensions are at least 30 times bigger in all cases.
552 particles and a fixed z dimension of 671 nm, the x and y dimensions of the cell ranged from 2014 nm at the lowest volume fraction to 822 nm at the highest volume fraction. Since the average particle diameter is 22 nm, the box dimensions are at least 30 times bigger in all cases.
Fig. 14 shows the top-down views of systems corresponding to H = 280 G, and Φ = 0.037 and 0.222. For each system, an orthographic view and a perspective view are shown, so that the presence of chains in the field direction can be discerned. In the case of the orthographic view, four periodic replicas are shown in the xy plane, so that any clusters cut by the box edge can be distinguished. At Φ = 0.037, it is clear that long chains of large particles have formed in the field direction, but many of the small particles are not part of any cluster. Some chains are one-particle thick, and others are zippered. The orthographic view – where the particle positions are projected on the plane – shows some clustering, but the distinction between clusters and free particles is not very clear. Increasing the volume fraction does not produce any interesting structure. As shown in Fig. 14, at Φ = 0.222, no distinct clusters can be identified clearly from either view.
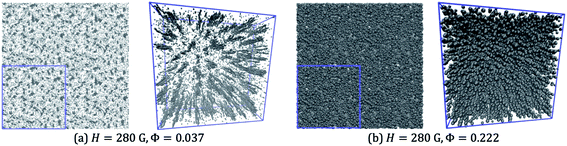 | ||
| Fig. 14 Snapshots from simulations with H = 280 G and (a) Φ = 0.037, and (b) Φ = 0.222. In each case, an orthographic view (with 4 periodic replicas) and a perspective view are shown. | ||
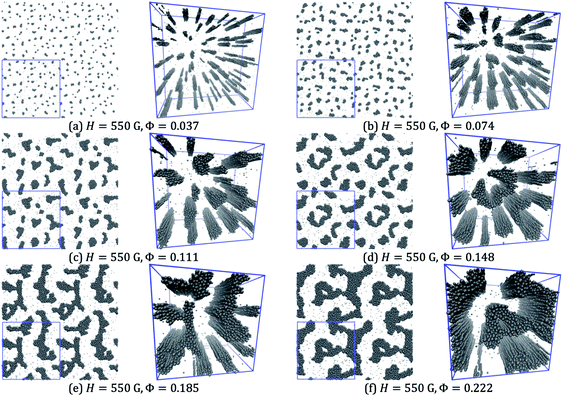
Higher field strengths are required to produce more distinct clusters. Fig. 15 shows snapshots from simulations at a field strength of 415 G (halfway between the experimental values of 280 G and 550 G), and at six volume fractions in the range Φ = 0.037–0.222. The results are dramatically different from those at the lower magnetic field strength. Firstly, a much greater proportion of particles are now associated with columns, meaning that the clusters are much more distinct in the snapshots. At the three lowest volume fractions (Φ = 0.037, 0.074, and 0.111), the columns mostly have cylindrical symmetry, and are evenly spaced in the xy plane, but without long-range ordering. At higher volume fractions (Φ ≥ 0.148), the columns have coalesced to form structures that are more extended in the direction perpendicular to the field, and as the volume fraction is increased, they begin to connect up further to form something resembling a continuous, labyrinthine structure. The perspective views clearly show the sheet-like structures formed by the coalescence of the columns.
Fig. 16 shows similar results but for a field strength of 550 G. The qualitative picture is very similar to that at 415 G. At low volume fractions, the particles are clustered into columns. There are fewer free, small particles at this field strength because of the increased magnetization and hence coupling constants of the particles. As the volume fraction is increased, the columns start to coalesce in the lateral dimension, forming sheet-like structures. At the highest volume fraction, these sheets connect up to form a labyrinthine structure; the snapshots very clearly show the two-dimensional nature of the sheets.
To estimate the length scales of the various structures being formed, the two-dimensional radial distribution function g(r) was computed by projecting all particle positions onto the xy plane. This is given by
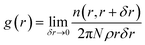 | (2) |
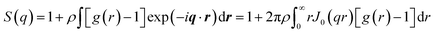 | (3) |
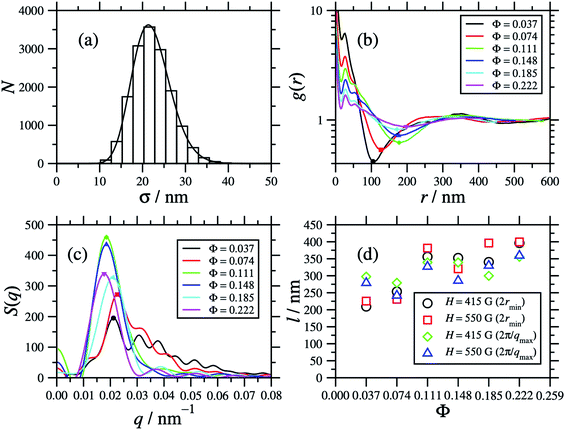
Fig. 13(d) shows the characteristic length scales obtained from both g(r) and S(q), as functions of the volume fraction, and for the field strengths H = 415 G and 550 G (no structure being discernible at 280 G). Firstly, the two routes give broadly similar results. Secondly, as the volume fraction increases (corresponding to the ingress of magnetic nanoparticles), the characteristic length scales approach values in the range 300 nm–400 nm, irrespective of the field strength. This suggests that the natural length scale of the stripe-like patterns should be in the region of 0.4 μm. In Section 4.1, it was observed that the distance between stripes at the highest field strength was about 0.7 μm. There are several unknown factors at play here (local size distribution, volume fraction, and magnetic field strength and gradient). Moreover, the simulations can only capture a very small volume and over much shorter timescales than in experiments (on the timescale of minutes). Nonetheless, the simulations show how columns coalesce to form sheets and that the spacing between sheets is at least of the right order of magnitude as compared to the experiment.
5. Conclusions
The effect of size polydispersity on field-induced equilibrium and non-equilibrium structures in magnetic nanofluids was probed systematically. Three different ferrofluids – labelled M1, M2, and M3 – containing magnetic nanoparticles with average crystallite diameters of 9.6 nm, 8.3 nm, and 10.5 nm, and with different polydispersities, respectively, were studied. Phase contrast optical microscopy images revealed that sample M3 showed structural transitions from isotropic columnar, through hexagonal close packed, to striped patterns on increasing the magnetic field strength from 0 G to 500 G. In contrast, samples M1 and M2 showed no such structural transitions. The formation of stripe/lamellar structures was completely reversible upon switching on and off the external magnetic field. The lamellar structures obtained in strong fields were dynamic and disappeared upon the removal of the external magnetic field. In sample M3, bubbles were formed at a very low magnetic field strength of 30 G, with an average intercolumn spacing of 3 μm, which was found to decrease with increasing magnetic field. Hexagonal close packed columnar structures were formed with an intercolumn spacing of 0.6 μm at 170 G. The average intercolumn spacing was found to vary inversely with the external magnetic field up to 170 G, beyond which the columns coalesced and formed striped patterns. At a very high magnetic field strength, an undulation due to the long-range magnetic coupling interaction between stripes gave rise to a zig-zag pattern. The isotropic, hexagonal columnar, and lamellar/stripe patterns observed in sample M3 indicate the prominent roles of larger sized particles and the applied magnetic field strength in structural transitions in ferrofluids. The lamellar structures were formed only at a high volume fraction of large particles and with strong magnetic fields. The intercolumn spacing decreased with ΦL and showed a power-law dependence. The intercolumn spacing varied inversely with the magnetic field strength. A phase diagram was constructed containing the different structures seen with different volume fractions and field strengths. The structural transitions observed with microscopy were also confirmed using light-scattering techniques, with each structure giving rise to characteristic features in the scattering pattern. In addition, time-resolved experiments showed that the aggregation and disaggregation kinetics are slow, but that the processes are essentially reversible. Finally, Brownian dynamics simulations were used to gain some insights into the formation of the magnetic sheets which give rise to the stripe-like patterns in the high-polydispersity sample (M3) seen with very strong magnetic fields. It was shown how thin chains coalesce to form sheets with increasing magnetic field, and although the ultimate equilibrium structures cannot be obtained on the simulation timescale, the emerging characteristic length scales were in approximate agreement with those seen in the microscopy experiments. Our work not only provide new insights into the role of the PDI in structural transitions but also opens up new opportunities to develop optical devices and access diverse structures by tuning size polydispersity. The obtained results are useful for the design of light-controllable magnetic-fluid-based devices such as light modulators and light switches, where the light transmission through the magnetic fluid can be controlled with an external magnetic field, size polydispersity and volume fraction of larger sized particles. The reversible and fast response of polydisperse samples will also be beneficial for microfluidics applications such as ferrofluid-based robots and lab-on-chip devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Shaju P. Albert, Dr S. Raju and Dr A. K. Bhaduri for their support and encouragement.References
- R. E. Rosensweig, Ferrohydrodynamics, Dover Publications, Inc., New York, 1997 Search PubMed.
- G. Gnanaprakash, J. Philip, T. Jayakumar and B. Raj, J. Phys. Chem. B, 2007, 111, 7978 CrossRef CAS PubMed.
- M. Wu, G. Liu, M. Li, P. Dai, Y. Ma and L. Zhang, J. Alloys Compd., 2010, 491, 689 CrossRef CAS.
- M. A. Almessiere, et al. , Ceram. Int., 2019, 45, 8222 CrossRef CAS.
- Y. Slimani, M. A. Almessiere, M. Nawaz, A. Baykal, S. Akhtar, I. Ercan and I. Belenli, Ceram. Int., 2019, 45, 6021 CrossRef CAS.
- K. D. Kim, S. S. Kim, Y.-H. Choa and H. T. Kim, J. Ind. Eng. Chem., 2007, 13, 1137 CAS.
- T. Muthukumaran and J. Philip, J. Nanosci. Nanotechnol., 2014, 15, 2715 CrossRef PubMed.
- Y. Slimani, M. A. Almessiere, M. Sertkol, S. E. Shirsath, A. Baykal, M. Nawaz, S. Akhtar, B. Ozcelik and I. Ercan, Ultrason. Sonochem., 2019, 57, 203 CrossRef CAS PubMed.
- Y. Slimani, et al. , Ultrason. Sonochem., 2019, 59, 104757 CrossRef CAS PubMed.
- M. A. Almessiere, Y. Slimani and A. Baykal, J. Alloys Compd., 2018, 762, 389 CrossRef CAS.
- A. Manikandan, M. Yogasundari, K. Thanrasu, A. Dinesh, K. K. Raja, Y. Slimani, S. K. Jaganathan, R. Srinivasan and A. Baykal, Phys. E, 2020, 124, 114291 CrossRef CAS.
- S. Akhtar, S. Rehman, M. A. Almessiere, F. A. Khan, Y. Slimani and A. Baykal, Nanomaterials, 2019, 9, 1635 CrossRef CAS PubMed.
- H. Tombuloglu, Y. Slimani, G. Tombuloglu, M. Almessiere and A. Baykal, Chemosphere, 2019, 226, 110 CrossRef CAS PubMed.
- G. Yasin, et al. , Diamond Relat. Mater., 2020, 104, 107763 CrossRef CAS.
- Y. Slimani, M. A. Almessiere, S. E. Shirsath, E. Hannachi, G. Yasin, A. Baykal, B. Ozcelik and I. Ercan, J. Magn. Magn. Mater., 2020, 510, 166933 CrossRef CAS.
- Y. Slimani, E. Hannachi, M. K. B. Salem, A. Hamrita, A. Varilci, W. Dachraoui, M. B. Salem and F. B. Azzouz, Phys. B, 2014, 450, 7 CrossRef CAS.
- L. Hu, R. Zhang and Q. Chen, Nanoscale, 2014, 6, 14064 RSC.
- T. Yao, S. Pu, J. Rao and J. Zhang, Sci. Rep., 2018, 8, 12352 CrossRef PubMed.
- D. K. Mohapatra and J. Philip, Opt. Mater., 2018, 76, 97 CrossRef CAS.
- L. Luo, S. Pu, J. Tang, X. Zeng and M. Lahoubi, Appl. Phys. Lett., 2015, 106, 193507 CrossRef.
- T. Pellegrino, S. Kudera, T. Liedl, A. M. Javier, L. Manna and W. Parak, Small, 2005, 1, 48 CrossRef CAS PubMed.
- S. Ranoo, B. B. Lahiri, T. Muthukumaran and J. Philip, Appl. Phys. Lett., 2019, 115, 043102 CrossRef.
- G. Barrera, P. Allia and P. Tiberto, Nanoscale, 2020, 12, 6360 RSC.
- M. F. Casula, A. Corrias, P. Arosio, A. Lascialfari, T. Sen, P. Floris and I. J. Bruce, J. Colloid Interface Sci., 2011, 357, 50 CrossRef CAS PubMed.
- V. Socoliuc and R. Turcu, J. Magn. Magn. Mater., 2020, 500, 166348 CrossRef.
- A. Y. Zubarev, Phys. Rev. E, 2019, 99, 062609 CrossRef CAS PubMed.
- A. V. Lebedev, V. I. Stepanov, A. A. Kuznetsov, A. O. Ivanov and A. F. Pshenichnikov, Phys. Rev. E, 2019, 100, 032605 CrossRef CAS PubMed.
- P. Ilg, Phys. Rev. E, 2019, 100, 022608 CrossRef CAS PubMed.
- J. Philip, G. G. Prakash, T. Jaykumar, P. Kalyanasundaram and B. Raj, Phys. Rev. Lett., 2002, 89, 268301 CrossRef PubMed.
- C. Holm and J. J. Weis, Curr. Opin. Colloid Interface Sci., 2005, 10, 133 CrossRef CAS.
- G. A. Flores, M. L. Ivey, J. Liu, M. Mohebi and N. Jamasbi, Int. J. Mod. Phys. B, 1996, 10, 3283 CrossRef CAS.
- A. J. Dickstein, S. Erramilli, R. E. Goldstein, D. P. Jackson and S. A. Langer, Science, 1993, 261, 1012 CrossRef CAS PubMed.
- F. Donado, J. M. Sausedo-Solorio and R. E. Moctezuma, Phys. Rev. E, 2017, 95, 022601 CrossRef CAS PubMed.
- S. L. Saville, et al. , Nanoscale, 2013, 5, 2152 RSC.
- J. M. Laskar, J. Philip and B. Raj, Phys. Rev. E, 2010, 82, 021402 CrossRef PubMed.
- M. Ivey, J. Liu, Y. Zhu and S. Cutilas, Phys. Rev. E, 2000, 63, 011403 CrossRef PubMed.
- C. Rablau, P. Vaishnava, C. Sudakar, R. Tackett, G. Lawes and R. Naik, Phys. Rev. E, 2008, 78, 051502 CrossRef PubMed.
- S. Garcia-Jimeno, J. Estelrich, J. Callejas-Fernandez and S. Roldan-Vargas, Nanoscale, 2017, 9, 15131 RSC.
- Z. Fu, Y. Xiao, A. Feoktystov, V. Pipich, M.-S. Appavou, Y. Su, E. Feng, W. Jin and T. Brückel, Nanoscale, 2016, 8, 18541 RSC.
- A. V. Nagornyi, V. Socoliuc, V. I. Petrenko, L. Almasy, O. I. Ivankov, M. V. Avdeev, L. A. Bulavin and L. Vekas, J. Magn. Magn. Mater., 2020, 501, 166445 CrossRef CAS.
- J. Promislow, A. P. Gast and M. Fermigier, J. Chem. Phys., 1995, 102, 5492 CrossRef CAS.
- F. M. Pedredo, A. E. Harrak, J. C. F. Tolenado, M. Tirado-Miranda, J. Baudry, A. Schmitt, J. Bibette and J. C. Fernandez, Phys. Rev. E, 2008, 78, 011403 CrossRef PubMed.
- Á. Sanz-Felipe and J. C. Martín, J. Magn. Magn. Mater., 2019, 474, 613 CrossRef.
- T. Ukai and T. Maekawa, Phys. Rev. E, 2004, 69, 032501 CrossRef PubMed.
- M. A. Salvador, A. S. Costa, M. Gaeti, L. P. Mendes, E. M. Lima, A. F. Bakuzis and R. Miotto, Phys. Rev. E, 2016, 93, 022609 CrossRef PubMed.
- D. Zablotsky, E. Blums and H. J. Herrmann, Soft Matter, 2017, 13, 6474 RSC.
- D. Heinrich, A. R. Goñi, T. M. Osan, L. M. C. Cerioni, A. Smessaert, S. H. L. Klapp, J. Faraudo, D. J. Pusiol and C. Thomsen, Soft Matter, 2015, 11, 7606 RSC.
- Z. M. Sherman, D. Ghosh and J. W. Swan, Langmuir, 2018, 34, 7117 CrossRef CAS PubMed.
- M. Wang, L. He and Y. Yin, Mater. Today, 2013, 16, 110 CrossRef CAS.
- F. Elias, C. Flament, J.-C. Bacri and S. Neveu, J. Phys., 1997, 7, 711 CAS.
- M. F. Islam, K. H. Lin, D. Lacoste, T. C. Lubensky and A. G. Yodh, Phys. Rev. E, 2003, 67, 021402 CrossRef CAS PubMed.
- D. Sornette, J. Phys., 1987, 48, 151 CrossRef.
- M. Seul and R. Wolfe, Phys. Rev. A, 1992, 46, 7519 CrossRef CAS PubMed.
- J. Bugase, J. Berner and T. M. Fischer, Soft Matter, 2016, 12, 8521 RSC.
- S. A. Langer, R. E. Goldstein and D. P. Jackson, Phys. Rev. A, 1992, 46, 4894 CrossRef PubMed.
- A. Cebers, Int. J. Mod. Phys. B, 2002, 16, 2345 CrossRef.
- J. Richardi, D. Ingert and M. P. Pileni, Phys. Rev. E, 2002, 66, 046306 CrossRef CAS PubMed.
- D. Lacoste and T. C. Lubensky, Phys. Rev. E, 2001, 64, 041506 CrossRef CAS PubMed.
- F. M. Ytreberg and S. R. McKay, Phys. Rev. E, 2000, 61, 4107 CrossRef CAS PubMed.
- P. J. Camp, E. A. Elfimova and A. O. Ivanov, J. Phys.: Condens. Matter, 2014, 26, 456002 CrossRef PubMed.
- P. D. Shima, J. Philip and B. Raj, J. Phys. Chem. C, 2010, 114, 18825 CrossRef CAS.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237 CrossRef CAS.
- J. J. Cerdà, V. Ballenegger, O. Lenz and C. Holm, J. Chem. Phys., 2008, 129, 234104 CrossRef PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1 CrossRef CAS.
- G. Gnanaprakash, S. Ayyappan, T. Jayakumar, J. Philip and B. Raj, Nanotechnology, 2006, 17, 5851 CrossRef CAS.
- H.-E. Horng, C.-Y. Hong, W. B. Yeung and H.-C. Yang, Appl. Opt., 1998, 37, 2674 CrossRef CAS PubMed.
- M. Seul and C. A. Murray, Science, 1993, 262, 558 CrossRef CAS PubMed.
- H.-E. Horng, C.-Y. Hong, S. L. Lee, C. H. Ho, S. Y. Yang and H. C. Yang, J. Appl. Phys., 2000, 88, 5904 CrossRef CAS.
- L. He, V. Malik, M. Wang, Y. Hu, F. E. Anson and Y. Yin, Nanoscale, 2012, 4, 4438 RSC.
- A. T. Skjeltorp, Phys. Rev. Lett., 1983, 51, 2306 CrossRef CAS.
- S. Ranoo, B. B. Lahiri, S. Vinod and J. Philip, J. Magn. Magn. Mater., 2019, 486, 165267 CrossRef CAS.
- A. O. Ivanov and E. V. Novak, Colloid J., 2007, 69, 302 CrossRef CAS.
- E. S. Minina, A. B. Muratova, J. J. Cerda and S. S. Kantorovich, J. Exp. Theor. Phys., 2013, 116, 424 CrossRef CAS.
- Z. Wang and C. Holm, Phys. Rev. E, 2003, 68, 041401 CrossRef PubMed.
- A. O. Ivanov and S. S. Kantorovich, Phys. Rev. E, 2004, 70, 021401 CrossRef PubMed.
- H. Ezzaier, J. A. Marins, I. Razvin, M. Abbas, A. B. H. Amara, A. Zubarev and P. Kuzhir, J. Chem. Phys., 2017, 146, 114902 CrossRef CAS PubMed.
- L. He, Y. Hu, H. Kim, J. Ge, S. Kwon and Y. Yin, Nano Lett., 2010, 10, 4708 CrossRef CAS PubMed.
- V. Malik, A. V. Petukhov, L. He, Y. Yin and M. Schmidt, Langmuir, 2012, 28, 14777 CrossRef CAS PubMed.
- Q. Zhang, M. Janner, L. He, M. Wang, Y. Hu, Y. Lu and Y. Yin, Nano Lett., 2013, 13, 1770 CrossRef CAS PubMed.
- V. Germain and M. P. Pileni, Adv. Mater., 2005, 17, 1424 CrossRef CAS.
- J. Richardi and M. P. Pileni, Phys. Rev. E, 2004, 69, 016304 CrossRef CAS PubMed.
- X. Zhong, X. Wang, N. Cooley, P. M. Farrell, S. Foletta and B. Moran, Opt. Commun., 2014, 313, 256 CrossRef CAS.
- S. Brojabasi, T. Muthukumaran, J. M. Laskar and J. Philip, Opt. Commun., 2015, 336, 278 CrossRef CAS.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley, New York, 1983 Search PubMed.
- J. M. Laskar, S. Brojabasi, B. Raj and J. Philip, Opt. Commun., 2012, 285(6), 1242 CrossRef CAS.
- E. Hasmonay, E. Dubois, J. C. Bacri, R. Perzynski, Y. L. Raikher and V. I. Stepanov, Eur. Phys. J. B, 1998, 5, 859 CrossRef CAS.
- D. K. Mohapatra, J. M. Laskar and J. Philip, J. Mol. Liq., 2020, 304, 112737 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |