Understanding nanodomain morphology formation in dip-coated PS-b-PEO thin films

Abstract

Block copolymer (BCP) thin films prepared by dip-coating are increasingly investigated, owing to the many promising application areas, the facility, and the industrial scalability of this technique. Yet, the effect of different dip-coating parameters on BCP nanostructure formation is still underdeveloped and the results of previous literature are limited to a few block copolymers. Here, we study the effect of the withdrawal rate and solvent selectivity on the morphology evolution of dip-coated polystyrene-b-poly(ethylene oxide) thin films by applying a wide range of dip-coating speeds and altering the volume ratio of the tetrahydrofuran–water solvent system. The dip-coated films were characterized using atomic force microscopy and ellipsometry. The nanodomain morphology, its feature sizes, its spanning, and the degree of ordering were investigated with regard to different dip-coating parameters. Notably, we have obtained a hexagonally packed BCP pattern with long-range order without the need for post-annealing processes. Overall, a solid understanding of the parameters affecting the formed surface patterns and their interplay was attained and explained, extending the knowledge of this field to more materials.

---

1. Introduction

Block copolymer (BCP) self-assembly into thin films has shown great potential for applicability in the semiconductor,^1–3 sensing,^4,5 electronics,⁶ membrane filtration,^7–9 and photovoltaic^10,11 industries. For such applications, it is crucial to control the orientation and evolution of the BCP nanopatterns accurately over relatively large areas. A wide range of well-ordered nanodomains in BCP thin films including spheres,^12,13 cylinders,^14–16 and lamellae^17,18 have been reported in literature. To form these nanodomains, different methods such as templated self-assembly,¹⁹ solvent annealing,²⁰ thermal annealing,²¹ zone annealing,²² soft-shear annealing,²³ and electrical²⁴ and magnetic field²⁵ ordering have been employed. However, these techniques often require external fields and complex instrumental set-ups. More importantly, such annealing steps involved in the post-processing of these methods can take hours or even days,²⁶ but the pattern formation and ordering should ideally take less than a few minutes for industrial applicability.²⁷ These pivotal technological barriers in cost-effectiveness and scalability have hindered the industrial manufacturing of BCP thin films so far.

Dip-coating is a simple and industrially scalable technique to fabricate ultrathin films²⁸ with great control over the film thickness.²⁹ Film thickness plays a crucial role in BCP morphology evolution,^30,31 which makes this technique especially attractive for pattern design. In a typical dip-coating process, a substrate is immersed into a solution containing the materials to be coated and withdrawn at a constant speed. A dried film can be obtained within seconds to a few minutes, depending on the chosen withdrawal speed, thus making this method of thin film creation more attractive than most previously mentioned techniques. Depending on the applied solvent, fast solvent evaporation conditions, which are known to favour the often desired perpendicular BCP morphology, can be reached.^14,32 Moreover, partial solvent annealing can occur due to the solvent vapor layer during the withdrawal of the film, so no further annealing step is required to create a surface pattern. Despite these advantages, the intricate interplay among different parameters influencing the drying process in a dip-coating experiment, in which a variety of kinetically trapped morphologies can be attained,^33–35 is usually difficult to control and interpret, and therefore still underutilized.

The thickness of thin films created by dip-coating, which plays a major role in the attained film morphology, depends on the withdrawal speed in a V-shaped manner, stemming from the presence of three distinct withdrawal regimes.^29,36 At slower withdrawal speeds, called the “capillary regime”, the thickness is dictated by convective capillarity and evaporation. In this regime, a slower withdrawal rate will lead to a greater film thickness due to prolonged capillary feeding. At faster withdrawal rates, the “viscous drag regime” or “draining regime”, the drag force of the solution dominates and the film thickness can be characterized by the conventional Landau–Levich equation for viscous flow.³⁷ Therefore, the film thickness in this regime increases with increasing withdrawal speed. The governing forces of these two regimes oppose each other, creating an intermediate withdrawal rate regime where the governing forces of both regimes are still relevant and almost cancel each other, allowing for the creation of the thinnest film. This clear relationship between the film thickness and withdrawal speed allows for the control of the thickness with nanometer accuracy.²⁹

The effect of several parameters like film thickness on the creation of BCP thin films has already been studied in combination with dip-coating. The morphology evolution of dip-coated supramolecular PS-b-P4VP films was investigated over a wide range of withdrawal speeds and the film morphology was found to be governed by the film thickness, film composition, and solvent properties.^38–41 Solvent selectivity was also found to affect the structure of the BCP in solution and thus, the final formation of the dried film morphology.⁴² Such studies to control dip-coated BCP films have mainly been limited to PS-b-P4VP by now.

While most of the research on dip-coated BCP films has focused on PS-b-P4VP, PS-b-PEO might be an even more interesting BCP due to the higher chemical contrast between the two blocks. This chemical contrast offers the selective binding of a broader range of additives to one of the blocks to control the size of the nanodomains as well as the desired physicochemical properties.^43–52 Most of the studies involving the combination of dip-coating and PS-b-PEO have focused on the fabrication of mesoporous films so far, in which a self-assembled PS-b-PEO structure was used as the template for preparing silica^50,52 or metal oxide mesopores.⁵¹ In all of these studies, the effect of the dip-coating speed on the final formed mesopores was not discussed, or limited to only one dip-coating regime. On top of that, thermal annealing was also involved to create better ordered patterns. This shows that despite the great potential of PS-b-PEO, there is little understood about the effect of dip-coating parameters on pattern formation.

To the best of our knowledge, there is no systematic investigation on the effect of dip-coating parameters on the morphology of PS-b-PEO thin films to date, which would be needed for intentional pattern design. Hence, the aim of this research was to extend the knowledge of dip-coated BCP films to PS-b-PEO and investigate the morphology evolution in relation to different dip-coating regimes and different solvent selectivities. By optimizing the solvent mixture and dip-coating rate, we have been able to obtain a relatively fast single-step method to create diverse BCP patterns, including a high degree of hexagonal ordering of vertical cylinders without the need for additional annealing. Finally, a general theory to understand the effect of various parameters on the pattern formation will be proposed.

2. Experimental section

2.1 Materials and polymer solution preparation

The block copolymer PS-b-PEO (M_n(PS) = 20 kg mol⁻¹ and M_n(PEO) = 9.5 kg mol⁻¹) was purchased from Polymer Source. Tetrahydrofuran (THF, ≥99.0%, ACS reagent) was purchased from Sigma Aldrich. Deionized Milli-Q (18.2 MΩ cm) water was used for all procedures. All chemicals were used as received unless stated otherwise. Experiments were conducted at room temperature.

Si (100) wafers were provided by Micronova Finland and cut into pieces of 1 × 1.5 cm. These Si substrates were then cleaned by immersion in piranha acid (a mixture of sulfuric acid and hydrogen peroxide with a volume ratio 7 : 3) for 20 min, followed by rinsing the substrates with deionized water and drying with nitrogen (caution: piranha is a strong oxidizing solution and must be used carefully).

A 10 mg ml⁻¹ polymer solution was obtained by dissolving 0.05 g PS-b-PEO in 5 ml solvent of pure THF or THF–water mixtures (2%, 5%, and 10% water by volume), for which different amounts of water were used. The solution was then stirred overnight and filtered through 0.45 μm Whatman® syringe filters (Sigma Aldrich). The size distribution of the PS-b-PEO structure in solution obtained by dynamic light scattering (Fig. S3b†) clearly indicates that there is no aggregation formed in the solution after the filtration.

2.2 Thin film fabrication

The Si substrates were dip-coated from the polymer solution using a KSV NIMA Single Vessel System (Biolin Scientific) dip-coater placed on an anti-vibration platform under ambient conditions. The Si substrates were immersed in the solution at a speed of 10 mm min⁻¹, followed by a dwell time of 30 s. The substrates were then withdrawn at varying speeds, ranging from 1 mm min⁻¹ to 100 mm min⁻¹, and left in a storage box to dry overnight prior to characterization steps.

2.3 Dynamic light scattering

Dynamic light scattering (DLS) measurements were carried out using a Zeta Sizer Nano ZS 90 instrument (Malvern) equipped with a 633 nm laser source. The backscattered measurement angle was 173° and the equilibrium time before each new measurement was 180 s. The data reported were calculated by averaging five autocorrelation functions for each sample, using cumulant analysis and non-negative least squares to fit the exponential to the correlation function and obtain the mean size and size distribution respectively.

2.4 Contact angle measurement

The static contact angle of a sessile drop of different solutions on cleaned Si substrates was measured with a CAM 200 goniometer (Biolin Scientific). For each measurement, a 4 μL drop was dispensed on the Si surface using a syringe pump, and the drop image was captured by using a high-resolution camera. The image was then analyzed using the contact angle plugin of ImageJ software (NIH). All reported values were the average of measurements of five distinct drops.

2.5 Thin film characterization

The film thickness was measured using an M-2000 spectroscopic ellipsometer (J.A. Woollam) with a fixed angle of 65°. For each sample, three measurements were conducted, and the Cauchy model was applied to fit the thickness data. For this, a 1.2 nm thick oxide layer was taken into account to obtain the final thickness values.

Tapping mode AFM imaging was done using a Multimode 8 atomic force microscope (Bruker) with non-contact AFM cantilevers (NCHV-A, tip radius 8 nm, frequency 320 kHz, and spring constant 40 N m⁻¹, Bruker). The readability of the patterns in the AFM images was enhanced by adjusting the image colour scale and using the flattening function in the NanoScope Analysis software (Bruker). The diameter of the dots was calculated via the particles analysis tool in ImageJ software and the width of the stripes was measured manually using the Nanoscope Analysis software. The average nanodomain sizes and their standard deviations were calculated from at least 20 measurements for each image.

Fast Fourier Transform (FFT) images were obtained via the 2D spectrum filter of the same software in which the images were recorded from multiple 1 × 1 μm height images at different areas within the same film.

For the TEM analysis of the sample cross section, the dip-coated films were first coated with a platinum layer of 15 nm with a Leica EM High Vacuum Coater ACE600 to provide mechanical protection for the weak polymer layers. Next, a JEOL JIB-4700F Multi Beam System was used to deposit an additional 1.18 μm layer of platinum, followed by cutting a cross-sectional lamella of dimensions 8 × 8 μm. The lamella was then loaded onto TEM half grids for subsequent analysis. The grid bound lamella containing a polymer cross section was vapor stained with ruthenium tetroxide in a glass covered dish for at least 10 min. TEM images were taken with a JEOL JEM 2800 instrument operated at an acceleration voltage of 200 kV.

Due to the edge effect, which leads to inhomogeneity in the film thickness in the top and bottom areas of a dip-coated thin film, all the ellipsometry and AFM data were measured from the middle area of the film.

3. Results and discussion

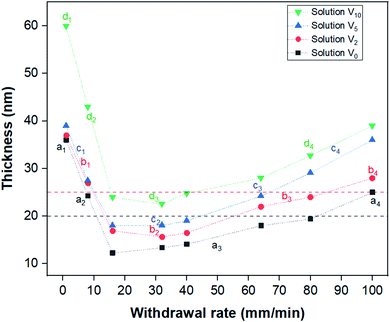
The aim of this research was to understand how different parameters affect the morphological patterns created by the spontaneous self-assembly of the block copolymer (BCP) into thin films via dip-coating. For this, films were dip-coated on Si substrates at different withdrawal speeds and from different solutions containing the same concentration of PS-b-PEO to investigate potential trends. The dip-coating speed was varied from 1 to 100 mm min⁻¹, and the same weight of PS-b-PEO to give a concentration of 10 mg ml⁻¹ was dissolved in solutions of either pure THF or a binary mixture of THF and water with 2%, 5%, and 10% water by volume. These solutions and their corresponding experiments will be referred to as V₀, V₂, V₅, and V₁₀ hereafter. At water contents greater than 10 v%, the solution turned opaque white, indicating the precipitation of BCP chains, so it was not a homogeneous solution as desired. In the following, the AFM morphologies from this experimental series will be described first, and then the effect of film thickness and solvent selectivity on these trends will be investigated by ellipsometry and DLS experiments.

In order to investigate the created morphologies, a series of topographical AFM images representing the surface patterns of the dip-coated films were acquired (Fig. 1). For the films dip-coated from the pure THF solution V₀ (Fig. 1(a₁–a₄)), a dot pattern with a low degree of ordering is observed as the surface morphology at the lowest withdrawal speed of 1 mm min⁻¹. The lighter phase in the AFM height image corresponds to the phase of a greater height at the surface. In this case, the lighter phase amounts to the dominant area in the image, which is why it is expected to represent the PS block with a greater weight fraction in the BCP used. The dot pattern could indicate either a spherical or cylindrical domain morphology in the film. However, due to the volume ratio of the individual polymer blocks, this dot pattern is expected to stem from the organization of PEO into cylindrical domains oriented vertically to the substrate, which was also confirmed by cross-sectional TEM (Fig. 2). At a withdrawal speed of 8 mm min⁻¹, this dot pattern only appeared in island-like regions and was surrounded by a flat featureless film (Fig. 1(a₂), see also in ESI Fig. S1†). At even greater speeds of 16–40 mm min⁻¹, a completely featureless film was observed. In the highest withdrawal speed range of 64–100 mm min⁻¹, the island-like regions of dot patterns appeared again. The average diameters of these cylinders corresponding to different withdrawal speeds where the nanostructures were obtained range from 11.0 to 12.4 nm as indicated in Table 1.

Fig. 1 Representative AFM height images of films dip-coated from 10 mg ml⁻¹ PS-b-PEO solutions containing varying contents of water in THF: (a₁–a₄) V₀, (b₁–b₄) V₂, (c₁–c₄) V₅ and (d₁–d₄) V₁₀. The white bar represents a scale of 200 nm.

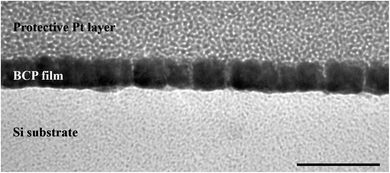Fig. 2 TEM cross-sectional image of the dot patterns. The samples were coated with platinum to protect the fragile polymer layer underneath. The scale bar represents 50 nm.

Table 1 The type and dimensions of the surface patterns observed in the investigated BCP films

Solvent used	Surface patterns	Nanodomain sizes, D (nm)
V 0	Dots	12.4 ± 1.5 (a1)
		11.3 ± 0.8 (a2)
		11.0 ± 0.8 (a4)
V 2	Dots	16.2 ± 1.6 (b1)
		16.0 ± 1.1 (b3)
		19.4 ± 3.3 (b4)
V 5	Dots (1–80 mm min^−1)	27.0 ± 2.1 (c1)
	Stripes (100 mm min^−1)	26.1 ± 1.8 (c3)
		32.9 ± 2.6 (c4)
V 10	Mixture of dots and stripes (1 mm min^−1) or stripes (8 mm min^−1)	37.2 ± 1.6 (d2)

---

The patterns of the films created from V₂ (Fig. 1(b₁–b₄)) exhibited a hexagonally ordered dot array at lower withdrawal speeds (1–8 mm min⁻¹) and featureless films at intermediate withdrawal speeds (16–40 mm min⁻¹). The dot pattern created by vertically oriented cylindrical domains reappeared within islands (64–80 mm min⁻¹) and covered the entire film at the highest withdrawal speed (100 mm min⁻¹). The diameter of these cylinders is greater than that for the films created from V₀, with an average value ranging from 16.2 to 19.4 nm. The cylinders at higher withdrawal speeds were also found to have a greater diameter (Table 1).

The films created from V₅ (Fig. 1(c₁–c₄)) exhibited a similar morphological evolution to the ones created from V₂. The dot pattern was present in the low withdrawal speed regime of 1–8 mm min⁻¹, a featureless film was observed for 16–40 mm min⁻¹, and the dot pattern re-emerged for 64–80 mm min⁻¹. Intriguingly, stripe patterns were formed inside bigger island-like regions at the greatest withdrawal speed of 100 mm min⁻¹. The diameter of the dots corresponding to the vertical cylinder morphology is around 26.1–27.0 nm and the width of the stripes is 32.9 nm.

The surface morphologies found for the films created from V₁₀ were stripes and featureless (Fig. 1(d₁–d₄)). At the lowest speed of 1 mm min⁻¹, a pattern that appeared to transition from the vertical cylindrical morphology to stripes, either indicating horizontally oriented cylinders or lamellae, emerged. Dip-coating films with withdrawal speeds of 8–16 mm min⁻¹ led to a striped surface morphology. For the highest speed range of 32–100 mm min⁻¹, the surface of the entire film was featureless.

These morphology data clearly show that there are different morphology trends, which are affected by the withdrawal speed and water content of the solution. Apart from the different patterns and the sizes of their features, it should be investigated what ensures that a surface pattern is formed at all. It is well known that the film thickness and the natural periodicity of the BCP need to commensurate for a surface pattern to extend widely, depending on the microdomain orientation of the film.^53,54 Moreover, the film thickness is affected by the withdrawal speed. Therefore, the withdrawal speed might impact whether a surface pattern is formed indirectly by determining the film thickness. To confirm this hypothesis, the thickness of all created films was measured to see if there is a clear trend between pattern emergence and formed film thickness.

3.1 Effect of film thickness

In order to comprehend the effect of film thickness on the formation of the BCP patterns, ellipsometry was employed to present the average thickness of the dip-coated films as a function of withdrawal speeds (Fig. 3). The measured thickness developed in a V-shape manner with respect to the withdrawal speed, which is in agreement with previous reports for dip-coated block copolymer thin films.^38,41,42 Here, the capillary regime occurred at dip-coating speeds of 1–8 mm min⁻¹, whereas the viscous drag regime is found for withdrawal speeds greater than 40 mm min⁻¹. The minimum film thickness of 12–25 nm for films from different solutions was found for films coated in the intermediate regime of the withdrawal speed from 16–40 mm min⁻¹. The thickness developed with the withdrawal speed in a similar manner for films created from each respective solution; however, a greater water content led to a greater overall thickness.

Fig. 3 Relationship between the film thickness and withdrawal rate for PS-b-PEO films dip-coated from solutions of different water contents in THF: V₀ (black squares), V₂ (red circles), V₅ (blue upward triangles) and V₁₀ (green downward triangles). The horizontal dashed black line represents the critical thickness below which featureless films were obtained for dot patterns. In the area between the dashed black line and dashed red line, films with island-like regions containing dot nanodomains were observed. The dotted lines connecting the data points are for the sole purpose of visual guidance. The standard deviation of each data point is estimated to be within 2 to 4% of the original average value.

It was attempted to link the spread of the created nanodomain surface patterns to the thickness of the films. All the featureless PS-b-PEO films created from the solutions V₀, V₂ and V₅ had a thickness of less than 19 nm (regions a₃, b₂ and c₂ in Fig. 3). This indicates that these films were formed by a single brush layer of the BCP, presumably with PEO preferably wetting the Si substrate and PS at the air interface to minimize the free surface energy.⁴⁹ This threshold thickness, below which a brush layer forms, depends on the individual BCP used, specifically its molecular weight and the wetting conditions of the blocks.^38,39 The films for which islands of surface patterns surrounded by a featureless film were observed possessed a thickness ranging from 20 to 25 nm (regions a₂, a₄, b₃, and c₃ in Fig. 3). Such island-like regions are known to form as a result of partial incommensurability of the film thickness and the natural periodicity of a BCP nanodomain pattern with an orientation parallel to the substrate.^53–55 Curiously though, the island-like surface morphologies in this case are attained in combination with a perpendicular nanodomain orientation. This might indicate that even for the formation of a perpendicularly oriented pattern there is a minimum thickness the pattern needs to develop for it to be energetically feasible. This especially makes sense in cases like ours, where the final BCP arrangement is still not in equilibrium. In cases where the overall film thickness is below this minimum requirement and above the threshold for brush layers (approximately the region between the red and black dashed lines in Fig. 3), such island regions might be formed at the expense of thinner featureless areas surrounding them, similarly to the case of incommensurability with parallel domain orientations. All of this shows that the thickness did indeed play a major role in determining how much of the film the nanodomain surface pattern covers, and only the samples created from V₁₀ behaved differently from the presented trend.

To understand the span of the pattern for the films created from V₁₀, it is important to keep the different domain morphologies of these films in mind. Unlike most other samples, these films exhibited either a featureless or a striped pattern at the surface. This indicates an either lamellar or a horizontally oriented cylindrical morphology. Depending on the morphology and orientation, these patterns will be commensurate with different film thickness ranges than that of the dot patterns. In this case, it appears that the striped patterns only occurred for samples with a thickness greater than 40 nm, indicating that a lower thickness than this did not match with the periodicity of the stripe BCP morphology. For a lamellar morphology, it has been found that a perpendicular orientation is attained when the film thickness is smaller than the interlamellar spacing,^56–59 making a parallel orientation highly unfeasible. A similar thickness driven orientation change might also be observed in our experiments if the stripes correspond to parallel cylinders, since they are only observed at greater film thicknesses. If the domain spacing is great in comparison to the film thickness for films of less than 40 nm, this might lead to a preference for the perpendicular orientation. This shows that in order to make predictions about the ideal thickness range to create patterns spanning the entire film surface, the specific morphology must also be taken into consideration.

After understanding the relationship between film thickness and pattern formation, it is crucial to understand how the different solvent systems affected this thickness. In the capillary regime at withdrawal speeds of 1–8 mm min⁻¹, the thickness of films dip-coated from V₀, V₂, and V₅ was very similar, ca. 36–39 nm. The films created from V₁₀ were considerably thicker than the ones created from other solutions, with about 60 nm at a 1 mm min⁻¹ withdrawal speed. Since the thickness in the capillary regime is governed by convective capillarity and evaporation,²⁹ a greater water content in the solution should decrease the evaporation rate, which would be expected to decrease the film thickness. However, the opposite was observed in this case, indicating that a change in the convective capillary flow counters this. A similar observation was also reported for PS-b-P4VP films, which were thicker when coated from toluene (lower evaporation rate) than from p-dioxane (higher evaporation rate).⁴² In the referenced work, it was suggested that the lower viscosity of toluene might cause an increase in capillary feeding, thereby leading to the creation of thicker films. In this research, however, the addition of water to THF increased the final viscosity of the solvent,⁶⁰ which still leads to thicker films, so the viscosity change cannot explain this thickness trend. Therefore, it was assumed that the enhanced capillary feeding for solutions with a greater water content was a result of increased surface tension, which would also increase the capillary force.⁶¹

In order to test the hypothesis that the addition of water to the solvent increased the surface tension, the contact angle between the different solutions and the Si substrate was measured as an indication. Greater contact angles between the solution and the Si substrate were indeed observed when the water content was greater in the solution (Fig. S2†), indicating a higher apparent surface tension, which is in good accordance with the theoretical value of the surface tension in Table 2. This confirms the assumption that a decreased wettability caused by the addition of water to THF leads to a greater capillary flow and thereby thicker films, which appears to have a greater effect on the capillary force than the increased viscosity, and a greater effect on the thickness than the evaporation rate in this case.

Table 2 Physical properties of the solvents used and their interaction with PS and PEO blocks

Solvents	Vapor pressure (mmHg) (ref. 62 and 63)	Surface tension (dynes per cm) (ref. 64 and 65)	Viscosity (cP) (ref. 64 and 65)	Solvent interaction parameter of the PS block^a (χPS-solvent)	Solvent interaction parameter of the PEO block^a (χPEO-solvent)
a The solvent interaction parameters of the PS and PEO blocks are calculated based on their solubility parameters^66 by using the equation χ = Vs(δs − δp)^2/RT + 0.34, where Vs is the molar volume of the solvent, and δs and δp are the solubility parameters of the solvent and the polymer, respectively.
THF	162	26.4	0.53	0.35	0.36
Water	24	72	0.89	4.40	1.26

---

In the viscous drag regime of withdrawal speeds greater than 40 mm min⁻¹, there is a clear trend of film thickness increasing with a greater water content in the solution coated from. In this regime, the thickness of the created films depends on the viscous drag force of the solution.²⁹ An increase of solvent viscosity, as we have when adding water to THF, would therefore lead to a greater viscous drag force. This force in turn ensures that more solution is entrained when the substrate is withdrawn, which will lead to a thicker film. Therefore, the thickness trend in the viscous drag regime can be explained by the trend of solvent viscosity affecting the viscous drag force.

The intermediate regime at withdrawal speeds of 16–40 mm min⁻¹ showed the same trend of increasing film thickness with increasing water content in the solution. Since the intermediate regime is formed by a combination of the effects from the capillary regime and the viscous drag regime, it is no surprise that the same correlation between water content and thickness was found.

3.2 Effect of solution composition

After the conditions for pattern emergence in this research, namely the right thickness, were better understood, we investigated what causes a specific pattern to emerge to explain the observed morphological evolution. It is well known that the volume fractions of the blocks play a major role in the pattern that is formed,^38,67 and this seems to be the case here as well. The increase in the water content in the solution clearly affected the feature sizes of the surface patterns created, as well as the type of the pattern. The dot size, which likely corresponds to the diameter of a PEO cylinder film morphology, increased with increasing water content if the withdrawal speed was kept similar (Table 1). From V₀ to V₅, the diameter of the dots increased more than two-fold on average at the lowest withdrawal speed, which would correspond to an almost five times greater volume of a cylinder. This observation indicates an increase in the volume fraction of the PEO block relative to the PS one, which can be achieved by selectively swelling this block.

In order to yield an indication about the preferential swelling of PEO with an increasing water content of the solution, DLS measurements were performed. The hydrodynamic radius of PS-b-PEO in the different solvent mixtures, R_h, is shown in Table 3. The respective interaction parameters of PS and PEO with THF are close to identical (Table 2), which indicates that THF is a nearly equally good solvent for both blocks. Therefore, the BCP is expected to adopt a random coil conformation in THF, which was confirmed by DLS. The R_h value of the PS-b-PEO sample in pure THF was ca. 8 nm, probably corresponding to the structure of a single polymer chain, as suggested by previous reports.^68,69 The addition of water to the solution leads to the increase of the R_h value to ca. 10.8, 10.9, and 16.1 nm for 2, 5, and 10 v% water respectively. According to similar studies done in the literature, in which water is added to a BCP dissolved in a non-selective solvent, the presence of water resulted in the self-organization of the single BCP chains into dynamic micelles, with the micelle size and count increasing with the water content of the solution.^68–70 The micelles reported in these works were found to have the hydrophobic block as the core, and the hydrophilic block as the corona. However, in our case, it is difficult to conclude about the exact structure of the BCP in the solution using solely DLS data. Despite the uncertainty about the BCP structure in solution, the DLS result still clearly demonstrates the proportional expansion of the PS-b-PEO structure with the amount of added water. This further indicates that a solution with a greater water content does indeed preferentially interact with the PEO block, leading to preferential swelling during film formation and a greater apparent volume fraction of PEO in the dried film.

Table 3 Hydrodynamic radius of the PS-b-PEO BCP in different solvent systems

Solvent used	V 0	V 2	V 5	V 10
Hydrodynamic radius of the BCP, Rh (nm)	8.0	10.8	10.9	16.1
Polydispersity	0.253	0.223	0.213	0.244

---

The preferential swelling explains why the cylinder diameter increases with increasing water content. Moreover, striped patterns are formed from V₁₀. By now it could not be confirmed whether this pattern emerges from horizontal cylindrical or lamellar domains. Therefore, a brief explanation for either option will be offered. The selective swelling of one block with a solvent or additive leads to a greater effective volume fraction of this block, which can induce a change in the domain morphology.^38,71,72 This could explain the transition from a cylindrical to a lamellar morphology, which occurs for more even volume fractions of the BCP blocks.⁶⁷ An explanation for the reorganization of the cylinders into a horizontal alignment could be the previously discussed change in the thickness, or the change in the evaporation rate of the solvent when more water is added. Dip-coating is known to favor perpendicular orientations due to the relatively fast solvent evaporation; thus, if this evaporation rate decreases, the cylindrical domains might orient differently. Therefore, the pattern evolution with increasing water content at a similar withdrawal speed can be explained by the preferential swelling of the PEO block and potentially the decreased solvent evaporation during the drying of the film.

What still needs to be explained is the morphological evolution of films coated from the same solution with increasing withdrawal speed. For V₂, the cylinder diameter at greater withdrawal speeds increased from 16.2 nm at lower speeds to 19.4 nm at 100 mm min⁻¹ (Fig. 1b₄). For films created from V₅, the relatively big dots at low withdrawal speeds changed to islands of stripes at fast withdrawal speeds. And for V₁₀, the striped pattern became more pronounced at higher withdrawal speeds (Fig. 1d₂), while it appeared to be more of a transitional pattern at the lowest speeds (Fig. 1d₁). Overall, the patterns at greater withdrawal speeds are reminiscent of patterns with a greater PEO volume fraction if we assume that the stripes represent lamellae, which can be induced by a greater water content in the solution.

It is known that at withdrawal speeds in the viscous drag regime, the entrained solution consolidates, whereas at withdrawal speeds in the capillary regime, capillary feeding occurs during the evaporation of the solution and formation of the film. Furthermore, while water is fully miscible with THF, it also evaporates slower than THF.⁶² Together with the small volume of the drying film and the large surface area of evaporation, this can lead to a gradual increase of the water ratio in the solution during solvent evaporation. Therefore, the appearance of a greater water ratio at higher withdrawal speeds might be true, since at lower withdrawal speeds the forming film is continuously fed with fresh solution. This feed of fresh solution could keep the volume fraction of water in the evaporating solution closer to the one of the bulk solution. This hypothesis also fits with the observation that the pattern and dot size for films created from V₀ do not change with the withdrawal speed, since this change in the other solutions would be created by the presence of a second solvent with a different evaporation rate in the solution. Therefore, the appearance of a lower water content of the solution at lower withdrawal speeds is likely caused by the inflowing bulk solution countering a potential faster evaporation of THF in the solvent system.

3.3 Lateral order of the pattern

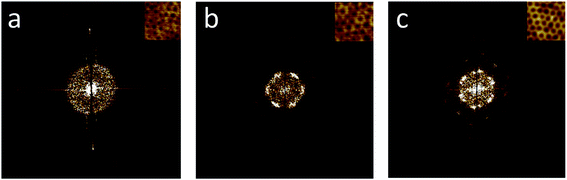
Many potential applications for BCP patterning require great control over the lateral ordering, especially those in the data storage and semiconductor industries.^73,74 Therefore, it is of great interest to determine the degree of order of the created patterns, and what this degree is affected by. The order of the hexagonally packed dot array stemming from vertical cylinders, which was obtained for films created from solutions with 0 to 5 v% water, can be determined by creating FFT images (Fig. 4). For films dip-coated from V₀, the FFT pattern is characterized by a continuous ring, indicating disorder (Fig. 4a). The six-spot patterns of the FFT images for solutions V₂ and V₅ (Fig. 4b and c), on the other hand, revealed that the degree of ordering did increase with increasing water content, as can be seen by the clarity and strength of the six-spot pattern. For V₅, the six-spot pattern was even surrounded by another set of spots (Fig. 4c), demonstrating a high degree of ordering. Probing different locations of the film by AFM revealed that the ordering is long-range. Therefore, it appears that the higher selectivity of the solvent with more water present, a property also inherently coupled to the evaporation rate, aided the organization of the domains into a better-ordered pattern.

Fig. 4 Fast Fourier transform (FFT) of AFM images for the evaluation of the ordering of the cylinders formed from different solutions: (a) V₀ (1, 8 and 100 mm min⁻¹), (b) V₂ (1–8, 64–80 and 100 mm min⁻¹) and (c) V₅ (1–8 and 64 mm min⁻¹). The size of the inset AFM images is 200 × 200 nm.

It has been observed earlier that a greater solvent selectivity, and specifically adding a solvent selective for the minor block, can greatly enhance the ordering of BCP domains during solvent annealing.^49,75–78 Solvent annealing commonly takes several hours, during which the polymer chains are mobile and can attain a state closer to equilibrium, leading to fewer defects in the ordering. Applying solvent annealing to enable the macromolecular diffusion required for removing the defects in the lateral ordering, but retaining the non-equilibrium vertical orientation of the morphology, is a delicate balance.^20,79,80 An effect similar to solvent annealing was likely observed for our experiments, since the addition of water did not only increase the selectivity of the solvent towards the minor block, but also increased the overall evaporation time. The combination of a solvent mixture with the dip-coating technique allowed us to reach a better lateral ordering of the nanodomains using a one-step method within minutes, thus making it more feasible for industrial applications.

3.4 Summarized theory of parameter interplay

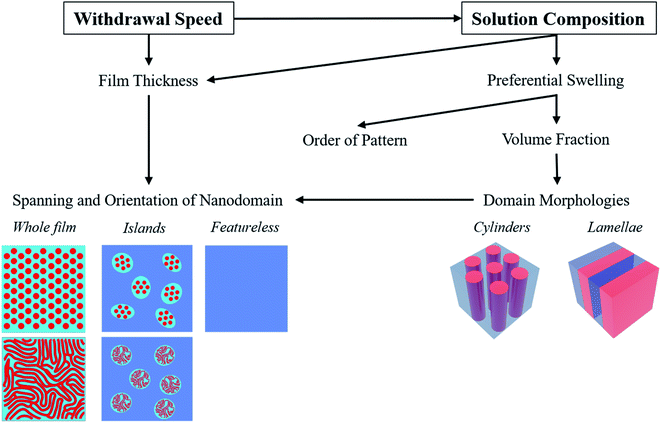
In this work, it was found that the withdrawal speed and solvent composition greatly determined the observed patterns (Fig. 5). The film thickness was the main factor in determining whether a surface pattern is created and how far it spans. This is a consequence of the commensurability requirements, which also depend on the specific nanodomain morphologies. The domain morphology itself appeared to mainly be determined by the apparent volume fractions of the blocks, which can be tailored by selective solvent swelling. Moreover, the different evaporation rates of components of a solvent mixture led to a greater solvent evolution during evaporation in the viscous drag regime, which further affected the patterns by changing the possible degree of domain swelling. Finally, the hexagonal ordering of surface dot patterns improved by increasing the selectivity of the solvent towards the minor block.

Fig. 5 Schematic illustration summarizing the interplay of the proposed main factors affecting the pattern evolution found for dip-coated PS-b-PEO thin films in this work. Note: the domain morphologies drawn are examples and not necessarily the ones present.

4. Conclusion

The effects of the dip-coating technique and related parameters on nanodomain morphology formation and ordering have not been investigated for most BCPs yet, which hinders intentional pattern design. Therefore, the morphological evolution of PS-b-PEO was investigated for different withdrawal speeds and solvent mixtures. The different surface patterns observed were dots, stripes, and featureless areas, varying with the withdrawal speed and solvent system used. The influence of film thickness and solvent composition on the final film morphology was investigated, and the withdrawal regime was also found to play a role in the solvent evolution. Overall, the hexagonal ordering of surface dot patterns could be improved by increasing the selectivity of the solvent towards the minor block. The discussed findings allow for a better overall understanding of the different parameters influencing the morphology formation and orientation and their interplay. Investigating the effect of predetermined surface orientations on morphologies by using random copolymer brush layers could be a next step for a more complete understanding of parameters and their interplay. This understanding will aid to pave the way for future applications based on the control of BCP patterning in thin films.

Author contributions

All the work of this manuscript has been conducted in the SUPER-WEAR project, funded by the Academy of Finland and led by Prof. Jaana Vapaavuori. All experiments have been conducted by Hoang M. Nguyen, and the TEM analysis was done by Swarnalok De. The development of the theory was a joint effort of both Hoang M. Nguyen and Ariane V. Mader. Hoang M. Nguyen and Ariane V. Mader wrote the first version of the manuscript, which was finally refined by all the co-authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

All the authors acknowledge the Academy of Finland SUPER-WEAR project (decision number: 322214) for generous funding. In addition, Dr Swarnalok De acknowledges the funding from Ella and Georg Ehrnrooth Foundation. This work made use of Aalto University Bioeconomy, Otanano Nanomicroscopy Center and RawMatters Facilities.

Notes and references

1. H. Yi, X. Y. Bao, R. Tiberio and H.-S. S. P. Wong, A General Design Strategy for Block Copolymer Directed Self-Assembly Patterning of Integrated Circuits Contact Holes Using an Alphabet Approach, Nano Lett., 2015, 15(2), 805–812,  DOI:10.1021/nl502172m.
2. M. Aizawa and J. M. Buriak, Block Copolymer Templated Chemistry for the Formation of Metallic Nanoparticle Arrays on Semiconductor Surfaces, Chem. Mater., 2007, 19(21), 5090–5101,  DOI:10.1021/cm071382b.
3. C. T. Black, K. W. Guarini, K. R. Milkove, S. M. Baker, T. P. Russell and M. T. Tuominen, Integration of Self-Assembled Diblock Copolymers for Semiconductor Capacitor Fabrication, Appl. Phys. Lett., 2001, 79(3), 409–411,  DOI:10.1063/1.1383805.
4. G. Wirnsberger, B. J. Scott and G. D. Stucky, PH Sensing with Mesoporous Thin Films, Chem. Commun., 2001, 1, 119–120,  10.1039/b003995k.
5. B. K. Kuila and M. Stamm, Transparent, Versatile Chemical Vapor Sensor Using Supramolecular Assembly of Block Copolymer and Carbon Nanotubes, Macromol. Rapid Commun., 2010, 31(21), 1881–1885,  DOI:10.1002/marc.201000383.
6. H. C. Kim, S. M. Park, W. D. Hinsberg and I. R. Division, Block Copolymer Based Nanostructures: Materials, Processes, and Applications to Electronics, Chem. Rev., 2010, 110(1), 146–177,  DOI:10.1021/cr900159v.
7. X. Qiu, H. Yu, M. Karunakaran, N. Pradeep, S. P. Nunes and K. V. Peinemann, Selective Separation of Similarly Sized Proteins with Tunable Nanoporous Block Copolymer Membranes, ACS Nano, 2013, 7(1), 768–776,  DOI:10.1021/nn305073e.
8. V. Abetz, Isoporous Block Copolymer Membranes, Macromol. Rapid Commun., 2015, 36(1), 10–22,  DOI:10.1002/marc.201400556.
9. W. A. Phillip, B. O’neill, M. Rodwogin, M. A. Hillmyer and E. L. Cussler, Self-Assembled Block Copolymer Thin Films as Water Filtration Membranes, ACS Appl. Mater. Interfaces, 2010, 2(3), 847–853,  DOI:10.1021/am900882t.
10. C. Guo, Y. H. Lin, M. D. Witman, K. A. Smith, C. Wang, A. Hexemer, J. Strzalka, E. D. Gomez and R. Verduzco, Conjugated Block Copolymer Photovoltaics with near 3% Efficiency through Microphase Separation, Nano Lett., 2013, 13(6), 2957–2963,  DOI:10.1021/nl401420s.
11. S. B. Darling, Block Copolymers for Photovoltaics, Energy Environ. Sci., 2009, 2(12), 1266–1273,  10.1039/b912086f.
12. A. P. Marencic, M. W. Wu, R. A. Register and P. M. Chaikin, Orientational Order in Sphere-Forming Block Copolymer Thin Films Aligned under Shear, Macromolecules, 2007, 40(20), 7299–7305,  DOI:10.1021/ma0713310.
13. R. A. Segalman, A. Hexemer and E. J. Kramer, Effects of Lateral Confinement on Order in Spherical Domain Block Copolymer Thin Films, Macromolecules, 2003, 36(18), 6831–6839,  DOI:10.1021/ma0257696.
14. W. A. Phillip, M. A. Hillmyer and E. L. Cussler, Cylinder Orientation Mechanism in Block Copolymer Thin Films upon Solvent Evaporation, Macromolecules, 2010, 43(18), 7763–7770,  DOI:10.1021/ma1012946.
15. I. Otsuka, S. Tallegas, Y. Sakai, C. Rochas, S. Halila, S. Fort, A. Bsiesy, T. Baron and R. Borsali, Control of 10 Nm Scale Cylinder Orientation in Self-Organized Sugar-Based Block Copolymer Thin Films, Nanoscale, 2013, 5(7), 2637–2641,  10.1039/c3nr00332a.
16. G. Singh, S. Batra, R. Zhang, H. Yuan, K. G. Yager, M. Cakmak, B. Berry and A. Karim, Large-Scale Roll-to-Roll Fabrication of Vertically Oriented Block Copolymer Thin Films, ACS Nano, 2013, 7(6), 5291–5299,  DOI:10.1021/nn401094s.
17. I. P. Campbell, G. J. Lau, J. L. Feaver and M. P. Stoykovich, Network Connectivity and Long-Range Continuity of Lamellar Morphologies in Block Copolymer Thin Films, Macromolecules, 2012, 45(3), 1587–1594,  DOI:10.1021/ma2025336.
18. S. Kim, P. F. Nealey and F. S. Bates, Directed Assembly of Lamellae Forming Block Copolymer Thin Films near the Order-Disorder Transition, Nano Lett., 2014, 14(1), 148–152,  DOI:10.1021/nl403628d.
19. J. Y. Cheng, A. M. Mayes and C. A. Ross, Nanostructure Engineering by Templated Self-Assembly of Block Copolymers, Nat. Mater., 2004, 3(11), 823–828,  DOI:10.1038/nmat1211.
20. C. Jin, B. C. Olsen, E. J. Luber and J. M. Buriak, Nanopatterning via Solvent Vapor Annealing of Block Copolymer Thin Films, Chem. Mater., 2017, 29(1), 176–188,  DOI:10.1021/acs.chemmater.6b02967.
21. F. Ferrarese Lupi, T. J. Giammaria, M. Ceresoli, G. Seguini, K. Sparnacci, D. Antonioli, V. Gianotti, M. Laus and M. Perego, Rapid Thermal Processing of Self-Assembling Block Copolymer Thin Films, Nanotechnology, 2013, 24(31), 315601,  DOI:10.1088/0957-4484/24/31/315601.
22. K. G. Yager, N. J. Fredin, X. Zhang, B. C. Berry, A. Karim and R. L. Jones, Evolution of Block-Copolymer Order through a Moving Thermal Zone, Soft Matter, 2009, 6(1), 92–99,  10.1039/b916200c.
23. G. Singh, K. G. Yager, B. Berry, H. C. Kim and A. Karim, Dynamic Thermal Field-Induced Gradient Soft-Shear for Highly Oriented Block Copolymer Thin Films, ACS Nano, 2012, 6(11), 10335–10342,  DOI:10.1021/nn304266f.
24. K. Amundson, E. Helfand, X. Quan and S. D. Smith, Alignment of Lamellar Block Copolymer Microstructure in an Electric Field. 1. Alignment Kinetics, Macromolecules, 1993, 26(11), 2698–2703,  DOI:10.1021/ma00063a010.
25. P. W. Majewski, M. Gopinadhan, W. S. Jang, J. L. Lutkenhaus and C. O. Osuji, Anisotropic Ionic Conductivity in Block Copolymer Membranes by Magnetic Field Alignment, J. Am. Chem. Soc., 2010, 132(49), 17516–17522,  DOI:10.1021/ja107309p.
26. M. Luo and T. H. Epps, Directed Block Copolymer Thin Film Self-Assembly: Emerging Trends in Nanopattern Fabrication, Macromolecules, 2013, 46(19), 7567–7579,  DOI:10.1021/ma401112y.
27. W. M. Arden, The International Technology Roadmap for Semiconductors - Perspectives and Challenges for the next 15 Years, Curr. Opin. Solid State Mater. Sci., 2002, 6(5), 371–377,  DOI:10.1016/S1359-0286(02)00116-X.
28. J. Puetz and M. A. Aegerter, Dip Coating Technique, in Sol-Gel Technologies for Glass Producers and Users, Springer US, 2004, pp. 37–48.  DOI:10.1007/978-0-387-88953-5_3.
29. D. Grosso, How to Exploit the Full Potential of the Dip-Coating Process to Better Control Film Formation, J. Mater. Chem., 2011, 21(43), 17033–17038,  10.1039/c1jm12837j.
30. M. J. Fasolka and A. M. Mayes, Block Copolymer Thin Films: Physics and Applications, Annu. Rev. Mater. Sci., 2001, 31(1), 323–355,  DOI:10.1146/annurev.matsci.31.1.323.
31. K. Brassat, D. Kool, C. G. A. Nallet and J. K. N. Lindner, Understanding Film Thickness-Dependent Block Copolymer Self-Assembly by Controlled Polymer Dewetting on Prepatterned Surfaces, Adv. Mater. Interfaces, 2020, 7(1), 1901605,  DOI:10.1002/admi.201901605.
32. M. Li, C. A. Coenjarts and C. K. Ober, Patternable Block Copolymers, Advances in Polymer Science, Springer, Berlin, Heidelberg, 2005, pp. 183–226.  DOI:10.1007/12_003.
33. Q. Zhang, O. K. C. Tsui, B. Du, F. Zhang, T. Tang and T. He, Observation of Inverted Phases in Poly(Styrene-b-Butadiene-b-Styrene) Triblock Copolymer by Solvent-Induced Order-Disorder Phase Transition, Macromolecules, 2000, 33(26), 9561–9567,  DOI:10.1021/ma001161q.
34. Y. Li, H. Huang, T. He and Y. Gong, The Effect of the Preferential Affinity of the Solvent on the Microstructure of Solution-Cast Block Copolymer Thin Films, J. Phys. Chem. B, 2010, 114(3), 1264–1270,  DOI:10.1021/jp908852u.
35. Y. Gong, Z. Hu, Y. Chen, H. Huang and T. He, Ring-Shaped Morphology in Solution-Cast Polystyrene-Poly(Methyl Methacrylate) Block Copolymer Thin Films, Langmuir, 2005, 21(25), 11870–11877,  DOI:10.1021/la052292t.
36. A. Gans, E. Dressaire, B. Colnet, G. Saingier, M. Z. Bazant and A. Sauret, Dip-Coating of Suspensions, Soft Matter, 2019, 15(2), 252–261,  10.1039/c8sm01785a.
37. L. Landau and B. Levich, Dragging of a Liquid by a Moving Plate, Dyn. Curved Front, 1988, 141–153,  DOI:10.1016/b978-0-08-092523-3.50016-2.
38. S. B. Roland, R. E. Prud’homme and C. G. Bazuin, Morphology, Thickness, and Composition Evolution in Supramolecular Block Copolymer Films over a Wide Range of Dip-Coating Rates, ACS Macro Lett., 2012, 1(8), 973–976,  DOI:10.1021/mz3003165.
39. S. Roland, D. Gaspard, R. E. Prud'Homme and C. G. Bazuin, Morphology Evolution in Slowly Dip-Coated Supramolecular PS-b-P4VP Thin Films, Macromolecules, 2012, 45(13), 5463–5476,  DOI:10.1021/ma3007398.
40. J. Vapaavuori, J. Grosrenaud, A. Siiskonen, A. Priimagi, C. Pellerin and C. G. Bazuin, Photocontrol of Supramolecular Azo-Containing Block Copolymer Thin Films during Dip-Coating: Toward Nanoscale Patterned Coatings, ACS Appl. Nano Mater., 2019, 2(6), 3526–3537,  DOI:10.1021/acsanm.9b00496.
41. J. Vapaavuori, J. Grosrenaud, C. Pellerin and C. G. Bazuin, In Situ Photocontrol of Block Copolymer Morphology during Dip-Coating of Thin Films, ACS Macro Lett., 2015, 4(10), 1158–1162,  DOI:10.1021/acsmacrolett.5b00483.
42. S. Roland, C. G. Gamys, J. Grosrenaud, S. Boissé, C. Pellerin, R. E. Prud'Homme and C. G. Bazuin, Solvent Influence on Thickness, Composition, and Morphology Variation with Dip-Coating Rate in Supramolecular PS-b-P4VP Thin Films, Macromolecules, 2015, 48(14), 4823–4834,  DOI:10.1021/acs.macromol.5b00847.
43. E. M. Freer, L. E. Krupp, W. D. Hinsberg, P. M. Rice, J. L. Hedrick, J. N. Cha, R. D. Miller and H. C. Kim, Oriented Mesoporous Organosilicate Thin Films, Nano Lett., 2005, 5(10), 2014–2018,  DOI:10.1021/nl051517h.
44. J. Gutierrez, A. Tercjak, I. Garcia, L. Peponi and I. Mondragon, Hybrid Titanium Dioxide/PS-b-PEO Block Copolymer Nanocomposites Based on Sol-Gel Synthesis, Nanotechnology, 2008, 19(15), 8,  DOI:10.1088/0957-4484/19/15/155607.
45. U. S. Jeng, Y. S. Sun, H. Y. Lee, C. H. Hsu, K. S. Liang, S. W. Yeh and K. H. Wei, Binding Effect of Surface-Modified Cadmium Sulfide on the Microstructure of PS-b-PEO Block Copolymers, Macromolecules, 2004, 37(12), 4617–4622,  DOI:10.1021/ma049722r.
46. J. P. Spatz, A. Roescher and M. Möller, Gold Nanoparticles in Micellar Poly(Styrene)b-Poly(Ethylene Oxide) Films - Size and Interparticle Distance Control in Monoparticulate Films, Adv. Mater., 1996, 8(4), 337–340,  DOI:10.1002/adma.19960080411.
47. V. Hlady and G. Jogikalmath, Albumin Binding and Insertion into PS-b-PEO Monolayers at Air-Water Interface, Colloids Surfaces B Biointerfaces, 2007, 54(2), 179–187,  DOI:10.1016/j.colsurfb.2006.10.018.
48. T. Ghoshal, C. Ntaras, M. T. Shaw, J. D. Holmes, A. Avgeropoulos and M. A. Morris, A Vertical Lamellae Arrangement of Sub-16 Nm Pitch (Domain Spacing) in a Microphase Separated PS-b-PEO Thin Film by Salt Addition, J. Mater. Chem. C, 2015, 3(27), 7216–7227,  10.1039/c5tc00485c.
49. T. Ghoshal, M. T. Shaw, C. T. Bolger, J. D. Holmes and M. A. Morris, A General Method for Controlled Nanopatterning of Oxide Dots: A Microphase Separated Block Copolymer Platform, J. Mater. Chem., 2012, 22(24), 12083–12089,  10.1039/c2jm30468f.
50. N. Suzuki, M. Imura, Y. Nemoto, X. Jiang and Y. Yamauchi, Mesoporous SiO2 and Nb2O5 Thin Films with Large Spherical Mesopores through Self-Assembly of Diblock Copolymers: Unusual Conversion to Cuboidal Mesopores by Nb2O5 Crystal Growth, CrystEngComm, 2011, 13(1), 40–43,  10.1039/c0ce00507j.
51. J. Hierso, P. Boy, K. Vallé, J. Vulliet, F. Blein, C. Laberty-Robert and C. Sanchez, Nanostructured Ceria Based Thin Films (≤1 μm) As Cathode/Electrolyte Interfaces, J. Solid State Chem., 2013, 197, 113–119,  DOI:10.1016/j.jssc.2012.08.021.
52. D. R. Ceratti, M. Faustini, C. Sinturel, M. Vayer, V. Dahirel, M. Jardat and D. Grosso, Critical Effect of Pore Characteristics on Capillary Infiltration in Mesoporous Films, Nanoscale, 2015, 7(12), 5371–5382,  10.1039/c4nr03021d.
53. P. F. Green and R. Limary, Block Copolymer Thin Films: Pattern Formation and Phase Behavior, Adv. Colloid Interface Sci., 2001, 94(1–3), 53–81,  DOI:10.1016/S0001-8686(01)00055-0.
54. J. N. L. Albert and T. H. Epps, Self-Assembly of Block Copolymer Thin Films, Mater. Today, 2010, 13(6), 24–33,  DOI:10.1016/S1369-7021(10)70106-1.
55. H. Hu, M. Gopinadhan and C. O. Osuji, Directed Self-Assembly of Block Copolymers: A Tutorial Review of Strategies for Enabling Nanotechnology with Soft Matter, Soft Matter, 2014, 10(22), 3867–3889,  10.1039/c3sm52607k.
56. T. L. Morkved and H. M. Jaeger, Thickness-Induced Morphology Changes in Lamellar Diblock Copolymer Ultrathin Films, Europhys. Lett., 1997, 40(6), 643–648,  DOI:10.1209/epl/i1997-00517-6.
57. D. G. Walton, G. J. Kellogg, A. M. Mayes, P. Lambooy and T. P. Russell, A Free Energy Model for Confined Diblock Copolymers, Macromolecules, 1994, 27(21), 6225–6228,  DOI:10.1021/ma00099a045.
58. M. Kikuchi and K. Binder, Microphase Separation in Thin Films of the Symmetric Diblock-Copolymer Melt, J. Chem. Phys., 1994, 101(4), 3367–3377,  DOI:10.1063/1.467584.
59. T. Geisinger, M. Müller and K. Binder, Symmetric Diblock Copolymers in Thin Films. I. Phase Stability in Self-Consistent Field Calculations and Monte Carlo Simulations, J. Chem. Phys., 1999, 111(11), 5241–5250,  DOI:10.1063/1.479778.
60. J. Hao, H. Cheng, P. Butler, L. Zhang and C. C. Han, Origin of Cononsolvency, Based on the Structure of Tetrahydrofuran-Water Mixture, J. Chem. Phys., 2010, 132(15), 154902,  DOI:10.1063/1.3381177.
61. X. Xiao and L. Qian, Investigation of Humidity-Dependent Capillary Force, Langmuir, 2000, 16(21), 8153–8158,  DOI:10.1021/la000770o.
62. R. L. Rowley, T. E. Daubert, N. A. Zundel, R. P. Danner and M. E. Adams, Physical and Thermodynamic Properties of Pure Chemicals: Data Compilation, Choice Rev. Online, 1990, 27(6), 27-3319,  DOI:10.5860/choice.27-3319.
63. D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, 2004, vol. 85,  DOI:10.1080/08893110902764125.
64. E. W. Flick, Industrial Solvents Handbook, 1999, vol. 37,  DOI:10.5860/choice.37-0335.
65. R. Philip Hammond, The Water Encyclopedia, CRC Press, 1971, vol. 12,  DOI:10.13182/nt71-a31041.
66. C. J. Knill and J. F. Kennedy, Polymer Handbook, Elsevier BV, 4th edn, 2001, vol. 46,  DOI:10.1016/s0144-8617(01)00238-7.
67. F. S. Bates and G. H. Fredrickson, Block Copolymer Thermodynamics: Theory and Experiment, Annu. Rev. Phys. Chem., 1990, 41(1), 525–557,  DOI:10.1146/annurev.pc.41.100190.002521.
68. C. Luo, X. Han, Y. Gao, H. Liu and Y. Hu, Aggregate Morphologies of PS-b-PEO-b-PS Copolymer in Mixed Solvents, J. Dispers. Sci. Technol., 2011, 32(2), 159–166,  DOI:10.1080/01932690903546843.
69. S. Wu, L. Wang, A. Kroeger, Y. Wu, Q. Zhang and C. Bubeck, Block Copolymers of PS-b-PEO Co-Assembled with Azobenzene-Containing Homopolymers and Their Photoresponsive Properties, Soft Matter, 2011, 7(24), 11535–11545,  10.1039/c1sm06316b.
70. A. Kroeger, L. Xingfu and A. Eisenberg, Dendrimer-Influenced Supramolecular Structure Formation of Block Copolymers, Langmuir, 2007, 23(21), 10732–10740,  DOI:10.1021/la701334r.
71. I. Tokarev, R. Krenek, Y. Burkov, D. Schmeisser, A. Sidorenko, S. Minko and M. Stamm, Microphase Separation in Thin Films of Poly(Styrene-Block-4-Vinylpyridine) Copolymer-2-(4’-Hydroxybenzeneazo)Benzoic Acid Assembly, Macromolecules, 2005, 38(2), 507–516,  DOI:10.1021/ma048864i.
72. S. W. Yeh, K. H. Wei, Y. S. Sun, U. S. Jeng and K. S. Liang, CdS Nanoparticles Induce a Morphological Transformation of Poly(Styrene-b-4-Vinylpyridine) from Hexagonally Packed Cylinders to a Lamellar Structure, Macromolecules, 2005, 38(15), 6559–6565,  DOI:10.1021/ma047653a.
73. M. P. Stoykovich and P. F. Nealey, Block Copolymers and Conventional Lithography, Mater. Today, 2006, 9(9), 20–29,  DOI:10.1016/S1369-7021(06)71619-4.
74. J. Bang, U. Jeong, D. Y. Ryu, T. P. Russell and C. J Hawker, Block Copolymer Nanolithography: Translation of Molecular Level Control to Nanoscale Patterns, Adv. Mater., 2009, 21(47), 4769–4792,  DOI:10.1002/adma.200803302.
75. S. H. Kim, M. J. Misner, T. Xu, M. Kimura and T. P. Russell, Highly Oriented and Ordered Arrays from Block Copolymers via Solvent Evaporation, Adv. Mater., 2004, 16(3), 226–231,  DOI:10.1002/adma.200304906.
76. T. H. Kim, J. Hwang, H. Acharya and C. Park, Ordered Nanostructure of PS-b-PEO Copolymer by Solvent Annealing with Mixture of Benzene/Water Vapor and Its Micropattern Fabrication, J. Nanosci. Nanotechnol., 2010, 10(10), 6883–6887,  DOI:10.1166/jnn.2010.2958.
77. T. H. Kim, J. Hwang, W. S. Hwang, J. Huh, H. C. Kim, S. H. Kim, J. M. Hong, E. L. Thomas and C. Park, Hierarchical Ordering of Block Copolymer Nanostructures by Solvent Annealing Combined with Controlled Dewetting, Adv. Mater., 2008, 20(3), 522–527,  DOI:10.1002/adma.200700651.
78. S. Kim, R. M. Briber, A. Karim, R. L. Jones and H. C. Kim, Environment-Controlled Spin Coating to Rapidly Orient Microdomains in Thin Block Copolymer Films, Macromolecules, 2007, 40(12), 4102–4105,  DOI:10.1021/ma0625298.
79. G. Seguini, F. Zanenga, T. J. Giammaria, M. Ceresoli, K. Sparnacci, D. Antonioli, V. Gianotti, M. Laus and M. Perego, Enhanced Lateral Ordering in Cylinder Forming PS-b-PMMA Block Copolymers Exploiting the Entrapped Solvent, ACS Appl. Mater. Interfaces, 2016, 8(12), 8280–8288,  DOI:10.1021/acsami.6b00360.
80. A. Baruth, M. Seo, C. H. Lin, K. Walster, A. Shankar, M. A. Hillmyer and C. Leighton, Optimization of Long-Range Order in Solvent Vapor Annealed Poly(Styrene)- Block -Poly(Lactide) Thin Films for Nanolithography, ACS Appl. Mater. Interfaces, 2014, 6(16), 13770–13781,  DOI:10.1021/am503199d.

---

Footnotes

† Electronic supplementary information (ESI) available: A graph of different contact angle measurements, representative AFM height images of the created films with larger areas (5 × 5 μm), the DLS autocorrelation function and size distribution of the BCP structure in solution, and the TEM images showing the cylindrical morphology giving rise to the dot pattern. See DOI: 10.1039/d1na00263e

‡ These authors contributed equally.

---