Open Access Article
Open Access ArticlePhotoacoustics for listening to metal nanoparticle super-aggregates†
Roberto
Li Voti
 *a,
Grigore
Leahu
a,
Concita
Sibilia
a,
Roberto
Matassa
*b,
Giuseppe
Familiari
b,
Sara
Cerra
*a,
Grigore
Leahu
a,
Concita
Sibilia
a,
Roberto
Matassa
*b,
Giuseppe
Familiari
b,
Sara
Cerra
 c,
Tommaso Alberto
Salamone
c and
Ilaria
Fratoddi
c,
Tommaso Alberto
Salamone
c and
Ilaria
Fratoddi
 *c
*c
aDepartment of Basic and Applied Sciences for Engineering (SBAI), Sapienza University of Rome, Via A. Scarpa 14, 00161 Rome, Italy. E-mail: roberto.livoti@uniroma1.it
bDepartment of Anatomical, Histological, Forensic and Orthopedic Sciences, Section of Human Anatomy, Sapienza University of Rome, Via A. Borelli 50, 00161, Rome, Italy. E-mail: roberto.matassa@uniroma1.it
cDepartment of Chemistry, Sapienza University of Rome, P.le A. Moro 5, 00185 Rome, Italy. E-mail: Ilaria.fratoddi@uniroma1.it
First published on 18th June 2021
Abstract
Photoacoustic signal detection has been used to build a new strategy to determine the mesoscale self-assembly of metal nanoparticles in terms of size distribution and aggregate packing density (metal nanoparticle filling factor). A synergistic approach integrating photoacoustic signal and theoretical studies, validated by conventional light scattering and electron microscopy techniques, allows us to obtain a well-defined morphological interpretation of nanoparticle-based super-aggregates. By pumping light in a complex system, the acousto-thermal effect was listened to, providing information on the aggregation phenomena. Super-aggregates of covalently interconnected silver nanoparticles (AgNPs) functionalized with an organometallic dithiol are identified in solution, as a proof of concept for the versatility of the photoacoustic approach. According to our results, tiny AgNPs (size less than 10 nm) assembled into a 3D-network of super-aggregates (SA-AgNPs) with sizes in the range 100–200 nm and a filling factor in the range of 30–50%. Low-cost, rapid, and easy photoacoustic measurement in the low frequency range (less than 100 Hz) was revealed to be an innovative method to characterize the fundamental structure/property correlation of metal nanoparticle super-aggregates. This morpho-optical approach, which uses the absorption and scattering properties of nanoparticles in the liquid phase, opens new perspectives for advanced biomedical and structural applications.
1. Introduction
Nanomaterials bring together different scientific approaches arising from physics, chemistry, and materials science, with the common goal of improving the living conditions of the world’s population.1 Some of the innovative applications of nanotechnology are not only in nanodevices, sensors, photonic and optical engineering,2 and nanomedicine,3 but also well beyond in sustainable energy.4 In this regard, nanoparticles play a crucial role in tailoring physico-chemical properties for improving performances in the above-mentioned applications. Among others, metal-based nanoparticles (MNPs),5 whose average size falls in the range from units to hundreds of nanometres, show interesting optical and electrical properties which can be tuned by varying synthesis parameters.6 MNPs and the corresponding covalent or non-covalent bioconjugates, obtained by interaction with drugs, enzymes, proteins, biomarkers, and antibodies,7 are leading materials in emerging fields such as nanomedicine including studies on biodistribution,8–10 cancer treatment,11 and drug delivery.12,13 The structural and morphological characterization of MNPs and bioconjugates is of fundamental interest to understand the interaction mechanism, where aggregation phenomena play an important role in understanding the controlled nanoparticle–drug interaction.14 Non-covalent aggregation is a dynamic process that occurs in suitable solvents, and covalently interconnected MNPs are also studied in the literature due to their intrinsic stability.15–17A common approach for the fabrication of functionalized nanoparticles is based on the reduction of metallic ions in solution in the presence of a reducing agent and of a ligand. Among others, thiol ligands show an intrinsic high covalent binding to metallic surfaces and bifunctional thiols can be used for the preparation of covalently interconnected nanoparticles.18 Our attention recently oriented towards MNPs functionalized with bifunctional organometallic thiols, containing Pt(II) centres and tributylphosphine ligands (among others trans,trans-4,4′-diethynyl(bistributylphosphine-Pt(II)thioacetyl) biphenyl, (Pt-DEBP)), to enhance solubility and achieve promising optoelectronic properties.19–21 The presence of two thiol terminal groups induces the interconnection into a superstructure network of MNPs.22,23 Optical and electrical properties are strongly affected by the proximity of nanoparticles, and the fine morphostructural characterization of interconnected networks of MNPs is challenging.24,25
A conventional strategy for characterizing large nanometric agglomerates formed in a selective self-assembly process involves different techniques, such as transmission electron microscopy (TEM), small angle X-ray scattering (SAXS), dynamic light scattering (DLS), and others. However, as the size of the super-aggregate increases, it becomes difficult to understand the self-assembly growth of the nanoparticles. Indeed, three-dimensional determination is challenging, and deep expertise is needed for SAXS and TEM techniques. The direct imaging method of electron microscopy techniques not only lacks in the elaboration of the size distribution because of the limited statistical analysis based on nanometric or micrometric region, but also might cause radiation damage.26
The indirect methods of X-ray diffraction techniques may provide more reliable size–shape information from the statistical point of view, and spatial averaging occurs due to the randomized orientation of the objects. X-ray diffraction is sensitive to the presence of the amorphous phase, enlarging the experimental diffraction peaks and consequently changing the size–shape structural information. The DLS method uses visible laser scattered light with a typical wavelength of several hundred nanometers, compromising the resolution with an overestimated average size of the aggregates appearing too large and hiding small particles; furthermore, impurities increase polydispersity formation,27 thereby DLS needs a very pure dispersion. However, these techniques need either expensive instruments with high energy consumption or complicated fabricating processes, making them unfavourable for industrial applications. Since the different single methods present some limitations, an approach based on a combination of different characterization techniques might yield realistic and complete information on the size–shape and the photonic properties of the investigated object. Although these techniques enable us to determine the dimensions of objects at the micron- and nano-scale, none of them is intrinsically suited for gaining both spectroscopy and shape–size information.
As an alternative, photoacoustic spectroscopy (PAS) can provide quantitative information for establishing the morpho-optical nature of the mesoscopic assemblies of aggregates,28 strictly correlated to their photonic and size–shape intrinsic properties.28–30 This represents an indisputable advantage for assessing their physical, chemical, and biological applications.31–33
The nanoarchitecture investigated here by the non-destructive PAS technique highlights another important issue for reliable nanostructured particle analysis. Freely diffusing nanoparticles in suspension undergo constant Brownian motion when probed using a heating focused beam, making it difficult to quantify their dimensions and limiting the achievable resolution. Therefore, expensive and complicated optical and mechanical systems are needed to obtain reliable analyses of nanoscale objects during long periods of data acquisition processes. Currently, there is significant interest in science and technology towards the development of a new method that allows us to obtain statistically meaningful information and that can be used to derive new principles on studying freely moving nanoparticles in suspension with single particle sensitivity.
For all these reasons, it would be highly beneficial to introduce the evolution of photoacoustic spectroscopy developed here which includes two steps: easy handling experiments and theoretical simulation.
Photoacoustic signal and theory have been employed in this work to build a novel strategy for determining well-defined nanostructured interconnected MNPs and their interesting optical behaviour. To better validate this complex superstructure governed by self-assembling mechanisms of a wet-synthesis approach, TEM imaging has been employed to visualize the silver nanoparticles covalently linked by the Pt-DEBP organometallic ligand forming a well-dispersed,22 stable super-aggregate network in the solid state. Moreover, DLS characterization in the solution phase was used to perform the statistics at a macroscopic scale on the NP diameter and super-aggregate sizes, as a comparison. Herein, an innovative evolution of photoacoustic spectroscopy (PAS) has been applied to characterize the structure/property correlation of AgNP super-aggregates (SA-AgNPs) in chloroform. This work aims at pooling information from an appropriate morpho-optical investigation by merging experimental and theoretical methods, taking advantage of photoacoustic signal.
2. Results and discussion
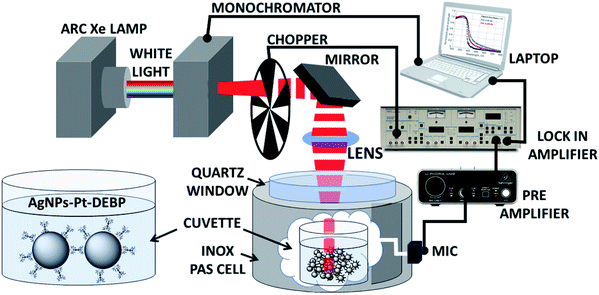
Photoacoustic spectroscopy combined with a theoretical approach is herein used to characterize AgNP super-aggregates and compare with TEM and DLS data. Photoacoustic spectroscopy (PAS) measurements in the UV-Vis region were carried out on SA-AgNPs in a chloroform suspension using variation of light diffusion and absorption across the plasmonic resonances. Fig. 1 presents a schematic illustration of the experimental setup of a PAS measurement system, showing the functionalized AgNP chemical structure, prepared according to our previous studies in the presence of the Pt-DEBP ligand.22A source of light is used to pump light; a monochromator allows the selection of the pump beam at a desired wavelength modulated by a mechanical chopper at a fixed frequency. The beam is focused through a photoacoustic cell onto the sample of AgNPs in chloroform placed inside a quartz cuvette. The PAS signal generated by light absorption induces primarily thermal waves to produce also an acoustic signal detected by a microphone; thereby the sample behaves as a “thermal piston” in which the intensity of the photoacoustic signal is proportional to the sample absorbance.
2.1 Photoacoustic spectroscopy experimental data compared with theoretical results
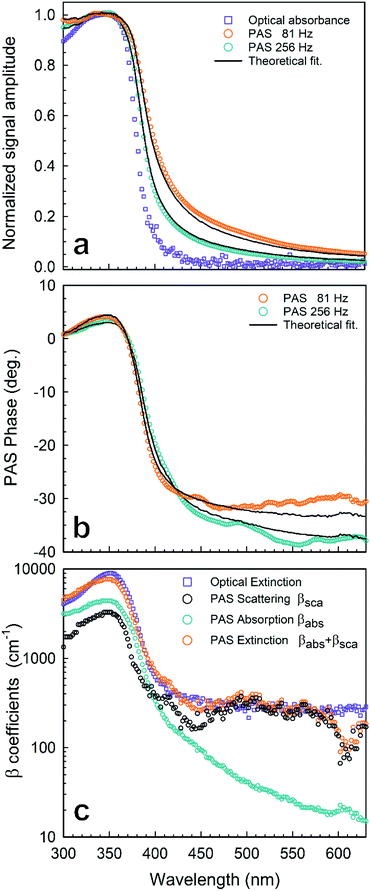 | ||
| Fig. 2 Photoacoustic spectroscopy experimental results of AgNPs in a chloroform solution (1 mg mL−1): (a) normalized amplitude of PAS at f = 81 Hz (○) and f = 256 Hz (○) compared with the optical absorbance (□); (b) phase of PAS at f = 81 Hz (○) and f = 256 Hz (○); (c) absorption and scattering coefficient spectra reconstructed from the PAS signal in Fig. 2 by using eqn (1): (○) βsca(λ) from PAS, (○) βabs(λ) from PAS, (○) βext = βabs + βsca from PAS, (□) βext = βabs + βsca from OT. Lines stand for numerical simulations. | ||
In this work, we follow the approach used by Helander et al. by which the photoacoustic signal for scattering media is proportional to eqn (1):36
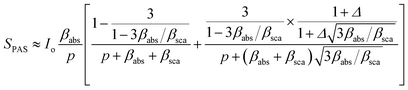 | (1) |
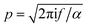 is the wavenumber of the thermal wave, f is the modulation frequency, and α is the thermal diffusivity of the media. The sample has been assumed to be optically and thermally thick. The thermal expansion of the sample has been neglected, and the photon scattering is assumed to be uniformly distributed in each of the forward and backward directions. Furthermore, the quantity Δ = ⅔(1 + 2r) determined by the boundary condition of the photon distribution function depends on the reflection r at the sample surface of the backward light. By considering the experimental parameters of chloroform thermal diffusivity (α = 7 × 10−8 m2 s−1), at modulation frequencies (f = 81 and 256 Hz), and of internal reflection (r = 0.035), p and Δ have been calculated. In accordance with the sample proposed, the PAS signal in eqn (1) allowed us to determine separately both βabs and βsca quantities.37 Instead, optical transmittance spectra can only be determined from the total extinction coefficient βext = βabs + βsca, as reported in Fig. 2c.
is the wavenumber of the thermal wave, f is the modulation frequency, and α is the thermal diffusivity of the media. The sample has been assumed to be optically and thermally thick. The thermal expansion of the sample has been neglected, and the photon scattering is assumed to be uniformly distributed in each of the forward and backward directions. Furthermore, the quantity Δ = ⅔(1 + 2r) determined by the boundary condition of the photon distribution function depends on the reflection r at the sample surface of the backward light. By considering the experimental parameters of chloroform thermal diffusivity (α = 7 × 10−8 m2 s−1), at modulation frequencies (f = 81 and 256 Hz), and of internal reflection (r = 0.035), p and Δ have been calculated. In accordance with the sample proposed, the PAS signal in eqn (1) allowed us to determine separately both βabs and βsca quantities.37 Instead, optical transmittance spectra can only be determined from the total extinction coefficient βext = βabs + βsca, as reported in Fig. 2c.
The maximum of both absorption and extinction curves is reached at 350 nm, arising from the light strongly absorbed by the Pt-DEBP thiols. The absorption peak of the AgNPs at around 410 nm is less intense and overlapped by the thiol absorption band. Instead, a broad scattering peak at around 500 nm has been observed which enabled us to unambiguously provide information on the morphometric features of super-aggregates.
The extinction, scattering, and absorption cross-sections have been here calculated for a sphere using the following mathematical series:24,44,45
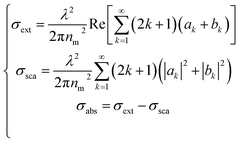 | (2) |
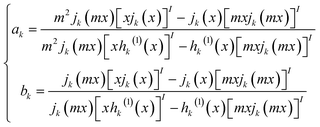 | (3) |
The diameter D of a sphere has been extrapolated using the dimensionless parameter x = πnmD/λ obtained from eqn (3). Furthermore, the quantities ns and nm are the refractive indices of the sphere and surrounding medium, respectively; m = ns/nm is their refractive index ratio (ns for metal is a complex number), primes indicate derivatives with respect to the argument in parentheses in eqn (3), and λ is the wavelength in a vacuum.
In Fig. 3a–c the absorption cross-sections of AgNPs calculated from eqn (2) and (3) with size in the 5–20 nm, 80–120 nm and 160–220 nm ranges are presented. The scattering cross-section has not been plotted in Fig. 3a due to it being much smaller than the absorption cross-section. Indeed, subwavelength nanospheres with D ≪ λ in the Rayleigh scattering condition are physically not evaluable. In such a case, eqn (2) can be calculated by using one term only (k = 1) corresponding to the dipole oscillation and neglecting the multipole contributions, so as to converge to the following expressions for the cross-sections normalized to the NS geometric section S = πD2/4.
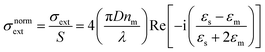 | (4a) |
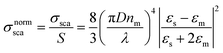 | (4b) |
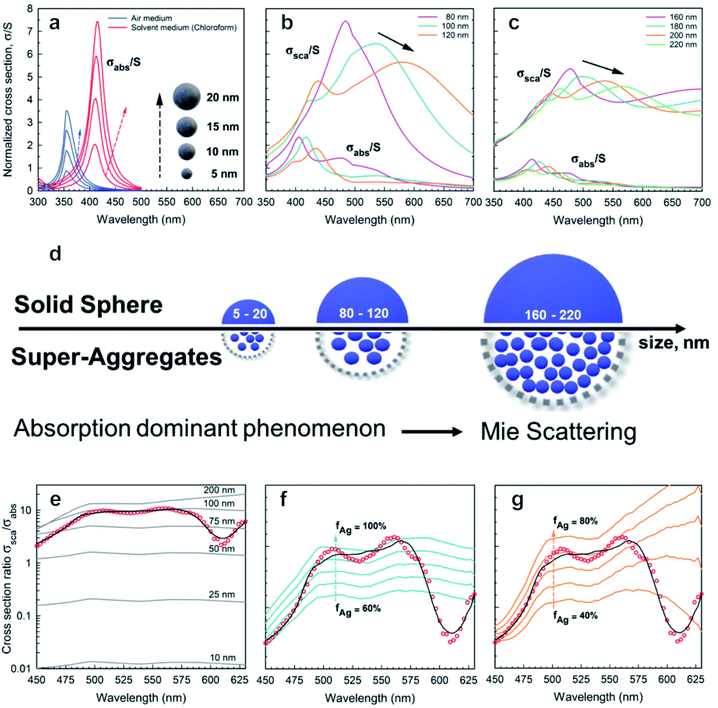 | ||
| Fig. 3 Absorption and scattering theoretical analysis applied to AgNPs: absorption cross-sections calculated from eqn (2) and (3) for AgNPs with diameters (a) 5–20 nm, (b) 80–120 nm, and (c) 160–220 nm; (d) schematic drawing illustrating the effect of size on absorption and scattering; (e) (red ●) experimental data; (black cont. lines) theoretical cross-section ratio σsca/σabs for a single Ag nanosphere as a function of wavelength and for different diameters D according to the exact theory in eqn (2); (f and g) (red ●) scattering coefficient normalized to absorption coefficient βsca/βabs calculated using PAS from Fig. 2c. (black curve) Best fit corresponding to the ensemble of nanoparticles with D = 100 nm (f) and D = 200 nm (g). The cont. lines correspond to different silver filling fractions. | ||
For the sake of clarity, a summary of the key features that emerged from Mie theory has been highlighted in the following statements:
(i) The surface plasmon resonance satisfies the condition Re[εs(λ)] = −2εm at a specific wavelength, which minimizes the denominator of eqn (4) and maximizes the extinction peak. For AgNPs in air (εm = 1), Re(εs) = −2 at λ = 354 nm, while in chloroform (εm = 2.1), Re(εs) = −4.2 at λ = 410 nm.
(ii) Two normalized cross-sections exhibit different behaviour with the nanosphere diameter D: in particular σnormext ∝ (D/λ) and σnormsca ∝ (D/λ)4. Therefore, the cross-section ratio σnormsca/σnormext (or equivalently σnormsca/σnormabs) is extremely sensitive to the nanosphere diameter D, showing a strong increase with the power law D3.
Fig. 3a–c show both normalized cross-sections σnormabs,σnormsca for silver nanospheres calculated from the theory in eqn (2). In Fig. 3d a schematic drawing illustrates the effect of size on absorption and scattering. Moreover, the quantity βsca/βabs is also plotted in Fig. 3e, for which the scattering coefficient normalized to the absorption coefficient has been calculated from the PAS in Fig. 2c. Although the corresponding experimental curve is poorly fitted by the theoretical expectation for nanospheres, the presence of NPs with a diameter of about 100 nm seems to be closer to the experimental data, probably the best effective size of the clustered nanospheres (see Fig. 3e). An accurate theoretical analysis leads to the best fit in agreement with the experimental one, corresponding to an ensemble of nanoparticles with size and density as shown in Fig. 3f and g.
Fig. 3a shows the absorption cross-sections calculated from eqn (2) and (3) for silver nanospheres of 5, 10, 15, and 20 nm diameter, both in air and in chloroform. The cross-sections are normalized (σabs/S) with respect to the nanosphere geometrical section S. Interestingly, surface plasmon resonance at around 350 nm (air medium) is shifted at 410 nm due to the silver nanospheres floating in chloroform solution, as calculated from eqn (4). By increasing the diameter of the sphere, the increasing absorption peaks also exhibit a weak redshift of a few nanometres (see blue and red curves in Fig. 3a). It should be asserted that the peak at about 410 nm due to AgNPs is overlapped by the dominant thiol absorption broadband, whose absorption coefficient βabs is equal to 300 cm−1 at 410 nm (see Fig. 3c and ESI-1†). Such a hiding effect limits the proposed method to determine the size of a few nanometres of the AgNPs with a concentration lower than N = βabs/σabs ≈ 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bil per mL; thereby the scattering phenomenon is negligible for small nanospheres. Further analysis reveals the presence of spheroidal super-aggregates of a few hundred nanometres in size, providing a broad scattering peak centered at a wavelength of 500 nm (Fig. 3).
000 bil per mL; thereby the scattering phenomenon is negligible for small nanospheres. Further analysis reveals the presence of spheroidal super-aggregates of a few hundred nanometres in size, providing a broad scattering peak centered at a wavelength of 500 nm (Fig. 3).
The numerical simulations, considering large diameter silver nanospheres, confirmed a compatible maximum of the scattering cross-sections. By considering these outcomes, the interpretation of the simulations clarifies the following points:
(i) Scattering cross-sections become dominant over the absorption (Fig. 3b and c).
(ii) A resonant phenomenon is theoretically observed for the scattering cross-section: the broad scattering of the primary peak increases with the nanosphere diameter (Fig. 3b and c).
(iii) Secondary peaks appear for large diameters corresponding to higher order resonances (see Fig. 3c).
(iv) The peak at λ = 500 nm does not correspond univocally to one diameter only. In Fig. 3b and c for example two diameters (D = 100 nm and D = 200 nm) exhibit a different behaviour but the same maximum at λ = 500 nm, due to higher order resonances.
(v) The scattering spectra in Fig. 3 may be expressed as a superposition of the curves in Fig. 3b and c, and the deconvolution of the data can allow us to determine the size distribution of the super-aggregates.
2.2 Determination of the size and density statistics of super-aggregates
The aggregation process generally causes a coupling of the silver nanoparticle plasma modes, which results in a redshift and broadening of the longitudinal plasma resonance in the optical spectrum.46 Since the interparticle coupling is stronger than the coupling within the surrounding medium, Mie's theory developed for very dilute solutions and isolated particles fails to describe the optical spectra. So far, the best approach is the effective-medium theories, predicted by J. C. Maxwell Garnett, which have been successfully applied to the evaluation of the optical absorbance behaviour of densely packed self-assembled metal nanoparticles.47–50 The Maxwell Garnett Theory (MGT) is strictly valid under the quasistatic limit (D < λ) of the smallest interparticle distances and can be generalized to various shapes of the particles.According to such an approach, the super-aggregates may be modelled as a spheroidal composite material. By assuming that the super-aggregates float in chloroform solution the effective optical properties of the inhomogeneous compound can be obtained from a weighted combination of the optical properties of the two major components i.e. the functionalizing thiol and the AgNPs; in particular, the effective permittivity εeff may be calculated according to MGT as follows:47,51
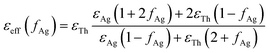 | (5) |
To improve the fit in Fig. 3e with the experimental ratio βsca/βabs, the comparison with the theoretical cross-section ratio σsca/σabs computed for different silver volume fractions has been shown for the two classes of possible diameters: D = 100 nm (see Fig. 3f) and D = 200 nm (see Fig. 3g).
In both Fig. 3f and g, the theoretical data lost the best fit at λ = 600 nm, suggesting that a more complete interaction is formed in the diluted solution, assuming an ensemble of aggregates with high variations in size and density. For these fundamental reasons, the scattering and absorption coefficients have been expressed, here, by a weighted superposition of the cross-sections of the different aggregates:
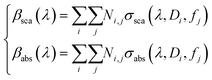 | (6) |
Fig. 4 shows the first evidence of the results obtained by using SVD for resolving the inverse problem of eqn (6). In particular, Fig. 4a shows the reconstructed concentration 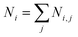 as a function of different diameters D (for any silver volume fraction). The ensemble contains two groups of super-aggregates with diameters ranging from 70 to 120 nm (green histogram) and from 180 to 220 nm (orange histogram) with similar concentrations. This measurement does not reveal aggregates in the range of 130–170 nm, probably due to a loss of assembly in this specific sample of SAs. Moreover, Fig. 4b highlights the composition of two groups, showing for each group the percentage of aggregates with a specific silver volume fraction. For instance, the group with diameters ranging from 70–120 nm has a wide distribution of silver filling factors centered at an fAg of about 50% (green histogram), while the group with larger diameters ranging from 180–220 nm exhibits a maximum percentage of cases with a filling factor fAg of about 30% (orange histogram) corresponding to a lower density of silver. This may be justified considering that the larger the aggregate, the less probable is its formation. Fig. 4c shows the experimental data of the scattering coefficient spectra fitted with SVD in the range of interest 450–630 nm (cont. red line), corresponding to the concentrations reported in Fig. 4a. The best fit between theoretical and experimental data allows us to determine not only the maximum scattering at 500 nm, but also the minimum at 600 nm. The best agreement of the fit is also confirmed by the cross-section ratio in Fig. 3. DLS results are reported in Fig. 4d: it is possible to observe the presence of a population of aggregated AgNPs with a mean size 〈RH〉 of about 100 nm, in good agreement with PAS based calculations and a less intense population of AgNPs with 〈2RH〉 = 10 nm due to dimers and low interconnected NPs. In Fig. 4e a schematic drawing of the SA-AgNPs is shown.
as a function of different diameters D (for any silver volume fraction). The ensemble contains two groups of super-aggregates with diameters ranging from 70 to 120 nm (green histogram) and from 180 to 220 nm (orange histogram) with similar concentrations. This measurement does not reveal aggregates in the range of 130–170 nm, probably due to a loss of assembly in this specific sample of SAs. Moreover, Fig. 4b highlights the composition of two groups, showing for each group the percentage of aggregates with a specific silver volume fraction. For instance, the group with diameters ranging from 70–120 nm has a wide distribution of silver filling factors centered at an fAg of about 50% (green histogram), while the group with larger diameters ranging from 180–220 nm exhibits a maximum percentage of cases with a filling factor fAg of about 30% (orange histogram) corresponding to a lower density of silver. This may be justified considering that the larger the aggregate, the less probable is its formation. Fig. 4c shows the experimental data of the scattering coefficient spectra fitted with SVD in the range of interest 450–630 nm (cont. red line), corresponding to the concentrations reported in Fig. 4a. The best fit between theoretical and experimental data allows us to determine not only the maximum scattering at 500 nm, but also the minimum at 600 nm. The best agreement of the fit is also confirmed by the cross-section ratio in Fig. 3. DLS results are reported in Fig. 4d: it is possible to observe the presence of a population of aggregated AgNPs with a mean size 〈RH〉 of about 100 nm, in good agreement with PAS based calculations and a less intense population of AgNPs with 〈2RH〉 = 10 nm due to dimers and low interconnected NPs. In Fig. 4e a schematic drawing of the SA-AgNPs is shown.
 | ||
| Fig. 4 PAS results of nanoaggregate population with sizes around 100 and 200 nm: (a) distribution of concentration vs. size and (b) concentration of the population with sizes of 100 (green color) and 200 nm (orange color) vs. silver filling factor; (c) scattering coefficient vs. wavelength (black dots are experimental, red line is the best fit, from Fig. 4a and b); (d) DLS results; (e) drawing of isolated NPs and SA-AgNPs, from dimers to 3D covalent aggregates. | ||
In conclusion, PAS seems the most appropriate technique to measure experimentally both absorption and scattering coefficients, separately in a single measurement. A new methodology is also given with PAS to analyse the βsca/βabs ratio allowing us to reveal the presence of super-aggregates giving a quantitative statistic of their size together with the metallic volume fraction.
2.3 Transmission electron microscopy studies
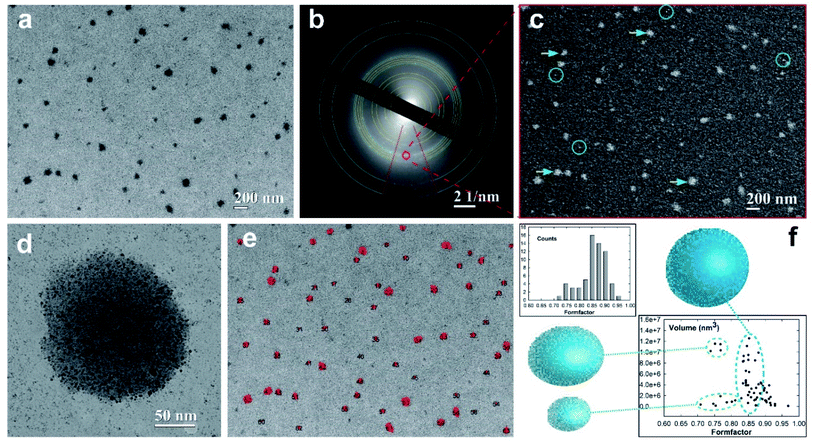
The morphology and morphometric characterization of well-separated super-aggregates of metal nanoparticles (SA-AgNPs) have been extensively investigated through electron microscopy techniques supported by quantitative imaging analysis (QIA), as shown in Fig. 5. The bright-field (BF) TEM image shows a monolayer of separated dark SA-NPs acquired at low magnification to improve the fundamental statistical observation/analysis of the nanostructured aggregates (Fig. 5a). To obtain structural information of the SA-AgNPs, selected area electron diffraction (SAED) measurements were performed in order to identify the atomic and structural compositions of the observed hybrid aggregates.55,56 The corresponding electron diffraction pattern (EDP) exhibits diffraction rings produced by random orientation of the polycrystalline material (Fig. 5b). By measuring the d-spacing of the diffraction rings, we were able to identify a superimposition of two different diffraction patterns. The strong signal of the diffraction rings indicated by blue arcs belongs to the typical Ag crystallites with a face-centered cubic (fcc) structure of the space group Fm3m, confirmed also by the intensive ring signal at d111 = 0.239 nm. The second EDP has been identified by considering the crystalline phase of the Pt-DEBP complex.22 The calculated d-spacing of a triclinic structure well matched with our experimental interplanar spacing of the diffraction rings (yellow arcs), wherein the highest intensity signal belongs to the (111) diffraction plane with an interplanar spacing of d111 = 0.470 nm. To visualize the crystalline feature of the SA-AgNPs, dark-field (DF) imaging was applied. DF images have been obtained by placing the objective aperture around a diffracted beam of the EDP (red circle of Fig. 5b), corresponding to both (111) and (144) Debye rings of the Ag and Pt-DEBP contents. The DF image shows bright dots in the SA-AgNPs consisting of silver crystallites interacting with the crystalline trans,trans-4,4′-diethynyl(bistributylphosphine-Pt(II)thioacetyl) biphenyl, indicated with yellow-blue arrowheads in Fig. 5c.Furthermore, the DF method was able to light up also the smallest or single Ag–Pt-DEBP nanoparticles located outside the SA-AgNPs (marked by blue circles).
This feature also allows us to confirm that the smallest dark spots observed in Fig. 5b correspond to well-separated silver-organic nanoparticles forming a sub-monolayer of a bi-dimensional network previously studied.22 These two types of crystalline architectures have been acquired at relative medium magnification for showing the potential ability of the Pt-DEBP organometallic bridge to assemble AgNPs covalently into both bi-dimensional and three-dimensional networks driven by wet-chemistry, as shown in Fig. 5d. A single SA-AgNP of more than 180 nm in dimension seems to be constituted of silver nanoparticle colloidal subunits with size less than 10 nm, while the bi-dimensional network of AgNPs–Pt-DEBP deposited on the carbon amorphous film can also be noticed.
Therefore, the wet-chemical synthesis via a reduction of the metal precursors was able to create an early intermediate bi-dimensional network of AgNPs which evolved into more complex agglomerates of metallic–organic quasispherical SAs consisting of self-assembled colloidal subunits. Appropriate QIA imaging analyses have been exploited to estimate the size–shape of the individual SA-AgNPs, paying attention to the statistical analysis. A 2D contour map of the distribution of 63 SA-AgNPs (black numbers) has been quantified on a probed area of 4.202 × 3.136 μm2, as displayed in Fig. 5e. The estimated size of the SAs provided a main average value of 116.07 ± 7.32 nm, having a low polydispersity of about 6.3%. The morphometric analysis exhibited a further formation of SAs with sizes of 176.08 ± 15.32 nm and polydispersity of about 8.7% in low amount.
In this regard, the estimated particles size allows direct quantitative comparison of the TEM experimental data with theoretical prediction based on the photoacoustic signal. The different size of about 20 nm among the two SA populations can be attributable to the different volume of the investigated sample, wherein PAS, similar to the DLS techniques, analyses a millimetric volume of the sample, providing average dimensional information. Instead, TEM is capable of analysing a local micrometric region with nanometric determination in terms of size–shape analyses. To evaluate the shape of the SA-NPs, the form-factor, a measure of the SA circularity (4π area/perimeter2), has been estimated in the histogram reported in the top part of Fig. 5f. The histogram profile exhibits a preferential high counting after the main bin centered at 0.86 ± 0.01 toward the direction of the circularity shape (form-factor equal to 1), confirming the quasi-spherical shape of the SA-AgNPs. Furthermore, the volume of the SA-AgNPs related to the form-factor has been reported at the bottom of Fig. 5f. The SA volumes show a linear increase with a similar form-factor of around 0.85 (blue dot line), indicating that the self-assembling wet chemistry is capable of growing SAs with a quasi-spherical shape, while the other two regions indicate the presence of a few SAs grown with a slightly elongated shape between 0.70 and 0.80 (green dot line).
3. Conclusion
Photoacoustic investigation revealed to be a robust and non-destructive technique for determining self-assembled nanostructures, with an improvement of the proposed methods in the literature.57–60 This study opens up prospects for PAS application for example in biomedical imaging. The use of a straightforward approach based on photoacoustic detection allows us to listen to both the absorption and scattering phenomena generated by nanoparticle suspensions.The extrapolated absorption and scattering spectra together with a theoretical study favour a quantitative method for determining the size of three-dimensional super-aggregates with nanometric accuracy. Well beyond the morpho-chemical characterization, these insights have been useful in developing new methods based on smart de-convolution of the data, providing quantitative size and filling factor (metal content) morpho-parameters. The photoacoustic results were compared with dynamic light scattering and local transmission electron microscopy measurements, allowing a well-defined interpretation of super-aggregates. DLS measurements highlighted a broad population of nano-objects ranging from 10 to 200 nm. The PAS main results evidenced the presence of different super-aggregates with mean sizes of 100 nm and 200 nm, whose mean filling factors are 50% and 30%, respectively. These morphological achievements are supported by local TEM imaging to evidence two similar size populations of nanoparticles self-assembled into nanostructured super-aggregates. Following the steps of A. G. Bell, who said “I heard the articulate speech by sunlight”,61 we can conclude that we have listened to the whispering of nanoparticles and their super-aggregates.
4. Experimental section
Materials synthesis is reported in the ESI,† together with spectroscopic characterization.The experimental PAS setup is described in Fig. 1. The measurements were carried out on a SA-AgNP chloroform suspension (1 mg mL−1) in the range from 300 to 600 nm. A Xe lamp (400 W) was used as a source to pump light. A monochromator (Jobin Yvon) and a mechanical chopper at a fixed frequency (in the 10 Hz to 100 Hz range) modulated the beam which was focused with a mirror onto the liquid sample in a quartz cuvette. Acquisition of the microphone signal (Brüel & Kjær 4166) was done with a lock-in amplifier (Brüel & Kjær 2660) and a preamplifier (EG&G 7260). Dynamic Light Scattering (DLS) measurements were acquired from suspensions of functionalized AgNPs in chloroform solution (1 mg mL−1) using a Zetasizer instrument (Malvern) at a temperature of 25.0 ± 0.2 °C. Transmission electron microscopy observations were performed using a ZEISS EM10 at 80 kV.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors gratefully acknowledge Ateneo Sapienza funding grants 2019 (RM11916B75D8FAF5) and 2020 (RM120172B6B660AB).References
- X. Y. Wong, A. Sena-Torralba, R. Álvarez-Diduk, K. Muthoosamy and A. Merkoçi, ACS Nano, 2020, 14, 2585 CrossRef CAS PubMed.
- K. J. Cash, C. Li, J. Xia, L. V. Wang and H. A. Clark, ACS Nano, 2015, 9, 1692 CrossRef CAS PubMed.
- M. Craig, A. L. Jenner, B. Namgung, L. P. Lee and A. Goldman, Chem. Rev., 2021, 121(6), 3352–3389 CrossRef CAS PubMed.
- J. Liu, J. Jiang, Y. Meng, A. Aihemaiti, Y. Xu, H. Xiang, Y. Gao and X. Chen, J. Hazard. Mater., 2020, 388, 122026 CrossRef CAS PubMed.
- I. Chakraborty and T. Pradeep, Chem. Rev., 2017, 117, 8208 CrossRef CAS PubMed.
- Ö. Karhan, Ö. B. Ceran, O. N. Şara and B. Şimşek, Ind. Eng. Chem. Res., 2017, 56, 8180 CrossRef.
- A. E. Nel, L. Mädler, D. Velegol, T. Xia, E. M. V. Hoek, P. Somasundaran, F. Klaessig and V. Castranova, Nat. Mater., 2009, 8, 543 CrossRef CAS PubMed.
- E. Okoampah, Y. Mao, S. Yang, S. Sun and C. Zhou, Colloids Surf., B, 2020, 196, 111312 CrossRef CAS PubMed.
- R. Shanmuganathan, I. Karuppusamy, M. Saravanan, H. Muthukumar, K. Ponnuchamy, V. S. Ramkumar and A. Pugazhendhi, Curr. Pharm. Des., 2019, 25, 2650 CrossRef CAS PubMed.
- J. Kim, S.-K. Lee, D. Schellingerhout, M. Nahrendorf, K. Kim, J. Kim and D. E. Kim, ACS Biomater. Sci. Eng., 2019, 5, 6389 CrossRef CAS PubMed.
- H. Barabadi, K. D. Kamali, F. J. Shoushtari, B. Tajani, M. A. Mahjoub, A. Alizadeh and M. Saravanan, J. Cluster Sci., 2019, 30, 1375 CrossRef CAS.
- M. Sharifi, F. Attar, A. A. Saboury, K. Akhtari, N. Hooshmand, A. Hasan, M. A. El-Sayed and M. Falahati, J. Controlled Release, 2019, 311, 170 CrossRef PubMed.
- P. Prasher, M. Sharma, H. Mudila, G. Gupta, A. K. Sharma, D. Kumar, H. A. Bakshi, P. Negi, D. K. Kapoor, D. K. Chellappan, M. M. Tambuwala and K. Dua, Colloid Interface Sci. Commun., 2020, 35, 100244 CrossRef CAS.
- S. Cerra, R. Matassa, A. M. Beltrán, G. Familiari, C. Battocchio, I. Pis, F. Sciubba, F. A. Scaramuzzo, A. Del Giudice and I. Fratoddi, Mater. Sci. Eng., C, 2020, 117, 111337 CrossRef CAS PubMed.
- N. Marro, F. della Sala and E. R. Kay, Chem. Sci., 2020, 11, 372 RSC.
- M. A. Squillaci, M. A. Stoeckel and P. Samorì, Nanoscale, 2019, 11, 19319 RSC.
- M. Quintiliani, M. Bassetti, C. Pasquini, C. Battocchio, F. Mura, R. Matassa, L. Fontana, M. V. Russo and I. Fratoddi, J. Mater. Chem. C, 2014, 2, 2517 RSC.
- J. C. Love, L. A. Estroff, J. K. Kriebel, R. G. Nuzzo and G. M. Whitesides, Chem. Rev., 2005, 105, 1103 CrossRef CAS PubMed.
- Z. Tian, X. Yang, B. Liu, J. Zhao, D. Zhong, Y. Wu, G. Zhou and W. Y. Wong, J. Mater. Chem. C, 2018, 6, 6023 RSC.
- Z. Tian, X. Yang, B. Liu, D. Zhong and G. Zhou, J. Organomet. Chem., 2019, 895, 28 CrossRef CAS.
- J. Zhang, L. Xu, C. L. Ho and W. Y. Wong, Top. Curr. Chem., 2017, 375, 77 CrossRef PubMed.
- R. Matassa, I. Fratoddi, C. Battocchio, R. Caminiti and M. V. Russo, J. Phys. Chem. C, 2012, 116, 15795 CrossRef CAS.
- S. Cerra, L. Fontana, E. Rossi, M. Bassetti, C. Battocchio, I. Venditti, L. Carlini, R. Matassa, G. Familiari and I. Fratoddi, Inorg. Chim. Acta, 2021, 516, 120170 CrossRef CAS.
- S. K. Ghosh and T. Pal, Chem. Rev., 2007, 107(11), 4797 CrossRef CAS PubMed.
- S. Wintzheimer, T. Granath, M. Oppmann, T. Kister, T. Thai, T. Kraus, N. Vogel and K. Mandel, ACS Nano, 2018, 12, 5093 CrossRef CAS PubMed.
- J. C. Azcárate, M. H. Fonticelli and E. Zelaya, J. Phys. Chem. C, 2017, 121(46), 26108 CrossRef.
- J. Stetefeld, S. A. McKenna and T. R. Patel, Biophys. Rev., 2016, 8, 409 CrossRef CAS PubMed.
- A. Rosencwaig, Anal. Chem., 1975, 47, 592A CrossRef CAS.
- R. Li Voti, G. Leahu, M. C. Larciprete, C. Sibilia, M. Bertolotti, I. Nefedov and I. V. Anoshkin, Int. J. Thermophys., 2015, 36, 342 Search PubMed.
- R. Li Voti, G. Leahu, S. Gaetani, C. Sibilia, V. Violante, E. Castagna and M. Bertolotti, J. Opt. Soc. Am. B, 2009, 1585 CrossRef CAS.
- S. Park, C. Lee, J. Kim and C. Kim, Biomed. Eng. Lett., 2014, 4, 213 CrossRef.
- G. Cesarini, G. Leahu, M. L. Grilli, A. Sytchkova, C. Sibilia and R. Li Voti, Phys. Status Solidi C, 2016, 13, 998 CrossRef CAS.
- M. Gandolfi, F. Banfi and C. Glorieux, Photoacoustics, 2020, 20, 100199 CrossRef PubMed.
- A. Rosencwaig and A. Gersho, J. Appl. Phys., 1974, 47, 64 CrossRef.
- P. Helander and I. Lundstrom, J. Appl. Phys., 1980, 51, 3841 CrossRef.
- P. Helander, J. Appl. Phys., 1983, 54, 3410 CrossRef CAS.
- F. R. Lamastra, M. L. Grilli, G. Leahu, A. Belardini, R. Li Voti, C. Sibilia, D. Salvatori, I. Cacciotti and F. Nanni, Nanotechnology, 2017, 28, 375704 CrossRef CAS PubMed.
- G. Chumanov, K. Sokolov, B. W. Gregory and T. M. Cotton, J. Phys. Chem., 1995, 99, 9466 CrossRef CAS.
- B. Palpant, B. Prével, J. Lermé, M. Treilleux, J. L. Vialle and M. Broyer, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 5, 1963 CrossRef.
- L. Novotny and B. Hecht in Principles of Nano-Optics, 545 Cambridge, UK, 2006 Search PubMed.
- J. Lin, W. Zhou and C. O'Connor, Mater. Lett., 2001, 49, 282 CrossRef CAS.
- A. Henglein, J. Phys. Chem., 1993, 97, 5457 CrossRef CAS.
- G. Mie, Ann. Phys., 1908, 25, 377 CrossRef CAS.
- A. J. Cox, A. J. De Weerd and J. Linden, Am. J. Phys., 2002, 70, 620 CrossRef.
- J. G. Van Bladel in Electromagnetic Fields, IEEE Press, Wiley, II edn, 2007 Search PubMed.
- A. N. Shipway, M. Lahav, R. Gabai and I. Willner, Langmuir, 2000, 16, 8789 CrossRef CAS.
- J. C. Maxwell Garnett, Philos. Trans. R. Soc., A, 1904, 203, 805 Search PubMed.
- J. C. Maxwell Garnett, Philos. Trans. R. Soc., A, 1906, 205, 237 Search PubMed.
- G. L. Hornyak, C. J. Patrissi and C. R. Martin, J. Phys. Chem. B, 1997, 10, 1548 CrossRef.
- C. A. Foss Jr, G. L. Hornyak, J. A. Stockert and C. R Martin, J. Phys. Chem., 1994, 98, 2963 CrossRef.
- G. Cesarini, G. Leahu, A. Belardini, M. Centini, R. Li Voti and C. Sibilia, Int. J. Therm. Sci., 2019, 146, 10606 CrossRef.
- M. Tomoda, R. Li Voti, O. Matsuda and O. B. Wright, Appl. Phys. Lett., 2007, 90, 041114 CrossRef.
- J. Ravi, Y. Lu, S. Longuemart, S. Paoloni, H. Pfeiffer, J. Thoen and C. Glorieux, J. Appl. Phys., 2005, 97, 014701 CrossRef.
- C. Glorieux and J. Thoen, J. Appl. Phys., 1996, 80, 65610 Search PubMed.
- R. Matassa, S. Orlanducci, G. Reina, M. C. Cassani, D. Passera and M. L. Terranova, Sci. Rep., 2016, 6, 31163 CrossRef CAS PubMed.
- E. Kraleva, M. L. Saladino, R. Matassa, E. Caponetti, S. Enzo and A. Spojakina, J. Struct. Chem., 2011, 52, 330 CrossRef CAS.
- B. Silvestri, P. Armanetti, G. Sanità, G. Vitiello, A. Lambert, G. Calì, A. Pezzella, G. Luciani, L. Menichetti, S. Luin and M. D'Ischia, Mater. Sci. Eng. C, 2019, 102, 788 CrossRef CAS PubMed.
- Z. Yasmin, E. Khachatryan, Y.-H. Lee, S. Maswadi, R. Glickman and K. L. Nash, Biosens. Bioelectr., 2015, 64, 676 CrossRef CAS PubMed.
- C. L. Bayer, S. Y. Nam, Y.-S. Chen and S. Y. Emelianov, J. Biomed. Opt., 2013, 18, 016001 CrossRef PubMed.
- P. K. Krivoshein, D. S. Volkov, O. B. Rogov and M. A. Proskurnina, Photoacoustics, 2020, 18, 100162 CrossRef PubMed.
- A. G. Bell, Am. J. Sci., 1880, S3–S20(118), 305 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00333j |
| This journal is © The Royal Society of Chemistry 2021 |