Open Access Article
Open Access ArticleMechanisms of sodiation in anatase TiO2 in terms of equilibrium thermodynamics and kinetics†
Zhongqiu
Tong
abc,
Tianxing
Kang
bc,
Jianming
Wu
a,
Rui
Yang
bc,
Yan
Wu
bc,
Ruqian
Lian
*d,
Hui
Wang
bc,
Yongbing
Tang
 e and
Chun Sing
Lee
e and
Chun Sing
Lee
 *bc
*bc
aCollege of Materials and Metallurgical Engineering, Guizhou Institute of Technology, Guiyang, 550003, Guizhou, China
bDepartment of Chemistry, City University of Hong Kong, Hong Kong, China. E-mail: apcslee@cityu.edu.hk
cCenter of Super-Diamond and Advanced Films (COSDAF), City University of Hong Kong, Hong Kong, China
dSchool of Physical Science and Technology, Hebei University, Baoding, 071002, China. E-mail: rqlian@126.com
eShenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, 518055, China
First published on 25th June 2021
Abstract
Anatase TiO2 is a promising anode material for sodium-ion batteries (SIBs). However, its sodium storage mechanisms in terms of crystal structure transformation during sodiation/de-sodiation processes are far from clear. Here, by analyzing the redox thermodynamics and kinetics under near-equilibrium states, we observe, for the first time, that upon Na-ion uptake, the anatase TiO2 undergoes a phase transition and then an irreversible crystal structure disintegration. Additionally, unlike previous theoretical studies which investigate only the two end points of the sodiation process (i.e., TiO2 and NaTiO2), we study the progressive crystal structure changes of anatase TiO2 upon step-by-step Na-ion uptake (NaxTiO2, x = 0.0625, 0.125, 0.25, 0.5, 0.75, and 1) for the first time. It is found that the anatase TiO2 goes through a thermodynamically unstable intermediate phase (Na0.25TiO2) before reaching crystalline NaTiO2, confirming the inevitable crystal structure disintegration during sodiation. These combined experimental and theoretical studies provide new insights into the sodium storage mechanisms of TiO2 and are expected to provide useful information for further improving the performance of TiO2-based anodes for SIB applications.
1. Introduction
Current research in titanium dioxide (TiO2) has made promising advances towards applications in photocatalysis,1 dye-sensitized solar cells,2 capacitors,3 and rechargeable batteries such as lithium-ion batteries (LIBs) and sodium-ion batteries (SIBs).4–6 Notably, TiO2 anode materials of SIBs show superiorities of high theoretical capacity (∼336 mA h g−1 corresponding to NaTiO2), moderate redox potential (from 0.5 to 1 V vs. Na+/Na), earth abundance, and low cost.7–9 Among various TiO2 polymorphs, anatase TiO2 (a-TiO2) possesses two-dimensional diffusion channels along the a and the b axes with a size of 3.72 × 3.78 Å, which are theoretically suitable for interstitial accommodation of Na-ions (1.02 Å).10,11 Plenty of a-TiO2 anode materials for SIBs have been synthesized which delivered high specific capacities, high-rate performance and long cycling stabilities.5,9,12–14However, the reaction mechanisms on which this remarkable performance is based are still not fully understood. The key issue is to determine the a-TiO2 crystal structure transformation during the sodiation/de-sodiation processes. In practice, three different mechanisms have been proposed: (1) reversible insertion/extraction of Na-ions in the crystalline lattice,15–18 (2) Na-ion storage occurring in intermediates of sodium titanium oxide phases produced from a-TiO2 during initial discharge/charge cycles,19,20 and (3) a multiphase complex (mainly formed by metallic Ti0, low-crystallinity sodium titanates and TixOy with poor crystallinity) derived from a completely collapsed a-TiO2 structure after the first sodiation/de-sodiation.14,21–23 All the three proposed Na-ion redox mechanisms find their own support from different experimental results.23–40 Recently, it was found that the sodiation processes in the internal region and near the surface region of a-TiO2 particles differed significantly.35,37,38,41 Furthermore, the literature also demonstrates that the sodiated phase compositions of a-TiO2 depend strongly on the morphology,33,42 crystallinity,43,44 surface status,24,45–47 particle size,48 cycling numbers,23,25,31,47,49 and solid electrolyte interphase (SEI)-controlled Na-ion diffusion kinetics.23,31,50 These phenomena clearly indicate that the sodiation kinetics occurring in the a-TiO2 are rather sluggish. The different mechanisms possibly stem from the fact that their corresponding supporting experiments have been carried out under different non-equilibrium sodiation/de-sodiation conditions. That is they are likely to be all correct but under different kinetics conditions. Unfortunately, this situation is difficult for researchers to establish the fundamental understanding of the thermodynamics of the sodiation process in a-TiO2. In fact, experimental investigations under near-equilibrium conditions have been shown to be useful for understanding the sodiation mechanisms in electrode materials such as NaFePO4 and hard carbons.51–55 However, until now, there have been no corresponding studies on the a-TiO2 anode for elucidating its sodiation mechanism.
In this work, we aim to fill this gap by combining experimental studies such as galvanostatic intermittent titration technique (GITT) and cyclic voltammetry (CV), and density functional theory (DFT) calculation to understand sodiation/de-sodiation in a-TiO2, for the first time. In addition, unlike previous theoretical studies which focus mainly on investigating the properties of the two end points (TiO2 and NaTiO2),22,43,46,53 we theoretically studied the crystal structure changes of anatase- and amorphous-derived NaxTiO2 under step-by-step Na-ion uptake conditions (x = 0.0625, 0.125, 0.25, 0.5, 0.75, and 1). By further supplementation with ex situ X-ray photoelectron spectroscopy (XPS) and transmission electron microscopy (TEM), we provide convincing evidence that defect-free a-TiO2 suffers crystal structure disintegration before reaching the final crystalline NaTiO2. Our results also demonstrate that the sodiation process is strongly influenced by the crystallinity of a-TiO2, applied discharge/charge current densities and potential windows.
2. Experimental
2.1 Preparation of TiO2 samples
TiO2 samples were prepared by standard hydrolysis and annealing using tetrabutyl titanate.5,9 Amorphous, low-crystalline and high-crystalline TiO2 materials (denoted as “amor-TiO2”, “low crys-TiO2” and “high crys-TiO2”, respectively) were prepared by annealing treatments of the hydrolysis-obtained precipitate in air at 310 °C for 1 h, 450 °C for 0.5 h and 500 °C for 10 h, respectively.2.2 Physical characterization
A thermogravimetry analysis/differential scanning calorimetry (TGA/DSC) system (Netzsch, STA 449C) was used to determine the suitable annealing temperature of the hydrolysis-obtained precipitate in air. The crystalline and morphology information was collected by X-ray diffraction (XRD, PANalytical X'Pert Pro X-ray diffractometer), transmission electron microscopy (TEM, FEI Tecnai G2F30, 300 kV), high-resolution TEM (HRTEM), selected area electron diffraction (SAED), and scanning electron microscopy (SEM, FEI Helios Nanolab 600i) examinations. X-ray photoelectron spectroscopy tests (XPS, PHI 5700ESCA System) and Raman spectra (JY Co. LABRAM-HR) were used to study chemical elements and bond characters. Nitrogen physisorption measurements were performed on a Quantachrome QDS-MP-30 analyzer (USA) at 77 K.2.3 Electrochemical measurements
For the electrochemical measurements, TiO2 slurry (80 wt% titania, 10 wt% conductive carbon and 10 wt% PVDF (poly(vinylidene fluoride))) was pasted on a copper substrate and dried in a vacuum. The mass loading of the active material was about 2 mg cm−2. Na-ion half-cells were assembled into 2032 type coin cells with a sodium foil counter electrode, a Whatman glass fiber separator, and 1 M NaClO4/ethylene carbonate–propylene carbonate (EC–PC, volume ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) electrolyte. Li-ion half-cells were assembled into 2032 type coin cells with a lithium foil counter electrode, a Whatman glass fiber separator, and 1 M LiClO4/ethylene carbonate-propylene carbonate (EC–PC, volume ratio of 1
1) electrolyte. Li-ion half-cells were assembled into 2032 type coin cells with a lithium foil counter electrode, a Whatman glass fiber separator, and 1 M LiClO4/ethylene carbonate-propylene carbonate (EC–PC, volume ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) electrolyte. Galvanostatic discharge/charge and galvanostatic intermittent titration technique (GITT) tests were conducted using an Arbin Instrument system. All the tests were conducted at room temperature.
1) electrolyte. Galvanostatic discharge/charge and galvanostatic intermittent titration technique (GITT) tests were conducted using an Arbin Instrument system. All the tests were conducted at room temperature.
2.4 DFT calculations
Calculations employing the density functional theory (DFT) + U method were implemented in the Vienna Ab initio Simulation Package (VASP), where U is the on-site Coulomb parameter.22 Valence electrons in these calculations were described using a plane-wave basis set with an energy cutoff of 500 eV. Interactions between core and valence electrons were described with the PAW method, with cores of [Mg] for Ti, [He] for O, and [Ne] for Na. Lattice systems were modeled with periodic boundary conditions. Full relaxation of all atomic positions was carried out until the forces on all atoms were less than 0.5 eV nm−1 for geometric and energetic convergence.3. Results and discussion
3.1 Physical characterization and electrochemical performance
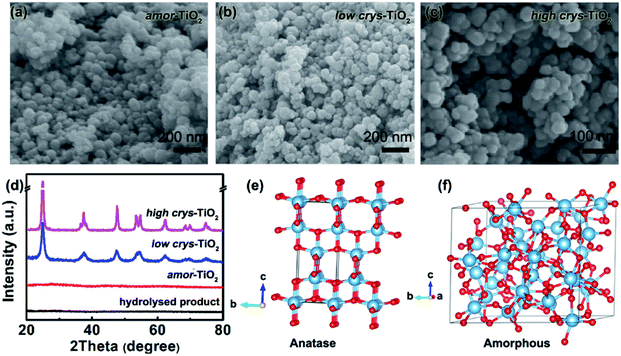
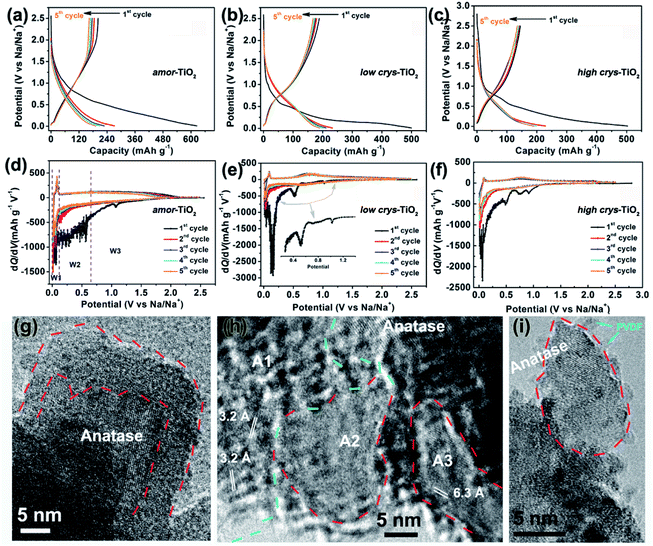
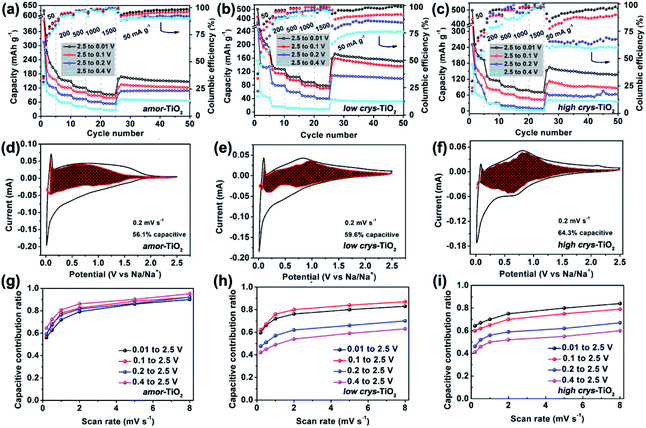
Because of the respectively controlled annealing treatments at temperatures of 310, 450 and 500 °C (Fig. S1a†), the amorphous, the low-crystallinity and the high-crystallinity TiO2 samples (denoted as “amor-TiO2”, “low crys-TiO2” and “high crys-TiO2”, respectively) exhibit nearly identical morphologies (Fig. 1a–c), almost the same specific surface areas (Fig. S1b†) but different degrees of crystallinity (Fig. 1d and S1c–f†). The crystalline structure of anatase TiO2 with two-dimensional diffusion channels is demonstrated in Fig. 1e. The random Ti and O atom arrangements of amorphous TiO2 are presented in Fig. 1f.The sodiation/de-sodiation performances of the three titania electrodes were studied at various current densities over the potential range of 0.01–2.5 V vs. Na/Na+. The discharge/charge profiles and the corresponding differential (dQ/dV) curves during the initial five cycles at 50 mA g−1 are shown in Fig. 2a–f. The Na-ion storage performances of a super P electrode (mixture of super P and PVDF) and pure high crys-TiO2 (mixture of high crys-TiO2 and PVDF) electrodes as well as the Li-ion storage performance of the amor-TiO2 electrode at 50 mA g−1 were also tested for comparison (Fig. S2a to f†). Based on the electrochemical properties, three points are notable.
(1) Compared to the three titania electrodes (Fig. 2a–f), the super P (Fig. S2a, b†) and the pure high crys-TiO2 (Fig. S2c, d†) electrodes demonstrate different discharge/charge profiles and low discharge/charge capacity, indicating that the super P component only acts as an efficient electron pathway to assist the efficient sodiation/de-sodiation in the active titania.
(2) Basically, in the 1st discharge process of the amor-TiO2 electrode (Fig. 2d), the differential (dQ/dV) curve of the 1st sodiation process can be roughly divided into three potential parts, W1 (0.01 to 0.11 V), W2 (0.11 to 0.65 V) and W3 (0.65 to 2.5 V). (i) In the W1 region, by comparing with the electrochemical features of the super P electrode over the same potential region (Fig. S2b†),55,56 plating of metallic sodium in the pores of the electrode film makes a large energy storage contribution. (ii) A large difference appeared in the W2 region. It is found that the 1st sodiation behavior of the amor-TiO2 electrode (Fig. 2d) is similar to that of its 1st lithiation process (Fig. S2f†) with mild metal-ion insertion-derived structure transformation and relaxation.8,9 In contrast, for the two crystalline titania samples (low crys-TiO2 and high crys-TiO2, Fig. 2e, f), their high dQ/dV values in the W2 region indicate that they undergo significant structure transformation during 1st Na-ion insertion. Furthermore, compared to that for the high crys-TiO2 electrode (Fig. 2f), a strong peak located at 0.14 V for the low crys-TiO2 electrode (Fig. 2e) indicates its sodiation feasibility because of low crystallinity.43,44 (iii) The dQ/dV peaks in the W3 region (Fig. 2d–f) can be assigned to the side reactions, including decomposition of electrolytes and formation of a solid-electrolyte interphase (SEI).57,58 (iv) The dQ/dV profiles of 1st de-sodiation and the following sodiation/de-sodiation cycles (2nd to 5th cycles) in the three titania electrodes are similar to each other as well as to those of the amor-TiO2 Li-ion electrode. This phenomenon indicates that the sodiated products might be of amorphous or low-crystallinity nature.8,9,59
(3) The amor-TiO2 electrode delivers better rate capability than the low crys-TiO2 and the high crys-TiO2 electrodes (Fig. S2g†). Capacities of 94.7, 80.2 and 72.1 mA h g−1 are observed at 1.5 A g−1 for the amor-TiO2, the low crys-TiO2 and the high crys-TiO2 electrodes, respectively. Additionally, the three titania electrodes demonstrate impressive cycling stability at 500 mA g−1 for 1000 cycles (Fig. S2h†).
The three titania electrodes under typical potentials of 0.65 and 0.01 V during the initial sodiation process were collected for further XPS analysis. The observation of only Ti4+ in the three titania electrodes confirms that no redox occurs above 0.65 V (Fig. S3a–c†). Additionally, the co-existence of Ti4+ and Ti3+ signals at 0.01 V indicates that the Na-ion storage is from the Ti4+/Ti3+ redox couple under 50 mA g−1 (Fig. S3d–f†). Meanwhile the different molar ratios of Ti4+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti3+ of the three titania electrodes indicate their crystallinity-dependent redox activity.
Ti3+ of the three titania electrodes indicate their crystallinity-dependent redox activity.
HRTEM analysis was used for studying the phases of high crys-TiO2 after the 1st full sodiation under 50 mA g−1. It is found that sodiation does not change the particle morphology of the sample (Fig. S4a†). Furthermore, as shown in the SAED pattern (Fig. S4b†), diffraction rings from unreacted a-TiO2, irregular diffraction points and amorphous diffraction signals confirm that the sodiated product is a mixture of these. As shown in Fig. 2g, the near-surface part of an a-TiO2 particle suffers Na-ion insertion-derived amorphization, generating a crystalline/amorphous core/shell structure. Fig. 2h demonstrates another typical sodiated titania microsite with complex phases. Besides the homogeneous contrast amorphous area (“A2”), two inhomogeneous contrast amorphous parts (“A1” and “A3”) are also found, which are believed to be generated from the non-equilibrium sodiation process.8,9,59,60 Interestingly, some ultra-small nanocrystals can be observed in the amorphous matrix. These nanocrystals could be assigned as Na2Ti6O13 (d20-1 = 0.63 Å, JCPDS no. 14-0277) and Na4TiO4 (d041 = 0.32 Å, JCPDS no. 25-1297). As shown in Fig. 2i demonstrating a nanoparticle marked with a dashed line, a large part of anatase TiO2 has been transformed into a product with low crystallinity, instead of amorphous sodium titanate. Additionally, an unreacted a-TiO2 nanoparticle is also observed (Fig. S4c†).
Based on the above analysis on the sodiation/de-sodiation performance and XPS results, the crystallinity-dependent sodiation confirms the sluggish redox kinetics in a-TiO2. Meanwhile, the complex sodiation products indicate the non-uniform and non-equilibrium sodiation in the a-TiO2 electrode under such conventional galvanostatic discharge/charge processes at 50 mA g−1.58,61 Thus, investigation of the Na-ion sodiation/de-sodiation in aspects of equilibrium thermodynamics and kinetics could be key to understanding the sodiation/de-sodiation redox mechanism of a-TiO2.51,52,54
3.2 GITT thermodynamic and kinetic analysis
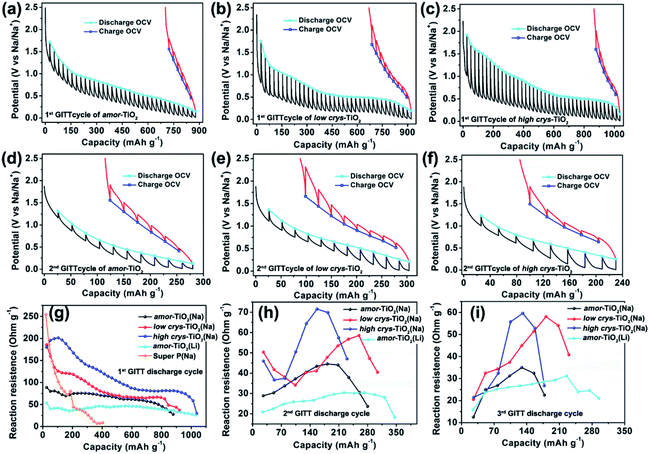
The galvanostatic intermittent titration technique (GITT), as a technique combining transient and steady-state measurements, is widely employed for studying redox thermodynamics and kinetics in systems at near-equilibrium states.51,52,54,62,63 During the GITT measurements, the three titania electrodes undergo discharge/charge at 25 mA g−1 for 1 h, followed by a 24 h relaxation process at room temperature (Fig. 3, S5†). GITT measurements of Na-ion redox of the super P (Fig. S6†) and Li-ion redox of the amor-TiO2 electrode (Fig. S7†) were also conducted for comparison. The open-circuit-voltage (OCV) at the end of relaxation is considered to be the thermodynamic equilibrium potential. The discharge (or charge) overpotential is defined as the absolute value of the difference between the OCV and the experimentally measured potential in the discharge (or charge) process.First, as shown in the 1st GITT sodiation (Fig. 3a) and the 1st GITT lithiation (Fig. S7a†) of the amor-TiO2 electrodes, the steadily decreased OCV is assigned to the redox nature of the amorphous hosts.38,51,52,54,62–65 Additionally, during the 1st GITT discharge process, the overpotential (voltage differences between the blue lines and the valley tips of the black lines in Fig. 3a–c) and reaction resistance (Fig. 3g) increase in the sequence of amor-TiO2, low crys-TiO2 and high crys-TiO2 electrodes. These phenomena demonstrate that high crystallinity leads to a high reaction barrier. Furthermore, for the low crys-TiO2 and the high crys-TiO2 electrodes, the irregular OCV (Fig. 3b, c) and reaction resistance (Fig. 3g) profiles comprise relatively flat and sloping parts. Such curve profiles indicate that sodiation in a-TiO2 might involve a phase transition reaction and crystalline structure conversion or disintegration.54,62,65 Notably, the 1st de-sodiation of the low crys-TiO2 (Fig. 3b) and the high crys-TiO2 (Fig. 3c) electrodes demonstrates similar GITT charge profiles to Na-/Li-ion GITT charge characteristics of the amor-TiO2 electrode (Fig. 3a, S7a†). This phenomenon indicates that the pristine a-TiO2 crystal structure cannot be recovered after 1st near-equilibrium GITT sodiation.54,62,65
To better study the near-equilibrium sodiation mechanisms, XPS measurements on Ti valence of the three titania electrodes at 1st GITT fully sodiated states were conducted. Ti signals in valences of 0, +2, +3, and +4 (Fig. S8†) are detected for the three titania electrodes. In contrast, as shown in Fig. S3d–f,† Ti signals in valences of only +3 and +4 are observed for the fully discharged titania electrodes treated by the conventional galvanostatic discharge process. The appearance of Ti0 and Ti2+ after GITT sodiation confirms the thermodynamic favorability of crystalline structure conversion or disintegration. This result is consistent with the previously reported sodiation/de-sodiation phenomena. It was reported that the phases of sodiated products are applied-current-dependent.31,35,39 There were differences in the sodiation kinetics occurring in the internal and surface/near-surface regions of a-TiO2 materials.35,37,38,41 These two phenomena appear upon non-equilibrium sodiation.
TEM measurements were also conducted to study the near-equilibrium sodiation. Fig. S9† shows typical TEM images of high crys-TiO2 taken after 1st full GITT sodiation. It can be observed that near-equilibrium GITT sodiation also does not change the particle morphology (Fig. S9a, b†). By comparing with the SAED pattern taken from the high crys-TiO2 electrode treated by the conventional galvanostatic discharge process (Fig. S4b†), it is found that near-equilibrium GITT discharge increases the sodiation-derived amorphization degree (Fig. S9c†). A typical HRTEM image (Fig. S9d†) shows that the sample consists mostly of the amorphous product and a small amount of low-crystallinity products (marked with blue arrow points). Additionally, the low-crystallinity SAED pattern of high crys-TiO2 (Fig. S9e,f†) after 1st GITT de-sodiation indicates that the sodiation-derived crystal structure disintegration is irreversible. In addition, as to the 2nd and 3rd GITT sodiation/de-sodiation cycles, the low crys-TiO2 and the high crys-TiO2 electrodes demonstrate similar OCV (Fig. 3e, f and S5a–c†) and reaction resistance (Fig. 3h,i) profiles to the amor-TiO2 as Na-ion (Fig. 3d, S5a†) and Li-ion (Fig. S7b, c†) electrodes. This confirms that the amorphous and low-crystallinity compounds produced during 1st GITT sodiation/de-sodiation act as Na-ion hosts during the following cycles.
Second, analysis of ion diffusion coefficients during the GITT sodiation/de-sodiation processes provides information about the Na-ion redox kinetics.51,52 The Na-ion diffusion coefficient (DNa) and Li-ion diffusion coefficient (DLi) are calculated based on Fick's second law using the equation:54,62,63
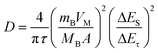 | (1) |
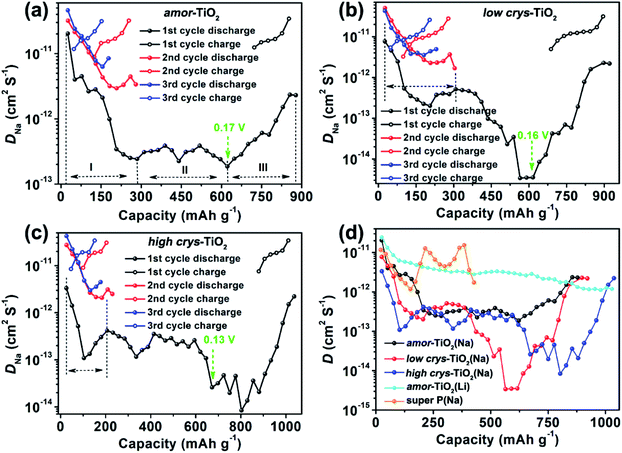
Compared to the steady decrease of DLi during the 1st GITT lithiation (Fig. 4d and S7d†), the 1st GITT sodiation in the amor-TiO2 electrode shows three distinct stages (marked as I, II and III in Fig. 4a). Before 285 mA h g−1 (ca. 0.48 V, stage I in Fig. 4a), the continuous DNa decrease indicates slow atomic deformation in amorphous titania to accommodate the inserted Na-ions.38,51,52,54,62–65 Then, the relatively stable DNa region from 0.57 to 0.17 V (i.e. from 207.2 to 622 mA h g−1, stage II in Fig. 4a) indicates that further sodiation undergoes a redox mechanism similar to that occurring in solid solution hosts.66–68 Finally, the increase of DNa from 0.17 to 0.01 V (stage III in Fig. 4a) can be assigned to the increased electrical conductivity due to the generation of metallic Ti0 and the plating of metallic sodium.55,56
On the other hand, a-TiO2 undergoes different sodiation kinetics before reaching NaTiO2 which corresponds to 336 mA h g−1 (Fig. 4b, c). They show U-shaped DNa profiles (marked with dashed lines in Fig. 4b, c) during the 1st GITT sodiation. Typically, as demonstrated by the plots of DLivs. capacity of a-TiO2 (Fig. S10†), the U-shaped plots of diffusion coefficient vs. capacity (Fig. S10†) indicate the phase transition reaction process.69–71 In two a-TiO2 electrodes, the observation of U-shaped DNa profiles before reaching the capacity of 336 mA h g−1 clearly indicates that they undergo a limited phase transition during the 1st sodiation processes (marked with dashed lines in Fig. 4b, c). Additionally, the GITT capacity from phase transition occurring in the low crys-TiO2 reaches 308 mA h g−1 (corresponding to 0.26 V, Fig. 4b), which is much higher than that of low crys-TiO2 (206 mA h g−1, corresponding to 0.44 V, Fig. 4c). This phenomenon clearly indicates that sodiation in a-TiO2 is sluggish and crystallinity-dependent.
Following the irreversible phase transition process of the 1st GITT sodiation process, the complex changes of DNa (Fig. 4d) clearly indicate that the a-TiO2 undergoes a crystal structure disintegration after the irreversible phase transition.51,52,54,62,63 The increase of DNa from below 0.2 V can be assigned to the increased electrical conductivity because of the generation of metallic Ti0 and the plating of metallic sodium.55,56 Notably, this is the first experimental demonstration that the a-TiO2 crystal structure transformation sequentially contains irreversible phase transition and crystal structure disintegration during initial sodiation under near-equilibrium processes.
3.3 Kinetic analysis based on cut-off potential-dependent sodiation/de-sodiation
The above analysis demonstrates that the crystal structure disintegration during 1st sodiation is key to influencing the redox performance of a-TiO2. Thus, it is believed that the sodiation/de-sodiation kinetics could be significantly influenced by discharge cut-off potentials. Fig. 5a–c, respectively, show rate performance of the amor-TiO2, the low crys-TiO2 and the high crys-TiO2 electrodes with different discharge cut-off potentials (0.01, 0.1, 0.2 and 0.4 V vs. Na/Na+). The discharge/charge profiles of the titania electrodes at 50 mA g−1 are shown in Fig. S11.† The amor-TiO2 electrodes, due to the facile and uniform redox kinetics below the potential of 0.48 V (Fig. 4a), exhibit an almost incremental increase of capacity along with the cut-off potential varying from 0.4 to 0.01 V (Fig. 5a). For the low crys-TiO2 electrode, because of the maximum crystal structure disintegration-derived dQ/dV values located at ca. 0.14 V (Fig. 2e), the rate capability varies significantly between cut-off potentials of 0.1 and 0.2 V (Fig. 5b). Additionally, the cut-off potential of 0.4 V neighbors the lower potential of the phase transition under near-equilibrium conditions (0.44 V, Fig. 4d). Thus, the poor rate performance of the low crys-TiO2 electrode over the potential range of 0.4 to 2.5 V can be derived from the lack of crystal structure disintegration (Fig. 5b). In the case of high crys-TiO2 electrodes, their increased sodiation barrier makes the influence of cut-off potential on capacity more obvious (Fig. 5c), compared to the low crys-TiO2 electrodes.Analysis of pseudocapacitance with different cut-off discharge potentials is also employed to study the sodiation/de-sodiation kinetics. For a specific CV scanning rate (v), the measured current (i) at a fixed potential (V) can be quantitatively separated into capacitive (k1v) and diffusion controlled (k2v1/2) responses according to the equation:72,73
| i(V) = k1v + k2v1/2 | (2) |
Fig. S12–S14†, respectively, demonstrate the CV curves at different scan rates with variable cut-off potentials for the amor-TiO2, the low crys-TiO2 and the high crys-TiO2 electrodes. The separated CV curves with a cut-off potential of 0.01 V at 0.2 mV s−1 of the three titania electrodes are demonstrated in Fig. 5d–f, respectively. The plots of capacitive contribution ratio versus scan rate with variable cut-off potentials for the amor-TiO2, the low crys-TiO2 and the high crys-TiO2 electrodes are presented for comparison in Fig. 5g–i, respectively. The amorphous titania demonstrates feasible structural relaxation below 0.4 V, leading to almost the same capacitive contribution ratio at a specific scan rate under different potential ranges (Fig. 5g). On the other hand, when the cut-off potentials are set as 0.01 and 0.1 V (Fig. 5h), the high and similar capacitive contribution ratios of the low crys-TiO2 electrodes are due to that these electrodes undergo sufficient crystal structure disintegration below 0.14 V. Additionally, the decrease of the cut-off potential from 0.4 to 0.1 V gradually increases the degree of crystal structure disintegration, leading to the almost incremental changes of capacitive contribution ratios for the low crys-TiO2 electrodes (Fig. 5h). Finally, the high crys-TiO2 electrodes demonstrate similar cut-off potential-dependent changes of capacitive contribution ratios to the low crys-TiO2 electrodes (Fig. 5i). This phenomenon further confirms that the crystal structure disintegration-derived amorphous and low-crystalline products are the main Na-ion storage hosts. Notably, in the case of a cut-off potential of 0.1 V, the low crys-TiO2 electrodes demonstrate higher capacitive contribution ratio than the high crys-TiO2 electrodes, further indicating the crystallinity-dependent sodiation/de-sodiation kinetics.
When the a-TiO2 materials are employed as Li-ion hosts in the potential range from 1 to 3 V (Fig. S15†),11 the low crys-TiO2 electrode demonstrates higher capacitive contribution ratio than the high crys-TiO2 electrodes. This result is consistent with the lower crystallinity of the former sample, given that a-TiO2 is a type of extrinsic pseudocapacitive Li-ion host.59
Electrochemical impedance spectroscopy (EIS) was also used to investigate the influence of Na-ion insertion-derived crystal structure disintegration on the redox reversibility. The Nyquist plots of the amor-TiO2, the low crys-TiO2 and the high crys-TiO2 electrodes after different discharge/charge cycles at 50 mA g−1 over the potential window of 0.01 to 2.5 V are illustrated in Fig. S16a–c,† respectively. Although the three electrodes demonstrate different charge-transfer resistances (Rct, which corresponds to the diameter of the semicircle) at the initial assembled state, the low crys-TiO2 and the high crys-TiO2 electrodes undergo almost the same changes of Rct as amor-TiO2 along with the increase of cycle numbers. This phenomenon indicates that the active materials which act as Na-ion hosts are similar after the activation of the initial discharge/charge process. The amorphous and low-crystallinity compounds produced after the initial discharge/charge cycle are the “true” hosts for Na-ion insertion/extraction during the following cycles.
Based on the above analysis, it is concluded that efficient crystal structure disintegration in a-TiO2 is key to obtaining high Na-ion storage. To further demonstrate this point, the rate performances of the three titania electrodes were studied with an initial current density of 15 mA g−1 (Fig. S17†). For both a-TiO2 electrodes, the increased capacity over the potential range from 0.4 to 0.01 V indicates the increased degree of crystal structure disintegration at 15 mA g−1 (Fig. S17b, c†), compared to those operating at 50 mA g−1 (Fig. 2b, c). Due to the reasonably increased degree of crystal structure disintegration in the low crys-TiO2 electrode, it demonstrates impressive rate performances with 157 and 119 mA h g−1 at 500 and 1500 mA g−1 (Fig. S17d†). In contrast, the low crys-TiO2 electrode only shows 109 and 80.2 mA h g−1 at 500 and 1500 mA g−1 when the initial current density is 50 mA g−1 (Fig. S2g†).
3.4 Density functional theory (DFT) calculations on sodiation in the a-TiO2
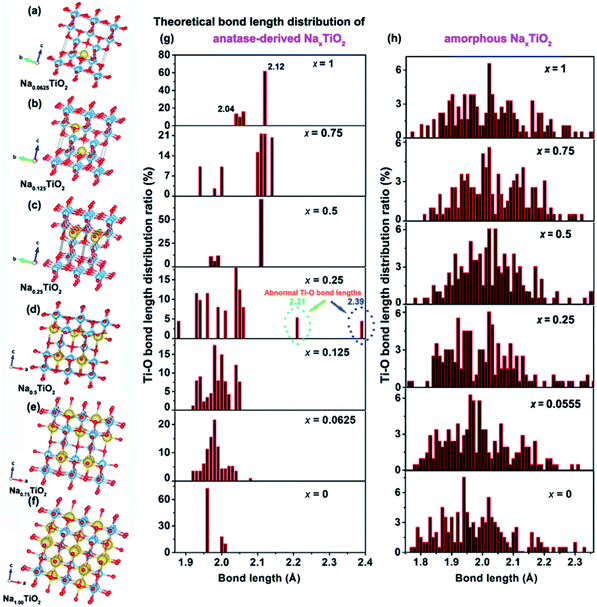
The above electrochemical studies demonstrate the importance of crystal structure disintegration for the a-TiO2 SIB anodes. This brings a question of why the crystal lattice of a-TiO2 cannot accommodate the Na-ions for facile insertion/removal, although the size of two-dimensional diffusion channels (a size of 3.72 × 3.78 Å) is much larger than the radius of Na-ions (1.02 Å).10,11 To answer this question, DFT calculations on the corresponding amorphous and anatase TiO2-derived NaxTiO2 were performed. Unlike previous theoretical studies which mainly investigate the two end points of the process (i.e. TiO2 and NaTiO2),22,43,46,53 we theoretically calculate the crystalline structure changes of amorphous and anatase TiO2 under step-by-step Na-ion uptake conditions. For sodiated amorphous TiO2-derived NaxTiO2, x is set in the sequence of 0.0555, 0.25, 0.5, 0.75, and 1 (Fig. S18†). For sodiated anatase TiO2-derived NaxTiO2, x is set in the sequence of 0.0625, 0.125, 0.25, 0.5, 0.75, and 1 (Fig. 6a–f). The Ti–O bond length distributions of sodiated anatase and amorphous TiO2-derived NaxTiO2 are summarized and presented in Fig. 6g and h, respectively. The Na-ion insertion energy (Eins) is computed as:| Eins = ETiO2:Na − ETiO2 − ENa | (3) |
| Samples | Insertion energy (eV) | a (Å) | b (Å) | c (Å) | Volume (Å3) | Theoretical capacity (mA h g−1) |
|---|---|---|---|---|---|---|
| Anatase TiO2 | — | 3.82 | 3.82 | 9.69 | 141.40 | — |
| Na0.0625TiO2 | −0.89 | 3.83 | 3.83 | 9.64 | 141.41 | 21 |
| Na0.125 TiO2 | −0.79 | 3.90 | 3.90 | 9.49 | 144.34 | 42 |
| Na0.2500TiO2 | −0.77 | 4.05 | 3.80 | 9.68 | 148.98 | 84 |
| Na0.500TiO2 | −0.71 | 4.12 | 4.12 | 9.08 | 154.13 | 168 |
| Na0.7500TiO2 | −0.83 | 4.21 | 4.21 | 9.00 | 159.29 | 252 |
| Na1.000TiO2 | −0.87 | 4.32 | 4.32 | 8.88 | 166.47 | 336 |
| Amorphous TiO2 | — | 11.59 | 11.53 | 9.87 | 1317.85 | — |
| Na0.0555TiO2 | −1.12 | 11.49 | 11.63 | 9.76 | 1304.45 | 19 |
| Na0.2500TiO2 | −0.72 | 12.26 | 11.53 | 9.92 | 1400.32 | 84 |
| Na0.5000TiO2 | −0.50 | 12.55 | 12.91 | 9.07 | 1470.13 | 168 |
| Na0.7500TiO2 | −0.47 | 13.30 | 13.14 | 9.14 | 1597.18 | 252 |
| Na1.0000TiO2 | −0.37 | 13.44 | 13.22 | 9.31 | 1654.24 | 336 |
For amorphous TiO2, a 153-atom supercell of size about 11.53 × 11.53 × 9.87 Å3 was used. The average coordination number of Ti (with a cutoff for the Ti–O bond of 2.5 Å) is 5.5 in the relaxed structure with an average Ti–O bond length of 1.99 Å, which are in good agreement with the measured experimental values for amorphous titania.74 As demonstrated in Table 1 and Fig. 6h, sodiation (0 ≤ x ≤ 1) only has mild effects on the Ti–O bond length distribution. This indicates that the random arrangement of Ti and O atoms of amorphous titania provides plenty of insertion sites for Na-ion insertion.43,75 The steadily increased but negative Eins further confirms the thermodynamically favorable conditions of amorphous TiO2 for Na-ion insertion (Table 1).
For anatase TiO2, a 2 × 2 × 1 supercell (146 atoms, 7.64 × 7.64 × 9.7 Å3) was used for the calculation of sodiation. As shown in Fig. 6a–f, the theoretically crystalline NaxTiO2 undergoes structure transformation along with Na-ion insertion (Fig. 6g). Similar to the previous results,22,43 Na-ions can thermodynamically accommodate in the one-dimensional zigzag chains consisting of distorted edge-sharing octahedra (Fig. 6f). The length of Ti–O bonds of anatase-derived crystalline NaTiO2 is in the range from 2.04 to 2.12 Å (top figure of Fig. 6g). Given that the Ti–O bond length of Ti2O3 varies over the 2.03–2.07 Å range76 and the Ti–O bond length of solid-phase reaction-prepared NaTiO2 is ca. 2.09,77 the simulated crystalline NaTiO2 could be favorable because there is only a small crystal structure deformation.78
On the other hand, the analysis of the Ti–O bond length changes along with the step-by-step sodiation provides some new insights. During the initial sodiation (x = 0.0625), the inserted Na-ions demonstrate a fivefold-coordinated environment and locate in the anatase octahedral sites with a displacement of ca. 0.5 Å, giving rise to prolonged and compensatorily shortened Ti–O bond lengths of 2.08 Å and 1.95 Å along the c axis (Fig. 6a). The small changes of Ti–O bonds and the Eins of −0.89 eV indicate the thermodynamic stability of crystalline Na0.0625TiO2.75 The sodiated anatase product of Na0.125TiO2 is also theoretically stable as demonstrated from the Ti–O bond length distribution and Eins (Fig. 6b). A significant difference occurs when x = 0.25 (Fig. 6c). In crystalline Na0.25TiO2, because of the strong electron overlap repulsion and Coulomb repulsion among adjacent Na-ions as well as between the Na-ions and Ti-ions,61,75 the lengths of Ti–O bonds along the c axis are further increased to 2.21 and 2.39 Å with compensatory Ti–O bond lengths of 1.89 Å and 1.88 Å in the opposite direction along the c axis (Fig. 6c). The prolonged Ti–O lengths of 2.21 and 2.39 Å are much larger than those of Ti2O3, indicating that it is kinetically and thermodynamically unfavorable. Thus, Na0.25TiO2 will disintegrate before NaTiO2 is obtained, although the crystalline Na0.5TiO2 (Fig. 6d) and Na0.75TiO2 (Fig. 6e) are theoretically stable. Furthermore, as demonstrated in the previous experimental and computational reports,5,10,17 the Na-ion transport in anatase TiO2 is by “hopping” between two octahedral vacant sites. Increased Ti–O bond length could reasonably increase the Na-ion transport path length, kinetically hindering further sodiation in crystalline Na0.25TiO2 to crystalline Na0.5TiO2. Such an increased Na-ion insertion barrier is reflected by the significantly increased Eins between Na0.25TiO2 (−0.77 eV) and Na0.5TiO2 (−0.71 eV) (Table 1). Fig. S19† demonstrates the theoretical discharge curves of amorphous and anatase TiO2 along with the increase of discharge capacity up to 336 mA h g−1 based on the calculation data shown in Table 1. As shown in Fig. S19,† the amorphous TiO2 theoretically demonstrates a continuous voltage decrease along with the Na-ion uptake, which is consistent with the experimental GITT discharge curve of amorphous TiO2 shown in Fig. 3a and 4a. On the other hand, theoretically, the anatase TiO2 should take in Na-ions in a phase transformation manner with a small voltage vibration between 0.7 and 0.9 V (Fig. S19†). In contrast, the practical GITT discharge curve shows an unstable phase transformation and a following crystal structure disintegration before reaching NaTiO2 (Fig. 3b, c and 4b, c). Thus, it is further confirmed that the inevitable crystal structure disintegration occurs in practical measurements using a-TiO2 as anodes for SIBs. Notably, as shown in Table 1, from a-TiO2 to Na0.25TiO2, the Na-ion uptake into the octahedral sites gives rise to the expansion of the lattice in the a-axis from 11.59 to 12.26 Å, i.e., theoretically small shifts of (200) and (101) crystalline plane XRD peaks to lower 2θ angles. Then crystal structure disintegration occurs upon further sodiation. These results are consistent with previously reported experimental phenomena about sodiation of high-crystallinity a-TiO2 nanoparticles. During sodiation/de-sodiation, a-TiO2 shows a small reversible shift of XRD peaks and a continuous decrease of XRD peak strength upon cycling.15,18,21,25,31,35,37,49 These phenomena can be assigned to some of the a-TiO2 particles that undergo reversible phase transition while the whole a-TiO2 suffers continuous crystal structure disintegration during cycling measurements. Furthermore, research has also demonstrated that the crystal structure disintegration can more feasibly occur in doped a-TiO2 (such as niobium-doped,79 nickel-doped80 and nickel/nitrogen-codoped TiO2 (ref. 81)), because their doped crystal structures are more susceptible to disintegration.
3.5 Proposed sodiation/de-sodiation mechanism in anatase TiO2
According to the above thermodynamics and kinetics analysis, a sodiation/de-sodiation mechanism of a-TiO2 is proposed. During the initial sodiation to 0.01 V, when the redox occurs under a near-equilibrium state, the sodium-ion uptake in a-TiO2 sequentially includes three states: (1) sodium-ion insertion-derived irreversible phase transition; (2) then structural relaxation into amorphous and low-crystallinity products; (3) further generation of metallic titanium and metallic sodium plating. In the following discharge/charge cycles, the amorphous and low-crystallinity products act as the main sodium storage hosts. Furthermore, the sodiation-derived compounds and electrochemical energy storage properties of a-TiO2 can be tuned using the applied discharge/charge current density, potential windows and crystallinity when the sodiation is under non-equilibrium conditions. Notably, the a-TiO2 materials with a relatively low crystallinity could demonstrate better rate performance because they can be more kinetically feasible to disintegration during the initial Na-ion uptake process. Furthermore, by doping a-TiO2 with suitable elements which can alleviate the a-TiO2 lattice integrity, the doped a-TiO2 also can demonstrate high rate performance because of the facilitated crystal structure disintegration of the initial Na-ion uptake process.3.6 Hybrid capacitors with anatase TiO2 anodes
Based on the above results, it is found that the low crys-TiO2 electrode delivers high capability after the electrochemical activation at 15 mA g−1, indicating its suitability for organic hybrid capacitors.57,59 The low crys-TiO2 nanoparticles and commercial activated carbon (AC, BET specific surface area of 2084.15 m2 g−1, XinSen Carbon Industry Co., Ltd) were, respectively, used as anode and cathode materials.Fig. S20a† shows the typical CV curves of the AC electrode from 2 to 50 mV s−1 between 2.5 and 4.0 V (vs. Na/Na+). The featureless shape indicates electrochemical double layer capacitance behavior.82 The specific capacity of the AC electrode was determined with galvanostatic charge/discharge measurements (Fig. S20b, c†). Furthermore, the unchanged CV curves at 20 mV s−1 for 100 cycles indicate its electrochemical stability (Fig. S20d†). For the assembly of hybrid capacitors, the optimum mass ratio of the anode and cathode is calculated using the specific capacity at 50 mA g−1 based on balancing the charge storages in the cathode and anode. The mass ratio of the low crys-TiO2 and the AC is set as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5. Before the assembly of the capacitor, the low crys-TiO2 electrode was run through one discharge/charge cycle and then fully sodiated in half-cells at 15 mA g−1. The assembled hybrid capacitor was named the low crys-TiO2//AC. The capacity of the capacitor was determined by the mass of anodes.
5. Before the assembly of the capacitor, the low crys-TiO2 electrode was run through one discharge/charge cycle and then fully sodiated in half-cells at 15 mA g−1. The assembled hybrid capacitor was named the low crys-TiO2//AC. The capacity of the capacitor was determined by the mass of anodes.
The charge/discharge profiles and rate performance of the assembled low crys-TiO2//AC capacitors are, respectively, demonstrated in Fig. S21a and b.† The galvanostatic charge/discharge profiles of the low crys-TiO2//AC exhibit an almost triangular shape with small deviations from linearity, indicative of the capacitive energy storage nature of the low crys-TiO2 (Fig. S21a†).82,83 Due to the high Na-ion storage in a-TiO2 anodes, the low crys-TiO2//AC hybrid capacitor demonstrates high capability performance over the potential window from 1 to 3 V. The hybrid capacitor delivers an energy density of 18.9 W h kg−1 in 11.3 min (Fig. S21b†). Notably, at 2 A g−1, a short time of 5.3 s is needed to fulfil the discharge with a highly maintained energy density of 5.79 W h kg−1. In addition, the assembled low crys-TiO2//AC capacitor shows impressive cycling stability. As shown in Fig. S21c,† after 2500 cycles at 200 mA g−1, 70% of the initial capacity of the low crys-TiO2//AC capacitor is retained, indicating the stable and reversible sodiation/de-sodiation kinetics in the low crys-TiO2 anodes. As shown in Fig. S22a, b,† TEM examination shows that the low crys-TiO2 nanoparticles maintain their morphology after 2500 cycles at 200 mA g−1. And the amorphous SAED pattern (Fig. S22c†) further confirms that there is a crystal structure disintegration process during the Na-ion uptake/release cycles.
4. Conclusions
In summary, the sodiation/de-sodiation thermodynamics and kinetics of a-TiO2 are investigated by combining experimental analysis in near-equilibrium redox states and theoretical calculation of sodiated compounds under step-by-step Na-ion uptake conditions. It is found that the a-TiO2 sequentially undergoes a phase transition and a following irreversible crystal structure disintegration during the initial Na-ion uptake process. Meanwhile, it is also found that the sodiation-derived compounds and the electrochemical energy storage properties are influenced by the applied discharge/charge current density, potential windows and crystallinity of a-TiO2 particles when the Na-ion insertion is under non-equilibrium conditions. Notably, based on the experimental and theoretical calculation results, given that the crystal structure disintegration of a-TiO2 is crystallinity-dependent, preparation of a-TiO2 materials with low crystallinity and/or doping could be effective approaches to achieve high performance in a-TiO2 anodes for sodium-ion batteries.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the NSFC/RGC Joint Research Scheme 2020/21 (Project No: N_CityU104/20) and the Science and Technology Foundation of Guizhou Province of China (No. qian ke he ji chu [2017] 1065).References
- J. You, Y. Guo, R. Guo and X. Liu, Chem. Eng. J., 2019, 373, 624–641 CrossRef CAS.
- F. W. Low and C. W. Lai, Renewable Sustainable Energy Rev., 2018, 82, 103–125 CrossRef CAS.
- X. Lu, G. Wang, T. Zhai, M. Yu, J. Gan, Y. Tong and Y. Li, Nano Lett., 2012, 12, 1690–1696 CrossRef CAS PubMed.
- Z. Liu, A. Daali, G. g. Xu, M. Zhuang, X. Zuo, C. Sun, Y. Liu, Y. Cai, M. Hossain, H. Liu, K. Amine and Z. Luo, Nano Lett., 2020, 20, 3844–3851 CrossRef CAS PubMed.
- C. Chen, Y. Wen, X. Hu, X. Ji, M. Yan, L. Mai, P. Hu, B. Shan and Y. Huang, Nat. Commun., 2015, 6, 6929 CrossRef CAS PubMed.
- L. Cao, X. Gao, B. Zhang, X. Ou, J. Zhang and W. Luo, ACS Nano, 2020, 14, 3610–3620 CrossRef CAS PubMed.
- Y. Kaneti, J. Zhang, Y. He, Z. Wang, S. Tanaka, Md. Hossain, Z. Pan, B. Xiang, Q. Yang and Y. Yamauchi, J. Mater. Chem. A, 2017, 5, 15356–15366 RSC.
- J. Wu a, J. Liu, J. Cui, S. Yao, M. Ihsan-Ul-Haq, N. Mubarak, E. Quattrocchi, F. Ciucci and J. Kim, J. Mater. Chem. A, 2020, 8, 2114–2122 RSC.
- N. Wang, C. Chu, X. Xu, Y. Du, J. Yang, Z. Bai and S. Dou, Adv. Energy Mater., 2018, 8, 1801888 CrossRef.
- D. Lin, L. Lyu, K. Li, G. Chen, H. Yaoa, F. Kang, B. Li and L. Zhou, J. Mater. Chem. A, 2021, 9, 9256–9265 RSC.
- Z. Tong, S. Liu, X. Li, L. Mai, J. Zhao and Y. Li, Nanoscale, 2018, 10, 3254–3261 RSC.
- Y. Li, S. Wang, Y. He, L. Tang, Y. Kaneti, W. Lv, Z. Lin, B. Li, Q. Yang and F. Kang, J. Mater. Chem. A, 2017, 5, 4359–4367 RSC.
- K. Li, B. Li, J. Wu, F. Kang, J. Kim and T. Zhang, ACS Appl. Mater. Interfaces, 2017, 9, 35917–35926 CrossRef CAS PubMed.
- J. Wu, M. Ihsan-Ul-Haq, F. Ciucci, B. Huang and J.-K. Kim, Energy Storage Mater., 2021, 34, 582–628 CrossRef.
- K.-T. Kim, G. Ali, K. Y. Chung, C. S. Yoon, H. Yashiro, Y.-K. Sun, J. Lu, K. Amine and S.-T. Myung, Nano Lett., 2014, 14, 416–422 CrossRef CAS PubMed.
- L. Zhao, T. Tang, W. Chen, X. Feng and L. Mi, Green Energy Environ., 2018, 3, 277–285 CrossRef.
- Z. Chen, L. Xu, Q. Chen, P. Hu, Z. Liu, Q. Yu, T. Zhu, H. Liu, G. Hu, Z. Zhu, L. Zhou and L. Mai, J. Mater. Chem. A, 2019, 7, 6740–6746 RSC.
- R. Luo, Y. Ma, W. Qu, J. Qian, L. Li, F. Wu and R. Chen, ACS Appl. Mater. Interfaces, 2020, 12, 23939–23950 CrossRef CAS PubMed.
- W. Li, M. Fukunishi, B. J. Morgan, O. J. Borkiewicz, K. W. Chapman, A. Maignan, O. I. Lebedev, J. Ma, H. Groult, S. Komaba and D. Dambournet, Chem. Mater., 2017, 29, 1836–1844 CrossRef CAS.
- Q. Zhang, H. He, X. Huang, J. Yan, Y. Tang and H. Wang, Chem. Eng. J., 2018, 332, 57–65 CrossRef CAS.
- L. M. Wu, D. Bresser, D. Buchholz, G. A. Giffin, C. R. Castro, A. Ochel and S. Passerini, Adv. Energy Mater., 2015, 5, 1401142 CrossRef.
- D. Su, S. Dou and G. Wang, Chem. Mater., 2015, 27, 6022–6029 CrossRef CAS.
- Z. Liu, W. Zhang, Z. Zhou, X. Liu, H. Zhang and M. Wei, ACS Appl. Energy Mater., 2020, 3, 3619–3627 CrossRef CAS.
- L. Ma, X. Gao, W. Zhang, H. Yuan, Y. Hu, G. Zhu, R. Chen, T. Chen, Z. Tie, J. Liu, T. Wu and Z. Jin, Nano Energy, 2018, 53, 91–96 CrossRef CAS.
- Y. Fang, Y. Zhang, C. Miao, K. Zhu, Y. Chen, F. Du, J. Yin, K. Ye, K. Cheng, J. Yan, G. Wang and D. Cao, Nano-Micro Lett., 2020, 12, 128 CrossRef CAS PubMed.
- Y. Liu, J. Liu, D. Bin, M. Hou, A. G. Tamirat, Y. Wang and Y. Xia, ACS Appl. Mater. Interfaces, 2018, 10, 14818–14826 CrossRef CAS PubMed.
- W. Wang, M. Wu, P. Han, Y. Liu, L. He, Q. Huang, J. Wang, W. Yan, L. Fu and Y. Wu, ACS Appl. Mater. Interfaces, 2019, 11, 3061–3069 CrossRef CAS PubMed.
- Z. Hong, K. Zhou, Z. Huang and M. Wei, Sci. Rep., 2015, 5, 11960 CrossRef PubMed.
- N. Louvain, A. Henry, L. Daenens, B. Boury, L. Stievano and L. Monconduit, CrystEngComm, 2016, 18, 4431–4437 RSC.
- D. Lin, K. Li, Q. Wang, L. Lyu, B. Li and L. Zhou, J. Mater. Chem. A, 2019, 7, 19297–19304 RSC.
- K. Li, J. Zhang, D. Lin, D. Wang, B. Li, W. Lv, S. Sun, Y. He, F. Kang, Q. Yang, L. Zhou and T. Zhang, Nat. Commun., 2019, 10, 725 CrossRef CAS PubMed.
- L. Ling, Y. Bai, Y. Li, Q. Ni, Z. Wang, F. Wu and C. Wu, ACS Appl. Mater. Interfaces, 2017, 9, 39432–39440 CrossRef CAS PubMed.
- W. Song, H. Zhao, J. Ye, M. Kang, S. Miao and Z. Li, ACS Appl. Mater. Interfaces, 2019, 11, 17416–17424 CrossRef CAS PubMed.
- C. Ding, T. Nohira and R. Hagiwara, Phys. Chem. Chem. Phys., 2016, 18, 30770–30776 RSC.
- J. Li, J. Liu, Q. Sun, M. N. Banis, X. Sun and T. Sham, J. Phys. Chem. C, 2017, 121, 11773–11782 CrossRef CAS.
- Y. Liu, F. Zhao, J. Li, Y. Li, J. A. McLeod and L. Liu, J. Mater. Chem. A, 2017, 5, 20005–20013 RSC.
- G. Santoro, J. M. Amarilla, P. Tartaj and M. B. Vázquez-Santos, Mater. Today Energy, 2018, 10, 23–27 CrossRef PubMed.
- C. Deng, C. Ma, M. L. Lau, P. Skinner, Y. Liu, W. Xu, H. Zhou, Y. Ren, Y. Yin, B. Williford, M. Dahl and H. Xiong, Electrochim. Acta, 2019, 321, 134723 CrossRef CAS.
- Z. Le, F. Liu, P. Nie, X. Li, X. Liu, Z. Bian, G. Chen, H. Wu and Y. Lu, ACS Nano, 2017, 11, 2952–2960 CrossRef CAS PubMed.
- M. Fehse, A. Henry, A. Zitolo, B. Boury, N. Louvain and L. Stievano, Appl. Sci., 2020, 10, 5547 CrossRef CAS.
- G. Greco, K. A. Mazzio, X. Dou, E. Gericke, R. Wendt, M. Krumrey and S. Passerini, ACS Appl. Energy Mater., 2019, 2, 7142–7151 CrossRef CAS.
- H. He, Q. Gan, H. Wang, G. Xu, X. Zhang, D. Huang, F. Fu, Y. Tang, K. Amine and M. Shao, Nano Energy, 2018, 44, 217–227 CrossRef CAS.
- M. Zhou, Y. Xu, J. Xiang, C. Wang, L. Liang, L. Wen, Y. Fang, Y. Mi and Y. Lei, Adv. Energy Mater., 2016, 6, 1600448 CrossRef.
- H. He, Q. Zhang, H. Wang, H. Zhang, J. Li, Z. Peng, Y. Tang and M. Shao, J. Power Sources, 2017, 354, 179–188 CrossRef CAS.
- H. He, D. Huang, W. Pang, D. Sun, Q. Wang, Y. Tang, X. Ji, Z. Guo and H. Wang, Adv. Mater., 2018, 30, 1801013 CrossRef PubMed.
- J. Chen, B. Luo, Q. Chen, F. Li, Y. Guo, T. Wu, P. Peng, X. Qin, G. Wu, M. Cui, L. Liu, L. Chu, B. Jiang, Y. Li, X. Gong, Y. Chai, Y. Yang, Y. Chen, W. Huang, X. Liu and M. Li, Adv. Mater., 2020, 32, 1905578 CrossRef CAS PubMed.
- N. Lee, J. Jung, J. Lee, H. Jang, I. Kim and W. Ryu, Electrochim. Acta, 2018, 263, 417–425 CrossRef CAS.
- W. Wei, M. Valvo, K. Edström and L. Nyholm, ChemElectroChem, 2018, 5, 674–684 CrossRef CAS.
- J. Wang, J. Li, X. He, X. Zhang, B. Yan, X. Hou, L. Du, T. Placke, M. Winter and J. Li, J. Power Sources, 2020, 461, 228129 CrossRef CAS.
- Z. Xu, K. Lim, K. Park, G. Yoon, W. Seong and K. Kang, Adv. Funct. Mater., 2018, 28, 1802099 CrossRef.
- T. Gao, X. Ji, S. Hou, X. Fan, X. Li, C. Yang, F. Han, F. Wang, J. Jiang, K. Xu and C. Wang, Adv. Mater., 2018, 30, 1704313 CrossRef PubMed.
- A. Ven, Z. Deng, S. Banerjee and S. Ong, Chem. Rev., 2020, 120, 6977–7019 CrossRef PubMed.
- A. Massaro, A. Muñoz-García, P. Maddalena, F. Bella, G. Meligrana, C. Gerbaldi and M. Pavone, Nanoscale Adv., 2020, 2, 2745–2751 RSC.
- Y. Zhu, Y. Xu, Y. Liu, C. Luo and C. Wang, Nanoscale, 2013, 5, 780–787 RSC.
- M. Wahid, D. Puthusseri, Y. Gawli, N. Sharma and S. Ogale, ChemSusChem, 2018, 11, 506–526 CrossRef CAS PubMed.
- M. Liu, P. Zhang, Z. Qu, Y. Yan, C. Lai, T. Liu and S. Zhang, Nat. Commun., 2019, 10, 3917 CrossRef PubMed.
- Z. Tong, S. Liu, Y. Zhou, J. Zhao, Y. Wu, Y. Wang and Y. Li, Energy Storage Mater., 2018, 13, 223–232 CrossRef.
- Y. Cao, T. Zhang, X. Zhong, T. Zhai and H. Li, Chem. Commun., 2019, 55, 14761–14764 RSC.
- V. Augustyn, P. Simon and B. Dunn, Energy Environ. Sci., 2014, 7, 1597–1614 RSC.
- Y. Huang, C. Zhu, S. Zhang, X. Hu, K. Zhang, W. Zhou, S. Guo, F. Xu and H. Zeng, Nano Lett., 2019, 19, 1118–1123 CrossRef PubMed.
- F. Bella, A. B. Muñoz-García, G. Meligrana, A. Lamberti, M. Destro, M. Pavone and C. Gerbaldi, Nano Res., 2017, 10, 2891–2903 CrossRef CAS.
- S. Gu, H. Wang, C. Wu, Y. Bai, H. Li and F. Wu, Energy Storage Mater., 2017, 6, 9–17 CrossRef.
- Z. Tong, J. Hao, K. Zhang, J. Zhao, B. Su and Y. Li, J. Mater. Chem. C, 2014, 2, 3651–3658 RSC.
- Z. Tong, H. Xu, G. Liu, J. Zhao and Y. Li, Electrochem. Commun., 2016, 69, 46–49 CrossRef CAS.
- C. Deng, M. Lau, H. Barkholtz, H. Xu, R. Parrish, M. Xu, T. Xu, Y. Liu, H. Wang, J. Connell, K. Smith and H. Xiong, Nanoscale, 2017, 9, 10757–10763 RSC.
- Z. Li, F. Du, X. Bie, D. Zhang, Y. Cai, X. Cui, C. Wang, G. Chen and Y. Wei, J. Phys. Chem. C, 2010, 114, 22751–22757 CrossRef CAS.
- M. Levi, K. Gamolsky, D. Aurbach, U. Heider and R. Oesten, J. Electroanal. Chem., 1999, 477, 32–40 CrossRef CAS.
- X. Wang, X. Yu, H. Li, X. Yang, J. McBreen and X. Huang, Electrochem. Commun., 2008, 10, 1347–1350 CrossRef CAS.
- Z. Cui, X. Guo and H. Li, Energy Environ. Sci., 2015, 8, 182–187 RSC.
- K. Tang, X. Yu, J. Sun, H. Li and X. Huang, Electrochim. Acta, 2011, 56, 4869–4875 CrossRef CAS.
- E. Allcorn, S. Kim and A. Manthiram, Phys. Chem. Chem. Phys., 2015, 17, 28837–28843 RSC.
- Z. Tong, R. Yang, S. Wu, D. Shen, T. Jiao, K. Zhang, W. Zhang and C. S. Lee, Small, 2019, 15, 1901272 CrossRef PubMed.
- Z. Tong, R. Yang, S. Wu, D. Shen, T. Jiao, K. Zhang, W. Zhang and C.-S. Lee, J. Mater. Chem. A, 2019, 7, 19581–19588 RSC.
- V. Petkov, G. Holzhüter, U. Tröge, T. Gerber and B. Himme, J. Non-Cryst. Solids, 1998, 231, 17–30 CrossRef CAS.
- F. Legrain, O. Malyi and S. Manzhos, J. Power Sources, 2015, 278, 197–202 CrossRef CAS.
- L. F. Mattheiss, J. Phys.: Condens. Matter, 1996, 8, 5987–5995 CrossRef CAS.
- D. Wu, X. Li, B. Xu, N. Twu, L. Liu and G. Ceder, Energy Environ. Sci., 2015, 8, 195–202 RSC.
- R. P. Kolli and A. Devaraj, Metals, 2018, 8, 506 CrossRef.
- F. Zhao, B. Wang, Y. Tang, H. Ge, Z. Huang and H. Liu, J. Mater. Chem. A, 2015, 3, 22969–22974 RSC.
- D. Yan, C. Yu, D. Li, X. Zhang, J. Li, T. Lu and L. Pan, J. Mater. Chem. A, 2016, 4, 11077–11085 RSC.
- D. Yan, C. Yu, X. Zhang, J. Li, J. Li, T. Lu and L. Pan, Electrochim. Acta, 2017, 254, 130–139 CrossRef CAS.
- Z. Tong, Y. Yang, J. Wang, J. Zhao, B. Su and Y. Li, J. Mater. Chem. A, 2014, 2, 4642–4651 RSC.
- S. Zhou, S. Wang, S. Zhou, H. Xu, J. Zhao, J. Wang and Y. Li, Nanoscale, 2020, 12, 8934–8941 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00359c |
| This journal is © The Royal Society of Chemistry 2021 |