The role of size and nature in nanoparticle binding to a model lung membrane: an atomistic study

Abstract

Understanding the uptake of nanoparticles (NPs) by different types of cellular membranes plays a pivotal role in the design of NPs for medical applications and in avoiding adverse effects that result in nanotoxicity. Yet, the role of key design parameters, such as the bare NP material, NP size and surface reactivity, and the nature of NP coatings, in membrane remodelling and uptake mechanisms is still very poorly understood, particularly towards the lower range of NP dimensions that are beyond the experimental imaging resolution. The same can be said about the role of a particular membrane composition. Here, we systematically employ biased and unbiased molecular dynamics simulations to calculate the binding energy for three bare materials (Ag/SiO₂/TiO₂) and three NP sizes (1/3/5 nm diameter) with a representative lung surfactant membrane, and to study their binding kinetics. The calculated binding energies show that irrespective of size, Ag nanoparticles bind very strongly to the bilayer, while the NPs made of SiO₂ or TiO₂ experience very low to no binding. The unbiased simulations provide insight into how the NPs and membrane affect each other in terms of the solvent-accessible surface area (SASA) of the NPs and the defect types and fluidity of the membrane. Using these systematic fine-grained results in coarsening procedures will pave the way for simulations considering NP sizes that are well beyond the membrane thickness, i.e. closer to experimental dimensions, for which different binding characteristics and more significant membrane remodelling are expected.

---

1. Introduction

The class of materials in which one of the physical dimensions is in the nanometer range, the so-called nanomaterials, has acquired an important position in industrial fabrication processes as well as in many aspects of our daily life. While some of these materials are designed towards performing one or more specific tasks at the nanoscale, for instance masking for nano-lithography, carriers for drug delivery, biosensors and environmental sensors, the majority takes the form of nanoparticles that enter our environment due to natural events (forest fires, dust storms and aerosols from outer space) and as undesired waste products stemming from human activities (combustion, wear, mining, or industrial exhaust). NPs are also actively mixed into consumer bulk products to enhance the properties of the matrix materials to which they are added (for instance, carbon black in tires, and titanium dioxide NPs in food products, toothpaste, and cosmetics^1,2). An interesting aspect of NPs is that their electromagnetic,³ optical,^4,5 mechanical, and various other material responses often significantly transcend those of their bulk form. This property, which is due to the significant increase in the surface area per volume ratio that leads surface atoms to dominate the NP properties,^6–8 can be exploited for design objectives. While NPs from more exotic materials have been produced for special purposes, most engineered NPs are made from metals or metal-oxides due to their relatively low cost of production and unique (electronic) properties. Among the most common ones are gold (Au), silver (Ag), silicon dioxide (SiO₂), and titanium dioxide (TiO₂), three of which will be considered in this study.

From the perspective of safety, also the yet unknown risks associated with (released) NPs entering a complex biological environment have to be considered before NPs are introduced in any type of application.⁹ Understanding NP interactions at the cellular level is one of the most essential steps in such a safe-by-design strategy. While such hazards have historically primarily been evaluated in the lab, material engineers generally tend to employ classical or extended DLVO theory^10,11 to assess the propensity to aggregate or bind to surfaces via the (effective) force acting between two rigid bodies, which can be two different NPs or a NP and a membrane. This force, which is a balance between (attractive) van der Waals forces and (repulsive) electrical double layer forces,¹² is obtained by integrating out more resolved contributions into two long-ranged terms for their centers of mass. While DLVO has been shown to be able to capture interactions between two bodies at longer separations, based on only a few phenomenological parameters such as the Hamaker constant and the Debye length, it is known to break down for smaller separations that are important in binding (and, hence, in the probability of uptake) and for small NPs that carry a size-dependent permittivity. Moreover, the interplay between NPs and lipid membranes will also depend on the chemical and physical structures that each of them carries or is able to responsively induce onto each other, a property that is not covered by DLVO theory. Recent studies, for instance, clarify that cationic and negatively charged nanoparticles interact quite differently with the same lipid bilayer.¹³ A more generic and detailed approach is therefore required to understand the interaction between nanoparticles and the cell membrane (Fig. 1).

Fig. 1 (a) Snapshot of the considered model lung membrane comprising DPPC, DOPC, POPC and cholesterol in a ratio of 5 : 2 : 2 : 1. For all the lipid molecules, the carbon, oxygen, phosphorus and nitrogen are shown as green, red, orange and blue spheres, respectively. Hydrogen atoms are omitted from the snapshot for clarity. (b) Snapshots of the SiO₂ NPs for the three considered diameters 1, 3, and 5 nm. For all the nanoparticles, the silicon, oxygen, and hydrogen are shown as yellow, red, and white spheres, respectively.

It is experimentally known that the ability of NPs to reach intracellular compartments depends critically on their size and surface properties. NPs with dimensions significantly smaller than the membrane thickness can cross the cell membrane through direct permeation,¹⁴ and large NPs can enter via a passive or activated endocytic pathway.¹⁵ Historically, the propensity of small NPs to permeate can be analysed via a (one dimensional) solubility-diffusivity model, while an elastic model can be applied for (passive) endocytosis, although both continuum descriptions do not account for the lipid sorting that can be induced by selective NP interactions. For the intermediate regime where the NP diameter is comparable to or slightly larger than the membrane thickness, however, there is no complete theoretical underpinning. Since these dimensions are generally also beyond the experimental resolution, the conditions for NP uptake often remain an open issue.¹⁶ It is known that as the particle size decreases, the probability of penetrating through the lipid membrane increases.

Penetration can have severe health effects,^17,18 with necrosis and damage to mitochondrial cell lines caused by small cationic Au nanoparticles being a prime example.¹⁹ Studies have shown that the toxic effects can emerge either from membrane damage or from the interaction of nanoparticles with the internal cell machinery once they are inside the cell. Therefore, an evaluation of possible risks should include an assessment of nanoparticles’ ability to adhere/bind prior to penetrating, modifying, or even destroying the cell membrane.

All atom molecular dynamics (AAMD or classical MD) provides effective but costly tools for gaining a better understanding of the interaction between NPs and a model lipid bilayer at an atomic resolution and for describing morphological membrane changes induced by NPs. In turn, these tools can rationalise causal relations and macroscopic observations provided by experiments and quantitative structure–activity relationship (QSAR) studies. The computational restrictions of molecular modelling at an atomistic resolution, however, have previously limited the focus of such approaches for simulating solvated NPs in small volumes. Unconstrained simulation of lipid bilayer–NP systems at much larger scales is usually considered at coarser resolutions, i.e. representations for which chemistry is described in terms of a significantly reduced number of degrees of freedom to attain the length and time scales needed to accurately describe the considered phenomena.^20–23 Yet, this gain in computational capabilities by mapping to coarser descriptions comes at the cost of a loss in fine-grained detail that is involved in, and may be important for, the interaction between the NPs, lipid bilayer, and water.

Here, we concentrate on computationally evaluating the hazards of bare NP uptake by the respiratory system, i.e. the lung membrane, at an atomistic resolution to capture all entropic and energetic factors that may play a role in a heterogeneous membrane. In practice, NPs are produced with a range of coatings for stabilization against coagulation and to enable tuning of their surface properties, and small molecule/protein coronas will quickly form around bare NPs upon entering any type of complex biological environment. Yet, including an ill-defined corona lends itself better to a coarser representation than a controlled atomistic setup. Carrying a much less diversified composition than the typical cellular membranes, i.e. a mixture of a few lipid types and a small amount of proteins, the lung membrane is both relevant and much better suited for atomistic simulation. Zwitterionic phosphatidylcholine (PC) lipids comprise about 90% of the lung membrane,^24,25 with cholesterol (≈5–10%) and small amounts of phosphatidylethanolamine (PE), fatty acids, lysolipids, and protein making up the rest. In our simulations, we omitted proteins, as their role is more likely in recognition rather than directly in membrane remodelling, which is believed to be more lipidic in nature. Moreover, we are not interested in the translocation pathway itself, since it would computationally be too costly to simulate such a process in a realistic manner at an atomistic resolution.

Thus far, very few atomistic MD simulations have been carried out to study NP–NP^26–28 and NP–membrane interactions.^13,29–34 Most of the simulation efforts have focused on employing coarse-grained (CG) and continuum (elastic) theories for obtaining a generic understanding of the factors that control the four stages – particle adhesion to the membrane, stalled partially wrapped states, budding followed by scission, and membrane rupture – in passive NP uptake via endocytosis. The group of Deserno was the first to draw a wrapping phase diagram using continuum (Helfrich) theory, by determining the equilibrium shape of an elastic fluid membrane, with a given bending rigidity κ and lateral tension σ, when a spherical NP adheres with some given strength.^35,36 In their approach, the cost of forced membrane bending, 8κA/d², where A is the wrapped area and d is the NP diameter, is balanced by the energetic gain of NP wrapping, −wA, where w is the adhesion energy per unit area. For the standard tensionless membrane that is also considered in this study, this theory predicted that NPs are either unbound or fully wrapped. Later coarse-grained (CG)MD simulations, which were based on a generic coarse lipid representation and implicit solvent, did identify stable partially wrapped states but interpreted them as metastable,³⁷ and Spangler et al.³⁸ analysed the results of a very similar CGMD treatment to extend the elastic theory of Deserno et al.^35,36 to much smaller NPs. In particular, they added a new term to the classical expression for the excess free energy considered by Deserno. This new contribution, due to the effective adhesion energy of the non-contact region, is indeed found to stabilize partially wrapped states, as observed in the CG simulations, and the adhesion energy strength required for wrapping is seen to increase with decreasing NP diameter d, as expected. Related generic coarse MD or continuum treatments have been used to study the binding of elastic nanoshells,^39,40 the adhesion of anisotropic NPs^41,42 and of functionalized NPs.^43,44 Also the role of bending and adhesion in the distribution of multiple NPs inside the membrane has been investigated, both in terms of a generic CG representation⁴⁵ and for specific systems using a chemically resolved CG representation like Martini.⁴⁶ Interestingly, the latter study, which focusses on the aggregation of ligated gold NPs inside one- and two-component membranes, points at an active role of lipids via lipid partitioning, which is out of the scope of the existing continuum and generic CG treatments.

The recent finding of Spangler et al. that partial wrapping dominates the membrane binding of small NPs with diameters d in the range of 1 nm < d < 5 nm, see Fig. 5 in ref. 38, makes one wonder why fully atomistic approaches have not been considered more systematically to validate these trends, particularly since classical MD is capable of capturing detailed packing effects and important interactions like hydrogen bonding that are (partially) integrated out at the coarser level. Yet, to date, AAMD studies of NP and membrane interactions are rather scarce and particular, because they usually concentrate on rationalising experiments that are equally scarce owing to the challenging stabilization of dispersions of small NPs. In addition, many of these atomistic studies focus on ‘model’ membranes with very restricted lipid diversity.

Our size-dependent investigations of binding with realistic lung tissue will therefore provide first insight into the detailed interactions of several types of common NPs with a bio-relevant and heterogeneous membrane, including the effect that NP proximity has on lipid partitioning and membrane stability. We particularly focus on calculating the binding energy for the considered NPs and the lung membrane, and on investigating how NP size and chemical nature control the membrane properties. While we are aware that the considered NP dimensions have only a limited experimental relevance, we note that this study is only a first step in obtaining a more systematic insight into NP binding for common NP materials, and a prerequisite for future systematic coarsening procedures towards a realistic coarse-grained representation of all considered setups. This next step will provide the much desired direct link that is needed to systematically evaluate the wrapping behavior for common NPs towards the experimentally accessible range. Moreover, it will enable a more complete extraction of size-dependent descriptors for QSAR studies.

2. Computational procedure

Initial configurations were generated using the CHARMM-GUI builder⁴⁷ for NPs consisting of three different materials, namely silver (Ag), silicon dioxide (SiO₂), and titanium dioxide (TiO₂), and three different diameters (1, 3 and 5 nm). The composition of the lipid bilayer was selected in line with the experimental information on the lipid content of the lung membrane,^24,25 that is, a mixture of dipalmitoylphosphatidylcholine (DPPC), 1,2-dioleoyl-sn-glycerol-3-phosphocholine (DOPC), 1-palmitoyl-2-oleoyl-sn-glycerol-3-phosphocholine (POPC), and cholesterol (CHOL) in a ratio of 5 : 2 : 2 : 1 (see Fig. 1). The CHARMM36 forcefield^48,49 was used for all the lipid species, while water was simulated using the TIP3P forcefield.⁵⁰ The SiO₂ and Ag parameters were obtained from the INTERFACE forcefield,^51,52 which is integrated within the CHARMM forcefield. For TiO₂, which is missing in the standard CHARMM force-field, we considered the parameters of Luan et al.⁵³ A 1.4 nm cutoff was used for both the Lennard–Jones and electrostatic interactions, while particle-mesh Ewald summation⁵⁴ was used to evaluate the long-range electrostatic interactions. Periodic boundary conditions were employed throughout this study as well as a 2 fs time step, and bonds involving hydrogen were constrained via the LINCS algorithm.⁵⁵ All MD simulations were performed at 310.15 K with the GROMACS 2016 (ref. 56) package.

In the constrained MD simulations, the potential of mean force (PMF) upon insertion of an individual nanoparticle into a lipid bilayer was computed using an umbrella sampling technique.⁵⁷ Free energy profiles were extracted using the weighted histogram analysis method (WHAM)^58,59 by considering the center of mass distance between the nanoparticle and the lipid membrane as a reaction coordinate. A force constant K = 500 kJ mol⁻¹ nm⁻² was applied to pull the nanoparticle towards the lipid membrane, resulting in 25–30 different configurational windows placed every ≈0.10 nm along the pathway. We report the results for NP diameters of 1, 3, and 5 nm, for which we used a lipid bilayer of 15.6 nm × 15.6 nm to avoid boundary artefacts. First, a short equilibration run was performed, followed by a 20 ns production run using the Nose–Hoover thermostat.⁶⁰ On all individual windows, we used semi-isotropic pressure coupling (1 bar) with a Parinello–Rahman barostat.⁶¹ The statistical uncertainties associated with umbrella sampling simulations were analyzed by a bootstrap analysis that is available within GROMACS.⁵⁶

Unbiased MD simulations were performed for all setups, with the NPs initially placed 2.5 nm above the lipid bilayer irrespective of their size and type. The reference system, i.e. a pristine membrane, was simulated in an 8.6 nm × 8.6 nm × 9 nm volume. The increasing diameter of the NPs is reflected in the simulation volumes and membrane area that we may consider while avoiding boundary artifacts: 5.5 nm × 5.5 nm × 11 nm (1 nm), 8.8 nm × 8.8 nm × 13 nm (3 nm), and 12.5 nm × 12.5 nm × 15.5 nm (5 nm). Minimization of the initial structure was performed by a standard steepest descent method. Following this step, a 20 ns NPT equilibration was conducted using the same thermostat and pressure coupling as for the constrained MD. Finally, a 400 ns production run in an NPT ensemble was performed, where the last 100 ns were used throughout for analysis. Defect constants associated with the membrane were calculated with the package PackMem⁶² to determine the role of NP binding in the exposure of the hydrophobic interior of the membrane. The membrane mean curvature that is induced by the NP was determined by the program “g lomepro”.⁶³ Bilayer thickness was calculated based on the position of the phosphate atom in the upper and the lower leaflet of the lipid bilayer. Area per lipid (APL) and the lipid acyl chain order parameter were calculated using VMD MEMPlugin.⁶⁴ Finally, the partial density for the whole system, the solvent accessible surface area (SASA) of the NPs, and the average number of contacts were calculated using the built-in GROMACS routines. The mean square displacement (MSD) as a function of time was computed using VMD diffusion coefficient tool plugin.⁶⁵ For visualisation, Visual Molecular Dynamics (VMD)⁶⁶ was used throughout.

3. Results

3.1 Potentials of mean force

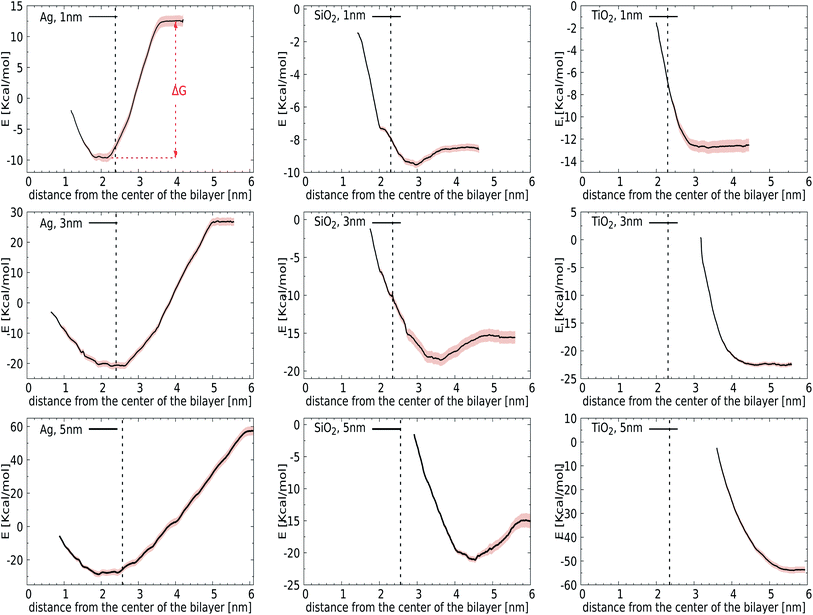
We first introduce bias potentials to enhance the sampling in regions of the (free) energy landscape where the sampling probability of unconstrained MD is expected to be very low. An example is the transfer of a polar NP from the water phase into the hydrophobic domain of the lipid bilayer, which is expected to be a rare event due to the presence of a significant energetic barrier. Thus the obtained potentials of mean force (PMF) provide direct access to the binding energies for the most relevant cases: NPs of TiO₂, Ag, and SiO₂ with a diameter of 1, 3 or 5 nm. Since the calculation of PMFs for such large and sluggish systems comes with inherent limitations, we carefully analyzed the convergence of PMF profiles as a function of the simulation time used in each window. The binding energy, ΔG, was determined as the difference between the minimum and the plateau value of the potential of mean force, see Fig. 2 (top-left). We observed considerable variation in this rate of convergence. For instance, the PMF for a 3 nm TiO₂ NP displays no significant alteration after 15 ns, while the final ΔG for a 5 nm Ag NP differs by 0.72 kcal mol⁻¹ from the value obtained after 15 ns. The final PMF profiles, displaying a signal-to-noise ratio that is sufficient to draw conclusions, are shown in Fig. 2.

Fig. 2 PMFs calculated for NP insertion in the lipid bilayer composed of DPPC, POPC, DOPC, and CHOL: (left) Ag, (center) SiO₂, and (right) TiO₂. Shaded regions correspond to standard deviations calculated using the bootstrapping technique of GROMACS. A dashed line is added as a reference for the position of the bilayer/water interface, obtained from the intersection point of the mass density profile of the lipid bilayer and the water.

Initially, we computed the PMFs for Ag NPs with sizes 1, 3, and 5 nm, see Fig. 2. For the 1 nm Ag NP, we observed a minimum at 2.05 nm, i.e. in the interior of the membrane, with a binding energy of ΔG = −22 kcal mol⁻¹. The PMF for 3 nm Ag NPs also contains one minimum at about 2.75 nm, respectively, at which the center-of-mass separation of a NP is inserted into the membrane and deforms it, see the graph in Fig. 2, showing similar behaviour to a 1 nm NP. While it is clear that hydrophobic Ag NPs prefer the hydrophobic core of the lipid bilayer over an aqueous environment, we can now associate a binding energy of ΔG = −47 kcal mol⁻¹ with this spontaneous process based on these calculations. A more pronounced binding is observed for even larger Ag NPs of 5 nm, for which the binding energy increases to ΔG = −85 kcal mol⁻¹. The fact that the binding energies do not scale with the ratio of the NP surface areas, A_{5 nm}/A_{3 cm} = 2.7, signals that the lipid reorganisation in the membrane, as reflected in the conformational entropy of all lipids, differs when going from a 3 nm to a 5 nm NP. The onset of a barrier that is observed at very small separations is due to the necessity for the membrane to bend and wrap around a bare NP when it is inserted in the interstitial space. Another factor that may play a role in this barrier is the repulsion from the head groups of the lower leaflet. The quantitative information obtained from these PMFs suggests that the adsorption of Ag NPs in the lipid membrane is a spontaneous process with a substantial binding energy.

For the other two materials, the situation is different. In the case of SiO₂, the PMFs for all the NPs show energy minima at the interface of the lipid membrane and water. The NPs gain ΔG = −1 (1 nm), −3 (3 nm), and −6 (5 nm) kcal mol⁻¹ upon transfer from the water phase to the bilayer–water interface, as shown in Fig. 2, by positioning positively charged hydrogen atoms at the NP surface close to negatively charged phosphate atoms in the membrane. On the other hand, TiO₂ NPs show no affinity towards the lipid bilayer whatsoever, irrespective of size, which can be attributed to their hydrophilic nature. It would be interesting to consider how hydrogenation would change this affinity.

Considering our Computational procedure, we want to highlight that reversing the process, i.e., biasing the sampling towards embedded NPs leaving the membrane, may require a different reaction coordinate and can show hysteresis. Hysteresis is a more general challenge in free energy calculations, as previously discussed for the extraction or insertion of single lipids from or into the membrane.⁶⁷ For NPs, insertion into the membrane from the aqueous phase results in membrane compression upon NP attachment prior to (partial) fusion, while exiting of NPs is known to occur with a pulling out into the aqueous phase of a lipid portion that remains attached to the NP surface. In particular, for NPs with higher adhesion strengths, a lipid domain will wrap around the NPs and shield them from the surrounding water after endocytosis.³⁸ Whether this translates into an asymmetric driving force for bare NPs is a question that we leave for future study. The same goes for the question how ligands and/or coronas of absorbed bio-molecules like proteins affect the driving forces for binding and membrane remodelling. Here, we just note that asymmetry or directionality has been previously discussed in the context of efficient trafficking of virus particles from and into cells.⁶⁸ In particular, PMFs for the lower leaflet are not required for the analysis of bare NP binding to the outside of the lung membrane, which is the focus of the current study.

3.2 Unconstrained MD simulations

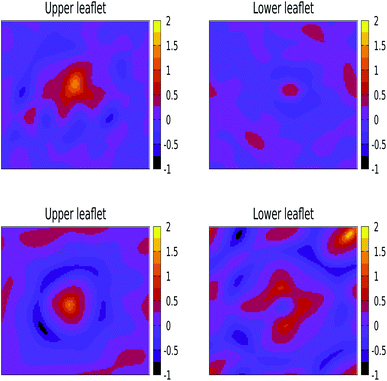
We have also performed 400 ns of unbiased MD simulation for all NPs. In all cases, a NP was initially positioned away from the membrane, in the aqueous phase, and approaches the lipid membrane within the initial 50 ns of simulation. We carefully analysed the binding kinetics as well as how the membrane is affected by the presence of the NP. An intriguing finding is that the properties of the lipids and the membrane as a whole can be affected by the NP even in the case that it does not bind.

3.2.1 General findings. Concentrating on the smallest 1 nm diameter considered, the SiO₂ and TiO₂ NPs can be seen to bind and unbind along the 400 ns trajectory, signalling a lack of preference towards the lipid bilayer. On the other hand, the Ag NP stays attached to the membrane upon binding after 10 ns of simulation, in agreement with the PMF calculations that predict a binding preference, and can be seen to regularly sink into the upper membrane leaflet. Concentrating on how this uptake affects the density profile, see the profile for the phosphate of the lipid head group in the ESI (Fig. S1 and S2†), we find that it does not significantly perturb the overall bilayer structure. Clearly, for NPs that are small (e.g. 1 nm) compared to the thickness of the unperturbed bilayer (±4 nm), uptake indeed takes place according to the proposed permeation-like mechanism, and can be analysed accordingly.

For larger 3 and 5 nm NPs, i.e. comparable in size to the membrane thickness, uptake is expected to take place via wrapping, and the balance between an energy gain upon NP adhesion and an energy loss due to enforced membrane bending becomes important.³⁸ For SiO₂ and TiO₂ NPs of these sizes we observe no significant wrapping. In particular, a 3 nm SiO₂ NP is found to transiently bind to the membrane, see Fig. S4,† but no well-defined curvature is induced. Yet, even in the case that the NP remains in the solvent phase during the entire simulations, the NP can be seen to affect the membrane properties (details are provided later on). We note that when the energy gain due to adhesion is low, the NP is unlikely to penetrate into the lipid bilayer in an unconstrained simulation as a result of a loss of rotational and translational entropy for both the lipids in the bilayer and NP, while the entropic gain for the water is relatively small. The lack of penetration of the SiO₂ and TiO₂ NPs into the bilayer signals that the adhesion energy for these NPs is indeed insufficient to enforce curvature, consistent with the PMF results (see Fig. S4 and S5†). On the other hand, adding 3 or 5 nm Ag NPs to an otherwise tensionless and flat membrane gives rise to binding and a significant alteration of the bilayer morphology, see Fig. 3. Our findings of stable partially wrapped states for both 3 and 5 nm Ag NPs over the course of 100 ns trajectories agree well with the predictions of Spangler et al.³⁸ based on continuum theory. A wrapping of the membrane around the NPs of equivalent dimensions clearly induces significant bending of the membrane, with the induced curvature being localised around the NP. In particular, a 3 nm Ag NP is seen to induce curvature only in the top leaflet, while the membrane deformation induced by a 5 nm NP is also observed in the lower leaflet.

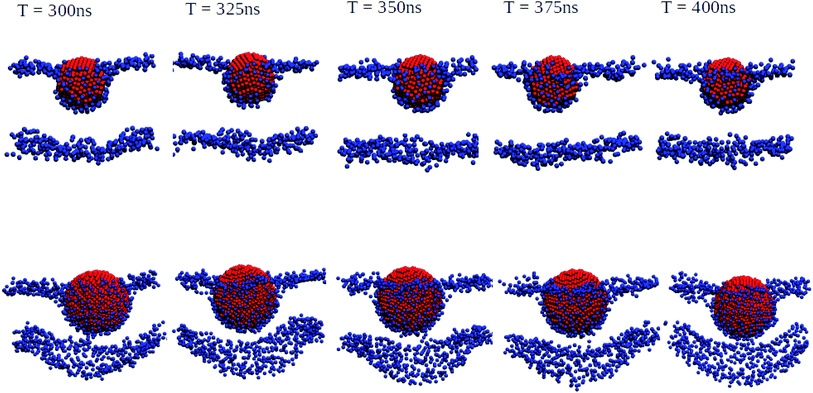Fig. 3 Orthogonal projections of simulation snapshots at selected time steps T for systems containing a 3 nm Ag (top) and a 5 nm Ag (bottom) NP illustrating the partial wrapping. As the nature of the lipids is not important at this stage, phosphorus and nitrogen atoms in DPPC, DOPC, and POPC are shown as blue spheres, and all other atom types are omitted for clarity. The Ag atoms in the NPs are shown as red spheres. As indicated, snapshots were generated at 25 ns intervals from the last 100 ns of a 400 ns production run. The wrapping angles θ extracted from the last 25 ns of the trajectories are 97.1° ± 1.35° for 3 nm and 117.4° ± 0.65° for 5 nm, see the ESI (Fig. S3†) for details.

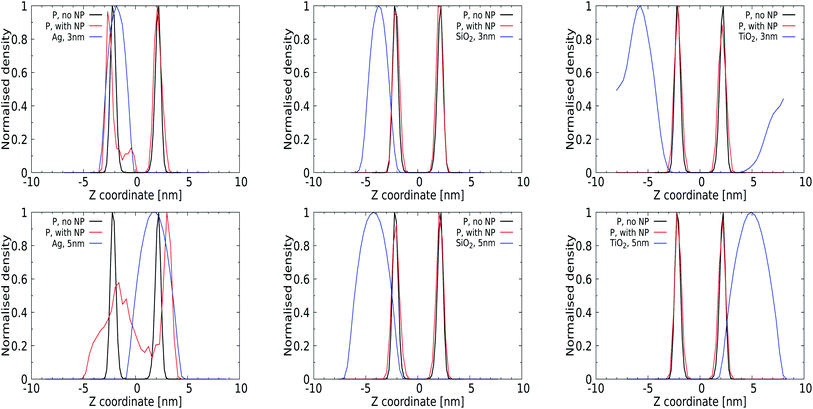
Quantitative analysis via the averaged density profiles perpendicular to the membrane interface for phosphate and NP atoms shown in Fig. 4 and the ESI (for a 1 nm NP, Fig. S1†) corroborates this finding. The density profiles for 3 and 5 nm Ag NPs show significant distortion in the phosphate domain, with lipids wrapping around the NPs and getting pushed away, see Fig. 4 (left panels). In all cases, 1 and 3 nm NPs can be seen to distort only the lipid layer which is in direct contact, leaving the opposing leaflet unperturbed. The SiO₂ NPs show affinity towards the membrane without distorting it, as expected from their PMFs, see Fig. 4 (middle panel), and no (3 nm) or only superficial binding without distortion (5 nm) is observed for both TiO₂ NPs. We note that the 3 nm TiO₂ NP can be seen to diffuse over the periodic boundaries to the other side of the lipid membrane, which is consistent with a lack of binding for this NP.

Fig. 4 Normalized density profiles for the phosphorus group of the DPPC, DOPC and POPC lipids in the bilayer (black line without a NP; red line with a NP) and for the NP itself (blue solid line): (left) Ag, (center) SiO₂, and (right) TiO₂. The origin is selected to correspond to the center of the lipid bilayer. Profiles were calculated from simulation data for the last 100 ns of a 400 ns production run, and obtained as an average over all lipids in both leaflets.

We also analysed the average number of contacts between the NPs and phosphorus atoms present in the lipid head groups, see Table 1, which we determined using a cutoff of 0.6 nm. We report absolute contact numbers, noting that the NP surface area scale as 1 : 9 : 25 for the considered diameters. For 1 nm NPs, the average number of contacts of 5 ± 1 for Ag is only slightly higher than the 2 ± 1 for SiO₂ and the 3 ± 1 for TiO₂. Yet, for 3 nm and 5 nm Ag NPs, these contacts increase drastically to 40 ± 1 and 97 ± 2, respectively, while showing only a slight increase for TiO₂ and SiO₂ NPs. These results again demonstrate the increased affinity of larger Ag NPs towards the lipid membrane compared to that of TiO₂ and SiO₂ as shown in Table 1.

Table 1 Bilayer thickness of a pure bilayer and in the presence of three types of NPs: Ag, SiO₂, and TiO₂ with three different diameters d (1 nm, 3 nm and 5 nm); average number of contacts between the NPs and phosphorus atoms; and average solvent accessible surface area (SASA) of each individual NP. Analysis of individual cases was performed using the last 100 ns of a 400 ns production run. The standard errors for all the average values are also shown

NP	d (nm)	D p–p (nm)	No. of contacts	SASA (nm^2)
No NP	—	4.27 ± 0.04	—	—
	1	4.26 ± 0.10	5 ± 1	4.65 ± 0.12
Ag	3	4.44 ± 0.06	40 ± 1	41.95 ± 0.93
	5	4.90 ± 0.05	97 ± 2	108.22 ± 0.80
	1	4.24 ± 0.07	2 ± 1	7.75 ± 0.24
SiO2	3	4.26 ± 0.05	9 ± 3	49.04 ± 0.71
	5	4.30 ± 0.03	24 ± 4	121.91 ± 1.56
	1	4.30 ± 0.07	3 ± 1	8.36 ± 0.19
TiO2	3	4.34 ± 0.04	7 ± 1	61.27 ± 0.68
	5	4.26 ± 0.04	14 ± 2	160.70 ± 1.26

---

Next, we focus on the average area per lipid A (see the ESI, Table S1†) and the bilayer thickness D_p–p for systems with and without a NP, see Table 1. Although a comparison of the lipid packing characteristics to experimental data is known to be challenging even for a single-component lipid membrane,⁶⁹ it makes sense to shortly discuss the values extracted for a pristine model lung membrane. Half of our membrane is composed of DPPC lipids, so one may relate our membrane properties to those of a pure DPPC membrane at 310 K, a temperature that is just below the experimentally measured gel-to-liquid transition temperature of 314 K. All-atom MD with an earlier version of our force field identified good correspondence between the measured and calculated areas per lipid of 0.68 nm² and 0.72 nm² for pure POPC and DOPC membranes at 310 K, respectively, and a lipid area of 0.64 nm² for a DPPC membrane at an elevated temperature of 325 K, i.e. in the liquid phase.⁷⁰ These values illustrate that decreasing the degree of saturation increases the area that each lipid occupies on average. An earlier computational study showed that adding up to 10% cholesterol to a DPPC, DOPC or POPC membrane gives rise to a condensation effect, and the average lipid area reduces compared to that of a pure membrane to values that are comparable to the ones determined in the current study.⁷¹ Another experimental study identified a lipid area for a pure POPC membrane, which behaves like a fluid above 271 K, as 0.64 nm² at 303 K and 0.67 nm² at 323 K,⁷² illustrating the historical challenge of selecting relevant experimentally measured membrane properties for force field adaptation and validation. Cholesterol alone is not capable of forming a lamellar phase, and its role in a mixed lipid membrane is versatile.⁷³ For our pristine membrane, which is a mixture of DPPC, DOPC and POPC and cholesterol in a 5 : 2 : 2 : 1 ratio, the reference area per lipid is determined from our MD simulations as 0.54 nm², see Table SI,† highly reduced compared to that of the pure counterparts. As this reduction may be the result of several factors, including condensation by the cholesterol, diffusion rates will provide more insight into the fluidity of the membrane.

Our main purpose here is to investigate whether the earlier determined binding and insertion characteristics correlate with a variation of the average lipid packing. It should be noted that the membrane area scales with the NP size as detailed in the Computational procedure section, meaning that the total number of lipids used in the averaging procedure varies. For the Ag NPs, an increasing NP diameter gives rise to a decreasing lipid area of all lipid types present in the membrane as well as an increasing membrane thickness, which is the average thickness calculated over the last 100 ns of the simulation time. While these are the hallmarks of gel-like behavior, the membrane deformation due to NP binding makes this determination very sensitive to the method used for analysis. In particular, the standard deviations of the lipid areas can be seen to increase substantially. Clearly, the membrane thickness does monotonically increase upon insertion of a 3 or 5 nm Ag NP, reflecting the increase of combined volume after the insertion of the NP and suggesting that lipids respond to the presence of the NP by stretching. For SiO₂ NPs, which are known to have a weak affinity for the membrane, and non-interacting TiO₂ NPs, the membrane thickness is indeed found very comparable to that of the pristine membrane. The small variations of the lipid areas for the different lipid types that are identified compared to the reference system suggest that the lipid packing is sensitive to the presence of a NP even in the unbound state.

3.2.2 Solvent accessible surface area of the NPs. The average solvent accessible surface area (SASA) was determined via a standard Gromacs routine, see Table 1. As expected, the SASA increases from 41.947 ± 0.931 nm² for a 3 nm Ag NP to 61.266 ± 0.682 nm² for a 3 nm TiO₂ NP. For 5 nm NPs, the reduced relative increase of the SASA from 108.220 ± 0.80 nm² for Ag to 121.906 ± 1.56 nm² for a SiO₂ NP suggests that the lipid coating of smaller 3 nm Ag NPs upon insertion is enhanced compared to the larger ones. As the surface area scales quadratically with the NP diameter d, the increased SASA going from 3 to 5 nm agrees with the increasing surface area. Yet, the wrapping angle θ determined from the last 20 ns of the simulations is larger for the 5 nm than for the 3 nm Ag NP, see the caption of Fig. 3, signalling that water is pulled into the NP–membrane interface region. Indeed, a water shell can be identified surrounding the inserted NP, see snapshots in the ESI (Fig. S6†). Since the SASA is often used to determine the transfer free energy required to move a NP from aqueous solvent to a lipid environment, our data show that the order of NP hydrophilicity is TiO₂ > SiO₂ > Ag.

3.2.3 NP-induced membrane curvature. Instantaneous and spatially resolved information complementary to the information in Fig. 3 is provided via two-dimensional color maps that represent the lateral position of the phosphate group for all systems as shown in Fig. 5 for Ag NPs. For other NPs, refer to the ESI (Fig. S7 and S8†). We used the last 20 ns of the 400 ns production run to extract the color maps, assuming that the NP position will not significantly vary in this window. To focus on the strongly curved portion of the membrane, we applied a bandpass filter between 0.5 nm⁻¹ and 2.0 nm⁻¹ over the trajectory. These color maps clearly illustrate the pronounced membrane deformation induced by Ag NPs. It also reveals that the deformation of the membrane upon binding is always structured. In particular, although all considered NPs are spherical, the membrane deformation upon insertion has a non-isotropic character as a result of the responsive lipid structure within the membrane. We note that such a feature is not included in the existing elastic models, which assume radially symmetric deformations around the NPs.³⁶ As expected, the color maps for TiO₂ and SiO₂ NPs do not show any height variation for both diameters considered.

Fig. 5 The mean curvature induced by 3 nm (top) and 5 nm (bottom) Ag NPs in a lipid bilayer composed of DPPC : DOPC : POPC : CHOL in a 5 : 2 : 2 : 1 proportion by applying a band pass filter with q_low = 0.5 nm⁻¹ and q_high = 2.0 nm⁻¹.

3.2.4 Exposure of the hydrophobic membrane core. The accessibility of the hydrophobic interior of the membrane is a property of interest, as packing defects at the interface between water and lipids can play a role in membrane stability and in the recruitment of NPs from the solvent phase. Next, we analyse the interfacial voids where lipids are more loosely packed via the PackMem tool with standard settings.⁶² PackMem identifies two types of defects, deep and shallow, depending on the depth of the cavity where the aliphatic atoms are accessible to the solvent (refer to the PackMem literature for more details). In Fig. 6 we report defect constants π (in units of nm²) that are obtained from fitting the probability of finding a lipid-packing defect of area A, P(A), to an exponentially decaying function as p(A) = b exp(−A/π), where b is a fit constant, in full agreement with standard practice. We note that π is a statistically relevant parameter and that its magnitude signals the abundance and size of lipid-packing defects. Moreover, we have combined the upper and lower leaflet in this analysis.

Fig. 6 Defect size constants as obtained with PackMem for the system without a NP and with Ag, SiO₂ and TiO₂ NPs of 1 nm (left), 3 nm (center) and 5 nm (right). Defects were determined during the last 100 ns, with block averaging to calculate standard deviations. The constant exponents are obtained by fitting; the higher, the more abundant are large lipid-packing defects.

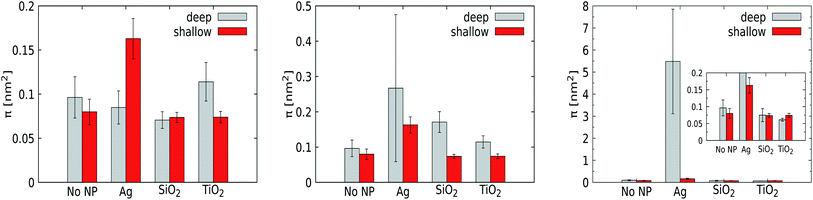
For a pristine lipid bilayer, i.e. in the absence of a NP, we find π = 0.1 ± 0.02 nm² for deep and π = 0.08 ± 0.01 nm² for shallow defects. Clearly, void formation is an inherent membrane property, and the heterogeneous composition apparently gives rise to slightly more deep defects than shallow ones. Turning to 1 nm NPs, the defect constant does not deviate much from that of a pristine membrane. Clearly, such small particles can come close or enter the membrane without significantly altering the lipid conformations. Somewhat surprisingly, the NP with the lowest adhesion strength, TiO₂, is found to express the highest defect constants, but the deviations from the reference case (a pristine membrane) are just slightly larger than the error margins. For the 3 nm Ag NP, we observe a significant increase in the deep defect constant (0.27 ± 0.26 nm²) compared to the 1 nm counterpart, although the error margins are huge. Also the defect constant for shallow defects does increase but not equivalently, showing that the curvature induced by NP penetration into the membrane generates mainly deeper defects as expected. For the other 3 nm NPs, the effect of the NP on the generation of membrane defects is weak (SiO₂) or absent (TiO₂). A substantial increase of the defect constant for deeper defects is also obtained for the 5 nm Ag NP, with a huge deep defect constant of 5.48 ± 2.37 nm², while the presence of the other NPs displays no genuine effect on the membrane properties. While the error margins for the Ag NP are again huge, the point to consider is that the defect constant appears to grow nonlinearly with an increasing NP radius for the most hydrophobic Ag NP. This suggests that the membrane stability is highly sensitive to the NP radius in this compact size range. At least part of this effect is due to the distortion of the lower leaflet of the membrane.

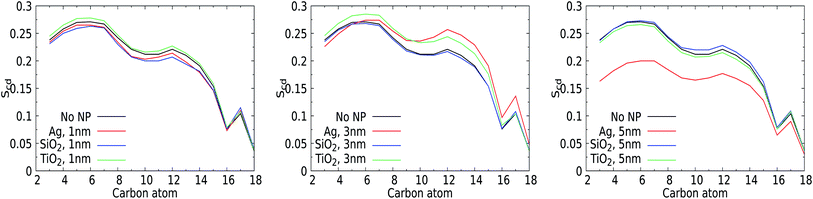
3.3 Orientational lipid order parameter

The perturbation induced by the considered NPs in the lipid orientation within the mixed membrane was further investigated via the lipid acyl orientation order parameter S_cd, reflecting the averaged bond orientation with respect to the trans-membrane direction. Since we consider a mixed membrane, we have averaged over the SN-1 and SN-2 acyl chains of DPPC, DOPC, and POPC lipid components in both leaflets, see Fig. 7. The order parameter for a characteristic bilayer composed of fully saturated lipids like DPPC is known to display a plateau-like region for the upper and middle section of the carbon chain, followed by a parabolic drop towards the end of the chain reflecting the reduced acyl density near the interleaflet space.⁷⁴ Moreover, the presence of unsaturated carbons along the acyl chains such as in POPC is known to give rise to a depression of the orientational order around their average position.⁷⁵ The signature of the order parameter for our pristine membrane, which is an average over the acyl tails and over saturated and unsaturated lipids, will thus be a weighted average of these two distinct signatures. Moreover, the presence of cholesterol can modulate the flexibility of lipids surrounding them.

Fig. 7 Order parameter (S_cd) for the acyl chains of lipid with and without NPs. (Left) – S_cd for 1 nm NPs of Ag, SiO₂, and TiO₂; (center) – S_cd for 3 nm NPs of Ag, SiO₂, and TiO₂, and (right) – S_cd for 5 nm NPs of Ag, SiO₂, and TiO₂. The results were measured for the last 100 ns of a 400 ns production run and were averaged over all the lipids in the both the leaflets.

For the smallest 1 nm NPs, for which uptake takes place via permeation, the S_cd values are not very sensitive to the presence of NPs. The orientational order closer to the water–membrane interface slightly decreases compared to that of the pristine membrane for the Ag and SiO₂ NPs. This effect is weak but still notable, very likely because the membrane area and thus also the total number of lipids are fairly limited in these simulations. Slightly higher order parameters are identified for TiO₂ NPs, which are not likely to enter the membrane due to the lack of affinity. One could attribute the decrease for Ag and SiO₂ to the NP-induced lipid bending and the increase for TiO₂ to transient binding effects. For 3 nm NPs, the average lipid orientation is found indifferent to the binding of a SiO₂ NP, while the orientational order increases for the TiO₂ NP, which has no affinity for the membrane, very similar to the case for a 1 nm TiO₂ NP. Clearly, while binding is only transient for TiO₂ NPs of 1 and 3 nm, the presence of a NP outside the membrane has a weak effect of lipid straightening on average. The 3 nm Ag NP, on the other hand, binds and deforms the membrane. As a result, the order is reduced closer to the solvent interface but increased further away, in line with the suggestion mentioned in the section discussing area per lipid. For the 5 nm NPs, the orientational order for the pristine membrane can be seen to overlap with those for the NPs that do not bind to the membrane, i.e. the SiO₂ and TiO₂ NPs, suggesting that the presence of the NP has no effect on average lipid orientations. The order parameter for the 5 nm Ag NP is significantly reduced. While this can be interpreted as an overall reduction of the orientational order of the lipids, we note that the introduction of a NP deep inside the membrane gives rise to membrane distortion and a spherical domain of NP-bound lipids. In combination, these two effects will contribute to an overall reduction of the orientational order parameter. Moreover, as NP binding will affect a significant part of membrane patches considered in our simulations, this effect is likely to dominate any increase of the orientational ordering of unbound lipids. In particular, the observed increase of the overall membrane thickness discussed in an earlier section suggests that lipids on average straighten to accommodate the NPs. Rather than analysing the orientational order of bound and unbound lipids separately, we will focus on the role of NP binding in lipid diffusion.

3.4 Lipid diffusion

Phospholipid bilayer membranes can adopt two distinctly different phases, a fluid and a solid or gel phase, which can coexist in mixed membranes and translate into a particular structure of the membrane as well as into a different mobility of lipids within the membrane. The transition between these two phases is to a great extent determined by the strength of the attractive van der Waals interactions between adjacent lipid molecules, particularly between the hydrocarbon tails,⁷⁶ and is specific to molecular lipid details⁷⁷ as well as the composition of the membrane. The transition temperatures for the considered DOPC, POPC, and DPPC lipids have been experimentally determined as 256 K, 271 K and 314 K, respectively, and stem from differences in the length and degree of saturation of their tails. Consequently, the highest (DPPC) content of our mixed membrane corresponds to a gel, while the POPC and DOPC contents should express liquid behavior. The phase behavior has been shown to be sensitive to the presence of cholesterol, which has a higher mobility and flip-flop rate than the other lipids and is known to change the lipid packing.

Internalization of small gold and silver NPs within a DPPC membrane has experimentally been shown to promote the fluidity of the membrane.^78,79 For quantum dots, NP uptake was found to give rise to the conglomerating transition from the ordered gel to the disordered gel phase and a widening of the melting region.⁸⁰ Here, we investigate the role of added NPs in membrane fluidity, i.e. without changing the thermodynamics conditions, by comparing lipid diffusion rates to the values obtained for a pristine membrane. Lateral diffusion coefficients D were calculated from the slope of the mean square displacement vs. time for DPPC lipid, along with cholesterol, as shown in Table 2. Since all simulations are performed at 310 K, i.e. below the fluid transition temperature of DPPC, which is the majority lipid fraction, the membrane is likely to feature the sluggish dynamics of a gel phase in the absence of a NP, even though particularly the 10% cholesterol may mediate this behavior. Diffusion constants of 8.3 × 10⁻⁸ cm² s⁻¹ and 7.8 × 10⁻⁸ cm² s⁻¹ were previously measured for DOPC and for POPC at 298 K, and 1.8 × 10⁻⁷ cm² s⁻¹ for DPPC at 318 K, all in the liquid phase.⁸¹ Adding 10% cholesterol to DMPC, which has a C₁₄ acyl tail versus the C₁₆ for DPPC, has a condensing effect and reduces the overall diffusion constant by a factor of two. For our pristine membrane, we extracted the mean-square displacement (MSD) for the least and most mobile membrane components, DPPC and cholesterol, respectively. Using the Einstein relation to convert them into diffusion constant, we find D_DPPC = 1.03 × 10⁻⁷ cm² s⁻¹ and D_CHOL = 2.18 × 10⁻⁷ cm² s⁻¹ as shown in Table 2. We conclude that these values are reasonable for a mixed membrane at 310 K. In particular, previous studies have concluded that different lipids diffuse in loosely defined clusters, i.e. in a concerted fashion, with a lifetime in the order of a microsecond.⁸²

Table 2 Diffusion constants for a pristine membrane and in the presence of Ag, SiO₂, and TiO₂ NPs of three different diameters d (1 nm, 3 nm and 5 nm). Analysis of individual cases was performed using the last 100 ns of a 400 ns production run. The standard errors for all the average values are also shown

NP	d (nm)	D DPPC (× 10^−7 cm^2 s^−1)	D CHOL (× 10^−7 cm^2 s^−1)
No NP	—	1.03 ± 0.00	2.18 ± 0.02
	1	1.57 ± 0.03	2.07 ± 0.14
Ag	3	0.81 ± 0.01	1.05 ± 0.02
	5	1.31 ± 0.02	1.37 ± 0.02
	1	2.38 ± 0.04	2.39 ± 0.07
SiO2	3	2.23 ± 0.03	2.18 ± 0.01
	5	1.44 ± 0.01	1.40 ± 0.03
	1	2.02 ± 0.02	2.18 ± 0.04
TiO2	3	1.47 ± 0.01	1.63 ± 0.01
	5	1.88 ± 0.04	2.38 ± 0.06

---

When we add the smallest 1 nm NPs to the membrane, lipid diffusion rates are found to increase for both DPPC and cholesterol, see Table 2. The small size of the NPs allows them to permeate transiently via insertion, diffusion, exiting, and rolling over the lipid membrane, a process that causes local changes in the lipid arrangement which increase the fluidity of the membrane on average. Yet, the magnitude of this increase depends on the NPs’ chemical nature. For SiO₂ and TiO₂, the lipid mobility increases more than for the Ag NPs, in line with the observation that the TiO₂ and SiO₂ only loosely bind with the lipid bilayer. The more frequent binding and unbinding from the water phase distort the membrane to a higher degree, while Ag is bound to the bilayer and can only roll over the surface.

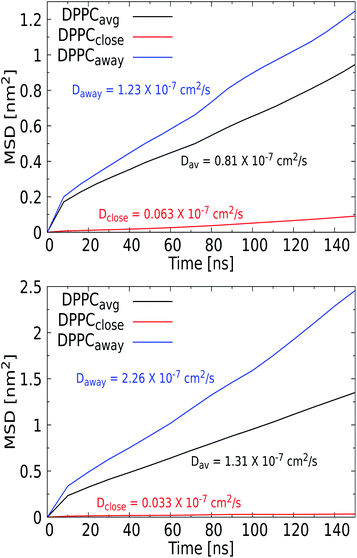
For the larger Ag NPs, which are wrapped upon binding, we observed a distinct feature. Close visual inspection revealed that the overall reduced DPPC mobility for the 3 nm Ag NP of 0.81 × 10⁻⁷ cm² s⁻¹, compared to the 1.57 × 10⁻⁷ cm² s⁻¹ for the 1 nm Ag counterpart, originates from the binding of lipids to a permanent coating of the NP, while unbound lipids are able to diffuse freely. An interesting observation is that cholesterol is pushed away from the NP upon insertion and thus always diffuses freely, see the radial distribution function and snapshots in the ESI (see Fig. S9 and S10†). Curvature induced by the NP in the lipid bilayer may also affect the distribution of cholesterol, which is known to play a key role in relaxing bilayer stresses via trans-bilayer motion (flip-flop). The time scale associated with spontaneous flip-flop events for a mobile molecule such as cholesterol has been found in the millisecond to minute range,⁸³ meaning that it is unlikely to observe a flip-flop during the tiny 200 ns AAMD trajectory considered. While we indeed observe no flip-flops for the 3 nm Ag NP, we do identify a single event for the 5 nm Ag NP, where a cholesterol switches from the upper to the lower leaflet in the vicinity of the NP. While this may be seen as a sign of NP-induced cholesterol repartitioning, it is clear that statistically more significant sampling is required to draw a firm conclusion. Consequently, the lipids in the coating are slaved to the NP motion, which results in a significantly reduced mobility for these bound lipids. This behavior was only observed for the Ag NP and identifies the formation of raft-like coating domains within the lipid membrane. To further investigate this feature, we calculated the MSD vs. time for the set of DPPC lipids that bind to the NP and further away from the NP, see Fig. 8, which indeed illustrates a distinct separation in diffusion rates. We note that similar raft-like coating domains have already been observed in the presence of gold NPs in a lipid bilayer by Montis et al.⁸⁴ Further increasing the Ag NP radius to 5 nm reveals a more distinct separation, with the diffusion rate of unbound lipids further increasing and that of lipids in the coating further decreasing compared to that for 3 nm Ag NPs. Since the coated lipids are slaved to the NP diffusion, which is known to slow down with increasing size, the latter is to be expected. We note that the more extensive distortion of the upper and lower leaflet of the lipid bilayer by the 5 nm NP is an additional factor in this process. The significant increase in the diffusion rate for lipids away from the NP is in line with the experimental findings.

Fig. 8 Mean-squared displacement versus time for DPPC in the presence of a 3 nm (top) and a 5 nm (bottom) Ag NP. Here, DPPC_avg (black) refers to average displacement of DPPC lipids, DPPC_close (red) refers to lipids that become entrapped/bound by the Ag NPs and DPPC away (blue) refers to DPPC molecules that remain far/unbound from Ag NPs during the whole simulation. The corresponding diffusion constants calculated from the MSD are added in matching colors. The MSD was calculated for the last 150 ns of a 400 ns production run.

For the SiO₂ NPs, the diffusion rates can be seen to decrease with the diameter of the NPs, although the diffusion coefficient for DPPC is always larger than in a pristine membrane. Moreover, for all SiO₂ NP diameters, the diffusion rates for DPPC and cholesterol are about equal. Although SiO₂ NPs do not feature a significant binding energy, i.e. ΔG = −3 and −6 kcal mol⁻¹ for 3 nm and 5 nm NPs, they will bind to the membrane. This shallow binding will induce a similar raft-like feature for the lipids that are in close proximity to the NP and are likely to bind. Although this effect will be much weaker than for Ag NPs, it apparently promotes diffusion in a concerted fashion in the entire membrane.⁸² The role of size in slowing down the diffusion for SiO₂ NPs can be explained by the fraction of the lipids that is affected by this process. A compelling finding is the increase of mobility of DPPC for a 3 nm and a 5 nm TiO₂ NP compared to that of the pristine membrane, since these NPs do not possess any binding affinity for the membrane, although the density profiles in Fig. 4 show that a NP does transiently bind to the membrane. Since fluid flows are known to couple to soft elastic surfaces such as membranes,⁸⁵ one may speculate that the tiny flow field induced by a NP in the solvent phase is an additional factor that can weakly perturb the diffusion characteristics of the membrane constituents, as shown for the TiO₂ NPs. Overall, we conclude that the presence of a NP indeed increases the diffusion rates of unbound lipids within the membrane.

4. Conclusions

In this work, we have studied the interaction between a model lung membrane and NPs of three different materials (Ag, SiO₂, and TiO₂) and three different sizes (1 nm, 3 nm, and 5 nm) by means of all-atom MD. Our aim is to derive new atomistic and thermodynamic descriptors for statistical models that aim at an in silico prediction of nano-toxicity prior to materials design, i.e. a safe-by-design strategy. Moreover, we provide new insight into NP binding and responsive membrane perturbation upon binding that are well beyond the experimental resolution. Last but not the least, we have generated atomistic data required for systematic coarse-graining in the next modelling step. The latter is particularly needed to address the role of NP size and shape in the nano-descriptors and in the specific mechanism for binding and subsequent membrane perturbation, which are known to vary with size in the lower end of the spectrum. The current study goes well beyond the literature in terms of the range of materials and NP sizes that are considered atomistically and in terms of the membrane response, which is generally modeled by an elastic continuum model without lipid details or by phenomenological CG descriptions that do not address lipid specificity. The considered model lung membrane mimics the DPPC, POPC, DOPC, and cholesterol contents of the actual lung membrane, in the ratio of 5 : 2 : 2 : 1.

Our free energy calculations provide quantitative binding energies for all considered NPs, i.e. as a function of material and size. Since binding precedes uptake, these new descriptors can be useful for understanding bare NP uptake by inhalation. We find that 3 and 5 nm Ag NPs gain substantial energy by binding and moving spontaneously and irreversibly inside the hydrophobic acyl core of the membrane, while SiO₂ NPs are likely to reside at the bilayer–water interface. The TiO₂ NPs have no affinity for the lipid bilayer. Structural and dynamic descriptors for the NP-induced membrane perturbations are provided by unconstrained AAMD simulations, which show that the lipid structure of the membrane, the membrane defects and the lipid mobility are affected by the NP even if the binding energy vanishes.

Three major findings of this study are shortly reviewed here. Although the adhesion energy density for Ag NPs has not been determined in this study, the wrapping angle extracted for the Ag NP simulations in principle enables a direct comparison with wrapping angle predictions for small NPs from elastic theory.³⁸ It is, however, unlikely that these two values will exactly match, in part owing to the second finding that the membrane curvature induced by the NP binding is not fully radially symmetric, as supposed by elastic theory, as a consequence of the underlying lipid structure. The third and last finding is that the lipids that bind to the NPs start to diffuse collectively, just like a lipid raft, and are therefore slaved to the NP diffusion, which is slow and decreases with NP diameter. The diffusion rate for the unbound DPPC lipids on the other hand is found to increase in the presence of the NP, in full agreement with experimental findings, even if the NP remains entirely in the solvent phase.

The data generated for this article will have a future purpose of providing a stepping stone for systematic mapping to a coarser MD description, which will enable simulation of a broader range of experimentally accessible NPs. Besides validation, systematic coarse-graining will enable us to calculate accurate descriptors for a much broader range of NP sizes. As a possible additional step, moving towards particle-field approaches^86–88 is a viable option to achieve even longer length and timescales.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the European Union's Horizon 2020 Research and Innovation Program under grant agreement 814426 (NanoInformaTIX). This work was carried out on the Dutch national e-infrastructure with the support of SURF Cooperative.

Notes and references

1. M. Skocaj, M. Filipic, J. Petkovic and S. Novak, Radiol. Oncol., 2011, 45, 227.
2. P.-J. Lu, S.-C. Huang, Y.-P. Chen, L.-C. Chiueh and D. Y.-C. Shih, J. Food Drug Anal., 2015, 23, 587–594.
3. S. Hu, E. L. Ribeiro, S. A. Davari, M. Tian, D. Mukherjee and B. Khomami, RSC Adv., 2017, 7, 33166–33176.
4. S. Hu, K. Cheng, E. L. Ribeiro, K. Park, B. Khomami and D. Mukherjee, Catal. Sci. Technol., 2017, 7, 2074–2086.
5. S. A. Davari, J. L. Gottfried, C. Liu, E. L. Ribeiro, G. Duscher and D. Mukherjee, Appl. Surf. Sci., 2019, 473, 156–163.
6. T. B. Rawal, A. Ozcan, S.-H. Liu, S. V. Pingali, O. Akbilgic, L. Tetard, H. ONeill, S. Santra and L. Petridis, ACS Appl. Nano Mater., 2019, 2, 4257–4266.
7. R. Service, Nanotoxicology: Nanotechnology Grows up, 2004.
8. D. T. Alexander, D. Forrer, E. Rossi, E. Lidorikis, S. Agnoli, G. D. Bernasconi, J. Butet, O. J. Martin and V. Amendola, Nano Lett., 2019, 19, 5754–5761.
9. Y. Yamagishi, A. Watari, Y. Hayata, X. Li, M. Kondoh, Y. Tsutsumi and K. Yagi, Pharmazie, 2013, 68, 178–182.
10. E. M. Hoek and G. K. Agarwal, J. Colloid Interface Sci., 2006, 298, 50–58.
11. M. Boström, D. Williams and B. Ninham, Phys. Rev. Lett., 2001, 87, 168103.
12. J. N. Israelachvili, Intermolecular and Surface Forces, Academic press, 2015.
13. E. Heikkila, H. Martinez-Seara, A. A. Gurtovenko, M. Javanainen, H. Hakkinen, I. Vattulainen and J. Akola, J. Phys. Chem. C, 2014, 118, 11131–11141.
14. N. Sadrieh, A. M. Wokovich, N. V. Gopee, J. Zheng, D. Haines, D. Parmiter, P. H. Siitonen, C. R. Cozart, A. K. Patri and S. E. McNeil, et al. , Toxicol. Sci., 2010, 115, 156–166.
15. E. Lavagna, J. Barnoud, G. Rossi and L. Monticelli, Nanoscale, 2020, 12, 9452–9461.
16. D. Smith, J. Phys. D: Appl. Phys., 2018, 51, 294004.
17. W. H. De Jong and P. J. Borm, Int. J. Nanomed., 2008, 3, 133.
18. T. Lunnoo, J. Assawakhajornsak and T. Puangmali, J. Phys. Chem. C, 2019, 123, 3801–3810.
19. Y. Pan, A. Leifert, D. Ruau, S. Neuss, J. Bornemann, G. Schmid, W. Brandau, U. Simon and W. Jahnen-Dechent, Small, 2009, 5, 2067–2076.
20. D. Bedrov, G. D. Smith, H. Davande and L. Li, J. Phys. Chem. B, 2008, 112, 2078–2084.
21. K. Yang and Y.-Q. Ma, Nat. Nanotechnol., 2010, 5, 579–583.
22. R. C. Van Lehn and A. Alexander-Katz, J. Phys. Chem. B, 2014, 118, 12586–12598.
23. E. Heikkila, A. A. Gurtovenko, H. Martinez-Seara, H. Hakkinen, I. Vattulainen and J. Akola, J. Phys. Chem. C, 2012, 116, 9805–9815.
24. R. Veldhuizen, K. Nag, S. Orgeig and F. Possmayer, Biochim. Biophys. Acta, Mol. Basis Dis., 1998, 1408, 90–108.
25. S. Baoukina and D. P. Tieleman, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 2431–2440.
26. G. Munaò, A. Correa, A. Pizzirusso and G. Milano, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 1–9.
27. L. Zhang, Q. Li, S. Tian and G. Hong, J. Nanomater., 2019, 2019 DOI:10.1155/2019/7612805.
28. S. Izvekov, A. Violi and G. A. Voth, J. Phys. Chem. B, 2005, 109, 17019–17024.
29. M. P. Aranha, D. Mukherjee, L. Petridis and B. Khomami, Langmuir, 2020, 36, 1043–1052.
30. M. Das, U. Dahal, O. Mesele, D. Liang and Q. Cui, J. Phys. Chem. B, 2019, 123, 10547–10561.
31. L. Wang, P. Quan, S. H. Chen, W. Bu, Y.-F. Li, X. Wu, J. Wu, L. Zhang, Y. Zhao and X. Jiang, et al. , ACS Nano, 2019, 13, 8680–8693.
32. L. Monticelli, J. Chem. Theory Comput., 2012, 8, 1370–1378.
33. G. Rossi, J. Barnoud and L. Monticelli, J. Phys. Chem. Lett., 2014, 5, 241–246.
34. I. U. Foreman-Ortiz, D. Liang, E. D. Laudadio, J. D. Calderin, M. Wu, P. Keshri, X. Zhang, M. P. Schwartz, R. J. Hamers and V. M. Rotello, et al. , Proc. Natl. Acad. Sci., 2020, 117, 27854–27861.
35. M. Deserno and W. M. Gelbart, J. Phys. Chem. B, 2002, 106, 5543–5552.
36. M. Deserno and T. Bickel, EPL, 2003, 62, 767.
37. T. Ruiz-Herrero, E. Velasco and M. F. Hagan, J. Phys. Chem. B, 2012, 116, 9595–9603.
38. E. J. Spangler, S. Upreti and M. Laradji, J. Chem. Phys., 2016, 144, 044901.
39. X. Yi, X. Shi and H. Gao, Phys. Rev. Lett., 2011, 107, 098101.
40. X. Yi and H. Gao, Soft Matter, 2015, 11, 1107–1115.
41. S. Dasgupta, T. Auth and G. Gompper, Soft Matter, 2013, 9, 5473.
42. S. Dasgupta, T. Auth and G. Gompper, Nano Lett., 2014, 14, 687–693.
43. R. Vacha, F. Martinez-Veracoechea and D. Frenkel, Nano Lett., 2011, 11, 5391–5395.
44. C. Huang, Y. Zhang, H. Yuan, H. Gao and S. Zhang, Nano Lett., 2013, 13, 4546–4550.
45. A. Saric and A. Cacciuto, Phys. Rev. Lett., 2012, 108, 118101.
46. P. Angelikopoulos, L. Sarkisov, Z. Cournia and P. Gkeka, Nanoscale, 2017, 9, 1040–1048.
47. S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865.
48. R. Pastor and A. MacKerell, Jr, J. Phys. Chem. Lett., 2011, 2, 1526–1532.
49. J. B. Klauda, R. M. Venable, J. A. Freites, J. W. OConnor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell, Jr and R. W. Pastor, J. Phys. Chem. B, 2010, 114, 7830–7843.
50. P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960.
51. H. Heinz, T.-J. Lin, R. Kishore Mishra and F. S. Emami, Langmuir, 2013, 29, 1754–1765.
52. T.-J. Lin and H. Heinz, J. Phys. Chem. C, 2016, 120, 4975–4992.
53. B. Luan, T. Huynh and R. Zhou, J. Chem. Phys., 2015, 142, 234102.
54. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
55. B. Hess, H. Bekker, H. J. Berendsen and J. G. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
56. D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718.
57. G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199.
58. B. Roux, Comput. Phys. Commun., 1995, 91, 275–282.
59. J. S. Hub, B. L. De Groot and D. Van Der Spoel, J. Chem. Theory Comput., 2010, 6, 3713–3720.
60. D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069–4074.
61. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
62. R. Gautier, A. Bacle, M. L. Tiberti, P. F. Fuchs, S. Vanni and B. Antonny, Biophys. J., 2018, 115, 436–444.
63. V. Gapsys, B. L. de Groot and R. Briones, J. Comput.-Aided Mol. Des., 2013, 27, 845–858.
64. R. Guixà-González, I. Rodriguez-Espigares, J. M. Ramírez-Anguita, P. Carrió-Gaspar, H. Martinez-Seara, T. Giorgino and J. Selent, Bioinformatics, 2014, 30, 1478–1480.
65. T. Giorgino, J. Open Source Software Process., 2019, 4, 1698.
66. W. Humphrey, A. Dalke and K. Schulten, et al. , J. Mol. Graphics, 1996, 14, 33–38.
67. N. Pokhrel and L. Maibaum, J. Chem. Theory Comput., 2018, 14, 1762–1771.
68. M. Deserno and T. Bickel, Europhys. Lett., 2003, 62, 767–773.
69. D. Poger and A. E. Mark, J. Chem. Theory Comput., 2010, 6, 325–336.
70. Z.-J. Wang and M. Deserno, New J. Phys., 2010, 12, 095004.
71. S. A. Pandit, S.-W. Chiu, E. Jakobsson, A. Grama and H. L. Scott, Langmuir, 2008, 24, 6858–6865.
72. N. Kučerka, M.-P. Nieh and J. Katsaras, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 2761–2771.
73. F. de Meyer and B. Smit, Proc. Natl. Acad. Sci., 2009, 106, 3654–3658.
74. R. Y. Patel and P. V. Balaji, J. Phys. Chem. B, 2005, 109, 14667–14674.
75. T. J. Piggot, J. R. Allison, R. B. Sessions and J. W. Essex, J. Chem. Theory Comput., 2017, 13, 5683–5696.
76. M. J. Janiak, D. M. Small and G. G. Shipley, Biochemistry, 1976, 15, 4575–4580.
77. S. Mabrey and J. M. Sturtevant, Proc. Natl. Acad. Sci., 1976, 73, 3862–3866.
78. S.-H. Park, S.-G. Oh, J.-Y. Mun and S.-S. Han, Colloids Surf., B, 2006, 48, 112–118.
79. S.-H. Park, S.-G. Oh, J.-Y. Mun and S.-S. Han, Colloids Surf., B, 2005, 44, 117–122.
80. G. D. Bothun, A. E. Rabideau and M. A. Stoner, J. Phys. Chem. B, 2009, 113, 7725–7728.
81. G. Lindblom and G. Orädd, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 234–244.
82. M. Javanainen, L. Monticelli, J. B. de la Serna and I. Vattulainen, Langmuir, 2010, 26, 15436–15444.
83. R.-X. Gu, S. Baoukina and D. P. Tieleman, J. Chem. Theory Comput., 2019, 15, 2064–2070.
84. C. Montis, D. Maiolo, I. Alessandri, P. Bergese and D. Berti, Nanoscale, 2014, 6, 6452–6457.
85. B. Rallabandi, N. Oppenheimer, M. Yah Ben Zion and H. Stone, Nat. Phys., 2018, 14, 1211–1215.
86. A. De Nicola, Y. Zhao, T. Kawakatsu, D. Roccatano and G. Milano, Theor. Chem. Acc., 2012, 131, 1–16.
87. E. Sarukhanyan, A. De Nicola, D. Roccatano, T. Kawakatsu and G. Milano, Chem. Phys. Lett., 2014, 595, 156–166.
88. A. De Nicola, T. Kawakatsu, F. Müller-Plathe and G. Milano, Eur. Phys. J.: Spec. Top., 2016, 225, 1817–1841.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00578b

---