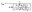Open Access Article
Open Access ArticleMechanistic insights into the anisotropic growth of ZnO nanoparticles deciphered through 2D size plots and multivariate analysis†
Zhihua
Zhao
ab,
Yinping
Wang
ab,
Céline
Delmas
c,
Christophe
Mingotaud
b,
Jean-Daniel
Marty
 *b and
Myrtil L.
Kahn
*b and
Myrtil L.
Kahn
 *a
*a
aLaboratory of Coordination Chemistry, CNRS UPR 8241, University of Toulouse, 205 Route de Narbonne, 31077 Toulouse, France. E-mail: myrtil.kahn@lcc-toulouse.fr
bLaboratoire des IMRCP, Université de Toulouse, CNRS UMR 5623, Université Paul Sabatier, 118, Route de Narbonne, 31062 Toulouse Cedex 9, France. E-mail: marty@chimie.ups-tlse.fr
cMIAT, Université de Toulouse, INRA, 31326 Castanet-Tolosan, France
First published on 14th September 2021
Abstract
The control and understanding of the nucleation and growth of nano-objects are key points for improving and/or considering the new applications of a given material at the nanoscale. Mastering the morphology is essential as the final properties are drastically affected by the size, shape, and surface structure. Yet, a number of challenges remain, including evidencing and understanding the relationship between the experimental parameters of the synthesis and the shape of the nanoparticles. Here we analyzed jointly and in detail the formation of anisotropic ZnO nanoparticles under different experimental conditions by using two different analytical tools enabling the analysis of TEM images: 2D size plots and multivariate statistical analysis. Well-defined crystalline ZnO nanorods were obtained through the hydrolysis of a dicyclohexyl zinc precursor in the presence of a primary fatty amine. Such statistical tools allow one to fully understand the effect of experimental parameters such as the hydrolysis rate, the mixing time before hydrolysis, the length of the ligand aliphatic chain, and the amount of water. All these analyses suggest a growth process by oriented attachment. Taking advantage of this mechanism, the size and aspect ratio of the ZnO nanorods can be easily tuned. These findings shed light on the relative importance of experimental parameters that govern the growth of nano-objects. This general methodological approach can be easily extended to any type of nanoparticle.
Introduction
Mechanisms underlying the synthetical pathways or properties of nanomaterials are of particular interest. Many chemical procedures have been developed to control the nanoparticles' (NPs) size, polydispersity, shape, surface, volume, chemical composition, etc.1–3 Metallic,4,5 II–VI or III–V semiconducting nanoparticles (NPs)6–11 are nowadays synthesized with a simple isotropic shape or a more elaborate core–shell structure.12 Cubes,13 stars,14 bipyramidal architectures,15 rods,16 nanowires,17etc., are also largely described. In general, the variation of the size and shape is dependent on the experimental chemical conditions and the proposed mechanisms.18–21 Yet, a number of challenges remain, including evidencing and understanding the relationship between the experimental parameters of the synthesis and the shape of the NPs, with the latter driving the NP's properties.The inherent complexity of such systems22 requires to have access to efficient analytical techniques to study them and to understand the correlation (if any) between the different involved parameters.23 Such a Holy Grail could be achieved with multivariate analysis or machine learning but one of the constraints is the lack of data, which is particularly problematic: the data set can be either dense (i.e. it covers a small fraction of the configuration space) or sparse (i.e. it covers a large fraction of the configuration space but with many of the data missing).
The aim of this article is to demonstrate how simple analytical tools based on statistical analysis can help us to decipher the anisotropic growth of NPs and to better understand and control the parameters governing this anisotropic growth. ZnO NPs were taken as a first model system and were prepared by taking advantage of the exothermic hydrolysis of a dicyclohexyl zinc precursor [ZnCy2]. In one step and under mild conditions (i.e. room temperature and atmospheric pressure), well-defined crystalline ZnO NPs can then be synthetized.24 In this process, the control of the morphology (i.e. either isotropic NPs or nanorods) is achieved by varying the experimental conditions: isotropic NPs are obtained in the presence of alkyl chain amine ligands in an organic solvent, while nanorods are obtained under the same experimental conditions but in the absence of solvent.25 Up to now, experimental results have suggested the critical role of different parameters like the composition of the reaction mixture, the amount of water, the kinetic parameters of the reaction, and the temperature.
To gain information on the parameters of importance for the growth of such nanorods and to better understand the growth processes, we studied the kinetics of the formation of anisotropic ZnO NPs under different conditions by using two different analytical tools enabling the analysis of TEM images: 2D size plots and multivariate statistical analysis. The first one, 2D size plot, enables the extraction of information on the correlation between the widths and lengths of anisotropic objects.26 For this, each particle is characterized by two sizes, denoted as D1 and D2, measured on perpendicular axes. These two sizes generally correspond to the length and width of the nano-objects. For each particle and on the same graph, we plot D1 as a function of D2 and also D2 as a function of D1. The proposed 2D plots enable the qualitative visualization of such a correlation. Nevertheless, the quantitative analysis of these data might be hampered by the presence of different sub-populations that could necessitate tedious procedures to separate them, especially when these populations overlap each other. In order to identify them numerically and to obtain their own statistical parameters like the average length and width, corresponding standard deviations, and correlation between the length and width, a complementary multivariate analysis needs to be performed.26 When a limited number of NPs can be counted, such an approach can also lead to improved accuracy in the statistical analysis by helping to discard minor sub-populations that are not representative of the samples. Here, we study the effect of the hydrolysis rate, the mixing time before hydrolysis, the length of the ligand aliphatic chain, and the amount of water on the anisotropic growth of ZnO NPs. All these experiments suggest growth by oriented attachment.
Results and discussion
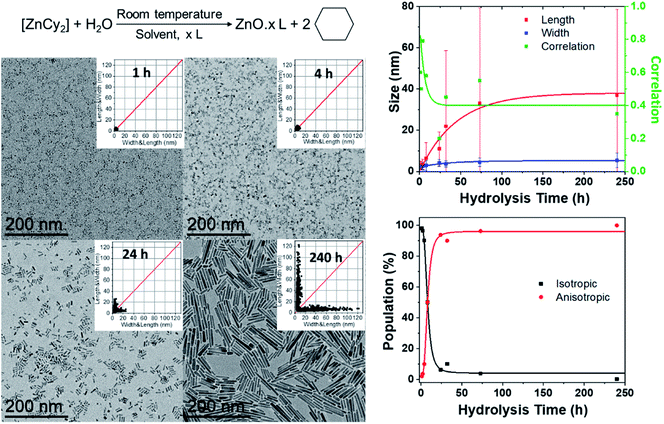
In a typical experiment, the dicyclohexyl zinc precursor [ZnCy2] is mixed at room temperature with two equivalents of alkylamine RNH2 (dodecylamine, DDA, R = C12H25) as the ligand (Fig. 1). No solvent was used. After 10 minutes, water is introduced by opening the vial. The atmospheric water vapor will induce a hydrolysis reaction leading to the formation of ZnO NPs (see details in the Experimental part below). 2D size plots were constructed from TEM pictures and the measurements were analyzed thanks to multivariate analysis (see details in ESI† Section A). This analysis gives information about the average characteristics of the sub-populations (number, orientation, average length and width, corresponding standard deviation and correlation). The number of sub-populations that composed the point clouds was chosen numerically thanks to the Bayesian Information Criterion (BIC criterion, see the ESI† for more details). In this study, its optimal value is found to be equal to one or two.2D size plots were used to analyze the effect of various experimental parameters on the growth and final morphology of ZnO. The following paragraphs will successively describe the effect of the time of hydrolysis, the mixing time of the mixture of reagents before hydrolysis, the amount of water, the speeding rate of water addition, and the length of the ligand aliphatic chain on the ZnO NP morphology. It has to be mentioned that the temperature of the reaction medium is also of crucial importance. Anisotropic NPs were only obtained when the temperature was kept below a critical value of 60 °C to maintain the local organization of the fatty amines surrounding the growing ZnO NPs.27 All the studies were therefore made at room temperature.
Effect of the time of hydrolysis
Advantageously, 2D size plots are of special interest to describe the modifications of NPs versus time during the growth or aging process. In a first series of experiments, TEM grids were prepared from the same synthesis followed over time. The width and length of these NPs extracted from the TEM pictures allow one to draw the 2D size plots as a function of time (Fig. 1 and S1 in the ESI†). The point clouds obtained at 1 and 2 h are centered on the median. This corresponds to the presence of isotropic NPs. The growth of ZnO NPs clearly starts with a nucleation step, in which pristine isotropic NPs are formed. The results of the multivariate analysis considering one cluster are depicted in Fig. 1 (see also Table S1 in the ESI†).Up to 4 h, the average size of the quasi-isotropic NPs slightly increases from 3.2 ± 1.6 to 3.5 ± 2.5 nm. During the first hours, these pristine NPs mature and their mean size increases. At 8 h, the 2D size plot shows that the point cloud starts to extend, suggesting that the anisotropic growth of the nanoparticles has begun. The correlation parameter (between the length and width) ρ up to ca. 0.80 is observed (Fig. 1 and Table S1†). In the subsequent hours, the point cloud extends more and more up to 35 nm, while remaining quasi-parallel to the 2D size plot axis at ca. 5–6 nm: the rods become longer but their widths are somewhat maintained. ρ decreases and a lower correlation between the length and the width is observed for these anisotropic NPs.
These results suggest that growth occurs mainly along the long axis of the NPs. A growth mechanism by oriented attachment could be suggested here.26,28 This hypothesis has been tested by considering two populations of NPs. Indeed, after four hours the point clouds are best fitted with two sub-populations: the first, N1, corresponds to the pristine isotropic ZnO NPs and the second, N2, corresponds to the growing nanorods. The results of the multivariate analysis considering these two clusters are listed in Table S2 (see the ESI†). Fig. 1 shows the percent of isotropic and anisotropic NPs over the time of hydrolysis. Clearly, isotropic NPs decrease very quickly in favor of anisotropic ones. This indicates that after the nucleation step, the number of isotropic NPs decreases rapidly. Less than 10% of isotropic NPs are indeed observed after 24 h. This result evidences that no nucleation occurs during the period of anisotropic growth. The nucleation and growth steps are uncorrelated and occurred sequentially in agreement with an oriented attachment process. In addition, after 24 h, the overall length of the nanorods is still increasing (Fig. 1), which strengthened the growth by oriented attachment. The isotropic NPs are consumed to the benefit of the length of the rods that increases concomitantly.29
Furthermore, C. Ribeiro et al. suggest that the growth of nanorods through an oriented attachment mechanism can be described as a “polymerization” reaction.30 In that case and following various simplifications, the number of NPs, xmax, which have undergone a coalescence process leading to a nanorod should follow the equation:
| L = xmaxW |
Quantitative information can be extracted from the data depicted in Fig. 1. In particular, the average growth rates along the two axes can be obtained by calculating the derivative at each point of the curves (Fig. S3†). An estimation based on the fitting of the experimental results using an exponential equation gives the initial growth rates – within the accuracy of the measurement – in the range of 0.9 nm h−1 for the length and one order of magnitude less (0.09 nm h−1) for the width. The growth in the width is therefore already very slow after one hour, while it continues to decrease significantly after 150 h for the length. It is however important to keep in mind that the instantaneous growth rate should be much higher in the early stages of the reaction as NPs of 3.2 ± 1.6 × 2.1 ± 1.1 nm are already observed after 1 h. This apparent anisotropic shape corresponds in fact to the isotropic growth of the nanocrystals. Indeed, considering the intrinsic structural parameters of ZnO (c = 0.521 and a = b = 0.325 nm), after one hour, the nanocrystals are composed of 6 unit cells that have isotropically grown.
While the initial nucleation reaction is fast (after 1 minute solutions became luminescent, which demonstrates the formation of ZnO NPs), the growth mechanism seems to be stopped only after 5 days. This halt in the growth is certainly due to the partial carbonation of alkylamines to ammonium carbamates which, as we have recently shown,29 leads to a complete modification of the organic stabilizing agents on the surface of the NPs. When NPs are only stabilized by alkylamines, and the latter are localized only along the lateral faces leaving the basal faces accessible for growth by oriented attachment,31–33 whereas in the presence of ammonium carbamates, they are located both on the lateral and the basal faces with a very strong affinity preventing the growth from continuing.29
Effect of the aging time of the reagent mixture before hydrolysis
Another parameter that has to be considered is the waiting time after mixing amine and zinc precursor reagents, before starting the hydrolysis step. Indeed, the viscosity of the solution increases slowly and, after 6 hours, the mixture behaves as a glass state gel.34 This waiting time was then varied from 10 min up to 24 h and the final shape of the obtained NPs was observed systematically 3 days after starting the hydrolysis process (Fig. 2, S4 and S5 in the ESI†). The 2D size plots up to a waiting time of 4 h are very similar to each other: they show an extended point cloud almost parallel to the graph axis, corresponding to a mean width diameter of ca. 4 ± 2 nm and a mean length of ca. 10 ± 8 nm up to 20 nm (Table S3†). As expected, the observed morphology is similar to that obtained at the final stage (three days) in the part depicting the effect of the hydrolysis time. When the mixing time reaches 5 h, anisotropic growth is almost totally prevented: the average length and width of these particles over time remain roughly constant with a mean width of ca. 2.1 ± 1.2 nm and a mean length of ca. 3.4 ± 2.5 nm. As previously observed, the calculated correlation values are significantly lower for populations with high anisotropy (aging time < 6 h); this could be related to the fact that the growth of the particles should occur essentially on their extremities in an oriented attachment mechanism.Again, the resulting point clouds were analyzed considering possible population mixing. The multivariate analysis leads to an optimal adjustment of the data set by considering, as before, two populations of particles: one isotropic and the second anisotropic, comprising N1 and N2 nanoparticles respectively, which are similar to that obtained after three days in the previous synthesis (Fig. S1†). They show an extended point cloud almost parallel to the graph axis, corresponding to a mean diameter of ca. 4 nm and a length of up to 20 nm of the nanorods. The multivariate analysis of these graphs was conducted as described previously. Results considering one cluster are listed in Table S3† and the percent of N1 and N2 is shown in Fig. 2 (see also Table S4†). In this case, up to a mixing time of 4 hours, the values of N1 and N2 remain constant with a mean value of more than 95% for N2 (i.e. anisotropic NPs) and less than 5% for N1 (i.e. isotropic NPs). Then, the percentages are abruptly reversed for a waiting time of 5 h. This reflects an abrupt transition from anisotropic NPs to isotropic ones. When the mixing time reaches 5 h, anisotropic growth is totally prevented. These results should be compared with rheological measurements of the reaction medium over time, which make it possible to measure the variation of the viscosity of the medium (Fig. S6†). Between 0 and 5 h, the values of G′ and G′′ increase slowly and reach respectively 0.5 and 0.1 Pa, which indicates a liquid medium whose viscosity increases progressively. At 5 h, G′ and G′′ increase abruptly, and G′ becomes higher than G′′, and the medium becomes very viscous and reaches a semi-glassy state within a few minutes.34 Clearly, a correlation between the viscosity of the medium and NP shape exists. The multivariate analysis of the data quantitatively corroborates the abrupt transition from anisotropic to isotropic NPs with an average diameter almost constant and equal to 4 nm from 10 minutes to 5 hours which decreases to 2 nm after 5 hours and a length (for which the uncertainties are large) of ca. 10 nm which reaches 2 nm after 5 h.
As suggest by C. Ribeiro et al., the kinetics related to an oriented attachment mechanism should consider the viscosity of the medium, η.35 The diffusion coefficient of the NPs controlling the collision process leading to contact and coalescence will decrease as 1/η with the viscosity as well as the kinetic constant associated with such a process. A longer waiting time (longer than 4–5 hours) leads to a very high viscosity, which should limit the diffusion speed and growth process of the NPs. This explains why shorter NPs are observed for such a long waiting time.
Effect of the speeding rate of water addition and the amount of water
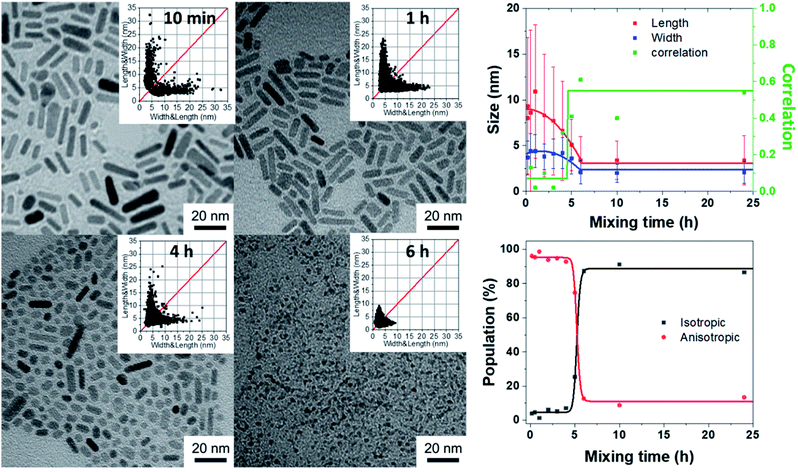
The effects of the hydrolysis time and mixing time illustrate the importance of the kinetic parameters of the reaction. The question then arises of the speed of arrival of water in the medium to lead by the hydrolysis of [ZnCy2] the formation of ZnO NPs. To study this effect, the speeding rate of water addition is varied from 10−7 down to 10−9 mol s−1 (see details in ESI† Section D) and the water amount from 2 to 100 equiv. relative to the Zn precursor. To avoid at maximum the observed gelation process, hydrolysis was initiated, in all the subsequent experiments, 10 minutes after the mixing process. Practically, the water feeding rate reaching the reactant mixture was controlled by using PTFE tubes of different lengths and diameters as depicted schematically in Scheme S1.†As shown in Fig. 3 (as well as Fig. S7 and S8 and Tables S5–S8†), anisotropic NPs with a mean length of 16.5 ± 11.6 nm could be prepared if the vial without a stopper was used. Interestingly, the length of the NPs decreased if, for a given diameter equal to 2 mm, longer tubes were used (i.e. lowering the feeding rate). For the longest 20 cm tube, quasi-isotropic 1.7 ± 1.1 nm ZnO NPs were thus obtained with, as expected for isotropic ZnO NPs, higher correlation values. Decreasing the feeding rate of water favored the gelation process to occur and prevented the formation of anisotropic NPs. As expected, the same tendency is observed when the diameter of the PTFE tube was increased from 2 mm to 4 mm. This increase in the diameter results in an increase of the water flow rate by a factor of 4 and therefore longer NPs were obtained with a larger tube for a given length. Moreover, as expected from the fact that the water flow should be inversely proportional to the tube length (see the ESI†), anisotropic NPs with a similar size were obtained when comparing tubes with respective lengths equal to 1 and 4 cm and diameters equal to 2 and 4 mm, respectively. Thus, as illustrated in Fig. 3, the size was found to be proportional to Φ2/L (where Φ and L are the diameter and length of the tubes, respectively), which is directly related to the water feeding rate (see details in ESI† Section D). In conclusion, increasing the amount of water reaching per unit of time the reaction medium (by using larger and/or longer tubes) enables the growth process to occur more rapidly than the gelation process and promotes the formation of anisotropic nanoparticles.
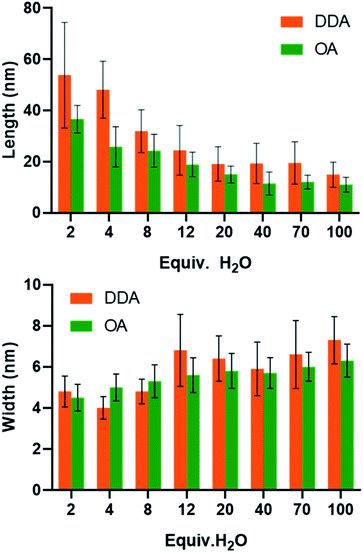
Apart from the kinetics of water feeding, the amount of water introduced into the vessel has been varied from 2 equiv. up to 100 equiv. relative to the zinc precursor as depicted in Scheme S2.† The results are reported Fig. 4 (see also Fig. S9 and Tables S9 and S10†). Increasing the amount of water leads to a decrease of the NP aspect ratio. In the case of NPs stabilized with 2 equiv. DDA and with 2 equiv. of water, the 2D size plots reveal a distribution of size where the average width and length are equal to 4.8 ± 1.5 nm and 53.8 ± 41.2 nm, respectively. As the amount of water increases, the 2D size plot exhibits a less and less extended length range, and the point cloud is more and more focused around the median line which is characteristic of a decrease of the aspect ratio. Especially for more than 8 equiv. of water, the width of the NPs increases from 5 nm up to 7 nm. Interestingly, the number of isotropic NPs increases as the amount of water increases (Table S10† and Fig. 4). This result suggests that a large amount of water favors multi-nucleation. As the quantity of zinc precursor is the same for all the experiments (0.25 mmol), multi-nucleation competes with growth and consequently, the aspect ratio decreases. Fig. 4 shows the evolution of the length, width and correlation as a function of the water amount. The correlation between the length and width remains roughly constant irrespective of the amount of added water. As previously discussed, an oriented attachment mechanism from isotropic NPs formed during the nucleation step can easily explain this observation.
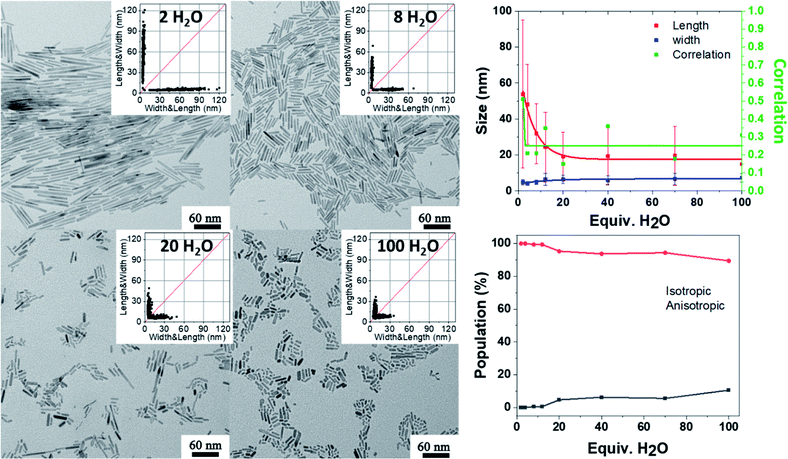 | ||
| Fig. 4 TEM images and the corresponding 2D size plots. The results obtained from multivariate analysis (with a single Gaussian). The red, blue and green lines depict the mean width, mean length and corresponding correlation respectively. The lines are just guides for the eye. See also Fig. S9.† | ||
Effect of the length of the fatty amine
The structure of the amine can also influence the morphology of the particles obtained. In order to measure this impact, an additional series of experiments were performed with octylamine, OA (C8H17–NH2) instead of DDA with varying amounts of water. The comparison of the results is shown Fig. 5 (see also Fig. S10–S12 and Tables S11 and S12†). As observed with DDA, increasing the final amount of water favors the formation of shorter and slightly larger nanorods with a lower aspect ratio. In addition, for an equivalent quantity of water, while the width of the nanorods is similar regardless of the ligand (Fig. 5), the aspect ratio is much higher when DDA is used instead of OA. The length of the NPs ranges from 5 to 65 and 15 to 100 nm for OA and DDA, respectively. Another important difference is the absence of isotropic NPs for 2 and 4 equiv. of water in the presence of DDA (see Fig. 4 and Table S10†). The effect of the alkyl chain can be related to the specific organization of the reaction medium before and during the hydrolysis process. This organization may be either due to the interaction of zinc ions with primary amine34 and/or due to the formation of well-organized liquid crystalline phases for the obtained hybrid materials.27 This organization is prone to modify the rheological behavior of the reaction medium and might be responsible for the differences observed between the different amines in the frame of the oriented attachment mechanism.Conclusions
In this work, we demonstrate how simple analytical tools based on statistical analysis can help us to decipher the anisotropic growth of NPs and to better understand and control the parameters governing this anisotropic growth. A fine comparison of the synthetic protocol of the role of the hydrolysis rate, the mixing time before hydrolysis, the length of the ligand aliphatic chain, and the amount of water allowed us to evidence the relative importance of those experimental parameters for the anisotropic growth of ZnO NPs. All the data suggest that the growth mechanism occurred through an oriented attachment process that is eventually hampered by a gelation process induced by the interaction of the zinc precursor or ZnO NPs with amine ligands. These findings shed light on the relative importance of experimental parameters that govern the growth of nano-objects and as such are crucial to identify, study, and control the design progress in nanoscience.Experimental
Materials and reagents
All starting compounds in this work are sensitive to oxygen and water and were manipulated in a MBraun glove box with an argon system. The zinc precursor [Zn(C6H11)2] (noted [ZnCy2]) was purchased from Nanomeps (http://www.nanomeps.fr). Octylamine (OA) and dodecylamine (DDA) were purchased from Sigma Aldrich. All compounds were stored at −20 °C in a glove box and used without any further purifications.Synthesis of ZnO NPs
All the above synthesis was performed under ambient temperature. The experiments were performed repeatedly to ensure the reproducibility of the experiments. The data provided correspond to the results of one of these experiments. The sample size is systematically given in the ESI† for each analysis. Regardless of the experimental conditions, ZnO samples exhibit the hexagonal zincite phase (space group P63mc) and exhibit similar UV-Visible absorption spectra.25The study of the ZnO NP size as a function of hydrolysis time (Fig. 1 and Section B in ESI†): in a glove box, 57.9 mg of [ZnCy2] was added into a 4 mL glass vial with 92.7 mg of DDA. After complete mixing (the total time in the glove box is 10 minutes), the vial was taken out of the glove box and exposed to air. TEM analysis was then performed at different reaction times from 1 h up to 240 h.
The influence of the gelation time on the ZnO NP size (Fig. 2 and Section C in the ESI†): 57.9 mg of [ZnCy2] was mixed in a 4 mL glass vial with 92.7 mg of DDA. After complete mixing, the mixture was aged in a glove box from 10 min up to 24 h. Samples were taken out of the glove box at different times and exposed to air for 3 days.
The study of the ZnO NP size as a function of the length of tubes (Fig. 3 and Section D in the ESI†): 57.9 mg of [ZnCy2] was added into a 4 mL glass vial with different lengths of PTFE tubes (from 0 to 20 cm) with 92.7 mg of DDA. After complete mixing (the total time in the glove box is 10 minutes), the vial was taken out of the glove box and exposed to air for 1 week.
The study of the ZnO NP size as a function of water content (Scheme S1,†Fig. 4 and Section D in the ESI†): 57.9 mg of [ZnCy2] was added into a 4 mL glass vial with 92.7 mg of DDA. After complete mixing (the total time in the glove box is 10 minutes), the vial was placed into a homemade reactor that allowed the slow diffusion of water into the sample. Different amounts of degassed water were injected in the reactor from 2 up to 100 equiv. After 3 days white luminescent powders were obtained and analyzed by TEM.
Transmission electron microscopy (TEM)
Samples for TEM were prepared by slow evaporation of droplets of colloidal solution deposited on a carbon-coated 200 mesh copper TEM grid from Ted Pella Company. TEM experiments were performed at the microscopy service of University Paul Sabatier (TEMSCAN) by using a JEOL JEM1011 electron microscope operating at 100 kV with a resolution point of 0.45 nm.Author contributions
Z. Z. and Y. W. prepared the samples, performed the TEM measurements and drew the 2D size plots. C. D. and J.-D. M. analyzed all data from multivariate analysis. C. M. and M. L. K. supervised the study. J.-D. M., C. M. and M. L. K. prepared the manuscript with contributions from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to thank the China Scholarship Council (CSC) and the CNRS for financial support. C. Roux is gratefully acknowledged for helpful discussions.References
- G. Schmid, Nanoparticles: from Theory to Application, Wiley-VCH, Weinheim, 2004 Search PubMed.
- X. Liang, S. Bai, X. Wang, X. Dai, F. Gao, B. Sun, Z. Ning, Z. Ya and Y. Jin, Chem. Soc. Rev., 2017, 46, 1730–1759 RSC.
- T. Song, F. Gao, S. Guo, Y. Zhang, S. Li, H. You and Y. Du, Nanoscale, 2021, 13, 3895 RSC.
- M. Zhou, C. Li and J. Fang, Chem. Rev., 2021, 121, 736–795 CrossRef CAS PubMed.
- C. Gao, F. Lyu and Y. Yin, Chem. Rev., 2021, 121, 834–881 CrossRef CAS PubMed.
- X.-M. Liu, X. Cui, K. Dastafkan, H.-F. Wang, C. Tang, C. Zhao, A. Chen, C. He, M. Han and Q. Zhang, J. Energy Chem., 2021, 53, 290–302 CrossRef.
- X.-L. Shi, J. Zou and Z.-G. Chen, Chem. Rev., 2020, 120, 7399–7515 CrossRef CAS PubMed.
- Z. Xie, Y. Duo, Z. Lin, T. Fan, C. Xing, L. Yu, R. Wang, M. Qiu, Y. Zhang, Y. Zhao, X. Yan and H. Zhang, Adv. Sci., 2020, 7, 1902236 CrossRef CAS PubMed.
- L. Cheng, X. Wang, F. Gong, T. Liu and Z. Liu, Adv. Mater., 2019, 1902333 Search PubMed.
- J. G. DiStefano, A. A. Murthy, S. Hao, R. dos Reis, C. Wolvertona and V. P. Dravid, Nanoscale, 2020, 12, 23897 RSC.
- S. R. Alvarado, Y. J. Guo, T. P. A. Ruberu, E. Tavasoli and J. Vela, Coord. Chem. Rev., 2014, 263, 182 CrossRef.
- G. D. Li and Z. Y. Tang, Nanoscale, 2014, 6, 3995–4011 RSC.
- H. J. Yang, S. Y. He, H. L. Chen and H. Y. Tuan, Chem. Mater., 2014, 26, 1785–1793 CrossRef CAS.
- M. W. Rotz, K. S. B. Culver, G. Parigi, K. W. MacRenaris, C. Luchinat, T. W. Odom and T. J. Meade, ACS Nano, 2015, 9, 3385–3396 CrossRef CAS PubMed.
- J. Jonca, A. Ryzhikov, M. L. Kahn, K. Fajerwerg, A. Chapelle, P. Menini and P. Fau, Chem.–Eur. J., 2016, 22, 10127–10135 CrossRef CAS PubMed.
- K. Thorkelsson, P. Bai and T. Xu, Nano Today, 2015, 10, 48–66 CrossRef CAS.
- G. L. Drisko, C. Gatel, P.-F. Fazzini, A. Ibarra, S. Mourdikoudis, K. Fajerwerg, P. Fau and M. L. Kahn, Nano Lett., 2018, 18, 1733–1738 CrossRef CAS PubMed.
- P. Melinon, S. Begin-Colin, J. L. Duvail, F. Gauffre, N. H. Boime, G. Ledoux, J. Plain, P. Reiss, F. Silly and B. Warot-Fonrose, Phys. Rep., 2014, 543, 163–197 CrossRef CAS.
- S. Mourdikoudis, V. Colliere, C. Amiens, P. Fau and M. L. Kahn, Langmuir, 2013, 29, 13491–13501 CrossRef CAS PubMed.
- Y. Xia, Y. Xiong, B. Lim and S. E. Skrabalak, Angew. Chem., Int. Ed., 2009, 48, 60–103 CrossRef CAS PubMed.
- Y. Xia, X. Xia and H. C. Peng, J. Am. Chem. Soc., 2015, 137, 7947–7966 CrossRef CAS PubMed.
- S. Gomez-Grana, F. Hubert, F. Testard, A. Guerrero-Martinez, I. Grillo, L. M. Liz-Marzan and O. Spalla, Langmuir, 2012, 28, 1453–1459 CrossRef CAS PubMed.
- N. D. Burrows, S. Harvey, F. A. Idesis and C. J. Murphy, Langmuir, 2017, 33, 1891–1907 CrossRef CAS PubMed.
- M. Monge, M. L. Kahn, A. Maisonnat and B. Chaudret, Angew. Chem., Int. Ed., 2003, 42, 5321–5324 CrossRef CAS PubMed.
- M. L. Kahn, A. Glaria, C. Pages, M. Monge, L. Saint Macary, A. Maisonnat and B. Chaudret, J. Mater. Chem., 2009, 19, 4044–4060 RSC.
- Z. Zhao, Z. Zheng, C. Roux, C. Delmas, J. D. Marty, M. L. Kahn and C. Mingotaud, Chem.–Eur. J., 2016, 22, 12424–12429 CrossRef CAS PubMed.
- Z. Zheng, R. Butynska, C. Valverde Serrano, J.-D. Marty, C. Mingotaud and M. L. Kahn, Chem.–Eur. J., 2016, 22, 15614–15618 CrossRef PubMed.
- X. Xue, R. L. Penn, E. R. Leite, F. Huang and Z. Lin, CrystEngComm, 2014, 16, 1419–1429 RSC.
- G. Spataro, Y. Champouret, Y. Coppel and M. L. Kahn, Chem. Phys. Chem., 2020, 21, 2454–2459 CrossRef CAS PubMed.
- C. Ribeiro, E. J. H. Lee, E. Longo and E. R. Leite, ChemPhysChem, 2006, 7, 664–670 CrossRef CAS PubMed.
- G. Spataro, Y. Champouret, P. Florian, Y. Coppel and M. L. Kahn, Phys. Chem. Chem. Phys., 2018, 20, 12413–12421 RSC.
- M. L. Kahn, T. Cardinal, B. Bousquet, M. Monge, V. Jubera and B. Chaudret, Chem. Phys. Chem., 2006, 7, 2392–2397 CrossRef CAS PubMed.
- Y. Coppel, G. Spataro, C. Pages, B. Chaudret, A. Maisonnat and M. L. Kahn, Chem.–Eur. J., 2012, 18, 5384–5393 CrossRef CAS PubMed.
- Z. Zhao, Y. Coppel, J. Fitremann, P. Fau, C. Roux, C. Lepetit, P. Lecante, J.-D. Marty, C. Mingotaud and M. L. Kahn, Chem. Mater., 2018, 30, 8959–8967 CrossRef CAS.
- C. Ribeiro, E. J. H. Lee, E. Longo and E. R. Leite, ChemPhysChem, 2005, 6, 690–696 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: 2D size plot and multivariate analysis, experimental TEM and 2D size plots. See DOI: 10.1039/d1na00591j |
| This journal is © The Royal Society of Chemistry 2021 |