Nanowire networks: how does small-world character evolve with dimensionality?†
Ryan K.
Daniels
 and
Simon A.
Brown
and
Simon A.
Brown
 *
*
The MacDiarmid Institute for Advanced Materials and Nanotechnology, School of Physical and Chemical Sciences, University of Canterbury, Christchurch, New Zealand. E-mail: simon.brown@canterbury.ac.nz
First published on 6th May 2021
Abstract
Networks of nanowires are currently under consideration for a wide range of electronic and optoelectronic applications. Nanowire devices are usually made by sequential deposition, which inevitably leads to stacking of the wires on top of one another. Here we demonstrate the effect of stacking on the topology of the resulting networks. We compare perfectly 2D networks with quasi-3D networks, and compare both nanowire networks to the corresponding Watts Strogatz networks, which are standard benchmark systems. By investigating quantities such as clustering, path length, modularity, and small world propensity we show that the connectivity of the quasi-3D networks is significantly different to that of the 2D networks, a result which may have important implications for applications of nanowire networks.
New conceptsNetworks of nanowires are routinely used for a number of emerging applications, ranging from transparent conducting devices to neuromorphic computing. In most cases devices are fabricated by sequential deposition of the nanowires, leading to stacking of the wires on top of each other. This stacking effect will clearly lead to different connectivity within the network compared to perfectly two-dimensional networks in which stacking is ignored. Remarkably, the effect of stacking on network connectivity has not been studied previously. Here we show using computer simulations that stacking leads to dramatic differences in network topology. In particular, we show that the ‘small world’ character of quasi-three-dimensional networks is much weaker than that of perfectly two-dimensional networks. These changes in network topology have the potential to influence the properties of real-world devices built from nanowires. Our results show that it should be possible to control network topology by controlling the number of deposited nanowires. |
Introduction
Networks of nanowires and nanotubes have a range of potential applications in photovoltaic, optoelectronic, and sensor devices such as flexible transparent electrodes, organic light emitting diodes, and bioelectric interfaces.1–9 More particularly, it has been proposed that the structures of self-assembled networks of nanowires (and nanoparticles10–12) mimic some of the complex biological structures of the brain, and therefore may be useful as novel systems for neuromorphic computing.13–15 Networks of nanowires exhibit a number of brain-like properties such as reconfiguration dynamics and short and long term memory.16–18 They exhibit winner-takes-all behaviour14 and have been proposed as systems for physical reservoir computing,13 able to perform tasks such as nonlinear transformations, sine wave auto-generation, and Mackey–Glass chaotic time series forecasting.19,20Randomly deposited networks of nanowires have been studied extensively within the framework of percolation theory.21–27 More recent work has addressed the topological structure of 2D nanowire networks using well-established techniques in graph and network theory. These networks have been shown to exhibit a small-world architecture similar to many biological systems,27,28i.e. the nodes are considered to be both highly clustered and have small path lengths between nodes.29 This concept is of interest because small-world architecture is thought to affect emergent behavior in complex systems,30,31 and to be important for information propagation across networks,32,33 with several groups also demonstrating that reservoir computing performance is impacted by small-world or scale-free network architectures.34,35
Previous modelling has however assumed that the nanowire networks are perfectly two-dimensional i.e. that the wires lie in a plane.23–28 This is clearly not the case for real-world nanowire networks in which the wires are stacked on top of one another during a deposition process. Given the importance of topological structure for information processing and a range of other network properties there is clearly a need for models which incorporate realistic stacking of the nanowires.
In the present work, we seek to understand the impact of stacking on the connectivity of a nanowire network. We build a physical model that explicitly considers the sequence in which the wires are deposited and the consequent stacking of the wires in a three-dimensional volume. It is important to note that because the network is built up by sequential deposition, it is quasi-three-dimensional (Q3D) and is therefore distinct from percolating systems21 in which the objects are randomly placed in a 3D space (without requiring that the wires rest on each other). We show here that perfectly 2D networks have much broader degree distributions and much larger mean degrees than the Q3D networks. We demonstrate the impact of dimensionality on the small-world nature of the networks, and conclude that experimentally realized Q3D networks of nanowires are likely to have very different network structures than model 2D structures.
Nanowire models
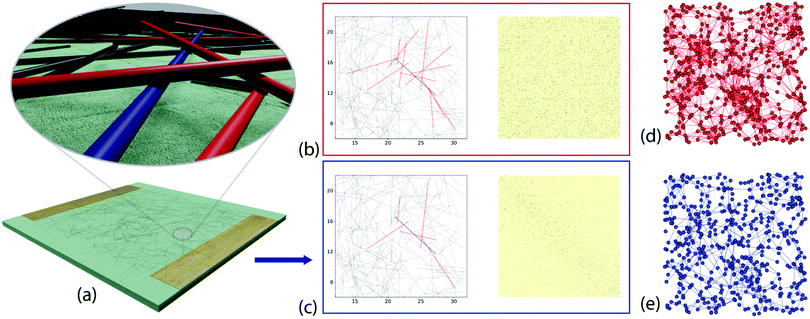
We consider networks of N wires, deposited on a Λ × Λ μm area, which is considered to be the xy-plane. For each wire in the network, the x- and y-coordinates of the mid-point of the wire were chosen at random from a uniform distribution over [0,Λ], and the angle the wire makes with the x-axis was drawn from a uniform distribution over [ −π/2, π/2]. Every point where two or more wires touch is taken to be a junction in the network. This connectivity is then stored in a N × N adjacency matrix, which also allows the number of connections between each wire and its neighbours (the degree, k) to be calculated. For the 2D network, every wire is considered to be a 1D line (i.e. with zero thickness). As a result, the wires lie exactly in the xy-plane, and every intercept is a junction (similar to that shown in Fig. 1c).In the Q3D network, each wire also has a diameter and therefore carves out a volume in space that cannot be occupied by any other wire. The wires are deposited sequentially, one at a time, and the vertical position of each new wire depends on the positions of the wires that have already been deposited. A comparison of Fig. 1b and c shows that stacking causes some wires that are in contact in the perfectly 2D system to become separated vertically in the Q3D system.
For each new wire, the algorithm determines firstly which wires are below it, and calculates the intercept points. In the simplest case, the new wire rests on top of the two previously deposited wires that provide the highest contact points. In the trivial case of there being no intercept points, the wire is deposited directly onto the target area. More generally, the point of intercept with the largest z-value acts as a pivot around which the new wire must rotate. The location of the centre of mass with respect to the pivot point determines the direction of rotation, and hence the location of the second point of contact. If the end of the wire reaches the substrate before making contact with a second wire, its end is at z = 0. This results in a network that is stacked vertically in a third dimension, the z-axis, as shown in Fig. 1a and ESI,† Fig. S1 and S2. As with the 2D model, every point of contact is a junction and the connections between wires are stored in an adjacency matrix (Fig. 1b and c). This allows construction of a graph representation of the network, where each node is taken to be the center of a wire and each edge represents a contact between two wires (Fig. 1d and e).
It is of course possible to consider additional processes during the wire deposition, including allowing the wires to settle, slide or bend. The purpose of the present work is to investigate the effect of dimensionality on network connectivity (rather than the detailed deposition dynamics) and so we focus on the simplest model that captures the essential features, i.e. the wires are perfectly rigid and do not move from their initial position after deposition. The effects of these processes have not previously been considered in detail but it is known that bending has minimal impact on the number of wires required to form a spanning group24 and therefore it seems likely that allowing bending in the simulation would not modify the network structure significantly.
In order to compare the nanowire networks with benchmark networks, we also generated four sets of Watts-Strogatz (WS) networks. The first step in generating WS networks is to calculate the mean degree ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) for each 2D or Q3D network. The WS network has the same N and
for each 2D or Q3D network. The WS network has the same N and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) but connections are rewired with probability p to another node chosen at random from all other available nodes.29 As shown in ESI,† Fig. S3, for each value of
but connections are rewired with probability p to another node chosen at random from all other available nodes.29 As shown in ESI,† Fig. S3, for each value of ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) N we construct two WS networks: one with p = 0, making a regular network, and the other with p = 1, making a random network. We then compare the 2D, Q3D, and the WS networks using a number of common measures from network theory (see Methods). These include the degree, path length (L), and average local clustering coefficient (C) distributions. We then also examine the community structure of the network, the modularity of a community partitioned network, and the small world propensity.
N we construct two WS networks: one with p = 0, making a regular network, and the other with p = 1, making a random network. We then compare the 2D, Q3D, and the WS networks using a number of common measures from network theory (see Methods). These include the degree, path length (L), and average local clustering coefficient (C) distributions. We then also examine the community structure of the network, the modularity of a community partitioned network, and the small world propensity.
Results and discussion
We varied the mean wire length λ, the dispersion d, and the number of nanowires in the network N. Values of λ were chosen to be 6, 6.5, 7, 7.5, 8, 8.5, and 9 μm. Values for the dispersion were chosen to be 0, 0.1, 0.2 and 0.5 (hence the minimum possible length of any given wire is λ − dλ and the maximum possible length is λ + dλ). Λ is fixed at 30 μm and the scaling of the network properties with λ and Λ is shown in ESI,† Fig S4. The scaling parameter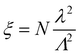 captures the key relationships between parameters,24 and makes it clear that for a fixed value of wire length, the critical number of wires Nc required to form a spanning group scales proportionally to the target area. Nc can also be scaled by keeping the target area fixed and varying the wire length. Our choice of parameters enables comparisons with existing literature on the topology of 2D nanowire networks.27 For the Q3D network, the wire diameter is chosen to be 20 nm. If the diameter of the wires is changed, this would change the final height of the stack of wires but would not affect the connectivity of the network. Tunnelling between wires that are not touching but which are in close proximity has a negligible effect on the overall connectivity (see ESI,† Fig. S5) and electrical properties.22,36–38
captures the key relationships between parameters,24 and makes it clear that for a fixed value of wire length, the critical number of wires Nc required to form a spanning group scales proportionally to the target area. Nc can also be scaled by keeping the target area fixed and varying the wire length. Our choice of parameters enables comparisons with existing literature on the topology of 2D nanowire networks.27 For the Q3D network, the wire diameter is chosen to be 20 nm. If the diameter of the wires is changed, this would change the final height of the stack of wires but would not affect the connectivity of the network. Tunnelling between wires that are not touching but which are in close proximity has a negligible effect on the overall connectivity (see ESI,† Fig. S5) and electrical properties.22,36–38
We considered networks in which the number of wires ranged from 50 (almost perfectly two-dimensional) to 2000 (highly three-dimensional as shown in ESI,† Fig. S1 and S2). For clarity of presentation we show data only for N = 100, 180, 500, 1000, and 2000 wires.
Degree and path length
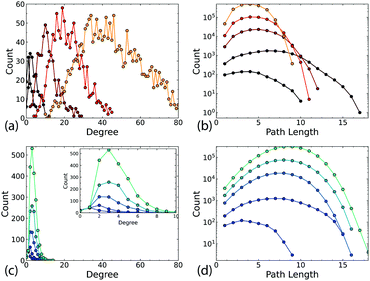
The difference in the connectivity of the networks (Fig. 1c and d) is reflected in the degree and path length distributions, as shown in Fig. 2 for typical networks for each N. The 2D networks in Fig. 2a and b have much broader degree distributions and generally narrower path length distributions than the Q3D networks (Fig. 2c and d). In the 2D network the number of intersections increases for each newly deposited wire. Therefore, we see an approximately linear increase in mean degree with increasing N (Fig. 3a). We also see a gradual decrease in path length as more connections become available (Fig. 3c). In contrast, for the Q3D networks![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) is much lower and it increases at a much slower rate. The growth of the height of the network (ESI,† Fig. S2) in the z-direction also results in a higher mean path length for the Q3D networks.
is much lower and it increases at a much slower rate. The growth of the height of the network (ESI,† Fig. S2) in the z-direction also results in a higher mean path length for the Q3D networks.
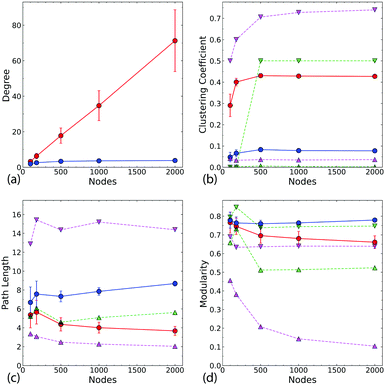 | ||
Fig. 3 (a) The dependence of average degree ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) on system size. The markers are the average values taken over all combinations of λ (6, 6.5, 7, 7.5, 8, 8.5, 9) and d (0, 0.1, 0.2, 0.5) (28 networks) for both the 2D (red) and Q3D (blue) networks. (b) Average clustering coefficient for the 2D and Q3D networks with the corresponding Watts-Strogatz networks for comparison. For each value of the mean degree, two WS networks were constructed: one with a rewiring probability of p = 0 (down triangle) and one with p = 1 (up triangle). This was done for degree values of both the 2D (magenta) and the Q3D (green) networks. (c) The average path lengths of the network. (d) The resulting maximized modularity after the partitioning of the networks using the Louvain algorithm. All error bars are one standard deviation of the data obtained from all 28 networks. Note that the regular WS (p = 0) networks corresponding to the 3D network have high values of L, and so are not displayed here. A modified version of this plot with a logarithmic y-scale is presented in ESI,† Fig. S6. on system size. The markers are the average values taken over all combinations of λ (6, 6.5, 7, 7.5, 8, 8.5, 9) and d (0, 0.1, 0.2, 0.5) (28 networks) for both the 2D (red) and Q3D (blue) networks. (b) Average clustering coefficient for the 2D and Q3D networks with the corresponding Watts-Strogatz networks for comparison. For each value of the mean degree, two WS networks were constructed: one with a rewiring probability of p = 0 (down triangle) and one with p = 1 (up triangle). This was done for degree values of both the 2D (magenta) and the Q3D (green) networks. (c) The average path lengths of the network. (d) The resulting maximized modularity after the partitioning of the networks using the Louvain algorithm. All error bars are one standard deviation of the data obtained from all 28 networks. Note that the regular WS (p = 0) networks corresponding to the 3D network have high values of L, and so are not displayed here. A modified version of this plot with a logarithmic y-scale is presented in ESI,† Fig. S6. | ||
Clustering and comparison with WS networks
Fig. 3b and c compare the clustering coefficients and path lengths of each nanowire network with the corresponding WS networks. The 2D network, has high clustering like the WS regular network (p = 0, ), but a low mean path length similar to that of the WS random network (p = 1,
), but a low mean path length similar to that of the WS random network (p = 1,  ). These are typical characteristics of a small world network. The Q3D model, on the other hand, exhibits a low degree of clustering, similar to that of the corresponding WS random network (
). These are typical characteristics of a small world network. The Q3D model, on the other hand, exhibits a low degree of clustering, similar to that of the corresponding WS random network ( ). The mean path lengths in the Q3D network are higher than those in the 2D network, but are still similar to those in the corresponding WS random network.
). The mean path lengths in the Q3D network are higher than those in the 2D network, but are still similar to those in the corresponding WS random network.
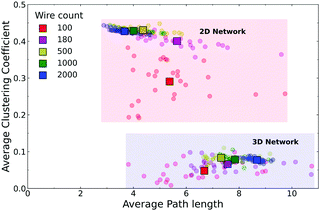
Fig. 4 shows a comparison of the average mean path lengths and average local clustering coefficients for a large number of realisations of both the 2D and Q3D networks, with different values of N, λ, and d. This alternative representation of the data shows clearly that the Q3D networks are significantly less clustered and have greater mean path lengths than the 2D networks. The mean values of L (square symbols) are similar for N = 100 but become more different as N increases: ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) decreases for the 2D networks, but increases for the Q3D networks. There is considerable scatter in the path lengths from network to network, but the clustering coefficients are only weakly dependent on N, wire length and dispersion for N > 100. For N = 100, in both the 2D and Q3D networks, there is significant variation in clustering because the system is close to the percolation threshold (Nc ∼ 50–150, see ESI,† Fig. S4).
decreases for the 2D networks, but increases for the Q3D networks. There is considerable scatter in the path lengths from network to network, but the clustering coefficients are only weakly dependent on N, wire length and dispersion for N > 100. For N = 100, in both the 2D and Q3D networks, there is significant variation in clustering because the system is close to the percolation threshold (Nc ∼ 50–150, see ESI,† Fig. S4).
Modularity and community structure
The separation of typical networks into modules is shown in Fig. 5. The 2D network is much more densely connected than the Q3D network, and the communities are more clearly defined. The communities in the Q3D network can also be clearly seen, but overlap much more than in the 2D network. Fig. 3d shows that the modularity, Q (see Methods for definition), for the Q3D network is higher for all network sizes. For both the 2D and Q3D networks, Q is similar to that of the regular WS networks (p = 0) with the same dimensionality ( and
and  respectively).
respectively).
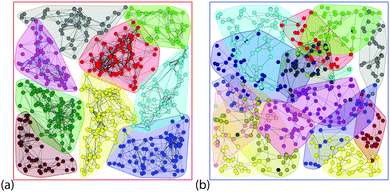 | ||
| Fig. 5 The partitioning of the 500 nanowire example network featured in Fig. 1 into communities based on the Louvain algorithm39 of modularity maximization. (a) 2D and (b) Q3D. | ||
The degree of modularity is of interest because it reflects the vulnerability of a network to different types of ‘attack’ by random removal of nodes.40 In the low modularity regime, removal of nodes fragments the modules internally and causes the network to collapse. For high modularity, the network undergoes a fragmentation process where, while the modules remain intact, they become disconnected from one another. Networks with a broader degree distribution tend to be more vulnerable to fragmentation in this way.40 This is because a broader degree distribution with the same average degree implies more low-degree nodes and hence fewer interconnections between nodes. Thus the higher modularity in the Q3D network is at least partly a consequence of the smaller average degree (see Fig. 2).
Small-world
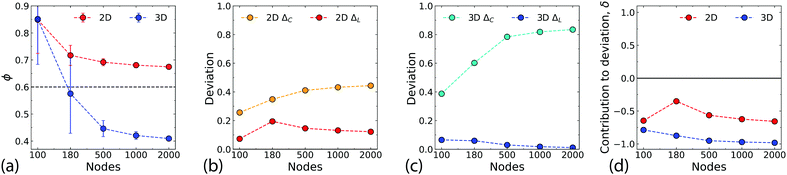
A small world architecture29 is characterised by a high degree of clustering and a small average path length between nodes, but the precise definition of the “small-world effect” has been the subject of some debate.41 Here, we use the small-world propensity ϕ (see Methods for definition) to quantify the “small-worldness” of the network.42The effects of system size on ϕ are shown in Fig. 6a. For N ∼ 100 the 2D and Q3D networks are almost identical because the density of the networks is low, with limited overlapping of wires. As groups of wires begin to span the network, the small-world propensity decreases. Muldoon et al. propose a pragmatic threshold value of ϕT = 0.6,42 with networks having ϕ > ϕT identified as having a strong small-world propensity. The 2D network remains consistently above this threshold (ϕ = 0.67 ± 0.01 for N = 2000). In contrast, for the Q3D networks it is clear that for N > Nc the stacking of the wires becomes important and ϕ drops below ϕT.
Fig. 6b–d further elucidate the contributions of the clustering coefficient and the path length to ϕ (ΔC and ΔL respectively – see methods for definitions). ΔC is high for the Q3D network (Fig. 6c) indicating a large divergence from the regular network due to lower clustering. The 2D network by comparison, has much lower values of ΔC (Fig. 6b). Both networks have low values of ΔL, due to their small path lengths, which are similar to those of the corresponding WS random networks. Fig. 6d shows the contribution, δ to the deviation (see methods and ESI,† Fig. S7 for more details). The negative values of δ for both networks indicate that the dominant contribution to ϕ is the low level of clustering compared with the corresponding WS regular network. This is especially evident in the Q3D network. Ultimately, the lower small world propensity for the Q3D networks results from a more dramatic decrease in clustering than is observed for the 2D networks.
Conclusion
We have shown that stacking of nanowires during deposition significantly affects the connectivity and topology of the resulting network. Perfectly 2D networks have much broader degree distributions and much larger mean degrees than the quasi-3D networks that result from stacking. Differences in connectivity are observable soon after the percolation threshold is exceeded i.e. as soon the number of wires is sufficient to connect opposite sides of the system (allowing current to flow through the network). More specifically the small world character of quasi-3D networks is significantly lower than in the 2D networks. The Q3D networks instead exhibit greater modularity. Perhaps surprisingly, the connectivity of the Q3D networks does not increase when additional nanowires are deposited.These differences in connectivity will have significant effects on the properties of real-world nanowire networks, and hence on potential applications such as neuromorphic computing. It is known for example that in network models of artificial neurons, segregated communities of activity emerge in pattern recognition tasks, mimicking the visual cortex.43 The modularity, a predictor of the robustness of networks to node deletion, can be important in nanowire networks which show “self-healing” properties44 – when a critical junction in a conducting path is deleted, the system quickly reconfigures into another low-resistance path. In addition, small world connectivity is advantageous for time series prediction within a reservoir computing framework35 and significantly affects synchronisability in oscillator networks.32,45 Ultimately, it is important that the impact of changes in connectivity of nanowire networks on the performance of reservoir computing tasks is tested experimentally.
Methods
The nanowire simulations were built using Python v3.7.7. The graph analysis measures were taken from the Python NetworkX46 and iGraph47 libraries, and the MATLAB Brain Connectivity Toolbox.48The midpoints of the nanowires are chosen randomly with a uniform distribution in the plane of the drop zone. Note that the boundary conditions are not periodic as in real physical devices. The end point of any given wire of length λ therefore can extend beyond the boundaries of the drop zone by at most λ/2. While in principle other distributions could be considered, in percolation theory21 the effect of the distribution of the size of the objects is usually found to be small, as is indeed the case here: see Fig. 3.
Since the connections between wires can be mapped to an adjacency matrix, we can use graph theory to analyze the networks. In order to simplify analysis, the corresponding graph is considered to be undirected and the edges unweighted – that is, the adjacency matrix is a symmetric binary matrix. Each wire is modelled as a node (or vertex) in a graph, and each contact between wires is an edge. The nanowire network is then treated as the graph G = (N, E), where N is the set of nodes and E the set of edges. The number of wires that are connected to wire i is the degree, ki. The mean degree ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) is then
is then
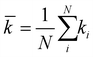 | (1) |
The degree distribution, P(k), captures some aspects of the connectivity of the network, but there are many other metrics. Watts and Strogatz introduced methods to characterise the path lengths and clustering of the network, as described below.
Given any two nodes in the network i and j, the path length Lij, is the shortest sequence of edges that connects them. The average path length (also sometimes called the characteristic path length) is then,
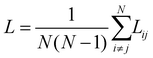 | (2) |
The local clustering coefficient is the fraction of the total allowable edges that exist between node i and its neighbours. For an undirected network with adjacency matrix A, the local clustering coefficient of node i with degree ki is given by
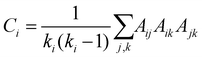 | (3) |
The global clustering coefficient is then the average of these values
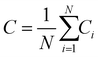 | (4) |
The small-world propensity, ϕ,42 was defined in order to quantify the deviation of the clustering coefficient, Cobs, and path length, Lobs, of the network from those of both regular and random networks with the same number of nodes and degree distribution in such a way as to account for variations in network density:
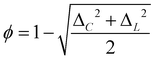 | (5) |
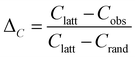 | (6) |
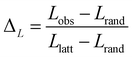 | (7) |
In addition to the small-world propensity, following the work of Muldoon et al., we also quantify the amount that ΔC and ΔL contribute to ϕ. This can be done by calculating the angular difference of the values of the network from the value of equal contribution of ΔC and ΔL (see ESI,† Fig. S7). This calculation is then called the contribution to the deviation,
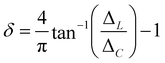 | (8) |
The method we used to partition the network was the Louvain method of community detection.39 In brief, nodes within the same community are more densely connected to one another than with nodes in other communities. Each node is assigned to one community, then pairs of communities are combined iteratively such that the number of connections within groups is maximized while the number of connections between groups is minimized. This is done by maximizing the modularity, a measure of the relative density of edges inside the groups with respect to edges outside the groups. For some partition of a network with m edges with node i having degree ki, into communities c, the modularity q of this is49
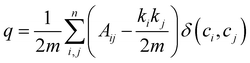 | (9) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Matt Arnold, Josh Mallinson, Susant Acharya, and Zac Heywood for useful discussions and input.References
- S. Ye, A. R. Rathmell, Z. Chen, I. E. Stewart and B. J. Wiley, Adv. Mater., 2014, 26, 6670–6687 CrossRef CAS PubMed.
- S. Park, M. Vosguerichian and Z. Bao, Nanoscale, 2013, 5, 1727–1752 RSC.
- T. Sannicolo, M. Lagrange, A. Cabos, C. Celle, J.-P. Simonato and D. Bellet, Small, 2016, 12, 6052–6075 CrossRef CAS PubMed.
- B. Tian and C. M. Lieber, Chem. Rev., 2019, 119, 9136–9152 CrossRef CAS.
- J. F. Fennell Jr., S. F. Liu, J. M. Azzarelli, J. G. Weis, S. Rochat, K. A. Mirica, J. B. Ravnsbæk and T. M. Swager, Angew. Chem., Int. Ed., 2016, 55, 1266–1281 CrossRef PubMed.
- H. Y. Zheng, O. A. Alsager, B. Zhu, J. Travas-Sejdic, J. M. Hodgkiss and N. O. V. Plank, Nanoscale, 2016, 8, 13659–13668 RSC.
- C.-H. Song, C. J. Han, B.-K. Ju and J.-W. Kim, ACS Appl. Mater. Interfaces, 2016, 8, 480–489 CrossRef CAS PubMed.
- J. Lee, K. An, P. Won, Y. Ka, H. Hwang, H. Moon, Y. Kwon, S. Hong, C. Kim, C. Lee and S. H. Ko, Nanoscale, 2017, 9, 1978–1985 RSC.
- W. Li, H. Zhang, S. Shi, J. Xu, X. Qin, Q. He, K. Yang, W. Dai, G. Liu, Q. Zhou, H. Yu, S. R. P. Silva and M. Fahlman, J. Mater. Chem. C, 2020, 8, 4636–4674 RSC.
- J. B. Mallinson, S. Shirai, S. K. Acharya, S. K. Bose, E. Galli and S. A. Brown, Sci. Adv., 2019, 5, aaw8438 CrossRef PubMed.
- S. Shirai, S. K. Acharya, S. K. Bose, J. B. Mallinson, E. Galli, M. D. Pike, M. D. Arnold and S. A. Brown, Network Neuroscience, 2020, 4, 432–447 CrossRef.
- M. D. Pike, S. K. Bose, J. B. Mallinson, S. K. Acharya, S. Shirai, E. Galli, S. J. Weddell, P. J. Bones, M. D. Arnold and S. A. Brown, Nano Lett., 2020, 20, 3935–3942 CrossRef CAS PubMed.
- A. V. Avizienis, H. O. Sillin, C. Martin-Olmos, H. H. Shieh, M. Aono, A. Z. Stieg and J. K. Gimzewski, PLoS One, 2012, 7, 1–8 CrossRef.
- H. G. Manning, F. Niosi, C. G. da Rocha, A. T. Bellew, C. O'Callaghan, S. Biswas, P. F. Flowers, B. J. Wiley, J. D. Holmes, M. S. Ferreira and J. J. Boland, Nat. Commun., 2018, 9, 3219 CrossRef.
- H. Tanaka, M. Akai-Kasaya, A. TermehYousefi, L. Hong, L. Fu, H. Tamukoh, D. Tanaka, T. Asai and T. Ogawa, Nat. Commun., 2018, 9, 2693 CrossRef PubMed.
- A. Z. Stieg, A. V. Avizienis, H. O. Sillin, C. Martin-Olmos, M. Aono and J. K. Gimzewski, Adv. Mater., 2012, 24, 286–293 CrossRef CAS.
- A. Diaz-Alvarez, R. Higuchi, P. Sanz-Leon, I. Marcus, Y. Shingaya, A. Z. Stieg, J. K. Gimzewski, Z. Kuncic and T. Nakayama, Sci. Rep., 2019, 9, 14920 CrossRef PubMed.
- G. Milano, G. Pedretti, M. Fretto, L. Boarino, F. Benfenati, D. Ielmini, I. Valov and C. Ricciardi, Adv. Intell. Syst., 2020, 2, 2000096 CrossRef.
- K. Fu, R. Zhu, A. Loeffler, J. Hochstetter, A. Diaz-Alvarez, A. Stieg, J. Gimzewski, T. Nakayama and Z. Kuncic, International Joint Conference on Neural Networks (IJCNN), 2020, pp. 1-8.
- Z. Kuncic, O. Kavehei, R. Zhu, A. Loeffler, K. Fu, J. Hochstetter, M. Li, J. M. Shine, A. Diaz-Alvarez, A. Stieg, J. Gimzewski and T. Nakayama, IEEE International Symposium on Circuits and Systems (ISCAS), 2020, pp. 1-5.
- D. Stauffer and A. Aharony, Introduction to Percolation Theory, Taylor and Francis, 2nd edn, 1992 Search PubMed.
- S. Fostner, R. Brown, J. Carr and S. A. Brown, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 075402 CrossRef.
- J. Li and S.-L. Zhang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 040104 CrossRef PubMed.
- D. P. Langley, M. Lagrange, N. D. Nguyen and D. Bellet, Nanoscale Horiz., 2018, 3, 545–550 RSC.
- S. I. White, R. M. Mutiso, P. M. Vora, D. Jahnke, S. Hsu, J. M. Kikkawa, J. Li, J. E. Fischer and K. I. Winey, Adv. Funct. Mater., 2010, 20, 2709–2716 CrossRef CAS.
- R. M. Mutiso, M. C. Sherrott, A. R. Rathmell, B. J. Wiley and K. I. Winey, ACS Nano, 2013, 7, 7654–7663 CrossRef CAS PubMed.
- A. Loeffler, R. Zhu, J. Hochstetter, M. Li, K. Fu, A. Diaz-Alvarez, T. Nakayama, J. M. Shine and Z. Kuncic, Front. Neurosci., 2020, 14, 184 CrossRef PubMed.
- R. D. Pantone, J. D. Kendall and J. C. Nino, Neural Networks, 2018, 106, 144–151 CrossRef PubMed.
- D. J. Watts and S. H. Strogatz, Nature, 1998, 393, 440–442 CrossRef CAS PubMed.
- A. Pascual-Garca, arXiv preprint arXiv:1610.02448, 2016.
- S. H. Strogatz, Nature, 2001, 410, 268–276 CrossRef CAS PubMed.
- T. Nishikawa, A. Motter, Y.-C. Lai and F. Hoppensteadt, Phys. Rev. Lett., 2003, 91, 014101 CrossRef PubMed.
- J. Lu, X. Yu, G. Chen and D. Cheng, IEEE Trans. Circuits Syst., 2004, 51, 787–796 CrossRef.
- A. Haluszczynski, J. Aumeier, J. Herteux and C. Räth, Chaos, 2020, 30, 063136 CrossRef PubMed.
- Z. Deng and Y. Zhang, IEEE Trans. Neural Netw., 2007, 18, 1364–1375 Search PubMed.
- G. Ambrosetti, C. Grimaldi, I. Balberg, T. Maeder, A. Danani and P. Ryser, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 155434 CrossRef.
- B. Nigro, C. Grimaldi, M. A. Miller, P. Ryser and T. Schilling, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 042140 CrossRef CAS PubMed.
- I. V. Vodolazskaya, A. V. Eserkepov, R. K. Akhunzhanov and Y. Y. Tarasevich, J. Appl. Phys., 2019, 126, 244903 CrossRef.
- V. D. Blondel, J.-L. Guillaume, R. Lambiotte and E. Lefebvre, J. Stat. Mech.: Theory Exp., 2008, P10008 CrossRef.
- S. Shai, D. Y. Kenett, Y. N. Kenett, M. Faust, S. Dobson and S. Havlin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 062805 CrossRef PubMed.
- M. Newman, J. Stat. Phys., 2000, 101, 819–841 CrossRef.
- S. F. Muldoon, E. W. Bridgeford and D. S. Bassett, Sci. Rep., 2016, 6, 22057 CrossRef CAS PubMed.
- L. Michiels van Kessenich, D. Berger, L. de Arcangelis and H. J. Herrmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2019, 99, 010302 CrossRef CAS PubMed.
- C. O'Callaghan, C. G. Rocha, F. Niosi, H. G. Manning, J. J. Boland and M. S. Ferreira, J. Appl. Phys., 2018, 124, 152118 CrossRef.
- M. Barahona and L. M. Pecora, Phys. Rev. Lett., 2002, 89, 054101 CrossRef PubMed.
- A. A. Hagberg, D. A. Schult and P. J. Swart, Proceedings of the 7th Python in Science Conference, Pasadena, CA USA, 2008, pp. 11–15.
- G. Csardi and T. Nepusz, InterJournal, 2006, Complex Systems, 1695 Search PubMed.
- M. Rubinov and O. Sporns, NeuroImage, 2010, 52, 1059–1069 CrossRef.
- A. Clauset, M. E. J. Newman and C. Moore, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 066111 CrossRef.
- M. E. J. Newman, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 8577–8582 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nh00693a |
| This journal is © The Royal Society of Chemistry 2021 |