Open Access Article
Open Access ArticleDirect observation of spin correlations in an artificial triangular lattice Ising spin system with grazing-incidence small-angle neutron scattering†
Petai
Pip‡
 *abc,
Artur
Glavic‡
*abc,
Artur
Glavic‡
 *d,
Sandra Helen
Skjærvø
ab,
Anja
Weber
*d,
Sandra Helen
Skjærvø
ab,
Anja
Weber
 ab,
Andrew
Smerald
e,
Kirill
Zhernenkov
f,
Naëmi
Leo
ab,
Andrew
Smerald
e,
Kirill
Zhernenkov
f,
Naëmi
Leo
 g,
Frédéric
Mila
g,
Frédéric
Mila
 h,
Laetitia
Philippe
i and
Laura J.
Heyderman
h,
Laetitia
Philippe
i and
Laura J.
Heyderman
 ab
ab
aLaboratory for Mesoscopic Systems, Department of Materials, ETH Zurich, 8093 Zurich, Switzerland. E-mail: ppip@student.ethz.ch
bLaboratory for Multiscale Materials Experiments, Paul Scherrer Institut, Villigen PSI, Switzerland
cLaboratory for Mechanics of Materials and Nanostructures, Empa (Swiss Federal Laboratories for Materials Testing and Research), 3602 Thun, Switzerland
dLaboratory for Neutron and Muon Instrumentation, Paul Scherrer Institut, Villigen PSI, Switzerland
eAtmospheric Environmental Research (IMK-IFU), Institute for Meteorology and Climate Research, Karlsruhe Institute of Technology, 82467 Garmisch-Partenkirchen, Germany
fJülich Centre for Neutron Science at Heinz Maier-Leibnitz Zentrum, Forschungszentrum Jülich GmbH, 85748 Garching, Germany
gCIC nanoGUNE BRTA, 20018 Donostia-San Sebastián, Spain
hInstitute of Physics, École Polytechnique Fédérale de Lausanne (EPFL), CH-1015 Lausanne, Switzerland
iManufacture des Montres ROLEX SA, Research & Development, CH-2501 Biel/Bienne, Switzerland
First published on 7th May 2021
Abstract
The triangular lattice with Ising magnetic moments is an archetypical example of geometric frustration. In the case of dipolar-coupled out-of-plane moments, the geometric frustration results in a disordered classical spin-liquid state at higher temperatures while the system is predicted to transition to an anti-ferromagnetic stripe ground state at low temperatures. In this work we fabricate artificial triangular Ising spin systems without and with uniaxial in-plane compression to tune the nature and temperature of the correlations. We probe the energy scale and nature of magnetic correlations by grazing-incidence small-angle neutron scattering. In particular, we apply a newly-developed empirical structure-factor model to describe the measured short-range correlated spin-liquid state, and find good agreement with theoretical predictions. We demonstrate that grazing-incidence neutron scattering on our high-quality samples, in conjunction with detailed modeling of the scattering using the Distorted Wave Born Approximation, can be used to experimentally quantify the spin-liquid-like correlations in highly-frustrated artificial spin systems.
New conceptsOur work advances the field of nanomagnetism with three important concepts. First, we used electron-beam lithography to create a 2D single crystal of macrospins that allowed us to observe strong and clean magnetic signals while suppressing structural signals in grazing-incidence small-angle neutron scattering experiments. This approach is applicable to any two-dimensional or layered nanostructure and can thus be employed to study many short-range correlated magnetic systems. Second, we used a newly developed empirical structure factor model to simulate the short-range correlated spin-liquid state of a triangular dipolar-coupled Ising-like lattice with out-of-plane moments. This allowed integration into the Distorted Wave Born Approximation (DWBA) for quantitative analysis of the scattering results. In previous studies these correlations were only described with Monte-Carlo simulated structure factors and the DWBA model was restricted to domains of ordered super-spins. We expect that other magnetic systems with short-range correlations can now be approximated in this way. Finally, we could fit our model structure factor specifically to theoretical predictions of the frustrated triangular lattice and thus directly correlate theory with experiment. This can be used in future temperature-dependent investigations of this fascinating system. |
1 Introduction
Magnetically corrrelated nanosystems, such as self-assemblies of magnetic nanoparticles1,2 or artificial spin systems,3 are of great interest due to their high potential for advanced applications such as computation, nanomagnetic logic gates4,5 and magnonic crystals.6 Such systems consist of arrangements of single-domain nanomagnets, where each nanomagnet can be considered to have a macroscopic magnetic moment, which interact through magnetostatic interactions. These interactions lead to complex magnetic correlations of fundamental physical interest7–12 that may not lead to long-range ordering. For experimental studies of such systems with short-range correlations a non-local probe is required that can further our understanding in the field.Since the early days, neutron scattering has been an excellent technique to probe the magnetic order of many systems due to the interaction between the intrinsic magnetic moment of the neutrons and the unpaired electrons in the material.13–17 Scattering experiments with polarised neutrons furthermore allow the direct probing of the magnetic structure, magnetic distribution and spin dynamics. While small angle neutron scattering (SANS) is a suitable technique for nanoscale investigations it is often not suitable for thin structures on surfaces as the amount of material is too low to produce the necessary signal. Specular neutron reflectometry, on the other hand, provides a measure of a depth-dependent magnetisation profile, but does not give information about the in-plane structural and magnetic correlations. Grazing-incidence small-angle neutron scattering (GISANS) closes this gap, as the experimental geometry gives a strong surface sensitivity and enhancement to the measured signal from samples with small amounts of material, as well as offering access to in-plane correlations.18,19 Therefore this surface-sensitive technique is the method of choice for thin nanoscale structures.20
In artificial spin systems, however, experiments have proven to be difficult to conduct and analyse compared with various nano-imaging techniques such as magnetic force microscopy21 or X-ray photoemission electron microscopy.8,22 One reason for this is the need for large scattering volumes that are orders of magnitude larger than the volumes needed for X-ray scattering.12,23 In addition, the magnetic scattering is much weaker than the nuclear signal, and modeling requires the inclusion of dynamic effects.
In this work, we use GISANS to probe emerging correlations in a nanoscale artificial spin system. These lithographically-designed magnetic nanostructures are ideal for this experimental technique, as it is possible to pattern large-area structures with a very high level of structural perfection. Here, we choose to focus on a triangular NiFe nanopillar array mimicking dipolar-coupled Ising macrospins, which allows for a rich phase diagram, including ordered phases and a classical spin liquid regime.11 To analyse the magnetic scattering data, we developed an empirical magnetic structure factor to model the emergent correlations in the system. We integrated the model into the open-source software BornAgain, which provides simulations within the framework of the distorted wave Born approximation (DWBA). In addition, we were able to fit our model to temperature dependent Monte-Carlo simulations, in order to determine the magnetic state of the system. As a result, we conclude that at room-temperature the measured arrays were in a weakly correlated paramagnetic phase. We emphasize that the approach described here for the analysis of GISANS results can be extended and applied to other magnetically correlated systems.
2 The dipolar-coupled triangular-lattice Ising spin system
Artificial spin systems are two-dimensional defined lattices of single-domain nanomagnets, which interact via magnetostatic interactions.3 Due to their pairwise coupling, which can be designed at will with careful placement of the nanomagnets, emergent properties can arise, including phase transitions to long-range ordered phases as well as complex short-range correlations, which can be described by spin-ice or spin-liquid models.3,7–12,24In this work we chose to investigate dipolar-coupled out-of-plane magnetic moments on the triangular lattice,25 a system for which the theoretically predicted but not yet experimentally verified magnetic ordering depends on the degree of geometrical frustration.
The interaction between the nanomagnets at positions i and j depends on their distance rj − ri as well as their moments mi = msi, where m denotes the net out-of-plane magnitude (which is identical for each nanomagnet), and si = ±1 its Ising spin degree of freedom. The dipolar Hamiltonian is given by the following equation, and can be simplified with a pairwise coupling strength Jij:
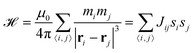 | (1) |
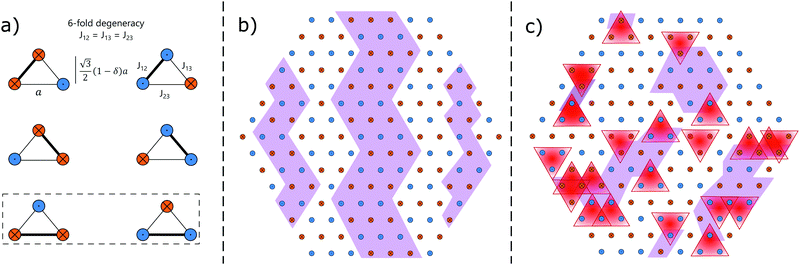
In the symmetric lattice the coupling between neighbouring spins is equivalent and favors an anti-ferromagnetic arrangement. Therefore, on a triangular spin plaquette, as shown in Fig. 1a, not all pairwise interactions can be satisfied simultaneously, leading to a six-fold degeneracy. For an extended lattice this results in a macroscopic number of low-energy configurations.
Considering the longer-range interactions from the dipolar coupling, however, a well-defined six-fold-degenerate stripe-ordered ground state below a critical temperature TC/JNN ∼ 0.2 is found (with JNN = J23 the coupling strength between neighboring moments).11 At temperatures closely above TC the quasi-degenerate manifold of low-energy states is explored leading to the formation of a stripe-domain superstructure (tri-state) without invoking the formation of energy-costly defect triangles, as illustrated in Fig. 1b. This results in spin-liquid-like correlations in a system of classical Ising moments. At temperatures Tpm ≳ 0.75JNN a crossover to weakly-correlated paramagnetic behavior is predicted, which is characterized by the formation of high-energy excitations, as shown in Fig. 1c.
Lowering the symmetry of the lattice through uniaxial in-plane compression results in a reduction of the ground-state degeneracy from six to two (see dashed box in Fig. 1a) and thus lifts the frustration inherent to the system. Consequently, the critical temperature for ground-state ordering increases, e.g. TC/J23 ≈ 0.75 for δ = 0.1, with J23 remaining unchanged by the lattice compression δ. As the nature of the phase transition changes, the region of spin liquid regime is further reduced, e.g. Tpm ≳ JNN for δ = 0.1.11 Therefore, the lattice compression parameter δ can be used to tune the frustration of the system, modifying dramatically the nature of the phase transition and of the short-range correlations close to the long-range ordered ground state.
The ability to design artificial spin systems at will via nanofabrication techniques means that we can experimentally explore large parts of the phase diagram of the dipolar-coupled triangular-lattice Ising system. With the aim to demonstrate a proof-of-principle of the characterization of the emergent short-range spin-liquid-like correlations, here we designed two artificial spin systems, one with no uniaxial in-plane compression, and one with 10% distortion (i.e. δ = 0.1).
3 Sample fabrication
We fabricated elongated NiFe nanomagnets with out-of-plane shape anisotropy arranged on a triangular lattice with electron-beam lithography and electrodeposition. To obtain meaningful results from GISANS experiments, the samples are required to have small lattice periods, spatial correlations over large distances, and large patterned areas. To achieve this, we have pushed the current limits of electron beam lithography and patterned porous templates to give pore diameters of 35 nm, lattice constants below 70 nm and a high structural coherence over a large area. The high structural coherence for patterned areas of the order of cm2 is far beyond the structural domain sizes of μm2 obtained from of self-ordered porous anodic alumina templates with comparable feature sizes.26 We then exploited the capability of electrodeposition to deposit NiFe nanomagnets into the porous templates. NiFe was chosen as magnetic material since it has a large moment and a small magnetocrystalline anisotropy. Therefore the magnetic shape anisotropy dominates and, as a result of the elongated shape, a magnetic single-domain state is formed in each nanomagnet with a net moment (macrospin) aligned along its length. Each macrospin interacts with its neighboring moments via magnetostatic interactions, leading to antiferromagnetic correlations in the lattice. Further details on the fabrication of the samples can be found in ESI,† S1.Here, we characterised three lattices: two symmetric triangular lattices with a nominal lattice constant (shown in Fig. 1) a = 60 nm and a = 70 nm, and a uniaxial in-plane compressed lattice with δ = 10% and with a nominal lattice constant of a = 60 nm. While demonstrating the high structural quality of the samples with unpolarised GISANS on the 70 nm lattice, we concentrated our further analysis on magnetic correlations in the 60 nm lattices for the better comparison of symmetric and compressed case (see Fig. 2). The diameter of the nanomagnets of each sample is 0.53a with a height of (150 ± 10) nm, (120 ± 10) nm and (150 ± 10) nm for the symmetric (a = 70 nm), symmetric (a = 60 nm) and the uniaxial compressed (a = 60 nm) array, respectively.
The samples have excellent structural ordering and filling ratio, as observed in the scanning electron microscope (SEM) images (see Fig. 2). We note that the structural coherence is maintained over the entire patterned sample area, which exceeds 1 cm2, and thus can be considered as a two-dimensional single crystal for the scattering experiment.
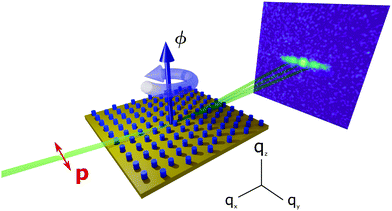
4 GISANS experiments
This work is based upon experiments performed at the MARIA reflectometer27 operated by the Jülich Centre for Neutron Science (JCNS) at the Heinz Maier-Leibnitz Zentrum (MLZ), Garching, Germany. The experimental geometry is illustrated in Fig. 3. The collimated neutron beam impinges at a small glancing angle on the sample's surface, giving a specular peak and additional structural and magnetic signals coming from the lattice. Two different instrument configurations were used, with the sample-detector distance fixed to 1.91 m and the distance between sample and collimation slits fixed to 4.5 m. Measurements with unpolarised neutrons were carried out at a wavelength of 10 Å and with collimation slits of 20 × 20 mm2, leading to a qy resolution full width at half maximum (FWHM) of approximately 6 × 10−2 nm−1. For polarisation analysis, we reduced the neutron wavelength to 7 Å and used collimation slits of size 14 × 20 mm2. While there is a lower qy resolution of 8 × 10−2 nm−1, this provided a sensitivity to the magnetic moment direction and a reduction of the specular scattering background for the spin–flip channels. An acquisition time of 1 h to 5 h was used for unpolarised experiments and to measure each channel (uu, dd, ud, du) for polarisation analysis.5 Model basis
Modeling of the GISANS experiment was performed using the Distorted Wave Born Approximation (DWBA) implemented in the BornAgain software28 version 1.17.0. The instrumental resolution was taken into account using the experimental geometry, including detector distance, beam size and divergence as well as wavelength resolution. All simulation parameters have been taken from the measurement and no further adjustment was performed during modeling.For material parameters, the bulk Scattering Length Densities (SLDs) as calculated from material density and elemental scattering lengths have been used. Film thicknesses and the ratios between the lattice parameter and cylinder radius were extracted from SEM images. For the structural model we have used the BornAgain 2D hexagonal lattice with a cylinder form factor.
6 Results and discussion
The GISANS measurements allow us to determine the structural quality of the samples as well as the magnetic correlations assigned to different phases that can vary from weakly-correlated to strongly-correlated, and from short-range to long-range.6.1 Structural order
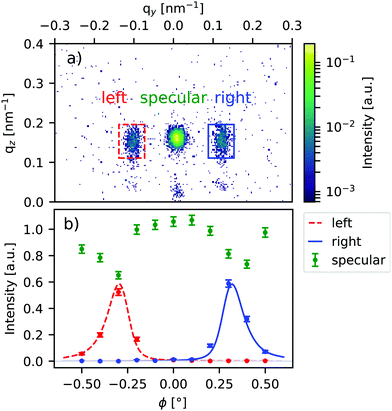
The measurement of unpolarised GISANS on varying the sample rotation angle ϕ in 0.1° steps allows the determination of the exact lattice period and an estimation of the structural coherence length. In contrast to most mesoscopic systems investigated with this technique, our samples have a large structural coherence. We thus expect very sharp Bragg peaks in the scattering plane that are only visible within a very narrow range of ϕ. In Fig. 4(a), the combined data of several measurements with different angles of ϕ are shown. In all measurements, one center peak is visible, corresponding to the specular reflection, while the two Bragg peaks at qy ≈ ±0.12 nm−1 show up in a small set of measurements only.The sharpness of the Bragg peaks means that they can be easily suppressed through the choice of ϕ. The scan data is used to determine the structural quality of the system. The resulting fitted intensity for both regions of interest (ROI) and the specular peak indicated in Fig. 4a is shown in Fig. 4b. Integration of the left and right Bragg peaks have been combined in one dataset and refined simultaneously. The applied DWBA model did not include any magnetic order and the only free structural parameters were lattice periodicity and correlation length. As a result, a lattice parameter a = (66.4 ± 0.5) nm and a correlation length of ξ = (20+40−10) μm were found.
6.2 Magnetic correlations
The regular- and compressed-lattice samples have superior structural quality, as shown by SEM images (Fig. 2) and confirmed by an unpolarised GISANS scan for different sample orientations (Fig. 4). We used polarised neutrons in order to validate the magnetic origin of the scattering signals and exploited the higher yield of unpolarised neutrons for more resolution and faster measurements. After the detailed structural characterisation, we reduce the non-magnetic background from the Bragg peaks as much as possible in order to measure the magnetic correlations of our samples (a = 60 nm) by orientating the samples with ϕ = 0° and 90°. For both samples, the strongest magnetic signal is observed for ϕ = 90° because of the larger structured surface area in this direction and the influence of the cylinder form factor. No non-spin–flip signal could be detected in either orientation, confirming that the magnetic moments are aligned out-of-plane and therefore perpendicular to the guide field.The spin–flip measurements for the symmetric and 10% distorted lattice can be found in Fig. 5. In both samples there is a clear magnetic signal above background, far exceeding experimental counting errors (light color area in Fig. 5b and d). The intensity around qy = 0 is the non spin–flip specular peak passing through the analyser due to the finite polarisation efficiency of polariser and analyser of the order of ≈99%. The magnetic scattering is significantly weaker than the structural peaks and much broader than the instrumental resolution.
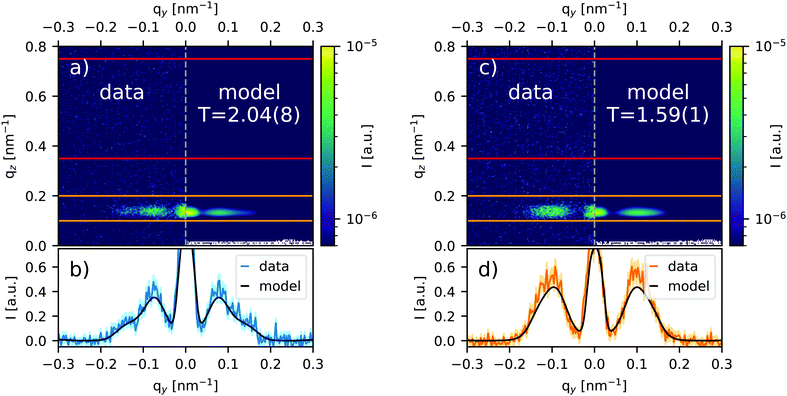 | ||
| Fig. 5 GISANS spin–flip measurement of symmetric (a and b) and 10% distorted (c and d) triangular lattice and model calculation with parameters from the structure factor fitting (Fig. 6). The magnetic guide field was aligned in-plane and parallel to the y-direction. Measurements were performed with the sample at ϕ = 90°. Red and orange horizontal lines in (a and c) denote the regions used to extract the background and Yoneda line intensity, respectively. The effective temperature T/JNN is determined by a fit of our model to temperature-dependent Monte-Carlo simulations. Bottom panels (b and d) show the Yoneda lines after background subtraction with one standard deviation indicated by the light color area and the fitted model indicated as a line. | ||
On further inspection of the distorted lattice measurement (Fig. 5c and d), we observe a broad peak around half the qy of the structural Bragg peak as would be expected for a short-range stripe order that is oriented along the a-axis. The symmetric sample (Fig. 5a and b) shows more structured scattering (i.e. overlapping peaks) at different qy values that are not consistent with this state. While not modeled separately, a dominant part of this apparent structure is described by the tri-state peaks explained below.
Both the presence of different correlation vectors in the symmetric lattice and the width of the magnetic scattering in both samples indicate the presence of magnetic correlations of limited range due to significant magnetic disorder. This means that we are observing magnetic configurations at effective temperatures well above the transition temperature to the long-range stripe-ordered ground state.
The observed short-range magnetic correlations are the result of statistical averages in agreement with theory that predicts that the magnetic structure factor evolves gradually in temperature from a spin-liquid to a paramagnetic state with broad correlations.11 The structure factors available in BornAgain either deal with disordered particles, isotropic short-range order or long-range ordered lattices. For the spin-liquid modeling of the statistical mixture of spin clusters in the glassy and paramagnetic regime a different treatment is needed.
6.3 Empirical magnetic structure factor
To the authors' knowledge there is no analytic solution for the structure factor of the dipolar coupled triangular lattice. There are, however, well established Monte-Carlo techniques that allow the determination of the spin–spin correlations (structure factor) on a limited-sized lattice with finite temperature. We have used the same modeling described in ref. 11 to calculate the structure factors for various temperatures of the two systems measured here. To be able to calculate the scattering intensity via the DWBA, we have then developed an empirical function to approximate this structure factor and integrated it into BornAgain as an interference function to be used in our model.The empirical structure factor consists of two components:
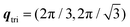 associated with the stripe-domain superstructure of the symmetric lattice.
associated with the stripe-domain superstructure of the symmetric lattice.
The amount of tri-state spectral weight is ηtri between 0 and 1. If ηtri = 0, our structure factor model is equivalent to the BornAgain implementation of a 2D lattice of antiferromagnetic particles with stripe-order and three orientations. A single stripe direction can be singled out with a scaling parameter for the main direction η23 = 1. Each peak uses 2D Lorentzian functions:
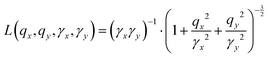 | (2) |
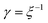 .
.
The peak shape for the tri-state is based on the Pseudo-Voigt function PV, a linear combination of 2D Lorentz L and Gauss G functions:
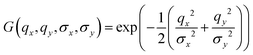 | (3) |
| PV(qx,qy,σx,σy,γx,γy,ηPV) = ηPVL(qx,qy,γx,γy) + (1 − ηPV)G(qx,qy,σx,σy) | (4) |
To generate the three-fold peak symmetry, a mapping of ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) is performed in polar coordinates with the origin at the peak center. While the radius is kept constant, the polar angle is multiplied by 3/2 to generate 3-fold symmetry from the existing 2-fold symmetry.
is performed in polar coordinates with the origin at the peak center. While the radius is kept constant, the polar angle is multiplied by 3/2 to generate 3-fold symmetry from the existing 2-fold symmetry.
In the model implementation an arbitrary reciprocal space vector is first scaled to the lattice size, translational symmetry is imposed by mapping the vector to the first Brillouin zone (BZ) and local point-symmetry around 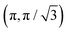 is imposed by mirroring half of the BZ around this point. In the resulting region, only one tri-state peak and three stripe-state peaks need to be calculated.
is imposed by mirroring half of the BZ around this point. In the resulting region, only one tri-state peak and three stripe-state peaks need to be calculated.
For the distorted lattice, the BZ is mapped on the symmetric lattice to keep the correct peak location. In addition to the possibility to have a dominant stripe direction using η23, it is possible to use different correlation lengths for these directions. One can observe in the Monte-Carlo results that the tri-state peaks tend to move closer to the dominant stripe-state peaks for increased distortion, making the structure factor more “rectangular”. To allow for this effect, another adjustment to qx can be defined using the scaling parameter ηrectify that projects qx to values closer to π.
The resulting function was then fitted to the temperature-dependent Monte-Carlo results. For temperatures above the transition to the long-range stripe-ordered phase, the parameters vary smoothly. Therefore, we have employed a global fit with linear or quadratic spline behaviour of all parameters.
We therefore can use the effective temperature T/J23 (see Fig. 1a) as a single fitting parameter to map the structure factor obtained from Monte-Carlo simulations to a phenomenological DWBA structure-factor model. The source code and a detailed comparison of the empirical model to the Monte-Carlo simulation are available via the Zenodo repository 10.5281/zenodo.4161444.
6.4 Magnetic modeling
While the structural long-range correlations of the sample are ideal for measuring emergent short-range magnetic correlations (as it allows the measurement of the Bragg peaks without significant structural background scattering), this violates the assumption of small in-plane scattering used in DWBA. This can already be seen from the experiment (Fig. 4b), where the specular reflection (green points) drops significantly for ϕ ≈ ±0.3° and the Bragg peak reaches approximately 30% of the specular intensity. The model calculates intensities far above the incident intensity, which is another hint that the DWBA calculation does not yield physically accurate intensity values.To circumvent this limitation for the analysis of the magnetic order we have therefore split the DWBA model into two parts that are later combined into one intensity. First we have performed the structural calculation as described in Section 6.1. This yields the specular reflection and residual structural Bragg peaks. For the magnetic part, the structural lattice is removed and replaced with a homogeneous layer material using the surface averaged SLD of the lattice. In this homogeneous material, magnetic cylinders are embedded and the structure factor model described above is applied to the particle system. As the magnetic order will have a far shorter correlation length, the scattering is small and DWBA can be used without issues.
Unpolarised measurements at ϕ = 0° and 90° have been used and the Yoneda line (given by the orange boundaries in Fig. 5) extracted. The background region at higher qz was subtracted from the data before it was co-refined with the magnetic model for the symmetric and 10% distorted lattice. Free parameters of the fit are nuclear and magnetic intensity for each direction as well as the normalised temperature T/J23 (see Fig. 1a).
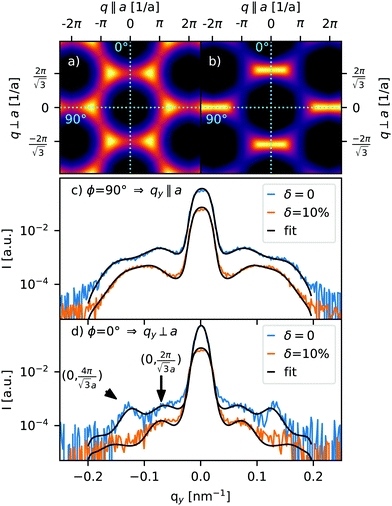
The results of the fits are shown in Fig. 6. In the top row, the pure§ structure factor used in the model for the full reciprocal unit cell is displayed. In addition to the structure factor, the Yoneda intensity is modulated by the cylinder form factor of the nanomagnets, which results in a drop of intensity for higher qy. The model can be directly compared to the theoretical predictions.11 Below, one can see the fit results (solid black line) for the two sample orientations ϕ = 90° and ϕ = 0°, corresponding to horizontal and vertical cuts in the structure factor, respectively. For the ϕ = 0° orientation, the magnetic contributions are very similar for both samples, with one relatively weak half order peak. The location of the peaks differ due to the lattice compression when viewed in this direction. Taking a look at the structure factor, this is not surprising as the cut is perpendicular to the honeycomb boundaries at 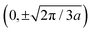 , which are always relatively narrow regardless of distortion and temperature. The outer peaks for this orientation are just the structural reflections from the lattice located at
, which are always relatively narrow regardless of distortion and temperature. The outer peaks for this orientation are just the structural reflections from the lattice located at 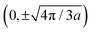 .
.
The interesting differences can be observed at ϕ = 90° where the distorted lattice displays a single broad peak and the symmetric system is more structured. Here the peaks directly resemble the tri-state peaks and stripe domain correlation structure around (±2π, 0). The symmetric lattice has a dominating tri-state fraction with a little intensity between the two peaks, while the distorted lattice is dominated by the stripe domains that are aligned along the uncompressed direction. While both structure factors show spin-liquid-like correlations, the distinct appearance indicate that the compression leads to a promotion of stripe-like correlations.
7 Conclusions
We have probed the magnetic correlations in an artificial triangular Ising spin system with grazing-incidence small-angle neutron scattering. We have developed an empirical magnetic structure factor in order to calculate scattering patterns including disordered magnetic moments, isotropic short-range order and long-range order in the DWBA, and have integrated this into the open-source software BornAgain. In addition, we were able to fit our model to temperature-dependent Monte-Carlo simulations. We determined that there is a very weakly correlated paramagnetic phase present in the symmetric and compressed system. The compressed lattice has a clear influence on the directionality of the structure factor and, as predicted by theory, favours stripe-like correlations with the propagation vector along the distorted direction.In order to determine whether the spin system is dynamic or static at room temperature, temperature-dependent measurements are needed. A fully rotatable sample stage could be used to give access to different parts of the structure factor in order to obtain more details about the magnetic configuration. For our system of out-of-plane Ising moments on a triangular lattice, this provides a means to observe the fascinating spin-liquid phase and stripe-ordered ground state quantitatively and in detail.
As demonstated in this work, our approach of simple, empirical functions within a custom DWBA structure factor can be used to model experimental GISANS data of numerous systems with magnetic short-range correlations. The comparison with theoretical predictions then allows the probing and verification of the properties of intriguing magnetic phases, and other systems with frustrated and competing interactions.
Conflicts of interest
There are no conflicts to declare.Appendix
The data that support this study are available via the Zenodo repository. See DOI: 10.5281/zenodo.4161444.Acknowledgements
The authors thank Vitaly Guzenko for support with the template fabrication. Petai Pip, Laetitia Philippe and Laura J. Heyderman acknowledge funding from the Swiss National Science Foundation (project no. 200020_172774). Naëmi Leo has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska Curie Grant Agreement No. 844304 (LICONAMCO). Frédéric Mila and Andrew Smerald acknowledge the Swiss National Science Foundation and its SINERGIA network “Mott physics beyond the Heisenberg model” (project number CRSII2_160765) for financial support.References
- C. Desvaux, C. Amiens, P. Fejes, P. Renaud, M. Respaud, P. Lecante, E. Snoeck and B. Chaudret, Nat. Mater., 2005, 4, 750–753 CrossRef CAS PubMed.
- E. Wetterskog, C. Jonasson, D.-M. Smilgies, V. Schaller, C. Johansson and P. Svedlindh, ACS Nano, 2018, 12, 1403–1412 CrossRef CAS PubMed.
- S. H. Skjærvø, C. H. Marrows, R. L. Stamps and L. J. Heyderman, Nat. Rev. Phys., 2019, 2, 13–28 CrossRef.
- H. Arava, P. M. Derlet, J. Vijayakumar, J. Cui, N. S. Bingham, A. Kleibert and L. J. Heyderman, Nanotechnology, 2018, 29, 265205 CrossRef PubMed.
- H. Arava, N. Leo, D. Schildknecht, J. Cui, J. Vijayakumar, P. M. Derlet, A. Kleibert and L. J. Heyderman, Phys. Rev. Appl., 2019, 11, 054086 CrossRef CAS.
- M. Krawczyk and D. Grundler, J. Phys.: Condens. Matter, 2014, 26, 123202 CrossRef CAS PubMed.
- S. Ladak, D. E. Read, G. K. Perkins, L. F. Cohen and W. R. Branford, Nat. Phys., 2010, 6, 359 Search PubMed.
- E. Mengotti, L. J. Heyderman, A. F. Rodríguez, F. Nolting, R. V. Hügli and H.-B. Braun, Nat. Phys., 2011, 7, 68 Search PubMed.
- V. Kapaklis, U. B. Arnalds, A. Harman-Clarke, E. T. Papaioannou, M. Karimipour, P. Korelis, A. Taroni, P. C. W. Holdsworth, S. T. Bramwell and B. Hjörvarsson, New J. Phys., 2012, 14, 035009 CrossRef.
- L. Anghinolfi, H. Luetkens, J. Perron, M. G. Flokstra, O. Sendetskyi, A. Suter, T. Prokscha, P. M. Derlet, S. L. Lee and L. J. Heyderman, Nat. Commun., 2015, 6, 8278 CrossRef CAS PubMed.
- A. Smerald and F. Mila, SciPost Phys., 2018, 5, 30 CrossRef.
- O. Sendetskyi, V. Scagnoli, N. Leo, L. Anghinolfi, A. Alberca, J. Lüning, U. Staub, P. M. Derlet and L. J. Heyderman, Phys. Rev. B, 2019, 99, 214430 CrossRef CAS.
- O. Halpern and M. H. Johnson, Phys. Rev., 1939, 55, 898–923 CrossRef CAS.
- T. J. Hicks, Adv. Phys., 1996, 45, 243–298 CrossRef CAS.
- S. W. Lovesey, Theory of Neutron Scattering from Condensed Matter: Volume 2: Polarization Effects and Magnetic Scattering. The International Series of Monographs on Physics, Oxford University Press, New York, 1986 Search PubMed.
- S. Maleev, V. Bar'yakhtar and R. Suris, Sov. Phys.-Solid State, 1963, 4, 2533–2539 Search PubMed.
- R. M. Moon, T. Riste and W. C. Koehler, Phys. Rev., 1969, 181, 920–931 CrossRef CAS.
- E. Kentzinger, H. Frielinghaus, U. Rücker, A. Ioffe, D. Richter and T. Brückel, Phys. B, 2007, 397, 43–46 CrossRef CAS.
- K. Theis-Bröhl, D. Mishra, B. P. Toperverg, H. Zabel, B. Vogel, A. Regtmeier and A. Hütten, J. Appl. Phys., 2011, 110, 102207 CrossRef.
- P. Müller-Buschbaum, Polym. J., 2013, 45, 34–42 CrossRef.
- R. F. Wang, C. Nisoli, R. S. Freitas, J. Li, W. McConville, B. J. Cooley, M. S. Lund, N. Samarth, C. Leighton, V. H. Crespi and P. Schiffer, Nature, 2006, 439, 303 CrossRef CAS PubMed.
- E. Mengotti, L. J. Heyderman, A. Fraile Rodríguez, A. Bisig, L. Le Guyader, F. Nolting and H. B. Braun, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 144402 CrossRef.
- O. Sendetskyi, L. Anghinolfi, V. Scagnoli, G. Möller, N. Leo, A. Alberca, J. Kohlbrecher, J. Lüning, U. Staub and L. J. Heyderman, Phys. Rev. B, 2016, 93, 224413 CrossRef.
- N. Rougemaille and B. Canals, Eur. Phys. J. B, 2019, 92, 62 CrossRef.
- G. H. Wannier, Phys. Rev., 1950, 79, 357–364 CrossRef.
- C. V. Manzano, J. P. Best, J. J. Schwiedrzik, A. Cantarero, J. Michler and L. Philippe, J. Mater. Chem. C, 2016, 4, 7658–7666 RSC.
- S. Mattauch, A. Koutsioubas, U. Rücker, D. Korolkov, V. Fracassi, J. Daemen, R. Schmitz, K. Bussmann, F. Suxdorf, M. Wagener, P. Kämmerling, H. Kleines, L. Fleischhauer-Fuß, M. Bednareck, V. Ossoviy, A. Nebel, P. Stronciwilk, S. Staringer, M. Gödel, A. Richter, H. Kusche, T. Kohnke, A. Ioffe, E. Babcock, Z. Salhi and T. Bruckel, J. Appl. Crystallogr., 2018, 51, 646–654 CrossRef CAS PubMed.
- G. Pospelov, W. Van Herck, J. Burle, J. M. Carmona Loaiza, C. Durniak, J. M. Fisher, M. Ganeva, D. Yurov and J. Wuttke, J. Appl. Crystallogr., 2020, 53, 262–276 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: S1: IPython notebooks, S2: Method details. See DOI: 10.1039/d1nh00043h |
| ‡ These authors contributed equally to this work. |
| § The pure magnetic structure factor only includes spin–spin correlations in the 2D and Born approximation, which is equivalent to the Fourier transform of the magnetic moment direction on the triangular lattice. |
| This journal is © The Royal Society of Chemistry 2021 |