Free volume dependence of dielectric behaviour in sandwich-structured high dielectric performances of poly(vinylidene fluoride) composite films
Lei
Yang
a,
Lanqiong
Yang
a,
Kun
Ma
a,
Yu
Wang
a,
Tong
Song
a,
Liliang
Gong
a,
Jian
Sun
a,
Ling
Zhao
a,
Zhihong
Yang
a,
Jianmei
Xu
a,
Qing
Wang
 b,
Guogang
Li
b,
Guogang
Li
 a and
Wei
Zhou
a and
Wei
Zhou
 *ac
*ac
aFaculty of Materials Science and Chemistry, China University of Geosciences, Wuhan 430074, China. E-mail: weizhou@cug.edu.cn
bDepartment of Materials Science and Engineering, The Pennsylvania State University, University Park, PA 16802, USA
cZhejiang Institute, China University of Geosciences, Hangzhou 311305, China
First published on 8th December 2020
Abstract
A dielectric film with a trilayer structure is fabricated to obtain both a high dielectric constant and superior electrical breakdown strength simultaneously. The outer layers of the trilayered composite film are composed of barium titanate (BTO) particles dispersed in poly(vinylidene fluoride) (PVDF) to ensure a relatively high dielectric constant, while the central layer of the composite film consists of exfoliated hexagonal boron nitride nanosheets (BNNS) dispersed in PVDF to provide high electrical breakdown strength. Compared with pristine PVDF, the dielectric constant and breakdown strength are simultaneously enhanced due to the sandwich structure, and the dielectric loss is maintained at a low level. Most important of all, positron annihilation lifetime spectroscopy (PALS) is applied to study the atomic-scale free volume holes of PVDF composite films and the effect of free volume holes on the dielectric constant and breakdown strength. Results show that the size of free volume holes of PVDF increased with the addition of BTO, but it decreased firstly and then increased with the BNNS loading. The correlation between dielectric properties and the size of free volume holes of the PVDF matrix was discussed in each layer. It is illustrated that the experimental dielectric constant of the PVDF/BTO single-layered film is consistent with the theoretical value at a lower BTO loading but smaller than the theoretical value at a higher BTO loading, which is probably ascribed to the increased size of free volume holes. The breakdown strength of the PVDF/BNNS film increased with the introduction of BNNS and the reduced size of free volume holes, which is ascribed to the reduced partial discharge phenomenon. The atomic-scale microstructure analysis based on free volume holes provides valuable ideas and new understanding for the study of the mechanism of the dielectric behaviour of polymer composites.
1. Introduction
Capacitors are widely used in consumer electronics and hybrid electric vehicles. As one of the key components of capacitors, dielectric materials must have a higher energy storage density to adapt to the development trend of product miniaturization and lightweight. Based on this, polymeric dielectric materials recently have attracted more and more attention due to their good comprehensive performances. Amongst different kinds of polymers, poly(vinylidene fluoride) (PVDF) has been paid much attention due to its superior physical properties such as low density, outstanding mechanical properties, being pollution free, extraordinary chemical resistance, piezoelectricity, dielectric properties, aging resistance, flexibility and excellent thermal stability.1–4 In terms of application, PVDF is used in various aspects like separation membranes5 and flexible capacitors.6However, it is still challenging to fabricate polymeric dielectric materials with a high dielectric constant and high electrical breakdown strength. On the other hand, when compared with their electrochemical counterparts, such as batteries and super capacitors, film capacitors are severely limited by the amount of energy that can be stored in dielectric materials. The energy density of commercially available biaxially oriented polypropylene (BOPP) capacitors is much lower than that of their electrochemical counterparts.7
Typically, the discharge energy density (Ue) of nonlinear dielectrics is determined by the applied electric field and electric displacement, which is relevant to the dielectric constant. For linear dielectric materials, Ue is dominated by the strength of applied electric field (E) and relative dielectric constant (εr), which is plotted as:
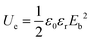 | (1) |
Polymers are preferred as dielectric materials for high energy density capacitors because of their superior breakdown strength and flexibility. However, the dielectric constant of polymers is relatively low, typically lower than 10. In this case, different kinds of ceramics, such as barium titanate (BTO) and lead zirconate titanate (PZT), were introduced into polymers to fabricate composites with improved dielectric properties.8–11 Besides, conductive metal particles12,13 or conductive carbon materials14–17 were also utilized on the basis of percolation theory. However, the high dielectric constant of composites is typically achieved at the expense of breakdown strength.7 The existence of inhomogeneous field distribution owing to the large contrast of the dielectric constant between the filler and the matrix yields sharply decreased Eb of the composites.18
Typically, simultaneous enhancements of the dielectric constant and breakdown strength have been achieved in the multilayered polymer composites.19,20 In sandwich-structured dielectric composites, enhancements of the dielectric constant and breakdown strength can be simultaneously achieved due to the integration of different functional layers of composites. Compared with single-layered composites, the introduction of a highly insulating layer could increase the breakdown strength of composites and a high dielectric constant could be achieved with the addition of a ceramic filler to provide high electrical polarization.21,22
In some other previous works, sandwich-structured composites were fabricated and showed relatively superior performance. However, most previous works23–25 are mainly focused on how to improve the dielectric properties of polymer composites through matrix and (or) filler selection, modification and structure design, but rare research studies touch deeply the discussion of the relationship between the dielectric properties and atomic-scale microstructure of the matrix and fillers.
The superior dielectric properties of PVDF are intensively correlated with the orientation of dipoles, which relies on the motion state of molecular chains and the motion space provided by free volume of the polymer.26,27 Besides, the breakdown strength is probably related to the defects brought by the free volume of the polymer. The free volume theory of polymers developed by Fox and Flory et al.28–31 is based on the idea that the motion of molecules in the bulk state is dependent on the existence of holes. And the free volume of polymers is considered to be closely related to many physical properties such as mechanical, thermal, electrical, diffusion and permeability properties. As a unique and non-destructive method, positron annihilation lifetime spectroscopy (PALS) is widely accepted for the characterization of atomic-scale free volume holes of polymers.32–34 PALS provides a powerful tool to study the influence of the molecular chain movement of the polymer matrix on the dielectric properties.
In this work, exfoliated ultra-thin boron nitride nanosheets and barium titanate were introduced to fabricate sandwich-structured composites with PVDF/BTO as outer layers and PVDF/BNNS as the central layer. Different from previous works,7,20 outer layers incorporate a high dielectric constant BTO filler and the central layer is functionalized with the introduction of exfoliated ultra-thin BNNS. The BNNS possesses unique properties including a wide band gap (≈5.9 eV), high mechanical strength, high thermal conductivity and low density.7,35,36 The BNNS is an efficient barrier against the leakage current and the space-charge conduction, thus enhancing breakdown strength and decreasing conduction loss of dielectric composites.37,38 On the other hand, BaTiO3 is a kind of typical ferroelectric ceramic with a high dielectric constant and is applicable to be introduced into a polymer as a filler with a high dielectric constant.20,39 Therefore, combining BNNS and BTO with PVDF is a predictably effective method to prepare composites with a simultaneously enhanced dielectric constant and breakdown strength.
In addition to focusing on the enhancement of dielectric properties, PALS is utilized to explore the effect of the addition of BTO or BNNS on the sizes of free volume holes and dielectric properties of polymers. The effects of atomic-scale free volume holes on the dielectric constant and breakdown strength were discussed based on the results of PALS and dielectric properties, providing a relatively novel approach and a new insight for the study of the mechanism of the dielectric behaviour of polymer composites.
2. Experimental section
2.1 Exfoliation of BNNS
Generally, boron nitride nanosheets are chemically exfoliated in organic solvents following a sonication-centrifugation process.37,40,41 In this work, N-methyl-2-pyrrolidone (NMP) was adopted as the solvent to exfoliate BNNS. Typically, 6 g h-BN powders (Aladdin) were dispersed in 450 mL NMP (Aladdin) under vigorous stirring for 10 h at room temperature. The BNNS dispersion was then subjected to tip-type sonication (Scientz-08, Scientz Biotechnology, China) with a power of 1680 W for 4 h, 8 h, 16 h, 20 h, 24 h, respectively. After sonication, the BNNS dispersion was centrifuged at 3000 rpm for 40 min and the supernatant was collected to obtain exfoliated BNNS. The supernatant was then centrifuged at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 20 min and the BNNS sediment was collected. After that, the collected BNNS sediment was washed with ethanol and dried at 70 °C for a certain amount of time.
000 rpm for 20 min and the BNNS sediment was collected. After that, the collected BNNS sediment was washed with ethanol and dried at 70 °C for a certain amount of time.
2.2 Fabrication of PVDF composite films
| Sample label | Sample type | Volume contents (vol%) | |||
|---|---|---|---|---|---|
| PVDF | BTO | BNNS | |||
| PVDF/10BTO | Single-layered film | 90 | 10 | 0 | |
| PVDF/2BNNS | Single-layered film | 98 | 0 | 2 | |
| 10-12-10 | SS film | Outer layers | 90 | 10 | 0 |
| Central layer | 88 | 0 | 12 | ||
2.3 Characterization
Scanning electron microscopy (SEM) measurements were performed with a Hitachi SU-8010 field emission electron microscope. X-ray diffraction (XRD) analysis was performed with a Bruker D8-ADVANCE, Germany with Cu Kα radiation (λ = 1.54 Å), a voltage of 40 kV and a current of 40 mA. Fourier Transform Infrared Spectrometry (FTIR) measurements were performed with a Fourier Transform Infrared Spectrometer, Thermo Fisher Nicolet iS50, USA, employing the attenuated total reflectance (ATR) mode. A differential scanning calorimeter (DSC) (NETZSCH STA409PC, Germany) was used to investigate the melting behaviour of samples. Samples were firstly heated from room temperature to 300 °C at a heating rate of 10 °C min−1 and were cooled down to room temperature at a cooling rate of 10 °C min−1. All the measurements were carried out under a nitrogen atmosphere. Positron lifetime measurements were performed on a conventional fast–fast coincidence lifetime spectrometer with a time resolution of 250 ps in full width at half maximum (FWHM). A 10 μCi 22Na source is sandwiched between two pieces of identical samples. For each sample, two lifetime spectra are collected with a total count of 106 for each spectrum. To meet the sample requirements of PALS measurement, the multilayer membranes were stacked together to ensure that their total thickness is larger than 1 mm on each side of the positron source. The temperature and relative humidity (RH) at which the tests were performed were at 23 °C and 55 RH%, respectively. Electrical breakdown strength measurements were performed with a voltage breakdown tester DDJ-50 kV, China, with an AC voltage rate-of-rise of 0.5 kV s−1. The dielectric constant and loss spectra were acquired using an Align Impedance Analyzer E4990A, USA. The holder used for samples was a High temperature dielectric measurement system HDMS-1000, Partulab, China. Before the measurement, gold was sputtered on both sides of the membranes to eliminate the contact resistance.3. Results and discussion
As illustrated in Fig. 1, the lateral size of BNNS is not obviously changed after sonication. However, the thickness of BNNS is clearly reduced with the sonication time increasing, which is shown in the distribution of thickness of BNNS in Fig. 2. It can be seen that the thickness of BNNS tends to be less when the sonication time is getting longer. As fewer-layer BNNS is more advantageous for the enhancement of breakdown strength,42,43 BNNS after sonication for 24 h has be adopted in the following experiments. As evidenced in the cross-section SEM images shown in Fig. 3, the fillers are well dispersed in the composite films. Fig. 3(a) shows that spherical BTO particles are well dispersed in the PVDF matrix even though the BTO content is up to 60 vol%. Similarly, nanosheets of boron nitride are clearly observed and well dispersed in the matrix, shown in Fig. 3(b). In addition, there are distinct boundaries between different functional layers in the trilayered composites, as shown in Fig. 3(c). The average thickness of the sandwich-structured composite film is about 21 μm. The thickness ratio of the two outer PVDF/BTO layers to the central PVDF/BNNS layer is approximately 1.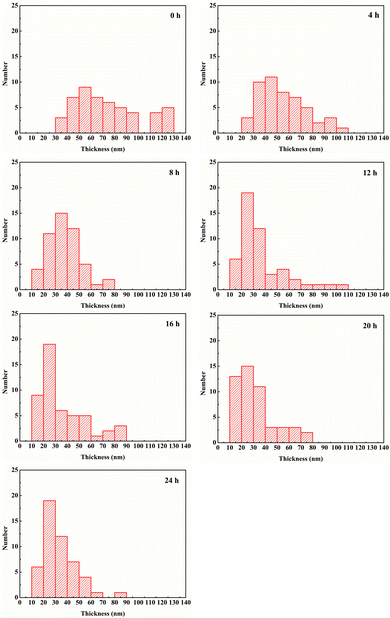 | ||
| Fig. 2 Distribution of the thickness of BNNS and 50 slices were counted for each group of samples. The time in the upper right corner of each figure represents the stripping time. | ||
The FTIR spectra of the single-layered and sandwich-structured PVDF composites are shown in Fig. 4. As illustrated in Fig. 4, the characteristic peaks of different crystal forms of PVDF appear in the spectra of composites. It can be demonstrated that α, β and γ crystal forms coexist in the polymer matrix. The absorption peaks appear at 416 cm−1, 480 cm−1, 604 cm−1, and 875 cm−1 are ascribed to α-phase of PVDF.44,45 Characteristic absorption peaks at 433 cm−1, 512 cm−1 and 1169 cm−1 are attributed to the presence of the β-phase.27 Besides, peaks at 512 cm−1, 835 cm−1, 1232 cm−1 and 1402 cm−1 correspond to the γ-phase of PVDF and the peak at 1071 cm−1 is ascribed to the wagging of –CH2 groups.27,44–47 From Fig. 4, characteristic absorption peaks of BTO and BNNS are obviously observed and no obvious chemical bonds are detected between the polymer and fillers.
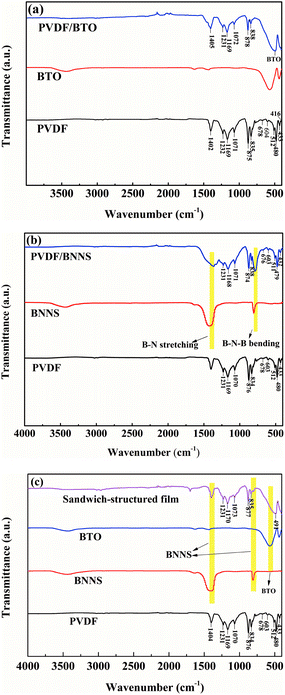 | ||
| Fig. 4 FTIR spectra of (a) BTO and PVDF/BTO composite, (b) BNNS and PVDF/BNNS composite, and (c) sandwich-structured PVDF composite. | ||
X-ray diffraction tests of different samples were performed and analysed further. As illustrated in Fig. 5(a), crystallization of exfoliated BNNS seems to be similar to that of unexfoliated BNNS. Characteristic peaks of BNNS appear at 26.9°, 41.8°, 44.0°, 50.2°, 55.2°, 76.1° and 82.3°, which correspond to the crystal plane (002), (100), (101), (102), (004), (110), and (112) of BNNS respectively. The spectrum of BTO is shown in Fig. 5(b) and characteristic peaks of BTO appear at 22.2°, 31.5°, 38.9°, 45.4°, 51.1°, 56.3°, 65.7°, 70.4° and 75.1°, corresponding to the crystal plane of (100), (101), (111), (200), (210), (211), (202), (212) and (310), respectively. As can be seen in Fig. 5(c), the characteristic peaks of BNNS at 26.9° and 55.2° are clearly observed in the single-layered PVDF/BNNS composite. Fig. 5(d) illustrates the crystal conditions of pristine PVDF and sandwich-structured composites. Characteristic peaks of PVDF at 18.4° and 39.0° are ascribed to the presence of the α-phase, and correspond to the crystal plane of (020) and (002) respectively.27,45–47 A diffraction peak at 20.3° is attributed to the β-phase corresponding to the (200) plane of PVDF.27
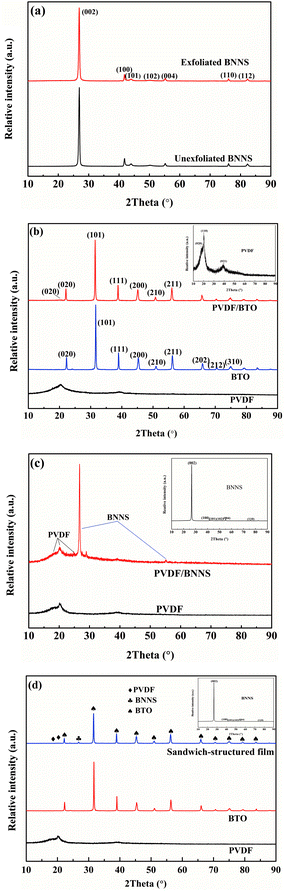 | ||
| Fig. 5 XRD patterns of (a) pristine and exfoliated BNNS, (b) BTO and PVDF/BTO composite, (c) BNNS and PVDF/BNNS composite, and (d) sandwich-structured PVDF composite. | ||
To clarify the change of melting temperature of composites with the addition of BTO and BNNS, DSC tests were performed. As shown in Fig. 6(a), with the addition of BTO, the melting point (Tm) of PVDF/BTO composites decreases gradually. Fig. 6(b) displays that the melting point of PVDF/BNNS composites seems to not change with the introduction of BNNS. In sandwich-structured composites, as shown in Fig. 6(c), melting point seems to be lower compared with neat PVDF and the Tm tends to gradually decrease with increasing BTO content, which is consistent with that of single-layer PVDF/BTO composites.
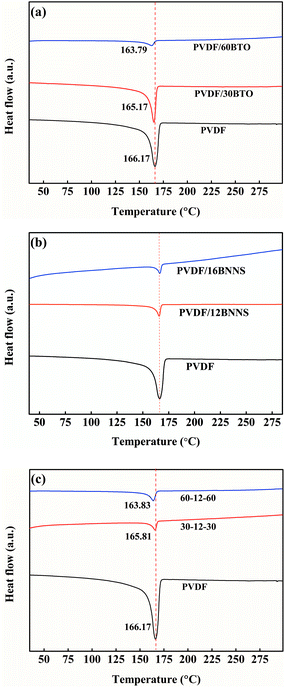 | ||
| Fig. 6 DSC spectra of (a) pristine PVDF and PVDF/BTO composite, (b) pristine PVDF and PVDF/BNNS composite, and (c) pristine PVDF and sandwich-structured PVDF composite. | ||
Analysis of positron lifetime spectra is conducted using the finite-term lifetime analysis PATFIT48 program. All the measured spectra are resolved into three components (τ1, τ2 and τ3) using PATFIT for discrete analysis. The long-lived component τ3 is ascribed to the o-Ps pick-off annihilation in free volume holes in amorphous regions.49 Assuming that the free-volume holes are spheres, the radius (R) and average size (V) of free volume holes are evaluated from τ3 from eqn (2) and (3), respectively:50
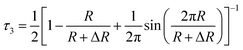 | (2) |
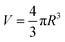 | (3) |
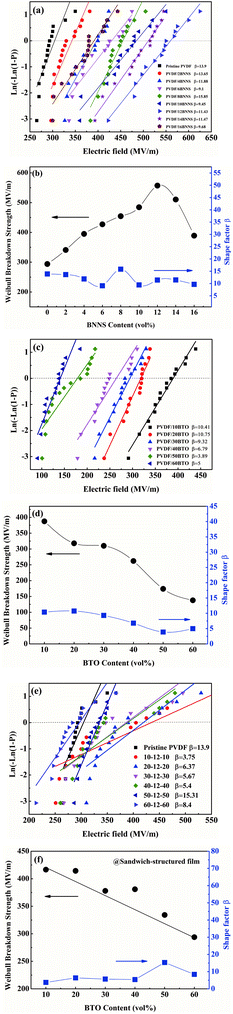
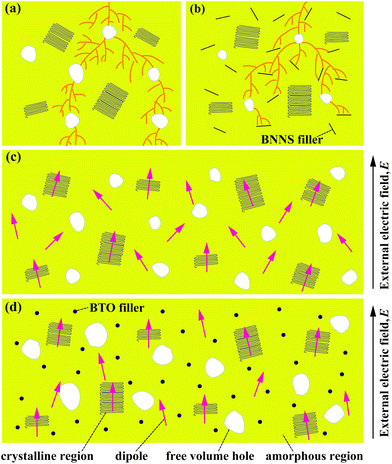
Generally speaking, the lifetime of o-Ps pick-off annihilation in polymers is mostly in the range from 1 to 10 ns, which is determined by the even size of the free volume holes. Besides, its intensity is proportional to the fraction of free volume holes. As shown in Fig. 7(a), o-Ps lifetime τ3 is slightly increased with the addition of BTO into single-layered PVDF/BTO composites, which means that the average size of free volume holes is improved. This is attributed to the motion of polymer molecular chains affected by the addition of the BTO filler. When BTO was introduced into the matrix, the stacking mode of PVDF was induced. The PVDF molecular chain segments were partly disarranged, resulting in the increase of the motility of molecules. Ultimately, the disarrangement of molecular chains causes the size of free volume holes to increase. In addition, the intensity of o-Ps lifetime, I3, shows dependence on the BTO content and is reduced as the BTO content increases, as shown in Fig. 7(b).
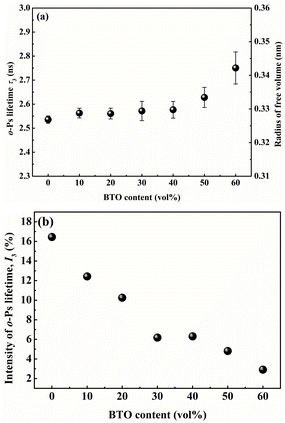 | ||
| Fig. 7 The BTO volume content dependence of (a) o-Ps lifetime and free volume radius of PVDF/BTO composites, and (b) the intensity of o-Ps lifetime of PVDF/BTO composites. | ||
In PVDF/BNNS composites, as shown in Fig. 8(a), o-Ps lifetime τ3 gradually decreases with BNNS content up to 12 vol% and increases with further increase of BNNS content, which means that the average size of free volume holes is firstly reduced and then increased. This is ascribed to the motion of polymer molecular chains affected by the addition of the BNNS filler. When the BNNS was introduced into the matrix, the conformation changes of PVDF were induced. The disarrangement of PVDF molecular chain segments due to the addition of BNNS will result in the increase of the motility of molecules. On the other hand, the probable interactions between the BNNS and matrix may probably limit the motion of the chains. Therefore, the variation of the size of free volume holes of the composites is the equilibrium of the above two influence factors52 and the change depends on which factor is predominant. Fig. 8(b) illustrates that the intensity of o-Ps lifetime, I3, shows dependence on the BNNS content and is reduced as the BNNS content increases.
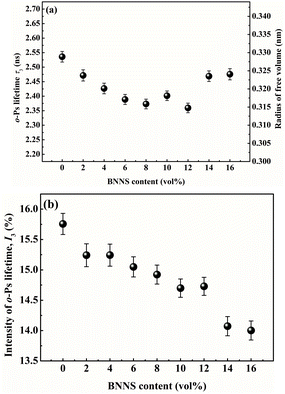 | ||
| Fig. 8 The BNNS volume content dependence of (a) o-Ps lifetime and free volume radius of the PVDF/BNNS composites, and (b) the intensity of o-Ps lifetime of PVDF/BNNS composites. | ||
The characteristic breakdown strength of the PVDF/BNNS composites is analyzed by a two-parameter Weibull statistic described as:42,53
| P(E) = 1 − exp[−(E/Eb)β] | (4) |
Based on the above results, 12 vol% was identified as the optimal BNNS content in the composites. Electrical breakdown strength of single-layer PVDF/BTO composites and sandwich-structured composites is also analyzed. As shown in Fig. 9(d), the breakdown strength of PVDF/BTO composite films decreased with the increase of the BTO content, and the PVDF/60BTO composite film has the lowest value of about 138 MV m−1. Subsequently, Eb of trilayered composites is measured and presented in Fig. 9(e). It is displayed that Eb reaches 410 MV m−1 in the sandwich-structured composite filled with 10 vol% BTO in the outer layers and 12 vol% BNNS in the central layer. Fig. 9(f) shows that when the BTO content increases further, breakdown strength of the composite gradually decreases.
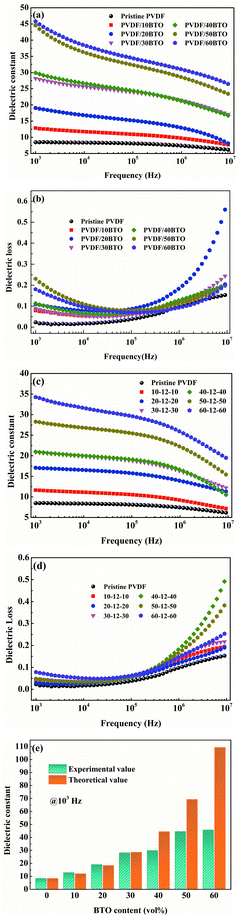
The dielectric properties of the single-layer PVDF/BTO composites and trilayer-structured composites with different BTO contents in the outer layers are presented in Fig. 11. As shown in Fig. 11(a) and (c), both the dielectric constants of single-layer PVDF/BTO composites and trilayer-structured composites increase steadily with the increase of BTO content. Moreover, based on the experiments and feasibility, the Jayasundere–Smith equation is utilized and the theoretical dielectric constant of PVDF/BTO composite films at 103 Hz is calculated:54,55
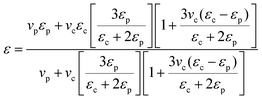 | (5) |
Based on the above analysis, the increased dielectric constant and differentiation of experimental and theoretical dielectric constants are probably attributed to the following factors. On the one hand, the increased size of free volume holes shown in Fig. 7(a) employs intrinsic dipoles in the polymer matrix additional space to orient themselves and more dipolar interfacial polarization exists according to the applied electric field,57,58 which is advantageous to enhance the dielectric constant. On the other hand, the increased size of free volume holes implies that the dipole density is reduced and more defects and holes exist in the composite films, indicating that there are more air components in the materials.59,60 This is definitely disadvantageous to the dielectric constant. Thus, the effect of the size of free volume holes on the dielectric constant is probably a competitive result of the above two factors. With low BTO loading, the positive and negative effects of the free volume holes are analogical, thus the experimental dielectric constant agrees well with the theoretical value. With high BTO loading, the size of free volume holes greatly increases, and the disadvantageous effect of free volume holes is predominant and resultantly the experimental dielectric constant is lower than the theoretical value. The free volume dependence mechanism of the dielectric constant of the PVDF/BTO composite film is diagrammatized in Fig. 10(c) and (d). Comparatively, in Fig. 11(c), with 60 vol% BTO in the outer layers of the trilayer-structured composite, the dielectric constant is increased from 8.4 of the PVDF matrix to about 35 measured at 1 kHz, which is lower than that of the single-layer PVDF/BTO composite with 60 vol% BTO loading. This is possibly ascribed to the relatively low dielectric constant of BNNS and reduced size of free volume holes in PVDF/BNNS composites. According to results in Fig. 8(a), the further reduced size of free volume holes decreases the space for intrinsic dipoles in PVDF to orient themselves in the applied electric field, which will negatively affect the dielectric constant. As shown in Fig. 11(a) and (c), the dielectric constant displays dependence on the frequency in the dielectric spectrum. This can be demonstrated that at lower frequency, the orientation polarization of dipoles and interface polarization can be achieved.61,62 However, at relatively high frequency, the change of the dipole moment orientation could not catch up with the frequency of the electric field63,64 and the displacement polarization of electrons and atoms is dominant. Dielectric loss of PVDF/BTO and trilayer-structured composites is shown in Fig. 11(b) and (d). Due to the addition of fillers, dielectric loss is increased compared with neat PVDF but still remains at a relatively low level. Interestingly, dielectric loss of trilayer-structured composites is lesser than that in single-layered composites which can be probably ascribed to the presence of BNNS.
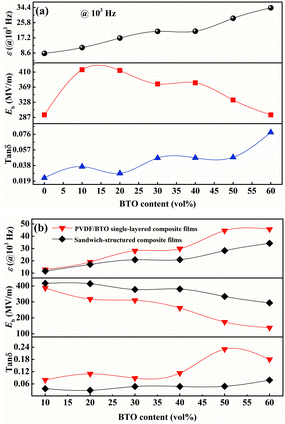
The change of dielectric constant (ε), breakdown strength (Eb) and dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of sandwich-structured composite films versus BTO content is plotted in Fig. 12(a). It presents that the sandwich-structured PVDF composite films display a greatly enhanced dielectric constant and breakdown strength, and dielectric loss maintains at a low level compared with pristine PVDF. Similarly, the comparison of sandwich-structured composite films and PVDF/BTO single-layered composite films is shown in Fig. 12(b). It shows that the dielectric constant of sandwich-structured composite films is smaller than that of PVDF/BTO single-layered composite films, which is ascribed to the relatively low dielectric constant of BNNS. It is noteworthy that the breakdown strength and dielectric loss of sandwich-structured composite films are superior to those of PVDF/BTO single-layered composite films due to the introduction of BNNS with outstanding insulating properties.
δ) of sandwich-structured composite films versus BTO content is plotted in Fig. 12(a). It presents that the sandwich-structured PVDF composite films display a greatly enhanced dielectric constant and breakdown strength, and dielectric loss maintains at a low level compared with pristine PVDF. Similarly, the comparison of sandwich-structured composite films and PVDF/BTO single-layered composite films is shown in Fig. 12(b). It shows that the dielectric constant of sandwich-structured composite films is smaller than that of PVDF/BTO single-layered composite films, which is ascribed to the relatively low dielectric constant of BNNS. It is noteworthy that the breakdown strength and dielectric loss of sandwich-structured composite films are superior to those of PVDF/BTO single-layered composite films due to the introduction of BNNS with outstanding insulating properties.
4. Conclusions
In general, PVDF-based single-layered and sandwich-structured composite films were prepared in this work. Compared with the pristine PVDF matrix, the substantially enhanced breakdown strength and enhanced dielectric constant have been simultaneously achieved from the sandwich-structured PVDF composite films. Compared with PVDF/BTO single-layered composite films, the breakdown strength of sandwich-structured PVDF composite films is further increased and the dielectric loss is reduced to a low level. Moreover, the atomic-scale free volume holes, which characterize the activity of polymer molecular chains, have also been discussed in this work, which are as important as the improvement of the dielectric performances mentioned above. The correlations between the dielectric properties and the size of free volume holes of the PVDF matrix were discussed in each layer. It is illustrated that the experimental dielectric constant of PVDF/BTO single-layered composite films is smaller than the theoretical value at a higher BTO loading, which is probably ascribed to the increased free volume hole size. The breakdown strength of the PVDF/BNNS composite film increased when the size of free volume holes decreased due to the reduced partial discharge phenomenon. The atomic-scale microstructure analysis based on free volume holes provides valuable ideas and new understanding for the study of the mechanism of the dielectric behaviour of polymer composite films.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (No. 11975212 and 11305145) and the Zhejiang Provincial Natural Science Foundation of China (No. LQY19A050001).Notes and references
- B. J. Chu, X. Zhou, K. L. Ren, B. Neese, M. R. Lin, Q. Wang, F. Bauer and Q. M. Zhang, Science, 2006, 313, 334–336 CrossRef CAS PubMed.
- P. Thomas, S. Satapathy, K. Dwarakanath and K. B. R. Varma, eXPRESS Polym. Lett., 2010, 4, 632–643 CrossRef CAS.
- B. C. Luo, X. H. Wang, Y. P. Wang and L. T. Li, J. Mater. Chem. A, 2014, 2, 510–519 RSC.
- Y. Wu, X. Y. Lin, X. Shen, X. Y. Sun, X. Liu, Z. Y. Wang and J. K. Kim, Carbon, 2015, 89, 102–112 CrossRef CAS.
- M. H. Razzaghi, A. Safekordi, M. Tavakolmoghadam, F. Rekabdar and M. Hemmati, J. Membr. Sci., 2014, 470, 547–557 CrossRef.
- M. F. Lin and P. S. Lee, J. Mater. Chem. A, 2013, 1, 14455–14459 RSC.
- F. H. Liu, Q. Li, J. Cui, Z. Y. Li, G. Yang, Y. Liu, L. J. Dong, C. X. Xiong, H. Wang and Q. Wang, Adv. Funct. Mater., 2017, 27, 1606292 CrossRef.
- R. Gregorio, M. Cestari and F. Bernardino, J. Mater. Sci., 1996, 31, 2925–2930 CrossRef CAS.
- A. K. Zak, W. C. Gan, W. A. Majid, M. Darroudi and T. S. Velayutham, Ceram. Int., 2011, 37, 1653–1660 CrossRef CAS.
- S. S. Kulkarni, P. B. Belavi and U. V. Khadke, AIP Conf. Proc., 2018, 1953, 090046 CrossRef.
- H. Tang and H. A. Sodano, Appl. Phys. Lett., 2013, 102, 063901 CrossRef.
- H. P. Xu, Z. M. Dang, N. C. Bing, Y. H. Wu and D. D. Yang, J. Appl. Phys., 2010, 107, 034105 CrossRef.
- Y. Zhang, Y. Wang, Y. Deng, M. Li and J. B. Bai, ACS Appl. Mater. Interfaces, 2012, 4, 65–68 CrossRef CAS PubMed.
- S. K. Rath, S. Dubey, G. S. Kumar, S. Kumar, A. K. Patra, J. Bahadur, A. K. Singh, G. Harikrishnan and T. U. Patro, J. Mater. Sci., 2014, 49, 103–113 CrossRef CAS.
- N. Yousefi, X. Y. Sun, X. Y. Lin, X. Shen, J. J. Jia, B. Zhang, B. Z. Tang, M. S. Chan and J. K. Kim, Adv. Mater., 2014, 26, 5480–5487 CrossRef CAS PubMed.
- R. Costa, J. Silva and S. L. Mendez, Composites, Part B, 2016, 93, 310–316 CrossRef.
- Y. Zhang, Y. Q. Wang, S. J. Qi, S. Dunn, H. S. Dong and T. Button, Appl. Phys. Lett., 2018, 112, 202904 CrossRef.
- J. Li, L. Zhang and S. Ducharme, Appl. Phys. Lett., 2007, 90, 132901 CrossRef.
- P. Hu, Y. Shen, Y. Guan, X. Zhang, Y. Lin, Q. Zhang and C. W. Nan, Adv. Funct. Mater., 2014, 24, 3172–3178 CrossRef CAS.
- Y. Wang, J. Cui, Q. Yuan, Y. Niu, Y. Bai and H. Wang, Adv. Mater., 2015, 27, 6658–6663 CrossRef CAS PubMed.
- P. Barber, S. Balasubramanian, Y. Anguchamy, S. Gong, A. Wibowo, H. Gao, H. Ploehn and H.-C. Zur Loye, Materials, 2009, 2, 1697–1733 CrossRef CAS.
- Y. Niu, Y. Bai, K. Yu, Y. Wang, F. Xiang and H. Wang, ACS Appl. Mater. Interfaces, 2015, 7, 24168–24176 CrossRef CAS PubMed.
- J. Chen, Y. F. Wang, X. W. Xu, Q. B. Yuan, Y. J. Niu, Q. Wang and H. Wang, J. Mater. Chem. A, 2019, 7, 3729–3736 RSC.
- M. A. Marwat, B. Xie, Y. W. Zhu, P. Y. Fan, W. G. Ma, H. M. Liu, M. Ashtar, J. Z. Xiao, D. Salamon, C. Samart and H. B. Zhang, Composites, Part A, 2019, 121, 115–122 CrossRef CAS.
- Z. Y. Li, F. H. Liu, H. Li, L. L. Ren, L. J. Dong, C. X. Xiong and Q. Wang, Ceram. Int., 2019, 45, 8216–8221 CrossRef CAS.
- A. Buchtemann, W. Stark and D. Geiss, Acta Polym., 1988, 39, 171–174 CrossRef.
- R. Gregorio and E. M. Ueno, J. Mater. Sci., 1999, 34, 4489–4500 CrossRef CAS.
- A. K. Doolittle, J. Appl. Phys., 1951, 22, 1471–1475 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1936, 4, 283–291 CrossRef CAS.
- T. G. Fox Jr. and P. J. Flory, J. Appl. Phys., 1950, 21, 581–591 CrossRef.
- Y. C. Jean, P. E. Mallon and D. M. Schrader, Principles and Applications of Positron and Positronium Chemistry, World Scientific, 2003 Search PubMed.
- P. M. Budd, N. B. McKeown and D. Fritsch, J. Mater. Chem., 2005, 15, 1977–1986 RSC.
- G. Golemme, J. B. Nagy, A. Fonseca, C. Algieri and Y. Yampolskii, Polymer, 2003, 44, 5039–5045 CrossRef CAS.
- D. Ponnamma, R. Ramachandran, S. Hussain, R. Rajaraman, G. Amarendra, K. T. Varughese and S. Thomas, Composites, Part A, 2015, 77, 164–171 CrossRef CAS.
- H. X. Tang, Z. Zhou and H. A. Sodano, ACS Appl. Mater. Interfaces, 2014, 6, 5450–5455 CrossRef CAS PubMed.
- Y. Song, Y. Shen, H. Y. Liu, Y. H. Lin, M. Li and C. W. Nan, J. Mater. Chem., 2012, 22, 8063–8068 RSC.
- Q. Li, K. Han, M. R. Gadinski, G. Z. Zhang and Q. Wang, Adv. Mater., 2014, 26, 6244–6249 CrossRef CAS PubMed.
- Q. Li, F. H. Liu, T. N. Yang, M. R. Gadinski, G. Z. Zhang, L. Q. Chen and Q. Wang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 9995–10000 CrossRef CAS PubMed.
- J. J. Li, J. Claude, L. E. Norena-Franco, S. I. Seok and Q. Wang, Chem. Mater., 2008, 20, 6304–6306 CrossRef CAS.
- C. Y. Zhi, Y. Bando, C. C. Tang, H. Kuwahara and D. Golberg, Adv. Mater., 2009, 21, 2889–2893 CrossRef CAS.
- J. N. Coleman, M. Lotya, A. O'Neill, S. D. Bergin, P. J. King, U. Khan, K. Young, A. Gaucher, S. De, R. J. Smith, I. V. Shvets, S. K. Arora, G. Stanton, H.-Y. Kim, K. Lee, G. T. Kim, G. S. Duesberg, T. Hallam, J. J. Boland, J. J. Wang, J. F. Donegan, J. C. Grunlan, G. Moriarty, A. Shmeliov, R. J. Nicholls, J. M. Perkins, E. M. Grieveson, K. Theuwissen, D. W. McComb, P. D. Nellist and V. Nicolosi, Science, 2011, 331, 568–571 CrossRef CAS PubMed.
- Q. Li, G. Z. Zhang, F. H. Liu, K. Han, M. R. Gadinski, C. X. Xiong and Q. Wang, Energy Environ. Sci., 2015, 8, 922–931 RSC.
- J. E. Padilha, R. B. Pontes and A. Fazzio, J. Phys.: Condens. Matter, 2012, 24, 075301 CrossRef.
- S. Dash, R. N. P. Choudhary and M. N. Goswami, J. Alloys Compd., 2017, 715, 29–36 CrossRef CAS.
- X. Xie, M. B. Zhou, L. Q. Lv, S. Y. Liu and J. Shen, Polymer, 2017, 132, 193–197 CrossRef CAS.
- R. S. Bharath, T. Chakraborthy, H. Nhalil, B. Masin, K. Ashok, H. Sreemoolanadhan, C. Oommen and S. Elizabeth, J. Mater. Chem. C, 2019, 7, 4484–4496 RSC.
- W. B. Zhang, Z. X. Zhang, J. H. Yang, T. Huang, N. Zhang, X. T. Zheng, Y. Wang and Z. W. Zhou, Carbon, 2015, 90, 242–254 CrossRef CAS.
- P. Kirkegaard, M. Eldrup, O. E. Mogensen and N. J. Pedersen, Comput. Phys. Commun., 1981, 23, 307–335 CrossRef CAS.
- L. M. Liu, P. F. Fang, S. P. Zhang and S. J. Wang, Mater. Chem. Phys., 2005, 92, 361–365 CrossRef CAS.
- S. Tao, J. Chem. Phys., 1972, 56, 5499–5510 CrossRef CAS.
- Y. C. Jean, Microchem. J., 1990, 42, 72–102 CrossRef CAS.
- W. Zhou, J. Wang, Z. Gong, J. Gong, N. Qi and B. Wang, Appl. Phys. Lett., 2009, 94, 021904 CrossRef.
- J. Claude, Y. Lu and Q. Wanga, Appl. Phys. Lett., 2007, 91, 212904 CrossRef.
- S. D. Cho, S. Y. Lee, J. G. Hyun and K. W. Paik, J. Mater. Sci.: Mater. Electron., 2005, 16, 77–84 CAS.
- R. Kota, A. F. Ali, B. I. Lee and M. M. Sychov, Microelectron. Eng., 2007, 84, 2853–2858 CrossRef CAS.
- C. J. Fu, N. Chen and G. P. Du, Ceram. Int., 2017, 43, 15927–15931 CrossRef CAS.
- Y. Thakur, R. Dong, M. R. Lin, S. Wu, Z. X. Cheng, Y. Hou, J. Bernholc and Q. M. Zhang, Nano Energy, 2015, 16, 227–234 CrossRef CAS.
- Y. Thakur, T. Zhang, C. Iacob, T. N. Yang, J. Bernholc, L. Q. Chen, J. Runt and Q. M. Zhang, Nanoscale, 2017, 9, 10992–10997 RSC.
- L. K. Lin, C. C. Hu, W. C. Su and Y. L. Liu, Chem. Commun., 2015, 51, 12760–12763 RSC.
- S. J. Park, H. S. Kim and F. L. Jin, J. Colloid Interface Sci., 2005, 282, 238–240 CrossRef CAS PubMed.
- Y. H. Li, M. Fan, K. Wu, F. L. Yu, S. G. Chai, F. Chen and Q. Fu, Composites, Part A, 2015, 73, 85–92 CrossRef CAS.
- S. H. Cho, M. Kim, J. S. Lee and J. Jang, ACS Appl. Mater. Interfaces, 2015, 7, 22301–22314 CrossRef CAS.
- Z. Q. Yang, Y. Yuan, F. L. Li and R. J. Liao, J. Appl. Polym. Sci., 2015, 132, 41385 Search PubMed.
- L. Y. Xie, X. Y. Huang, Y. H. Huang, K. Yang and P. K. Jiang, J. Phys. Chem. C, 2013, 117, 22525–22537 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |