Open Access Article
Open Access ArticleOptical magnetic lens: towards actively tunable terahertz optics†
Georgii
Shamuilov
 a,
Katerina
Domina
bc,
Vyacheslav
Khardikov
bc,
Alexey Y.
Nikitin
a,
Katerina
Domina
bc,
Vyacheslav
Khardikov
bc,
Alexey Y.
Nikitin
 *def and
Vitaliy
Goryashko
*def and
Vitaliy
Goryashko
 *a
*a
aDepartment of Physics and Astronomy, Uppsala University, Lägerhyddsvägen 1, Uppsala, 75120, Sweden. E-mail: vitaliy.goryashko@physics.uu.se
bSchool of Radio Physics, V. N. Karazin Kharkiv National University, 4, Svobody Square, Kharkiv 61022, Ukraine
cInstitute of Radio Astronomy of National Academy of Sciences of Ukraine, 4, Mystetstv Street, Kharkiv 61002, Ukraine
dDonostia International Physics Center (DIPC), 20018 Donostia-San Sebastián, Spain. E-mail: alexey@dipc.org
eIKERBASQUE, Basque Foundation for Science, 48013 Bilbao, Spain
fCIC nanoGUNE BRTA, Tolosa Hiribidea 76, E-20018 Donostia-San Sebastián, Spain
First published on 11th November 2020
Abstract
As we read this text, our eyes dynamically adjust the focal length to keep the image in focus on the retina. Similarly, in many optics applications the focal length must be dynamically tunable. In the quest for compactness and tunability, flat lenses based on metasurfaces were introduced. However, their dynamic tunability is still limited because their functionality mostly relies upon fixed geometry. In contrast, we put forward an original concept of a tunable Optical Magnetic Lens (OML) that focuses photon beams using a subwavelength-thin layer of a magneto-optical material in a non-uniform magnetic field. We applied the OML concept to a wide range of materials and found out that the effect of OML is present in a broad frequency range from microwaves to visible light. For terahertz light, OML can allow 50% relative tunability of the focal length on the picosecond time scale, which is of practical interest for ultrafast shaping of electron beams in microscopy. The OML based on magneto-optical natural bulk and 2D materials may find broad use in technologies such as 3D optical microscopy and acceleration of charged particle beams by THz beams.
The lens as a tool for focusing transmitted light has been around for four thousand years.1 It imprints a proper phase shift onto a light wavefront making the wavefront converging. Conventional optical components (lenses, waveplates, prisms) are optically thick,2 and rely on their geometry to imprint required phase shifts by means of the difference in refractive indices. This approach faces a fundamental limitation: the lack of transparent materials with a high contrast of indices of refraction (a higher index of refraction implies lower transparency because of the Kramers–Kronig relations).
In contrast, a new field of planar or flat optics has been thriving for the past decade. The concept consists in imprinting abrupt, controlled phase shifts onto transmitted light by a 2D array of subwavelength-thin nanoresonators, metasurface.3–10 Thus, planar optical components can be made nanometre thin and comply with industrial lithography fabrication.
One of the desired functionalities of both conventional and planar lenses is the active tunability of focal length: think of the eye. Nature's solution realised in mammals’ eyes is to tune the focal length by changing the curvature of the lens with the ciliary muscle and by employing a slight gradient of the index of refraction.11 A number of eye-inspired approaches and metasurface-based methods have been demonstrated using mechanical or electric control.12–24 Meanwhile, active ultrafast and wide tunability is still challenging.13
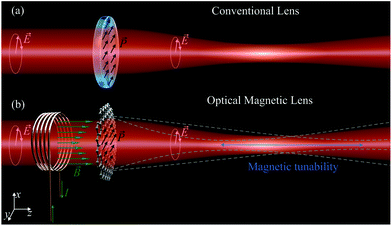
At the same time, actively tunable lenses have been used for around a century in electron microscopy to focus charged particle beams by spatially non-uniform magnetic fields. However, magnetic focusing does not apply to chargeless photon beams. In this article, we put forward an original concept of an Optical Magnetic Lens (OML) that focuses photon beams using a subwavelength-thin layer of a magneto-optical material immersed into a non-uniform magnetic field, sec. I. We set forth the physics of the OML and exemplify its performance in different frequency bands with bulk and 2D materials, sec. II.
The OML features tunability of the focal length via changing the strength or curvature of the magnetic field. Specifically, the wavefront of an optical beam incident onto the OML receives a phase shift according to the transverse distribution of the magnetic field strength (Fig. 1). The effect is the most profound in the vicinity of cyclotron resonance in the chosen material, with a phase shift up to one rad, resulting in cm-scale focal distances. An analysis of the practical realisation of the OML shows that a quite simple experimental setup can be used to test the OML concept, sec. III.
I. Brief theory
To illustrate our concept, let us examine the transformation of a Gaussian optical beam by the OML. Consider a subwavelength-thin, infinitely wide, flat layer of an isotropic medium, supporting free charges. The layer is immersed into an axially symmetric, static, non-uniform magnetic field B. The magnetic field is normal to the layer and its strength varies quadratically with distance in the medium [such as the field of a coil or ring, see Fig. 1]. Let the origin of a Cartesian coordinate system (x, y, z) be aligned with the extremum of the magnetic field in the layer and the z-axis being normal to the layer. A Gaussian optical beam is normally incident onto the layer with the beam waist positioned in the layer: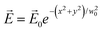 . Here,
. Here, 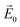 and w0 are the amplitude and waist, respectively. A sinusoidal behaviour in time at frequency ω is assumed.
and w0 are the amplitude and waist, respectively. A sinusoidal behaviour in time at frequency ω is assumed.
We treat the layer as an anisotropic medium with its charge carriers oscillating in the combined optical and static magnetic field. Solving the equations of motion for charge carriers in the layer and relating the electric current to the electric field, we find the tensor of dielectric permittivity [see ref. 25 and ESI (D)†]
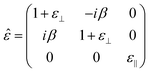 | (1) |
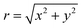 because the static magnetic field depends on r as B = B0p(r), with B0 being the field amplitude and p(r) the radial profile. For field inhomogeneity small on the wavelength scale, λd(log
because the static magnetic field depends on r as B = B0p(r), with B0 being the field amplitude and p(r) the radial profile. For field inhomogeneity small on the wavelength scale, λd(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p)/dr < 1, with λ being the wavelength, the functional form of
p)/dr < 1, with λ being the wavelength, the functional form of ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) remains unchanged [see ESI (D)†].
remains unchanged [see ESI (D)†].
The electric field of the Gaussian beam propagating through the layer in the positive z direction is governed by the inhomogeneous paraxial wave equation26
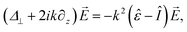 | (2) |
| (Δ⊥ + 2ik∂z)E± = −k2(ε⊥ ∓ β)E±. | (3) |
Outside the layer, the longitudinal field component Ez can be found from the Coulomb law 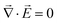 .
.
The reflected Gaussian beam propagating in the negative z direction is described by the same paraxial equation as (3) with the only difference that the wavenumber k must be replaced by −k. As usual in electrodynamics, the boundary conditions consist in the continuity of the electric field E± and its derivative with respect to the propagation coordinate z.
Since the layer is subwavelength thin, diffraction can be safely disregarded and the mathematical problem becomes essentially one-dimensional. The analytical solution for reflected and transmitted waves is described in terms of reflection,  , and transmission,
, and transmission, 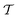 , Fresnel coefficients, respectively. Namely, the electric field of the transmitted optical beam reads as
, Fresnel coefficients, respectively. Namely, the electric field of the transmitted optical beam reads as 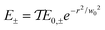 . For normal incidence, the Fresnel coefficients take on a simple and well known form27
. For normal incidence, the Fresnel coefficients take on a simple and well known form27
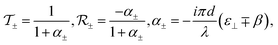 | (4) |
For a 2D material with conductivity σ±, the parameter α± is simply the normalised conductivity: α± = (2π/c)σ±. Furthermore, for a 2D material the coefficients 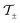 and
and 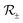 in eqn (4) are exact for any value of α±. Note that it is common to describe 2D materials by a conductivity tensor but we choose to use the permittivity tensor to unify the notations for 2D materials and thin layers of bulk materials.
in eqn (4) are exact for any value of α±. Note that it is common to describe 2D materials by a conductivity tensor but we choose to use the permittivity tensor to unify the notations for 2D materials and thin layers of bulk materials.
The Fresnel coefficients in eqn (4) depend on a local static magnetic field, 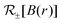 ,
, 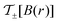 , thus setting the spatial phase profile of the reflected and transmitted electromagnetic fields of the beam. The inhomogeneous phase shift
, thus setting the spatial phase profile of the reflected and transmitted electromagnetic fields of the beam. The inhomogeneous phase shift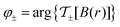 in eqn (4) impacts the shape of the transmitted wavefront. In particular, a quadratic profile of the magnetic field
in eqn (4) impacts the shape of the transmitted wavefront. In particular, a quadratic profile of the magnetic field
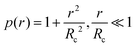 | (5) |
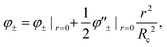 | (6) |
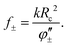 | (7) |
Image formation by the lens is well known in optics and discussed in ESI (B)† for completeness.
Examine the contents of results (4) and (7). First, the homogeneous part of the phase shift φ± leads to the Faraday rotation of linearly polarised light. Second, within the layer, the left and right circularly polarised components of the electric field experience different effective permittivities α±, and the focal length (7) contains different signs. Thus, the polarisation components have different focal lengths. Third, a comparison with full-wave simulations showed that the solution (7) is accurate under a constraint of w0 < 2Rc, more relaxed than the one in eqn (5). Fourth, the reflectivity of the layer can be high and thus allows for OML operation in reflecting telescope or mirror geometry.
To obtain an explicit expression for f± as a function of parameters of the film, let us proceed to the elements of the tensor ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) , eqn (1). The charges oscillate around the applied magnetic field with a frequency
, eqn (1). The charges oscillate around the applied magnetic field with a frequency 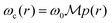 . Here, ω0 = qB0/mec is the reference (on-axis) cyclotron frequency with me being the electron mass,
. Here, ω0 = qB0/mec is the reference (on-axis) cyclotron frequency with me being the electron mass, 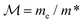 is the mass reduction ratio, q and m* are the charge and effective mass of the particle, respectively. In fact, the elements of the tensor
is the mass reduction ratio, q and m* are the charge and effective mass of the particle, respectively. In fact, the elements of the tensor ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) correspond to a magnetised plasma (Drude model)29–31 and read
correspond to a magnetised plasma (Drude model)29–31 and read
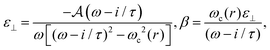 | (8) |
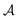 is a material-specific constant [s−2] and τ is the relaxation time. Particular cases with more familiar expressions for ε⊥ and β can be found in ESI (A).† Following eqn (4), we obtain a simple expression for the focal length for LH and RH circularly polarised waves transmitted through a layer of thickness d as
is a material-specific constant [s−2] and τ is the relaxation time. Particular cases with more familiar expressions for ε⊥ and β can be found in ESI (A).† Following eqn (4), we obtain a simple expression for the focal length for LH and RH circularly polarised waves transmitted through a layer of thickness d as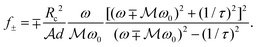 | (9) |
This simple result allows one to calculate the focal length of the OML for different materials as illustrated below. Due to the term 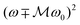 in the denominator in eqn (9), f± has a resonant behaviour for one of the polarisations of the optical beam for a given magnetic field orientation. Specifically, for a longitudinal magnetic field oriented along the positive direction of the z-axis, the cyclotron resonance,
in the denominator in eqn (9), f± has a resonant behaviour for one of the polarisations of the optical beam for a given magnetic field orientation. Specifically, for a longitudinal magnetic field oriented along the positive direction of the z-axis, the cyclotron resonance, 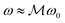 , occurs for the LH circularly polarised optical beam E+. In general, at the resonance eqn (9) simplifies to
, occurs for the LH circularly polarised optical beam E+. In general, at the resonance eqn (9) simplifies to 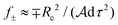 .
.
II. Examples of materials
Consider potential practical realisations of the OML for different frequency bands.Materials suitable for magnetic focusing in the microwave range are magnetic dielectrics, or ferrites, such as Yttrium Iron Garnet (YIG). Instead of charge carriers, there are unpaired spins precessing in the applied magnetic field. The functional form of ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) , eqn (1), and its components remain unchanged. Hence, the result in eqn (9) can be applied directly to ferrites, where ω0 should be understood as the Larmor frequency [see ESI (A)†].32 Practical results for the OML in the microwave region are presented in Table 1. A focal length of tens of centimeters is feasible. Ferrite-coated mirrors can potentially be used for tunable focusing of quasi-optical microwave beams in fusion experiments, e.g. for plasma probing or electron-cyclotron-resonance heaters.33,34
, eqn (1), and its components remain unchanged. Hence, the result in eqn (9) can be applied directly to ferrites, where ω0 should be understood as the Larmor frequency [see ESI (A)†].32 Practical results for the OML in the microwave region are presented in Table 1. A focal length of tens of centimeters is feasible. Ferrite-coated mirrors can potentially be used for tunable focusing of quasi-optical microwave beams in fusion experiments, e.g. for plasma probing or electron-cyclotron-resonance heaters.33,34
| Parameter | Graphene (T) | Graphene (R) | InSb (T) | InSb (R) | YIG (T) |
|---|---|---|---|---|---|
| Light frequency ω/2π | 1 THz | 1 THz | 3 THz | 2 THz | 50 GHz |
| Relaxation time τ | 0.5 ps | 1 ps | 3 ps | 3 ps | ≈0.1 μs |
| Efficiency (|T|2 or |R|2) | 32% | 55% | 27% | 66% | 72% |
| On-axis field B0 | 0.2 T | 0.2 T | 2.1 T | 1.7 T | 1.8 T |
| Field curvature Rc | 0.32 cm | 0.3 cm | 1.5 cm | 1.5 cm | 70 cm |
| Film thickness d | Monolayer | Monolayer | 0.6 μm | 3 μm | 0.1 μm |
| Focal length f | 8 cm | 40 cm | 16 cm | 40 cm | 51 cm |
To operate above microwaves, we need a material with a high mass reduction factor 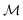 ,
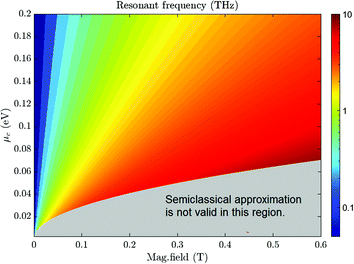
, 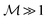 . Doped graphene is an outstanding candidate for a higher-frequency OML. We use the semiclassical model to describe doped graphene in magnetic fields.35 This model accounts only for intraband transitions, but is valid in a broad range covering the terahertz and mid-infrared bands under the condition
. Doped graphene is an outstanding candidate for a higher-frequency OML. We use the semiclassical model to describe doped graphene in magnetic fields.35 This model accounts only for intraband transitions, but is valid in a broad range covering the terahertz and mid-infrared bands under the condition 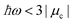 .35 Here, μc is the chemical potential and ħ is the reduced Planck constant.
.35 Here, μc is the chemical potential and ħ is the reduced Planck constant.
To use eqn (9) directly for a graphene sheet with a conductivity ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) , we approximate graphene by a layer with a finite thickness d and introduce an effective dielectric permittivity tensor
, we approximate graphene by a layer with a finite thickness d and introduce an effective dielectric permittivity tensor ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) eff = (4πi/ωd)
eff = (4πi/ωd)![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) .27 Then, the elements of
.27 Then, the elements of ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) eff assume the form given by eqn (8). As it should be for a 2D material, the dependence on d in f± cancels out. For doped graphene,
eff assume the form given by eqn (8). As it should be for a 2D material, the dependence on d in f± cancels out. For doped graphene, 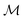 is meVF2/|μc|. We see that graphene poses an intriguing possibility of increasing the mass reduction factor M by increasing the Fermi velocity vF and operating with a small chemical potential μc. From the practical point of view this implies that the cyclotron resonance can be reached for lower magnetic fields for the same THz frequency. Recent experiments in the THz and IR regions show that the Fermi velocity can be engineered by placing graphene on a suitable dielectric substrate.36,37 Assuming a chemical potential μc = 0.19 eV and Fermi velocity VF = 2.5·106 m s−1, we estimate
is meVF2/|μc|. We see that graphene poses an intriguing possibility of increasing the mass reduction factor M by increasing the Fermi velocity vF and operating with a small chemical potential μc. From the practical point of view this implies that the cyclotron resonance can be reached for lower magnetic fields for the same THz frequency. Recent experiments in the THz and IR regions show that the Fermi velocity can be engineered by placing graphene on a suitable dielectric substrate.36,37 Assuming a chemical potential μc = 0.19 eV and Fermi velocity VF = 2.5·106 m s−1, we estimate 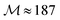 and
and 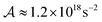 . The remaining parameters are listed in the Table 1.
. The remaining parameters are listed in the Table 1.
Let us take a closer look at the optical response of a graphene layer in a uniform magnetic field. First, we recall that for a longitudinal magnetic field oriented along the positive z-axis, the LH circularly polarised optical beam E+ exhibits a cyclotron resonance, see eqn (9). This is illustrated in Fig. 2, which shows a clear resonant behaviour of the transmitivity, reflectivity and phase shifts at the cyclotron resonance of 0.2 T. The distributions in the figure remain exactly the same for the RH circular polarisation for a reversed direction of the magnetic field due to the problem symmetry. The maximum of the derivative of the phase shift with respect to the magnetic field, dφ/dB0, suggests an operating point of the OML in a non-uniform magnetic field. Namely, for B0 ≈ 0.2 T, dφ/dB0 is maximal, and the graphene OML would attain the minimal value of f+ in a non-uniform field, given that other parameters are fixed. One should keep in mind that the OML focusing effect is dictated by the form of the spatial distribution of the magnetic field whereas the cyclotron resonance can only enhance the focusing effect but does not change its nature. The inverse relaxation time of graphene, 1/τ, plays the role of the resonance bandwidth: larger values of τ (high-purity graphene) provide a sharper resonance and thus a larger phase shift (on the order of one radian). At the same time, the OML appears tolerant to smaller τ values so that the graphene OML does not require high-quality graphene flakes for its reasonable performance.
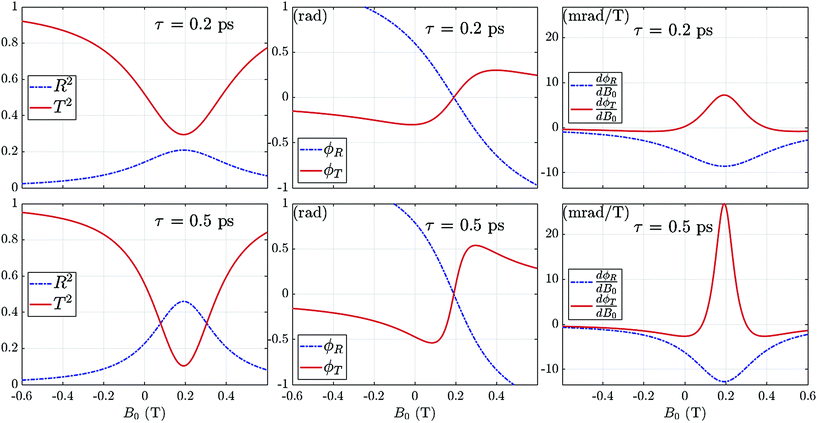 | ||
| Fig. 2 Transmission, reflection, phase shift and derivative dφ/dB0 of an LH circularly polarised optical beam calculated via Fresnel coefficients (4) for a graphene layer w.r.t. applied magnetic field B0 (uniform). The chemical potential is 0.19 eV. | ||
For practical applications, the cyclotron frequency for graphene can be written in the engineering form as
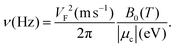 | (10) |
The behaviour of ν vs. B0 and |μc| for a representative set of parameters is shown graphically in Fig. 3.
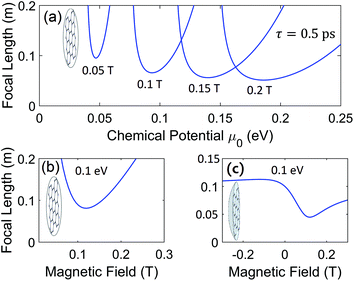
For the resonant LH circular polarisation of the optical beam incident onto graphene OML, we calculate a focal length of some cm with a wide adjustment range given by the field amplitude B0, Fig. 4b. Additional active adjustment of the focal length can be done by varying the chemical potential μc, Fig. 4a. Furthermore, f+ can be tuned by adjusting the curvature of the magnetic field, for example, by using a combination of a permanent ring magnet and a tunable current coil. Thus, the OML can bring vast tunability into existing THz optics.
We note that only one circular polarisation component undergoes resonant focusing by the OML [ , see eqn (9) and ESI (A)†], while the other circular polarisation component is barely affected. Unlike other materials considered in this article, graphene exhibits a striking difference between LH and RH circular polarisations. Hence, such a lens allows for selective focusing by choosing the direction of the external magnetic field. This effect can be potentially used for polarisation-sensitive detection of THz light.
, see eqn (9) and ESI (A)†], while the other circular polarisation component is barely affected. Unlike other materials considered in this article, graphene exhibits a striking difference between LH and RH circular polarisations. Hence, such a lens allows for selective focusing by choosing the direction of the external magnetic field. This effect can be potentially used for polarisation-sensitive detection of THz light.
The OML can also be used in combination with conventional lenses, substantially improving the performance of the latter. As an example, Fig. 4c shows 50% relative tunability of a conventional lens, having a fixed focal length f of 10 cm, decorated with the graphene OML. The focal distance of the combined lens can be tuned from around 5 to 12 cm as the magnetic field goes through the cyclotron resonance at 0.1 T. For negative (non-resonant) values of the magnetic field, the OML tuning effect is negligible.
To visualise the effect of the OML as well as to cross-check our analytical results, we run full-wave simulations for the particular example of graphene OML. We use commercial software COMSOL Multiphysics. Thanks to the azimuthal symmetry of the problem, the model can be built in 2D to reduce required computation power. The incident Gaussian beam (background field) is defined analytically and the graphene layer is represented as a surface current density given by a 2D conductivity tensor.27,31,35 The non-uniform magnetic field is included analytically via the components of the conductivity tensor.31 The final field distribution is calculated as the field scattered by the graphene layer.
The focusing effect is clearly seen in Fig. 5. If no magnetic field is applied (lens is “off”), the Gaussian beam diverges in the region to the right from the graphene OML (top plot). In contrast, a new waist of the beam appears (bottom plot), when a profiled magnetic field is applied (lens is “on”). The focal lengths calculated analytically, 6.5 cm, and numerically, 6.4 cm, match very well, thus validating our analytical approach, eqn (1)–(9). The simulated transmission efficiency defined as the ratio of the transmitted power to the incident one is 42%.
In Fig. 5, for having a sharper image and clearer visual illustration, we partly compensated for lens aberrations by adding a term −0.8r6/Rc6 to the magnetic field profile p(r). In the simulation, τ = 0.5 ps, μ0 = 0.1 eV, B0 = 0.09 T, Rc = 1.2w0, w0 = 6λ with λ = 300 μm.
Semiconductors and their heterostructures are another important example of materials for the OML. The sophisticated underlying mechanism of charge transport significantly reduces the effective mass of electrons,38,39 which can increase OML operating frequencies. The highest value of 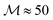 in this class of materials is achieved for indium antimonide (InSb).40 Assuming parameters tabulated in ref. 41, we calculate
in this class of materials is achieved for indium antimonide (InSb).40 Assuming parameters tabulated in ref. 41, we calculate 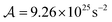 and the focal length of about 16 cm (see Table 1). Compared to graphene, tunability in InSb is limited to magnetic field only. Also, InSb exhibits phonon modes in the same frequency range suppressing resonant focusing at phonon frequencies.
and the focal length of about 16 cm (see Table 1). Compared to graphene, tunability in InSb is limited to magnetic field only. Also, InSb exhibits phonon modes in the same frequency range suppressing resonant focusing at phonon frequencies.
We also anticipate a possibility to use an array of ferromagnetic nanoresonators (e.g. TbCo42,43) for the OML at optical frequencies. Operating conditions are similar to those for ferrites discussed above. The focusing effect is weaker than in the THz range (the inhomogeneous phase shift is on the order of 10 mrad for B0 ∼ 1 T), but allows for fine-tuning of the focal length if the array is deposited on the surface of a plano-convex lens, similar to the example with graphene in Fig. 4c.
From a different perspective, the OML effect may impact propagation of electromagnetic waves in space similarly to a gravitational lens. Namely, a wavefront transformation may occur in cosmic plasma exposed to non-uniform magnetic fields generated by different massive astrophysical objects, thus affecting divergence of light from a remote source [see ESI (A)†].
III. Experimental considerations
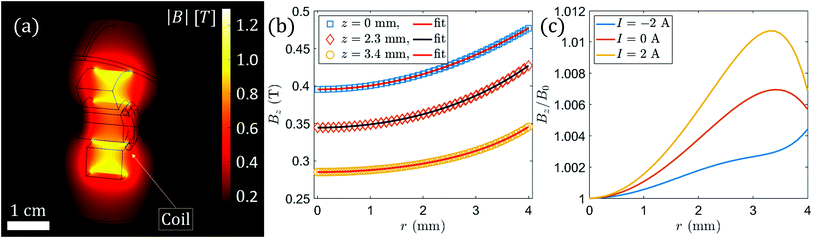
Let us describe a possible experimental setup for focusing THz light with a graphene-based lens. Reduced to its essentials, the setup can consist of just four key components: (1) the lens itself: a transparent substrate decorated with large-scale doped graphene fabricated with chemical vapour deposition;44 (2) a THz source based on optical rectification from, e.g., a zinc telluride crystal45 to generate an optical beam with a spectrum peaking at 1 THz; (3) a simple ring magnet to set the shape and focal length of the optical beam; (4) a THz beam imager based, for instance, on electro-optical sampling45 or an array of microbolometers.46 In practice, it is advantageous to place an additional thin current coil next to the ring magnet for fine tuning of the magnetic field curvature.Note that the phase shift of the transmitted light φ± given by the Fresnel coefficient (4) is a complex function of B and hence a complex function of r. Hence, in the regime of strong focusing (large non-uniformity of the magnetic field) the optical quality of the proposed OML suffers from spherical aberrations if a simple quadratic profile of the magnetic field is applied. To correct for the aberrations, the transverse profile of the magnetic field must have not only a quadratic component (r2), but also a component depending on r6. For instance, in the simulation in Fig. 5 the optimal transverse profile of B is (1 + r2/Rc2 − 0.8r6/Rc6). This profile can be realised in practice by properly choosing the longitudinal position of the graphene layer with respect to the ring magnet plane.
In Fig. 6, we show the magnetic field distribution for a typical commercial ring magnet. The transverse distribution of the longitudinal component of the magnetic field, Fig. 6b, changes with the longitudinal position. For certain longitudinal positions, close to the centre of the ring magnet, the magnetic field profile results in aberration-corrected focusing with the OML. In addition, a current coil can be used for fine tuning of the magnetic field profile.
For typical OML operation the radius of curvature of the magnetic field must be larger than the THz beam waist, Rc ≈ (1.2–1.3)w. At the same time, for a ring magnet Rc is often smaller than the physical radius of the ring R, see Fig. 6. Hence, nearly 100% transmission of the THz beam through the aperture of the ring is possible since R ≈ 1.5w. The typical numerical aperture is 0.1.
Thus, we have four different knobs in the OML magnet design to compensate for spatial aberrations: (i) the graphene layer position w.r.t. the ring magnet, (ii) the separation between the ring magnet and the current coil, (iii) the coil radius and (iv) the number of windings.
IV. Discussion
At THz frequencies, the response time of the graphene-based OML can potentially be as short as a few picoseconds. Though the physical mechanism of the phase shift induced in the OML is resonant and relies on cyclotron resonance, the relaxation time is typically less than a picosecond. That allows for ultrafast tuning. In practice, the response time will be limited by technical auxiliaries such as the response time of an electromagnetic coil used to create the required magnetic field profile. However, there is a promising solution for tuning the graphene-based OML on the picosecond time scale: to use quasi-half-cycle THz pulses45,47 to additionally control the chemical potential, see Fig. 4a, and correspondingly adjust the focal length.In contrast to sinusoidal electromagnetic pulses, quasi-half-cycle pulses maintain their electric field oriented in the preferential direction. Hence, the effect of such pulses on the graphene layer can be thought of as an instantaneous DC voltage. A permanent magnet can be used to preset a desired focal length of the OML and the electric field of an additional quasi-half-cycle THz pulse will modify the chemical potential on the picosecond time scale thus adjusting the focal length.
Compared to other tunable metalenses discussed in the literature, the OML offers (i) wide tunability of the operating frequency by one order of magnitude, see Fig. 3; (ii) 50% relative tunability of the focal length, see Fig. 4; (iii) the operating bandwidth of around 1 THz, see Fig. 2 and the discussion therein; and (iv) the transmission efficiency of 40%, see Fig. 5. To contrast our OML with other tunable metalenses, below we give a brief overview of the present state-of-the-art of the field. The existing designs of tunable metalens can broadly be divided into several classes. We consider representative examples from different classes irrespective of the frequency band since many designs can be extended to a longer wavelength regime.
In the class of electro-mechanically tunable lenses,16,18,48 mechanically stretchable substrates are used in the lens design. For instance, an infrared metalens on a dielectric elastomer actuator18 has a 100% relative tunability of the focal length. The reported response time is about 30 ms. In the near-infrared range, 130% focal length tuning is shown16 with the response time similar to the above. In the microwave range, an inverse-designed stretchable metalens48 allows for 75% relative tunability and about 70% transmission. In addition, Zhu et al.49 demonstrate a tunable microwave lens based on an array of cavities that can be filled with liquid metal using microfluidic technology and pneumatic valves. The lens shows an efficiency of 10% with a focal tunability of around 50%.
Many results are reported in the class of metalens based on phase-change materials.50–54 Tunability of the focal length of around 10–15% is typically reported with a focusing efficiency of 20%. However, the transmitted intensity usually changes dramatically as the focal length is tuned. In the case of a heat-induced phase change, the metalens response time of 2 minutes is reported.50
For tunable metalenses based on electrical control of the chemical potential of graphene,55–57 the focal length tunability of 10–20% is reported with efficiencies of 20–40%. The response time of such lenses is limited only by the switching time of a power supply, which can be on a microsecond scale. At the same time, for this class of lenses the operating frequency tunability is limited to some per cents as the operating frequency is set by the lens predefined geometry.
From the brief overview of the field, one can clearly see that the OML offers some advantages in terms of broad tunability of the focal length and operating frequency, wide operating bandwidth and high focusing efficiency. A very fast intrinsic response time of the OML is another intriguing feature interesting for ultrafast applications.
In summary, we introduced a concept of the magnetically tunable flat lens. It takes advantage of the resonant magnetic-field-dependent phase shift and features tunability by means of magnetic field control. We applied our model to a wide range of materials (semiconductors, graphene, ferrites and nanoparticle arrays), and found out that, with varying efficiency, the OML can be realised in a broad frequency range from microwaves to visible light. Moreover, using other magnetic field profiles, our OML can be reconfigured to operate as another optical component, e.g. as a beam deflector with a linear field profile or a grating with periodic field profile. We anticipate that the OML, based on available magneto-optical bulk and 2D materials, can find wide use in many optoelectronic technologies in a broad spectral range.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Prof. Oleg Kochukhov and Assoc. Prof. Vassilios Kapaklis (Uppsala University) for fruitful discussions, and Prof. Paolo Vavassori (CIC NanoGUNE).V. G. acknowledges the support of Swedish Research Council (Vetenskapsrådet) (grant no. 2016-04593) and A. Y. N. acknowledges the Spanish Ministry of Science, Innovation and Universities (national project MAT2017-88358-C3-3-R) and Basque Department of Education (PIBA-2020-1-0014).
References
- H. King, The History of the Telescope, Dover Publications, 2003 Search PubMed.
- B. E. Saleh and M. C. Teich, Fundamentals of photonics, John Wiley & Sons, 2019 Search PubMed.
- N. Yu, P. Genevet, M. A. Kats, F. Aieta, J.-P. Tetienne, F. Capasso and Z. Gaburro, Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction, Science, 2011, 334, 333–337 CrossRef CAS.
- L. Huang, X. Chen, H. Mühlenbernd, G. Li, B. Bai, Q. Tan, G. Jin, T. Zentgraf and S. Zhang, Dispersionless Phase Discontinuities for Controlling Light Propagation, Nano Lett., 2012, 12, 5750–5755 CrossRef CAS.
- P. Genevet, J. Lin, M. A. Kats and F. Capasso, Holographic detection of the orbital angular momentum of light with plasmonic photodiodes, Nat. Commun., 2012, 3, 1278 CrossRef.
- F. Aieta, P. Genevet, M. A. Kats, N. Yu, R. Blanchard, Z. Gaburro and F. Capasso, Aberration-Free Ultrathin Flat Lenses and Axicons at Telecom Wavelengths Based on Plasmonic Metasurfaces, Nano Lett., 2012, 12, 4932–4936 CrossRef CAS.
- X. Chen, L. Huang, H. Mühlenbernd, G. Li, B. Bai, Q. Tan, G. Jin, C.-W. Qiu, S. Zhang and T. Zentgraf, Dual-polarity plasmonic metalens for visible light, Nat. Commun., 2012, 3, 1198 CrossRef.
- A. Pors, M. G. Nielsen, R. L. Eriksen and S. I. Bozhevolnyi, Broadband Focusing Flat Mirrors Based on Plasmonic Gradient Metasurfaces, Nano Lett., 2013, 13, 829–834 CrossRef CAS.
- N. Yu and F. Capasso, Flat optics with designer metasurfaces, Nat. Mater., 2014, 13, 139–150 CrossRef CAS.
- F. Capasso, The future and promise of flat optics: a personal perspective, Nanophotonics, 2018, 7, 953–957 Search PubMed.
- D. J. Coleman, Unified model for accommodative mechanism, Am. J. Ophthalmol., 1970, 69, 1063–1079 CrossRef CAS.
- E. Arbabi, A. Arbabi, S. M. Kamali, Y. Horie, M. Faraji-Dana and A. Faraon, MEMS-tunable dielectric metasurface lens, Nat. Commun., 2018, 9, 812 CrossRef.
- S. M. Kamali, E. Arbabi, A. Arbabi and A. Faraon, A review of dielectric optical metasurfaces for wavefront control, Nanophotonics, 2018, 7, 1041–1068 CAS.
- A. She, S. Zhang, S. Shian, D. Clarke and F. Capasso, 2017 Conference on Lasers and Electro-Optics (CLEO), 2017, pp. 1–1.
- A. She, S. Zhang, S. Shian, D. R. Clarke and F. Capasso, Large area metalenses: design, characterization, and mass manufacturing, Opt. Express, 2018, 26, 1573 CrossRef CAS.
- S. M. Kamali, E. Arbabi, A. Arbabi, Y. Horie and A. Faraon, Highly tunable elastic dielectric metasurface lenses, Laser Photonics Rev., 2016, 10, 1002–1008 CrossRef CAS.
- H.-S. Ee and R. Agarwal, Tunable Metasurface and Flat Optical Zoom Lens on a Stretchable Substrate, Nano Lett., 2016, 16, 2818–2823 CrossRef CAS.
- A. She, S. Zhang, S. Shian, D. R. Clarke and F. Capasso, Adaptive metalenses with simultaneous electrical control of focal length, astigmatism, and shift, Sci. Adv., 2018, 4, eaap9957 CrossRef.
- S. Colburn, A. Zhan and A. Majumdar, Tunable metasurfaces via subwavelength phase shifters with uniform amplitude, Sci. Rep., 2017, 7, 40174 CrossRef CAS.
- J. Sautter, I. Staude, M. Decker, E. Rusak, D. N. Neshev, I. Brener and Y. S. Kivshar, Active Tuning of All-Dielectric Metasurfaces, ACS Nano, 2015, 9, 4308–4315 CrossRef CAS.
- S.-Q. Li, X. Xu, R. M. Veetil, V. Valuckas, R. Paniagua-Domínguez and A. I. Kuznetsov, Phase-only transmissive spatial light modulator based on tunable dielectric metasurface, Science, 2019, 364, 1087–1090 CrossRef CAS.
- A. L. Holsteen, A. F. Cihan and M. L. Brongersma, Temporal color mixing and dynamic beam shaping with silicon metasurfaces, Science, 2019, 365, 257–260 CrossRef CAS.
- F. Ding, Y. Yang and S. I. Bozhevolnyi, Dynamic Metasurfaces Using Phase-Change Chalcogenides, Adv. Opt. Mater., 2019, 7, 1801709 CrossRef.
- Q. He, S. Sun and L. Zhou, Tunable/Reconfigurable Metasurfaces: Physics and Applications, Research, 2019, 2019, 1–16 Search PubMed.
- T. H. Stix, Waves in plasmas, Springer Science & Business Media, 1992 Search PubMed.
- A. Siegman, Lasers, University Science Books, 1986 Search PubMed.
- S. Maier, Handbook of Metamaterials and Plasmonics, World Scientific, 2016, vol. 4 Search PubMed.
- M. Born and E. Wolf, Principles of optics: electromagnetic theory of propagation, interference and diffraction of light, Elsevier, 2013 Search PubMed.
- V. Nikolskiy and T. Nikolskaya, Electrodynamics and radio wave propagation, Nauka Publ., 1989, p. 508 Search PubMed.
- J. Bergman, The magnetized plasma permittivity tensor, Phys. Plasmas, 2000, 7, 3476–3479 CrossRef CAS.
- M. Tymchenko, A. Y. Nikitin and L. Martín-Moreno, Faraday Rotation Due to Excitation of Magnetoplasmons in Graphene Microribbons, ACS Nano, 2013, 7, 9780–9787 CrossRef CAS.
- D. Pozar, Microwave Engineering, Wiley, 4th edn, 2011 Search PubMed.
- S. Alberti, Plasma heating with millimetre waves, Nat. Phys., 2007, 3, 376–377 Search PubMed.
- External heating systems for ITER, 2019, https://www.iter.org/mach/Heating.
- A. Ferreira, J. Viana-Gomes, Y. V. Bludov, V. Pereira, N. M. R. Peres and A. H. C. Neto, Faraday effect in graphene enclosed in an optical cavity and the equation of motion method for the study of magneto-optical transport in solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 235410 CrossRef.
- C. Hwang, D. A. Siegel, S.-K. Mo, W. Regan, A. Ismach, Y. Zhang, A. Zettl and A. Lanzara, Fermi velocity engineering in graphene by substrate modification, Sci. Rep., 2012, 2, 590 CrossRef.
- P. R. Whelan, Q. Shen, B. Zhou, I. G. Serrano, M. V. Kamalakar, D. M. A. Mackenzie, J. Ji, D. Huang, H. Shi, D. Luo, M. Wang, R. S. Ruoff, A.-P. Jauho, P. U. Jepsen, P. Bøggild and J. M. Caridad, Fermi velocity renormalization in graphene probed by terahertz time-domain spectroscopy, 2D Mater., 2020, 7, 035009 CrossRef CAS.
- N. Tang, B. Shen, M. Wang, Z. Yang, K. Xu, G. Zhang, T. Lin, B. Zhu, W. Zhou and J. Chu, Effective mass of the two-dimensional electron gas and band nonparabolicity in Alx Ga1−x N/Ga N heterostructures, Appl. Phys. Lett., 2006, 88, 172115 CrossRef.
- T. Wang, X. Wang, Z. Chen, X. Sun, P. Wang, X. Zheng, X. Rong, L. Yang, W. Guo and D. Wang, et al., High-Mobility Two-Dimensional Electron Gas at InGaN/InN Heterointerface Grown by Molecular Beam Epitaxy, Adv. Sci., 2018, 5, 1800844 CrossRef.
- V. Agranovich, Surface Polaritons, Elsevier Science, 2012, pp. 47–52 Search PubMed.
- E. Palik and G. Ghosh, Handbook of Optical Constants of Solids, Elsevier Science, 1991, vol. 1, pp. 491–494 Search PubMed.
- A. Ciuciulkaite, K. Mishra, M. V. Moro, I.-A. Chioar, R. M. Rowan-Robinson, S. Parchenko, A. Kleibert, B. Lindgren, G. Andersson, C. Davies, A. Kimel, M. Berritta, P. M. Oppeneer, A. Kirilyuk and V. Kapaklis, Design of Amorphous TbxCo100−x Alloys for All-Optical Magnetization Switching, Phys. Rev. Mater., 2020, 4, 104418 CrossRef.
- R. M. Rowan-Robinson, J. Hurst, A. Ciuciulkaite, I.-A. Chioar, M. Pohlit, M. Zapata, P. Vavassori, A. Dmitriev, P. M. Oppeneer and V. Kapaklis, Spectrally reconfigurable magnetoplasmonic nanoantenna arrays, 2020, https://arxiv.org/abs/2005.14478 Search PubMed.
- I. Vlassiouk, P. Fulvio, H. Meyer, N. Lavrik, S. Dai, P. Datskos and S. Smirnov, Large scale atmospheric pressure chemical vapor deposition of graphene, Carbon, 2013, 54, 58–67 CrossRef CAS.
- P. Salén, M. Basini, S. Bonetti, J. Hebling, M. Krasilnikov, A. Y. Nikitin, G. Shamuilov, Z. Tibai, V. Zhaunerchyk and V. Goryashko, Matter manipulation with extreme terahertz light: Progress in the enabling THz technology, Phys. Rep., 2019, 836–837, 1–74 CrossRef.
- Z. Liu, Z. Liang, W. Tang and X. Xu, Design and fabrication of low-deformation micro-bolometers for THz detectors, Infrared Phys. Technol., 2020, 105, 103241 CrossRef CAS.
- J. Hebling, G. Almasi, I. Kozma and J. Kuhl, Velocity matching by pulse front tilting for large area THz-pulse generation, Opt. Express, 2002, 10, 1161 CrossRef CAS.
- F. Callewaert, V. Velev, S. Jiang, A. V. Sahakian, P. Kumar and K. Aydin, Inverse-designed stretchable metalens with tunable focal distance, Appl. Phys. Lett., 2018, 112, 091102 CrossRef.
- W. Zhu, Q. Song, L. Yan, W. Zhang, P.-C. Wu, L. K. Chin, H. Cai, D. P. Tsai, Z. X. Shen, T. W. Deng, S. K. Ting, Y. Gu, G. Q. Lo, D. L. Kwong, Z. C. Yang, R. Huang, A.-Q. Liu and N. Zheludev, A Flat Lens with Tunable Phase Gradient by Using Random Access Reconfigurable Metamaterial, Adv. Mater., 2015, 27, 4739–4743 CrossRef CAS.
- X. Yin, T. Steinle, L. Huang, T. Taubner, M. Wuttig, T. Zentgraf and H. Giessen, Beam switching and bifocal zoom lensing using active plasmonic metasurfaces, Light: Sci. Appl., 2017, 6, e17016–e17016 CrossRef CAS.
- W. Bai, P. Yang, S. Wang, J. Huang, D. Chen, Z. Zhang, J. Yang and B. Xu, Actively Tunable Metalens Array Based on Patterned Phase Change Materials, Appl. Sci., 2019, 9, 4927 CrossRef CAS.
- W. Bai, P. Yang, J. Huang, D. Chen, J. Zhang, Z. Zhang, J. Yang and B. Xu, Near-infrared tunable metalens based on phase change material Ge2Sb2Te5, Sci. Rep., 2019, 9, 5368 CrossRef.
- M. Y. Shalaginov, S. An, Y. Zhang, F. Yang, P. Su, V. Liberman, J. B. Chou, C. M. Roberts, M. Kang, C. Rios, Q. Du, C. Fowler, A. Agarwal, K. A. Richardson, C. Rivero-Baleine, H. Zhang, J. Hu and T. Gu, Reconfigurable all-dielectric metalens for diffraction-limited imaging, Active Photonic Platforms, 2020, XII, 114610M Search PubMed.
- X. Li, S. Li, G. Wang, Y. Lei, Y. Hong, L. Zhang, C. Zeng, L. Wang, Q. Sun and W. Zhang, Tunable doublet lens based on dielectric metasurface using phase-change material, Mod. Phys. Lett. B, 2020, 34, 2050313 CrossRef CAS.
- Z. Li, K. Yao, F. Xia, S. Shen, J. Tian and Y. Liu, Graphene Plasmonic Metasurfaces to Steer Infrared Light, Sci. Rep., 2015, 5, 12423 CrossRef.
- Z. Wang, B. Hu, B. Li, W. Liu, X. Li, J. Liu and Y. Wang, Active focal control of an ultrathin graphene-metal metasurface lens, Mater. Res. Express, 2016, 3, 115011 CrossRef.
- P. Ding, Y. Li, L. Shao, X. Tian, J. Wang and C. Fan, Graphene aperture-based metalens for dynamic focusing of terahertz waves, Opt. Express, 2018, 26, 28038 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/D0NR06198K |
| This journal is © The Royal Society of Chemistry 2021 |