Fingerprinting branches on supercoiled plasmid DNA using quartz nanocapillaries†
Sumanth Kumar
Maheshwaram
,
Koushik
Sreenivasa
and
Gautam Vivek
Soni
 *
*
Raman Research Institute, Bangalore, India. E-mail: gvsoni@rri.res.in
First published on 7th December 2020
Abstract
DNA conformation, in particular its supercoiling, plays an important structural and functional role in gene accessibility as well as in DNA condensation. Enzyme driven changes of DNA plasmids between their linear, circular and supercoiled conformations control the level of condensation and DNA distal-site interactions. Much effort has been made to quantify the branched supercoiled state of DNA to understand its ubiquitous contribution to many biological functions, such as packaging, transcription, replication etc. Nanopore technology has proven to be an excellent label-free single-molecule method to investigate the conformations of the translocating DNA in terms of the current pulse readout. In this paper, we present a comprehensive study to detect different branched-supercoils on individual plasmid DNA molecules. Using a detailed event charge deficit (ECD) analysis of the translocating molecules, we reveal, for the first time, the distributions in size and the position of the plectoneme branches on the supercoiled plasmid. Additionally, this analysis also gives an independent measure of the effective nanopore length. Finally, we use our nanopore platform for measurement of enzyme-dependent linearization of these branched-supercoiled plasmids. By simultaneous measurement of both single-molecule DNA supercoiled conformations and enzyme-dependent bulk conformational changes, we establish nanopore sensing as a promising platform for an in-depth understanding of the structural landscapes of supercoiled DNA to decipher its functional role in different biological processes.
Introduction
Supercoiling which acts as a topological constraint on DNA is a key control mechanism in regulating the transcription, replication, and compaction of DNA in both prokaryotes and eukaryotes.1–3 It has been a topic of great interest to physicists and biologists alike, due to the strong interdependence between its structure and function.4–6 Almost all organisms have negatively supercoiled DNA7,8 except for hyperthermophilic archaea that have positively supercoiled DNA.9 Supercoiled DNA can assume a variety of interwound branched structures, called plectonemes, which form due to the interplay between the twisting and bending energy of DNA.1,3 Plectonemes with branches protruding out of the super helical axis were initially observed by electron microscopy1 and later studied in detail using AFM10–12 under physiological conditions. Fluorescence and AFM based single molecule studies have revealed that the plectoneme formation depends on the underlying sequence as it governs the local DNA curvature.13–15 Interwinding and branching can juxtapose multiple distant sites which are important for processes such as the enhancer–promoter interaction.16,17 Negative supercoiling favours the local untwisting of DNA, thereby affecting the activity of transcription18 and restriction digestion.19 Studies on the kinetics of interconversion between the linear, circular and supercoiled plasmid conformations20 need to be carried out as DNA inside a cell is highly dynamic due to its interaction with various types of enzymes during processes like nucleosome formation, recombination, viral genome integration, etc. Mechanisms involved in the maintenance of supercoiling, and the kinetics of modulating the supercoiling of DNA by topoisomerases and gyrases have been studied using single molecule techniques like magnetic tweezers21,22 and rotor bead assays.23 However, there is a dearth of single molecule measurements required for quantification of the native branched structures and enzyme dependent conformational changes in DNA supercoiling.The nanopore platform has recently emerged as an excellent platform for detecting various polymers. The nanopore device works on the principle of the resistive pulse technique developed by Coulter.24 Here the nanopore acts as a channel between two reservoirs filled with an electrolyte. When a bias voltage is applied across the nanopore, the open pore current is measured due to the movement of electrolyte ions. For the duration an analyte particle translocates through the nanopore, it displaces ions in the nanopore resulting in conductance drop. These electrical events (conductance drops) contain details about the size and shape of the particle. Various types of nanopores are used which are made from silicon oxide,25 silicon nitride,26 carbon nanotubes,27 graphene,28 and glass capillaries.29–31 They have been used to detect molecules like DNA, RNA, proteins and protein–DNA complexes.32–39 The application of nanopores in the detection of conformational changes in proteins is also demonstrated.40–42 They have been used for measuring the kinetics of biomolecular reactions42–47 and to study the conformations of DNA in the distribution of knot conformations,48,49 G-quadruplexes50 and supercoiled DNA.51–53 However, until now, high resolution detection of different branched populations and the length and position analysis of naturally occurring plectonemes on supercoiled plasmid DNA have not been possible.
In this work, we demonstrate the nanopore platform as a promising label-free technique to quantitatively measure a variety of branched DNA structures in aqueous solutions at nanometre resolution. We present a detailed event charge deficit (ECD) based analysis to quantify the DNA lengths in these supercoiled branches. This analysis also provided us a method to determine the effective length of the nanopore. Finally, we apply the nanopore measurements to study the kinetics of enzyme dependent conformational changes in supercoiled DNA. Our work extracts a wealth of information about the branched sub-structures in supercoiled DNA demonstrating facets of the nanopore platform useful in the study of the dynamic conformational changes of DNA at high resolution.
Materials and methods
Sample preparation
For nanopore translocation experiments on λ-DNA (New England Biolabs), the sample was heated at 65 °C for 10 min to linearize the DNA and then added into the sample well at a final concentration of 4.2 ng μl−1. The experiments with supercoiled DNA were performed using the plasmid pGEM3z601b54,55 (a gift from Cees Dekker's lab). This plasmid was amplified by growing in E. coli DH5α and extracted using a Midi Prep kit (Qiagen). The circular form of the plasmid was obtained by nicking with Nt. BspQI enzyme (New England Biolabs, NEB) and the linear form was obtained by single-cut digesting of the supercoiled plasmid in 1× CutSmart Buffer (NEB) by NdeI, ScaI or EcoRI restriction enzymes (NEB) at a concentration of 0.14 U μl−1 (1×). The samples are purified using a PCR purification kit (Qiagen) followed by ethanol precipitation. For enzyme kinetics experiments, the digestion reactions with NdeI enzyme were performed in 50 mM Tris, 100 mM NaCl, 5 mM MgCl2 pH 7.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 at 1/6× enzyme concentration (see Fig. S9†). The digestion reaction was arrested at different time points (see the Results section) by the addition of EDTA to a final concentration of 100 mM and plunging immediately on ice. All the translocation experiments on plasmids were performed at a final concentration of 0.8 ng μl−1.
20 at 1/6× enzyme concentration (see Fig. S9†). The digestion reaction was arrested at different time points (see the Results section) by the addition of EDTA to a final concentration of 100 mM and plunging immediately on ice. All the translocation experiments on plasmids were performed at a final concentration of 0.8 ng μl−1.
Nanopore experiment
The nanopores were fabricated using quartz capillaries with a filament (OD = 1 mm and ID = 0.5 mm: QF-100-50-7.5, Sutter Instruments). After cleaning with water (MilliQ, Millipore) and ethanol and then drying under nitrogen, capillaries were pulled using Sutter Puller P-2000G with the following two-line program. Line 1: heat (810), filament (3), velocity (35), delay (145), pull (75), line 2: heat (660), filament (0), velocity (15), delay (128), pull (200). We have consistently achieved pore diameters in the range of 40–80 nm using the above program. Note that the pore diameters are affected by local conditions such as puller condition, cleanliness of capillaries, humidity, temperature, room vibrations and laser stability. These nanopores on capillary tips were further shrunk to the desired size using a 3 keV beam of a scanning electron microscope, SEM (Carl Zeiss Ultraplus FESEM) as described previously.31 The nanopores were then cleaned in oxygen plasma for 1 min at 50 W of RF power and 250 mtorr of oxygen pressure using a PlasmaPrep-III system (SPI Supplies). The capillary was then glued into the Teflon fluid cell and filled with the Nanopore Buffer (NPB) (4 M LiCl in 10 mM Tris-HCl, 1 mM EDTA at pH 8) as shown in the schematic in Fig. 1C (inset: top). To remove any air bubbles present inside the capillary, the fluid cell was kept in a vacuum desiccator for 15 min. The Ag/AgCl electrodes and Axopatch 200B amplifier (Molecular Devices) were used to apply a voltage and measure the current through the nanopore. In order to reduce the noise in electrical measurements, the nanopore setup was isolated from the external environment by placing it in a copper Faraday cage. For analyte detection, we select pores with a stable baseline (baseline drifts less than 5% per hour for the typical experiment duration of 10–50 minutes). Data acquisition was performed using NI DAQ PCI-6251 (National Instruments) at a sampling frequency of 200 kHz. The translocation data were acquired and analysed using custom-written codes in LabVIEW (National Instruments). For data analysis, the translocation data for λ-DNA and plasmids were low-pass filtered at 5 kHz and 25 kHz respectively. A translocation event is defined as a trace where the current drops below the threshold value 5 times the standard deviation of noise in the baseline. Branch analysis was performed using a custom-written code in MATLAB. When comparing samples measured on the same nanopore, the fluid cell and the nanopore were washed thoroughly with buffer and a stable baseline was confirmed before adding each sample to ensure that there is no sample left behind from the previous experiment.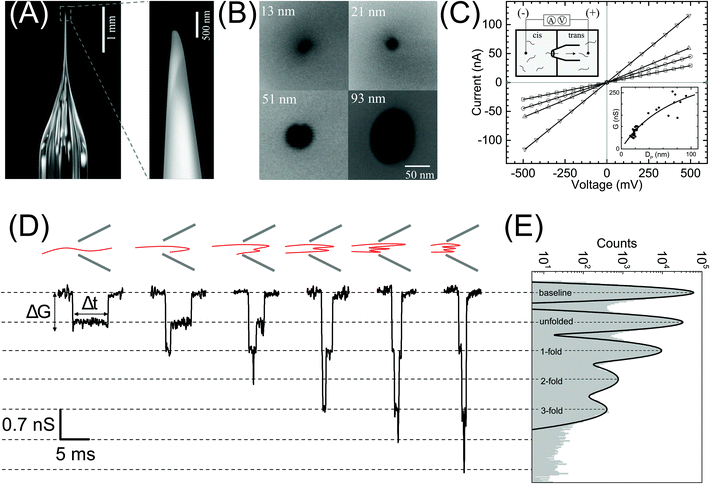 | ||
| Fig. 1 Nanopore characterization and observation of multiple conformations of λ-DNA in a glass nanopore. (A) Left: The side-on optical image of a typical quartz capillary pulled with the laser puller. The average taper length of these capillaries was 2.8 ± 0.3 mm. Right: A zoomed image of the tip of the nanocapillary using an SEM microscope. (B) The representative SEM images of nanopores at the tip of the nanocapillary, with sizes ranging from 13 nm to 93 nm, used in this study. (C) I–V curves of the representative nanopores (13 nm – squares, 21 nm – circles, 51 nm – up triangles and 93 nm – down triangles) showing linear characteristics are plotted. The top-left inset shows a schematic of the Teflon fluid cell mounted with a nanocapillary. The bottom-right inset shows pore conductance as a function of pore diameter plotted for N = 37 different nanopores. The solid line is the fit to eqn (1). (D) Representative events showing different levels of folding during λ-DNA translocation through a 20 nm pore (500 mV). Four different blockade levels, corresponding to different folded DNA conformations, are seen along with some rare events beyond the fourth level. A schematic of the possible conformations that could generate the corresponding events is shown above them. (E) Histogram of the nanopore conductance G (nS) during sample translocation. The histogram shows peaks (dotted lines) at integral levels corresponding to the folds of λ-DNA. | ||
Results
Characterization of nanopores and translocation of λ-DNA
In Fig. 1 we show the fabrication and characterization of our quartz nanopores for single molecule detection. All the custom-made nanopores are characterized by optical microscopy and SEM imaging to measure the taper length and tip geometry of the pore respectively (Fig. 1A). Fig. 1B shows the representative SEM images of nanopores with a diameter ranging from 13 to 93 nm. The quartz nanopore is mounted on the fluid cell and filled with nanopore buffer (Fig. 1C inset top-left) and checked for linearity in its I–V characteristics in the range of ±500 mV. We observed linear IV curves for all our nanopores as shown in Fig. 1C. The open pore conductance of nanopores is modelled very well with the previously established double-cone model. Here, the first cone is the tapered portion of the capillary tube with the cone length as the taper length, LT, and the base diameter, DT, as the I.D. of the quartz capillary and the second cone is the conductance cone near the tip of the capillary with a cone length and base diameter of Lcond and Dcond respectively. Nanopore conductance, G (nS), for a pore of diameter DP, in the double-cone model is given by:29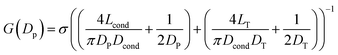 | (1) |
Here, σ is the conductivity of buffer (NPB, σ = 18.0 S m−1), as measured using a conductivity meter. The conductance G (nS) for each pore is calculated from the linear fits to their respective IV curves and is plotted for 37 different nanopores of varying diameter in Fig. 1C (inset on bottom-right). The experimental data were fitted by the above equation giving fitting parameters Lcond and Dcond as 427 ± 101 nm and 176 ± 25 nm respectively. This signifies the region where the major fraction of resistance of the conical nanopore falls. Given the spread in the data around the fit curve, we note that the internal geometry of each custom-made pore is slightly different and plays a crucial role in determining the true value of nanopore conductance.
We demonstrate the capability of our quartz nanopores in detecting multiple DNA conformations using a linearized 48.5 kb long λ-DNA translocating through a nanopore of diameter 20 nm at 500 mV bias voltage. In Fig. 1D the representative events corresponding to different levels of folding in DNA are shown where ΔG and Δt represent the conductance drop and dwell time of the event, respectively. The conductance drop increases in well-defined steps (dotted lines) and the dwell time decreases with the increase in the number of folds.26,56 These multi-level events correspond to multiply-folded DNA conformations as they translocate through the nanopore. The possible conformations that can result in the events shown are drawn schematically above the corresponding event. In Fig. 1E, we plot the baseline subtracted conductance histograms (G histograms) for the translocation data and show the familiar equally-spaced multi-peak histogram showing conductance drop levels corresponding to different folded conformations of linear DNA.30 We have fitted the conductance histogram with a multi-peak Gaussian function. Here, the first peak is from the open pore baseline and serves as a reference for the measurement of ΔG values (ΔG = Gpeak − Gbaseline) for the different current levels. We find that the peaks corresponding to the events are located at 0.70 ± 0.07, 1.4 ± 0.1, 2.1 ± 0.2, and 2.8 ± 0.2 nS relative to the baseline. These ΔG values are integer multiples of 0.70 nS (unfolded configuration) and represent populations of multiply-folded conformations of λ-DNA. There are events beyond 3-fold level but they constitute only 9.3% of the total number of events and hence didn't result in a clear peak in Fig. 1E. We have presented the events with higher-folds for completion.
Characterization of plasmid conformations
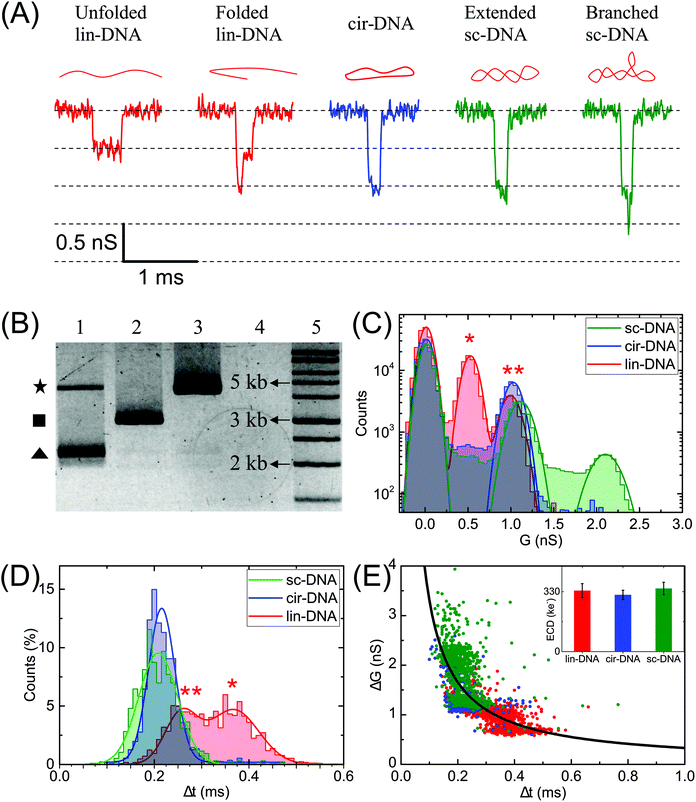
Next, we compare different forms of a 3 kb plasmid DNA which is in linear (lin-), circular (cir-) and supercoiled (sc-) conformations. Fig. 2A shows the representative electrical events of the three types of DNA conformations when compared on the same nanopore (pore diameter 19 nm). The experiments were performed on the same nanopore, one sample at a time, with extensive washes between different sample measurements, as described in the Material and methods section. Fig. 2B shows the gel image of the 3 forms of the plasmid DNA. The representative current traces for different conformations are shown in Fig. S1A.†Fig. 2C–E compare the ΔG, Δt, ΔG–Δt scatter plots and the ECD values of the detected events when each conformation of the plasmid DNA was measured individually. Gaussian fits were used to identify different peaks. The linear DNA sample shows two populations corresponding to ΔG values of 0.5 ± 0.1 nS and 1.0 ± 0.1 nS respectively and two populations in Δt histograms corresponding to dwell times of 0.26 ± 0.03 ms and 0.37 ± 0.05 ms (Fig. 2C and D, lin-DNA, red). The ΔG value for the second peak is almost double that of the first peak indicating that the two populations correspond to the unfolded (smaller ΔG, longer Δt values, marked by *) and folded forms (higher ΔG, shorter Δt values, marked by **) of the linear plasmid DNA, respectively. The percentage of events in the unfolded DNA peak is 33.4% when measured using this pore. This value was measured using multiple 20 nm nanopores and we find it to be highly reproducible with a mean percentage of 36.5 ± 3.1 of the events in the unfolded DNA peak (Table S1†). We later apply this approach to quantify the amount of linear DNA from a mixture of lin-DNA and sc-DNA from individual nanopores (see Fig. 5 and Fig. S8†). The circular DNA sample, measured in the same nanopore, shows a dominant single population (90.3% of total events) corresponding to a ΔG value of 1.0 ± 0.1 nS and a single peak in the Δt histogram at 0.22 ± 0.03 ms (Fig. 2C and D respectively, cir-DNA, blue). In the cir-DNA sample, the absence of any folded events is possibly due to its total length of 514.25 nm being closer to the dsDNA persistence length when compared to the linear plasmid DNA (1028.5 nm total length). Longer DNA, such as λ-DNA in Fig. 1D, however shows many more levels of folding and supports this possibility.
The supercoiled DNA sample measured in the same nanopore showed a primary population with 34.9% of total events corresponding to a ΔG value of ΔG1 = 1.1 ± 0.1 nS and Δt of 0.21 ± 0.04 ms (Fig. 2C and D, green). Being similar to the ΔG value for the circular plasmid, we attribute this population to an extended form of sc-DNA. Interestingly, we found a large number of events (65.1%) with a broad range of ΔG values which are higher than the first peak. Such a representative event is shown in Fig. 2A. Since these deeper events present themselves with additional current spikes which are not multiples of the extended sc-DNA event level and also noting that the persistence length of sc-DNA is (∼100 nm), about double that of lin- or cir-DNA,57 we disregarded these events as folded sc-DNA as they are energetically not favorable. However, since it is well known that due to the torsional energy stored in sc-DNA it can assume higher order branched structures,1,10 we attribute the deeper ΔG events detected in the sc-DNA sample to these branched structures on the supercoiled plasmid. We note that these spiked events, due to the branched sc-DNA, are resolvable from the extended sc-DNA events only because of the choice of the nanopore. Later, we present the role of nanopore diameter on its resolution (see Fig. 3). Different sized branched structures on sc-DNA produce current spikes of different amplitudes. It is evident that these structures are mechanically stable as the high electric field gradient near the pore was unable to extend them. These events have a broad range of ΔG values which finally culminate into a population seen as the second peak with a ΔG value of ΔG2 = 2.1 ± 0.1 nS. This second population suggests that either a large population of supercoiled DNA has a specific size of the branched structure or a cut-off in the detectable branch size that depends on the nanopore dimensions (see discussion for Fig. 4). We also note that compared to the unfolded-linear conformation of DNA, the folded-linear, circular and supercoiled conformations of DNA take about half the time to translocate through the pore. This is supported by the fact that their lengths are half of the unfolded lin-DNA and suggests that the translocation dynamics of different DNA conformations remain the same. In our experiments of measuring both samples on the same pore, event rates for lin- and sc-DNA were found to be 0.82 ± 0.13 and 0.77 ± 0.54 s−1 respectively from multiple nanopores (DP = 20 ± 2 nm). We note that under the current conditions, our experiments are not sensitive to conformation dependent changes in capture rates for lin- and sc-DNA of 3025 bp (∼1.028 μm) plasmid.
 | ||
| Fig. 3 Role of the nanopore size in resolving the branched populations of supercoiled DNA. (A) Density contour plots of conductance drop versus dwell time are compared for various pore diameters – pores used here are: P24 (13 nm, n = 755), P31 (19 nm, n = 960), P30 (39 nm, n = 1233), P08 (50 nm, n = 1436), P02 (76 nm, n = 410), and P03 (93 nm, n = 926). Here the darker regions represent a higher density of data points. For visual clarity scatter plots have a common Y-axis and independent time axis scale bars are shown at the bottom of each contour plot which starts from 0 ms and ends at 0.5 ms. Inset: Conductance drop (1st peak, ΔG1) (300 mV) during translocation of a supercoiled plasmid is plotted as a function of pore diameter when measured for N = 37 different nanopores. The solid line is the fit to eqn (S1).† (B) Representative events showing different conformations of sc-DNA as resolved by a 13 nm pore (300 mV). A schematic of the DNA conformation corresponding to each event is shown above it. | ||
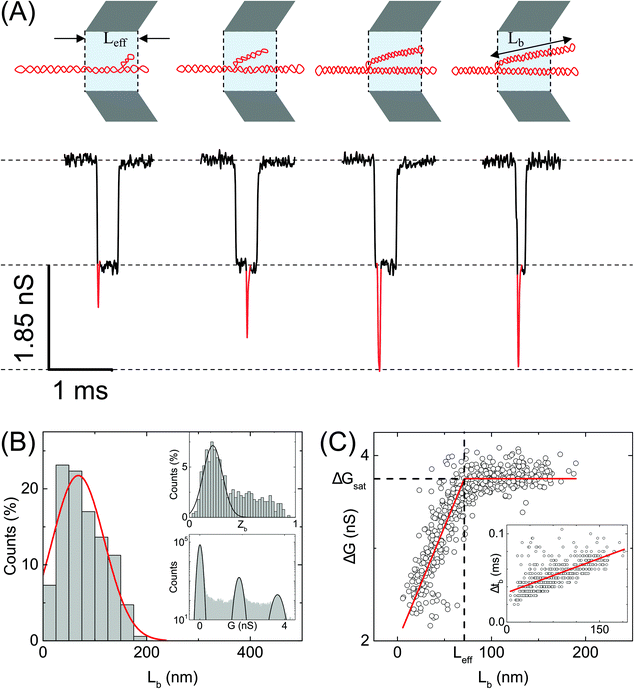 | ||
| Fig. 4 Analysis of branches in sc-DNA translocation. (A) Typical events measured with sc-DNA showing different branch lengths translocating through the nanopore P25 (17 nm, n = 979) (left to right: 25, 50, 100, 150 nm length of the branched region). Here the sample is driven from outside of the pore to inside (left to right movement). Red traces show the current spikes due to the branched regions of the sc-DNA sample. A schematic of the possible DNA conformations corresponding to each event is shown on the top. (B) shows the histogram of the branch length measured in the nanopore. Top inset: Histogram of relative branch positions along the length of the DNA molecule. Bottom inset: Conductance histogram for sc-DNA. (C) shows the conductance drop of the event (ΔG) plotted against the branch length (Lb). Inset: Dwell times of the branched region plotted against the branch length showing a linear relationship. In the ESI (Fig. S5–S7†) we compare the same trends across multiple other pores. | ||
We estimate the event charge deficit (ECD), defined as the integral of the current drop over the dwell time duration, for every translocation event.58 It is computed according to the equation,
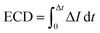 | (2) |
In Fig. 3 we show the role of nanopore size in resolving multiple populations corresponding to different conformations on the sc-DNA plasmid. Translocation experiments for sc-DNA were performed in a total of 37 nanopores with the pore size ranging from 13 nm to 93 nm. We compare ΔG corresponding to the extended sc-DNA conformation (first ΔG peak in Fig. 2C, ΔG1) for different pore sizes. We show, in Fig. 3A, that sc-DNA can be detected in nanopores in this entire size range with the ΔG1 values increasing non-linearly with decreasing pore diameter (see Fig. 3A inset & Table S2†). ΔG1versus DP is fitted with eqn (S1).†42,59–61 We note that in larger pores, the entire sample set is detected as a single peak in the ΔG histogram and is unable to distinguish between branched and unbranched forms. For pore sizes of 39 nm and smaller we see sc-DNA with branches being detected as a population separate from extended sc-DNA. This can be clearly seen from their ΔG histograms as well, as shown in Fig. S2.† Among all the pore diameters, we find the highest resolution in the 13 nm pore which presents us with a large plethora of event heterogeneity as seen in the representative events shown in Fig. 3B. The possible branched conformation that may result in the event is shown as a schematic above every event. Given the high throughput, reproducibility and sufficient resolution, all further experiments to quantify the branched samples were performed with nanopores of diameters around 20 nm.
Quantification of branches in supercoiled DNA using ECD analysis
We quantify the branches in sc-DNA using ECD analysis of the translocation events. Fig. 4A shows the typical translocation events of sc-DNA through a 17 nm pore. In each translocation event, the blockade level corresponding to an extended form of sc-DNA is shown in black and the red trace represents the detected spike on top of the event which corresponds to the branched region translocating through the pore. The size and location of the spike correspond to the size and location of the branch on the translocating sc-DNA molecule.49,62 The ECD of an event corresponds to the total amount of ions displaced by the molecule which depends on the size (length, in the case of a linear polymer) of the molecule and is independent of its conformation during translocation. We use this analysis to quantify the linear lengths (Lb) and positions (Zb) of the branches in sc-DNA using the following equations, for all events that display the branch signatures: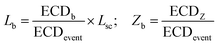 | (3) |
We next correlate the branch length of individual molecules with the corresponding ΔG value. In Fig. 4C, we plot the ΔG values against the estimated branch length (Lb) for all the branched molecules. We find that the ΔG increases linearly with Lb and then saturates to a constant value (ΔGsat) for all higher Lb values. We see this behavior in the raw data (Fig. 4A) and understand it by following the argument: increasing branch lengths block a larger portion of the pore resulting in increasing ΔG values, however for molecules with branch lengths (Lb) equal to or longer than the pore length (Leff), it will result in ΔG values twice that of extended sc-DNA (ΔG1). Fig. 4A (top) shows the cylindrical model of quartz nanopores with a length of Leff and the shaded portion is its sensing region. The sc-DNA translocating through this cylindrical volume causes the conductance drop (event) and the branches on the sc-DNA cause the spikes on top of the event. The larger the branch length traversing the nanopore the larger the ΔG value of the event. As we go from left to right in Fig. 4A, we see that with increasing branch length the event depth (ΔG) increases. This argument is also supported by the fact that the second conductance drop peak (ΔG2), as shown in Fig. 4B (inset, bottom), matches the saturation conductance drop value (ΔGsat) for the nanopore. We confirm this behavior to be consistent with the measurements across multiple pores (see Table S3†). By fitting the data to a piecewise function which defines the two connected straight lines with different slopes, we can obtain the exact point at which the saturation happens. This value gives us the effective length of the pore which turned out to be 71 ± 1 nm for the pore P25 (17 nm) as shown in Fig. 4C. This is also in close agreement with the pore length value of 67 ± 4 nm as estimated from the model of conductance drop vs. pore diameter in Fig. 3A (inset). This analysis provided us with a direct estimation of the effective length of the nanopore, one of the major bottlenecks in the accurate quantification of molecular sizing due to uncertainty in pore length in glass nanocapillaries.61,63
Fig. 4C (inset) shows the variation in the dwell time of the branch as a function of its length and shows a linear relationship. The slope of this curve provides the velocity of sc-DNA translocation. We found the average translocation velocity to be 11 ± 2 bp μs−1 when measured on multiple nanopores (N = 7) with diameters of 18 ± 2 nm (see Table S4†). This analysis helped us understand and model the relationship between the event characteristics (ΔG and Δt) and polymer size in conical nanopores which had been difficult to do until now.
Supercoiled DNA can have the branch located at any position along the length of the molecule as observed from the previous reports in the literature.1,10 The branch location was estimated for each event using eqn (3) and plotted as a branch position (Zb) histogram in Fig. 4B inset (top). Here, Zb is scaled such that Zb = 1 corresponds to the linear length of sc-DNA (514.25 nm). We observe that the location of branches on sc-DNA is predominantly towards the beginning (peak value of 0.22 ± 0.1) of the event. The observed bias in the position of the branches is likely due to the greater propensity of the charge-dense branched region to enter the pore first. These results were tested and found to be consistent across multiple nanopores and the data are shown in Fig. S5–S7 in the ESI.† From the above analysis, we understand that sc-DNA in its natural form exists in both unbranched and branched structures with a wide range of sizes.
NdeI-dependent changes in plasmid conformations
Finally, we perform quantification of NdeI dependent linearization of sc-DNA using our nanopore platform. The supercoiled plasmid was digested with NdeI enzyme for various durations 0, 5, 10, 30 & 60 min and then the samples were analysed by both gel electrophoresis (Fig. 5A) and nanopore platform (Fig. 5B and C). Since the NdeI enzyme is highly reactive, we chose to work at a low enzyme concentration (1/6×) allowing us to access the intermediate reaction time points. Reaction rates at different enzyme concentrations are shown in Fig. S9B.†Fig. 5B shows the translocation experiments performed on samples digested for 0, 5, 30 & 60 min. All samples were measured back-to-back in the same nanopore of diameter 17 nm. The ΔG histogram for the sample incubated for 0 min (which is the undigested supercoiled plasmid) shows the primary peak at 0.66 nS and a plethora of higher ΔG events ending with a peak at 1.14 nS, similar to what is seen in Fig. 2. After 5 min reaction, we observe the emergence of events with a mean ΔG of 0.38 nS confirming the formation of linearized-DNA upon NdeI digestion (as also seen in lane-2 of Fig. 5A). For visual clarity, the regions in the ΔG histograms corresponding to linear and supercoiled conformations are shaded in light and dark grey respectively. With increasing reaction times, the lin-DNA peak increases, as expected. Given the percentage of linearized DNA showing up as folded (or partially folded), the correct amount of DNA in the lin-DNA peak is quantified as done in Fig. 2B and confirmed with known mixtures of linearized and sc-DNA as detailed in ESI Fig. S8.† We quantified the amount of lin-DNA in the samples with increasing reaction times to be 3.8%, 22.4%, 41.5% and 55.2% respectively as shown in Fig. 5C and listed in Table S5.† The data are fitted with first-order rate constants, as shown in eqn (4) for the restriction digestion:64| [L(t)] = [SC]max (1 − e−kt) | (4) |
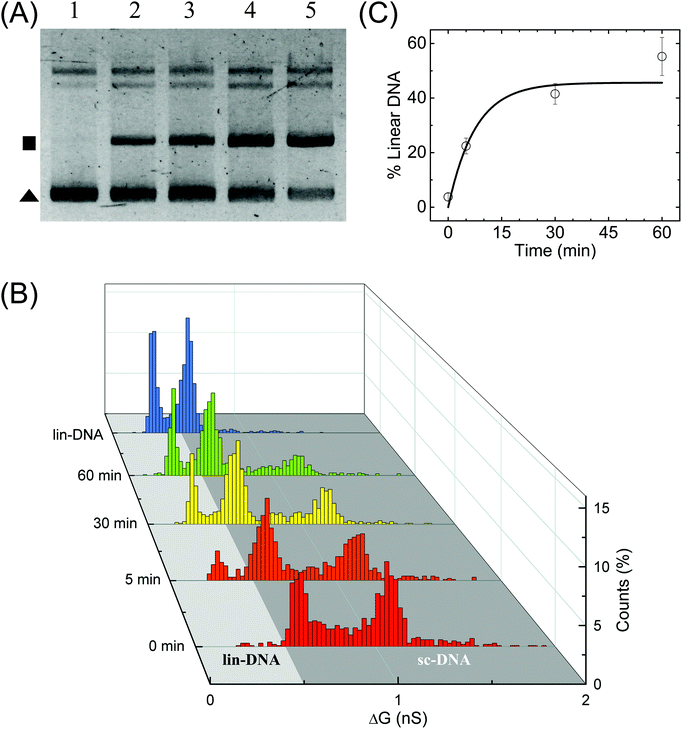 | ||
| Fig. 5 Enzymatic linearization of branched supercoiled DNA. Time dependent linearization of supercoiled plasmid DNA by NdeI restriction enzyme was quantified using nanopores. (A) Gel image shows time-dependent linearization of supercoiled plasmid by NdeI restriction enzyme at 1/6× concentration. Lanes 1–5 show the result of the restriction digestion assay when the reaction was stopped at 0, 5, 10, 30 and 60 min time points. The solid triangle marks the location of the supercoiled plasmid band and the square marks the linearized DNA band. (B) shows the nanopore data of ΔG histograms for NdeI-digested samples with increasing reaction times (as shown on the left axis) obtained on a 17 nm pore (P32). The time dependent increase in the lin-DNA peak and the corresponding decrease in sc-DNA peak are evident from the data. A ΔG histogram for 100% linear DNA is also shown for comparison. Here, n = 951 (0 min), 905 (5 min), 1102 (30 min), 1018 (60 min), 1470 (lin-DNA). (C) shows quantification of lin-DNA (in percentage) produced by the enzyme, at different reaction time points as measured by our nanopore data (N = 3, 2 datasets from P32 and 1 dataset from P35). The solid line is the fit to the kinetics model (eqn (4)) giving the reaction rate constant k = 0.13 ± 0.07 min−1. | ||
Here k is the first-order rate constant of reaction, [L] and [SC] are the time-dependent concentrations of linear and supercoiled plasmid DNA respectively and [SC]max is the maximum amount of sc-DNA that can be digested under the given conditions. The values of rate constant were found to be 0.13 ± 0.07 and 0.12 ± 0.02 min−1 from nanopore (Fig. 5C) and gel data (Fig. S9B,† black curve) respectively which are in excellent agreement with each other. Upon performing ECD analysis on these datasets, we find that the mean branch lengths (Lb) on sc-DNA remain constant as the enzyme reaction progresses confirming the well-established all-or-none mechanism65 where the DNA cut by the enzyme removes all branches from sc-DNA. This work establishes the nanopore platform to study thermal and enzyme dependent conformational changes in biomolecules at the single molecule level.
Conclusions
In this work, we demonstrate the application of the quartz nanopore platform in high resolution measurements of conformational details of supercoiled DNA. We showed the controlled fabrication of quartz nanopores of various sizes ranging from 13 nm to 93 nm with their conductance values in agreement with the standard theoretical model. The signal to noise ratio in nanopores was suitable for distinguishing the folded configurations of long λ-DNA as well as the three conformations of the plasmid DNA due to the differences in their electrical signatures. We observed that supercoiled DNA has two sub-populations as seen in the ΔG histogram, which were identified as unbranched (or extended) and branched supercoiled DNA. Using a customized ECD analysis, we could fingerprint the branch sizes as well as their relative positions on the molecule. An interesting outcome of this analysis was an independent measurement of the effective length of the pore which could lead to a significant technological advancement in accurate quantification of macromolecular sizes. Finally, we demonstrated nanopore based quantification of NdeI dependent conformational changes in supercoiled DNA. The values of first-order rate constants are calculated from the nanopore and gel electrophoresis data and they agree reasonably well with each other. We conclude that the nanopore technique is highly promising for studying conformational changes in DNA and it has potential applications in real time kinetics measurements of biomolecular reactions. The results presented here also pave the way for immediate further studies on the role of key parameters such as sequence, supercoiling density, environment, etc., in the global topology of supercoiled DNA using nanopores.Data availability
The authors declare that the data supporting the findings of this study are available within the paper and its Supplementary information files. Additional and relevant data are available from the corresponding authors on reasonable request.Author contributions
M. S. K. & G. V. S. designed research; M. S. K. & K. S. performed research; M. S. K., K. S., and G. V. S. analyzed data; M. S. K. & G. V. S. wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The project was funded by RRI core funding and the Ramalingaswami fellowship. We acknowledge Serene, Divya and Lavanya in the Bio-lab for help with plasmid purification and digestion, Mr Yatheendran for use of RRI Scanning Electron Microscopy facility & RRI machine-shop and the EEG group for low-noise fluid cell measurements. We also thank Prof. V. A. Raghunathan and Prof. Yashodhan Hatwalne for critical discussions on the manuscript.References
- J. Vinograd, J. Lebowitz, R. Radloff, R. Watson and P. Laipis, The twisted circular form of polyoma viral DNA, Proc. Natl. Acad. Sci. U. S. A., 1965, 53, 1104–1111 CrossRef CAS PubMed.
- P. R. Cook, The organization of replication and transcription, Science, 1999, 284, 1790–1795 CrossRef CAS PubMed.
- D. Andrew, Bates, Anthony Maxwell, DNA Topology, Oxford University Press, 2005 Search PubMed.
- C. Lavelle, Pack, unpack, bend, twist, pull, push: The physical side of gene expression, Curr. Opin. Genet. Dev., 2014, 25, 74–84 CrossRef CAS PubMed.
- L. Baranello, D. Levens, A. Gupta and F. Kouzine, The importance of being supercoiled: How DNA mechanics regulate dynamic processes, Biochim. Biophys. Acta, Gene Regul. Mech., 2012, 1819, 632–638 CrossRef CAS.
- R. Cortini, et al., The physics of epigenetics, Rev. Mod. Phys., 2016, 88, 025002 CrossRef.
- A. Worcel and E. Burgi, On the structure of the folded chromosome of Escherichia coli, J. Mol. Biol., 1972, 71, 127–147 CrossRef CAS.
- P. R. Kramer and R. R. Sinden, Measurement of unrestrained negative supercoiling and topological domain size in living human cells, Biochemistry, 1997, 36, 3151–3158 CrossRef CAS PubMed.
- P. Forterre, A. Bergerat and P. Lopez-Garcia, The unique DNA topology and DNA topoisomerases of hyperthermophilic archaea, FEMS Microbiol. Rev., 1996, 18, 237–248 CrossRef CAS.
- Y. L. Lyubchenko and L. S. Shlyakhtenko, Visualization of supercoiled DNA with atomic force microscopy in situ, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 496–501 CrossRef CAS PubMed.
- P. Bettotti, et al., Structure and Properties of DNA Molecules over the Full Range of Biologically Relevant Supercoiling States, Sci. Rep., 2018, 8, 6163 CrossRef PubMed.
- T. Brouns, et al., Free energy landscape and dynamics of supercoiled DNA by high-speed atomic force microscopy, ACS Nano, 2018, 12, 11907–11916 CrossRef CAS PubMed.
- E. A. Oussatcheva, et al., Influence of global DNA topology on cruciform formation in supercoiled DNA, J. Mol. Biol., 2004, 338, 735–743 CrossRef CAS PubMed.
- M. T. J. Van Loenhout, M. V. De Grunt and C. Dekker, Dynamics of DNA supercoils, Science, 2012, 338, 94–97 CrossRef CAS PubMed.
- S. Hyun Kim, et al., DNA sequence encodes the position of DNA supercoils, eLife, 2018, 7, e36557 CrossRef.
- Y. Liu, V. Bondarenko, A. Ninfa and V. M. Studitsky, DNA supercoiling allows enhancer action over a large distance, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 14883–14888 CrossRef CAS PubMed.
- R. Kanaar, P. Van De Putte and N. R. Cozzarelli, Gin-mediated DNA inversion: Product structure and the mechanism of strand exchange, Proc. Natl. Acad. Sci. U. S. A., 1988, 85, 752–756 CrossRef CAS PubMed.
- J. G. Brahms, S. Brahms, Y. Ohara and V. Vagner, Activation and Inhibition of Transcription by Supercoiling, J. Mol. Biol., 1985, 181, 455–465 CrossRef CAS PubMed.
- G. Snounou and A. D. B. Malcolm, Supercoiling and the mechanism of restriction endonucleases, Eur. J. Biochem., 1984, 138, 275–280 CrossRef CAS PubMed.
- S. E. Halford, N. P. Johnson and J. Grinsted, The reactions of the EcoRI and other restriction endonucleases, Biochem. J., 1979, 179, 353–365 CrossRef CAS PubMed.
- T. R. Strick, V. Croquette and D. Bensimon, Single-molecule analysis of DNA uncoiling by a type II topoisomerase, Nature, 2000, 404, 901–904 CrossRef CAS PubMed.
- D. A. Koster, V. Croquette, C. Dekker, S. Shuman and N. H. Dekker, Friction and torque govern the relaxation of DNA supercoils by eukaryotic topoisomerase IB, Nature, 2005, 434, 671–674 CrossRef CAS PubMed.
- J. Gore, et al., Mechanochemical analysis of DNA gyrase using rotor bead tracking, Nature, 2006, 439, 100–104 CrossRef CAS.
- W. H. Coulter, Means for Counting Particles Suspended in a Fluid, U.S. Patent No2656508, 1953 Search PubMed.
- A. J. Storm, et al., Fast DNA translocation through a solid-state nanopore, Nano Lett., 2005, 5, 1193–1197 CrossRef CAS PubMed.
- J. Li, M. Gershow, D. Stein, E. Brandin and J. A. Golovchenko, DNA molecules and configurations in a solid-state nanopore microscope, Nat. Mater., 2003, 2, 611–615 CrossRef CAS PubMed.
- L. Liu, C. Yang, K. Zhao, J. Li and H. C. Wu, Ultrashort single-walled carbon nanotubes in a lipid bilayer as a new nanopore sensor, Nat. Commun., 2013, 4, 2989 CrossRef PubMed.
- G. F. Schneider, et al., DNA translocation through graphene nanopores, Nano Lett., 2010, 10, 3163–3167 CrossRef CAS PubMed.
- L. J. Steinbock, R. D. Bulushev, S. Krishnan, C. Raillon and A. Radenovic, DNA translocation through low-noise glass nanopores, ACS Nano, 2013, 7, 11255–11262 CrossRef CAS PubMed.
- L. J. Steinbock, O. Otto, C. Chimerel, J. Gornall and U. F. Keyser, Detecting DNA folding with nanocapillaries, Nano Lett., 2010, 10, 2493–2497 CrossRef CAS PubMed.
- J. A. Bafna and G. V. Soni, Fabrication of low noise borosilicate glass nanopores for single molecule sensing, PLoS One, 2016, 11, e0157399 CrossRef PubMed.
- C. Dekker, Solid-state nanopores, Nat. Nanotechnol., 2007, 2, 209–215 CrossRef CAS PubMed.
- D. Branton, et al., The potential and challenges of nanopore sequencing, Nat. Biotechnol., 2008, 26, 1146–1153 CrossRef CAS PubMed.
- M. Wanunu, Nanopores: A journey towards DNA sequencing, Phys. Life Rev., 2012, 9, 125–158 CrossRef.
- S. M. Iqbal and R. Bashir, Nanopores: Sensing and Fundamental Biological Interactions, Springer, 2011 Search PubMed.
- R. D. Bulushev, et al., Measurement of the position-dependent electrophoretic force on DNA in a glass nanocapillary, Nano Lett., 2014, 14, 6606–6613 CrossRef CAS.
- N. E. Weckman, et al., Multiplexed DNA identification using site specific dCas9 barcodes and nanopore sensing, ACS Sens., 2019, 4, 2065–2072 CrossRef CAS PubMed.
- S. M. Lu, Y. Y. Peng, Y. L. Ying and Y. T. Long, Electrochemical Sensing at a Confined Space, Anal. Chem., 2020, 92, 5621–5644 CrossRef CAS.
- R. J. Yu, Y. L. Ying, R. Gao and Y. T. Long, Confined Nanopipette Sensing: From Single Molecules, Single Nanoparticles, to Single Cells, Angew. Chem., Int. Ed., 2019, 58, 3706–3714 CrossRef CAS PubMed.
- P. Waduge, et al., Nanopore-based measurements of protein size, fluctuations, and conformational changes, ACS Nano, 2017, 11, 5706–5716 CrossRef CAS.
- H. Chae, D. K. Kwak, M. K. Lee, S. W. Chi and K. B. Kim, Solid-state nanopore analysis on conformation change of p53TAD-MDM2 fusion protein induced by protein-protein interaction, Nanoscale, 2018, 10, 17227–17235 RSC.
- X. Wang, et al., Single-molecule nanopore sensing of actin dynamics and drug binding, Chem. Sci., 2020, 11, 970–979 RSC.
- R. Nouri, Y. Jiang, X. L. Lian and W. Guan, Sequence-Specific Recognition of HIV-1 DNA with Solid-State CRISPR-Cas12a-Assisted Nanopores (SCAN), ACS Sens., 2020, 5, 1273–1280 CrossRef CAS.
- A. Fennouri, et al., Single molecule detection of glycosaminoglycan hyaluronic acid oligosaccharides and depolymerization enzyme activity using a protein nanopore, ACS Nano, 2012, 6, 9672–9678 CrossRef CAS PubMed.
- T. Ma, E. Balanzat, J. M. Janot and S. Balme, Single conical track-etched nanopore for a free-label detection of OSCS contaminants in heparin, Biosens. Bioelectron., 2019, 137, 207–212 CrossRef CAS PubMed.
- N. Giamblanco, J. M. Janot, A. Gubbiotti, M. Chinappi and S. Balme, Characterization of Food Amyloid Protein Digestion by Conical Nanopore, Small Methods, 2020, 4, 1900703 CrossRef CAS.
- T. Ma, J. M. Janot and S. Balme, Dynamics of long hyaluronic acid chains through conical nanochannels for characterizing enzyme reactions in confined spaces, Nanoscale, 2020, 12, 7231–7239 RSC.
- C. Plesa, et al., Direct observation of DNA knots using a solid-state nanopore, Nat. Nanotechnol., 2016, 11, 1093–1097 CrossRef CAS PubMed.
- R. Kumar Sharma, I. Agrawal, L. Dai, P. S. Doyle and S. Garaj, Complex DNA knots detected with a nanopore sensor, Nat. Commun., 2019, 10, 4473 CrossRef PubMed.
- F. Bošković, J. Zhu, K. Chen and U. F. Keyser, Monitoring G-Quadruplex Formation with DNA Carriers and Solid-State Nanopores, Nano Lett., 2019, 19, 7996–8001 CrossRef PubMed.
- D. Fologea, E. Brandin, J. Uplinger, D. Branton and J. Li, DNA conformation and base number simultaneously determined in a nanopore, Electrophoresis, 2007, 28, 3186–3192 CrossRef CAS PubMed.
- Q. Chen, S. Diao and C. Wu, How does a supercoiled DNA chain pass through a small conical glass pore?, Soft Matter, 2012, 8, 5451–5458 RSC.
- E. Krueger, et al., Modeling and analysis of intercalant effects on circular DNA conformation, ACS Nano, 2016, 10, 8910–8917 CrossRef CAS PubMed.
- A. Gansen, K. Tóth, N. Schwarz and J. Langowski, Structural variability of nucleosomes detected by single-pair förster resonance energy transfer: Histone acetylation, sequence variation, and salt effects, J. Phys. Chem. B, 2009, 113, 2604–2613 CrossRef CAS PubMed.
- N. P. Hazan, et al., Nucleosome core particle disassembly and assembly kinetics studied using single-molecule fluorescence, Biophys. J., 2015, 109, 1676–1685 CrossRef CAS PubMed.
- A. J. Storm, J. H. Chen, H. W. Zandbergen and C. Dekker, Translocation of double-strand DNA through a silicon oxide nanopore, Phys. Rev. E, 2005, 71, 051903 CrossRef CAS PubMed.
- S. S. Zakharova, et al., Dimensions of plectonemically supercoiled DNA, Biophys. J., 2002, 83, 1106–1118 CrossRef CAS PubMed.
- D. Fologea, et al., Detecting single stranded DNA with a solid state nanopore, Nano Lett., 2005, 5, 1905–1909 CrossRef CAS PubMed.
- S. W. Kowalczyk, A. Y. Grosberg, Y. Rabin and C. Dekker, Modeling the conductance and DNA blockade of solid-state nanopores, Nanotechnology, 2011, 22, 315101 CrossRef PubMed.
- E. C. Yusko, et al., Controlling protein translocation through nanopores with bio-inspired fluid walls, Nat. Nanotechnol., 2011, 6, 253–260 CrossRef CAS PubMed.
- L. J. Steinbock, et al., Probing the size of proteins with glass nanopores, Nanoscale, 2014, 6, 14380–14387 RSC.
- W. Yang, et al., Detection of CRISPR-dCas9 on DNA with Solid-State Nanopores, Nano Lett., 2018, 18, 6469–6474 CrossRef CAS PubMed.
- W. Li, et al., Single protein molecule detection by glass nanopores, ACS Nano, 2013, 7, 4129–4134 CrossRef CAS PubMed.
- B. M. Reinhard, J. M. Yassif, P. Vach and J. Liphardt, Plasmon rulers as dynamic molecular rulers in enzymology, in Methods in Enzymology, Academic Press Inc., 2010, vol. 475, pp. 175–198 Search PubMed.
- S. E. Halford, Hopping, jumping and looping by restriction enzymes, Biochem. Soc. Trans., 2001, 29, 363–373 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: 9 figures and 5 tables. See DOI: 10.1039/d0nr06219g |
| This journal is © The Royal Society of Chemistry 2021 |