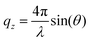Tuneable interfacial surfactant aggregates mimic lyotropic phases and facilitate large scale nanopatterning

Abstract

It is shown that the air–liquid interface can be made to display the same rich curvature phenomena as common lyotropic liquid crystal systems. Through mixing an insoluble, naturally occurring, branched fatty acid, with an unbranched fatty acid of the same length, systematic variation in the packing constraints at the air–water interface could be obtained. The combination of atomic force microscopy and neutron reflectometry is used to demonstrate that the water surface exhibits significant tuneable topography. By systematic variation of the two fatty acid proportions, ordered arrays of monodisperse spherical caps, cylindrical sections, and a mesh phase are all observed, as well as the expected lamellar structure. The tuneable deformability of the air–water interface permits this hitherto unexplored topological diversity, which is analogous to the phase elaboration displayed by amphiphiles in solution. It offers a wealth of novel possibilities for the tailoring of nanostructure.

---

Introduction

The concept of a packing parameter to determine the size and shape of micelles, and the structures within mesophases, has played a paramount role in the understanding of surfactant self-assembly in solution and lyotropic liquid crystals.^1–3 While essentially a simple concept, relating the volume of a hydrophobic moiety to the area of a polar headgroup allows understanding of the intrinsic curvature of structures found in emulsions, foams, micelles etc.⁴ Such thermodynamically driven self-assembly of surface-active molecules is, for example, essential in the formation of cell walls,^5,6 as well as in bio-lubrication⁷ and our ability to breathe.⁸ Knowledge of the underlying processes of self-assembly has not only contributed to an understanding that has resulted in the precise fine-tuning of micellar structures (for example via charge screening or increased hydrophobic interaction^9–11), but has also prompted the discovery of myriad intriguing surfactant phases, now being exploited for technological development.^4,12–16 Such self-assembly structures are not restricted to bulk phases: admicelles, surface micelles or hemi-micelles forming at the solid–water interface have been imaged in situ with atomic force microscopy (AFM),^17,18 and shown to adopt various surface structures consistent with the concept of a packing parameter, and which can be tuned by controlling the surfactant structure, charge and concentration as well as the ionic strength and pH, and specific substrate–adsorbate headgroup interactions.^19–24

The presence of two-dimensional surface micelles at the air–water interface was suggested over a century ago for insoluble surfactant monolayers studied using the Langmuir technique,²⁵ which has since been rationalized using thermodynamic arguments based on the non-linearity observed in first order phase transitions in pressure–area isotherms.^26,27 However, experimental methods to validate such interfacial structures were lacking at the time. The hypothesis was nevertheless further strengthened by theoretical predictions of 2D surface micelles, proposed as an intuitive extrapolation of the packing parameter responsible for bulk micelles.²⁸ 2D surface micelle dimensions were predicted to possess a diameter of two molecular lengths and display a cartwheel structure lying on the surface. Vibrational sum frequency spectroscopy (VSFS) has also been used to infer the transition from 2D “cartwheel” micelles to a monolayer at higher surface coverage.^29,30 Recently, large circular aggregates have been observed by using the Langmuir–Blodgett technique^31–33 to deposit insoluble monolayers of partially fluorinated long chain fatty acids from the air–water interface onto a solid substrate, followed by characterisation of the monolayer structure with AFM.³⁴ Regularly sized, circular, two dimensional domains composed of monolayers of low molecular weight surfactants were shown to form regularly ordered 2D domains with aggregation numbers of roughly 700 molecules. This study was followed by several examples of similar surface patterning of short-lived 2D domains transferred from the air–water interface to solid substrates.^35–38 These domains consisted of circular, monodisperse monolayer patches, rather than the 2D cartwheel micelles mentioned above.

Surface patterning of transferred monolayers was observed for the 18-methyleicosanoic acid (18-MEA³⁹) system: an antepenultimately methyl-branched fatty acid found as the major constituent of barrier lipids covalently bound to the outermost surface of mammalian hair.^40–43 Its role is multi-functional, working as a lubricant between hair strands,^44–46 providing hair surface cell adhesion,⁴⁷ and possibly anti-microbial properties.^48,49 Several suggestions have been made to explain the role and the positioning of the methyl branch. For instance, it may induce a larger degree of disorder compared to its unbranched analogue, leading to a decreased melting point,^50,51 which is normally achieved biologically via unsaturation,⁵ which is an unviable approach in the oxidative environment of air.⁵² Additionally, increased packing frustration increases the occupied area per molecule at a surface, which could better correspond to the limited number of cysteine binding sites in the underlying protein matrix of the hair.^45,53

Using VSFS at the air–water interface, and AFM on deposited monolayers, 18-MEA was studied together with its penultimately branched and straight chain analogues, 19-MEA and eicosanoic acid (EA), respectively.³⁹ The branched fatty acids—but not the straight chain analogue—were observed to form surface domains with dimensions dependent on the methyl branch positioning. This engendered the hypothesis that the domains at the air–water interface not only pattern the water surface, but in fact texture it in three dimensions to accommodate the packing constraints of the aliphatic chain—induced by the methyl branch—while maintaining a small headgroup area. Such an argument is in line with the principles of the packing parameter—a curvature induced by the competing constraints of the hydrophobic and hydrophilic moieties, and is not controversial in that context. What was controversial is that a 3D patterning of the air–water interface had never been suggested in the numerous studies of Langmuir films that had been conducted over the previous 100 years. Normally Langmuir films are considered to be 2D monolayers atop a completely planar air–water interface, apart from thermally induced capillary waves, which would normally cause perturbations in the order of 3 Å, albeit dependent on surface pressure.^54,55 (Obviously, 3D topography can occur, for example in a protein or nanoparticle film, but such topography is associated with the constituents of the film, rather than the water interface itself.) Recently, the hypothesis of 3D texturing received strong support, using neutron reflectometry (NR) and its inherent isotope dependent interaction potential to quantify an effective induced roughening of the water surface.⁵⁶ The effective roughening of this system well surpassed what could be expected from capillary waves, and could be explained only by an organised topography of the water interface induced by surfactant self-assembly.

Since deposited monolayers of 18-MEA display monodisperse domains, which have been inferred to originate from spherical caps on the water surface, and EA forms featureless planar monolayers, it is reasonable to hypothesise that the self-assembly behaviour of mixtures of these two fatty acids should display a systematic variation of structure depending on their proportions. Assuming that the two fatty acids are miscible and that there is no phase separation in the surface film, the prediction is that a tuneable curvature would result. Below it is demonstrated that the systematic tuning of self-assembly properties leads to changes in the geometry of the domains formed on the surface, and that there is an associated, systematic change in the topography of the water interface. These textures lead to tuneable structures ranging from spherical caps, through cylindrical segments to complex topologies, and eventually flat films of lower density. These 3D textures provide not only a facile means to control the topography of water, but also a method to pattern solid substrates with uniform patterns over large areas, limited only by the dimensions of a Langmuir trough.

Results and discussion

Initially, the following 18-MEA : EA ratios were studied in an attempt to understand whether it is possible to tune systematically the curvature: 100 : 0, 75 : 25, 50 : 50 and 25 : 75 in weight percent; the mole fraction of 18-MEA is thus slightly less by ∼1%. As explained in a succeeding paragraph, it was found necessary to subsequently perform an additional study at the ratio 38 : 62. (Pure EA, that is to say the 0 : 100 ratio, has been extensive studied elsewhere, and corresponding results for the flat featureless monolayer can be seen for example in ref. 39). The subphase conditions for the deposition were chosen to be the same as ref. 39, such that there is both significant dissociation of the carboxylates but also sufficiently small headgroup area to allow the alkyl chain properties to moderate the packing.

AFM was used in tapping mode to image the deposited films using both topography and phase shift. The phase image results shown in Fig. 1 correspond to films deposited on silicon substrates. Corresponding height images are shown in Fig. S1 in the ESI.† All monolayers were deposited at a surface pressure of 20 mN m⁻¹, where the Langmuir films are in a region which would conventionally be identified as the tilted condensed phase, and which is nonetheless far from monolayer fracture collapse in each case.^33,57 (Isotherms are shown in Fig. S2.†) In images A–D, a 2D Fourier transform (FT) inset is shown in the top left corner of each image. Image analysis of FTs was used to determine characteristic length scales in each image, corresponding to domain dimensions and ordering, as illustrated in Fig. S3, and further detailed in the ESI.†

Fig. 1 AFM tapping mode imaging of 18-MEA : EA monolayers formed at the air–water interface and deposited on silicon wafers. Phase images are shown to emphasise the contrast to the silicon substrate. Fractions in wt% for 18-MEA : EA are shown in the bottom right for each deposition. A Fourier transform is shown as inset to the top left of each image, except for the 25 : 75 mixture where no correlated surface structure is observed. Phase shift scalebars all start at zero degrees. All depositions were made at 20 mN m⁻¹. The phase in C has been inverted, and it should also be noted that this image spans 5 μm compared to 3 μm of the other figures, for improved statistics on the FT due to the larger domain size. The corresponding 3 μm height image is shown in Fig. S1 in the ESI.†

A deposited film of neat 18-MEA (Fig. 1A), shows monodisperse ellipse-like domains with semi-axis lengths of 39 and 31 nm, as determined by the FT analysis (see Table S1†). The domains are ordered hexagonally on the surface showing a clear correlation to next nearest neighbour. The domains have a “tower karst” morphology between 2.0 and 2.5 nm in height (determined by a line profile in a higher resolution AFM image shown in Fig. S4†), which is reasonable compared to the theoretically determined maximum length of about 2.7 nm for the extended contour length of an all-trans C20 hydrocarbon chain.^2,3 The domain elongation is parallel to the direction of deposition of the film. With the introduction of 25 wt% straight chain fatty acid, as seen in the image from the 75 : 25 ratio (Fig. 1B), monodisperse domains still cover the surface. The domains are still elongated in the direction of deposition, but show an increased size, with semi-axis lengths of 42 and 55 nm. In this case, the domains display translational ordering to the next nearest neighbour and even weak ordering to the third nearest neighbour in the direction perpendicular to the domain long axis, determined by the FT image analysis. With further increased EA proportion, in the image from the 50 : 50 ratio (Fig. 1C), significantly larger, circular domains cover the surface, showing a characteristic size of 165 nm. Fig. 1D shows the image from the 38 : 62 ratio, where the circular and ellipsoidal shapes are replaced by ordered lines of elongated domains with an equidistant spacing of 90 nm perpendicular to the line direction. In Fig. 1E, the image for the 25 : 75 ratio shows large, flat, irregularly shaped regions covering the surface. There are nonetheless clear boundaries separating the large grains.

As a solid surface is passed through the water–air interface the surface film transferred to the surfaces could be expected to undergo significantly different local forces. One possibility is that the structure is a result of such influences; however neither the 25 : 75 nor the 0 : 100^39,56 case form regular domains. This suggests, equivocally, that the observed topographical features observed for other ratios do not originate from artefacts of the deposition technique, but instead reveal the presence of discrete aggregates that had been present at the air–water interface. The fact that the diameter of the domains increases systematically with decreasing 18-MEA content up until 50 : 50, and the shape thereafter becomes parallel stripes and then featureless monolayers, is highly supportive of the tuneable 3D texturing hypothesis. A “packing parameter” argument, such as that suggested by Israelachvili³ for self-assembly structures in bulk would follow a sequence from small spheres, through larger spheres, cylinders, and finally lamellar structures as the packing constraints are relaxed from high curvature to zero.³ The patterns observed in the AFM images are necessarily two-dimensional in the sense that the headgroup region has been constrained to a rigid planar substrate. The air–water interface is deformable; it can thus curve to accommodate a constant headgroup area (constant surface tension) and the different areas per alkyl chain expected for the mixtures, leading to a 3D curvature of the water–headgroup interface. (The deposited films are thus flattened replicas of these curved structures. Note that the deposited fatty acid film itself has a thickness, and the fact that the film consists of domains leads to a trivial 3D structure, particularly at the domain boundaries, which is observed in Fig S4.†).

It is interesting to note that, at a different pressure to the data in Fig. 1, yet another texture can be induced in the surface for the case of 38 : 62 ratio. At low surface pressure, indeed at 0 mN m⁻¹, but close to the lift-off pressure, the pattern shown in Fig. 2 was observed. In most fatty acid ratios, the same texture was observed, although with an increasing order, as the pressure was increased; but in this case, the pattern is rather different. It is tempting to speculate that this low pressure pattern may reflect a two dimensional analogy of a bicontinuous cubic phase, but it is also possible that these structures are random tubes of the same nature as seen in Fig. 1D, and that the parallel ordering and reduced lateral dimension in that figure are a result of the increased level of confinement associated with the higher pressure.

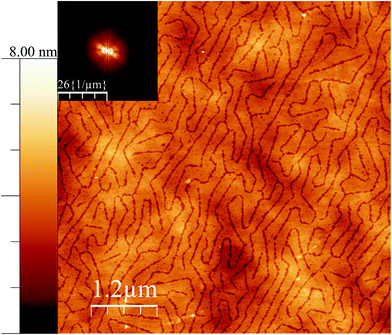Fig. 2 AFM height mode image of a film deposited on silicon wafers close to the surface pressure lift off but still at 0 mN m⁻¹ for the case of 38 : 62 18-MEA : EA (same Langmuir experiment as Fig. 1D). A Fourier transform is shown as inset to the top left. The height scalebar start at zero nanometre.

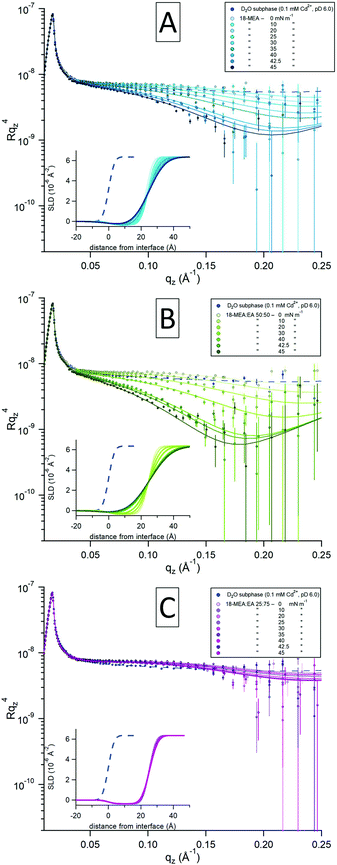
To further test the hypothesis that the 3D texture of the water surface can be tuned, NR was used to study the fatty acid mixtures in situ at the air–water interface. Using this technique it is possible to quantify the extent of any self-assembly induced topography as a function of the both the composition and the surface pressure. The data are presented in Fig. 3 for 18-MEA : EA ratios of 100 : 0 (A), 50 : 50 (B), and 25 : 75 (C). The three plots show intensities of the specular reflectivity as a function of the momentum transfer q_z, normal to the interface. The reflected intensity is shown as Rq_z⁴ to emphasise the intrinsic loss of reflectivity with increasing q_z. Each plot contains a series of consecutive measurements, indicated with darker shades for increasing surface pressure of the system. Model fits (solid lines) to the experimental data (circular markers) were optimized through least-squared regression, and the inset in each plot shows the scattering length density (SLD) profile generated for each fit to the experimental data. The smaller blue markers and dashed lines in each graph represent a reference measurement of a neat D₂O-buffer with no fatty acid and its fit to capillary wave theory, respectively.

Fig. 3 Specular neutron reflectometry results shown for 18-MEA (A) and the two mixtures 18-MEA : EA 50 : 50 (B) and 18-MEA : EA 25 : 75 (C). The data are presented as a function of Rq_z⁴ to emphasise the drop-off in reflectivity with increasing q_z. Lines are fits to the data (filled circles) using a two-layer model, and insets show SLD profiles corresponding to the fits. Reflectometry collected at increasing surface pressure is distinguished by a darkening colour gradient in the data and fits. The smaller blue markers and dashed lines represent a reference measurement on a neat D₂O-buffer subphase.

Due to its isotopic dependency, the neutron probe is intrinsically rather insensitive to hydrocarbons. Thus, to maximize the sensitivity of the measurement to the topography of the water surface, hydrogenous fatty acids were spread on a subphase of D₂O for all the NR measurements. To reliably assess molecular information, such as the thickness and density of the films as well as the degree of hydration of the headgroup, Langmuir films of 18-MEA and EA were also studied using X-ray reflectometry (XRR). These data, together with additional NR of the mixed systems, and appurtenant fits, are presented in the ESI,† where the details of the fitting procedure are also elaborated. To ensure rigour, the X-ray and neutron reflectivity data were fitted self-consistently.

At low surface pressures (<20 mN m⁻¹), the data are similar for all the samples studied with different fatty acid ratios and display a relatively minor increase in the reflectivity around 0.10 Å⁻¹ compared to the neat subphase. This slight increase originates from the contribution of hydrocarbon scattering. With increasing surface pressure, 18-MEA : EA 100 : 0 (Fig. 3A) starts to undergo a decrease in specular reflection at around 0.05 Å⁻¹, which evolves with increasing q_z. The greatest decrease in specular reflectivity is observed at the highest surface pressure. A similar trend is observed for the case of 50 : 50 (Fig. 3B), and the reduction in specular reflection is even more pronounced here, where once again the higher surface pressure results in the larger loss of specular reflection. In contrast, the 25 : 75 (Fig. 3C) ratio is apparently insensitive to changes in surface pressure, and there is almost no reduction in specular reflection compared to the neat D₂O surface. Since the hydrogenous aliphatic chain only has minor influence on the reflectivity profile, these observations reveal differences in the surface topography of the underlying water surface.

A two-layer slab model of the fatty acid was used to fit the data using an equivalent approach to that in ref. 56: that is to say a semi-infinite ambient medium of air, a hydrocarbon chain layer in contact with the air, a solvated headgroups layer in contact with the subphase, and a semi-infinite D₂O subphase. With the molecular dimensions and SLDs for each layer obtained from XRR, only the interfacial topography needed to be fitted. (The only exception to this was the hydrocarbon chain SLD at low pressures, where the SLD was closer to that of air due to inhomogeneities in the monolayer at zero surface pressure.) For a slab model consisting of a thin layer this is most reliably done by invoking a Gaussian interfacial “roughness” and constraining every interface to have the same value.^56,58 This is shown in ref. 58 to provide dependable fits to experimental data for several systems with systematically varied isotopic contrasts, and further strengthened in ref. 56, where this two-layer model was demonstrated to be equivalent to a conventional slicing model. While conventionally used to describe the small scale roughness associated with capillary waves, this “roughness” can also be used as a measure of the topographical modulation by self-assembly curvature. It was not possible to fit the NR data without invoking an increase in topography in this way. It is noteworthy that the topography increases only as the film is constrained to nonzero values of the surface pressure, as the area of the trough is decreased.

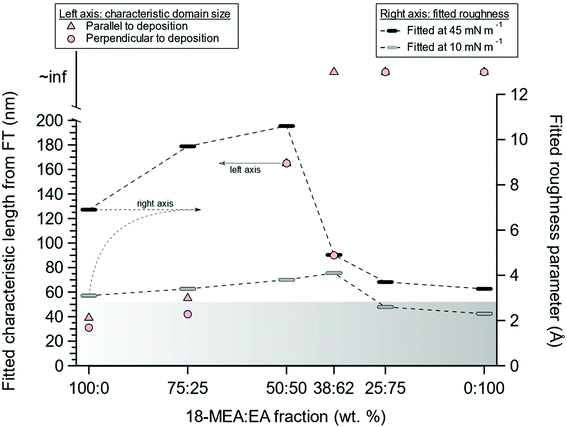
The fitted effective surface roughness parameters at relatively high (45 mN m⁻¹) and low (10 mN m⁻¹) values of the surface pressure are shown for all the 18-MEA : EA ratios in Fig. 4, together with the corresponding domain sizes from FT analysis of AFM imaging of deposited monolayers. Additionally, the gradient banner represents a capillary wave roughness of 2.8 Å, as determined from a neat D₂O buffer. With increasing EA proportion from 0% to 50%, the fitted topography increased (right axis), coinciding with the increased domain size observed in AFM (left axis). At higher EA proportions, the topography was reduced and became comparable to that observed for a neat EA monolayer. The rather dramatic change in topography between the 50 : 50 sample and the 25 : 75 samples was what prompted the additional ratio of 38 : 62 to be included in the study.

Fig. 4 Summary of results from AFM imaging and NR as a function of 18-MEA : EA fraction in wt%. The left-hand axis relates the filled circles and triangles to the fitted characteristic lengths found via FT analysis of AFM images of deposited monolayers. The right-hand axis corresponds to the fitted roughness parameters from fits to NR data, using a two-layer model, for low (10 mN m⁻¹) and high (45 mN m⁻¹) surface pressures, indicated by grey and black bars, respectively. The dashed lines between the bars are guides for the eye, and the gradient banner represents a capillary wave roughness of 2.83 Å, as measured from a neat D₂O buffer with NR.

The concomitant variation in the topography with the changes in the morphology of the deposited film is highly suggestive of—if not absolute proof of—a systematic variation in the self-assembly curvature. The large topography associated with the air–water interface is much larger than can be explained by, for example, capillary waves.^54–56 Additional support for the argument comes from considering the size of the domains for different positions of the methyl branch. The location of the branch at the C19 position should impose a lower curvature than at the C18 position, which in the latter case should lead to a larger curvature and smaller domains. This is indeed what is observed.^39,56

Furthermore, comparing surface roughness parameters measured with NR for neat 18-MEA and 19-MEA,⁵⁶ shows a smaller surface perturbance for the antepenultimately branched 18-MEA. Once again, this supports—but does not necessarily prove—the hypothesis of an aliphatic chain packing constraint at the air–water interface, responsible for the shape and size of surface domains.³⁹ A necessary condition for this hypothesis is that 18-MEA and EA mix homogeneously in the film, and that the introduction of EA to the monolayer would separate the branched 18-MEA molecules, relaxing the packing constraint from the methyl branch. The assumption of mixing appears justified: there is only a single domain size for each proportion, characteristic of an energy minimum for the system, and the AFM phase images are uniform, indicating the absence of phase separation.

Conclusion

By analogy to a lyotropic liquid crystal, relaxation of the packing constraint should lead to two observations. First, an overall decrease in the ratio of branched molecules should lead to a larger radius of curvature of surface domains observed with AFM. Second, changes in the radius of curvature should lead to changes in the surface roughness at the air–water interface, as observed with NR. It is striking that both these criteria are met as the 18-MEA : EA ratio is varied, i.e. an increased ratio of EA gradually leads to larger domains and higher surface roughness, as expected for a system constrained by packing arguments. Particularly compelling is the transition from spherical caps to the two-dimensional equivalent of a hexagonal phase (parallel cylindrical segments), and then to a two-dimensional lamellar phase (a featureless, flat monolayer). It is important to recognise that the domains are caps and segments, rather than hemispheres and hemicylinders; thus no unambiguous radius of curvature can be extracted from the measurements, particularly as the topography parameter represents a Gaussian roughness rather than an absolute “height” of the caps. The exact factors determining the height of the cap for a given radius (and thus the size of the domains) do not fall naturally from the analysis. It is likely that energetically unfavourable “edge effects” and line tension are responsible for regulating the final dimensions. At the borders of the domains the curvature arguments predict hydrocarbon–water contact and opposite curvature of the air–water interface. (Simulations of disc-like aggregates curvature of the hydrocarbon–water interface.⁵⁹) Nonetheless, the results unambiguously confirm the initial, and novel, hypothesis that the air–water interface can be textured into different patterns by systematic control of the packing constraints governing the surface self-assembly, and that these extremely well ordered three-dimensional patterns can be transferred to a solid surface, albeit in two dimensions. In addition to controlling the self assembly structure via the alkyl region as done here, the mismatch between alkyl chain area and headgroup area should also be tuneable by addressing the charge and hydration of the headgroup region via subphase characteristics such as pH and ionic strength. Two manuscripts addressing these aspects are in preparation. It follows that this phenomenon should also be observed for systems of similar packing constraints, such as floating films of branched or unsaturated phospholipids, double chained cationic surfactants, partially fluorinated chains etc. Such systems will form the basis of future studies.

Experimental methods

All chemicals were used as received. All water used was provided through a MilliQ (Merck MilliPore, United States) water purification system with constantly monitored resistivity and total organic content of >18.2 MΩ cm and <4 ppb, respectively. All mixture compositions are chosen as weight percent to facilitate sample preparation. This only leads to a 1% difference in mole percent.

In-house

Solutions of 1 mg mL⁻¹ 18-methyleicosanoic acid (99%, Larodan, Sweden), and eicosanoic acid (≥99%, Sigma-Aldrich, United States) were made through dissolution in chloroform (>99% with 50 ppm amylene, from Alfa Aesar, United States). The subphase was a 0.1 mM cadmium chloride (CdCl₂ >99.0%, Sigma-Aldrich), 0.1 mm sodium bicarbonate (NaHCO₃ 99.5%, Sigma-Aldrich) solution buffered to pH 6.0 with hydrochloric acid (HCl, Fluka, United States).

At FIGARO beamline

Solutions of 1 mg mL⁻¹ 18-methyl eicosanoic acid (99%, Larodan, Sweden) and eicosanoic acid (≥99%, Sigma-Aldrich) were made through dissolution in chloroform (99.5% with 100–200 ppm amylene, Sigma-Aldrich). The subphase was a 0.1 mm cadmium chloride (CdCl₂ >99.0%, Sigma-Aldrich), 0.1 mm sodium bicarbonate (NaHCO₃ 99.5%, Sigma-Aldrich) deuterium (D₂O 99.8 atom % D, Sigma-Aldrich) solution buffered to pD 6.0 (corresponding pH of 5.6⁶⁰) with deuterium chloride (DCl, Sigma-Aldrich).

AFM

A Multimode Microscope LN (Bruker, United States) was used in tapping mode for imaging of deposited fatty acid monolayers. Silicon cantilevers (HQ:NSC35/AL BS, MikroMasch, Switzerland) with a nominal radius of 8 nm were used. The nominal resonance frequency and force constant of the cantilevers were 150 kHz and 5.4 Nm,¹ respectively. Prior to measurement, cantilevers were cleaned under UV-light for 10 min. AFM images were analysed using the WsXM software.⁶¹

Langmuir–Blodgett deposition

A KSV NIMA 5000 system (Biolin Scientific, Sweden) was used for isotherms and depositions. It was equipped with a 580 × 150 × 4 mm PTFE (polytetrafluoroethylene) trough with hydrophilic POM (polyoxymethylene) barriers. Wilhelmy plates from lint free paper (Biolin Scientific) were used to monitor surface pressure to a certainty of ±0.01 mN m⁻¹. The subphase temperature was controlled to 22.0 ± 0.1 °C. Barriers were compressed by 4.5 cm² min⁻¹ and depositions were performed at 1 mm min⁻¹ with the surface pressure kept constant. The cadmium-buffer was chosen to increase the compressibility of the monolayer, and the solution was kept at pH 6.0 for increased monolayer stability. Depositions were made on silicon wafers which were cleaned through immersion in 5% chromosulfuric acid followed by thorough rinsing with MilliQ water. After spreading of the monolayer, the chloroform was allowed to evaporate for 10–15 minutes before the start of isotherm or deposition. A sequence of depositions at increasing surface pressure were made on the same silicon wafer.

Neutron reflectometry (NR)

NR was measured at the horizontal time-of-flight reflectometer FIGARO at Institut Laue-Langevin (ILL) in Grenoble, France.⁶² Specular reflection at the air–water interface can be described by intensity variations of reflected radiation with respect to the momentum transfer vector q_z normal to the interface:
where θ is the incident angle and λ is the radiation wavelength. Reflectivity data were collected at two incident angles: a low angle (0.62°) with a high reflectivity and short counting time, and a higher angle (3.78°) with lower reflectivity and longer counting time, yielding data from 0.01–0.26 Å⁻¹ in q_z. Data were collected at both angles only at the lowest and highest surface pressures (0 and 45 mN m⁻¹) as the intermittent measurements provided no additional structural information at low q_z-values. Raw data were reduced using COSMOS⁶³ and the normalized NR data were analysed using Motofit.⁶⁴

X-ray reflectometry (XRR)

XRR measurements were performed using a Panalytical X'Pert Pro instrument at ANSTO, in Lucas Heights Australia. Cu Kα (λ = 1.54 Å) radiation was used to collect reflectometry data at 0.1–1.5° and 1.2–7.0° at angular increments of 0.01° and 0.1°, respectively. To reduce shock waves during X-ray (and neutron) measurements, the Langmuir trough was situated on an antivibration table. The water subphase was kept at 22.0 ± 0.02 °C by a circulation bath. XRR data was analysed with Motofit.⁶⁴

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We thank the ILL for the provision of neutron beam time on FIGARO (DOI:10.5291/ILL-DATA.9-10-1487 and 10.5291/ILL-DATA.9-10-1515), and ANSTO for the provision of XRR beam time on Platypus (Proposal: P6419). M. R. and E. B. acknowledge support from the Swedish Research Council via grant VR 2013-04384. P. M. B. acknowledges funding from the Excellence Cluster Nanosystems Initiative Munich (NIM) and the Center for NanoScience (CeNS). We thank Deborah Wakeham, Anna Oleshkevych, Adrian Rennie, and Philippe Fontaine for useful discussions.

References

1. H. V. Tartar, J. Phys. Chem., 1956, 59, 1195–1199.
2. C. Tanford, J. Phys. Chem., 1972, 76, 3020–3024.
3. J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525–1568.
4. S. Hyde, Z. Blum, T. Landh, S. Lidin, B. W. Ninham, S. Andersson and K. Larsson, The Language of Shape, Elsevier, 1996.
5. C. D. Stubbs and A. D. Smith, Biochim. Biophys. Acta, Rev. Biomembr., 1984, 779, 89–137.
6. A. A. Spector and M. A. Yorek, J. Lipid Res., 1985, 26, 1015–1035.
7. W. H. Briscoe, S. Titmuss, F. Tiberg, R. K. Thomas, D. J. McGillivray and J. Klein, Nature, 2006, 444, 191–194.
8. S. Rugonyi, S. C. Biswas and S. B. Hall, Respir. Physiol. Neurobiol., 2008, 163, 244–255.
9. H. Wennerström and B. Lindman, Phys. Rep., 1979, 52, 1–86.
10. F. M. Menger, Acc. Chem. Res., 1979, 12, 111–117.
11. J. Israelachvili, Intermolecular and Surface Forces, Academic Press, 2011.
12. T. Yanagisawa, T. Shimizu, K. Kuroda and C. Kato, Bull. Chem. Soc. Jpn., 1990, 63, 988–992.
13. C. T. Kresge, M. E. Leonowicz, W. J. Roth, J. C. Vartuli and J. S. Beck, Nature, 1992, 359, 710–712.
14. V. Luzzati and P. A. Spegt, Nature, 1967, 215, 701–704.
15. J. M. Seddon and R. H. Templer, Philos. Trans. R. Soc. London, Ser. A, 1993, 344, 377–401.
16. R. Holyst, Nat. Mater., 2005, 4, 510–511.
17. S. Manne, J. P. Cleveland, H. E. Gaub, G. D. Stucky and P. K. Hansma, Langmuir, 1994, 10, 4409–4413.
18. E. J. Wanless and W. A. Ducker, J. Phys. Chem., 1996, 100, 3207–3214.
19. W. A. Ducker and E. J. Wanless, Langmuir, 1996, 12, 5915–5920.
20. L. M. Grant and W. A. Ducker, J. Phys. Chem. B, 1997, 101, 5337–5345.
21. V. Subramanian and W. A. Ducker, Langmuir, 2000, 16, 4447–4454.
22. V. Seredyuk, E. Alami, M. Nydén, K. Holmberg, A. V. Peresypkin and F. M. Menger, Colloids Surf., A, 2002, 203, 245–258.
23. H. Domínguez, Langmuir, 2009, 25, 9006–9011.
24. S. Inoue, T. Uchihashi, D. Yamamoto and T. Ando, Chem. Commun., 2011, 47, 4974–4976.
25. A. Pockels (Rayleigh), Nature, 1891, 43, 437–439.
26. B. Y. Yue, C. M. Jackson, J. A. G. Taylor, J. Mingins and B. A. Pethica, J. Chem. Soc., Faraday Trans. 1, 1976, 72, 2685–2693.
27. O. Albrecht, H. Gruler and E. Sackmann, J. Phys., 1978, 39, 301–313.
28. J. Israelachvili, Langmuir, 1994, 10, 3774–3781.
29. E. Tyrode, C. M. Johnson, A. Kumpulainen, M. W. Rutland and P. M. Claesson, J. Am. Chem. Soc., 2005, 127, 16848–16859.
30. E. Tyrode, C. M. Johnson, M. W. Rutland and P. M. Claesson, J. Phys. Chem. C, 2007, 111, 11642–11652.
31. I. Langmuir, Trans. Faraday Soc., 1920, 15, 62–74.
32. K. B. Blodgett, J. Am. Chem. Soc., 1934, 56, 495.
33. J. B. Peng, G. T. Barnes and I. R. Gentle, Adv. Colloid Interface Sci., 2001, 91, 163–219.
34. T. Kato, M. Kameyama and M. Kawano, Thin Solid Films, 1996, 273, 232–235.
35. M. Maaloum, P. Muller and M. P. Krafft, Angew. Chem., Int. Ed., 2002, 41, 4331–4334.
36. P. Fontaine, M. Goldmann, P. Muller, M. C. Fauré, O. Konovalov and M. P. Krafft, J. Am. Chem. Soc., 2005, 127, 512–513.
37. L. De Viguerie, R. Keller, U. Jonas, R. Berger, C. G. Clark, C. O. Klein, T. Geue, K. Müllen, H. J. Butt and D. Vlassopoulos, Langmuir, 2011, 27, 8776–8786.
38. S. M. Malone, S. Trabelsi, S. Zhang, T. R. Lee and D. K. Schwartz, J. Phys. Chem. B, 2010, 114, 8616–8620.
39. J. F. D. Liljeblad, E. Tyrode, E. Thormann, A.-C. Dublanchet, G. Luengo, C. M. Johnson and M. W. Rutland, Phys. Chem. Chem. Phys., 2014, 16, 17869–17882.
40. R. Evans, Adv. Phys., 1979, 28, 143–200.
41. P. W. Wertz and D. T. Downing, Lipids, 1988, 23, 878–881.
42. R. I. Logan, D. E. Rivett, D. J. Tucker and A. H. F. Hudson, Text. Res. J., 1989, 59, 109–113.
43. A. Körner and G. Wortmann, Proceedings of 11th Int. Wool Textile Res. Conf., Leeds UK, 2005, p. 11.
44. L. N. Jones and D. E. Rivett, Micron, 1997, 28, 469–485.
45. J. A. Swift, J. Cosmet. Sci., 1999, 50, 23–47.
46. S. Breakspear, J. R. Smith and G. Luengo, J. Struct. Biol., 2005, 149, 235–242.
47. L. N. Jones, D. J. Peet, D. M. Danks, A. P. Negri and D. E. Rivett, J. Invest. Dermatol., 1996, 106, 461–464.
48. B. Caven, B. Redl and T. Bechtold, Text. Res. J., 2019, 89, 510–516.
49. U. Roze, D. C. Locke and N. Vatakis, J. Chem. Ecol., 1990, 16, 725–734.
50. S. Abrahamsson, S. Ställberg-Stenhagen and E. Stenhagen, Prog. Chem. Fats Other Lipids, 1964, 7(Part 1), 1–157.
51. J. R. Nunn, J. Chem. Soc., 1951, 1740–1744.
52. J. F. D. Liljeblad, V. Bulone, E. C. Tyrode, M. C. Johnson and M. W. Rutland, Biophys. J., 2012, 102, 591a.
53. D. W. Cheong, F. C. H. Lim and L. Zhang, Langmuir, 2012, 28, 13008–13017.
54. A. Braslau, P. S. Pershan, G. Swislow, B. M. Ocko and J. Als-Nielsen, Phys. Rev. A, 1988, 38, 2457–2470.
55. S. K. Sinha, E. B. Sirota and S. Garoff, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 2297–2311.
56. E. Bergendal, R. A. Campbell, G. A. Pilkington, P. Müller-Buschbaum and M. W. Rutland, Nanoscale Horiz., 2020, 5, 839–846.
57. V. Kaganer, H. Möhwald and P. Dutta, Rev. Mod. Phys., 1999, 71, 779–819.
58. R. A. Campbell, Y. Saaka, Y. Shao, Y. Gerelli, R. Cubitt, E. Nazaruk, D. Matyszewska and M. J. Lawrence, J. Colloid Interface Sci., 2018, 531, 98–108.
59. G. M. C. Silva, P. Morgado, P. Lourenço, M. Goldmann and E. J. M. Filipe, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 14868–14873.
60. A. Krezel and W. Bal, J. Inorg. Biochem., 2004, 98, 161–166.
61. I. Horcas, R. Fernández, J. M. Gómez-Rodríguez, J. Colchero, J. Gómez-Herrero and A. M. Baro, Rev. Sci. Instrum., 2007, 78, 13705.
62. R. A. Campbell, H. P. Wacklin, I. Sutton, R. Cubitt and G. Fragneto, Eur. Phys. J. Plus, 2011, 126, 107.
63. P. Gutfreund, T. Saerbeck, M. A. Gonzalez, E. Pellegrini, M. Laver, C. Dewhurst and R. Cubitt, J. Appl. Crystallogr., 2018, 51, 606–615.
64. A. Nelson, J. Appl. Crystallogr., 2006, 39, 273–276.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary AFM height modulation images, Langmuir isotherms, AFM FT analysis, AFM height image line profiles, X-ray and neutron fitting procedures, supplementary X-ray and neutron data, X-ray and neutron fitting results (PDF). See DOI: 10.1039/d0nr06621d

---