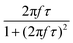Magneto-fluorescent nanocomposites: experimental and theoretical linkage for the optimization of magnetic hyperthermia†
Kosmas
Vamvakidis
 ,
Nikolaos
Maniotis
,
Nikolaos
Maniotis
 and
Catherine
Dendrinou-Samara
and
Catherine
Dendrinou-Samara
 *
*
Laboratory of Inorganic Chemistry, Department of Chemistry, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece. E-mail: samkat@chem.auth.gr
First published on 26th March 2021
Abstract
Magneto-fluorescent nanocomposites have been recognized as an emerging class of materials displaying great potential for improved magnetic hyperthermia assisted by optical imaging. In this study, we have designed a series of hybrid composites that consist of zinc doped ZnxFe3−xO4 ferrites functionalized by polyethylene-glycol (PEG8000) and an orange-emitting platinum complex [Pt(phen)Cl2]. Experimental and theoretical studies on the optimization of their magnetically-mediated heating properties were conducted. PEG was assembled around particles’ surface by two different approaches; in situ and post-PEGylation. PEGylation ensured the optimal distance between the magnetic core and Pt(II)-complex to maintain significant luminescence in the composite. The successful inclusion of the complex to the organic matrix was confirmed by a variety of spectroscopic techniques. A theoretical model was developed, based on linear response theory, in order to examine the composites’ power losses dependence on their properties. Within this model, inter-particle interactions were quantified by inserting a mean dipolar energy term in the estimation of Néel relaxation time, and consequently, the size and concentration that maximize power loss were derived (20 nm and 4 mg mL−1). Moreover, a decrease in the anisotropy of nanoparticles resulted in an increase in specific loss power values. Theoretical estimations are validated by experimental data when heating aqueous dispersions of composites in 24 kA m−1, 765 kHz AMF for various values of concentration and size. Magnetic hyperthermia results showed that the theory-predicted values of optimum concentration and size delivered the maximum-specific loss power which was found equal to 545 W g−1. By the present approach, a quantitative link between the particles’ dipolar interactions and their heating properties is established, while opening new perspectives to nanotheranostic applications.
1. Introduction
Since the pioneering studies on the rational synthesis of individual magnetic nanoparticles (MNPs), the research focus has shifted towards the development of more complicated nanoarchitectures headed for biomedical multitasking applications.1,2 These nanostructures of the next generation are composed of different functional modalities and are able to perform several tasks in parallel, such as simultaneous cancer imaging and therapy.3–5 One of the most favorable dual-modality combinations is the integration of magnetic resonance imaging (MRI) with magnetic hyperthermia (MH) in a single probe.6,7 However, other traditional diagnostic techniques have been seeking to endow combined properties with MH.Optical fluorescence imaging (OFI) counts as an important real-time imaging technique that is used to study molecular effects,8–10 while recently, it has been recommended for the imaging-guided surgery.11,12 The most proposed optical imaging probes for OFI are fluorescent lipids,13 quantum dots (QDs)14–16 and organic dyes.17–19 These systems show much promise but suffer from one or more shortcomings. Photo-bleaching and low chemical stability are some of the major drawbacks of organic dyes functionalized with ferrite nanoparticles.20,21 Even though QDs present high quantum yields, they are considered toxic to the human body.22,23 Lately, photoluminescent metal complexes (PTMCs) have drawn much attention as imaging agents due to their long-term optical stability.24 These complexes are able to emit intense light via a metal-to-ligand charge transfer (MLCT) process and can serve as long-living dyes in various aqueous solutions. Among PTMCs, square planar platinum(II) complexes display interesting photophysical properties, appropriate for OFI. Since the approval of cisplatin for the treatment of various cancers, Pt-complexes have been applied as theranostics through encapsulation into host matrices at the surface of the individual and/or clustered MNPs.25–27
The efficacy of magnetic hyperthermia is usually measured using specific loss power (SLP), which is the power released by MNPs in the form of heat. MH depends on many factors such as magnetic field characteristics (frequency and amplitude), MNPs composition and concentration, size, saturation magnetization and magnetic anisotropy, internal structure and hydrodynamic behavior. In addition, dipolar interactions can also play an important role in MH. By fine-tuning the external field's parameters with MNP properties, it is possible to increase the efficiency of the experiment by orders of magnitude. Thus, a comprehensive analysis of SLP becomes a multi-parametric task that requires modeling the experimental conditions and properties of involved materials.28
The synergistic combination of OFI-MH in a single nanocomposite can exploit both the high sensitivity of OFI for real-time monitoring of the ongoing cancer therapy and the local heat-up of MH for treatment. Such hybrid magneto-fluorescent nanostructures are rarely designed, while theoretical studies on their induction heating properties are still rare. During the preparation of this manuscript, Das et al. presented the development of a novel magnetoluminescent nanocomposite.29 Their research centered on the grafting procedure of luminophores on the particle core but not on the optimization of hyperthermia performance.
An extra concern about the synthesis of an OFI-MH dual agent arises from the presence of MNPs near the environment of the imaging probe, which can cause quenching of luminescence via an energy transfer process.15,28–31 To overcome this effect, the formation of a stable silica (SiO2) shell around MNPs’ surface prior to the introduction of the fluorescent molecule has been proposed.32–34 However, the precise control of the thickness of SiO2 is complicated,31 while Si–O–Si bonds are prone to hydrolysis when exposed to harsh environments, such as highly saline conditions encountered in biological media.35–37 Another drawback of silica is the possible reduction of magnetization of the produced OFI-MRI composites due to a large amount of magnetically inert organic layer.38,39
In the present study, we investigate an OFI-MH dual agent based on the combination of MNPs and PTMCs. In particular, a series of doped zinc ferrites MNPs (ZnxFe3−xO4, x = 0.3, 0.4, 0.45, 0.53) of small size and high Ms values have been synthesized,40 as well as the orange-emitting complex [Pt(phen)Cl2]. The Pt-phenanthroline complex presents π–π stacking in the solid-state, resulting in electronic interactions associated with Pt⋯Pt orbital overlap.41 Apart from its optical properties, it demonstrates cytotoxic, apoptotic effects and is capable of suppressing tumor formation in a dose-dependent manner.42 To anticipate the quenching issue we excluded the use of silica and the hybrid composites were surface-functionalized with polyethylene glycol (PEG) that also acted as an organic template for the absorption of the Pt-complex. PEG has the advantage of the highest solubility and smallest hydrodynamic size among other coatings (dextran, silica, etc.) while PEGylation effectively eliminates cytotoxicity and provides protection against sedimentation for long. The physicochemical characterization of the composites was conducted to verify their successful formation and stability over time. To understand their in-depth performance as MH agents, we conducted a theory-driven optimization of SLP values that predicted a strong influence of dipolar interactions on SLP, being capable of both increasing and decreasing it, while its dependence on other MNP parameters such as size, anisotropy and concentration was also revealed. Those properties were tailored by using the linear response theory (LRT) combined with a mean-field model. The heating evaluation of these hybrid magneto-fluorescent nanocomposite systems, accompanied by a comprehensive theoretical analysis for optimization, is presented for the first time and serves as a strategy for their potential employment as nanotheranostic agents.
2. Materials and methods
2.1 Materials
All the required reagents were of analytical grade and were used without any further purification: iron(III) acetylacetonate Fe(C5H7O2)3 [Fe(acac)3, Fluka, ≥97%], zinc chloride ZnCl2 (Fluca, ≥97%), 1,2-propylene glycol C3H8O2 (PG, Sigma, ≥98%), triethylene glycol C6H14O4 (TrEG, Sigma ≥98%), tetraethylene glycol C8H18O5 (TEG, Sigma, ≥99%), potassium tetrachloroplatinate(II) K2PtCl4 (Sigma, ≥99.99%), 1,10-phenanthroline C12H8N2 (phen, Sigma, ≥99%), sodium chloride NaCl (Sigma, ≥99%), hydrochloric acid HC1 (Sigma, ACS reagent, 37%), polyethylene glycol-8000 (PEG-8000, Alfa Aesar), ethanol C2H5OH (Bruggemann, GmbH, ≥96%), dimethyl sulfoxide C2H6OS (DMSO, Sigma ≥99.7%).2.2 Synthesis of ZnxFe3−xO4 MNPs
For the preparation of the ferrite MNPs, a microwave-assisted polyol process and a modified solvothermal method were adopted that are described extensively in our previous works.39,43 Briefly, Fe(acac)3 (2.7 mmol) and ZnCl2 (1.3 mmol) were dissolved in 0.9 mmol of polyol (PG, TrEG, TEG and PEG8000) and the mixture transferred to an autoclave. After the reaction, at 240 °C for 30 min for the microwave approach, the autoclave was cooled to room temperature and the particles were washed three times with ethanol and isolated by centrifugation (5000 rpm). According to the polyol that was involved, the three samples were labeled as ZnxFe3−xO4@PG, ZnxFe3−xO4@TrEG and ZnxFe3−xO4@TEG. For ZnxFe3−xO4@PEG, a solvothermal approach was adopted. The solvothermal reaction occurred at 200 °C for 24 h, while the isolation of MNPs was performed for the above samples.2.3 Synthesis of [Pt(phen)Cl2]
The Pt-complex was prepared according to the literature procedure.44 Potassium tetrachloroplatinate(II) (0.05 mmol), 1,10-phenanthroline (0.05 mmol), NaCl (67 mg) and HC1 (0.1 ml) were dissolved in 50 ml of water in a 100 ml round-bottomed flask. A stir bar was added and the flask was attached to a condenser and set to reflux for 3 h. The light yellow product that precipitated was filtered out, washed with hot water and dried under vacuum; yield 80%.2.4 Absorption of [Pt(phen)Cl2] onto PEGylated MNPs
First, in a stable aqueous (10 mL) suspension of the polyol-coated MNPs (15 mg), 5 mL of the aqueous solution of PEG (100 mg) was added. The mixture was left to stir for 24 h during which PEG gradually self-assembled on the surface of the particles. The PEGylated MNPs were magnetically isolated, washed three times with ethanol, and dried under vacuum. In the second step, PEGylated MNPs (15 mg) were dispersed in distilled water (15 mL), where [Pt(phen)Cl2] (15 mg) was added and the mixture was stirred at room temperature. After 24 h, the formed nano-molecular composites were collected using a permanent magnet, washed three times with ethanol and dried at room temperature under vacuum.2.5 Magnetic hyperthermia
For magnetic hyperthermia (MH) measurements, a commercial 2-turn solenoid coil (25 mm in diameter and 10 mm in height) resonating at 765 kHz capable of generating a homogenous field in a volume of approximately 5 cm3, ensuring that the whole sample was immersed in a region with a uniform amplitude, was used. The applied alternating magnetic field amplitude was set at 24 kA m−1 that is a typical condition employed in MH experiments.45 The desirable magnetic field could be achieved by adjusting the coil current. Moreover, the cooling system is based on a constant flow of water, which is automatically adjusted in order to keep the temperature of the water flowing at a specific value. It is worth noting that the presence of cooling water flowing through the coil keeps the latter at a constant temperature to avoid overheating. Water temperature was found to be 11 °C while the room temperature was 25 °C. A time step of 0.4 s was selected between consecutive temperature recordings and the total experimental process lasted 1200 s, composed of heating (field on) and cooling (field off) parts. A fiber-optic thermometer system was used to record the temperature of the samples with an accuracy of ±0.1 °C. All the hyperthermia measurements were performed under similar conditions, i.e., the sample holder (glassy vial) and its volume (1 mL), its position within the magnetic field, MH measurement time (1200 s including 600 s of sample heating and 600 s of cooling), and at the same alternating magnetic field (AMF) frequency and amplitude.2.6 Characterization techniques
The primary particle size and morphology were determined by conventional transmission electron microscopy (TEM) images obtained with a JEOL JEM 1010 microscope operating at an acceleration voltage of 100 kV. For TEM observations, we used suspensions of nanoparticles deposited onto carbon-coated copper grids. The elemental composition of primary MNPs was estimated via ICP-AES analysis (iCAP 6300, Thermo Scientific). The hydrodynamic size and surface charge of the composites were determined by dynamic light scattering (DLS) and zeta potential measurements, carried out at 25 °C, utilizing a Nano ZS Malvern apparatus. The elemental composition of samples was tested using scanning electron microscopy (SEM, JEOL 840A), where energy dispersive X-ray spectrometry (EDS) spectra were obtained. Thermogravimetric analysis (TGA) was carried out from room temperature to 900 °C at a heating rate of 10 °C min−1 under an N2 atmosphere on a SETARAM SetSys-1200 instrument. Fourier transform infrared spectroscopy (400–4000 cm−1) was performed on a Nicolet FT-IR 6700 spectrometer, (Thermo Electron, Waltham, MA, USA), with pellet samples prepared using KBr. UV-Visible measurements were performed on a spectrophotometer (2001 Hitachi, Kagoshima, Japan). The emission spectra were measured on a Horiba fluorescence spectrometer equipped with a powder sample holder. The light source was a 450 W xenon arc lamp (220–1000 nm) and the detector was a red-sensitive Hamamatsu R928 photomultiplier tube. Magnetic measurements on the samples in powdered form were performed with a vibrating sample magnetometer (Oxford Instruments 1.2 H/CF/HT VSM). The maximum-applied field was equal to 1 T with a field rate of 0.5 T min−1.3. Results and discussion
3.1 Design and formation of composites
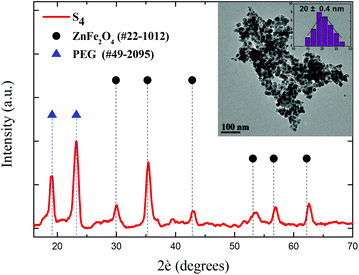
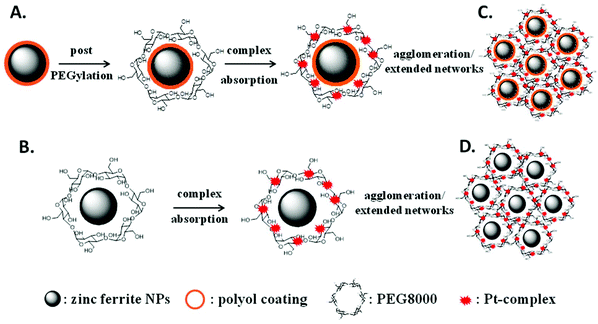
Based on our previous results,39 primary doped zinc ferrites ZnxFe3−xO4 (0.3 ≤ x ≤ 0.5) MNPs were isolated using a microwave-assisted polyol process in the presence of 1,2-propylene glycol (PG), triethylene glycol (TrEG) and tetraethylene glycol (TEG). Each polyol resulted in a different Zn2+ doping level according to its reductive ability and further ensured the dispersion of MNPs in water. Fundamentally, the reducing ability of polyols depends on their molecular weight; as the molecular weight of polyol decreases, b.p. decreases, and the reducing ability is increased.46 The composition of three synthesized ZnxFe3−xO4 MNPs was estimated by ICP-AES as Zn0.6Fe2.4O4, Zn0.45Fe2.55O4, and Zn0.3Fe2.7O4 for TrEG, PG, and TEG, respectively. The average nanoparticle sizes (dTEM) were found 14, 11 and 9 nm for the samples: S1-Zn0.45Fe2.55O4@PG, S2-Zn0.6Fe2.4O4@TrEG and S3-Zn0.3Fe2.7O4@TEG, respectively (Fig. S1†).39 The relatively small size variations are attributed to the different molecular weight of polyol that was used at each synthetic protocol. Another sample (S4) of zinc ferrite MNPs was solvothermally prepared in the presence of PEG solely performing a triple role: solvent, reducing agent and coating. Fig. 1 shows the XRD pattern and the TEM image of S4-Zn0.53Fe2.47O4@PEG with an average size (dTEM) 20 nm, while further physicochemical properties are given in ESI (ESI, Fig. S1†).Post-PEGylation has been attempted for S1–S3, where PEG was self-assembled on particles’ surface after synthesis, while in situ PEGylation, where PEG was attached on the surface during synthesis, was utilized for sample (S4). After PEGylation, all samples (S1–4) were able to function as absorbents for the platinum complex. The poor solubility of the complex in water was the driving force that facilitated its incorporation into the polymer's hydrophobic chains. Immobilization of the prepared complex on the PEGylated MNPs resulted in the formation of the desired nanocomposites named for clarity as Sb@Pt, (b = 1, 2, 3, 4). The process for the synthesis of novel hybrid magneto-fluorescent agents is presented in Scheme 1A and B, respectively.
3.2 Characterization of composites
The successful incorporation of the complex into PEG chains was evidenced from EDS, FT-IR, UV-Vis and fluorescence spectroscopy measurements. Compositional analysis of the composites was estimated using energy-dispersive X-ray (EDS) spectroscopy. Besides the detection of zinc and iron, peaks of platinum substantiated the presence of the complex. Furthermore, the relative atomic abundance (%) obtained from the spectra were S1 (1.07%), S2 (1.74%), S3 (0.80%) and S4 (3.75%) (ESI, Fig. S2†). The differential Pt content is attributed to the variation in PEG content as indicated by DLS measurements, given in the context below.FT-IR spectra of the composites are presented in Fig. 2, where several bands are identified belonging to both Pt-complex and organic coating as well as to ferrite MNPs. The high-frequency bands located in 3082 and 3054 cm−1 regions are assigned to symmetrical (νs) and asymmetrical (νas) stretching vibrations of CH3 and CH2 of PEG. Characteristic peaks of the phenyl ring, such as the out-plane bending vibration of the C–H bond, have been shifted slightly, appearing at 712 cm−1 in the composites and 717 cm−1 in the complex.47 The peak at 570 cm−1 corresponds to the motion of oxygen with respect to cations in Td and Oh sites of the spinel structure, demonstrating the existence of MNPs in the composites.48 Fig. 5S† presents the thermogravimetric analysis (TGA) of the hybrid nanocomposites. The presence of a double layer is common for all samples. The first step at about 420 °C is attributed to the initial polyol coating, while the second one at about 730 °C stems from PEG polymer. The cumulative contents were found to be 58, 44, 39 and 66 w/w%, for S1@Pt to S4@Pt, respectively.
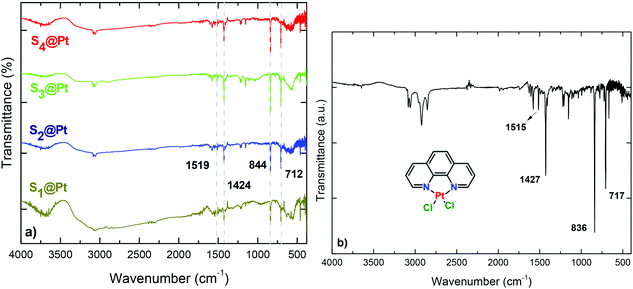 | ||
| Fig. 2 FT-IR spectra of (a) hybrid magneto-fluorescent composites in comparison with the (b) synthesized platinum complex, [Pt(phen)Cl2]. | ||
Dynamic light scattering (DLS) of aqueous dispersions of four composites was carried out to investigate their hydrodynamic diameter and ζ-potential (Fig. S3†) The diameters of the samples prepared by the post-PEGylation route (S1–3@Pt) was found to be similar, ranging from 349 to 404 nm, while for the in situ PEGylated sample (S4@Pt) the size was greater (620 nm). Owning to the electrical neutrality of PEG, the zeta potential of the samples was quite negligible. However, particles retained their aqueous dispersion ability, thanks to the steric stabilization stemming from polymer chains. As such, and as expected, PEGylation led to an increase in size and concomitantly to a reduction in the magnitude of surface charge. Moreover, the presence of PEG between Pt complexes and zinc ferrite MNPs makes the whole conjugate stable in biological solutions without serious toxic effects.49 The increased hydrodynamic sizes in comparison with sizes from TEM can be considered as a result of the large organic content and swelling of PEG in the water, while agglomeration/extended network formation cannot be excluded, as shown in Scheme 1C and D.50
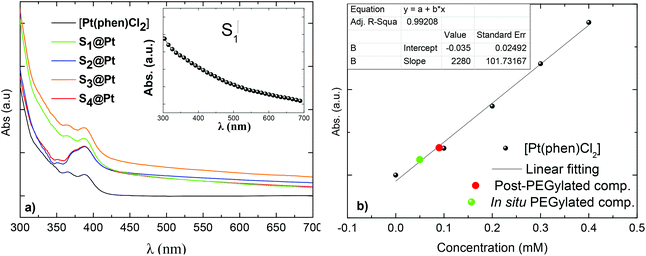
The electronic absorption spectra of magneto-fluorescent composites together with the pure Pt-complex in DMSO are shown in Fig. 3a. The Pt-complex exhibits the characteristic intraligand π–π* transition of phenanthroline at 365 nm and an extra shoulder at 388 nm, that are assigned to d(Pt)–π*(phenanthroline) charge transfer.35 On the other hand, PEGylated MNPs in the same concentration show no typical absorption in the spectrum range studied (inset of Fig. 3a). Only an exponential decay is observed originating from the Rayleigh scattering of the electromagnetic spectrum.51 In contrast, hybrid composites, owning to the absorbed Pt-complex, displayed weak shoulders which disturbed their exponential decay, and confirm the successful attachment of [Pt(phen)Cl2] to PEGylated MNPs.
As the absorbance of the composites is derived solely from the presence of the complex, its concentration in each sample can be calculated from their absorbance at 388 nm. Firstly, a calibration curve was obtained from the plot of the complex concentration versus the ratio of the integrated intensities of the absorption band (Fig. 3b). After that, the absorption of the composites was recorded and the amount of the complex was obtained from the experimental curve. No significant differences were detected in the concentration of the complex in post-PEGylated samples (0.09 mM) and that is the reason why all values are represented in the same red dot. For the in situ PEGylated composite, the amount was higher (green dot: 0.16 mM), in accordance with the EDS analysis.
The stability of composites before and after each hyperthermia measurement was further evaluated by UV-Vis studies in order to assess the possible leaching of the complex from PEGylated MNPs. Thus, after each hyperthermia measurement, hybrid composites were magnetically isolated by a permanent magnet (Nd2Fe14B) and the absorption of the supernatant was monitored (ESI, Fig. 4S†). Results disclosed that there was no conspicuous emission remaining in solutions, and as such, there was no loss of the complex during hyperthermia measurements. The above experimental observations provided through evidence for the compact nature of the hybrid magneto-fluorescent composites.
3.3 Fluorescence properties of composites
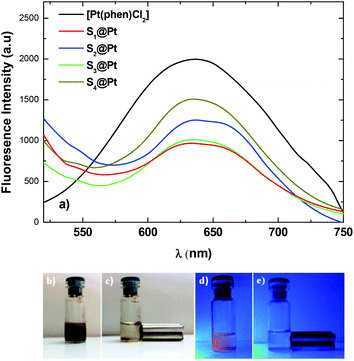
Emission spectra of [Pt(phen)Cl2] and nano-molecular composites were recorded under an excitation λexc = 400 nm at room temperature in the wavelength range of 450–750 nm (Fig. 4a). A strong emission in the visible spectral regime from the platinum complex is observed at 637 nm due to an efficient energy transfer from phenanthroline to platinum(II) ions.52 Upon absorption of the complex onto the surface of MNPs, the luminescence intensity of the composites was decreased compared to that of the pure complex due to the visible absorption of the magnetic nanoparticles. However, the interlayer of PEG/polymer effectively reduces the total fluorescence-quenching of the complex and fluorescence remains at acceptable levels.53Indicative digital photos of the composite S3@Pt were taken first under daylight and then under ultraviolet with the excitation wavelength of 365 nm (Fig. 4b–e). Under daylight, the aqueous dispersion showed a brown color (Fig. 4b), while under UV excitation an orange color was indicated (Fig. 4d), which is in good agreement with the fluorescent properties of the system. Also, the magneto-fluorescent composite completely separated to the side of the vial with a magnet in 5 min and the solution became completely clear (Fig. 4e). The rapid magnetic separation is attributed to the cooperative magnetophoresis effect of the applied external magnetic field induced agglomeration among MNPs.54
3.4 Magnetic properties of composites
Magnetic measurement data on the samples S1@Pt, S2@Pt, S3@Pt, and S4@Pt are shown in Fig. 5, where the values of saturation magnetization Ms were found equal to 53 (100), 52 (96), 66 (114) and 77 (126) emu g−1, respectively. The corresponding net magnetization values, per gram of magnetic core, at the maximum field applied (1 T) are also reported in brackets. Despite the addition of the Pt-complex, Ms values are still among the highest values reported for functionalized Zn ferrite MNPs by using polyols as surfactants.55–59 The central part of magnetization versus field cycles is presented in ESI in Fig. S7† together with a table (Table S1†) where the values of a coercive field are reported for all samples.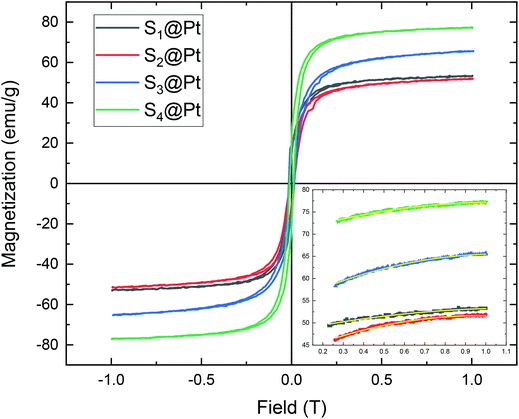 | ||
| Fig. 5 The magnetization versus the magnetic field, M(H), dependence for the MNP samples after different degrees of polyol functionalization. The magnetization curves were obtained at 300 K. The inset is the fitted magnetization-field data with the law of approach described by eqn (1). The symbols, following the same color indexing to the entire M(H) curves, are the experimental data and the yellow lines are the fittings. | ||
Magnetic anisotropy is an intrinsic property that affects drastically MNPs magnetic and heating properties. In order to estimate the effective anisotropy constant K of the samples, the magnetization curves using the law of approach to saturation60 were fitted as:
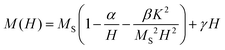 | (1) |
3.5 Evaluation of magnetic hyperthermia properties
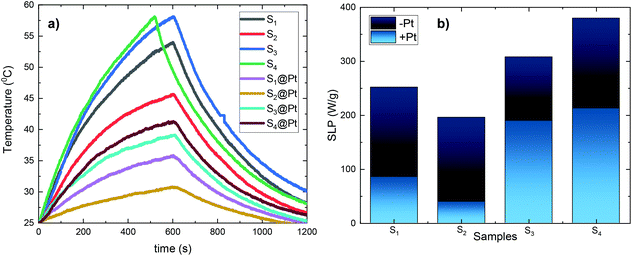
For magnetic hyperthermia experiments and calorimetric measurements of SLP, aqueous dispersions of all samples with a frequently used concentration67–69 of 2 mg mL−1 were initially prepared. All the hyperthermia measurements were performed under similar conditions, i.e., the sample holder (glassy vial) and its volume (1 mL), its position within the magnetic field, and MH measurement time (1200 s including 600 s of sample heating and 600 s of cooling), the same AMF frequency and amplitude. Magnetic hyperthermia curves for all samples, with and without the addition of the Pt-complex, are presented in Fig. 6a. Note that the optical fiber endures up to 90 °C, and thus, for safety reasons, the MH device was turned off when the temperature was approaching 60 °C. This is the case for sample S4, where due to its high heating rate, the AMF exposure time was shorter than 600 s. It is obvious that after the addition of Pt-complex a decrease of the heating efficiency in all samples was triggered, while none of the magneto-fluorescent composites entered the magnetic hyperthermia therapeutic window of 41–45 °C.In order to quantify the heating diminution, the resulting SLP values were estimated from eqn (2):
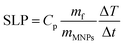 | (2) |
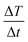 the initial (calculated in the first 100 s) slope of temperature increase curves. For reasons for comparison, in addition to SLP, the intrinsic loss power (ILP) is also reported taking into account the frequency f and amplitude H0 of the excitation field. ILP is given as ILP = SLP/(H20·f). According to the results shown in Fig. 6b, the reduction of SLP values is evidenced for all samples. It is worth mentioning that the superior magnetic performance of samples S4 and S4@Pt is also reflected through their heating performance resulting in higher heating rates than that for all the other samples. More specifically, for sample S1, it is decreased from 252 W g−1 (ILP = 0.57 nHm2 kg−1) to 86 W g−1 (ILP = 0.19 nHm2 kg−1), for sample S2 from 196 W g−1 (ILP = 0.44 nHm2 kg−1) to 40 W g−1 (ILP = 0.10 nHm2 kg−1), for sample S3 from 308 W g−1 (ILP = 0.70 nHm2 kg−1) to 190 W g−1 (ILP = 0.43 nHm2 kg−1) and for sample S4 from 380 W g−1 (ILP = 0.86 nHm2 kg−1) to 213 W g−1 (ILP = 0.48 nHm2 kg−1). This initial evaluation motivated us to develop a theoretical approach to simultaneously optimize SLP and accurately interpret the experimental results. Thus, the efficiency of the samples was further investigated under a theoretical prism.
the initial (calculated in the first 100 s) slope of temperature increase curves. For reasons for comparison, in addition to SLP, the intrinsic loss power (ILP) is also reported taking into account the frequency f and amplitude H0 of the excitation field. ILP is given as ILP = SLP/(H20·f). According to the results shown in Fig. 6b, the reduction of SLP values is evidenced for all samples. It is worth mentioning that the superior magnetic performance of samples S4 and S4@Pt is also reflected through their heating performance resulting in higher heating rates than that for all the other samples. More specifically, for sample S1, it is decreased from 252 W g−1 (ILP = 0.57 nHm2 kg−1) to 86 W g−1 (ILP = 0.19 nHm2 kg−1), for sample S2 from 196 W g−1 (ILP = 0.44 nHm2 kg−1) to 40 W g−1 (ILP = 0.10 nHm2 kg−1), for sample S3 from 308 W g−1 (ILP = 0.70 nHm2 kg−1) to 190 W g−1 (ILP = 0.43 nHm2 kg−1) and for sample S4 from 380 W g−1 (ILP = 0.86 nHm2 kg−1) to 213 W g−1 (ILP = 0.48 nHm2 kg−1). This initial evaluation motivated us to develop a theoretical approach to simultaneously optimize SLP and accurately interpret the experimental results. Thus, the efficiency of the samples was further investigated under a theoretical prism.
3.6 Coupled theoretical and experimental investigation
When superparamagnetic MNPs of volume V are exposed to low AMFs of frequency f and amplitude H0 their volumetric power dissipation P is given by the linear response theory (LRT):72
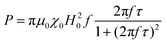 | (3) |
| τN ≈ exp(σ + γσ2) | (4) |
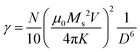 | (5) |
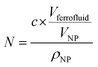
In eqn (4), N is the total number of MNPs and D the mean distance between MNPs. The MNPs number is given by:
 | (6) |
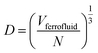 | (7) |
Finally, the Brownian relaxation time τB reads:
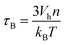 | (8) |
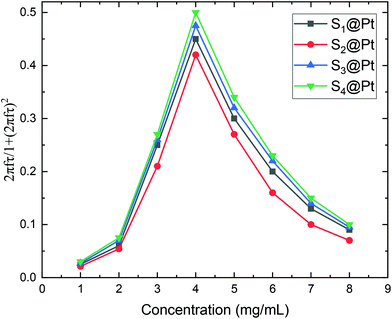
After all, and based on eqn (3), three cases can be distinguished regarding the role of dipolar interactions in the frequency factor of the susceptibility dissipative component 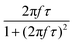 of MNPs energy losses: (a) when 2πfτ < 1 dipolar interactions increase P, (b) when 2πfτ = 1 P is maximum and (c) when 2πfτ > 1 dipolar interactions decrease P.
of MNPs energy losses: (a) when 2πfτ < 1 dipolar interactions increase P, (b) when 2πfτ = 1 P is maximum and (c) when 2πfτ > 1 dipolar interactions decrease P.
The applicability of LRT is also revealed by the ratio between the applied magnetic field amplitude and the anisotropy field (HK = 2K/μ0Ms) of samples. For values H0/HK ≪ 1, the linear response theory can quantify74 the experimental results. In the present study, for all samples, this ratio was in the order of 10−2.
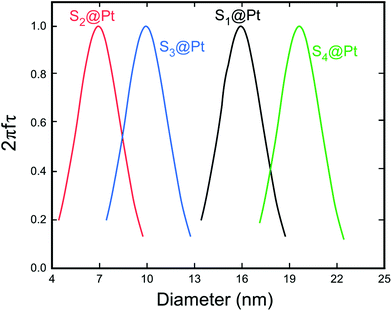 | ||
| Fig. 7 Dependence of the factor 2πfτ on the MNP diameter for the whole set of samples. This maximum corresponds to the resonant size of our MNPs for the working frequency of 765 kHz. The relaxation time τ was calculated by taking into account the Néel and Brown moment relaxation mechanisms that were obtained from eqn (3) and (7), respectively. | ||
Moreover, Fig. 8 elucidates the SLP attenuation portrayed in Fig. 6b. The addition of PEG and Pt-complex increases the spacing between the nanoparticles and thus decreases the strength of dipolar interactions between them. At low concentrations, like the one used here (2 mg mL−1), this decrease results in the reduction of power dissipation of MNPs as analyzed above and shown in Fig. 6b. When comparing the SLP values among the samples of each concentration, we found that the sample which had the highest saturation magnetization, the largest size, closer to the optimum one, and the lowest effective anisotropy constant value, showed the highest SLP values.
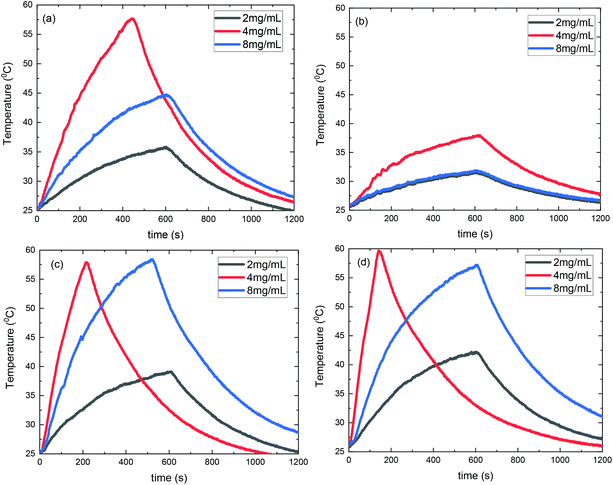
Consequently, SLP values calculated from eqn (2) are presented in Fig. 10. A good agreement with the theory arises from the fact that SLP behavior is consistent with the frequency factor dependence on the concentration shown in Fig. 8. A deviation from theory is observed in Fig. 10 for samples S3@Pt and S4@Pt at a concentration of 8 mg mL−1, where the SLP of the former is slightly higher than the SLP of the latter. This result is attributed to better dispersion of sample S3@Pt in the high concentration aqueous solution. A higher dispersion would decrease dipolar interactions between MNPs by increasing inter-particle distance. This tendency is beneficial for the heating efficiency of MNPs at high concentrations, higher than 4 mg mL−1, where decreasing dipolar interactions increase SLP as expected by theory and shown in Fig. 8.
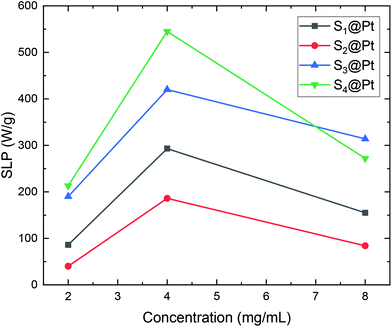 | ||
| Fig. 10 SLP values of samples S1@Pt, S2@Pt, S3@Pt and S4@Pt for the three different concentrations (2, 4 and 8 mg mL−1) used in magnetic hyperthermia experiments. | ||
From our results, it is clear that S4@Pt and S3@Pt MNPs presented higher SLP values, 545 W g−1 (ILP = 1.25 nHm2 kg−1) and 420 W g−1 (ILP = 0.96 nHm2 kg−1), respectively, at the optimum concentration compared to the other samples. In any case, all SLP values are considered to be quite adequate, if we also take into account the inevitable reduction due to the addition of Pt-complex, when compared to results attained in the literature on zinc ferrite MNPs.79,80 Moreover, with the exception of S2@Pt, all the other samples appeared to be suitable candidates for MH since they surpassed the MH temperature threshold of 41 °C. As indicated by theory, the concentration of 4 mg mL−1 generated the highest SLP value compared to 2 and 8 mg mL−1, for all the samples examined, since the quantity 2πfτ for those two values deviated significantly from the unit as derived from our calculations. At low concentrations and when σ is low enough, 2πfτ < 1, the low-barrier regime occurs, where MNPs magnetic moment rotation is frequent, but the released energy in each rotation is small. By raising the concentration, and so the dipolar interactions, the anisotropy barrier increases and thus takes the system closer to the optimum condition 2πfτ = 1. Conversely, when σ is larger, 2πfτ > 1, the high-barrier regime appears, where external AMF already has substantial difficulty in promoting the rotations. Thus, the amplification of dipolar interactions through MNPs’ concentration, the anisotropy barrier merely increases, even more, hampering further the efficacy of the heating process. This also shows the importance of choosing the appropriate frequency to increase the heating efficiency of high interacting MNPs systems. AMF amplitude of 24 kA m−1 used in MH experiments is appropriate for the validity of LRT approximation28,76 which is extended by using a mean-field model in order to analyze the role of dipolar interactions through the evaluation of MNPs concentration in SLP in the context of MH.
4. Conclusions
Zinc ferrites MNPs (ZnxFe3−xO4, x = 0.3, 0.4, 0.45, 0.53) with optimal magnetic characteristics for MH have been combined with a Pt-complex as an OFI probe through the post and in situ PEGylation to form stable hybrid magneto-fluorescent nanocomposites. PEGylation effectively hindered the quenching of emission light and preserved magnetization at high levels. The results of the initial MH measurements showed a sample-oriented-dependent behavior vis-à-vis SLP and prompted the application of a theoretical model in order to interpret and optimize them. Thus, the optimum size and concentration that maximize MNP power losses are estimated by theoretical calculations, where the contribution from inter-particle interactions has been considered by inserting a mean dipolar energy term in the estimation of Néel relaxation time. Next, our theoretical approach is validated by further MH outcomes regarding the dependence of time-temperature curves and SLP values on MNPs concentration. In this way, the experimental results are decoded by theory and vice versa. Additionally, considering that the primary MNPs presented high relaxivity values r2,39 we expect that the current magneto-fluorescent nanocomposites would also be able to perform as a sensitive probe for MRI applications.Author contributions
Conceptualization, K.V., N.M. and C.D.S.; methodology, K.V. and N.M.; formal analysis, K.V. and N.M.; investigation, K.V. and N.M.; resources, K.V. and N.M.; data curation, K.V. and N.M.; writing-original draft preparation, K.V. and N.M.; writing-review & editing, K.V., N.M. and C.D.S.; supervision, C.D.S. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This research is co-financed by Greece and the European Union (European Social Fund-ESF) through the Operational Programme (Human Resources Development, Education and Lifelong Learning 2014–2020) in the context of the project “Nanostructured agents of dual imaging capability with simultaneously therapeutic action for neoplastic cells” (MIS 5047857).References
- N. Knežević, I. Gadjanski and J. O. Durand, J. Mater. Chem. B, 2019, 7, 9–23 RSC.
- G. Chen, I. Roy, C. Yang and P. N. Prasad, Chem. Rev., 2016, 116, 2826–2885 CrossRef CAS PubMed.
- J. Zhao, J. Chen, S. Ma, Q. Liu, L. Huang, X. Chen, K. Lou and W. Wang, Acta Pharm. Sin. B, 2018, 8, 320–338 CrossRef PubMed.
- E. K. Lim, T. Kim, S. Paik, S. Haam, Y. M. Huh and K. Lee, Chem. Rev., 2015, 115, 327–394 CrossRef CAS PubMed.
- Z. Liu, X. Zhan, M. Yang, Q. Yang, X. Xu, F. Lan, Y. Wu and Z. Gu, Nanoscale, 2016, 8, 7544–7555 RSC.
- L. Lartigue, C. Innocenti, T. Kalaivani, A. Awwad, M. D. M. Sanchez Duque, Y. Guari, J. Larionova, C. Gueírin, J. L. G. Montero, V. Barragan-Montero, P. Arosio, A. Lascialfari, D. Gatteschi and C. Sangregorio, J. Am. Chem. Soc., 2011, 133, 10459–10472 CrossRef CAS PubMed.
- C. G. Hadjipanayis, M. J. Bonder, S. Balakrishnan, X. Wang, H. Mao and G. C. Hadjipanayis, Small, 2008, 4, 1925–1929 CrossRef CAS PubMed.
- F. Stuker, J. Ripoll and M. Rudin, Pharmaceutics, 2011, 3.2, 229–274 CrossRef PubMed.
- E. J. Sutton, T. D. Henning, S. Boddington, S. Demos, C. Krug, R. Meier, J. Kornak, S. Zhao, R. Baehner, S. Sharifi and H. Daldrup-Link, Mol. Imaging, 2010, 9, 278–290 CrossRef PubMed.
- W. Stummer, U. Pichlmeier, T. Meinel, O. D. Wiestler, F. Zanella and H. J. Reulen, Lancet Oncol., 2006, 7, 392–401 CrossRef CAS PubMed.
- L. Bu, B. Shen and Z. Cheng, Adv. Drug Delivery Rev., 2014, 76, 21–38 CrossRef CAS PubMed.
- G. M. Van Dam, G. Themelis, L. M. A. Crane, N. J. Harlaar, R. G. Pleijhuis, W. Kelder, A. Sarantopoulos, J. S. De Jong, H. J. G. Arts, A. G. J. Van Der Zee, J. Bart, P. S. Low and V. Ntziachristos, Nat. Med., 2011, 17, 1315–1319, DOI:10.1038/nm.2472.
- W. J. M. Mulder, G. J. Strijkers, G. A. F. Van Tilborg, D. P. Cormode, Z. A. Fayad and K. Nicolay, Acc. Chem. Res., 2009, 42, 904–914 CrossRef CAS PubMed.
- N. Li, H. Li, D. Chen, H. Liu, F. Tang, Y. Zhang, J. Ren and Y. Li, J. Nanosci. Nanotechnol., 2009, 9, 2540–2545 CrossRef PubMed.
- S. A. Corr, Y. P. Rakovich and Y. K. Gun'Ko, Nanoscale Res. Lett., 2008, 3, 87–104, DOI:10.1007/s11671-008-9122-8.
- T. T. Jiang, N. Q. Yin, L. Liu, J. M. Lei, L. X. Zhu and X. L. Xu, Chin. Phys. B, 2013, 22, 126102–126102 CrossRef.
- N. Chekina, D. Horák, P. Jendelová, M. Trchová, M. J. Bene, M. Hrubý, V. Herynek, K. Turnovcová and E. Syková, J. Mater. Chem., 2011, 21.21, 7630–7639, 10.1039/c1jm10621j.
- A. Louie, Chem. Rev., 2010, 110.5, 3146–3195, DOI:10.1021/cr9003538.
- M. K. Yoo, I. K. Park, H. T. Lim, S. J. Lee, H. L. Jiang, Y. K. Kim, Y. J. Choi, M. H. Cho and C. S. Cho, Acta Biomater., 2012, 8.8, 3005–3013, DOI:10.1016/j.actbio.2012.04.029.
- G. Wang and X. Su, Analyst, 2011, 136.9, 1783–1798 RSC.
- A. Quarta, R. Di Corato, L. Manna, A. Ragusa and T. Pellegrino, IEEE Trans. Nanobioscience, 2007, 6.4, 298–308 Search PubMed.
- C. Kaewsaneha, P. Tangboriboonrat, D. Polpanich and A. Elaissari, ACS Appl. Mater. Interfaces, 2015, 7.42, 23373–23386 CrossRef PubMed.
- D. Vollath, Adv. Mater., 2010, 22.39, 4410–4415, DOI:10.1002/adma.201001743.
- C. F. Markwalter, A. G. Kantor, C. P. Moore, K. A. Richardson and D. W. Wright, Chem. Rev., 2019, 119.2, 1456–1518 CrossRef PubMed.
- K. Cheng, S. Peng, C. Xu and S. Sun, J. Am. Chem. Soc., 2009, 131.30, 10637–10644, DOI:10.1021/ja903300f.
- J. Hernández-Gil, M. Cobaleda-Siles, A. Zabaleta, L. Salassa, J. Calvo and J. C. Mareque-Rivas, Adv. Healthcare Mater., 2015, 4.7, 1034–1042, DOI:10.1002/adhm.201500080.
- E. Voulgari, A. Bakandritsos, S. Galtsidis, V. Zoumpourlis, B. P. Burke, G. S. Clemente, C. Cawthorne, S. J. Archibald, J. Tuček, R. Zbořil, V. Kantarelou, A. G. Karydas and K. Avgoustakis, J. Controlled Release, 2016, 243, 342–356, DOI:10.1016/j.jconrel.2016.10.021.
- C. Iacovita, G. F. Stiufiuc, R. Dudric, N. Vedeanu, R. Tetean, R. I. Stiufiuc and C. M. Lucaciu, Magnetochemistry, 2020, 6, 23 CrossRef CAS.
- A. Das, S. Mohanty, R. Kumar and B. K. Kuanr, ACS Appl. Mater. Interfaces, 2020, 12, 42016–42029 CrossRef CAS PubMed.
- Y. Xu, A. Karmakar, D. Wang, M. W. Mahmood, F. Watanabe, Y. Zhang, A. Fejleh, P. Fejleh, Z. Li, G. Kannarpady, S. Ali, A. R. Biris and A. S. Biris, J. Phys. Chem. C, 2010, 114.11, 5020–5026, DOI:10.1021/jp9103036.
- E. K. Lim, J. Yang, C. P. N. Dinney, J. S. Suh, Y. M. Huh and S. Haam, Biomaterials, 2010, 31.35, 9310–9319, DOI:10.1016/j.biomaterials.
- C. W. Lai, Y. H. Wang, C. H. Lai, M. J. Yang, C. Y. Chen, P. T. Chou, C. S. Chan, Y. Chi, Y. C. Chen and J. K. Hsiao, Small, 2008, 4.2, 218–224, DOI:10.1002/smll.200700283.
- B. Xia, J. Li, J. Shi, Y. Zhang, Q. Zhang, Z. Chen and B. Wang, ACS Biomater. Sci. Eng., 2017, 3, 2579–2587 CrossRef CAS PubMed.
- A. Z. M. Badruddoza, M. T. Rahman, S. Ghosh, M. Z. Hossain, J. Shi, K. Hidajat and M. S. Uddin, Carbohydr. Polym., 2013, 95.1, 449–457, DOI:10.1016/j.carbpol.2013.02.046.
- M. J. Sailor and E. J. Lee, Adv. Mater., 1997, 9.10, 783–793, DOI:10.1002/adma.19970091004.
- J. M. Buriak, Chem. Rev., 2002, 102, 1271–1308 CrossRef CAS PubMed.
- S. Ciampi, J. B. Harper and J. J. Gooding, Chem. Soc. Rev., 2010, 39, 2158–2183 RSC.
- L. Li, C. Liu, L. Zhang, T. Wang, H. Yu, C. Wang and Z. Su, Nanoscale, 2013, 5, 2249–2253 RSC.
- P. Sun, H. Zhang, C. Liu, J. Fang, M. Wang, J. Chen, J. Zhang, C. Mao and S. Xu, Langmuir, 2010, 26.2, 1278–1284, DOI:10.1021/la9024553.
- K. Giannousi, O. Antonoglou and C. Dendrinou-Samara, ACS Chem. Neurosci., 2019, 10, 3796–3804 CrossRef CAS PubMed.
- Y. herng Chen, J. W. Merkert, Z. Murtaza, C. Woods and D. P. Rillema, Inorg. Chim. Acta, 1995, 240, 41–47 CrossRef.
- R. B. Bostancıoğlu, K. Işık, H. Genç, K. Benkli and A. T. Koparal, J. Enzyme Inhib. Med. Chem., 2012, 27, 458–466 CrossRef PubMed.
- K. Vamvakidis, M. Katsikini, G. Vourlias, M. Angelakeris, E. C. Paloura and C. Dendrinou-Samara, Dalton Trans., 2015, 44, 5396–5406 RSC.
- F. A. Palocsay and J. V. Rund, Inorg. Chem., 1969, 8.3, 524–528, DOI:10.1021/ic50073a022.
- M. Angelakeris, Biochim. Biophys. Acta, Gen. Subj., 2017, 1861.6, 1642–1651 CrossRef PubMed.
- A. J. Biacchi and R. E. Schaak, The Solvent Matters: Kinetic versus Thermodynamic Shape Control in the Polyol Synthesis of Rhodium Nanoparticles, ACS Nano, 2011, 10, 8089–8099 CrossRef PubMed.
- X. Wang, G. Jia, Y. Yu, Y. Gao, W. Zhang, H. Wang, Z. Cao and J. Liu, Quim. Nova, 2015, 38, 298–302 CAS.
- X. Wang, G. Jia, Y. Yu, Y. Gao, W. Zhang, H. Wang, Z. Cao and J. Liu, Quim. Nova, 2015, 38, 298–302 CAS.
- V. Wagner, A. Dullaart, A. K. Bock and A. Zweck, Nat. Biotechnol., 2006, 24, 1211–1217 CrossRef CAS PubMed.
- J. S. Suka, Q. Xua, N. Kima, J. Hanesa and L. M. Ensigna, PEGylation as a strategy for improving nanoparticle-based drug and gene delivery, Adv. Drug Delivery Rev., 2016, 99, 28–51 CrossRef PubMed.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley, 1998 Search PubMed.
- F. P. Dwyer and E. C. Gyarfas, Chelate complexes of 1,10-phenanthroline and related compounds, Chem. Rev., 1954, 54, 959–1017 CrossRef.
- P. Xi, K. Cheng, X. Sun, Z. Zeng and S. Sun, Fluorescent magnetic nanoparticles based on a ruthenium complex and Fe3O4, J. Mater. Chem., 2011, 21, 11464–11467 RSC.
- S. P. Yeap, J. Lim and B. S. Ooi, et al., Agglomeration, colloidal stability, and magnetic separation of magnetic nanoparticles: collective influences on environmental engineering applications, J. Nanopart. Res., 2017, 19, 368 CrossRef.
- P. M. Zélis, G. A. Pasquevich, S. J. Stewart, M. B. F. Van Raap, J. Aphesteguy, I. J. Bruvera, C. Laborde, B. Pianciola, S. Jacobo and F. H. Sánchez, J. Phys. D: Appl. Phys., 2013, 46, 125006 CrossRef.
- X. Liu, J. Liu, S. Zhang, Z. Nan and Q. Shi, J. Phys. Chem. C, 2016, 120, 1328–1341 CrossRef CAS.
- Y. Hadadian, A. P. Ramos and T. Z. Pavan, Sci. Rep., 2019, 9.1, 1–14, DOI:10.1038/s41598-019-54250-7.
- O. Yelenich, S. Solopan, T. Kolodiazhnyi, Y. Tykhonenko, A. Tovstolytkin and A. Belous, J. Chem., 2015, 532198, DOI:10.1155/2015/532198.
- S. K. Sharma, Complex magnetic nanostructures: Synthesis, assembly and applications, Springer International Publishing, 2017 Search PubMed.
- J. Herbst and F. Pinkerton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 10733–10739 CrossRef CAS.
- M. Thakur, K. De, S. Giri, S. Si, A. Kotal and K. Mandali, J. Phys.: Condens. Matter, 2008, 20, 149801 CrossRef.
- N. Modaresi, R. Afzalzadeh, B. Aslibeiki, P. Kameli, A. Ghotbi Varzaneh, I. Orue and V. A. Chernenko, J. Magn. Magn. Mater., 2019, 482, 206–218 CrossRef CAS.
- A. Goldman, Handbook of Modern Ferromagnetic Materials, Springer US, 1999 Search PubMed.
- F. Bødker, S. Mørup and S. Linderoth, Phys. Rev. Lett., 1994, 72, 282–285 CrossRef PubMed.
- F. Gazeau, J. C. Bacri, F. Gendron, R. Perzynski, Y. L. Raikher, V. I. Stepanov and E. Dubois, J. Magn. Magn. Mater., 1998, 186, 175–187 CrossRef CAS.
- A. A. McGhie, C. Marquina, K. O'Grady and G. Vallejo-Fernandez, J. Phys. D: Appl. Phys., 2017, 50, 455003 CrossRef.
- A. Das, S. Mohanty, R. Kumar and B. K. Kuanr, ACS Appl. Mater. Interfaces, 2020, 12, 42016–42029 CrossRef CAS PubMed.
- A. Rajan, M. Sharma and N. K. Sahu, Sci. Rep., 2020, 10, 15045, DOI:10.1038/s41598-020-71703-6.
- R. R. Shah, T. P. Davis, A. L. Glover, D. E. Nikles and C. S. Brazel, J. Magn. Magn. Mater., 2015, 387, 96–106 CrossRef CAS PubMed.
- R. P. Tan, J. Carrey and M. Respaud, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 214421 CrossRef.
- B. Mehdaoui, R. P. Tan, A. Meffre, J. Carrey, S. Lachaize, B. Chaudret and M. Respaud, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 174419 CrossRef.
- R. E. Rosensweig, J. Magn. Magn. Mater., 2002, 252, 370–374, DOI:10.1016/S0304-8853(02)00706-0.
- G. T. Landi, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 014403 CrossRef.
- S. Ruta, R. Chantrell and O. Hovorka, Sci. Rep., 2015, 5, 1–7 Search PubMed.
- I. Hilger, Int. J. Hyperthermia, 2013, 29.8, 828–834 CrossRef.
- X. L. Liu, H. M. Fan, J. B. Yi, Y. Yang, E. S. G. Choo, J. M. Xue, D. Di Fan and J. Ding, J. Mater. Chem., 2012, 22, 8235–8244 RSC.
- J. Carrey, B. Mehdaoui and M. Respaud, J. Appl. Phys., 2011, 109, 083921 CrossRef.
- A. LeBrun, R. Ma and L. Zhu, J. Therm. Biol., 2016, 62, 129–137 CrossRef PubMed.
- E. Myrovali, N. Maniotis, T. Samaras and M. Angelakeris, Nanoscale Adv., 2020, 2, 408–416 RSC.
- H. F. Rodrigues, G. Capistrano, F. M. Mello, N. Zufelato, E. Silveira-Lacerda and A. F. Bakuzis, Phys. Med. Biol., 2017, 62, 4062–4082 CrossRef CAS PubMed.
- A. Skumiel, K. Kaczmarek, D. Flak, M. Rajnak, I. Antal and H. Brząkała, J. Mol. Liq., 2020, 304, 112734 CrossRef CAS.
- P. Appa Rao, K. Srinivasa Rao, T. R. K. Pydi Raju, G. Kapusetti, M. Choppadandi, M. Chaitanya Varma and K. H. Rao, J. Alloys Compd., 2019, 794, 60–67 CrossRef CAS.
- M. S. A. Darwish, H. Kim, H. Lee, C. Ryu, J. Y. Lee and J. Yoon, Nanomaterials, 2019, 9, 1176 CrossRef CAS PubMed.
- C. Martinez-Boubeta, K. Simeonidis, D. Serantes, I. Conde-Leborán, I. Kazakis, G. Stefanou, L. Peña, R. Galceran, L. Balcells, C. Monty, D. Baldomir, M. Mitrakas and M. Angelakeris, Adv. Funct. Mater., 2012, 22, 3737–3744 CrossRef CAS.
- J. w. Kim, J. Wang, H. Kim and S. Bae, Concentration-dependent oscillation of specific loss power in magnetic nanofluid hyperthermia, Sci. Rep., 2021, 11, 733 CrossRef CAS PubMed.
- J. G. Ovejero, D. Cabrera, J. Carrey and T. Valdivielso, Effects of inter-and intra-aggregate magnetic dipolar interactions on the magnetic heating efficiency of iron oxide nanoparticles, Phys. Chem. Chem. Phys., 2016, 18, 10954–10963 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr00121c |
| This journal is © The Royal Society of Chemistry 2021 |