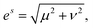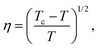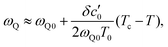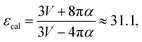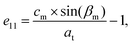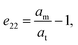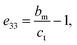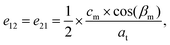DOI:
10.1039/D0QI00981D
(Research Article)
Inorg. Chem. Front., 2021,
8, 156-163
Anomalous dielectric behaviour during the monoclinic to tetragonal phase transition in La(Nb0.9V0.1)O4†
Received
13th August 2020
, Accepted 23rd October 2020
First published on 27th October 2020
Abstract
La(Nb0.9V0.1)O4 has been shown by in situ Raman spectroscopy and X-ray diffraction to undergo a ferroelastic phase transition from monoclinic fergusonite to tetragonal scheelite (TM–T) at 350 °C, accompanied by 3.55% spontaneous strain and an abrupt change in the thermal expansion coefficient (αL) from +15.5 ppm °C−1 to +11.4 ppm °C−1. Assuming a linear relationship between polarizability and temperature, an anomalous decrease in relative permittivity (εr) at TM–T is predicted from the Clausius–Mosotti relation and Shannon's additive rule. Such an anomalous decrease in εr in a phase transition has not previously been observed in ferroic and linear dielectrics and may aid in the design of novel microwave dielectric composites.
Introduction
Microwave (MW) dielectric ceramic materials are widely used as dielectric resonators, filters, antenna substrates, and capacitors for wireless and mobile communication, and radar and satellite positioning systems.1–4 The large εr (real part of permittivity) of MW dielectric ceramic materials helps in reducing the dimensions of MW devices and the low dielectric loss (high quality factor, Q) enhances the frequency selectivity.2–5 Furthermore, their temperature stability with respect to resonant frequency (TCF) ensures that related devices work from −45 to 85 °C. 5th generation wireless systems (5G) have gradually come on-line in recent years and offer ultra-wideband, ultra-high speed, and ultra-low latency.6–8 The frequency spectrum of 5G is generally divided into millimeter wave, mid-band and low-band. The millimeter wave (above 24 GHz) is yet to be exploited but materials with εr < 10 are likely to be utilised.7–10 Low-band refers to available frequency ranges at <1 GHz, whereas mid-band exploits the 2–6 GHz interval and is the most widely deployed. To attain the required data transmission rates, massive MIMO (multiple input and multiple output) and Multi-User MIMO (MU-MIMO) antennas are employed that are composed of large numbers of interconnected devices.11–15 Massive MIMO functions through mini base stations and exploits materials with εr = 20, such as MgTiO3–CaTiO3, (Ca1+xSm1−x)(Al1−xTix)O4, and Li2TiO3 due to their high Q and low TCF.7,16–19
Alongside the three materials mentioned above, fergusonite-structured LnNbO4 (Ln = La, Sm, Nd etc.) ceramics have attracted attention due to their high Q and εr ∼ 20.20–23 Kim et al. first reported the microwave dielectric properties of LaNbO4 ceramic sintered at 1250 °C with εr = 19.3, a high Qf (Q × resonant frequency, f) ∼ 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 GHz and TCF = +9 ppm °C−1.20 Substitutions of La or Nb by isovalent ions plus the use of sintering aid in further improving the microwave dielectric properties.21–23 In our previous work,21 we demonstrated that 10 mol% substitution of V5+ for Nb5+ increases the TCF from +9 ppm °C−1 to +110 ppm °C−1.
400 GHz and TCF = +9 ppm °C−1.20 Substitutions of La or Nb by isovalent ions plus the use of sintering aid in further improving the microwave dielectric properties.21–23 In our previous work,21 we demonstrated that 10 mol% substitution of V5+ for Nb5+ increases the TCF from +9 ppm °C−1 to +110 ppm °C−1.
TCF is approximately half the temperature coefficient εr (τε) according to:
| | 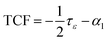 | (1) |
where
αl is the linear thermal expansion coefficient (below +15 ppm °C
−1 for ceramics). Hence, any abrupt change in TCF is normally attributed to a change in
τε usually caused by a structural phase transition. Phase transitions which show an increase in
εr are commonplace in ferroic materials as commonly observed for paraelectric to ferroelectric/antiferroelectric, ferroelectric to ferroelectric, octahedral tilt and paraelastic to ferroelastic transformations.
24–31
All the above phase transitions occur through classical softening of a transverse optical mode, consistent with the Lyddane–Sach–Teller relation.32 Since the maximum value of εr occurs at the phase transition temperature (PTT/TC), τε is largely positive below, but negative above the PTT, provided εr is not too high. This principle is the basis for the well-established relationship between the tolerance factor and τε described by Reaney et al.33 in which octahedral tilting induces an increase in εr at the PTT in Sr- and Ba-based complex perovskites. The TCF follows the inverse trend. Similarly BiVO4 undergoes a second-order ferroelastic phase transition from the monoclinic (I2/a) to tetragonal scheelite (I41/a) structure at 255 °C, at which temperature a maximum value of εr is observed.31,34–38 Furthermore in (Li0.5xBi1−0.5x)(MoxV1−x)O4 (0 ≤ x ≤ 0.25) ceramics, peaks in εr are observed at the PTT38,39 with the corresponding changes in TCF.
LaNbO4 also undergoes a ferroelastic phase transition from a monoclinic fergusonite to tetragonal scheelite structure at ∼480 °C.40–45 From previous studies,21,46 V5+ substitutes for Nb5+ on the B site and lowers the PTT to room temperature, where the tetragonal scheelite structure is stabilized for x = 0.225. However, in La(Nb,V)O4 solid solutions, the TCF decreases from a large positive (+100 ppm °C−1) to a large negative value (−40 ppm °C−1), the opposite trend to that which is typically observed at PTTs. This anomalous behaviour may be further elucidated by undertaking a detailed study of the crystal structure as a function of temperature. In the present work, therefore, we present in situ XRD and Raman data in combination with thermal expansion measurement which are interpreted through Landau theory, Shannon's additive rule, and the Clausius–Mosotti relation. Understanding this behavior might lead to design of temperature stable composite materials in the future.
Materials and methods
Material synthesis
Preparation of the La(Nb0.9V0.1)O4 ceramic was described in detail in our previous work.21
Material characterization
Room temperature XRD patterns were acquired using a Bruker D2 Phaser in the 2θ range of 10–70°, with a step size of 0.02. In situ XRD patterns were collected using a Siemens D5000 diffractometer from 30–500 °C using Pt foil as the holder for high temperature measurements. Results were analyzed by the Rietveld profile refinement method, using the FULLPROF program. In situ Raman spectra were obtained with a Renishaw Raman microscope (model InVia) using a 532 nm solid state (100 mW) laser and a Linkam stage (model THMS600). Dielectric properties measurements were performed on sintered ceramics, diameter ∼ 10 mm and thickness ∼ 1 mm, coated with gold using an LCR (Agilent E4980A) and homemade heating system from 25 to 680 °C at 10 kHz, 100 kHz, 250 kHz and 1 MHz with a heating rate of 1 °C min−1.
Results and discussion
In situ XRD patterns of the La(Nb0.9V0.1)O4 ceramic in the temperature range 30–500 °C and cell parameters as a function of temperature are shown in Fig. 1(a) and (b). At room temperature, La(Nb0.9V0.1)O4 crystallized with a monoclinic fergusonite structure (I2/c), with V5+ ions substituting for Nb5+. As the temperature increased, some characteristic peaks such as (121) and (130), (002) and (200) converged and merged into a single peak at ∼350 °C, indicating a continuous structural transition from a monoclinic fergusonite structure to a tetragonal scheelite structure (I41/a). The cell parameter a decreased with temperature while c increased and became equal to a at 350 °C, commensurate with a linear decrease in β from 93° to 90°, Fig. 1(b). All data are therefore consistent with the premise that ∼10 mol% V5+ substitutes for Nb5+, decreasing the distortion of the BO4 tetrahedra, and lowering the ferroelastic phase transition temperature from 480 °C to 350 °C for undoped LaNbO4 and La(Nb0.9V0.1)O4, respectively.
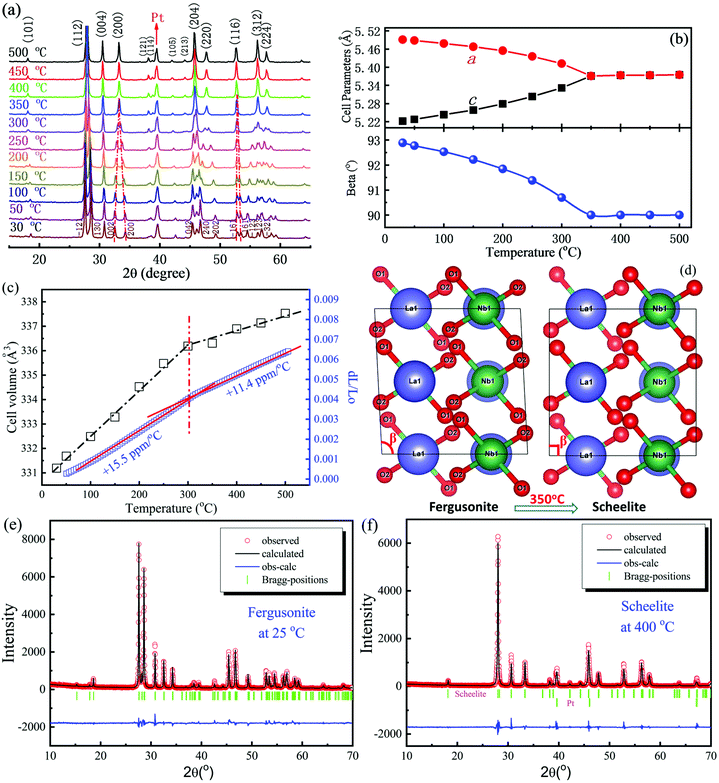 |
| | Fig. 1 (a) In situ XRD patterns of the La(Nb0.9V0.1)O4 ceramic from 30–500 °C. (b) Cell parameters as a function of temperature. (c) Cell volume and thermal expansion vs. temperature. (d) Schematic of the change in the crystal structure projected along the b axis. (e and f) Experimental (circles) and calculated (line) XRD profiles for La(Nb0.9V0.1)O4 at room temperature (Rp = 8.34%, Rwp = 11.5%, and Rexp = 6.52%) and 400 °C (Rp = 10.9%, Rwp = 14.9%, and Rexp = 9.84%). (The short vertical lines below the patterns mark Bragg reflections. The bottom continuous line is the difference between the observed and the calculated intensity.) | |
Fig. 1(c) shows the cell volume and thermal expansion data of La(Nb0.9V0.1)O4 as a function of temperature. As the temperature increased from 25 °C to 300 °C, the cell volume increased linearly from 331.19 Å3 to 336.19 Å3 corresponding to a gradient of +56 ppm °C−1. The cell volume further increased to 337.53 Å3 at 500 °C, but the gradient decreased to +20 ppm °C−1, suggesting a structural phase transition at ∼350 °C. Thermal expansion coefficients also followed the same trend (Fig. 1(c)), abruptly changing from +15.5 ppm °C−1 to +11.4 ppm °C−1 at the proposed PTT. Fig. 1(d) is a schematic illustrating the change in the crystal structure along the b axis. In the fergusonite structure, B site ions (Nb,V) are located in the center of distorted tetrahedra with two B–O bond lengths, resulting in different values of a and c, and a β angle >90 degrees. Above 350 °C, the B–O bond lengths in the tetrahedra become equal and the tetrahedral distortion disappears, coincident with β approaching 90 degrees. Cell refinements of fergusonite- and scheelite-structured La(Nb0.9V0.1)O4 at room temperature and 400 °C are shown in Fig. 1(e) and (f), respectively. The refined lattice parameters of La(Nb0.9V0.1)O4 at room temperature are a = 5.23654(7) Å, b = 11.6033(4) Å, c = 5.50762(4) Å, and β = 92.894 (4) ° with the space group I2/c (15) using data (ICSD # 81616) from Machida et al.47 The refined lattice parameters of scheelite La(Nb0.9V0.1)O4 at 400 °C are a = c = 5.3781(5) Å, b = 11.6783(7) Å with a space group I41/a (88) from (ICSD # 37139) reported by David.48 The atomic fractional coordinates and structural details are listed in Tables 1 and 2. Clear domains could be observed from the room temperature TEM images of the La(Nb0.9V0.1)O4 ceramic as shown in Fig. S1 in the ESI† and agree well with the XRD data.
Table 1 Refined atomic fractional coordinates from XRD data for the La(Nb0.9V0.1)O4 sample at room temperature and the lattice parameters are a = 5.23654(7) Å, b = 11.6033(4) Å, c = 5.50762(4) Å, β = 92.894 (4) °. The space group is I2/c (15)
| Atom |
Site |
Occ. |
x
|
y
|
z
|
| La |
4e |
0.5 |
0.25000 |
0.13539 |
0.00000 |
| Nb |
4e |
0.45 |
0.25000 |
0.61890 |
0.00000 |
| V |
4e |
0.05 |
0.25000 |
0.61890 |
0.00000 |
| O1 |
8f |
1.00 |
0.04142 |
0.71988 |
0.28695 |
| O2 |
8f |
1.00 |
1.02836 |
0.44614 |
0.19333 |
Table 2 Refined atomic fractional coordinates from the XRD data for the La(Nb0.9V0.1)O4 sample at 400 °C and the lattice parameters are a = c = 5.3781(5) Å, b = 11.6783(7) Å. The space group is I41/a (88)
| Atom |
Site |
Occ. |
x
|
y
|
z
|
| La |
4b |
0.25 |
0.00000 |
0.25000 |
0.62500 |
| Nb |
4a |
0.20 |
0.00000 |
0.25000 |
0.12500 |
| V |
4a |
0.05 |
0.00000 |
0.25000 |
0.12500 |
| O |
16f |
1.000 |
0.15639 |
0.02148 |
0.20595 |
The ferroelastic phase transition from monoclinic fergusonite to tetragonal scheelite is associated with an increase in point group symmetry from 2/m to 4/m and results in merging of two crystal orientation states (S1 and S2) above the PTT. Hence, second-rank strain tensors can be employed to describe these two orientation states caused by the relative ‘monoclinic’ displacements to the paraelastic scheelite phase:49,50
| | 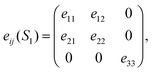 | (2) |
where R and R
T are the 90° rotation matrix and its transposition, respectively. As reported by Schlenker
et al.,
51 strain tensor components can be calculated from the cell parameters:
where
am,
bm,
cm and
βm are the cell parameters of the monoclinic phase, and
ct and
cb are the extrapolated tetragonal phase cell parameters. As described by Aizu,
49 ferroelasticity can be quantified using the spontaneous strain tensors and the two possible orientation states of La(Nb
0.9V
0.1)O
4 are presented as follows:
| | 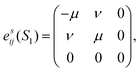 | (4) |
| | 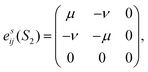 | (5) |
where
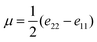
is the longitudinal strain and
ν =
e12 is the shear strain. It follows that the magnitude of the spontaneous strain is:
| | 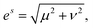 | (6) |
The spontaneous strain of the La(Nb0.9V0.1)O4 ceramic is ∼3.55% at room temperature, approximately half of that of undoped LaNbO4 ceramic (6.79%).
According to Landau's theory,52 the order parameter η (eqn (7)) may be used to describe the deviation from the paraelastic phase:
| | 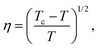 | (7) |
where
Tc is the PTT, (350 °C) and
T is temperature. The magnitude of the spontaneous strain of La(Nb
0.9V
0.1)O
4 is proportional to
η according to:
where
k is a constant (0.03725). The
η ×
k and
es values as a function of temperature are plotted in
Fig. 2. From room to the phase transition temperature, the agreement between
η ×
k and
es is obtained, confirming that the transition is of second order.
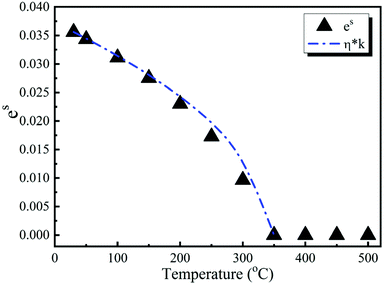 |
| | Fig. 2 Magnitude of the spontaneous strain and order parameter η of the La(Nb0.9V0.1)O4 ceramic as a function of temperature. | |
Group theory predicts that there are 18 Raman active modes for a monoclinic fergusonite structure (I2/a) and the irreducible representation of the modes is:53,54
| | | Γ = 8Ag + 10Bg + 8Au + 10Bu, | (9) |
where
Ag and
Bg are Raman active while
Au and
Bu are IR active. For the tetragonal scheelite structure (
I4
1/
a), the irreducible representation according to the group theory is given by:
55,56| | | Γ = 3Ag + 5Bg + 5Eg + 5Au + 3Bu + 5Eu, | (10) |
where all the
Ag,
Bg and
Eg are Raman active and all the
Au and
Eu are IR active. The correlation of the representations is at
Γ points of the
I2/
a and
I4
1/
a space groups. The phase transition in La(Nb
0.9V
0.1)O
4 may be described as a proper ferroelastic with strain as the primary order parameter, dominated by a soft acoustic phonon (marked
Q in
Fig. 3a). Based on Landau's theory,
54ωQ below the PTT (
TC) is given as follows:
| | 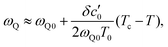 | (11) |
where
ωQ0 is the frequency at
TC,
δc′
0 is a spontaneous shear strain parameter, and
T0 is the temperature at which the ferroelastic phase becomes unstable.
ωQ decreases linearly with temperature in the ferroelastic phase but remains constant in the paraelastic phase, which agrees with the experimental results,
Fig. 3b, where
ωQ0 is ∼90 cm
−1. For BiVO
4, the ferroelastic → paraelastic phase transition is driven by a temperature-dependent
Bg optic mode coupled to the acoustic soft mode as described by Pinczuk
et al.37,57 In contrast to BiVO
4, no soft optical mode has been observed from room temperature to 500 °C, which defines the phase transition in LaNbO
4 to be purely ferroelastic with strain as the sole order parameter.
54,58 Hence, the Lyddane–Sachs–Teller (LST) relation is not followed.
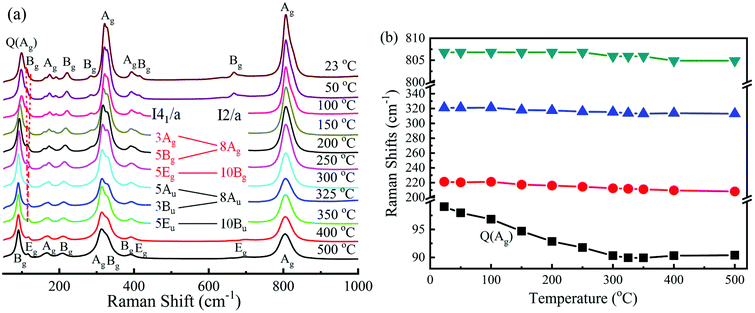 |
| | Fig. 3 (a) Raman shifts of La(Nb0.9V0.1)O4 from 25–500 °C and (b) selected modes as a function of temperature. | |
ε
r and dielectric loss of the La(Nb0.9V0.1)O4 ceramic as a function of temperature at different frequencies (10 kHz, 100 kHz, 250 kHz, 1 MHz and 8.5 GHz) are shown in Fig. 4. Different from BiVO4 ferroelastic ceramics and other ferroics as shown in Fig. 5b, an anomalous εr minimum value was observed at 10 kHz, 100 kHz, 250 kHz, and 1 MHz. Due to the limitation in microwave dielectric measurement, we did not obtain the wide temperature microwave εr spectrum but the present data show an apparent decrease of permittivity vs. temperature, which gives a large positive TCF value. Compared with εr, there is no abnormality observed from dielectric loss as shown Fig. 4(b). In the microwave region, polarizability is the sum of both ionic and electronic components. Shannon59 suggested that the molecular polarizability (α) of complex substances may be estimated by summing α of the constituent ions which for La(Nb0.9V0.1)O4 is:
| | | αLa(Nb0.9V0.1)O4 = αLa3+ + 0.9 × αNb5+ + 0.1 × αV5+ + 4αO2− = 17.98 Å3, | (12) |
where the ionic polarizabilities of La
3+, Nb
5+, V
5+ and O
2− are 6.07 Å
3, 3.97 Å
3, 2.92 Å
3 and 2.01 Å
3, respectively.
59 Considering the Clausius–Mosotti (C–M) relation,
60| | 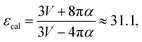 | (13) |
where
V is the cell volume (331.19/4 = 82.8 Å
3). The calculated
εr is 31.1, much larger than the measured value (∼20) at room temperature. As reported by Tsunekawa
et al.,
40,44,53 BO
4 tetrahedra are distorted in the fergusonite structure. The distorted tetrahedra have reduced B–O bond lengths, dampened B–O lattice vibrations and thereby decreased polarizability. Furthermore, macroscopic polarizability also includes additional terms related to the crystal structure and local anisotropy. As reported by Feteira
et al.,
61 polarizabilities of lanthanides (Ln) were derived from the rare-earth aluminates system and it became evident that Ln (
e.g. La
3+ = 4.68 Å
3) has lower values than reported by Shannon.
59
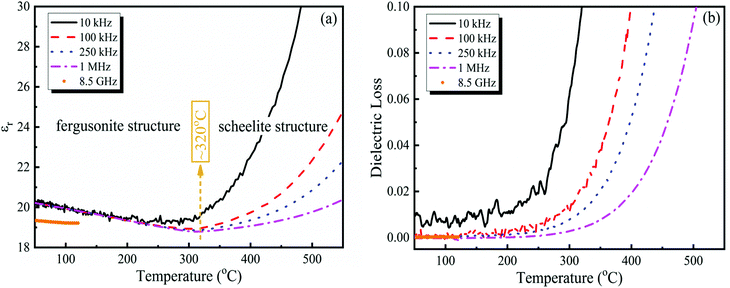 |
| | Fig. 4 (a and b) εr and dielectric loss of the La(Nb0.9V0.1)O4 ceramic as a function of temperature at different frequencies (10 kHz, 100 kHz, 250 kHz, 1 MHz and 8.5 GHz). | |
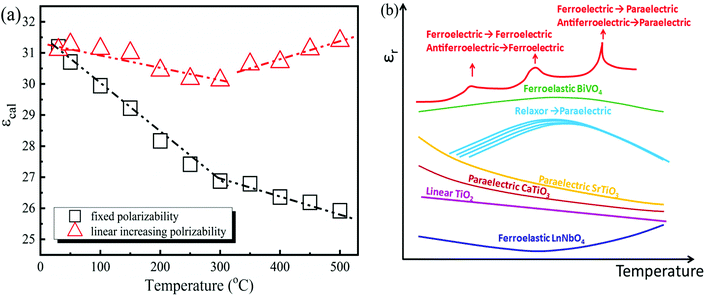 |
| | Fig. 5 (a) Calculated dielectric constant of the La(Nb0.9V0.1)O4 ceramic on assumptions of fixed and linear increasing polarizabilities and (b) schematic of εr of typical electro-ceramics vs. temperature. | |
The C–M relationship indicates that the εr of a specific compound is determined both by the cell volume and molecular polarizability. For La(Nb0.9V0.1)O4, as the temperature increased, the cell volume increased linearly below and above 350 °C but with different gradients. Based on the assumption that the molecular polarizability does not change with temperature, εr, calculated using eqn (13), is plotted in Fig. 5a which reveals a linear decrease below and above 350 °C but at different gradients. There is therefore an anomaly at 350 °C but not a minimum value of εr. However, if we assume that the molecular polarizability increases with temperature and follows a simple linear relation
| | | αLa(Nb0.9V0.1)O4 = α0 + (T − TR) × k, | (14) |
where
α0 is the room temperature molecular polarizability, 17.975 Å
3,
TR is room temperature and
k (0.00075) is a temperature-dependent constant; the combined effect of the cell volume and molecular polarizability
vs. T gives a minimum value of
εr at the PTT as shown in
Fig. 5a. Although this is a rough calculation, it gives a clear explanation for the dielectric minimum of the La(Nb
0.9V
0.1)O
4 ceramic at the PTT, at which point a decrease in thermal expansion coefficient occurs. In
Fig. 5b, we summarize the possible curves of
εrvs. T for a ferroelectric, relaxor, antiferroelectric, ferroelastic, paraelectric and linear dielectric material. The purely ferroelastic character and the sudden decrease in thermal expansion coefficient for La(Nb
0.9V
0.1)O
4 are anomalous compared with conventional ferroics and dielectrics.
Conclusions
The La(Nb0.9V0.1)O4 ceramic was determined by in situ XRD analysis to undergo a ferroelastic phase transition from a monoclinic fergusonite structure to a tetragonal scheelite structure at ∼350 °C. Raman analysis identified strain as the sole order parameter with a value of 3.55% at room temperature, almost half of that of the pure LaNbO4 ceramic. At the PTT, there was an abrupt change of the thermal expansion coefficient from +15.5 ppm °C−1 to +11.4 ppm °C−1, related to the anomalous change in the cell volume. Assuming a linear increase in polarizability, the minimum value of εr at the PTT for La(Nb0.9V0.1)O4 was predicted from the Clausius–Mosotti relation and Shannon's additive rule. Compared with ferroelectrics, relaxors, antiferroelectrics, ferroelastics, paraelectrics and linear dielectrics, the behaviour of εr in La(Nb0.9V0.1)O4vs. temperature is anomalous and may have novel applications in temperature stable composite ceramics.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Key Research and Development Program of China (Grant 2017YFB0406301), the Sustainability and Substitution of Functional Materials and Devices EPSRC (EP/L017s563/1), the National Natural Science Foundation of China (51972260, 52072295), the State Key Laboratory of Electrical Insulation and Power Equipment (Grant EIPE19210), the Fundamental Research Funds for the Central University, and the 111 Project of China (B14040).
References
- I. M. Reaney and D. Iddles, Microwave dieletric ceramics for resonators and filters in mobile phone networks, J. Am. Ceram. Soc., 2006, 89, 2063–2072 CAS.
- T. Fujii, A. Ando and Y. Sakabe, Characterization of dielectric properties of oxide materials in frequency range from GHz to THz, J. Eur. Ceram. Soc., 2006, 26, 1857–1860 CrossRef CAS.
- H. Ohsato, T. Tsunooka, A. Kan, Y. Ohishi, Y. Miyauchi, Y. Tohdo, T. Okawa, K. Kakimoto and H. Ogawa, Microwave-millimeterwave dielectric materials, Key Eng. Mater., 2004, 269, 195–198 CAS.
- M. T. Sebastian and H. Jantunen, Low loss dielectric materials for LTCC applications: a review, Int. Mater. Rev., 2008, 53, 57–90 CrossRef CAS.
- M. T. Sebastian, R. Ubic and H. Jantunen, Low-loss dielectric ceramic materials and their properties, Int. Mater. Rev., 2015, 60, 392–412 CrossRef.
- D. Zhou, L. X. Pang, D. W. Wang, C. Li, B. B. Jin and I. M. Reaney, High permittivity and low loss microwave dielectrics suitable for 5G resonators and low temperature co-fired ceramic architecture, J. Mater. Chem. C, 2017, 5, 10094–10098 RSC.
- H. H. Guo, D. Zhou, C. Du, P. J. Wang, W. F. Liu, L. X. Pang, Q. P. Wang, J. Z. Su, C. Singh and S. Trukhanov, Temperature stable Li2Ti0.75(Mg1/3Nb2/3)0.25O3-based microwave dielectric ceramics with low sintering temperature and ultra-low dielectric loss for dielectric resonator antenna applications, J. Mater. Chem. C, 2020, 8, 4690–4700 RSC.
- H. H. Guo, D. Zhou, W. F. Liu, L. X. Pang, D. W. Wang, J. Z. Su and Z. M. Qi, Microwave dielectric properties of temperature-stable zircon-type (Bi, Ce)VO4 solid solution ceramics, J. Am. Ceram. Soc., 2020, 103, 423–431 CrossRef CAS.
- C. H. Lee, N. D. Orloff, T. Birol, Y. Zhu, V. Goian, E. Rocas, R. Haislmaier, E. Vlahos, J. A. Mundy, L. F. Kourkoutis, Y. Nie, M. D. Biegalski, J. Zhang, M. Bernhagen, N. A. Benedek, Y. Kim, J. D. Brock, R. Uecker, X. X. Xi, V. Gopalan, D. Nuzhnyy, S. Kamba, D. A. Muller, I. Takeuchi, J. C. Booth, C. J. Fennie and D. G. Schlom, Exploiting dimensionality and defect mitigation to create tunable microwave dielectrics, Nature, 2013, 502, 532–536 CrossRef CAS.
- N. M. Dawley, E. J. Marksz, A. M. Hagerstrom, G. H. Olsen, M. E. Holtz, V. Goian, C. Kadlec, J. Zhang, X. Lu, J. A. Drisko, R. Uecker, S. Ganschow, C. J. Long, J. C. Booth, S. Kamba, C. J. Fennie, D. A. Muller, N. D. Orloff and D. G. Schlom, Targeted chemical pressure yields tuneable millimetre-wave dielectric, Nat. Mater., 2020, 19, 176–181 CrossRef CAS.
- O. Elijah, C. Y. Leow, T. A. Rahman, S. Nunoo and S. Z. Iliya, A comprehensive survey of pilot contamination in Massive MIMO—5G system, IEEE Commun. Surv. Tutor., 2016, 18, 905–923 Search PubMed.
- K. Xiao, L. Gong and M. Kadoch, Opportunistic multicast NOMA with security concerns in a 5G Massive MIMO system, IEEE Commun. Mag., 2018, 56, 91–95 Search PubMed.
-
M. B. Krishna and J. Lloret Mauri, Advances in mobile computing and communications: perspectives and emerging trends in 5G networks, CRC Press, Boca Raton, 2016 Search PubMed.
- Y. H. Jung, J. Lee, Y. Qiu, N. Cho, S. J. Cho, H. Zhang, S. Lee, T. J. Kim, S. Gong and Z. Ma, Stretchable twisted-pair transmission lines for microwave frequency wearable electronics, Adv. Funct. Mater., 2016, 26, 4635–4642 CrossRef CAS.
- I. Khan, M. Zafar, M. Jan, J. Lloret, M. Basheri and D. Singh, Spectral and energy efficient low-overhead uplink and downlink channel estimation for 5G Massive MIMO systems, Entropy, 2018, 20, 92 CrossRef.
- H. Li, B. Tang, X. Li, Z. Qing, Y. Li, H. Yang, Q. Wang and S. Zhang, The structure and properties of 0.95MgTiO3–0.05CaTiO3 ceramics doped with Co2O3, J. Mater. Sci., 2014, 49, 5850–5855 CrossRef CAS.
- X. C. Fan and X. M. Chen, Effects of Ca/Ti cosubstitution upon microwave dielectric characteristics of CaSmAlO4 ceramics, J. Am. Ceram. Soc., 2009, 92, 433–438 CrossRef CAS.
- L. X. Pang and D. Zhou, Microwave dielectric properties of low–firing Li2MO3 (M=Ti, Zr, Sn) Ceramics with B2O3–CuO addition, J. Am. Ceram. Soc., 2010, 93, 3614–3617 CrossRef CAS.
- H. H. Guo, D. Zhou, L. X. Pang and J. Z. Su, Influence of (Mg1/3Nb2/3) complex substitutions on crystal structures and microwave dielectric properties of Li2TiO3 ceramics with extreme low loss, J. Materiomics, 2018, 4, 368–382 CrossRef.
- D. W. Kim, D. K. Kwon, S. H. Yoon and K. S. Hong, Microwave dielectric properties of rare-earth ortho-niobates with ferroelasticity, J. Am. Ceram. Soc., 2006, 89, 3861–3864 CrossRef CAS.
- D. Guo, D. Zhou, W. B. Li, L. X. Pang, Y. Z. Dai and Z. M. Qi, Phase evolution, crystal structure, and microwave dielectric properties of water-insoluble (1-x)LaNbO4-xLaVO4 (0 ≤ x ≤ 0.9) ceramics, Inorg. Chem., 2017, 56, 9321–9329 CrossRef CAS.
- H. W. Lee, J. H. Park, S. Nahm, D. W. Kim and J. G. Park, Low-temperature sintering of temperature-stable LaNbO4 microwave dielectric ceramics, Mater. Res. Bull., 2010, 45, 21–24 CrossRef CAS.
- F. Vullum, F. Nitsche, S. M. Selbach and T. Grande, Solid solubility and phase transitions in the system LaNb1−xTaxO4, J. Solid State Chem., 2008, 181, 2580–2585 CrossRef CAS.
- A. R. V. Hippel, Ferroelectricity, domain structure, and phase transitions of barium titanate, Rev. Mod. Phys., 1950, 22, 221–237 CrossRef.
- M. Acosta, N. Novak, V. Rojas, S. Patel and J. Rödel, BaTiO3-based piezoelectrics: Fundamentals, current status, and perspectives, Appl. Phys. Rev., 2017, 4, 041305 Search PubMed.
- B. Noheda, N. Cereceda, T. Iglesias, G. Lifante and L. W. Yong, Composition dependence of the ferroelectric-paraelectric transition in the mixed system PbZr1-xTixO3, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 16388–16391 CrossRef CAS.
- A. K. Tagantsev, K. Vaideeswaran, S. B. Vakhrushev, A. V. Filimonov, R. G. Burkovsky, A. Shaganov, D. Andronikova, A. I. Rudskoy, A. Q. Baron, H. Uchiyama, D. Chernyshov, A. Bosak, Z. Ujma, K. Roleder, A. Majchrowski, J. H. Ko and N. Setter, The origin of antiferroelectricity in PbZrO3, Nat. Commun., 2013, 4, 2229 CrossRef CAS.
- G. Shirane and R. Pepinsky, Phase transitions in antiferroelectric PbHfO3, Phys. Rev., 1953, 91, 812–815 CrossRef CAS.
- D. L. Corker, A. M. Glazer, W. Kaminsky, R. W. Whatmore, J. Dec and K. Roleder, Investigation into the crystal structure of the perovskite lead hafnate, PbHfO3, Acta Crystallogr., 1998, 54, 18–28 Search PubMed.
- P. D. Dernier and J. P. Remeika, Synthesis and symmetry transformation in the perovskite compounds PbHfO3 and CdHfO3, Mater. Res. Bull., 1975, 10, 187–192 CrossRef CAS.
- R. M. Hazen and J. W. E. Mariathasan, Bismuth vanadate: a high-pressure, high-temperature crystallographic study of the ferroelastic-paraelastic transition, Science, 1982, 216, 991–993 CrossRef CAS.
- R. H. Lyddane, R. G. Sachs and E. Teller, On the polar vibrations of alkali halides, Phys. Rev., 1941, 59, 673–676 CrossRef CAS.
- I. M. Reaney, E. L. Colla and N. Setter, Dielectric and structural characteristics of Ba-based and Sr-based complex perovskites as a function of tolerance factor, Jpn. J. Appl. Phys., 1994, 33, 3984–3990 CrossRef CAS.
- J. D. Bierlein and A. W. Sleight, Ferroelasticity in BiVO4, Solid State Commun., 1975, 16, 69–70 CrossRef CAS.
- W. I. F. David, A. M. Glazer and A. W. Hewat, The structure and ferroelastic phase transition of BiVO4, Phase Transitions, 1979, 1, 155–169 CrossRef CAS.
- A. W. Sleight, H. Y. Chen, A. Ferretti and D. E. Cox, Crystal growth and structure of BiVO4, Mater. Res. Bull., 1979, 14, 1571–1581 CrossRef CAS.
- A. Pinczuk, B. Welber and F. H. Dacol, Mechanism of the ferroelastic transition of BiVO4, Solid State Commun., 1979, 29, 515–518 CrossRef CAS.
- D. Zhou, W. G. Qu, C. A. Randall, L. X. Pang, H. Wang, X. G. Wu, J. Guo, G. Q. Zhang, L. Shui, Q. P. Wang, H. C. Liu and X. Yao, Ferroelastic phase transition compositional dependence for solid-solution [(Li0.5Bi0.5)xBi1−x][MoxV1−x]O4 scheelite-structured microwave dielectric ceramics, Acta Mater., 2011, 59, 1502–1509 CrossRef CAS.
- D. Zhou, C. A. Randall, H. Wang, L. X. Pang and X. Yao, Ultra-low firing high-k scheelite structures based on [(Li0.5Bi0.5)xBi1−x][MoxV1−x]O4 microwave dielectric ceramics, J. Am. Ceram. Soc., 2010, 93, 2147–2150 CrossRef CAS.
- S. Tsunekawa and H. Takei, Domain switching behaviour of ferroelastic LaNbO4 and NdNbO4, J. Phys. Soc. Jpn., 1976, 40, 1523–1524 CrossRef CAS.
- L. H. Brixner, J. F. Whitney, F. C. Zumsteg and G. A. Jones, Ferroelasticity in the LnNbO4-type rare earth niobates, Mater. Res. Bull., 1977, 12, 17–24 CrossRef CAS.
- V. S. STUBIČAN, High-temperature transitions in rare-earth niobates and tantalates, J. Am. Ceram. Soc., 1964, 47, 55–58 CrossRef.
- K. A. Gingerich and H. E. Bair, Relation between ionic radii and transformation temperature in rare earth niobates, Adv. X-Ray Anal., 1964, 7, 22–30 CrossRef CAS.
- H. Takei and S. Tsunekawa, Growth and properties of LaNbO4 and NdNbO4 single crystals, J. Cryst. Growth, 1977, 38, 55–60 CrossRef CAS.
-
W. I. F. David, Structural phase transitions in ferroic ABO4 crystals, PH. D. thesis, University of Oxford, 1981 Search PubMed.
- S. Wachowski, A. Mielewczyk-Gryn and M. Gazda, Effect of isovalent substitution on microstructure and phase transition of LaNb1-xMxO4 (M=Sb, V or Ta; x=0.05–0.3), J. Solid State Chem., 2014, 219, 201–209 CrossRef CAS.
- M. Machida, J. Kido, T. Kobayashi, S. Fukui, N. Koyano and Y. Suemune, X-ray investigation on the crystal and domain structures of LaNbO4, Annu. Rep. Res. React. Inst., Kyoto Univ., 1995, 28, 25–32 CAS.
- W. I. F. David, The high-temperature paraelastic structure of LaNbO4, Mater. Res. Bull., 1983, 18, 749–756 CrossRef CAS.
- K. Aizu, Possible species of ferromagnetic, ferroelectric, and ferroelastic crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 1970, 2, 754–772 CrossRef.
- P. Satin, R. W. Hughes, D. R. Lowry, Z. D. Apostolov and W. M. Kriven, High-temperature properties and ferroelastic phase transitions in rare-earth niobates (LnNbO4), J. Am. Ceram. Soc., 2014, 97, 3307–3319 CrossRef.
- J. L. Schlenker, G. V. Gibbs and M. B. Boisen, Strain-tensor components expressed in terms of lattice parameters, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1978, 34, 52–54 CrossRef.
- L. D. Landau, On the theory of phase transitions, Zh. Eksp. Teor. Fiz., 1937, 7, 19–32 CAS.
- S. Tsunekawa, H. Takei and M. Ishigame, Study on the room temperature phase of LaNbO4 crystals, Mater. Res. Bull., 1977, 12, 1087–1094 CrossRef CAS.
- M. Wada, Y. Nakayama, A. Sawada, S. Tsunekawa and Y. Ishibashi, Raman scattering and fluorescence spectra of LaNbO4, J. Phys. Soc. Jpn., 1979, 47, 1575–1580 CrossRef CAS.
- M. Nicol and J. F. Durana, Vibrational Raman spectra of CaMoO4 and CaWO4 at high pressures, J. Chem. Phys., 1971, 54, 1436–1440 CrossRef CAS.
- D. Christofilos, G. A. Kourouklis and S. Ves, A high pressure Raman study of calcium molybdate, J. Phys. Chem. Solids, 1995, 56, 1125–1129 CrossRef.
- A. Pinczuk, G. Burns and F. H. Dacol, Soft optical phonon in ferroelastic BiVO4, Solid State Commun., 1977, 24, 163–165 CrossRef CAS.
- B. Y. Gu, H. Z. Cummins, S. L. Qiu and M. Copic, Acoustic soft modes and the ferroelastic phase transition in BiVO4 and LaNbO4, Ferroelectrics, 1983, 52, 45–57 CrossRef CAS.
- R. D. Shannon, Dielectric polarizabilities of ions in oxides and fluorides, J. Appl. Phys., 1993, 73, 348–366 CrossRef CAS.
- P. V. Rysselberghe, Remarks concerning the Clausius-Mossotti law, J. Phys. Chem., 1932, 36, 1152–1155 CrossRef.
- A. Feteira, D. C. Sinclair and M. T. Lanagan, Structural and electrical characterization of CeAlO3 ceramics, J. Appl. Phys., 2007, 101, 064110 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0qi00981d |
|
| This journal is © the Partner Organisations 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a,
Huan-Huan
Guo
a,
Mao-Sen
Fu
b,
Xiao-Gang
Yao
c,
Hui-Xing
Lin
c,
Wen-Feng
Liu
d,
Li-Xia
Pang
e,
Charanjeet
Singh
f,
Sergei
Trukhanov
ghi,
Alex
Trukhanov
*a,
Huan-Huan
Guo
a,
Mao-Sen
Fu
b,
Xiao-Gang
Yao
c,
Hui-Xing
Lin
c,
Wen-Feng
Liu
d,
Li-Xia
Pang
e,
Charanjeet
Singh
f,
Sergei
Trukhanov
ghi,
Alex
Trukhanov
 ghi and
Ian M.
Reaney
*j
ghi and
Ian M.
Reaney
*j
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 GHz and TCF = +9 ppm °C−1.20 Substitutions of La or Nb by isovalent ions plus the use of sintering aid in further improving the microwave dielectric properties.21–23 In our previous work,21 we demonstrated that 10 mol% substitution of V5+ for Nb5+ increases the TCF from +9 ppm °C−1 to +110 ppm °C−1.
400 GHz and TCF = +9 ppm °C−1.20 Substitutions of La or Nb by isovalent ions plus the use of sintering aid in further improving the microwave dielectric properties.21–23 In our previous work,21 we demonstrated that 10 mol% substitution of V5+ for Nb5+ increases the TCF from +9 ppm °C−1 to +110 ppm °C−1.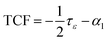
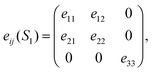
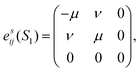
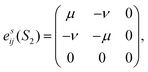
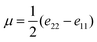 is the longitudinal strain and ν = e12 is the shear strain. It follows that the magnitude of the spontaneous strain is:
is the longitudinal strain and ν = e12 is the shear strain. It follows that the magnitude of the spontaneous strain is: