DOI:
10.1039/D0RA07425J
(Paper)
RSC Adv., 2021,
11, 11204-11214
Efficient removal of chromate ions from aqueous solution using a highly cost-effective ferric coordinated [3-(2-aminoethylamino)propyl]trimethoxysilane–MCM-41 adsorbent†
Received
29th August 2020
, Accepted 19th October 2020
First published on 17th March 2021
Abstract
The present investigation involves synthesis and characterization of MCM-41–AEAPTMS–Fe(III)Cl using coordinated Fe(III) on MCM-41–AEAPTMS for efficient removal of hazardous Cr(VI) ions from aqueous solution. The adsorbent MCM-41–AEAPTMS–Fe(III)Cl was characterized using small-angle X-ray diffraction (SAX), transmission electron microscopy (TEM), scanning electron microscopy (SEM), energy dispersive X-ray (EDX), Fourier-transform infrared (FT-IR) and Brunauer–Emmett–Teller (BET) surface analyzer techniques. The BET surface area was found to be 87.598 m2 g−1. The MCM-41–AEAPTMS–Fe(III)Cl effectively adsorbs Cr(VI) with an adsorption capacity acquiring the maximum value of 84.9 mg g−1 at pH 3 at 298 K. The data followed pseudo-second-order kinetics and obeyed the Langmuir isotherm model. The thermodynamic data proved the exothermic and spontaneous nature of Cr(VI) ion adsorption on MCM-41–AEAPTMS–Fe(III). Further, the higher value of ΔH° (−64.339 kJ mol−1) indicated that the adsorption was chemisorption in nature.
1. Introduction
Chromium is a versatile metal and finds its utility in numerous industrial applications such as in textiles, tannery, metallurgical, electroplating, pigments, etc.1 Regardless of being a profoundly demandable metal the magnitude of its toxicity has led it to be categorized among the top-most inorganic contamination by the US Environmental Protection Agency (EPA) and International Agency for Research on Cancer.2–4 Being a transition metal ion, chromium (Cr) exhibits a variable oxidation state and hence is found in nature ranging from II to VI oxidation states. Among these, Cr(VI) and Cr(III) are most stable. Cr(III) being insoluble is moderately toxic and is required as a nutrient for the metabolism of lipids and sugar in the body.5,6 In contrast, Cr(VI) is exceedingly water soluble, highly toxic. The toxicity of Cr(VI) is due to the fact that Cr(VI) as the CrO42− ion is isostructural to the SO42− ion and thus exploits the transmembrane sulfate channel to penetrate into the cell where it gets reduced to Cr(V), Cr(IV) and ultimately to the thermodynamically more stable Cr(III) ion by ascorbate (Asc), cysteine (Cys), glutathione (GSH).7 The tendency to exhibit a variable oxidation state allows Cr(VI) to undergo Fenton's type reaction and generate reactive oxygen species (ROS) inside the cell causing oxidative stress, tissue damage, injuring and disrupting the functioning of vital organs such as liver, kidney, stomach, etc. and finally leading to death of the individual.8,9 The carcinogenic and mutagenic nature of Cr(VI) has also been documented.10 Therefore, high Cr(VI) concentration can lead to a detrimental effect on plant and animal life and the environment. Hence it's desirable to limit its concentration in these effluents to acceptable limit before discharging into the environment. According to EPA, the tolerable level of Cr(VI) in consumable water to 0.1 mg L−1.11–13 Cr(VI) exists as HCrO4−, Cr2O72− and CrO42− in aqueous solution. Several methodologies have been implemented to eliminate these species from waste water. These involve ion exchange, reduction–precipitation, adsorption, membrane separation, electrochemical treatment, solvent extraction, biological treatment etc. Adsorption being simple and economical is widely preferred over the other techniques.14–16 Moreover, the adsorbed metal can be isolated and reused. Numerous adsorbent has been reported for eliminating hazardous Cr(VI) from industrial effluents. The common feature involved in these removal process involves either removing the hexavalent chromium as anionic species or simultaneous reducing and isolating it as Cr(III).12,17–23 The commonly used adsorbent includes nanomaterials, clay, ion exchange resins, zeolites, activated carbon, nanotubes, magnetic material, impregnated photocatalyst etc. These materials have poor adsorption capacity and selectivity. To overcome these drawbacks, ordered mesoporous silica-based material like MCM-41 is frequently used. MCM-41 is an attractive adsorbent owing to high thermal stability, uniform pore size, high surface area, etc. Several reports have confirmed the excellent absorption capacity of pure MCM-41 towards Cr(VI) removal.24–26 In order to enhance the adsorption capability of MCM-41, numerous surface modification have been reported.9,27–31 Some surface modification includes decorating MCM-41 with amino ligands, EDCC ligand, grafting of TiO2 with MCM-41, impregnation of CuO on ZrO–MCM-41 for the reduction of Cr(VI) to less toxic Cr(III) etc.32–35 Very few reports are available regarding the adsorption of Cr(VI) using metal ion complex.36 We report here Fe(III) chelated MCM-41–AEAPTMS for the abstraction of Cr(VI). Kinetic and equilibrium experiments were then performed. The material showed excellent removal capacity at pH 3. Small-angle X-ray scattering (SAX), Fourier-transform infrared (FT-IR) spectrometry, BET adsorption isotherms, UV-visible spectroscopy, SEM, and TEM were used to investigate the morphology and chemical composition of the adsorbent. Elemental analysis was performed using SEM-EDX. The batch process was used to investigate the effect of pH, adsorbent dosage, contact time, temperature, on the effectiveness of Cr(VI) removal using the synthesized adsorbent. Kinetics and thermodynamics studied were carried out to know the mechanism and feasibility of the Cr(VI) uptake using MCM-41–AEAPTMS–Fe(III). Finally, a regeneration experiment was performed for 5 cycles to check the reusability and stability of the adsorbent.
2. Experimental
2.1 Materials
Fumed silica (Sigma Aldrich) as silica source, cetyltrimethylammonium bromide (CTAB, Sigma Aldrich) as structural directing agent, absolute ethanol (99%, Merck), [3-(2-aminoethylamino)propyl]trimethoxysilane (AEAPTMS, 99%, Sigma Aldrich), K2Cr2O7 (Merck, India), 1,5-diphenylcarbazide (DiPC, Merck, India), sodium hydroxide (Merck, India), hydrochloric acid (Merck, India), distilled water. All the chemicals used were of analytical grade and used without further purification.
2.2 Synthesis of MCM-41
MCM-41 was synthesized based on previously reported articles with minor modifications.37–40 The process involved dissolving cetyltrimethylammonium bromide (CTAB, 9.840 g), tetramethylammonium hydroxide (TMAOH, 9.0 mL), NaOH (1.032 g) in H2O (60.0 mL) at 35 °C. To this clear solution, fumed silica (6.0 g) was added under continuous stirring for an hour. A white gel was obtained having the composition SiO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25 CTAB
0.25 CTAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.20 TMAOH
0.20 TMAOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40H2O. The pH of this gel was adjusted to 10.0 and transferred to Teflon lined autoclave and subjected heated at 100 °C for 24 h under autogenous pressure. The solid product was subsequently washed with water, dried at 80 °C, and subjected to calcination at 550 °C for 6 hours with 1° min−1 being the heating rate. This was termed as MCM-41.
40H2O. The pH of this gel was adjusted to 10.0 and transferred to Teflon lined autoclave and subjected heated at 100 °C for 24 h under autogenous pressure. The solid product was subsequently washed with water, dried at 80 °C, and subjected to calcination at 550 °C for 6 hours with 1° min−1 being the heating rate. This was termed as MCM-41.
2.2.1. Functionalization of MCM-41 with AEAPTMS (MCM-41–AEAPTMS). The as syn. MCM-41 (1.0 g) was dried at 150 °C and suspended in 60 mL of absolute ethanol. Thereafter AEAPTMS (1.0 mL) was added dropwise and the suspension was refluxed for 24 h. The above product was filtered, washed using ethanol, dried at 80 °C. This product was termed MCM-41–AEAPTMS.41,42
2.2.2. Incorporation of Fe3+ on MCM-41–AEAPTMS [MCM-41–AEAPTMS–Fe(III)Cl]. MCM-41–AEAPM (1.0 g) was suspended in absolute ethanol and to it 0.1 M ferric chloride solution was added and stirred for 3 h at 25 °C. Thereafter the powdered was filtered, washed with ethanol and finally drying at 80 °C. This was termed MCM-41–AEAPTMS–Fe(III).43,44
2.2.3. Batch experiments for Cr(VI) removal. Batch process was employed under equilibrium condition to investigate the role of various parameters such as pH, adsorbent dosage, temperature, initial Cr(VI) concentration, contact time, on the efficiency of chromate removal. The chromate concentration of desired strength was obtained by diluting the standard solution of potassium dichromate. For investigating the influence of pH, chromate solution (50 mL, 50 ppm) at varying pH (2, 3, 4, 5, 6) was taken and to it, adsorbent (50 mg) was added followed by agitating the suspension for 24 h at 25 °C and 100 rpm (thermostatic shaker, Narang Scientific). NaOH (0.1 M) and HCl (0.1 M) were employed to adjust the pH of the chromate solution to a preset value. Thereafter the suspension was centrifuged and the solution was extracted using a 0.45 μm PTFE syringe filter (Millipore, USA). The residual concentration of Cr(VI) was obtained employing the DiPC method and using a UV-vis spectrophotometer (Thermos, Evolution 201) measuring the absorbance at 540 nm. For investigating the influence of adsorbate dosage, experiment was performed by fixing the Cr(VI) concentration (50 ppm, 50 mL) at a pH of 3 and altering the adsorbent dosage (10 mg, 20 mg, 30 mg, 40 mg, 50 mg) and at different temperature of 25, 35 and 45 °C. For the adsorption experiments, initially, chromate solution (50 mL) of varying concentration (10, 25, 50, 100, and 200 ppm) were taken in a conical tube (50 mL) containing 50 mg of MCM-41–AEAPTMS–Fe(III)Cl adsorbent at a varying temperature of 25, 35 and 45 °C and agitated at 100 rpm. Subsequently, the suspension was centrifuged, the residual chromate solution was extracted using a 0.45 μm PTFE syringe filter and its concentration was evaluated using the following equation.| |
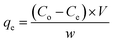 | (1) |
| |
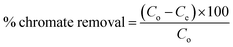 | (2) |
where qe is the amount of Cr(VI) adsorbed per unit mass of adsorbent, Co, Ce are the initial and equilibrium chromate concentration in ppm, V (L) is the volume of the chromate solution and w (g) is the amount of MCM-41–AEAPTMS–Fe(III)Cl in the experiment respectively. The effect of contact time on the adsorption of chromate was examined by suspending the adsorbent (50 mg) in chromate solution (50 ppm, 50 mL) at pH 3 and agitating for 200 minutes at 298K at 100 rpm. Thereafter, the solution collected at regular interval of time starting from 10 minutes to 200 minutes, centrifuged, filtered the chromate concentration was measured as stated earlier. The following equation was employed to calculate the residual chromate concentration as a function of time| |
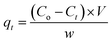 | (3) |
where qt (mg g−1) is the amount of chromate adsorbed on the mass of adsorbent w (g), at the time interval t (minutes). Co, Ct (ppm) are chromate concentration present initially and at time t (minutes), V (L) is the volume of the Cr(VI) solution respectively.
2.2.4. Characterization. Small-angle X-ray scattering (SAXS) was performed employing the Anton Paar SAX Space instrument, which utilizes Cu-Kα as an X-ray source, operating at 40 kV, 50 mA. The diffracted X-ray data were collected at 2θ values ranging between 1.2° to 10°. The morphology of the adsorbent was obtained using transmission electron microscopy (TEM, Tecnai G220 TWIN) and scanning electron microscopy (SEM, EVO MA15/18) operating at a voltage of 200 kV and 20 kV respectively. Elemental analysis was performed using SEM-energy dispersive X-ray (SEM-EDX, 51N1000 – EDS System). Fourier transform infrared (FTIR, PerkinElmer 1605) spectra were obtained between 400–4000 cm−1 range using KBr pellets for solid samples. N2 adsorption–desorption isotherms were performed at −196 °C using an automated gas sorption analyzer (quanta chrome autosorb iQ2). The samples were initially degassed at heating 100 °C for 3 h and Brunauer–Emmett–Teller (BET) technique was employed to obtain the specific surface area and pore size distribution was calculated using Barrett–Joyner–Halenda (BJH) method. The ultraviolet (UV) absorption spectra were obtained using an ultraviolet-visible spectrophotometer (Thermos, Evolution 201).
3. Result and discussion
The XRD pattern of MCM-41 (Fig. 1) is consistent with the earlier reports. The high-intensity peak at 2θ = 2.5° corresponds to reflection from (100) plane while the weak peaks between 2θ = 3–5° arise due to reflection from (110) and (200) planes respectively. The existence of all three peaks indicates the formation of highly ordered MCM-41. Upon functionalization with AEAPTMS and subsequent introduction of Fe(III) and Cr(VI) ions, shifts the peak position to higher 2θ value as well as reduces the peak intensity of (100) and eliminates the higher-order peaks. The slight shifting of the peaks to higher 2θ value is due to a decrease in the d spacing and lattice parameter (ao) while the missing peaks indicate a slight decrease in the pore ordering.40,45 The parameters of the unit cell were calculated using the following equation| |
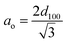 | (4) |
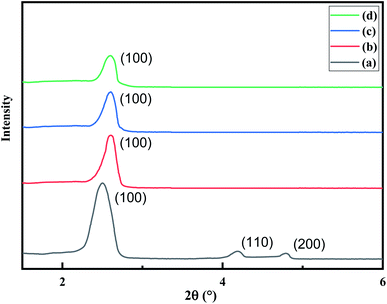 |
| | Fig. 1 XRD pattern of (a) MCM-41, (b) MCM-41–AEAPTMS, (c) MCM-41–AEAPTMS–Fe(III)Cl (d) MCM-41–AEAPTMS–Fe(III)–Cr(VI). | |
The d-spacing was found to be 33.9 Å while the calculated value of the lattice parameter (ao) was found to be 32.9 Å.
3.1 Surface analysis
The TEM images of AEAPTMS–Fe(III)–Cr(VI) are shown in Fig. 2. Fig. 2a substantiates the existence of hexagonally periodic arranged of the pore channels with P6mm symmetry as reported previously.46 The d spacing calculated from TEM (32.9 Å) and the XRD analysis (33.9 Å) is in close agreement. Fig. 2b confirms the existence of undistorted symmetry in regenerated MCM-41–AEAPTMS–Fe(III)Cl even after 5 cycles. The SEM-EDX spectrum of the MCM-41–AEAPTMS–Fe(III) (Fig. 3c) shows the peaks of all the elements. The additional peak (Fig. 3d) corresponding to Cr(VI) appears at 5.4 and 5.9 keV. The appearance of Cr(VI) peaks is marked by the reduction in the elemental composition of Cl− confirming the exchange of Cl− by Cr(VI) respectively.
 |
| | Fig. 2 TEM image of (a) MCM-41–AEAPTMS–Fe(III)–Cr(VI) and (b) MCM-41–AEAPTMS–Fe(III) regenerated after 5 cycles. | |
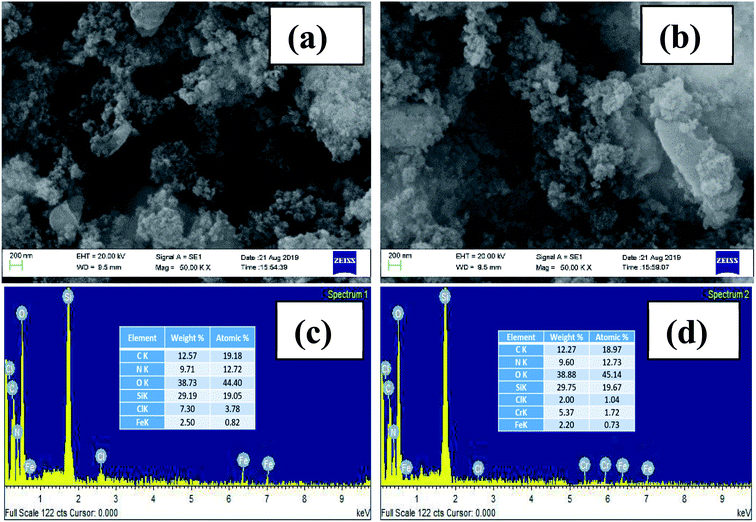 |
| | Fig. 3 SEM-image of MCM-41–AEAPTMS–Fe(III)Cl (a) prior to adsorption and (b) after adsorption of Cr(VI). SEM-EDX spectra of (c) MCM-41–AEAPTMS–Fe(III)Cl (d) MCM-41–AEAPTMS–Fe(III)–Cr(VI). | |
The FTIR spectra were obtained to confirm the desired modification on MCM-41. Fig. 4 compares the FTIR spectrum of MCM-41 and MCM-41–AEAPTMS. A broad band in Fig. 4x and y between 3600–3000 cm−1 and a band centered at 1636 cm−1 are due to the symmetrical stretching and bending mode of vibration associated with the adsorbed water molecule on the surface of the silinol. The vibrations at 1084, 1230, and 800 cm−1 are associated with antisymmetric and symmetric vibrations mode of Si–O–Si. A peak at 970 cm−1 arises from Si–OH vibration. Upon functionalization with AEAPTMS (Fig. 4y), new peaks appear at around 2900, 2800 cm−1. These peaks are generally associated with the C–H stretching and bending mode of vibrations. Peaks at 1510, 693 cm−1 are typically associated with –NH2 and N–H bending vibration respectively.47,48 The C–N stretching vibration usually appears at 1000–1200 cm−1 overlaps with Si–O–Si stretch appearing at 1000–1130 cm−1 range and so remains unresolved.45 As inferred from the Fig. 3, upon loading Fe(III), there is a slight increase in the intensity of the C–H stretching and N–H bending while Si–O–Si stretch remains unaltered indicating that the structure of MCM-41 remains stable. Similar observation have been documented in the literature in association with metal amine complex.49
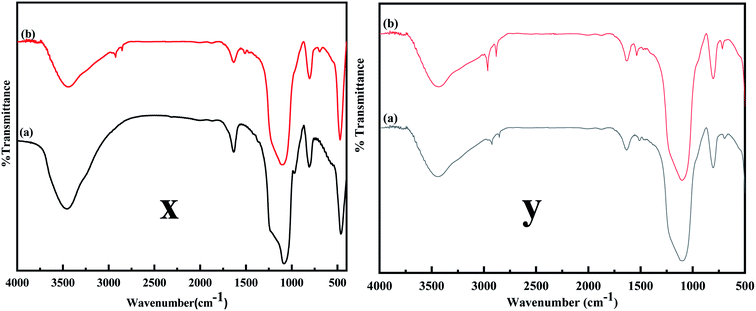 |
| | Fig. 4 (x) FT-IR spectra of (a) MCM-41, (b) MCM-41–AEAPTMS, (y) (a) MCM-41–AEAPTMS, (b) MCM-41–AEAPTMS–Fe(III)Cl. | |
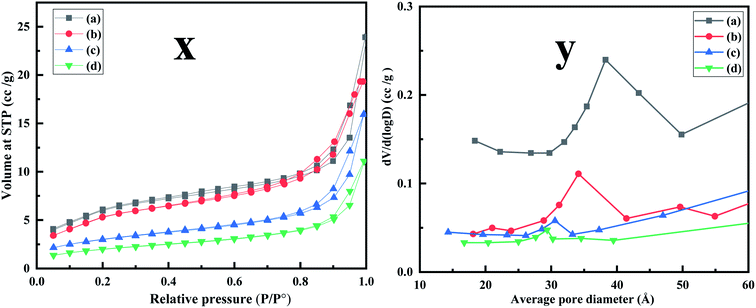 |
| | Fig. 5 (x) N2 adsorption–desorption isotherm performed at 77 K (a) MCM-41 (b) MCM-41–AEAPTMS (c) MCM-41–AEAPTMS–Fe(III)Cl (d) MCM-41–AEAPTMS–Fe(III)–Cr(VI). (y) BJH pore size distribution of (a) MCM-41 (b) MCM-41–AEAPTMS (c) MCM-41–AEAPTMS–Fe(III)Cl (d) MCM-41–AEAPTMS–Fe(III)–Cr(VI). | |
Table 1 BET surface area, pore volume, and pore size
| Sample |
SBET (m2 g−1) |
Vp (cm3 g−1) |
Dp (nm) |
| MCM-41 |
338.087 |
0.378 |
3.826 |
| MCM-41–AEAPTMS |
133.591 |
0.244 |
3.414 |
| MCM-41–AEAPTMS–Fe(III)Cl |
87.598 |
0.175 |
3.058 |
| MCM-41–AEAPTMS–Fe(III)–Cr(VI) |
57.743 |
0.122 |
3.023 |
Fig. 5 and Table 1 depict the nitrogen adsorption–desorption isotherms and the corresponding distribution of pore size of MCM-41, MCM-41–AEAPTMS, MCM-41–AEAPTMS–Fe(III)Cl and MCM-41–AEAPTMS–Fe(III)–Cr(VI) respectively performed at 77 K. The presence of type IV isotherms is indicative of the mesoporous nature of the adsorbent while the H1 hysteresis confirms narrow pore size distribution.29 The successive decline in the surface area, pore-volume, and pore size on the introduction of AEAPTMS, Fe(III), and Cr(VI) along with the FTIR signals and SEM EDX data confirms the presence of these elements on the MCM–AEAPTMS matrix.
3.2 Cr(VI) adsorption on MCM-41–AEAPTMS–Fe(III)Cl
3.2.1. Effect of pH on the adsorption of Cr(VI). The adsorption of the Cr(VI) ion from the solution depends on the charge of the adsorbent as well as on the speciation of the Cr(VI) ion. Both these factors are greatly influenced by the solution pH, therefore pH plays a significant role in sequestering Cr(VI) ion from aqueous waste. When the pH is around 1, Cr(VI) predominantly exists as hydrogen chromate (H2CrO4) while at pH > 2, HCrO4− predominates. At pH ≥ 6 chromate (CrO42−) and dichromate (Cr2O72−) dominates. At intermediate pH between 2 and 6, Cr(VI) exists all the three forms as HCrO4−, CrO42− and Cr2O72−.50 The experimental findings (Fig. 6a) reveal that the effectiveness with which Cr(VI) is removed increases significantly from 81.0% to 95.0% on going from pH 2 to 3 and thereafter reduces to 59.6% on arriving at pH 6. This is due to the fact that at low pH, there exists a strong electrostatic interaction between the positively charged adsorbent sites and chromate anion while at higher pH the negatively charged Cr(VI) and OH− ion competes for the positively charged adsorption sites.51 As the best result was obtained at pH 3, further investigation was performed at this pH.
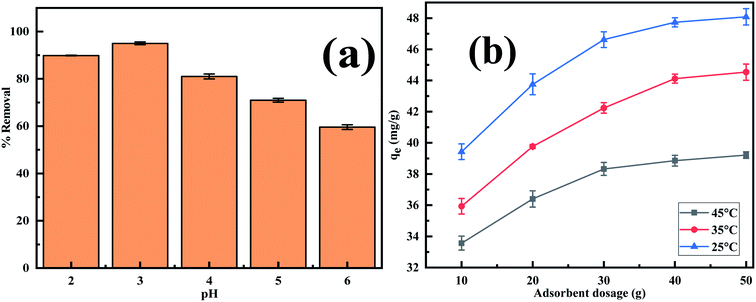 |
| | Fig. 6 Effect of (a) pH (b) adsorbent dosage on Cr(VI) adsorption on MCM-41–AEAPTMS–Fe(III)Cl as functions of Cr(VI) concentration (50 mg L−1, 50 mL). | |
3.2.2. Effect of adsorbent dosage on the adsorption of Cr(VI). It is obvious from Fig. 6b, that adsorbent capacity increases from an initial value (qe = 39.4 mg g−1) to a limiting value (qe = 48.1 mg g−1) on increasing the adsorbent dosage from 10 mg to 50 mg at 25 °C. Similar trends are observed at 35 and 45 °C. This finding is ascribed to the fact that with increasing adsorbent dosage there is an increment in the number of active sites responsible for Cr(VI) uptake but with increasing Cr(VI) the active site responsible for capturing the pollutant reduces drastically causing the adsorption capacity to reach a limiting value.52
3.2.3. Adsorption kinetics. The adsorption kinetics is an essential parameter governing the efficiency of the adsorption process.53 Fig. 7x reveals that the rate of Cr(VI) uptake is rapid for the initial 100 min with absorbent capacity (qt) reaching the value of 49.5 mg g−1 and removal capacity being 49.5% at around 180 min. The rapid adsorption of the metal ion indicates that active sites are largely available on the surface.54,55 Further, the time profile curve shows that the initial rapid adsorption is followed by a steady rise in the adsorption value to a saturation point indicating the formation of a monolayer of the adsorbate. As the equilibrium kinetic was reached at 180 min, a contact time of 200 min was finally chosen as the contact time for carrying further investigation. Thereafter the data were fed into the pseudo-first-order, pseudo-second-order kinetics, and the kinetic parameters were estimated after linearizing the kinetic model. Lagergren equation, used to express the pseudo-first-order is represented as| |
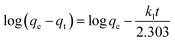 | (5) |
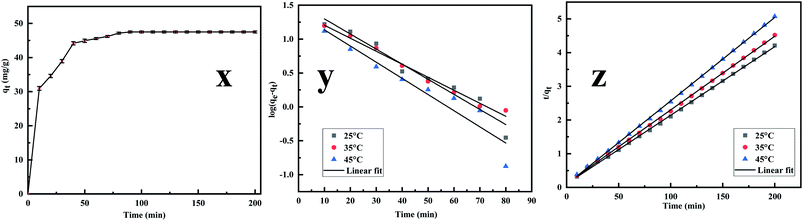 |
| | Fig. 7 (x) Effect of Cr(VI) adsorption on MCM-41–AEAPTMS–Fe(III)Cl as functions of contact time, adsorbent dosage (50 mg), solution volume (50 mL), 200 rpm, 25 °C, Cr(VI) concentration (50 mg L−1), (y) kinetics of pseudo-first order for Cr(VI) removal using MCM-41–AEAPTMS–Fe(III)Cl, contact time (200 min), adsorbent dosage (50 mg), solution volume (50 mL), 200 rpm, 25 °C, Cr(VI) concentration (50 mg L−1), (z) kinetics plot of pseudo-second order for Cr(VI) removal using MCM-41–AEAPTMS–Fe(III)Cl, contact time (140 min) adsorbent dosage (50 mg), solution volume (50 mL), 200 rpm, 25 °C, Cr(VI) concentration (50 mg L−1). | |
Pseudo-second order is typically expressed as
| |
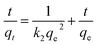 | (6) |
where qe, qt are the Cr(VI) (mg g−1) adsorbed at equilibrium and any instance t (min). k1 (min−1) and k2 (g mg−1 min−1) are the pseudo-first-order and pseudo-second-order rate constant respectively. Fig. 7y and z depict the pseudo-first and pseudo-second-order plot and Table 2 summaries the calculated and the experimental data. The compatibility of the calculated value of qe with that of the experimental value and the coefficient value approaching unity suggesting that the adsorption follows pseudo-second-order kinetics.
Table 2 Pseudo-first order and pseudo-second-order kinetics data for the adsorption of Cr(VI) by MCM-41–AEAPTMS–Fe(III)Cl
| Temperature (K) |
Pseudo-first order model |
Pseudo-second order model |
qe (exp) (mg g−1) |
| qe (cal) (mg g−1) |
k1 (min−1) |
R2 |
qe (cal) (mg g−1) |
k2 (g mg−1 min−1) |
R2 |
| 298 |
33.2 |
0.051 |
0.947 |
49.1 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 007.85 007.85 |
0.999 |
49.5 |
| 308 |
24.9 |
0.044 |
0.988 |
45.7 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 699.53 699.53 |
0.999 |
44.2 |
| 318 |
23.7 |
0.054 |
0.901 |
40.4 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 083.34 083.34 |
0.999 |
39.4 |
3.2.4. Adsorption isotherms. The influence of temperature on the adsorption capacity of the MCM-41–AEAPTMS–Fe(III)Cl was investigated by conducted experiments at three different temperatures. Fig. 8 depicts the adsorption capacity (qe) of Cr(VI) at 298 K, 308 K, and 318 K respectively. It is found that qe increases sharply, reaches a limiting value, and thereafter becoming constant. The increment in qe can be correlated to the availability of numerous active sites whereas the decline in the qe with rising temperature revels the exothermic nature of the interaction between the positively charged Fe(III) centers present on MCM-41–AEAPTMS–Fe(III) and Cr(VI) ions present in its vicinity.56
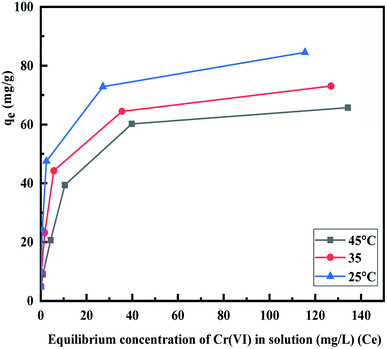 |
| | Fig. 8 Effect of temperature on Cr(VI) adsorption using MCM-41–AEAPTMS–Fe(III)Cl, contact time (200 min), adsorbent dosage (50 mg), solution volume 50 mL, 100 rpm, Cr(VI) concentration (50 mg L−1). | |
For investigating the adsorption isotherms, Langmuir, Freundlich, Temkin, and Dubinin–Radushkevich (D–R) isotherm model were employed (Fig. 9). The Langmuir model considers the adsorbent to be composed of finite numbers of equivalent active sites, having an identical affinity for the approaching adsorbent moiety. The absence of lateral interaction among the adsorbate and the presence of limited active sites causes the formation of a monolayer of Cr(VI) on MCM-41–AEAPTMS–Fe(III).57 The general form of the Langmuir equation is represented as
| |
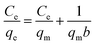 | (7) |
where Ce (mg L−1) is the equilibrium Cr(VI) concentration, qe (mg g−1) is the Cr(VI) adsorbed per unit mass of MCM-41–AEAPTMS–Fe(III)Cl, qm (mg g−1) is the maximum adsorption capacity of Cr(VI) on MCM-41–AEAPTMS–Fe(III)Cl and b (L mg−1) is the Langmuir isotherm constant or binding constant, related to the heat of adsorption. The decreasing value of b and qm with temperature (Fig. 8, 9, and Table 3) are indicative of the exothermic nature of the interaction between the adsorbate and adsorbent. According to Hall et al., a dimensionless parameter called separation factor (RL) can be utilized to ascertain the effectiveness of an adsorption process. It is defined by as| |
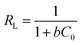 | (8) |
where C0 (mg L−1) is the initial Cr(VI) concentration. An isotherm with RL = 0 indicates an irreversible process, RL > 1 indicates an unfavorable process while 0 < RL < 1 indicates a favorable process.58 The RL value was found to be between 0.03–0.1 which indicated favorable interaction between the adsorbate and the adsorbent. The multilayer adsorption on the heterogeneous surface can be explained using the Freundlich adsorption model is expressed aswhere KF and n are the Freundlich adsorption capacity and adsorption intensity. For a favorable adsorption n > 1. The logarithmic form of Freundlich equation is expressed as| |
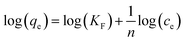 | (10) |
 |
| | Fig. 9 (a) Langmuir isotherm, (b) Freundlich isotherm (c) Temkin isotherm (d) D–R isotherm Cr(VI) adsorption using MCM-41–AEAPTMS–Fe(III)Cl, contact time (140 min), adsorbent dosage (50 mg), solution volume 50 mL, 100 rpm, Cr(VI) concentration (50 mg g−1). | |
Table 3 Various parameters of Langmuir, Freundlich, Temkin and D–R adsorption isotherm for Cr(VI) adsorbed on MCM-41–AEAPTMS–Fe(III)Cl
| Temp. |
Langmuir isotherm |
Freundlich isotherm |
Temkin isotherm |
D–R isotherm |
| qm |
b |
R2 |
RL |
n |
KF |
R2 |
b |
BT |
KT |
R2 |
qmax |
β |
E |
R2 |
| 25 °C |
84.9 |
0.5 |
0.996 |
0.04 |
3.5 |
29.2 |
0.824 |
299.1 |
8.28 |
1.78 |
0.870 |
41.1 |
1.06 × 10−8 |
6.85 |
0.730 |
| 35 °C |
74.4 |
0.3 |
0.998 |
0.06 |
2.7 |
16.3 |
0.940 |
259.9 |
9.85 |
1.30 |
0.965 |
43.1 |
4.85 × 10−8 |
3.21 |
0.849 |
| 45 °C |
68.8 |
0.1 |
0.998 |
0.17 |
2.4 |
11.1 |
0.952 |
266.3 |
9.92 |
1.78 |
0.896 |
33.5 |
6.27 × 10−8 |
2.82 |
0.649 |
The value of KF and n are evaluated from the intercept and slope of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe vs. log
qe vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce plot. Table 3 represents the Freundlich adsorption data. The positive value of n and KF are indicative of favorable adsorbate–adsorbent interaction. It is evident from the table that the linear regression coefficient (R2) is closer to unity for the Langmuir model indicating that it is better equipped to explain the adsorption process. The Temkin isotherm which is applicable at the intermediate concentration of the absorbent was employed to understand the nature of the interaction between the adsorbate and the adsorbent. It assumes that as the active sites get covered, the heat of adsorption decreases linearly.59 The model is expressed linearly as
Ce plot. Table 3 represents the Freundlich adsorption data. The positive value of n and KF are indicative of favorable adsorbate–adsorbent interaction. It is evident from the table that the linear regression coefficient (R2) is closer to unity for the Langmuir model indicating that it is better equipped to explain the adsorption process. The Temkin isotherm which is applicable at the intermediate concentration of the absorbent was employed to understand the nature of the interaction between the adsorbate and the adsorbent. It assumes that as the active sites get covered, the heat of adsorption decreases linearly.59 The model is expressed linearly as
| |
qe = BT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(KT) + BT ln(KT) + BT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Ce) ln(Ce)
| (11) |
where 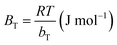 is the heat of sorption, bT = Temkin constant, KT (L g−1) is the Temkin equilibrium binding constant corresponding to maximum binding energy, R is the universal gas constant (8.314 J K−1 mol−1) and T is the temperature in absolute scale (K). It is evident from Table 3 that the (R2 = 0.870–0.965) indicating the Temkin model does not satisfactorily fits with the experimental data. The value of BT was found to 8.28–9.92 and KT was 1.30–1.78.
is the heat of sorption, bT = Temkin constant, KT (L g−1) is the Temkin equilibrium binding constant corresponding to maximum binding energy, R is the universal gas constant (8.314 J K−1 mol−1) and T is the temperature in absolute scale (K). It is evident from Table 3 that the (R2 = 0.870–0.965) indicating the Temkin model does not satisfactorily fits with the experimental data. The value of BT was found to 8.28–9.92 and KT was 1.30–1.78.
The D–R isotherm model is another model to understand the nature of adsorbate–adsorbent interaction.60 The D–R isotherm in linearized form is typically expressed as
| |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = −βε2 + ln qe = −βε2 + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qmax qmax
| (12) |
where qe (mol g−1) is the equilibrium concentration of Cr(VI) (mol g−1), qmax (mol g−1) is saturation adsorption capacity, β (mol2 J−2) is the D–R constant and ε (J mol−1) is the Polanyi potential expressed as| |
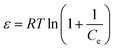 | (13) |
where Ce (mol L−1) is the equilibrium Cr(VI) concentration. The D–R constant β and the mean energy E (kJ mol−1) associated with the adsorption process is expressed| |
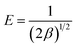 | (14) |
The values of E are used to evaluate the nature of adsorbate–adsorbent interaction. The physical adsorption is associated with E value ranging between 1 to 8 kJ mol−1, while ion-exchange corresponds to E values between 8 and 16 kJ mol−1, and diffusion controlled is associated with E > 16 kJ mol−1. Table 3 indicates that the D–R model (R2 = 0.649–0.849) does not fit the experimental data. The value of qmax, β, and E was found to lie between 33.5–43.1, 1.06 × 10−8 to 6.27 × 10−8, and 2.82–6.85 respectively. It is evident from the Table 3 that the Langmuir model fits quite accurately with the experimental data followed by Freundlich, Temkin and D–R model respectively. The calculated value of qm obtain from Langmuir model was 84.9 mg g−1 (25 °C), 74.4 mg g−1 (35 °C) and 68.8 mg g−1 (45 °C) are significantly close to the experimental value of qm (exp) of 84.5 mg g−1 (25 °C), 73.0 mg g−1 (35 °C), and 65.7 mg g−1 (45 °C) respectively. The decreasing value of b from 0.5 to 0.1 indicates the exothermic nature of interaction while the RL value between 0.04–0.17 indicated the favorable adsorbate–adsorbent interaction. In order to substantiate the finding, non-linear Langmuir fit (supplementary addition) was obtained and the evaluated data were found to be similar to the linear fit.
3.2.5. The thermodynamic of adsorption. The thermodynamic parameters associated with adsorption of Cr(VI) on MCM-41–AEAPTMS–Fe(III)Cl, were evaluated to understand the nature of adsorption| |
ΔG° = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KD KD
| (15) |
| |
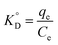 | (16) |
From the van't Hoff equation, we have
| |
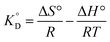 | (17) |
where ΔG° is the free energy change, entropy change (ΔS°), enthalpy change (ΔH°), associated with the adsorption process in the standard state. 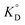 is the adsorption equilibrium constant, R is the universal gas constant (8.3104 J K−1 mol−1), T is the temperature in absolute scale, ΔH° and ΔS° are assessed from the slope and intercept of the plot of van't Hoff plot (Fig. 10) and are represented in Table 4. The exothermic nature of the adsorption process is evident by the negative value of ΔH° while chemisorption is confirmed by the higher value of ΔH° (−64.339 kJ mol−1).61 The negative value of ΔS° (−191.564 J mol−1 K−1) demonstrates that the adsorption process is accompanied by the reduction in the randomization of the Cr(VI) at the interphase of MCM-41–AEAPTMS–Fe(III) and chromium solution and is devoid of any structural change in the adsorbent.62 The spontaneous nature of the adsorption of Cr(VI) on MCM-41–AEAPTMS–Fe(III) is confirmed by the negative value of ΔG°. The progressively unfavorable nature of adsorption with increasing temperature is indicated by the diminishing value of ΔG° (Table 4).63,64 A relative adsorption capacities of different adsorbents for Cr(V) reported in previous literatures have been given in Table 5.
is the adsorption equilibrium constant, R is the universal gas constant (8.3104 J K−1 mol−1), T is the temperature in absolute scale, ΔH° and ΔS° are assessed from the slope and intercept of the plot of van't Hoff plot (Fig. 10) and are represented in Table 4. The exothermic nature of the adsorption process is evident by the negative value of ΔH° while chemisorption is confirmed by the higher value of ΔH° (−64.339 kJ mol−1).61 The negative value of ΔS° (−191.564 J mol−1 K−1) demonstrates that the adsorption process is accompanied by the reduction in the randomization of the Cr(VI) at the interphase of MCM-41–AEAPTMS–Fe(III) and chromium solution and is devoid of any structural change in the adsorbent.62 The spontaneous nature of the adsorption of Cr(VI) on MCM-41–AEAPTMS–Fe(III) is confirmed by the negative value of ΔG°. The progressively unfavorable nature of adsorption with increasing temperature is indicated by the diminishing value of ΔG° (Table 4).63,64 A relative adsorption capacities of different adsorbents for Cr(V) reported in previous literatures have been given in Table 5.
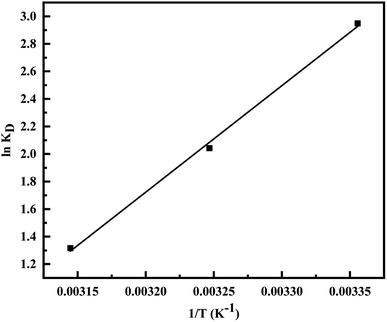 |
| | Fig. 10 van't Hoff plot for the evaluation of thermodynamic parameter. | |
Table 4 Thermodynamic parameter for the adsorption of Cr(VI) on MCM-41–AEAPTMS–Fe(III)Cl
| T (K) |
KD |
ΔG° (kJ mol−1) |
ΔH° (kJ mol−1) |
ΔS° (J mol−1 K−1) |
| 298 |
19.071 |
−7.304 |
−64.339 |
−191.564 |
| 308 |
7.705 |
−5.228 |
|
|
| 318 |
3.729 |
−3.480 |
|
|
Table 5 Comparison of adsorption capacity of Cr(VI) on MCM-41–AEAPTMS–Fe(III) with that of other adsorbents
| Sample |
Adsorption capacity (mg g−1) |
Optimum pH |
References |
| (3-Mercaptopropyl)trimethoxysilane functionalized acid-activated sepiolite (MASEP) |
7.73 |
4.7 |
64 |
| Cetyltrimethylammonium bromide stevensite (CTA-stevensite) |
10.27 |
2.0–6.0 |
65 |
| AMS–MNPs |
34.25 |
2.0 |
66 |
| m-HNTs/Fe3O4 |
49.81 |
2.0 |
67 |
| SG-AEMH |
63.3 |
4.0 |
68 |
| LDHs@MoS2 |
76.3 |
5.0 |
69 |
| EVOH/PPy nanofiber |
90.74 |
2.0 |
70 |
| MP@ZIF-8 |
136.56 |
5.0 |
71 |
| MCM-41 |
904 |
4.0 |
26 |
| TiO2–MCM-41 |
|
5.5 |
34 |
| s-MCM-41–NH2 & I-MCM-41–NH2 |
86.4 & 63.3 |
2.0 |
32 |
| EDCC–MCM |
49.044 |
2.0 |
33 |
| MCM-41–AEAPTMS–Fe(III)Cl |
84.9 |
3.0 |
This work |
3.2.6. Regeneration and reusability. Regeneration experiments were performed according to the previous report to evaluate the reusability of the adsorbent.24,72 Firstly, MCM-41–AEAPTMS–Fe(III)–Cr(VI) was regenerated by treating it with a 0.1 M HCl solution. This desorbed the Cr(VI) ions and involved the loss of some coordinated Fe(III) ion. Hence reloading of Fe(III) was performed by treating with 0.1 M FeCl3 solution and the adsorption experiment was performed using 50 mg of the adsorbent. It's found that the adsorption capacity decrease from 91.0% to 49.2% on performing 5 cycles (Fig. 11). This is due to the loss of the amine group and the subsequent loss of a substantial amount of coordinated ferric ion accountable for the capture of Cr(VI). The TEM image of the regenerated adsorbent shows that the structure of the adsorbent remains stables during the regeneration process.
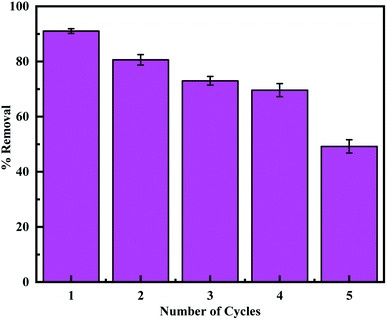 |
| | Fig. 11 The adsorption capacity of regenerated MCM-41–AEAPTMS–Fe(III) using 0.1 M HCl. | |
4. Conclusion
The SAX and IR data confirmed the synthesis of MCM-41 and the successful complexing of Fe(III) using AEAPTMS. The adsorption capacity of 84.9 mg g−1 was attained at pH 3 at 295 K and was found to increase with increasing adsorbent dosage. The adsorption of Cr(VI) on MCM-41–AEAPTMS–Fe(III)Cl followed pseudo-second-order kinetics and thermodynamic studies confirmed the exothermic nature of adsorption accompanied by reduction in the adsorption capacity with elevating temperature. The experimental data obeyed the Langmuir isotherm model with correlation coefficient approaching closer to unity. SEM-EDX data confirm the uptake Cr(VI) on Fe(III) using AEAPTMS by substituting Cl−.
Conflicts of interest
There are no conflicts of interest.
Acknowledgements
Authors thankfully acknowledge Board of Research in Nuclear Sciences (BRNS) for providing financial assistance and central instrumental facility center (CIFC), IIT(BHU) Varanasi for instrumental facilities.
References
- R. Jobby, P. Jha, A. K. Yadav and N. Desai, Chemosphere, 2018, 207, 255–266 CrossRef CAS PubMed.
- M. Costa, Crit. Rev. Toxicol., 1997, 27, 431–442 CrossRef CAS PubMed.
- Y. Xie, S. Holmgren, D. M. Andrews and M. S. Wolfe, Environ. Health Perspect., 2017, 125, 181–188 CrossRef PubMed.
- M. Li, S. Zhou, Y. Xu, Z. Liu, F. Ma, L. Zhi and X. Zhou, Chem. Eng. J., 2018, 334, 1621–1629 CrossRef CAS.
- C. M. Davis and J. B. Vincent, JBIC, J. Biol. Inorg. Chem., 1997, 2, 675–679 CrossRef CAS.
- D. M. Hausladen, A. Alexander-Ozinskas, C. McClain and S. Fendorf, Environ. Sci. Technol., 2018, 52, 8242–8251 CrossRef CAS PubMed.
- A. Elahi, I. Arooj, D. A. Bukhari and A. Rehman, Appl. Microbiol. Biotechnol., 2020, 104, 3729–3743 CrossRef CAS PubMed.
- C. Karthik, S. Barathi, A. Pugazhendhi, V. S. Ramkumar, N. B. D. Thi and P. I. Arulselvi, J. Hazard. Mater., 2017, 333, 42–53 CrossRef CAS PubMed.
- S. K. Soni, R. Singh, M. Singh, A. Awasthi, K. Wasnik and A. Kalra, Arch. Environ. Contam. Toxicol., 2014, 66, 616–627 CrossRef CAS PubMed.
- G. Lytras, C. Lytras, D. Argyropoulou, N. Dimopoulos, G. Malavetas and G. Lyberatos, J. Hazard. Mater., 2017, 336, 41–51 CrossRef CAS PubMed.
- K. Salnikow and A. Zhitkovich, Chem. Res. Toxicol., 2008, 21, 28–44 Search PubMed.
- V. Srivastava, Y. Sharma and M. Sillanpää, Appl. Surf. Sci., 2015, 326, 257–270 CrossRef CAS.
- D. Vu, Z. Li, H. Zhang, W. Wang, Z. Wang, X. Xu, B. Dong and C. Wang, J. Colloid Interface Sci., 2012, 367, 429–435 CrossRef CAS PubMed.
- P. R. Gogate and A. B. Pandit, Adv. Environ. Res., 2004, 8, 501–551 CrossRef CAS.
- M. A. Oturan and J.-J. Aaron, Crit. Rev. Environ. Sci. Technol., 2014, 44, 2577–2641 CrossRef CAS.
- X. Tian, W. Wang, Y. Wang, S. Komarneni and C. Yang, Microporous Mesoporous Mater., 2015, 207, 46–52 CrossRef CAS.
- X. Sun, L. Yang, Q. Li, Z. Liu, T. Dong and H. Liu, Chem. Eng. J., 2015, 262, 101–108 CrossRef CAS.
- X.-Q. Zhang, Y. Guo and W.-C. Li, RSC Adv., 2015, 5, 25896–25903 RSC.
- T. Liu, Z.-L. Wang, X. Yan and B. Zhang, Chem. Eng. J., 2014, 245, 34–40 CrossRef CAS.
- B. Liu and Y. Huang, J. Mater. Chem., 2011, 21, 17413–17418 RSC.
- L. J. Yu, S. S. Shukla, K. L. Dorris, A. Shukla and J. Margrave, J. Hazard. Mater., 2003, 100, 53–63 CrossRef CAS PubMed.
- B. Sarkar, R. Naidu and M. Megharaj, Water, Air, Soil Pollut., 2013, 224, 1704 CrossRef.
- V. N. Montesinos, N. Quici, E. B. Halac, A. G. Leyva, G. Custo, S. Bengio, G. Zampieri and M. I. Litter, Chem. Eng. J., 2014, 244, 569–575 CrossRef.
- K. F. Lam, K. L. Yeung and G. Mckay, Microporous Mesoporous Mater., 2007, 100, 191–201 CrossRef CAS.
- M. Ghiaci, R. Kia, A. Abbaspur and F. Seyedeyn-Azad, Sep. Purif. Technol., 2004, 40, 285–295 CrossRef CAS.
- L. Tian, G. Xie, R.-x. Li, X.-h. Yu and Y.-q. Hou, Desalin. Water Treat., 2011, 36, 334–343 CrossRef CAS.
- I. I. Slowing, J. L. Vivero-Escoto, B. G. Trewyn and V. S.-Y. Lin, J. Mater. Chem., 2010, 20, 7924–7937 RSC.
- N. A. Fellenz, I. O. P. De Berti, A. L. Soldati, S. J. Stewart, S. G. Marchetti and J. F. Bengoa, Ceram. Int., 2015, 41, 15057–15066 CrossRef CAS.
- H. Yoshitake, J. Mater. Chem., 2010, 20, 4537–4550 RSC.
- D. Pérez-Quintanilla and I. Sierra, J. Porous Mater., 2014, 21, 71–80 CrossRef.
- A. Walcarius and L. Mercier, J. Mater. Chem., 2010, 20, 4478–4511 RSC.
- N. Fellenz, F. J. Perez-Alonso, P. P. Martin, J. L. García-Fierro, J. F. Bengoa, S. G. Marchetti and S. Rojas, Microporous Mesoporous Mater., 2017, 239, 138–146 CrossRef CAS.
- B. A. Shah, A. V. Patel, M. I. Bagia and O. A. Oluyinka, J. Dispersion Sci. Technol., 2019, 40, 1827–1841 CrossRef CAS.
- K. Parida, K. G. Mishra and S. K. Dash, J. Hazard. Mater., 2012, 241, 395–403 CrossRef PubMed.
- B. Nanda, A. C. Pradhan and K. Parida, Chem. Eng. J., 2017, 316, 1122–1135 CrossRef CAS.
- T. Yokoi, T. Tatsumi and H. Yoshitake, J. Colloid Interface Sci., 2004, 274, 451–457 CrossRef CAS PubMed.
- M. Ghiaci, A. Abbaspur, R. Kia and F. Seyedeyn-Azad, Sep. Purif. Technol., 2004, 40, 217–229 CrossRef CAS.
- Q. Cai, Z.-S. Luo, W.-Q. Pang, Y.-W. Fan, X.-H. Chen and F.-Z. Cui, Chem. Mater., 2001, 13, 258–263 CrossRef CAS.
- C. Kresge, M. Leonowicz, W. J. Roth, J. Vartuli and J. Beck, Nature, 1992, 359, 710–712 CrossRef CAS.
- J. S. Beck, J. Vartuli, W. J. Roth, M. Leonowicz, C. Kresge, K. Schmitt, C. Chu, D. H. Olson, E. Sheppard and S. McCullen, J. Am. Chem. Soc., 1992, 114, 10834–10843 CrossRef CAS.
- F. Zheng, D. N. Tran, B. J. Busche, G. E. Fryxell, R. S. Addleman, T. S. Zemanian and C. L. Aardahl, Ind. Eng. Chem. Res., 2005, 44, 3099–3105 CrossRef CAS.
- H. Yao, Q. Ding, H. Zhou, Z. Zhao, G. Liu and G. Wang, RSC Adv., 2016, 6, 27039–27046 RSC.
- N. Bailey, D. Cummins, E. McKenzie and J. Worthington, Inorg. Chim. Acta, 1981, 50, 111–120 CrossRef CAS.
- G.-P. Tao, Q.-Y. Chen, X. Yang, K.-D. Zhao and J. Gao, Colloids Surf., B, 2011, 86, 106–110 CrossRef CAS PubMed.
- T. Joseph, S. Deshpande, S. Halligudi, A. Vinu, S. Ernst and M. Hartmann, J. Mol. Catal. A: Chem., 2003, 206, 13–21 CrossRef CAS.
- M. H. Lim, C. F. Blanford and A. Stein, J. Am. Chem. Soc., 1997, 119, 4090–4091 CrossRef CAS.
- X. Wang, K. S. Lin, J. C. Chan and S. Cheng, J. Phys. Chem. B, 2005, 109, 1763–1769 CrossRef CAS PubMed.
- W. Chouyyok, R. J. Wiacek, K. Pattamakomsan, T. Sangvanich, R. M. Grudzien, G. E. Fryxell and W. Yantasee, Environ. Sci. Technol., 2010, 44, 3073–3078 CrossRef CAS PubMed.
- K. Parida, K. G. Mishra and S. K. Dash, Ind. Eng. Chem. Res., 2012, 51, 2235–2246 CrossRef CAS.
- M. Jain, V. Garg and K. Kadirvelu, Bioresour. Technol., 2011, 102, 600–605 CrossRef CAS PubMed.
- J. Huang, M. Ye, Y. Qu, L. Chu, R. Chen, Q. He and D. Xu, J. Colloid Interface Sci., 2012, 385, 137–146 CrossRef CAS PubMed.
- V. E. Pakade, N. T. Tavengwa and L. M. Madikizela, RSC Adv., 2019, 9, 26142–26164 RSC.
- H. Demiral, I. Demiral, F. Tümsek and B. Karabacakoğlu, Chem. Eng. J., 2008, 144, 188–196 CrossRef CAS.
- S. K. Lagergren, Sven. Vetenskapsakad. Handingarl., 1898, 24, 1–39 Search PubMed.
- N. K. Hamadi, X. D. Chen, M. M. Farid and M. G. Lu, Chem. Eng. J., 2001, 84, 95–105 CrossRef CAS.
- A. Sharma and K. G. Bhattacharyya, Adsorption, 2005, 10, 327–338 CrossRef.
- E. Malkoc and Y. Nuhoglu, Sep. Purif. Technol., 2007, 54, 291–298 CrossRef CAS.
- K. R. Hall, L. C. Eagleton, A. Acrivos and T. Vermeulen, Ind. Eng. Chem. Fundam., 1966, 5, 212–223 CrossRef CAS.
- M. Temkin, Acta physicochimica URSS, 1940, 12, 327–356 CAS.
- Q. Hu and Z. Zhang, J. Mol. Liq., 2019, 277, 646–648 CrossRef CAS.
- K. R. Hall, L. C. Eagleton, A. Acrivos and T. Vermeulen, Ind. Eng. Chem. Fundam., 1966, 5, 212–223 CrossRef CAS.
- S. S. Thakur and G. S. Chauhan, Ind. Eng. Chem. Res., 2014, 53, 4838–4849 CrossRef CAS.
- T. A. Saleh, Desalin. Water Treat., 2016, 57, 10730–10744 CrossRef CAS.
- M. Maretto, R. Vignola, C. D. Williams, R. Bagatin, A. Latini and M. P. Papini, Microporous Mesoporous Mater., 2015, 203, 139–150 CrossRef CAS.
- M. Tahergorabi, A. Esrafili, M. Kermani and M. Shirzad-Siboni, Desalin. Water Treat., 2016, 57, 19834–19845 CrossRef CAS.
- A. Benhammou, A. Yaacoubi, L. Nibou and B. Tanouti, J. Hazard. Mater., 2007, 140, 104–109 CrossRef CAS PubMed.
- S. H. Araghi, M. H. Entezari and M. Chamsaz, Microporous Mesoporous Mater., 2015, 218, 101–111 CrossRef.
- K. Zhu, Y. Duan, F. Wang, P. Gao, H. Jia, C. Ma and C. Wang, Chem. Eng. J., 2017, 311, 236–246 CrossRef CAS.
- S. Nayab, H. Baig, A. Ghaffar, E. Tuncel, Z. Oluz, H. Duran and B. Yameen, RSC Adv., 2018, 8, 23963–23972 RSC.
- J. Wang, P. Wang, H. Wang, J. Dong, W. Chen, X. Wang, S. Wang, T. Hayat, A. Alsaedi and X. Wang, ACS Sustainable Chem. Eng., 2017, 5, 7165–7174 CrossRef CAS.
- K. Zhu, C. Chen, H. Xu, Y. Gao, X. Tan, A. Alsaedi and T. Hayat, ACS Sustainable Chem. Eng., 2017, 5, 6795–6802 CrossRef CAS.
- J. Lee, J.-H. Kim, K. Choi, H.-G. Kim, J.-A. Park, S.-H. Cho, S. W. Hong, J.-H. Lee, J. H. Lee and S. Lee, Sci. Rep., 2018, 8, 1–11 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra07425j |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Dhanesh Tiwari* and
Indrajit Sinha
,
Dhanesh Tiwari* and
Indrajit Sinha
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25 CTAB
0.25 CTAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.20 TMAOH
0.20 TMAOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40H2O. The pH of this gel was adjusted to 10.0 and transferred to Teflon lined autoclave and subjected heated at 100 °C for 24 h under autogenous pressure. The solid product was subsequently washed with water, dried at 80 °C, and subjected to calcination at 550 °C for 6 hours with 1° min−1 being the heating rate. This was termed as MCM-41.
40H2O. The pH of this gel was adjusted to 10.0 and transferred to Teflon lined autoclave and subjected heated at 100 °C for 24 h under autogenous pressure. The solid product was subsequently washed with water, dried at 80 °C, and subjected to calcination at 550 °C for 6 hours with 1° min−1 being the heating rate. This was termed as MCM-41.
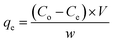
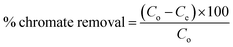
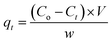
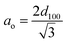




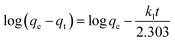
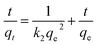
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 007.85
007.85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 699.53
699.53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 083.34
083.34
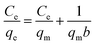
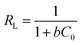
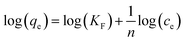
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe vs. log
qe vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce plot. Table 3 represents the Freundlich adsorption data. The positive value of n and KF are indicative of favorable adsorbate–adsorbent interaction. It is evident from the table that the linear regression coefficient (R2) is closer to unity for the Langmuir model indicating that it is better equipped to explain the adsorption process. The Temkin isotherm which is applicable at the intermediate concentration of the absorbent was employed to understand the nature of the interaction between the adsorbate and the adsorbent. It assumes that as the active sites get covered, the heat of adsorption decreases linearly.59 The model is expressed linearly as
Ce plot. Table 3 represents the Freundlich adsorption data. The positive value of n and KF are indicative of favorable adsorbate–adsorbent interaction. It is evident from the table that the linear regression coefficient (R2) is closer to unity for the Langmuir model indicating that it is better equipped to explain the adsorption process. The Temkin isotherm which is applicable at the intermediate concentration of the absorbent was employed to understand the nature of the interaction between the adsorbate and the adsorbent. It assumes that as the active sites get covered, the heat of adsorption decreases linearly.59 The model is expressed linearly as![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(KT) + BT
ln(KT) + BT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Ce)
ln(Ce)
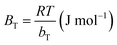 is the heat of sorption, bT = Temkin constant, KT (L g−1) is the Temkin equilibrium binding constant corresponding to maximum binding energy, R is the universal gas constant (8.314 J K−1 mol−1) and T is the temperature in absolute scale (K). It is evident from Table 3 that the (R2 = 0.870–0.965) indicating the Temkin model does not satisfactorily fits with the experimental data. The value of BT was found to 8.28–9.92 and KT was 1.30–1.78.
is the heat of sorption, bT = Temkin constant, KT (L g−1) is the Temkin equilibrium binding constant corresponding to maximum binding energy, R is the universal gas constant (8.314 J K−1 mol−1) and T is the temperature in absolute scale (K). It is evident from Table 3 that the (R2 = 0.870–0.965) indicating the Temkin model does not satisfactorily fits with the experimental data. The value of BT was found to 8.28–9.92 and KT was 1.30–1.78.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = −βε2 + ln
qe = −βε2 + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qmax
qmax
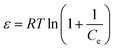
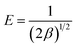
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KD
KD
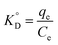
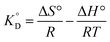
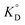 is the adsorption equilibrium constant, R is the universal gas constant (8.3104 J K−1 mol−1), T is the temperature in absolute scale, ΔH° and ΔS° are assessed from the slope and intercept of the plot of van't Hoff plot (Fig. 10) and are represented in Table 4. The exothermic nature of the adsorption process is evident by the negative value of ΔH° while chemisorption is confirmed by the higher value of ΔH° (−64.339 kJ mol−1).61 The negative value of ΔS° (−191.564 J mol−1 K−1) demonstrates that the adsorption process is accompanied by the reduction in the randomization of the Cr(VI) at the interphase of MCM-41–AEAPTMS–Fe(III) and chromium solution and is devoid of any structural change in the adsorbent.62 The spontaneous nature of the adsorption of Cr(VI) on MCM-41–AEAPTMS–Fe(III) is confirmed by the negative value of ΔG°. The progressively unfavorable nature of adsorption with increasing temperature is indicated by the diminishing value of ΔG° (Table 4).63,64 A relative adsorption capacities of different adsorbents for Cr(V) reported in previous literatures have been given in Table 5.
is the adsorption equilibrium constant, R is the universal gas constant (8.3104 J K−1 mol−1), T is the temperature in absolute scale, ΔH° and ΔS° are assessed from the slope and intercept of the plot of van't Hoff plot (Fig. 10) and are represented in Table 4. The exothermic nature of the adsorption process is evident by the negative value of ΔH° while chemisorption is confirmed by the higher value of ΔH° (−64.339 kJ mol−1).61 The negative value of ΔS° (−191.564 J mol−1 K−1) demonstrates that the adsorption process is accompanied by the reduction in the randomization of the Cr(VI) at the interphase of MCM-41–AEAPTMS–Fe(III) and chromium solution and is devoid of any structural change in the adsorbent.62 The spontaneous nature of the adsorption of Cr(VI) on MCM-41–AEAPTMS–Fe(III) is confirmed by the negative value of ΔG°. The progressively unfavorable nature of adsorption with increasing temperature is indicated by the diminishing value of ΔG° (Table 4).63,64 A relative adsorption capacities of different adsorbents for Cr(V) reported in previous literatures have been given in Table 5.






