Open Access Article
Open Access ArticleRevealing a masked Verwey transition in nanoparticles of coexisting Fe-oxide phases
David González-Alonso†
 *a,
Jesús González
*a,
Jesús González a,
Helena Gavilánb,
Jeppe Fock‡
a,
Helena Gavilánb,
Jeppe Fock‡
 c,
Lunjie Zengd,
Kerstin Witte§
e,
Philipp Bender¶
c,
Lunjie Zengd,
Kerstin Witte§
e,
Philipp Bender¶
 a,
Luis Fernández Barquín
a,
Luis Fernández Barquín a and
Christer Johanssonf
a and
Christer Johanssonf
aDepartment CITIMAC, Faculty of Science, University of Cantabria, 39005 Santander, Spain
bInstituto de Ciencia de Materiales de Madrid, ICMM/CSIC, 28049 Madrid, Spain
cTechnical University of Denmark, 2800 Kongens Lyngby, Denmark
dChalmers University of Technology, 41296 Göteborg, Sweden
eInstitute of Physics, University of Rostock, 18051 Rostock, Germany
fRISE Research Institutes of Sweden, 411 33, Göteborg, Sweden
First published on 23rd December 2020
Abstract
The attractive electronic and magnetic properties together with their biocompatibility make iron-oxide nanoparticles appear as functional materials. In Fe-oxide nanoparticle (IONP) ensembles, it is crucial to enhance their performance thanks to controlled size, shape, and stoichiometry ensembles. In light of this, we conduct a comprehensive investigation in an ensemble of ca. 28 nm cuboid-shaped IONPs in which all the analyses concur with the coexistence of magnetite/maghemite phases in their cores. Here, we are disclosing the Verwey transition by temperature dependent (4–210 K) Raman spectroscopy.
Considered as the oldest known magnetic material, magnetite (Fe3O4) has been revealed as a prototypical multifunctional material in the last decades.1–7 The renewed interest is especially connected to applications associated with the reduction of such a compound to the nanoscale. Some of its fascinating applications are related to electronics and magnetism,1–3 catalysis4,5 and especially in biomedicine,6,7 in which the use of magnetic ensembles of IONPs are gathering increasing attention. One of the reasons relies on their biocompatibility, which enables them to be used as vectors for drug delivery, therapeutic instruments for hyperthermia therapy, and contrast agents for magnetic resonance imaging.7–9
Current progress in the uniform synthesis of controllable IONPs in size and shape has unfolded their potentialities.8,10–12 To investigate their structure and magnetic properties, a variety of techniques are required. X-ray diffraction, transmission electron microscopy (TEM), dynamic light scattering, and DC-magnetization are commonly used techniques.13 It is widely known that magnetite IONPs may experience a progressive oxidation to maghemite (γ-Fe2O3) and which consequently changes their properties. However, examining the existence of magnetite within an ensemble of IONPs remains a challenging task, despite the enormous effort devoted to the study of these compounds.
The Verwey transition that characterizes magnetite could shed light on this issue.14 Though it still remains contentious,15 this complex phase transition involving magnetic, electric, and structural degrees of freedom16 is extremely sensitive to oxygen vacancies.17,18 That is the reason why it was frequently found that the characteristic Verwey transition appeared inhibited in oxidized magnetite. X-ray diffraction may help to identify magnetite,18 whereas Mössbauer spectroscopy pinpoints magnetite by quantifying the presence of Fe2+ ions in the sample.19
Recently, this transition has been positively observed in magnetite nanocrystals (above 10 nm) by different techniques, i.e., heat capacity, conductance, magnetization, nuclear magnetic resonance, and tunneling microscopy.20–22 However, the Verwey transition can be hampered depending upon the particle size and shape.11,20,23,24 The transition is not observed in small spherical IONPs, whereas it is clearly exhibited in cuboid-shaped nanoparticles (NPs) of similar size.23 We associate the masked Verwey transition in spherical Fe3O4 NPs with surface effects that not only do increase the spin disorder along with the oxygen vacancies at the surface, but also reduce the saturation magnetization.25 Additional studies show similar phenomena in IONPs with defects in their cores.26 This underlines the importance of the surface anisotropy27 to detect the Verwey transition in nanosized (4–15 nm) Fe3O4 NPs.
In this work, we are providing direct evidence of a masked Verwey transition in IONPs with coexisting Fe3O4/γ-Fe2O3 phases by Raman spectroscopy. The ensemble of IONPs has been carefully selected with a mixture of Fe3O4/γ-Fe2O3 and a controlled size and shape. To assess our findings, a thorough study has been conducted to characterize the IONPs. Additionally, other magnetite counterparts are included here to draw a complete comparison.
The IONPs were synthesized by an oxidative precipitation process described elsewhere,28,29 followed by a dextran coating procedure under high-pressure homogenization conditions. Finally, the IONPs were magnetically fractionated using a commercial magnetophoresis setup SEPMAG-Q100 system to refine size inhomogeneities.29 Transmission electron microscopy (TEM) and high-resolution transmission electron microscopy (HRTEM) were performed, respectively, in a FEI Tecnai G2 T20 (equipped with LaB6 electron gun) and a FEI Titan 80-300. In both cases the sample was prepared by depositing droplets of water-dispersed IONPs on a carbon-coated copper grid. The transmission high-energy X-ray diffraction (XRD) study was conducted in Debye–Scherrer geometry at HEMS beamline P07b located at PETRAIII (DESY), Hamburg (Germany). A Si (220) monochromator was used to select a wavelength of λ = 0.1424 Å.30,31 The diffraction pattern was collected with a Perkin Elmer image plate detector, characteristic of a resolution of 2048 × 2048 pixels and a pixel size of 200 μm, at a sample to detector distance of 1254 mm. The experimental setup was calibrated using a standard Al2O3 powder. The transmission Mössbauer spectrum was recorded at room-temperature (RT) with a built in-house Mössbauer spectrometer equipped with a 57Co source in Rh foil and operating in constant acceleration mode. Specific heat CP was measured within the temperature range 5 K ≤ T ≤ 300 K. A standard two-τ relaxation method was used to obtain the absolute value of CP in a Quantum Design PPMS-system. Prior to the CP(T) measurement, the IONPs powder was compressed into a pellet of 5 mm diameter and a thickness of ca. 1 mm. To guarantee a good thermal contact, apiezon N grease was used to stick the sample to the sample holder. Instrumental (and adhesive grease) contributions to the CP(T) signal have been subtracted. Magnetic AC-susceptibility was performed in a Quantum Design MPMS-system at a frequency of 0.5 Hz using a field amplitude of μ0Hac ≈ 0.3 mT. Unpolarized micro-Raman scattering measurements were carried out with a triple monochromator Horiba-Jobin-Yvon T64000 spectrometer in subtractive mode backscattering configuration, equipped with a Horiba Symphony liquid-nitrogen-cooled CCD detector. The 647 nm line of a Coherent Innova 70Ar+-Kr+ laser was focused on the sample with a 20× objective for micro-Raman, and the laser powder was kept below 2 mW to avoid heating effects. The laser spot was 20 μm in diameter and the spectral resolution was better than 0.6 cm−1. An Oxford Microstat He optical cryostat attached to the Raman microscope was used for temperature-dependent measurements between 4 and 210 K.
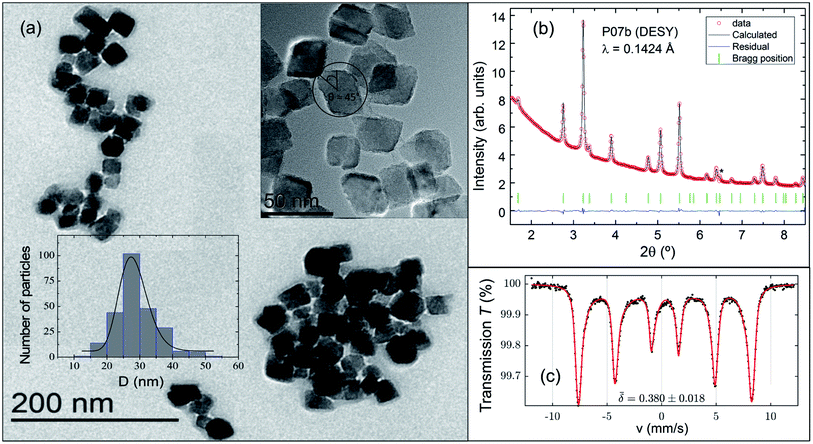
Fig. 1(a) shows a representative TEM image of an ensemble of single-core IONPs displaying a variety of aggregates ranging from 4 units up to several dozens. The synthesis method produces cuboid-shaped IOPNs with nearly monodispersed single-cores as it is illustrated in Fig. 1(a). The size-distribution was examined with TEM by counting 250 particles (see bottom-left inset of Fig. 1(a)). A number-weighted mean value of 28 nm with a standard deviation of 4 nm was obtained using a log-normal distribution.
In Fig. 1(b) we show the Rietveld refinement of the synchrotron XRD pattern using the FULLPROF program.32 It should be noted that magnetite crystallizes at RT in an inverse-spinel with a cubic Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group,33 whereas maghemite can present different crystal structures depending on the vacancy ordering.34 Bearing this in mind, the analysis satisfactorily accounts for all the reflections with a lattice parameter of a = 8.3741(1) Å. This value suggests the presence of a mixture of maghemite (γ-Fe2O3, a ≈ 8.34 Å (ref. 35)) and magnetite phases (Fe3O4, a ≈ 8.40 Å (ref. 36)) in the core of the IONPs. The main structural parameters refined at RT, together with the agreement factors, are compiled in Table 1. The average crystal-size obtained from the Rietveld refinement is slightly deviated from the size estimated with TEM by a factor of ca. 0.7. We can properly explain this mismatch by applying the correction factor proposed for cuboid-shaped NPs,37 DRietveld ≈ <DTEM>·cos(π/4), as depicted in the top-right inset of Fig. 1(a). Therefore, the average size obtained with TEM and XRD (synchrotron) is ca. 28 nm.
m space group,33 whereas maghemite can present different crystal structures depending on the vacancy ordering.34 Bearing this in mind, the analysis satisfactorily accounts for all the reflections with a lattice parameter of a = 8.3741(1) Å. This value suggests the presence of a mixture of maghemite (γ-Fe2O3, a ≈ 8.34 Å (ref. 35)) and magnetite phases (Fe3O4, a ≈ 8.40 Å (ref. 36)) in the core of the IONPs. The main structural parameters refined at RT, together with the agreement factors, are compiled in Table 1. The average crystal-size obtained from the Rietveld refinement is slightly deviated from the size estimated with TEM by a factor of ca. 0.7. We can properly explain this mismatch by applying the correction factor proposed for cuboid-shaped NPs,37 DRietveld ≈ <DTEM>·cos(π/4), as depicted in the top-right inset of Fig. 1(a). Therefore, the average size obtained with TEM and XRD (synchrotron) is ca. 28 nm.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group at RT [FeA-site at (1/8, 1/8, 1/8), FeB-site at (1/2, 1/2, 1/2), O at (u, u, u)]. The Goodness of fit χ2 and standard agreement factors Rp, Rwp, RBragg are 3.5, 6.9%, 5.8% and 1.4%, respectively
m space group at RT [FeA-site at (1/8, 1/8, 1/8), FeB-site at (1/2, 1/2, 1/2), O at (u, u, u)]. The Goodness of fit χ2 and standard agreement factors Rp, Rwp, RBragg are 3.5, 6.9%, 5.8% and 1.4%, respectively
| Parameters | RT-values |
|---|---|
| Oxygen coordinate u | 0.2528(1) |
| Lattice parameter, a (Å) | 8.3741(1) |
| Crystal size, D (nm) | 20(1) |
| Strain, ε (0/000) | 24(3) |
Fig. 1(c) displays the Mössbauer spectrum conducted at RT. Provided the 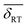 isomer-shift variation obtained from the analysis of the RT Mössbauer data, Fock and Bogart et al. showed that a quantitative evaluation of the amount of magnetite is feasible in solid-solutions of mixed maghemite-magnetite phases.19 The evaluation of the amount of magnetite is estimated through the expressions
isomer-shift variation obtained from the analysis of the RT Mössbauer data, Fock and Bogart et al. showed that a quantitative evaluation of the amount of magnetite is feasible in solid-solutions of mixed maghemite-magnetite phases.19 The evaluation of the amount of magnetite is estimated through the expressions 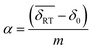 and
and 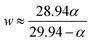 . The quantity α designates the atomic percentage of Fe2+ ions in the sample, whereas w indicates the weight percentage of magnetite. The parameters δ0 and m are evaluated to be 0.321 ± 0.002 mm s−1 and 0.21 ± 0.01 mm s−1, respectively, by the calibration-curve described in.19 In this ensemble of IONPs, the corresponding
. The quantity α designates the atomic percentage of Fe2+ ions in the sample, whereas w indicates the weight percentage of magnetite. The parameters δ0 and m are evaluated to be 0.321 ± 0.002 mm s−1 and 0.21 ± 0.01 mm s−1, respectively, by the calibration-curve described in.19 In this ensemble of IONPs, the corresponding 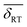 is 0.38 ± 0.02 mm s−1, and consequently a weight percentage of 28 ± 10 (wt%) in magnetite is estimated. Therefore, the structural analysis conveys that our ensemble of IONPs constitutes a good example of coexisting Fe3O4/γ-Fe2O3 phases.
is 0.38 ± 0.02 mm s−1, and consequently a weight percentage of 28 ± 10 (wt%) in magnetite is estimated. Therefore, the structural analysis conveys that our ensemble of IONPs constitutes a good example of coexisting Fe3O4/γ-Fe2O3 phases.
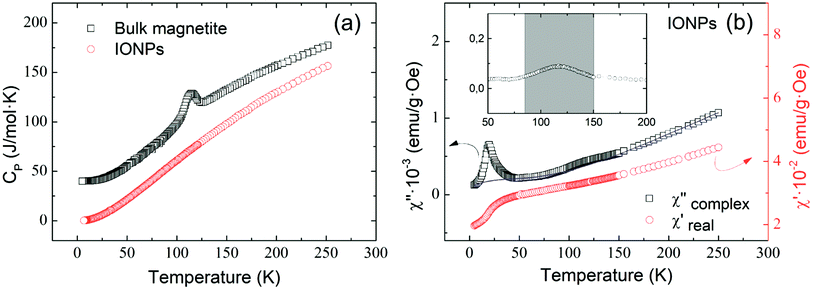
Fig. 2(a) shows the temperature dependence of specific heat for the ensemble of IONPs (red circles) and for a bulk polycrystalline magnetite sample (black squares) for comparison. It is worth noting that no distinctive peak is observed for the IONPs, whereas the bulk magnetite exhibits the characteristic peak identifying the Verwey transition at ca. 114 K.38,39 Fig. 2(b) depicts the temperature evolution of the real χ′(T) and the complex χ′′(T) components of the AC-susceptibility.16 No trace of the Verwey transition is observed neither in χ′(T) nor in zero-field-cooled DC-magnetization (not shown here). However, a low-temperature kink (below 50 K) is perceived in Fig. 2(b). This is usually associated with magnetic clustering (spin-glass-like transition) of IONPs,40 but it has also been related to spin polarization effects.41,42 Additionally, χ′′(T) exhibits an absorption peak at T ≈ 27 K that is surely connected with the mentioned magnetic clustering of IONPs. For the work presented here, it is relevant to ascertain the presence of magnetite as a very weak hump appearing centered around 120 K and illustrated in the inset of Fig. 2(b). In view of this result, we surmise that this feature provides a feeble indication of the Verwey transition in the ensemble of IONPs.15,43
Unpolarized Raman spectra recorded at temperatures well below and above the Verwey transition temperature (TV) are represented in Fig. 3(a). In the spectra, a clear peak around 670 cm−1 is visible for all temperatures between 4-210 K. This peak must be related to an active Raman mode. To understand the origin of such a peak it is necessary to briefly review the theoretical expectations governing the Raman modes. According to group theory and considering that magnetite crystallizes in a cubic inverse-spinel structure, the irreducible modes in the cubic phase at the zone center are the following:44
| Γ = A1g(R) + Eg(R) + 3T2g(R) + 2 A2u(S) + 2Eu(S) + 5T1u(IR) + 2T2u(S) | (1) |
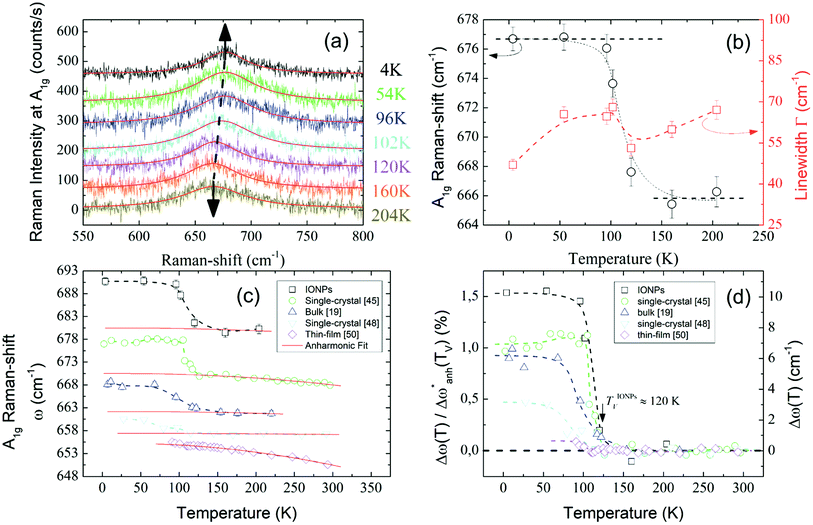 | ||
Fig. 3 (a) Raman spectra of the A1g mode. Arrows indicate the shift in the frequency. Solid red lines are the Lorentzian fits. (b) Thermal evolution of both Raman-shift (black circles) and linewidth (red squares) of the A1g mode around TV. (c) A1g Raman-shift of different samples are displayed for comparison and summarized in Table 2. Raman spectra have been vertically displaced for clarity. Solid red curves are the fits of the anharmonic contribution (d) Relative frequency change 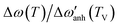 (left axis) and frequency change Δω (right axis) of the A1g mode after subtracting the harmonic term w0 and the anharmonic contributions. Dashed lines are guides to the eye. (left axis) and frequency change Δω (right axis) of the A1g mode after subtracting the harmonic term w0 and the anharmonic contributions. Dashed lines are guides to the eye. | ||
In light of the above considerations, in Fig. 3(a) the arrows are indicative of the A1g Raman-shift across TV. Solid red lines represent the fitting to a Lorentzian function, 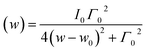 , where Γ0, ω0, and I0 are the phonon linewidth (full width at half maximum), frequency, and intensity of the Raman scattering, respectively. The frequency and linewidth of the A1g mode hallmarking the Verwey transition are clearly depicted in Fig. 3(b). The thermal evolution of the frequency shows a clear increase of ca. 10 cm−1 across TV upon cooling. Moreover, the linewidth draws a monotonous reduction down to a temperature around 110 K from which it experiences a sudden variation nearby TV.50 All these phenomena confirm the transition around TV.
, where Γ0, ω0, and I0 are the phonon linewidth (full width at half maximum), frequency, and intensity of the Raman scattering, respectively. The frequency and linewidth of the A1g mode hallmarking the Verwey transition are clearly depicted in Fig. 3(b). The thermal evolution of the frequency shows a clear increase of ca. 10 cm−1 across TV upon cooling. Moreover, the linewidth draws a monotonous reduction down to a temperature around 110 K from which it experiences a sudden variation nearby TV.50 All these phenomena confirm the transition around TV.
In Fig. 3(c) we compare the A1g Raman-shift of the ensemble of IONPs with respect to other investigated magnetite samples (bulk,19 single-crystals,45,48 and thin-film50) close to TV. There, all samples show a jump in the Raman-shift at a similar temperature, however in the thin-film case, the frequency variation is extremely small in comparison. To account for the temperature dependence of the Raman-shift of a phonon, one can write:50,51
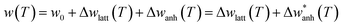 | (2) |
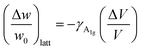 . Regarding the reported Grüneisen parameter of this mode γA1g = 0.96,52 and the small relative volume change (ΔV/V)Fe3O4 across TV that varies from ca. 0.2% (ref. 53) to 0.004%,54 this term does not explain alone the change in the frequency displayed in Fig. 3(c).
. Regarding the reported Grüneisen parameter of this mode γA1g = 0.96,52 and the small relative volume change (ΔV/V)Fe3O4 across TV that varies from ca. 0.2% (ref. 53) to 0.004%,54 this term does not explain alone the change in the frequency displayed in Fig. 3(c).
Below we perform the subtraction of the anharmonic contribution and the harmonic frequency to highlight the intrinsic change across TV. For this, we evaluate the 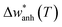 term. This term represents the anharmonic effects of phonon–phonon interactions at a constant volume, along with the harmonic frequency w0, and can be described by the following equation:55
term. This term represents the anharmonic effects of phonon–phonon interactions at a constant volume, along with the harmonic frequency w0, and can be described by the following equation:55
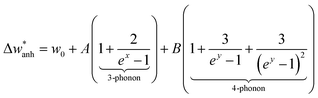 | (3) |
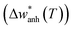 are represented by solid red lines, and their main parameters are compiled in Table 2. The fit adequately describes the behavior above the transition. However, other contributions are needed to explain the variation of the frequency below TV, e.g., electron–phonon interactions.56 The fine interpretation of these interactions is restricted to highly stoichiometric single-crystal magnetite, and is consequently beyond the scope of this work.
are represented by solid red lines, and their main parameters are compiled in Table 2. The fit adequately describes the behavior above the transition. However, other contributions are needed to explain the variation of the frequency below TV, e.g., electron–phonon interactions.56 The fine interpretation of these interactions is restricted to highly stoichiometric single-crystal magnetite, and is consequently beyond the scope of this work.
| Δω (cm−1) | Δω/w0 | TVa (K) | ΔT (K) | A (cm−1) | B (cm−1) | Fe3O4 samples |
|---|---|---|---|---|---|---|
| a TV appears to coincide with the temperature at which the frequency starts to vary upon cooling. | ||||||
| ∼10 | ∼1.5 | ∼120 | ∼11 | 1.39 | −0.92 | IONPs |
| ∼7 | ∼1.0 | ∼120 | ∼14 | 2.58 | −1.59 | Single-crystal45 |
| ∼6 | ∼0.9 | ∼114 | ∼30 | 1.37 | −0.71 | Bulk magnetite19 |
| ∼3.4 | ∼0.5 | ∼121 | ∼48 | 0.012 | −0.11 | Single-crystal48 |
| ∼0.5 | ∼0.1 | ∼119 | ∼9 | 1.1 | −2.2 | Thin-film50 |
In Fig. 3(d) we show the frequency change of the A1g mode and the relative frequency change that are respectively defined as, 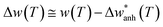 , and
, and 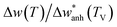 . Although it is difficult to draw a comparison among samples of different stoichiometry and shape, our ensemble of IONPs with coexisting Fe-phases exhibits a sharp phase transition at ca. 120 K with a small ΔT temperature span (see Table 2). Such a small ΔT in the IONPs is similar to the magnitudes provided in.45,50 By comparison with the magnetite samples in Table 2, the ensemble of IONPs shows the largest frequency change (ca. 10 cm−1) and relative frequency change (1.5%). Hereby, it needs to be considered that the spectral resolution is 0.6 cm−1 in the Raman-shift (see Fig. 3(b)). Hence, we surmise that the magnetite nanocrystals within the ensemble of IONPs are highly stoichiometric. We suggest that the main cause for the variety of ΔT values listed in Table 2 is caused by texture effects. This fact may merit future investigations.
. Although it is difficult to draw a comparison among samples of different stoichiometry and shape, our ensemble of IONPs with coexisting Fe-phases exhibits a sharp phase transition at ca. 120 K with a small ΔT temperature span (see Table 2). Such a small ΔT in the IONPs is similar to the magnitudes provided in.45,50 By comparison with the magnetite samples in Table 2, the ensemble of IONPs shows the largest frequency change (ca. 10 cm−1) and relative frequency change (1.5%). Hereby, it needs to be considered that the spectral resolution is 0.6 cm−1 in the Raman-shift (see Fig. 3(b)). Hence, we surmise that the magnetite nanocrystals within the ensemble of IONPs are highly stoichiometric. We suggest that the main cause for the variety of ΔT values listed in Table 2 is caused by texture effects. This fact may merit future investigations.
In conclusion, we have performed a thorough investigation and have proven that the ensemble of IONPs are constituted of coexisting Fe3O4/γ-Fe2O3 phases with an average size of ca. 28 nm. No sign of the Verwey transition was noticed either by specific heat or within the real component of the AC-susceptibility. However, an extremely feeble hump appears centered at around 120 K in χ′′(T). A temperature-dependent analysis of Raman scattering on the A1g mode has been carried out. The outcome is a conspicuous change in the frequency at around 120 K. This has allowed us to reveal the masked Verwey transition in the ensemble of IONPs. This finding highlights Raman spectroscopy as a powerful tool for the evaluation of Fe3O4 existence in iron-oxide compounds and towards the improvement of synthesis routes in ensembles of IONPs.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by EU FP7 604448 (NanoMag) and MAT2017-83631-C3-R. Dr Norbert Schell is acknowledged for the time at the HEMS beamline, and J. F. thanks MUDP (MST-141-01415).Notes and references
- R. Ramos, T. Kikkawa, K. Uchida, H. Adachi, I. Lucas, M. H. Aguirre, P. Algarabel, L. Morellón, S. Maekawa, E. Saitoh and M. R. Ibarra, Appl. Phys. Lett., 2013, 102, 072413 CrossRef.
- S. de Jong, R. Kukreja, C. Trabant, N. Pontius, C. F. Chang, T. Kachel, M. Beye, F. Sorgenfrei, C. H. Back, B. Bräuer, W. F. Schlotter, J. J. Turner, O. Krupin, M. Doehler, D. Zhu, M. A. Hossain, A. O. Scherz, D. Fausti, F. Novelli, M. Esposito, W. S. Lee, Y. D. Chuang, D. H. Lu, R. G. Moore, M. Yi, M. Trigo, P. Kirchmann, L. Pathey, M. S. Golden, M. Buchholz, P. Metcalf, F. Parmigiani, W. Wurth, A. Föhlisch, C. Schüßler-Langeheine and H. A. Dürr, Nat. Mater., 2013, 12, 882 CrossRef CAS.
- L. Zhang, W. Hou, G. Dong, Z. Zhou, S. Zhao, Z. Hu, W. Ren, M. Chen, C.-W. Nan, J. Ma, H. Zhou, W. Chen, Z.-G. Ye, Z.-D. Jiang and M. Liu, Mater. Horiz., 2018, 5, 991 RSC.
- A. Pratt, L. Lari, O. Hovorka, A. Shah, C. Woffinden, S. P. Tear, C. Binns and R. Kröger, Nat. Mater., 2014, 13, 26 CrossRef CAS.
- M. Muñoz, Z. M. de Pedro, J. A. Casas and J. J. Rodriguez, Appl. Catal., B, 2015, 176–177, 249 CrossRef.
- Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, R167 CrossRef CAS.
- B. Pelaz, C. Alexiou, R. A. Alvarez-Puebla, F. Alves, A. M. Andrews, S. Ashraf, L. P. Balogh, L. Ballerini, A. Bestetti, C. Brendel, S. Bosi, M. Carril, W. C. W. Chan, C. Chen, X. Chen, X. Chen, Z. Cheng, D. Cui, J. Du, C. Dullin, A. Escudero, N. Feliu, M. Gao, M. George, Y. Gogotsi, Z. Gu, N. J. Halas, N. Hampp, R. K. Hartmann, M. C. Hersam, P. Hunziker, J. Jian, X. Jiang, P. Jungebluth, P. Kadhiresan, K. Kataoka, A. Khademhosseini, J. Kopeček, N. A. Kotov, H. F. Krug, D. S. Lee, C. M. Lehr, K. W. Leong, X.-J. Liang, M. L. Lim, L. M. Liz-Marzán, X. Ma, P. Macchiarini, H. Meng, H. Möhwald, P. Mulvaney, A. E. Nel, S. Nie, P. Nordlander, T. Okano, J. Oliveira, T. H. Park, R. M. Penner, M. Prato, V. Puntes, V. M. Rotello, A. Samarakoon, R. E. Schaak, Y. Shen, S. Sjöqvist, A. G. Skirtach, M. G. Soliman, M. M. Stevens, H.-W. Sung, B. Z. Tang, R. Tietze, B. N. Udugama, J. S. VanEpps, T. Weil, P. S. Weiss, I. Willner, Y. Wu, L. Yang, Z. Yue, Q. Zhang, Q. Zhang, X.-E. Zhang, Y. Zhao, X. Zhou, A. Grünweller and W. J. Parak, ACS Nano, 2017, 11, 2313 CrossRef CAS.
- A. G. Roca, R. Costo, A. F. Rebolledo, S. Veintemillas-Verdaguer, P. Tartaj, T. González-Carreño, M. P. Morales and C. J. Serna, J. Phys. D: Appl. Phys., 2009, 42, 224002 CrossRef.
- P. Tartaj, M. P. Morales, T. Gonzalez-Carreño, S. Veintemillas-Verdaguer and C. J. Serna, Adv. Mater., 2011, 23, 5243 CrossRef CAS.
- S. Sun and H. Zeng, J. Am. Chem. Soc., 2002, 124, 8204 CrossRef CAS.
- J. Santoyo Salazar, L. Perez, O. de Abril, L. T. Phuoc, D. Ihiawakrim, M. Vazquez, J. M. Greneche, S. Begin-Colin and G. Pourroy, Chem. Mater., 2011, 23, 1379 CrossRef CAS.
- R. Costo, V. Bello, C. Robic, M. Port, J. Marco, M. Morales and S. Veintemillas-Verdaguer, Langmuir, 2012, 28, 178 CrossRef.
- P. Bender, L. K. Bogart, O. Posth, W. Szczerba, S. E. Rogers, A. Castro, L. Nilsson, L. J. Zeng, A. Sugunan, J. Sommertune, A. Fornara, D. González-Alonso, L. Fernández Barquín and C. Johansson, Sci. Rep., 2017, 7, 45990 CrossRef CAS.
- E. J. Verwey, Nature, 1939, 144, 327 CrossRef CAS.
- G. Perversi, E. Pachoud, J. Cumby, J. M. Hudspeth, J. P. Wright, S. A. J. Kimber and J. P. Attfield, Nat. Commun., 2019, 10, 2857 CrossRef.
- F. Walz, J. Phys.: Condens. Matter, 2002, 14, R285 CrossRef CAS.
- J. M. Honig, J. Alloys Compd., 1995, 229, 24 CrossRef CAS.
- J. B. Yang, X. D. Zhou, W. Yelon, W. J. James, Q. Cai, K. Gopalakrishnan, S. K. Malik, X. C. Sun and D. E. Nikles, J. Appl. Phys., 2004, 95, 7540 CrossRef CAS.
- J. Fock, L. K. Bogart, D. González-Alonso, J. I. Espeso, M. F. Hansen, M. Varón, C. Frandsen and Q. A. Pankhurst, J. Phys. D: Appl. Phys., 2017, 50, 265005 CrossRef.
- J. Lee, S. G. Kwon, J. G. Park and T. Hyeon, Nano Lett., 2015, 15, 4337 CrossRef CAS.
- S. Lim, B. Choi, S. Y. Lee, S. Lee, H. H. Nahm, Y. H. Kim, T. Kim, J. G. Park, J. Lee, J. Hong, S. G. Kwon and T. Hyeon, Nano Lett., 2018, 18, 1745 CrossRef CAS.
- A. Hevroni, M. Bapna, S. Piotrowski, S. A. Majetich and G. Markovich, J. Phys. Chem. Lett., 2016, 7, 1661 CrossRef CAS.
- A. Mitra, J. Mohapatra, S. S. Meena, C. V. Tomy and M. Aslam, J. Phys. Chem. C, 2014, 118, 19356 CrossRef CAS.
- H. Gavilán, O. Posth, L. K. Bogart, U. Steinhoff, L. Gutiérrez and M. Puerto Morales, Acta Mater., 2017, 125, 416 CrossRef.
- Z. Nedelkoski, D. Kepaptsoglou, L. Lari, T. Wen, R. A. Booth, S. D. Oberdick, P. L. Galindo, Q. M. Ramasse, R. F. L. Evans, S. Majetich and V. K. Lazarov, Sci. Rep., 2017, 7, 45997 CrossRef CAS.
- E. Wetterskog, C. W. Tai, J. Grins, L. Bergström and G. Salazar-Alvarez, ACS Nano, 2013, 7, 7132 CrossRef CAS.
- G. Salazar-Alvarez, J. Qin, V. Sepelák, I. Bergmann, M. Vasilakaki, K. N. Trohidou, J. D. Ardisson, W. Macedo, M. Mikhaylova, M. Muhammed, M. Baró and J. Nogués, J. Am. Chem. Soc., 2008, 130, 13234 CrossRef CAS.
- M. Andrés Vergés, R. Costo, A. Roca, J. Marco, G. Goya, C. Serna and M. P. Morales, J. Phys. D: Appl. Phys., 2008, 41, 134003 CrossRef.
- C. Grüttner, K. Müller, J. Teller, F. Westphal, A. Foreman and R. Ivkov, J. Magn. Magn. Mater., 2007, 311, 181 CrossRef.
- N. Schell, A. King, F. Beckmann, H. Ruhnau, R. Kirchhof, R. Kiehn, M. Müller and A. Schreyer, AIP Conf. Proc., 2010, 1234, 391 CrossRef CAS.
- N. Schell, A. King, F. Beckmann, T. Fischer, M. Müller and A. Schreyer, Mater. Sci. Forum, 2014, 772, 57 Search PubMed.
- J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55 CrossRef.
- M. Iizumi, T. F. Koetzle, G. Shirane, S. Chikazumi, M. Matsui and S. Todo, Acta Cryst. B, 1982, 38, 2121 CrossRef.
- C. Pecharromán, T. González-Carreño and J. E. Iglesias, Phys. Chem. Miner., 1995, 22, 21 CrossRef.
- A. N. Shmakov, G. N. Kryukova, S. V. Tsybulya, A. L. Chuvilin and L. P. Solovyeva, J. Appl. Crystallogr., 1995, 28, 141 CrossRef CAS.
- H. Okudera, K. Kihara and T. Matsumoto, Acta Crystallogr., Sect. B: Struct. Sci., 1996, 52, 450 CrossRef.
- F. Vereda, J. de Vicente, M. del Puerto Morales, F. Rull and R. Hidalgo-Álvarez, J. Phys. Chem. C, 2008, 112, 5843 CrossRef CAS.
- E. F. Westrum and F. Gronvold, J. Chem. Thermodyn., 1969, 1, 543 CrossRef CAS.
- J. P. Shepherd, J. W. Koenitzer, R. Aragón, J. Spalek and J. M. Honig, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 8461 CrossRef CAS.
- Z. Svindrych, Z. Janu, A. Kozlowski and J. M. Honig, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 214406 CrossRef.
- M. Alexe, M. Ziese, D. Hesse, P. Esquinazi, K. Yamauchi, T. Fukushima, S. Picozzi and U. Gösele, Adv. Mater., 2009, 21, 4452 CrossRef CAS.
- S. F. Alvarado, W. Eib, F. Meier, D. T. Pierce, K. Sattler, H. C. Siegmann and J. P. Remeika, Phys. Rev. Lett., 1975, 34, 319 CrossRef CAS.
- L. V. Gasparov, A. Rush, G. Güntherodt and H. Berger, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 144303 CrossRef.
- W. B. White and B. DeAngelis, Spectrochim. Acta, Part A, 1967, 23, 985 CrossRef CAS.
- L. V. Gasparov, D. B. Tanner, D. B. Romero, H. Berger, G. Margaritondo and L. Forró, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 7939 CrossRef CAS.
- J. L. Verble, Phys. Rev. B: Solid State, 1974, 9, 5236 CrossRef CAS.
- M. S. Senn, J. P. Wright and J. P. Attfield, Nature, 2012, 481, 173 CrossRef CAS.
- R. Gupta, A. K. Sood, P. Metcalf and J. M. Honig, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104430 CrossRef.
- M. S. Senn, J. P. Wright, J. Cumby and J. P. Attfield, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 024104 CrossRef.
- A. Kumar, S. Chaudhary, D. K. Pandya and S. K. Sharma, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 024302 CrossRef.
- M. Maczka, M. Ptak, K. Hermanowicz and A. Majchrowski, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 174439 CrossRef.
- O. N. Shebanova and P. Lazor, J. Chem. Phys., 2003, 119, 6100 CrossRef CAS.
- J. Wright, J. Attfield and P. Radaelli, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 214422 CrossRef.
- J. Blasco, J. García and G. Subías, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 104105 CrossRef.
- M. Balkanski, R. F. Wallis and E. Haro, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 1928 CrossRef CAS.
- E. Granado, A. García, J. A. Sanjurjo, C. Rettori, I. Torriani, F. Prado, R. D. Sánchez, A. Caneiro and S. B. Oseroff, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 11879 CrossRef CAS.
Footnotes |
| † Present address: Departament of Physics, Campus de Viesques, University of Oviedo, 33203 Gijón, Spain. |
| ‡ Present address: Blusense Diagnostics Aps, DK-2100, Denmark. |
| § Present address: Leibniz Institute for Plasma Science and Technology, Felix-Hausdorff-Str. 2, 17489 Greifswald, Germany. |
| ¶ Present address: Heinz Maier-Leibnitz Zentrum (MLZ), Technische Universität München, D-85748 Garching, Germany. |
| This journal is © The Royal Society of Chemistry 2021 |