Open Access Article
Open Access ArticleThermodynamics of the double sulfates Na2M2+(SO4)2·nH2O (M = Mg, Mn, Co, Ni, Cu, Zn, n = 2 or 4) of the blödite–kröhnkite family†
Juraj Majzlan *a,
Delyana Marinovab and
Edgar Dachsc
*a,
Delyana Marinovab and
Edgar Dachsc
aInstitute of Geosciences, Friedrich-Schiller University, Burgweg 11, 07749 Jena, Germany. E-mail: Juraj.Majzlan@uni-jena.de
bInstitute of General and Inorganic Chemistry, Bulgarian Academy of Sciences, 1113 Sofia, Bulgaria
cDepartment of Chemistry and Physics of Materials, University of Salzburg, Jakob-Haringer-Strasse 2a, 5020 Salzburg, Austria
First published on 23rd December 2020
Abstract
The double sulfates with the general formula Na2M2+(SO4)2·nH2O (M = Mg, Mn, Co, Ni, Cu, Zn, n = 2 or 4) are being considered as materials for electrodes in sodium-based batteries or as precursors for such materials. These sulfates belong structurally to the blödite (n = 4) and kröhnkite (n = 2) family and the M cations considered in this work were Mg, Mn, Co, Ni, Cu, Zn. Using a combination of calorimetric methods, we have measured enthalpies of formation and entropies of these phases, calculated their Gibbs free energies (ΔfG°) of formation and evaluated their stability with respect to Na2SO4, simple sulfates MSO4·xH2O, and liquid water, if appropriate. The ΔfG° values (all data in kJ mol−1) are: Na2Ni(SO4)2·4H2O: −3032.4 ± 1.9, Na2Mg(SO4)2·4H2O: −3432.3 ± 1.7, Na2Co(SO4)2·4H2O: −3034.4 ± 1.9, Na2Zn(SO4)2·4H2O: −3132.6 ± 1.9, Na2Mn(SO4)2·2H2O: −2727.3 ± 1.8. The data allow the stability of these phases to be assessed with respect to Na2SO4, MSO4·mH2O and H2O(l). Na2Ni(SO4)2·4H2O is stable with respect to Na2SO4, NiSO4 and H2O(l) by a significant amount of ≈50 kJ mol−1 whereas Na2Mn(SO4)2·2H2O is stable with respect to Na2SO4, MnSO4 and H2O(l) only by ≈25 kJ mol−1. The values for the other blödite–kröhnkite phases lie in between. When considering the stability with respect to higher hydrates, the stability margin decreases; for example, Na2Ni(SO4)2·4H2O is still stable with respect to Na2SO4, NiSO4·4H2O and H2O(l), but only by ≈20 kJ mol−1. Among the phases studied and chemical reactions considered, the Na–Ni phase is the most stable one, and the Na–Mn, Na–Co, and Na–Cu phases show lower stability.
1. Introduction
The most common energy storage systems are batteries whose storage capacity surpasses by far mechanical or latent-heat storage systems.1 Batteries based on lithium were developed and optimized in the last decades2 and are used widely in many modern applications. For large-scale grid application, however, their use may be restricted by limited geological reserves of lithium and earth-abundant alternatives are needed. Studies smoothly pass through the development of dual metal ion batteries and hybrid metal ion batteries.3 One of the possible solutions is the development and implementation of batteries based on sodium whose geological reserves are essentially limitless. Such a possibility is being extensively investigated.4–7 Some of the phases proposed for use in such batteries are isostructural with the minerals blödite [nominally Na2Mg(SO4)2·4H2O] and kröhnkite [nominally Na2Cu(SO4)2·2H2O].Thermodynamic stability is one of the criteria for a successful development of commercial batteries. The phases that make up the anodes and cathodes must retain their properties over many redox cycles. Natrochalcite (Na[Cu2(OH)(H2O)(SO4)2]), as an example, turns amorphous when operating as an anode, but recrystallizes back during the subsequent charge.6 H2O as a component in the batteries may be problematic because sulfates tend to be soluble and reactive towards water.8 Hence, anhydrous sulfates may be preferred9 but hydrous sulfates are being tested as well.10 Thermodynamic data suggest which phase assemblage are located energetically downhill and predict if, and with what driving force, the phases of interest for the battery development may tend to convert to other ones.
In this work, we address the question of thermodynamic properties and thermodynamic stability of a series of binary sodium-transition metal sulfates isostructural with blödite or kröhnkite. Some of them were previously tested as precursors for possible use in sodium-based batteries. The thermodynamic data were derived by a combination of acid-solution and relaxation calorimetry. Of particular interest is then the question is the title compounds have a tendency to decompose to simple sulfates.
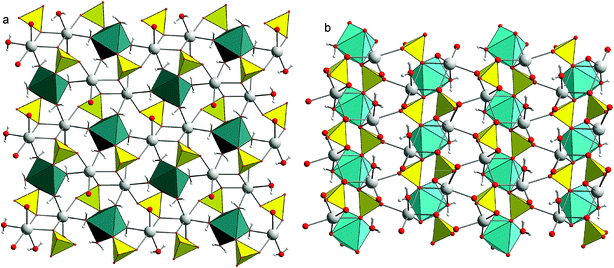
2. Crystal structures of blödite and kröhnkite
The crystal structure of blödite [Fig. 1a, nominally Na2Mg(SO4)2·4H2O]11,12 consists of [Mg(SO4)2(H2O)4]2− clusters that are interlinked by Na-centered polyhedra and hydrogen bonds. The ionic conductivity of these phases is facilitated by Na ions positioned in channels running along the [100] direction. Apart from Mg2+, the structures of this type could also incorporate divalent Fe, Co, Ni, Zn. The crystal structure of kröhnkite [Fig. 1b, nominally Na2Cu(SO4)2·2H2O]13 is more condensed than that of blödite. It consists of heteropolyhedral chains composed of CuO4(H2O)2 octahedra and sulfate tetrahedra.14,15 In kröhnkite itself, the octahedra are strongly distorted owing to the Jahn–Teller effect but these structures accept other cations that do not have the tendency to distort the octahedra.3. Experimental section
3.1. Synthesis
Syntheses of the phases investigated in this work were extensively described.16–20 The double salts Na2M2+(SO4)2·nH2O (M = Mg, Mn, Co, Ni, Cu, Zn n = 2 or 4) were obtained by crystallization from ternary solutions according to the solubility diagrams of the three-component Na2SO4–MSO4–H2O systems at 25 °C. Essentially, saturated high-temperature solutions at about 60–70 °C, were cooled subsequently to 25 °C, thereby forming a solid phase. The suspensions were stirred vigorously for 2 days until complete homogenization and then filtered. The concentration of M2+ ions was determined by different titrimetric methods of analysis and by calculations using the method of algebraic indirect identification of solid-phase compositions.3.2. Characterization
After the syntheses, but also prior to each calorimetric experiment, phase purity of the samples was tested by powder X-ray diffraction (XRD). The data were collected with a Bruker D8 ADVANCE with DAVINCI design, and with Cu Kα radiation, Ni filter, and a Lynxeye 1D detector. A step size of 0.02° 2θ and a 0.25 s time per step of were used. Lattice parameters were refined using the JANA2006 program.213.3. Calorimetric methods
For the solution calorimetric experiments at T = 25 °C, we used a commercial IMC-4400 isothermal microcalorimeter (Calorimetry Sciences Corporation) which we modified for the purposes of acid-solution calorimetry.22 The liquid bath of the calorimeter was held at a constant temperature of 298.15 K with fluctuations smaller than 0.0005 K. The calorimetric solvent was 25 g of deionized water or 25 g of 5 N HCl contained in a polyetheretherketone (PEEK) cup with a total volume of 60 mL. The cup was then closed with a PEEK screw lid and inserted into the calorimeter well. The calorimeter stabilized after ≈8 hours. During the stabilization and the experiment, the solvent was stirred by a SiO2 glass stirrer by a motor positioned about 40 cm from the active zone of the instrument. The samples were pressed into a pellet and weighed on a micro-balance with a precision of 0.002 mg (as stated by the manufacturer). The pellets were then dropped through an SiO2 glass tube into the solvent and the heat produced or consumed during the dissolution was measured. The heat flow between the reaction cup and the constant temperature reservoir was then integrated to calculate the caloric effect. A typical experiment lasted 50–60 minutes and the end of the experiment was judged from the return of the baseline to the pre-experiment position. The pellet mass of each measured phase was calculated according to the stoichiometry of the thermochemical cycle. Further details on operation, calibration, and accuracy checks can be found in.22Heat capacity was measured by relaxation calorimetry using a commercial Physical Properties Measurement System (PPMS, from Quantum Design, San Diego, California) at the University of Salzburg, Austria. With due care, accuracy can be within 1% for 5 K to 300 K, and 5% for 0.7 K to 5 K.23 Powdered samples were wrapped in a thin Al foil and compressed to produce ≈0.5 mm thick pellets, which were then placed onto the sample platform of the calorimeter for measurement.
4. Results
All samples used in this study were crystalline, with sharp peaks in their powder XRD patterns. The refined lattice parameters are summarized in Table 1. The structures corresponded to the structures previously determined for the minerals blödite12 and kröhnkite.25 The starting models for the full-profile fits were taken from these publications.| a (Å) | b (Å) | c (Å) | β (°) | V (Å3) | |
|---|---|---|---|---|---|
| Na2M(SO4)2·4H2O, space group P21/a | |||||
| M = Ni | 11.0373(7) | 8.1870(5) | 5.5302(4) | 100.503(4) | 491.35(6) |
| M = Mg | 11.1295(2) | 8.2459(2) | 5.5412(1) | 100.849(2) | 499.44(2) |
| M = Co | 11.1023(5) | 8.2471(4) | 5.5376(3) | 100.358(3) | 498.77(4) |
| M = Zn | 11.1154(9) | 8.2423(7) | 5.5406(3) | 100.738(5) | 498.72(6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Na2M(SO4)2·2H2O, space group P21/c | |||||
| M = Cu24 | 5.8054(7) | 12.659(2) | 5.5145(6) | 108.454(6) | 384.42(9) |
| M = Mn | 5.8203(6) | 12.992(2) | 5.4919(6) | 106.076(6) | 399.05(8) |
Enthalpies of dissolution in 5 N HCl, measured by acid-solution calorimetry, were converted to enthalpies of formation via the appropriate thermochemical cycles (Table 2). A suite of simple metal sulfates, metal oxides, and Na2SO4 were used as reference phases in this process.22 The dissolution of all samples was rapid and no problems were encountered during the calorimetric experiments.
| Na2M(SO4)2·nH2O = 2Na+ + M2+ + 2SO42− + nH2O | (1) |
| Na2SO4 = 2Na+ + SO42− | (2) |
| MSO4·mH2O = M2+ + SO42− + mH2O | (3) |
| MO + 2H+ = M2+ + H2O | (4) |
| H2O(l) = H2O (aq.) | (5) |
| 2Na + S + 2O2 = Na2SO4 | (6) |
| M + S + (2 + m/2)O2 + mH2 = MSO4·mH2O | (7) |
| M + (1/2)O2 = MO | (8) |
| H2 + (1/2)O2 = H2O | (9) |
| 2Na + M + 2S + (4 + n/2)O2 + nH2 = Na2M(SO4)2·nH2O | (10) |
| For a thermodynamic cycle closed with the simple metal sulfate (MSO4·mH2O, M = Mg, Ni, Co, Cu): ΔH10 = ΔfH° = −ΔH1 + ΔH2 + ΔH3 + (n–m)ΔH5 + ΔH6 + ΔH7 + (n–m)ΔH9 | |
| For a thermochemical cycle closed with the metal oxide (MO, M = Mn, Zn), MgSO4, and MgO: ΔH10 = ΔfH° = −ΔH1 + ΔH2 + ΔH3,MgSO4 + ΔH4,MO + nΔH5 − ΔH4,MgO + ΔH6 + ΔH7,MgSO4 + ΔH8,MO + nΔH9 − ΔH8,MgO |
| Dissolution/dilution enthalpies | Formation enthalpies |
|---|---|
| ΔH1,Co = ΔsolH[Na2Co(SO4)2·4H2O] = 51.62 ± 0.31(6) | |
| ΔH1,Cu = ΔsolH[Na2Cu(SO4)2·2H2O] = 54.18 ± 0.38(4) | |
| ΔH1,Mg = ΔsolH[Na2Mg(SO4)2·4H2O] = 42.21 ± 0.21(5) | |
| ΔH1,Mn = ΔsolH[Na2Mn(SO4)2·2H2O] = 37.97 ± 0.17(5) | |
| ΔH1,Ni = ΔsolH[Na2Ni(SO4)2·4H2O] = 49.27 ± 0.15(6) | |
| ΔH1,Zn = ΔsolH[Na2Zn(SO4)2·4H2O] = 65.22 ± 0.17(5) | |
| ΔH2 = ΔsolH(Na2SO4) = 21.08 ± 0.14(6) | ΔH6 = ΔfH°(Na2SO4) = −1387.8 ± 0.4 (ref. 26) |
| ΔH3,Co = ΔsolH(CoSO4·7H2O) = 44.66 ± 0.31(6) | ΔH7,Co = ΔfH°(CoSO4·7H2O) = −2979.3 ± 1.5 (ref. 27) |
| ΔH3,Cu = ΔsolH(CuSO4·5H2O) = 49.71 ± 0.19(17) | ΔH7,Cu = ΔfH°(CuSO4·5H2O) = −2279.5 ± 3.4 (ref. 27) |
| ΔH3,Mg = ΔsolH(MgSO4) = −53.50 ± 0.48(7) | ΔH7,Mg = ΔfH°(MgSO4) = −1288.64 ± 1.28 (ref. 28) |
| ΔH3,Ni = ΔsolH(NiSO4·7H2O) = 41.26 ± 0.58(9) | ΔH7,Ni = ΔfH°(NiSO4·7H2O) = −2976.8 ± 1.5 (ref. 27) |
| ΔH4,Mg = ΔsolH(MgO) = −149.68 ± 0.60(9) | ΔH8,Mg = ΔfH°(MgO) = −601.6 ± 0.3 (ref. 26) |
| ΔH4,Mn = ΔsolH(MnO) = −113.35 ± 0.05(3) | ΔH8,Mn = ΔfH°(MnO) = −385.2 ± 0.5 (ref. 26) |
| ΔH4,Zn = ΔsolH(ZnO) = −70.24 ± 0.11(4) | ΔH8,Zn = ΔfH°(ZnO) = −350.5 ± 0.3 (ref. 26) |
| ΔH5 = ΔdilutionH = −0.54 | ΔH9 = ΔfH°(H2O,l) = −285.8 ± 0.1 (ref. 26) |
Low-temperature heat capacities (Cp) were measured from 2 up to 310 K and the raw data is presented in Tables S1–Sx.† The data were fit with a set of polynomials. At low temperatures (T < 18 K), the extended Debye polynomial Cp = A3T3 + A5T5 was used for Na2M(SO4)2·nH2O with M = Co, Mg, Zn. For M = Mn and Ni, the Cp data showed low-temperature anomalies centered at 2.5 and 2.6 K, respectively (Fig. 2). These anomalies are related most likely to the magnetic properties of Mn2+ and Ni2+. Because of the low temperatures at which they are located, a full shape of the Cp anomalies was not determined. In this region for M = Mn and Ni, we used polynomials Cp = ΣApTp (with p = 1–6) for the fits. There is an additional, very small Cp anomaly at T = 15.2 in the data for M = Mn whose nature is not clear. At higher temperatures, several orthogonal polynomials Cp = ΣApTp (with p = 0–8 or 0–9) were used. The polynomials were joined and used for the determination of thermodynamic functions between 0–300 K. The results, including values of smoothed Cp and entropy at evenly spaced temperature intervals, are listed in Tables S1–S10.†
 | ||
| Fig. 2 Low-temperature heat capacity of the studied Na2M(SO4)2·nH2O phases. Note the Cp anomalies in the data for M = Ni and Mn. | ||
The enthalpies of formation and entropies of formation (Table 3) were used to calculate Gibbs free energies of formation. Auxiliary data needed for these calculations (entropies of elements in their standard state) were taken from ref. 26.
| ΔfH° kJ mol−1 | S° J mol−1 K−1 | ΔfS° J mol−1 K−1 | ΔfG° kJ mol−1 | |
|---|---|---|---|---|
| Na2Ni(SO4)2·4H2O | −3492.5 ± 1.7 | 407.3 ± 2.9 | −1543.2 ± 2.9 | −3032.4 ± 1.9 |
| Na2Mg(SO4)2·4H2O | −3896.4 ± 1.5 | 396.7 ± 2.8 | −1556.6 ± 2.8 | −3432.3 ± 1.7 |
| Na2Co(SO4)2·4H2O | −3494.0 ± 1.6 | 409.3 ± 2.9 | −1541.4 ± 2.9 | −3034.4 ± 1.9 |
| Na2Zn(SO4)2·4H2O | −3588.9 ± 1.7 | 431.8 ± 3.0 | −1530.5 ± 3.1 | −3132.6 ± 1.9 |
| Na2Cu(SO4)2·2H2O24 | −2791.7 ± 3.5 | 315.5 ± 3.8 | −1171.8 ± 3.8 | −2442.3 ± 3.6 |
| Na2Mn(SO4)2·2H2O | −3066.8 ± 1.7 | 347.4 ± 2.4 | −1138.7 ± 2.5 | −2727.3 ± 1.8 |
5. Discussion
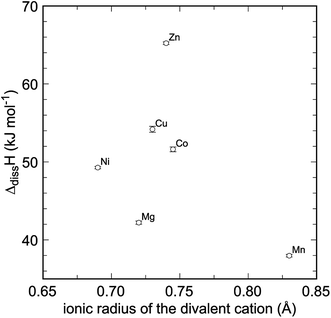
The enthalpies of dissolution of the title compounds in 5 N HCl are endothermic, with small magnitude (Table 2), as expected for hydrated sulfates. They show no linear correlation between the ionic radii (IR) of the divalent metals (Fig. 3), as reported for similar Li phases.29 With the exception of Mn2+ (IR = 0.83 Å), the ionic radii of the divalent metals considered here are fairly similar to each other. We assume that a simple relationship29 is obscured by the structural variations between the blödite- and kröhnkite-like sulfates. In addition, the introduction of H2O molecules in these structures induces structural depolymerization, as opposed to the anhydrous phases. Such depolymerization can allow relaxation of the structures and flexibility in the uptake of various divalent cations to a certain extent. Detailed studies16–20 showed that mixing is severely limited in many solid solutions of these phases and, therefore, the flexibility is also limited.There is no simple (i.e., linear) relationship between the chemical composition and formation enthalpies or Gibbs free energies. To decipher such relationship, detailed studies of the electronic structure of the title compounds, using ab initio calculations, may be needed. Such calculations are, however, beyond the scope of this contribution. Even though the question of interplay of crystal structures and thermodynamic properties is intriguing and recurring, this study cannot provide satisfactory answers to it.
Gibbs free energies of formation (Table 3) allow to evaluate the stability of the title phases quantitatively with respect to the simple sulfates. Considering the reaction
| Na2M(SO4)2·nH2O(cr) = Na2SO4·xH2O(cr) + MSO4·mH2O(cr) + (n–m–x)H2O(l) |
A set of equilibria can be evaluated. If the batteries should be operated with such phases, the presence of additional free water (aqueous solution) is unlikely. The implication for this reaction is that m < n, and hence higher hydrates are not considered in these calculations. For consistency, all Gibbs free energies of formation (ΔfG°) for the transition-metal sulfates were taken from ref. 30, even though the thermodynamic data for some systems have been updated since then, e.g.,27 The ΔfG° value for CoSO4·H2O was corrected because the values of formation enthalpy and entropy, listed by,30 do not add up to her ΔfG° for this phase. The ΔfG° values for magnesium sulfates were adopted from ref. 31 that for Na2SO4 from ref. 26.
The ΔRG° values for this reaction are graphically shown for all Na2M(SO4)2·nH2O(cr) phases in Fig. 4. We note that these values are approximate as only pure H2O(l) is considered. As mentioned above, the Na–M sulfates are highly soluble and aqueous solutions, if present, would likely have high ionic strength and affect the equilibria. Because of the uncertainties regarding the composition of such solutions and the appropriate activity-molality models, calculations involving aqueous solutions with Na, M, and sulfate as solutes were not performed here.
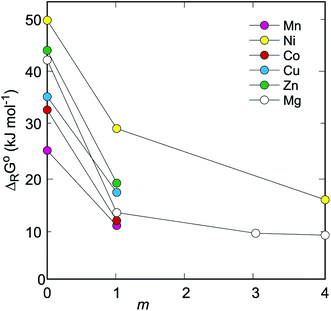 | ||
| Fig. 4 Gibbs free energies of decomposition (ΔRG°) of Na2M(SO4)2·nH2O to simple sulfates. The reaction considered is Na2M(SO4)2·nH2O(cr) → Na2SO4·xH2O(cr) + MSO4·mH2O(cr) + (n–m–x)H2O(l). For all reactions considered, x = 0 and n = 2 or 4, as specified in Tables 1 and 3. The uncertainties are smaller than the symbols. The lines that connect the individual points are only guides to the eye. | ||
6. Conclusions
All Na2M(SO4)2·nH2O phases are stable with respect to the assemblages of Na2SO4, MSO4·mH2O, and H2O(l). However, the differences among the Na2M(SO4)2·nH2O phases with different M2+ cations are significant. When considering their stability with respect to Na2SO4, MSO4, and H2O(l), the Gibbs free energies vary from ≈25 kJ mol−1 for M = Mn up to ≈50 kJ mol−1 for M = Ni. The differences, although smaller in magnitude, remain also for higher sulfates (MSO4·mH2O). For the tetrahydrates (MSO4·4H2O), the difference between M = Ni and M = Mg is only ≈7 kJ mol−1 (Fig. 4). Hence, the thermodynamic calculations document the stability of the Na2M(SO4)2·nH2O phases. They also show that the stability margin is relatively small. Should the Na2M(SO4)2·nH2O phases be decomposed during desodiation cycles, the driving force for the re-assembling of their structures is small and their recrystallization, similar to that observed for natrochalcite,6 could be problematic. From the set investigated here, the Na2Ni(SO4)2·4H2O phase is the most stable one with respect to the simple sulfates. If Na2Fe(SO4)2·2H2O should turn out as a promising candidate for the sodium batteries,7,10 the stability of the dihydrate with M = Ni should be also explored with respect to the stabilization of the materials in the batteries.Conflicts of interest
The authors declare no conflict of interest.References
- M. A. Hannan, M. M. Hoque, A. Mohamed and A. Ayob, Renewable Sustainable Energy Rev., 2017, 69, 771 CrossRef.
- M. Li, J. Lu, Z. Chen and K. Amine, Adv. Mater., 2018, 30, 1800561 CrossRef.
- R. Stoyanova, V. Koleva and A. Stoyanova, Chem. Rec., 2019, 19, 474 CrossRef CAS.
- M. Reynaud, M. Ati, S. Boulineau, M. T. Sougrati, B. C. Melot, G. Rousse, J. N. Chotard and J. M. Tarascon, ECS Trans., 2013, 50, 11 CrossRef.
- C. Masquelier and L. Croguennec, Chem. Rev., 2013, 113, 6552 CrossRef CAS.
- Z. Liu, H. J. Zhou, S. S. Ang and J. J. Zhang, Electrochim. Acta, 2016, 211, 619 CrossRef CAS.
- T. Watcharatharapong, J. T. Thienprasert, S. Chakraborty and R. Ahuja, Nano Energy, 2019, 55, 123 CrossRef CAS.
- T. Jin, H. Li, K. Zhu, P.-F. Wang, P. Liu and L. Jiao, Chem. Soc. Rev., 2020, 49, 2342 RSC.
- P. Barpanda, G. Oyama, S. Nishimura, S.-C. Chung and A. Yamada, Nat. Commun., 2014, 5, 4358 CrossRef CAS.
- P. Barpanda, G. Oyama, C. D. Ling and A. Yamada, Chem. Mater., 2014, 26, 1297 CrossRef CAS.
- M. Giglio, Acta Crystallogr., 1958, 11, 789 CrossRef CAS.
- F. C. Hawthorne, Can. Mineral., 1985, 23, 669 CAS.
- B. Dahlman, Ark. Mineral. Geol., 1952, 1, 339–366 CAS.
- M. Fleck, U. Kolitsch and B. Hertweck, Z. Kristallogr., 2002, 217, 435 CAS.
- U. Kolitsch and M. Fleck, Eur. J. Mineral., 2006, 18, 471 CrossRef CAS.
- M. Georgiev, T. Bancheva, D. Marinova, R. Stoyanova and D. Stoilova, International Journal of Scientific Research in Science and Technology, 2016, 2, 279 Search PubMed.
- M. Georgiev, D. Marinova, T. Bancheva and D. Stoilova, J. Chem. Technol. Metall., 2017, 52, 902 CAS.
- D. Marinova, M. Georgiev, T. Bancheva and D. Stoilova, International Journal of Scientific Research in Science and Technology, 2016, 2, 283 Search PubMed.
- D. Marinova, M. Georgiev, T. Bancheva, R. Stoyanova and D. Stoilova, J. Therm. Anal. Calorim., 2017, 130, 1925 CrossRef CAS.
- D. Marinova, M. Wildner, T. Bancheva, R. Stoyanova, M. Georgiev and D. G. Stoilova, Phys. Chem. Miner., 2018, 45, 801 CrossRef CAS.
- V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr., 2014, 229, 345 Search PubMed.
- J. Majzlan, Acta geol. Slovaca, 2017, 9, 171 Search PubMed.
- C. A. Kennedy, M. Stancescu, R. A. Marriott and M. A. White, Cryogenics, 2007, 47, 107 CrossRef CAS.
- J. Majzlan, A. Zittlau, K. D. Grevel, J. Schliesser, B. F. Woodfield, E. Dachs, M. Števko, J. Plášil and S. Milovská, Can. Mineral., 2015, 53, 937 CrossRef CAS.
- F. C. Hawthorne and R. B. Ferguson, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1975, 31, 1753 CrossRef.
- R. A. Robie and B. S. Hemingway, United States Geol. Surv. Bull., 1995, 2131, 461 Search PubMed.
- K. D. Grevel and J. Majzlan, Chem. Geol., 2011, 286, 301 CAS.
- R. J. Lemire, D. A. Palmer, P. Taylor and H. Schlenz, Chemical Thermodynamics of Iron, Part 2. OECD Nuclear Energy Agency, 2020, p. 921 Search PubMed.
- A. V. Radha, L. Lander, G. Rousse, J. M. Tarascon and A. Navrotsky, J. Mater. Chem. A, 2015, 3, 2601 RSC.
- C. W. DeKock, Information Circular, Bureau of Mines, 1982, 8910, p. 45 Search PubMed.
- K. D. Grevel and J. Majzlan, Geochim. Cosmochim. Acta, 2009, 73, 6805 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra09501j |
| This journal is © The Royal Society of Chemistry 2021 |