Open Access Article
Open Access ArticleEnhanced nonlinear optical response of graphene-based nanoflake van der Waals heterostructures†
Sumandeep Kaur a,
Ravindra Pandey
a,
Ravindra Pandey *a and
Shashi P. Karna*b
*a and
Shashi P. Karna*b
aDepartment of Physics, Michigan Technological University, Houghton, Michigan 49931, USA. E-mail: pandey@mtu.edu
bWeapons and Materials Research Directorate, U.S. Army Research Laboratory, ATTN: RDRL-WM, Aberdeen Proving Ground, Aberdeen, Maryland 21005-5069, USA. E-mail: shashi.p.karna.civ@mail.mil
First published on 29th January 2021
Abstract
The nonlinear optical properties of van der Waals bilayer heterostructures composed of graphene/h-BN and graphene/phosphorene nanoflakes are investigated using time-dependent density functional theory. Our calculated results show a significant enhancement of the first-hyperpolarizability value, β in heterostructures relative to the pristine nanoflakes at λ = 1064 nm. The calculated enhancement in optical nonlinearity mainly results from in-plane anisotropy induced by the interlayer electronic coupling between the adjacent nanoflake layers; a higher degree of anisotropy is induced by puckered phosphorene compared to atomically flat h-BN yielding χ(2) value corresponding to the second harmonic generation of ∼50 pm V−1 in the zigzag graphene/phosphorene bilayer heterostructure. The calculated results clearly show that graphene-based nanoflake heterostructures giving large NLO coefficients together with high electron mobility of these materials offer new opportunities as candidate materials of choice for next-generation photonics and integrated quantum technologies.
1. Introduction
In recent years, two-dimensional (2D) materials including graphene have attracted extensive research interest due to their novel properties and important applications in emerging electronics, photonics, and optoelectronics technologies. Specifically, 2D materials have been found to have large optical nonlinearities and ultra-fast optical responses and are, therefore, proposed as candidate materials for ultrafast laser systems, optical imaging, and nanophotonics.1–5 Graphene, the most prominent member of the family, exhibits ultrafast NLO response resulting from a sub pico to femtosecond carrier dynamics.6 The nonlinear effects observed in graphene now include saturable absorption,7 third-order generation,8 high-harmonic generation,9 and nonlinear Kerr effect.10In its purest, defect-free form, graphene lacks a second-order NLO response due to the inversion symmetry of its hexagonal lattice. However, a weak second harmonic generation (SHG) was observed from graphene supported on the oxidized silicon (001) due to substrate-induced symmetry breaking.11 Furthermore, calculations have shown that the application of an in-plane electric field can induce tunable second-order nonlinear susceptibility in the AB-stacked bilayer graphene.12 In trilayers, the stacking-induced SHG has been reported in ABA-stacked configuration, while no such response is observed in ABC-stacking, which retains inversion symmetry.13 In-plane anisotropy can also be induced in a hexagonal lattice of graphene by forming bilayer heterostructures of graphene with the hexagonal (h)-BN monolayer. In such a heterostructure, the interlayer interaction leads to the inequivalent carbon sublattices that, in turn, results in a non-centrosymmetric configuration.14–16
The NLO properties of the h-BN monolayer, which is an isoelectronic system with graphene, but an insulator with a large bandgap of ≈6 eV in contrasts to the gapless graphene, has been the subject of several recent theoretical17–19 and experimental20–25 investigations. A pristine h-BN sheet exhibits NLO properties.23 Theoretical calculations have emphasized the role of electron–hole-interaction,17 as well as inversion symmetry, breaking in the lattice.19 In addition to the symmetry breaking due to orientation-dependent stacking, experimental measurements have also revealed the effects of stacking order (odd–even number of layers),21 presence of mechanical stress-induced wrinkles,22 and microscopic defects,25 on enhanced SHG response of h-BN nanosheets. In fact, as a natural hyperbolic metamaterial,26 h-BN is considered an excellent material for a wide range of integrated photonic device applications.27
Among the elemental 2D materials, the recently exfoliated phosphorene, which is stable in a puckered configuration due to the preference of the hybridized sp3 orbitals over in-plane sp2 orbitals at the surface,28,29 has been shown to possess a broadband linear30 and NLO31 response from the visible to the mid-infrared region of the spectrum. Recent experiments have also observed high NLO susceptibility corresponding to four-wave mixing32 and saturation absorption33 in phosphorene.
In view of their exotic NLO properties, graphene (semimetal), phosphorene (tunable semiconductor), and h-BN (insulator) are potential candidates for tunable, broadband photonic devices, especially for power limiting and higher harmonic generation applications. Therefore, it is of interest to explore the NLO properties of these materials are brought together, i.e., when the two of them are stacked to form a heterostructure. This is what we have addressed in this paper performing a time-dependent density functional theory (TD-DFT) study of graphene/h-BN and graphene/phosphorene nanoflakes with an aim to gain an understanding of their NLO responses at λ = 1064 nm.
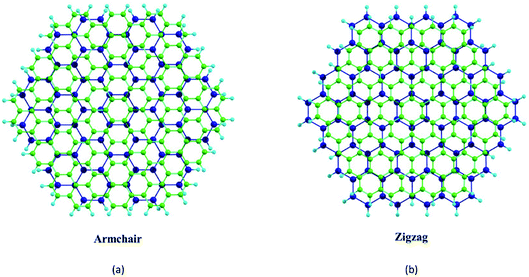
Graphene nanoflakes are well characterized by both experimental and theoretical methods.34–38 Depending upon the edge structures, they can be classified as zigzag or armchair nanoflakes. Note that graphene being zero-gap material exhibits zero optical emission, while the graphene nanoflakes are semiconducting with finite gaps. Several applications of graphene nanoflakes have been proposed, including its use in the spin-photovoltaic device,39 and tumor-targeting theranostic drug-delivery vehicles.40 Furthermore, the zigzag and armchair nanoflakes of h-BN and phosphorene were reported to be stable with finite band gaps.41–47 It is worth mentioning that both h-BN monolayer and phosphorene form stable heterostructures with graphene.48,49 Moreover, the use of h-BN instead of SiO2 as a substrate for the graphene-based devices was reported to provide better mobility and carrier inhomogeneity.50
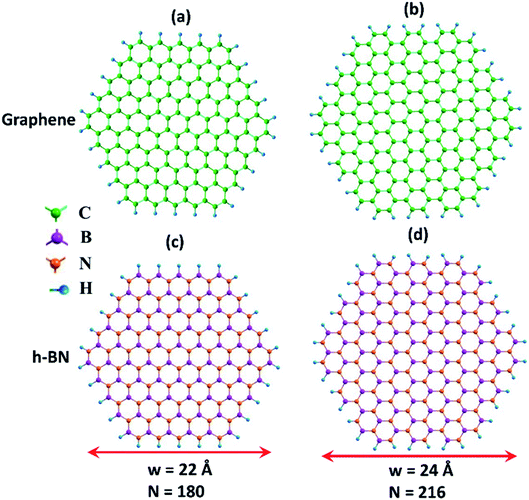
Fig. 1 shows the hexagonal-shaped nanoflakes of graphene, and h-BN in both the zigzag and armchair edge structures considered for NLO calculations. For graphene, a zigzag C150H60 nanoflake has a width of ∼22 Å, and an armchair C180H72 flake has a width of ∼24 Å. These nanoflakes are significantly larger than the C54H18 nanoflake with a width of ∼12 Å, which was predicted to be stable by the semi-empirical PM3 molecular orbital calculations.51 For the case of h-BN, the zigzag and armchair nanoflakes considered are B75N75H60 (∼22 Å) and B90N90H72 (∼24 Å), respectively. The zigzag and armchair phosphorene nanoflakes considered are of P96H24 (∼22 Å) and P84H24 (∼24 Å), respectively (Fig. S1, ESI†). Note that the edge atoms are passivated with H atoms, which has been suggested to minimize the reconstruction of its hexagonal-shaped configuration.52
The static and dynamic linear polarizability (α) and first- and second-hyperpolarizability, β, and γ, respectively, were calculated using TD-DFT theory implementation of the coupled-perturbed Hartree–Fock approach53,54 in the Gaussian 09 quantum chemistry package. Table 1 lists α calculated as 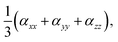 β calculated as
β calculated as 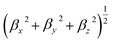 corresponding to the static β (0; 0, 0) effect, electro-optic Pockels effect, β (−ω; ω, 0), and the second harmonic generation (SHG), β (−2ω; ω, w). The second hyperpolarizability is calculated for the static case, γ (0; 0, 0, 0), optical Kerr effect (OKE) γ (−ω; ω, 0, 0), and electric field induced second harmonic generation (EFISHG) γ (−2ω; ω, ω, 0). The values of the dynamic α, β, and γ values were reported for a fundamental wavelength (λ) of 1064 nm.
corresponding to the static β (0; 0, 0) effect, electro-optic Pockels effect, β (−ω; ω, 0), and the second harmonic generation (SHG), β (−2ω; ω, w). The second hyperpolarizability is calculated for the static case, γ (0; 0, 0, 0), optical Kerr effect (OKE) γ (−ω; ω, 0, 0), and electric field induced second harmonic generation (EFISHG) γ (−2ω; ω, ω, 0). The values of the dynamic α, β, and γ values were reported for a fundamental wavelength (λ) of 1064 nm.
| Zigzag graphene nanoflake (C150H60) | Exchange and correlational functional | ||||||
|---|---|---|---|---|---|---|---|
| PBE | PBE+GD2 | B3LYP | wB97XD | M062X | PBE0+GD3 | ||
| μ (D) | 0 | 0 | 0 | 0 | 0 | 0 | |
| 〈α〉 (×10−22 esu) | (0) | 4.5 | 4.5 | 4.3 | 3.7 | 4.0 | 4.0 |
| (−ω) | 7.3 | 7.3 | 5.5 | 4.1 | 4.8 | 4.8 | |
| β (×10−33 esu) | (0) | 1.0 | 3.6 | 0.8 | 0 | 0 | 0 |
| (−ω) | 27.2 | 148.4 | 2.7 | 0 | 0 | 0 | |
| (−2ω) | 295.8 | 1184.8 | 3.0 | 0 | 0 | 0 | |
| γxxxx/γyyyy (×10−36 esu) | (0) | 2831.7 | 2822.9 | 2401.0 | 1285.0 | 1630.0 | 2134.9 |
| (−ω) | 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 419.5 419.5 |
98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 045.0 045.0 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520.0 520.0 |
2341.7 | 3438.5 | 7120.1 | |
| (−2ω) | −208![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 343.3 343.3 |
−221![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.3 298.3 |
4050.0 | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 856.6 856.6 |
−114![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 384 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 966.5 966.5 |
|
| γyyxx (×10−36 esu) | (0) | 948.0 | 940.4 | 840.0 | 428.3 | 545.3 | 715.0 |
| (−ω) | 127![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 715.3 715.3 |
97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 624.8 624.8 |
9859.0 | 1161.7 | 1814.1 | 4741.8 | |
| (−2ω) | −266![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 351.7 351.7 |
−255![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 805.0 805.0 |
2432.0 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 836.7 836.7 |
−78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 158 158 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 910.3 910.3 |
|
2. Computational method
In DFT calculations, the range-separated hybrid wB97XD exchange and correlation functional55 that incorporates a version of Grimme's dispersion term56 and long-range correction terms57 was employed. In general, the addition of the D2 dispersion term is necessary for an accurate description of the interlayer interactions in the graphene-based heterostructures.15 The 6-31G basis set as given in the Gaussian 09 program package58 was used for the constituent atoms of the nanoflake heterostructures. The convergence criteria for the RMS density matrix and total energy were set at 10−8 and 10−6 eV, respectively. For the geometry optimizations, the maximum force convergence criterion was set at 10−4 eV Å−1.To establish the suitability of the basis set for NLO calculations, we calculated the hyperpolarizability values of a graphene nanoflake using the 6-31G and 6-31G+(d,p) basis sets within the wB97XD implantation of DFT. Note that the 6-31G basis set is the spilt-valence basis set, whereas the 6-31G+(d,p) basis set is supplemented by a diffuse function together with d and p-type polarization functions on H and other heavy atoms, respectively. As listed in Table S1 (ESI†), the calculated β values for zigzag graphene nanoflake are nearly zero due to the inversion symmetry of its hexagonal lattice. The negligibly small values of β may be a result of the edge passivation of nanoflakes. The calculated γ values the correct order, γ (0) < γ (−ω) < γ (−2ω), and only show a relatively small variation in going from 6-31G to 6-31+G(d,p) basis set. Thus considering the higher computational cost involved with the latter, the split-valence 6-31G basis set appears to be adequate to provide reliable values for NLO coefficients of graphene-based nanoflakes considered in this study. It is also worthwhile to note that the split-valence basis set has been shown to provide reasonable β values for heterocyclic organic molecules including pyrrole.59
Next, we investigated the appropriateness of the exchange and correlational functionals for NLO calculations by considering additional functional forms, namely the generalized gradient approximation (PBE),60 hybrid B3LYP,61 M062X,62 and PBE0.63 In general, the PBE functional form has been shown to provide reliable values of NLO properties of small molecules64 and crystalline solids.65 However, we find that this is not the case for the zigzag graphene nanoflake (Table 1). Both the PBE and PBE+GD2 functionals yield a large β for the pristine graphene nanoflake, though it should be nearly zero by symmetry. On the other hand, the hybrid B3LYP wB97XD, PBE0+GD3, and M062X functionals yield a nearly zero value of β.
Further, as listed in Table 1, the results obtained with B3LYP do not follow the expected correct order of γ (0) < γ (−ω) < γ (−2ω). Also, the in-plane principal components, γxxxx (−2ω) and γyyyy (−2ω) predicted to be negative for PBE, PBE+GD2, M062X functionals for zigzag graphene nanoflake and the PBE0+GD3 functional form yields a negative γ (−2ω) value for armchair graphene nanoflake (Table S2 and Fig. S2, ESI†). Such discrepancies associated with the choice of the exchange and correlation functional form have been observed in previous studies66 as well. Note that the negative γ value is associated with the self-defocusing effect of incident light.67 Overall, the wB97XD functional form appears to be the appropriate choice to calculate the hyperpolarizability values of graphene-based nanoflakes.
para-Nitroaniline (p-NA) has been used in the literature68–71 to benchmark the accuracy and appropriateness of basis sets and different methods. Note that p-nitroaniline consists of a benzene ring in which a nitro group is at the para position to an amino group [Fig. S3, ESI†]. Our calculated static and frequency-dependent β values for p-NA are slightly larger than those obtained using the TDHF method68 but smaller than the corresponding values obtained using either the DFT (LDA)69 or the DFT (B3LYP)70 method. Also, it has been shown that the wB97XD functional form with the 6-311+G(d,p) basis set predicts the value of the β‖ (−2w; w, w) (i.e. component parallel to plane) to be 1032 a.u., which is in excellent agreement with the corresponding experimental value of 1072 a.u.81 Moreover, we also performed additional calculations using the M062X, and PBE0+GD3 functional forms. The results are listed in Table S3 (ESI†) showing that the β(M062X), β(wB97XD), and β(PBE0+GD3) values are nearly similar, with β(PBE0+GD3) being slightly closer to the experimental value.
Overall, the DFT values for β (λ = 1064 nm) are predicted to be in the range of 11–17 (×10−30 esu), showing good agreement with the corresponding experimental value of 15.4 (×10−30 esu) measured in the gas phase (Table S3, ESI†).71
3. Results and discussion
3.1 Pristine nanoflakes
We begin with an investigation of the stability of the pristine nanoflakes which is defined in terms of the binding energy (EB) as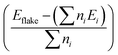 where Eflake is the total energy of the flake, ni is the number of i atoms in the flake, and Ei is the energy of the isolated i atom (e.g. C, H, B, N, or P). For the (∼22 Å) zigzag and (∼24 Å) armchair graphene nanoflakes, EB values are 8.03 and 8.05 eV per atom, respectively. For both the edge structures, the C–C and C–H bond lengths are 1.43 and 1.02 Å, respectively. A finite gap between the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) is found to be sensitive to the edges of the nanoflakes;72 a higher gap for the armchair nanoflake (∼4.4 eV) is predicted as compared to that for the zigzag nanoflake (∼3.5 eV) which displays the localized edge states [Fig. S2, ESI†].
where Eflake is the total energy of the flake, ni is the number of i atoms in the flake, and Ei is the energy of the isolated i atom (e.g. C, H, B, N, or P). For the (∼22 Å) zigzag and (∼24 Å) armchair graphene nanoflakes, EB values are 8.03 and 8.05 eV per atom, respectively. For both the edge structures, the C–C and C–H bond lengths are 1.43 and 1.02 Å, respectively. A finite gap between the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) is found to be sensitive to the edges of the nanoflakes;72 a higher gap for the armchair nanoflake (∼4.4 eV) is predicted as compared to that for the zigzag nanoflake (∼3.5 eV) which displays the localized edge states [Fig. S2, ESI†].
For h-BN nanoflakes, both the (∼22 Å) zigzag and (∼24 Å), armchair configurations have nearly the same B–N bond length of 1.45 Å, and the binding energy of 7.05 eV. The HOMO–LUMO gap of about ∼10.3 eV is found to be insensitive to the edge structure, which is in agreement with, previously reported results.73 This is also the case with (∼24 Å) zigzag and (∼22 Å) armchair phosphorene nanoflakes who do not show edge-dependent properties; the calculated P–P bond length and the binding energy values, and HOMO–LUMO gaps are 2.37 Å, ∼3.70 eV, ∼6.6 eV, respectively. Overall, the calculated values of the structural and electronic properties of graphene, BN, and phosphorene nanoflakes are in excellent agreement with previously reported values.
Table 2 lists the NLO polarizabilities of graphene, BN, and phosphorene nanoflakes. Due to the absence of inversion symmetry in the armchair graphene flake, we find that β (armchair) > β (zigzag) as expected. We also note that γxxxx = γyyyy due to the symmetry of its structure. Furthermore, γxxxx values calculated for the zigzag and armchair graphene nanoflakes are consistent with previously reported values.74,75 For example, the hybrid DFT calculations reported γxxxx to be 210 (×10−36 esu) for a (C84H24) armchair nanoflake with a width of ∼16 Å (ref. 74) compared to our wB97XD value of γxxxx of 1415 (×10−36 esu) for the (C180H72) armchair flake with a width of ∼24 Å (Table 2). For phosphorene, calculations predict relatively small values of γ, which may be associated with its puckered ground state configuration.45 Note that the delocalized π-electron cloud in graphene yields significantly higher values of γ in contrast to those in the case of h-BN and phosphorene nanoflakes.
| Zigzag | Armchair | ||||||
|---|---|---|---|---|---|---|---|
| Graphene (C150H60) | BN (B75N75H60) | Phosphorene (P96H24) | Graphene (C180H72) | BN (B90N90H72) | Phosphorene (P84H24) | ||
| Symmetry | C2H | CS | C1 | C1 | CS | C1 | |
| μ (D) | 0 | 0.1 | 0.3 | 0 | 0.1 | 0 | |
| E(HOMO–LUMO gap) (eV) | 3.9 | 10.3 | 6.6 | 4.2 | 10.3 | 6.7 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Polarizabilities | |||||||
| 〈α〉 (×10−22 esu) | (0) | 3.8 | 1.9 | 5.1 | 4.2 | 2.3 | 4.4 |
| (−ω) | 4.2 | 1.9 | 5.3 | 4.6 | 2.3 | 4.5 | |
| β (×10−33 esu) | (0) | ∼0 | 39.6 | 9.6 | 6.4 | 35 | 11.1 |
| (−ω) | ∼0 | 40.7 | 11.4 | 7.6 | 213.8 | 14.8 | |
| (−2ω) | ∼0 | 43.1 | 14.5 | 7.5 | 224.3 | 16.4 | |
| γxxxx/γyyyy (×10−36 esu) | (0) | 1285.0 | 45.0 | 95.0 | 1415.0 | 56.7 | 73.3 |
| (−ω) | 2341.7 | 48.3 | 128.3 | 2301.7 | 60.0 | 98.3 | |
| (−2ω) | 3585.0 | 55.0 | 175.0 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 665.0 665.0 |
68.3 | 135.0 | |
| γyyxx (×10−36 esu) | (0) | 428.3 | 14.9 | 31.7 | 473.3 | 18.3 | 25.0 |
| (−ω) | 1161.7 | 16.1 | 43.3 | 1013.3 | 20.0 | 33.3 | |
| (−2ω) | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 836.7 836.7 |
18.5 | 61.7 | 5490.0 | 23.3 | 48.3 | |
3.2 Nanoflake heterostructures
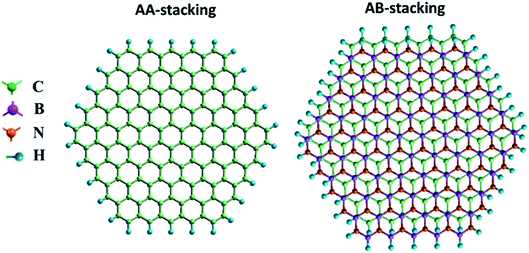 | ||
| Fig. 2 Top views of (a) AA- and (b) AB-stacked zigzag graphene/BN nanoflake heterostructures. Color code: C: green, B: purple, N: orange, H: blue. | ||
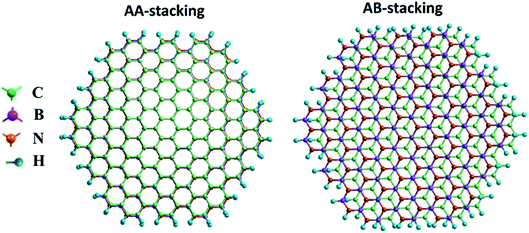 | ||
| Fig. 3 Top views of (a) AA- and (b) AB-stacked armchair graphene/BN nanoflake heterostructures. Color code: C: green, B: purple, N: orange, H: blue. | ||
For the zigzag heterostructure, the calculated interlayer binding energy of the AA-stacked and AB-stacked configurations with respect to the constituent monolayers is 0.23 eV per atom and 0.19 eV per atom, respectively. The results suggest that both stacking configurations are nearly degenerate. This is also the case with the armchair nanoflake where the energy difference between AA- and AB-stacking configurations being 6 meV. In both, the AA- and AB-stacked heterostructures, as noted earlier, the intra-layer atomic bond-distance is 1.43 Å for graphene and is 1.45 Å for the h-BN monolayer. The calculated interlayer distance for the graphene/BN heterostructure is 3.4 Å and 3.2 Å for the AA- and AB-stacked configurations, respectively. The bandgap is calculated to be 3.44 and 3.86 eV for the AA- and AB-stacked zigzag heterostructures, respectively. These values are in good agreement with the previously reported results for graphene/BN bilayer heterostructure.14
The calculated values of the NLO polarizabilities for the graphene/BN nanoflake heterostructures are listed in Table 3. β values for the heterostructure, while significantly larger than those calculated for the pristine monolayers (Fig. 4), are higher in magnitude for the AB- over AA-stacked configurations. The calculated results lack a clear trend due to the flake edge difference (zigzag vs. armchair) in the heterostructures. For example, whereas β (0) and β (−ω) for armchair bilayer are considerably larger than their values in zigzag nanoflakes, the reverse is true for β (−2ω), which has much higher magnitudes in the latter arrangement than in the former. We also note that, while the expected order in the frequency-dependent value of β, i.e. β (−2ω) > β (−ω) > β (0), is generally maintained for zigzag (AA as well as AB stacking) bilayers, the armchair nanoflakes only show this for the AB stacking. The calculation fails to predict the correct order between β (−ω) and β (−2ω) for the armchair bilayer in the AA stacking. Judging from the correct qualitative and quantitative trends predicted by the current method for PNA molecule, as discussed in the previous section, it should be pointed out that the present calculations predict considerably high β (−ω) coefficients at ∼105 × 10−33 esu for the AB-stacked graphene/BN bilayer, regardless of the edge geometry. The experimentally measurable βzzz, which is zero for the pristine nanoflakes, is calculated to be as high as ∼104 × 10−33 esu for the heterostructure.
| Graphene/BN nanoflake heterostructures | |||||
|---|---|---|---|---|---|
| Zigzag | Armchair | ||||
| AA-stacked | AB-stacked | AA-stacked | AB-stacked | ||
| Symmetry | C3V | C1 | C1 | C1 | |
| Interlayer distance, Å | 3.4 | 3.2 | 3.4 | 3.2 | |
| Interlayer binding energy, eV | 0.23 | 0.19 | 0.19 | 0.19 | |
| E(HOMO–LUMO gap), eV | 3.4 | 3.9 | 4.2 | 3.9 | |
| Dipole moment, μ (D) | 3.3 | 3.5 | 3.4 | 4.3 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Polarizabilities | |||||
| 〈α〉 (×10−22 esu) | (0) | 5.4 | 5.0 | 5.8 | 5.8 |
| (−ω) | 6.1 | 5.4 | 6.1 | 6.2 | |
| β (×10−33 esu) | (0) | 5620.8 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 521.8 521.8 |
6993.4 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 221.2 221.2 |
| (−ω) | 7116.5 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 028.1 028.1 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 539.2 539.2 |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 760.1 760.1 |
|
| (−2ω) | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504.8 504.8 |
596![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 865.1 865.1 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 657.4 657.4 |
103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 297.9 297.9 |
|
| γxxxx/γyyyy (×10−36 esu) | (0) | 1630.0 | 1043.3 | 1108.3 | 1081.7 |
| (−ω) | 4160.0 | 1988.3 | 1858.7 | 1796.7 | |
| (−2ω) | −695.0 | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 535.0 535.0 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 304.7 304.7 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 956.7 956.7 |
|
| γyyxx (×10−36 esu) | (0) | 542.6 | 335.0 | 596.7 | 588.3 |
| (−ω) | 2543.7 | 958.3 | 1083.3 | 1051.7 | |
| (−2ω) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 659.5 659.5 |
49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 201.7 201.7 |
7276.7 | 4450.0 | |
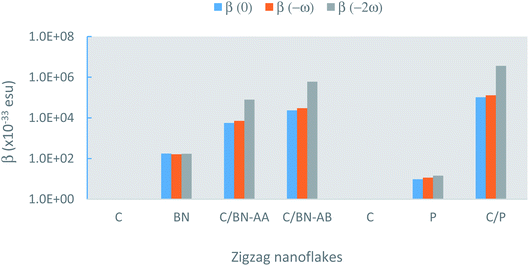 | ||
| Fig. 4 The frequency-dependent β for the pristine and zigzag bilayers calculated at a fundamental wavelength, λ of 1064 nm. C is graphene, BN is boron nitride, and P is phosphorene. | ||
Unlike β, the calculated γ coefficients exhibit a rather higher degree of consistency in magnitude with respect to the stacking as well as edge configurations, except γ (−2ω) for AA-stacked zigzag bilayer, which is calculated to have a negative value that may be associated with the self-defocusing effect of incident light.67 In general, the in-plane principal components (γxxxx/γyyyy) for the AA-stacked bilayers have larger values than their AB-stacked counterparts do, with the zigzag configuration giving higher values than the armchair. For the γyyxx component, no clear pattern emerges. This may be due to the sensitivity of third harmonics to the details of the edge-dependent gap. On the other hand, β values are inversely proportional to the energy gap given by the HOMO–LUMO gap in the present case.
 | ||
| Fig. 5 Top views of graphene/phosphorene heterostructures: (a) armchair and (b) zigzag. Color code: C: green, P: dark blue, H: light blue. | ||
Table 4 lists some of the structural and electronic properties of the graphene/phosphorene nanoflake hetero-bilayers. The zigzag and armchair configurations have nearly the same interlayer binding energy of 0.2 eV per atom, and an interlayer distance of about 3.5 Å. The calculated HOMO–LUMO gap of 3.9 and 4.2 eV for the zigzag and armchair heterostructures, respectively, exhibit a slight edge-dependence. It is also noteworthy that the calculated dipole moments are significantly larger than the dipole moments calculated for the pristine monolayer nanoflakes, suggesting an interlayer coupling-induced large asymmetric charge distribution in the heterostructures. This, in turn, results in significant enhancement of β values, which are significantly larger in magnitude compared to those predicted for graphene/BN heterostructures.
| Graphene/phosphorene nanoflake heterostructures | |||
|---|---|---|---|
| Zigzag | Armchair | ||
| Symmetry | C1 | C1 | |
| Interlayer distance, Å | 3.5 | 3.6 | |
| Interlayer binding energy, eV | 0.21 | 0.20 | |
| E (HOMO–LUMO gap) eV | 3.9 | 4.2 | |
| Dipole moment, μ (D) | 8.6 | 8.2 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Polarizabilities | |||
| 〈α〉 (×10−22 esu) | (0) | 7.3 | 7.1 |
| (−ω) | 7.7 | 7.5 | |
| β (×10−33 esu) | (0) | 102![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 595.5 595.5 |
80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 663.0 663.0 |
| (−ω) | 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010.6 010.6 |
94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 616.0 616.0 |
|
| (−2ω) | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 624 624![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 891.0 891.0 |
132![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134.0 134.0 |
|
| γxxxx/γyyyy (×10−36 esu) | (0) | 576.7 | 615.0 |
| (−ω) | 1078.3 | 1006.7 | |
| (−2ω) | −190![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 798.3 798.3 |
6452.6 | |
| γyyxx (×10−36 esu) | (0) | 190.00 | 205.0 |
| (−ω) | 525.7 | 436.7 | |
| (−2ω) | 118![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 491.2 491.2 |
3068.3 | |
It is worth mentioning that the β (−2ω) value of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 624
624![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 891 × 10−33 esu calculated for the zigzag graphene/phosphorene hetero-bilayer structure is comparable to the β (−2ω) value of the widely used NLO materials; e.g. β333 at 1064 nm for potassium titanyl phosphate (KTP) is measured76 to be 31
891 × 10−33 esu calculated for the zigzag graphene/phosphorene hetero-bilayer structure is comparable to the β (−2ω) value of the widely used NLO materials; e.g. β333 at 1064 nm for potassium titanyl phosphate (KTP) is measured76 to be 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 × 10−33 esu. In the organic crystals, one of the largest β is reported to be 2
600 × 10−33 esu. In the organic crystals, one of the largest β is reported to be 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480
480![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 × 10−33 esu associated with thiophene compounds.77,78
000 × 10−33 esu associated with thiophene compounds.77,78
The calculated results clearly show that the NLO coefficients for the graphene/phosphorene heterostructures have significantly higher values than those for graphene/BN. It can be associated with the anisotropic nature of phosphorene leading to distinctly different structural and electronic properties compared to those exhibited by the atomically flat BN nanoflakes. In phosphorene, for example, HOMO is associated with the localized (lone pair) pz orbitals, and LUMO is associated with delocalized sp3 hybridized orbitals. This is not the case with BN nanoflakes, where the frontier molecular orbitals (HOMO, LUMO) describe the delocalized multi-center bonding feature. Furthermore, we show a simplified model of the chemical bonding in the pristine graphene, h-BN monolayer, and phosphorene in Fig. S4 (ESI†). In the case of phosphorene, the lone pair electrons lead to a highly polarizable delocalized electron charge density. This is reflected in the charge density plots [Fig. S5 (ESI†)], clearly showing the delocalized nature of electron density in graphene/phosphorene heterostructure.
In general, an occurrence of the light-induced second harmonic depends on the dipole-allowed transition between frontier orbitals, facilitated by a non-centrosymmetric structure. Its magnitude depends on the transition's oscillator strength, which is determined by the extent of overlap of the electronic wave functions associated with valence and conduction bands of the material and the electronic bandgap. The degree of overlap, in a bilayer configuration, is associated with the strength of the interlayer electronic coupling between the constituent monolayers.79 This can be also verified by performing calculations of the second harmonic coefficient by varying the interlayer distance. A decrease in the interlayer distance corresponds to an increased overlap between the wave functions of the individual monolayers (i.e. strength of the interlayer electronic coupling) as reflected in the increased value of the calculated dipole moment of graphene/BN (Table S4, ESI†). The calculated results for the zigzag AA-stacked graphene/BN show that a mere 10% decrease in the interlayer distance leads to about 50% enhancement in the second harmonic coefficient (Fig. S6, ESI†).
To facilitate a comparison of the calculated β values with experiments, we now estimate the SHG intensity, defined in terms of the macroscopic second-order susceptibility, χ(2), using the following expression:80
| SHG = χ(2)/2 = ((β × 2 × π)/V)/2 | (1) |
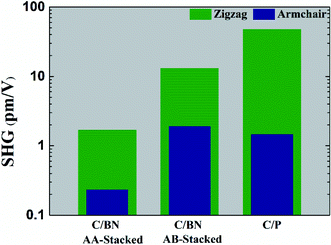
Fig. 6 displays the SHG intensity that follows the trend exhibited by β values in showing significant enhancement in heterostructures relative to pristine nanoflakes. For the zigzag case, the estimated SHG values are 2.2, 17.1, and 50 pm V−1 for AA-stacked graphene/BN, AB-stacked graphene/BN, and graphene/phosphorene heterostructures. On the other hand, the estimated SHG values are 0.3, 2.4, and 1.5 pm V−1 for AA-stacked graphene/BN, AB-stacked graphene/BN, and graphene/phosphorene armchair heterostructures. Therefore, it is worth stressing that the zigzag nanoflake heterostructures exhibit a strong SHG response, which is comparable to that exhibited by the widely used inorganic crystals, e.g. KTP.74
4. Summary
The NLO response of the graphene-based nanoflake heterostructures was investigated using time-dependent density functional theory. Since a graphene bilayer configuration is centrosymmetric, in-plane asymmetry is induced by forming the bilayer heterostructures with h-BN or phosphorene in either zigzag or armchair configurations. Test calculations on PNA and comparison with literature suggest that the wB97XD functional together with the 6-31G basis set are adequate to provide reliable values microscopic NLO coefficients.The results show that the interlayer electronic coupling of graphene with h-BN or phosphorene significantly enhances the first-order NLO response in a given nanoflake hetero-bilayer structure. Moreover, the delocalized π-electron cloud in graphene leads to significantly higher values of the second-order NLO coefficients, γ, in these heterostructures. Our study clearly shows that graphene-based nanoflake heterostructures giving large NLO coefficients together with high electron mobility of these materials offer new opportunities as candidate materials of choice for next-generation photonics and integrated quantum technologies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Michel Rérat, Dr Ashok Kumar, Dr Max Seel, Geeta Sachdeva, and Dr S. Gowtham for helpful discussions. SK acknowledges the financial support provided by Michigan Technological University. Computational resources at Michigan Technological University with SUPERIOR high-performance computing cluster were utilized. The research was partially supported by the Army Research Office (ARO) through grant number W911NF-14-2-0088.References
- X. Fengnian, H. Wang, D. Xiao, M. Dubey and A. Ramasubramaniam, Two-dimensional material nanophotonics, Nat. Photonics, 2014, 8, 899–907 CrossRef.
- M. Feng, H. Zhan and Y. Chen, Nonlinear optical and optical limiting properties of graphene families, Appl. Phys. Lett., 2010, 96, 33107 CrossRef.
- X. Liu, Q. Guo and J. Qiu, “Emerging Low-Dimensional Materials for Nonlinear Optics and Ultrafast Photonics, Adv. Mater., 2017, 29, 1605886 CrossRef.
- A. Autere and H. Jussila, et al., Nonlinear Optics with 2D Layered Materials, Adv. Mater., 2018, 30, 1705963 CrossRef.
- S. Yamashita, Nonlinear optics in a carbon nanotube, graphene, and related 2D materials, APL Photonics, 2019, 4, 034301 CrossRef.
- S. Dong, Z.-K. Wu, C. Divin, X. Li, C. Berger, W. A. de Heer, P. N. First and T. B. Norris, Ultrafast relaxation of excited Dirac fermions in epitaxial graphene using optical differential transmission spectroscopy, Phys. Rev. Lett., 2008, 101, 157402 CrossRef.
- M. Amos and Z. Sun, Nanotube and graphene saturable absorbers for fibre lasers, Nat. Photonics, 2013, 7, 842 CrossRef.
- S. Antti, L. Karvonen, J. Riikonen, W. Kim, S. Mehravar, R. A. Norwood, N. Peyghambarian, H. Lipsanen and K. Kieu, Rapid Large-Area Multiphoton Microscopy for Characterization of Graphene, ACS Nano, 2013, 7, 8441 CrossRef.
- Y. Naotaka, T. Tamaya and K. Tanaka, High-harmonic generation in graphene enhanced by elliptically polarized light excitation, Science, 2017, 356, 736 CrossRef.
- Y. Shaoliang, X. Wu, K. Chen, B. Chen, X. Guo, D. Dai, L. Tong, W. Liu and Y. R. Shen, All-optical graphene modulator based on optical Kerr phase shift, Optica, 2016, 3, 541 CrossRef.
- J. J. Dean and H. M. van Driel, Second-harmonic generation from graphene and graphitic films, Appl. Phys. Lett., 2009, 95, 261910 CrossRef.
- S. Wu, L. Mao, A. M. Jones, W. Yao, C. Zhang and X. Xu, Quantum-Enhanced Tunable Second-Order Optical Nonlinearity in Bilayer Graphene, Nano Lett., 2012, 12, 2032–2036 CrossRef CAS.
- S. Yuwei, Y. Li, D. Huang, Q. Tong, W. Yao, W.-T. Liu and S. Wu, Stacking symmetry governed second-harmonic generation in graphene trilayers, Sci. Adv., 2018, 4, eaat0074 CrossRef.
- Z. Xiaoliang, Y. K. Yap, R. Pandey and S. P. Karna, First-Principles Study of Strain-Induced Modulation of Energy Gaps of Graphene/BN and BN Bilayers, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 193403 CrossRef.
- R. Balu, X. Zhong, R. Pandey and S. P. Karna, Effect Of Electric Field On The Band Structure Of Graphene/boron Nitride And Boron Nitride/boron Nitride Bilayers, Appl. Phys. Lett., 2012, 100, 52104 CrossRef.
- X. Zhong, R. G. Amorim, R. H. Scheicher, R. Pandey and S. P. Karna, Electronic Structure And Quantum Transport Properties Of Trilayers Formed From Graphene And Boron Nitride, Nanoscale, 2012, 4, 5490 RSC.
- M. Grüning and C. Attaccalite, Second-harmonic generation in h-BN and MoS2 monolayers: Role of electron-hole interaction, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 081102 CrossRef.
- M. Grüning and C. Attaccalite, Erratum: Second-harmonic generation in h-BN and MoS2 monolayers: Role of electron-hole interaction, Physical Review B, 89, 081102(R) (2014)], Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 199901 CrossRef.
- V. A. Margulis, E. E. Muryumin and E. A. Gaiduk, Optical second-harmonic generation from two-dimensional hexagonal crystals with broken space inversion symmetry, J. Phys.: Condens. Matter, 2013, 25, 195302 CrossRef.
- Y. Li, Y. Rao, K. F. Mak, Y. You, S. Wang, C. R. Dean and T. F. Heinz, Probing symmetry properties of few-layer MoS2 and h-BN by optical second-harmonic generation, Nano Lett., 2013, 13, 3329–3333 CrossRef CAS.
- C. J. Kim, L. Brown, M. W. Graham, R. Hovden, R. W. Havener, P. L. McEuen, D. A. Muller and J. Park, Stacking order dependent second harmonic generation and topological defects in h-BN bilayers, Nano Lett., 2013, 13, 5660–5665 CrossRef CAS.
- C. K. Oliveira, E. F. Gomes, M. C. Prado, T. V. Alencar, R. Nascimento, L. M. Malard and R. J. Batista, et al., Crystal-oriented wrinkles with origami-type junctions in few-layer hexagonal boron nitride, Nano Res., 2015, 8, 1680–1688 CrossRef CAS.
- K. Pathik, A. K. Kole, C. S. Tiwary, S. Biswas, S. Vinod, J. Taha-Tijerina, U. Chatterjee and P. M. Ajayan, Nonlinear optical properties and temperature-dependent UV-vis absorption and photoluminescence emission in 2D hexagonal boron nitride nanosheets, Adv. Opt. Mater., 2015, 3, 828–835 CrossRef.
- S. Biswas, C. S. Tiwary, S. Vinod, A. K. Kole, U. Chatterjee, P. Kumbhakar and P. M. Ajayan, Nonlinear optical properties and temperature-dependent photoluminescence in hBN-GO heterostructure 2D material, J. Phys. Chem. C, 2017, 121, 8060–8069 CrossRef.
- C. Renan, A. Cadore, S. LLM Ramos, K. Watanabe, T. Taniguchi, S. Kim, A. S. Solntsev, I. Aharonovich and L. M. Malard, Second-harmonic generation in defective hexagonal boron nitride, J. Phys.: Condens. Matter, 2020, 32, 19LT01 CrossRef.
- J. D. Caldwell, A. V. Kretinin, Y. Chen, V. Giannini, M. M. Fogler, Y. Francescato, C. T. Ellis, J. G. Tischler, C. R. Woods, A. J. Giles and M. Hong, Sub-diffractional volume-confined polaritons in the natural hyperbolic material hexagonal boron nitride, Nat. Commun., 2014, 5, 1–9 Search PubMed.
- J. D. Caldwell, I. Aharonovich, G. Cassabois, J. H. Edgar, B. Gil and D. N. Basov, Photonics with hexagonal boron nitride, Nat. Rev. Mater., 2019, 4, 552–567 CrossRef CAS.
- G. Wang, W. J. Slough, R. Pandey and S. P. Karna, Degradation Of Phosphorene In Air: Understanding At Atomic Level, 2D Mater., 2016, 3, 25011 CrossRef.
- L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Black phosphorus field-effect transistors, Nat. Nanotechnol., 2014, 9, 372 CrossRef CAS.
- M. Buscema, D. J. Groenendijk, S. I. Blanter, G. A. Steele, H. S. Van Der Zant and A. Castellanos-Gomez, Fast and broadband photoresponse of few-layer black phosphorus field-effect transistors, Nano Lett., 2014, 14, 3347–3352 CrossRef CAS.
- S. B. Lu, L. L. Miao, Z. N. Guo, X. Qi, C. J. Zhao, H. Zhang, S. C. Wen, D. Y. Tang and D. Y. Fan, Broadband nonlinear optical response in multi-layer black phosphorus: an emerging infrared and mid-infrared optical material, Opt. Express, 2015, 23, 11183–11194 CrossRef CAS.
- S. Uddin, P. C. Debnath, K. Park and Y.-W. Song, Nonlinear Black Phosphorus for Ultrafast Optical Switching, Sci. Rep., 2017, 7, 43371 CrossRef.
- J. Sotor, G. Sobon, W. Macherzynski, P. Paletko and K. M. Abramski, Black phosphorus saturable absorber for ultrashort pulse generation, Appl. Phys. Lett., 2015, 107, 051108 CrossRef.
- A. M. Silva, et al., Graphene Nanoflakes: Thermal Stability, Infrared Signatures, and Potential Applications in the Field of Spintronics and Optical Nanodevices, J. Phys. Chem. C, 2010, 114, 17472 CrossRef CAS.
- A. Kuc, T. Heine and G. Seifert, Graphene nanoflakes – structural and electronic properties, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 81, 085430 CrossRef.
- W. Hu, L. Lin, C. Yang and J. Yang, Electronic Structure of Large-Scale Graphene Nanoflakes, J. Chem. Phys., 2014, 141, 214704 CrossRef.
- H. Wang, ‘Excitonic effects and optical spectra of graphene nanoflakes”, J. Appl. Phys., 2017, 122, 084301 CrossRef.
- R. Esteban-Puyuelo, R. K. Sonkar, B. Pujari, O. Grånäs and B. Sanyal, Tailoring the optoelectronic response of graphene nanoflakes by size and shape optimization, Phys. Chem. Chem. Phys., 2020, 22, 8212–8218 RSC.
- S. Zamani and R. Farghadan, Molecular spin–photovoltaic device based on a graphene nanoflake, J. Opt. Soc. Am. B, 2020, 37, 593–600 CrossRef CAS.
- J. Lamb, E. Fischer, M. Rosillo-Lopez, C. G. Salzmann and J. P. Holland, Multi-functionalised graphene nanoflakes as tumour-targeting theranostic drug-delivery vehicles, Chem. Sci., 2019, 10, 8880–8888 RSC.
- A. Yamanaka and S. Okada, Energetics and Electronic Structure of h-BN Nanoflakes, Sci. Rep., 2016, 6, 30653 CrossRef CAS.
- V. Kumar, K. Nikhil, P. Roy, D. Lahiri and I. Lahiri, Emergence of fluorescence in boron nitride nanoflakes and its application in bioimaging, RSC Adv., 2016, 6, 48025–48032 RSC.
- G.-J. Lee, M.-K. Lee, J.-J Park, D. Y. Hyeon, C. K. Jeong and K.-I. Park, Piezoelectric Energy Harvesting from Two-Dimensional Boron Nitride Nanoflakes, ACS Appl. Mater. Interfaces, 2019, 11, 37920–37926 CrossRef CAS.
- P. Bhatia, R. Swaroop and A. Kumar, Shape-dependent electronic properties of blue phosphorene nano-flakes, AIP Conf. Proc., 2016, 1728, 020598 CrossRef.
- E. M. Olmeda, C. G. Vera and S. Fomine, Electronic structure of phosphorene nanoflakes. A theoretical insight, Comput. Theor. Chem., 2018, 1130, 33–45 CrossRef CAS.
- M. Y. Bakir, H. D. Ozaydin, T. Gorkan, O. Ü. Aktürk, G. Gökoğlu, E. Aktürk and S. Ciraci, Free-standing and supported phosphorene nanoflakes: shape- and size-dependent properties, Appl. Surf. Sci., 2020, 506, 144756 CrossRef CAS.
- F. Xu, B. Ge, J. Chen, L. Xin, H. Ma, C. Zhu, W. Xia, H. Min, Z. Li, S. Li, K. Yu, L. Wu, Y. Cui, L. Sun and Y. Zhu, Scalable shear-exfoliation of high-quality phosphorene nanoflakes with reliable electrochemical cyclability in nano batteries, 2D Mater., 2016, 3, 025005 CrossRef.
- P. Järvinen, S. K. Hämäläinen, K. Banerjee, P. Häkkinen, M. Ijäs, A. Harju and P. Liljeroth, Molecular Self-Assembly on Graphene on SiO2 and h-BN Substrates, Nano Lett., 2013, 13, 3199 CrossRef.
- J. E. Padilha, A. Fazzio and A. J. R. Da Silva, Van Der Waals Heterostructure of Phosphorene and Graphene: Tuning the Schottky Barrier and Doping by Electrostatic Gating, Phys. Rev. Lett., 2015, 114, 066803 CrossRef CAS.
- J. Wang, F. Ma and M. Sun, Graphene, Hexagonal Boron Nitride, and Their Heterostructures: Properties and Applications, RSC Adv., 2017, 7, 16801 RSC.
- N. Wohner, P. K. Lam and K. Sattler, Energetic Stability of Graphene Nanoflakes and nanocones, Carbon, 2014, 67, 721–735 CrossRef CAS.
- A. Kuc, T. Heine and G. Seifert, Structural and electronic properties of graphene nanoflakes, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085430 CrossRef.
- J. E. Rice and N. C. Handy, The calculation of frequency-dependent polarizabilities as pseudo-energy derivatives, J. Chem. Phys., 1991, 94, 4959 CrossRef CAS.
- S. P. Kama and M. Dupuis, Frequency-Dependent Nonlinear Optical Properties of Molecules: Formulation and Implementation in the HONDO Program, J. Comput. Chem., 1991, 12, 487–504 CrossRef.
- U. Salznerr and A. Aydin, “Improved Prediction of Properties of π-Conjugated Oligomers with Range-Separated Hybrid Density Functionals, J. Chem. Theory Comput., 2011, 7, 2568–2583 CrossRef.
- S. Grimme, Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Long-Range Corrected Hybrid Density Functionals with Damped Atom–atom Dispersion Corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- J. Frisch, M. GAUSSIAN 09, http://www.gaussian.com/2009 Search PubMed.
- V. Keshari, M. K. P. Wijekoon, P. N. Prasad and S. P. Karna, Hyperpolarizabilities of Organic Molecules: Ab Initio Time-Dependent Coupled Perturbed Hartree-Fock-Roothaan Studies of Basic Heterocyclic Structures, J. Phys. Chem., 1995, 99, 9045–9050 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- A. D. Becke, Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 38, 3098 CrossRef.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: the PBE0 model, J. Chem. Phys., 1999, 110, 6158–6169 CrossRef CAS.
- Y. Takimoto, C. M. Isborn, B. E. Eichinger, J. J. Rehr and B. H. Robinson, Frequency and Solvent Dependence of Nonlinear Optical Properties of Molecules, J. Phys. Chem. C, 2008, 112, 8016 CrossRef CAS.
- Z. Lin, X. Jiang, L. Kang, P. Gong, S. Luo and M.-H. Lee, First-Principles Materials Applications and Design of Nonlinear Optical Crystals, J. Phys. D: Appl. Phys., 2014, 47, 253001 CrossRef.
- S. P. Karna, G. B. Talapatra, M. P. K. Wijekoon and P. N. Prasad, Frequency Dependence of Linear and Nonlinear Optical Properties of Conjugated Polyenes: An Ab Initio Time-Dependent Coupled Hartree-Fock Study, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 2763 CrossRef CAS.
- Y. Shen, The Principles of Nonlinear Optics, Wiley, New York, 1984 Search PubMed.
- S. P. Karna and P. N. Prasad, “Nonlinear optical properties of p-nitroaniline: an ab initio time-dependent coupled perturbed Hartree–Fock study, J. Chem. Phys., 1991, 94, 1177 CrossRef.
- S. J. A. van Gisbergen, J. G. Snijders and E. J. Baerends, Calculating frequency-dependent hyperpolarizabilities using time-dependent density functional theory, J. Chem. Phys. 109, 10644 (1998) – Erratum, J. Chem. Phys., 1999, 111, 6652 CrossRef CAS.
- P. Sałek, O. Vahtras, T. Helgaker and H. Ågren, Density-functional theory of linear and nonlinear time-dependent molecular properties, J. Chem. Phys., 2002, 117, 9630 CrossRef.
- P. Kaatz, E. A. Donley and D. P. Shelton, A comparison of molecular hyperpolarizabilities from gas and liquid phase measurements, J. Chem. Phys., 1998, 108, 849 CrossRef CAS.
- C. Mansilla Wettstein, F. P. Bonafé, M. B. Oviedo and C. G. Sánchez, Optical Properties of Graphene Nanoflakes: Shape Matters, J. Chem. Phys., 2016, 144, 224305 CrossRef.
- A. Yamanaka and S. Okada, Energetics and Electronic Structure of h-BN Nanoflakes, Sci. Rep., 2016, 6, 30653 CrossRef CAS.
- H. Nagai, M. Nakano, K. Yoneda, H. Fukui, T. Minami, S. Bonness, R. Kishi, H. Takahashi, T. Kubo and K. Kamada, et al., Theoretical Study on Third-Order Nonlinear Optical Properties in Hexagonal Graphene Nanoflakes: Edge Shape Effect, Chem. Phys. Lett., 2009, 477, 355 CrossRef CAS.
- K. Yoneda, H. Matsui, K. Fukuda, S. Takamuku, R. Kishi and M. Nakano, Open-Shell Characters and Second Hyperpolarizabilities for Hexagonal Graphene Nanoflakes Including Boron Nitride Domains, Chem. Phys. Lett., 2014, 595, 220 CrossRef.
- A. H. Reshak, X. Chen, S. Auluck, H. Kamarudin, J. Chyský, A. Wojciechowski and I. V. Kityk, Linear and Nonlinear Optical Susceptibilities and the Hyperpolarizability of Borate LiBaB9O15 Single-Crystal: Theory and Experiment, J. Phys. Chem. B, 2013, 117, 14141 CrossRef CAS.
- M. C. R. Castro, M. Belsley, A. M. C. Fonseca and M. M. M. Raposo, Synthesis and characterization of novel second-order NLO-chromophores bearing pyrrole as an electron donor group, Tetrahedron, 2012, 68, 8147 CrossRef CAS.
- M. Marinescu, Synthesis and nonlinear optical studies on organic compounds in laser deposited films, Appl. Surf. Sci., 2018, 1–26 Search PubMed.
- M. D. Corato, C. Cocchi, D. Prezzi, M. J. Caldas, E. Molinari and A. Ruini, Optical Properties of Bilayer Graphene Nanoflakes, J. Phys. Chem. C, 2014, 118, 23219–23225 CrossRef.
- https://www.crystal.unito.it/Manuals/crystal17.pdf.
- A. J. Garza, G. E. Scuseria, S. B. Khan and A. M. Asiri, Assessment of long-range corrected functionals for the prediction of non-linear optical properties of organic materials, Chem. Phys. Lett., 2013, 575, 122–125 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra09636a |
| This journal is © The Royal Society of Chemistry 2021 |