Open Access Article
Open Access ArticleThermal-stability of the enhanced piezoelectric, energy storage and electrocaloric properties of a lead-free BCZT ceramic†
Soukaina Merselmiz *a,
Zouhair Hanani
*a,
Zouhair Hanani abf,
Daoud Mezzaneac,
Anna G. Razumnayacd,
M'barek Amjouda,
Lahoucine Hajjia,
Svitlana Terenchuke,
Brigita Rožič
abf,
Daoud Mezzaneac,
Anna G. Razumnayacd,
M'barek Amjouda,
Lahoucine Hajjia,
Svitlana Terenchuke,
Brigita Rožič f,
Igor A. Luk'yanchukce and
Zdravko Kutnjakf
f,
Igor A. Luk'yanchukce and
Zdravko Kutnjakf
aIMED-Lab, Cadi Ayyad University, Marrakesh, 40000, Morocco. E-mail: soukaina.mers@gmail.com
bICMCB, University of Bordeaux, Pessac, 33600, France
cLPMC, University of Picardy Jules Verne, Amiens, 80039, France
dFaculty of Physics, Southern Federal University, Rostov-on-Don, 344090, Russia
eDepartment of Building Materials, Kyiv National University of Construction and Architecture, Kyiv, 03680, Ukraine
fJožef Stefan Institute, Ljubljana, 1000, Slovenia
First published on 2nd March 2021
Abstract
The lead-free Ba0.85Ca0.15Zr0.10Ti0.90O3 (BCZT) relaxor ferroelectric ceramic has aroused much attention due to its enhanced piezoelectric, energy storage and electrocaloric properties. In this study, the BCZT ceramic was elaborated by the solid-state reaction route, and the temperature-dependence of the structural, electrical, piezoelectric, energy storage and electrocaloric properties was investigated. X-ray diffraction analysis revealed a pure perovskite phase, and the temperature-dependence of Raman spectroscopy, dielectric and ferroelectric measurements revealed the phase transitions in the BCZT ceramic. At room temperature, the strain and the large-signal piezoelectric coefficient 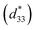 reached a maximum of 0.062% and 234 pm V−1, respectively. Furthermore, enhanced recovered energy density (Wrec = 62 mJ cm−3) and high-energy storage efficiency (η) of 72.9% at 130 °C were found. The BCZT ceramic demonstrated excellent thermal stability of the energy storage variation (ESV), less than ±5.5% in the temperature range of 30–100 °C compared to other lead-free ceramics. The electrocaloric response in the BCZT ceramic was explored via the indirect approach by using the Maxwell relation. Significant electrocaloric temperature change (ΔT) of 0.57 K over a broad temperature span (Tspan = 70 °C) and enhanced coefficient of performance (COP = 11) were obtained under 25 kV cm−1. The obtained results make the BCZT ceramic a suitable eco-friendly material for energy storage and solid-state electrocaloric cooling devices.
reached a maximum of 0.062% and 234 pm V−1, respectively. Furthermore, enhanced recovered energy density (Wrec = 62 mJ cm−3) and high-energy storage efficiency (η) of 72.9% at 130 °C were found. The BCZT ceramic demonstrated excellent thermal stability of the energy storage variation (ESV), less than ±5.5% in the temperature range of 30–100 °C compared to other lead-free ceramics. The electrocaloric response in the BCZT ceramic was explored via the indirect approach by using the Maxwell relation. Significant electrocaloric temperature change (ΔT) of 0.57 K over a broad temperature span (Tspan = 70 °C) and enhanced coefficient of performance (COP = 11) were obtained under 25 kV cm−1. The obtained results make the BCZT ceramic a suitable eco-friendly material for energy storage and solid-state electrocaloric cooling devices.
1. Introduction
Lead-based piezoceramics such as lead zirconium titanate (PbZrxTi1−xO3, PZT) systems have aroused substantial interest due to their outstanding piezoelectric, electrocaloric and energy storage performances.1–4 However, due to the environmental and human concerns caused by their toxicity, the integration of lead-based materials in future applications will be restricted.3,5,6 In 2009, Liu and Ren reported a Ba0.85Ca0.15Zr0.10Ti0.90O3 (BCZT) material with excellent electrical and piezoelectric properties as a revolutionary discovery in the field of ferroelectrics, which can substitute the Pb-based materials.7 The high piezoelectricity observed in BCZT was ascribed to the low energy barrier for polarisation rotation, i.e., energy landscape flattening at the morphotropic phase boundary.7–9The assessment of various application-relevant properties like the cost, reproducibility, electrical conductivity, and lifetime is required to transfer the lead-free piezoceramics into products.3 More important, the thermal-stability of the electrical properties over a broad operating temperature is a crucial requirement for the actual integration of the lead-free materials.3,10 For this purpose, BCZT ferroelectric relaxor can fulfil this necessity due to its diffuse ferroelectric transition.11–13 Hanani et al.11 reported the thermal-stability of the energy storage and electrocaloric properties of BCZT ceramic elaborated by low-temperature hydrothermal processing, and found a small energy storage variation (ESV) of 12.7% between 27 and 127 °C, alongside with enhanced recovered energy storage (Wrec) of 414.1 mJ cm−3 at 107 °C. In addition, Puli et al.14 investigated the energy storage performances in (1 − x)BZT–xBCT (x = 0.10, 0.15, 0.20) system and observed improved Wrec and high energy storage efficiency (η) of 680 mJ cm−3 and 72.8%, respectively, at x = 0.15 under 170 kV cm−1. Besides, Cai et al.15 studied the effect of grain size on the dielectric, ferroelectric, piezoelectric and energy storage performances, and observed that the piezoelectric coefficient (d33) gradually increases with the grain size increasing, however, despite the enhanced η, low Wrec and modest ESV were reported.
For eco-friendly solid-state refrigeration, BCZT ceramic demonstrated enhanced electrocaloric properties.13,16–21 Zhou et al.18 investigated the electrocaloric effect (ECE) in lead-free (1 − x)BZT–xBCT system under a moderate electric field of 28 kV cm−1 and reported high ECE response of 0.56 K at x = 0.6. In addition, Ben Abdessalem et al.22 studied the electrocaloric effect (ECE) in BCZT indirectly using Maxwell relation under 30 kV cm−1 and obtained ΔT = 0.565 K around TC = 119 °C. Besides, Hanani et al.11 reported a significant electrocaloric temperature change (ΔT) of 1.479 K with remarkable refrigerant capacity (RC) of 140.33 J kg−1, and a high coefficient of performance (COP = input power/output cooling power)23 of 6.29 under 55 kV cm−1.
Recently, miniaturised devices required materials with multifunctional properties, e.g., piezoelectric, electrocaloric and energy storage.24 In this study, we report, simultaneously, the thermal-stability of the piezoelectric, energy storage and electrocaloric properties of lead-free BCZT ceramic between 30 and 150 °C under 25 kV cm−1. The temperature-dependence of the structural properties in BCZT ceramic are investigated by in situ Raman spectroscopy. The electrocaloric effect in BCZT ceramic is revealed by an indirect approach through Maxwell relation.
2. Experimental section
Lead-free Ba0.85Ca0.15Zr0.1Ti0.9O3 (BCZT) ceramic was prepared by the conventional solid-state reaction route. The detailed experimental procedure and samples' characterisations are provided in Section S1 in the ESI.†3. Results and discussions
3.1 Structural properties
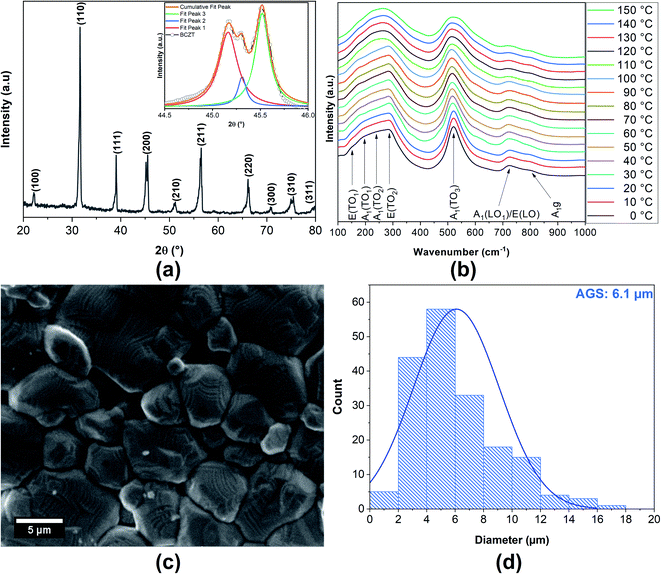
The room-temperature XRD pattern obtained for BCZT sample is displayed in Fig. 1a. The BCZT ceramic was crystallised in a pure perovskite structure without any secondary phase or impurities. The reflection peaks can be indexed according to standard BaTiO3 perovskite structures with orthorhombic (O, space group: Amm2) (PDF #75-1608) as well as tetragonal (T, space group: P4mm). The amplified XRD fitting pattern around 2θ ≈ 45° using Lorentz fitting method is plotted in the inset of the Fig. 1a. This inset clearly illustrates that BCZT sample exhibits a triplet around 45° which is attributed to (022)O/(200)T/(200)O characterising the formation of BCZT sample at the Morphotropic Phase Boundary (MPB) with the coexistence of O and T-phases.25,26The dynamic properties of BCZT sample were thoroughly investigated by Raman spectroscopy within the temperature range 0–150 °C. The results of the measurements are depicted in Fig. 1b. Below room temperature, we observe the most intensive Raman peaks at frequencies of ∼164, 210, 261, 294, 520, 724 and 800 cm−1, which correspond to the E(TO1), A1(TO1), A1(TO2), E(TO2), A1(TO3), A1(LO2)/E(LO) and A1g modes respectively. The E(TO, LO)- and A1(TO, LO)-type modes are polar and associated with the ferroelectric phase in perovskite oxides.27 On heating, their intensities steadily decrease, indicating the approach to the ferroelectric-to-paraelectric phase transition.11,13,17 Above the Curie temperature, in the cubic paraelectric phase, they disappear and only two disorder-activated broad peaks centred at 260 and 514 cm−1 are observed. It is worth noting that the A1g octahedral breathing mode at ∼800 cm−1 persisting in the whole range of the temperatures is not related with the structural distortion of the ferroelectric phase but results instead from the local distortions, caused either by the presence of B-sites occupied by cations of different sizes (Zr4+/Ti4+) or from donor A-site substitutions.13,28
The surface morphology and the grain size (GS) distribution of BCZT ceramic examined by SEM analysis are depicted in Fig. 1c and d, respectively. It is observed that the BCZT sample exhibits a compact and dense microstructure (bulk density of 5.25 g cm−3) with a non-uniform shape and dimensional grain distribution with an average grain size of 6.1 ± 3.0 μm. Also, clear grain boundaries with no porous microstructure were observed.
3.2 Dielectric properties
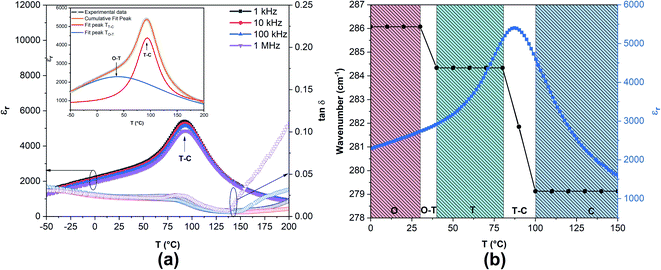
The thermal-evolution of the dielectric constant (εr) and the dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) registered in the selected frequency window from 1 kHz to 1 MHz in the temperature range of −50 to 200 °C of BCZT ceramic are plotted in Fig. 2a. The broad anomaly corresponds to the tetragonal–cubic (T–C) phase transition around the Curie point (TC = 93 °C), where εr and tan
δ) registered in the selected frequency window from 1 kHz to 1 MHz in the temperature range of −50 to 200 °C of BCZT ceramic are plotted in Fig. 2a. The broad anomaly corresponds to the tetragonal–cubic (T–C) phase transition around the Curie point (TC = 93 °C), where εr and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ reached 5400 and 0.019 at 1 kHz, respectively. The broad bump around room temperature was fitted using Lorentz fitting method to reveal the inherent O–T transition in BCZT ceramic29,30 and a broad peak at 35 °C was found as depicted in the inset of Fig. 2a. In a nutshell, the detailed analysis of temperature-dependence Raman spectroscopy can provide the evidence of the O–T and T–C phase transitions.31,32 Fig. 2b presents the thermal-evolution of the dielectric constant at 1 kHz with the peak positions of the E(TO2) Raman mode. The three apparent Raman shift plateaus correspond to the O, T and C phases, respectively, and the two drops match the O–T (<40 °C) and T–C (<100 °C) phase transitions. A typical relaxor behaviour is revealed by increasing the frequency due to the shift of the TO–T and TC peaks to the high temperatures (reminiscent of relaxor behaviour).33 The detailed discussion of the relaxor properties of BCZT ceramic is provided in Section S2 in the ESI.† Hence, BCZT ceramic exhibits a γ value of 1.74 and a degree of deviation (ΔTm) of the εr from the Curie–Weiss law above TC of 32 °C. These values indicate a strong diffused phase transition. Hanani et al.29 reported comparable values of 1.75 and 37 °C for γ and ΔTm, respectively, for the same BCZT composition.
δ reached 5400 and 0.019 at 1 kHz, respectively. The broad bump around room temperature was fitted using Lorentz fitting method to reveal the inherent O–T transition in BCZT ceramic29,30 and a broad peak at 35 °C was found as depicted in the inset of Fig. 2a. In a nutshell, the detailed analysis of temperature-dependence Raman spectroscopy can provide the evidence of the O–T and T–C phase transitions.31,32 Fig. 2b presents the thermal-evolution of the dielectric constant at 1 kHz with the peak positions of the E(TO2) Raman mode. The three apparent Raman shift plateaus correspond to the O, T and C phases, respectively, and the two drops match the O–T (<40 °C) and T–C (<100 °C) phase transitions. A typical relaxor behaviour is revealed by increasing the frequency due to the shift of the TO–T and TC peaks to the high temperatures (reminiscent of relaxor behaviour).33 The detailed discussion of the relaxor properties of BCZT ceramic is provided in Section S2 in the ESI.† Hence, BCZT ceramic exhibits a γ value of 1.74 and a degree of deviation (ΔTm) of the εr from the Curie–Weiss law above TC of 32 °C. These values indicate a strong diffused phase transition. Hanani et al.29 reported comparable values of 1.75 and 37 °C for γ and ΔTm, respectively, for the same BCZT composition.
3.3 Ferroelectric properties
The thermal-evolution of the polarisation–electric field hysteresis loops (P–E) obtained under 25 kV cm−1 and at 10 Hz for BCZT ceramic are plotted in Fig. 3a. The coercive field (Ec), the remnant polarisation (Pr) and the maximum polarisation (Pmax) obtained at room temperature are 4.65 kV cm−1, 6.33 and 15.31 μC cm−2, respectively. With rising the temperature, the P–E loops turn out to be slimmer, and the ferroelectric parameters decline gradually due to the disappearance of ferroelectric domains. Below the Curie temperature (TC = 93 °C), the P–E curves are slim but not linear, which is the paraelectric state's characteristic. This nature can be related to the ferroelectric clusters or residual polar nanoregions (PNR), which can be attributed to relaxor behaviour.11 | ||
Fig. 3 Temperature-dependence of (a) P–E, (b) J–E, (c) S–E loops measured at 25 kV cm−1 and 10 Hz and (d) the large-signal piezoelectric coefficient  determined in BCZT ceramic. determined in BCZT ceramic. | ||
Correspondingly, the temperature-dependence of the current density–electric field (J–E) curves of BCZT ceramic are displayed in Fig. 3b. It is worthy to note that when an electric field is applied to ferroelectric materials, two types of current density signals are detected, leakage current and current due to domain switching phenomena. Therefore, the electric peak appeared around the coercive field is mostly attributed to the ferroelectric domain switching.13 Meanwhile, the Ec value obtained in the P–E and J–E curves is almost the same.34 The domain switching current density peak around the Ec confirms the domain structure and long-range ferroelectric order of BCZT ceramic. As increasing the applied electric field to reach 25 kV cm−1, the magnitude of leakage current becomes very low.34 However, as increasing the temperature, the domain switching current peaks practically disappear, demonstrating long-range ferroelectric order disruption.13,35
3.4 Piezoelectric properties
The piezoelectric effect is a unique property of certain crystals that generate an electric field or a current if subjected to physical constraints and vice versa.36 When an electric field is imposed on the crystal, stress on its structure is induced (indirect piezoelectric effect), this property is mostly used in actuators.37 To evaluate the indirect piezoelectric effect's thermal-stability, the temperature-dependence of the strain–electric field (S–E) hysteresis loops of BCZT ceramic at 25 kV cm−1 is presented in Fig. 3c. A butterfly-like shape was observed at temperatures below TC due to the lattice distortion and the switching and movement of domain walls by the electric field.15,38,39 Consequently, the maximal average strain (Smax) was found to be 0.062%. However, a sprout-like shape was noticed at higher temperatures due to the ferroelectricity's gradual disruption.40 The corresponding large-signal piezoelectric coefficient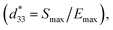 where, Smax is the maximum strain measured at the maximum electric field Emax. The thermal-evolution of the average value of
where, Smax is the maximum strain measured at the maximum electric field Emax. The thermal-evolution of the average value of 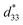
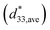 at the positive and the negative electric field is depicted in Fig. 3d. A small variation of
at the positive and the negative electric field is depicted in Fig. 3d. A small variation of 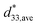 was observed below 50 °C, nevertheless, as increasing the temperature, a gradual decrease of
was observed below 50 °C, nevertheless, as increasing the temperature, a gradual decrease of 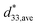 was detected letting a maximal
was detected letting a maximal 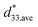 value of 234 pm V−1 at 30 °C.
value of 234 pm V−1 at 30 °C.
Praveen et al.41 stated that BZT–52BCT ceramic exhibits a comparable strain and 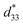 values of 0.076% and 250 pm V−1, respectively, under 30 kV cm−1 and at 40 °C, this value is comparable to that obtained in our BCZT ceramic. Moreover, Merselmiz et al.38 reported that Ba0.80Ca0.20Zr0.02Ti0.98O3 ceramic displays a maximum value of strain and
values of 0.076% and 250 pm V−1, respectively, under 30 kV cm−1 and at 40 °C, this value is comparable to that obtained in our BCZT ceramic. Moreover, Merselmiz et al.38 reported that Ba0.80Ca0.20Zr0.02Ti0.98O3 ceramic displays a maximum value of strain and 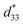 of 0.078% and 310 pm V−1, respectively, under 25 kV cm−1 and at 110 °C. Besides, Chaiyo et al.42 stated that Ba0.80Ca0.20Zr0.05Ti0.95O3 ceramic exhibits
of 0.078% and 310 pm V−1, respectively, under 25 kV cm−1 and at 110 °C. Besides, Chaiyo et al.42 stated that Ba0.80Ca0.20Zr0.05Ti0.95O3 ceramic exhibits 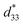 of 284 pm V−1 under 30 kV cm−1. However, at the similar electric field, Pisitpipathsin et al.43 reported high strain and
of 284 pm V−1 under 30 kV cm−1. However, at the similar electric field, Pisitpipathsin et al.43 reported high strain and 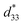 of 0.15% and 513 pm V−1, respectively, in Ba0.91Ca0.09Zr0.04Ti0.96O3 ceramic around 123 °C. Moreover, at 70 kV cm−1, Ba0.85Ca0.15Zr0.90Ti0.10O3 ceramic shows a similar strain (0.066%) and high
of 0.15% and 513 pm V−1, respectively, in Ba0.91Ca0.09Zr0.04Ti0.96O3 ceramic around 123 °C. Moreover, at 70 kV cm−1, Ba0.85Ca0.15Zr0.90Ti0.10O3 ceramic shows a similar strain (0.066%) and high 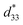 value of 942 pm V−1 at room temperature, as reported by Praveen et al.44 Besides, Cai et al.15 observed that as increasing the grain size (from 8.25 μm to 44.37 μm), the strain increases (0.086% to 0.115%) and correspondingly,
value of 942 pm V−1 at room temperature, as reported by Praveen et al.44 Besides, Cai et al.15 observed that as increasing the grain size (from 8.25 μm to 44.37 μm), the strain increases (0.086% to 0.115%) and correspondingly, 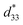 values enhanced (from 427.7 to 574.25 pm V−1). It should be mentioned that the piezoelectric parameters depend strongly on the extrinsic contribution, which occurs principally from the motion of the domain walls owing to the grain size effect.44 In other words, the domain in the coarse and large grain is easier to switch than in small grain, leading to an improved piezoelectric response.15 Furthermore, the differences in the results could be likewise ascribed to the chemical compositions, the sintering temperature, the applied electric field, the poling effect and the measurement conditions.45
values enhanced (from 427.7 to 574.25 pm V−1). It should be mentioned that the piezoelectric parameters depend strongly on the extrinsic contribution, which occurs principally from the motion of the domain walls owing to the grain size effect.44 In other words, the domain in the coarse and large grain is easier to switch than in small grain, leading to an improved piezoelectric response.15 Furthermore, the differences in the results could be likewise ascribed to the chemical compositions, the sintering temperature, the applied electric field, the poling effect and the measurement conditions.45
3.5 Energy storage performances
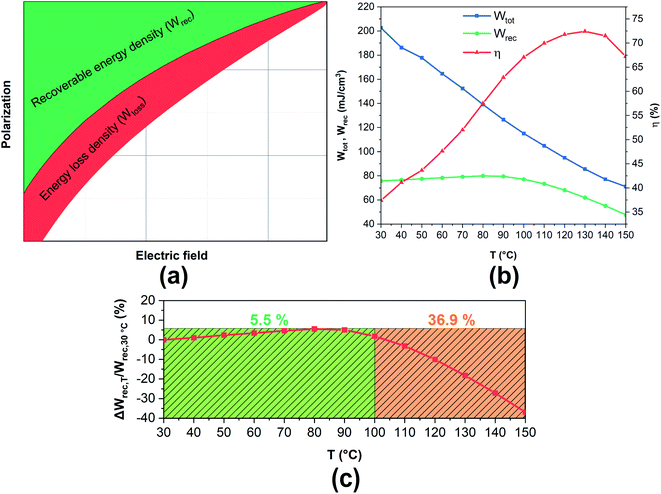
BCZT ferroelectric relaxor materials draw much attention for energy applications due to their excellent dielectric and ferroelectric properties.46–48 The energy storage density can be easily obtained from the polarisation versus electric field (P–E) curves by integrating the area between the polarisation axis and the P–E curve.11 As shown in Fig. 4a, the green area is equal to the recoverable energy density (Wrec), which corresponds to the released energy density in the discharging process. Meanwhile, the red area is equivalent to the dissipated energy density (Wloss) due to the dielectric material's losses. The overall area of the two parts equals the total energy density stored in the charging process. It is also required to estimate energy efficiency (η) for evaluating the energy storage performances. Thus, Wtot and Wrec, including η, could be estimated by employing eqn (1)–(3), where P, Pr, Pmax, E, denote polarisation, remnant polarisation, maximum polarisation, and electric field, respectively.
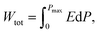 | (1) |
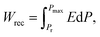 | (2) |
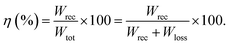 | (3) |
It is worth recalling that optimising the electrical breakdown strength, maximal polarisation, dielectric constant and dielectric loss of relaxor ferroelectric based-ceramics is the main avenue to realise extremely high energy storage densities and efficiencies.49 The thermal-evolution of the energy storage parameters of BCZT sample at 25 kV cm−1 is displayed in Fig. 4b. At room temperature, Wtot, Wrec and η were found to be 202, 75 mJ cm−3 and 37%, respectively. However, as increasing the temperature, Wtot declines continuously, and Wrec remains steady then decreases gradually above 90 °C. Correspondingly, η drops to reach 72.9% at 130 °C (Wtot = 85 mJ cm−1 and Wrec = 62 mJ cm−3), then decreases. It should be noted that P–E loops were not fully saturated; thus, by further increasing the applied electric field, the energy density could be enhanced even more. However, the electric field was kept at 25 kV cm−1 to avoid the electric breakdown at high temperatures.
To compare the energy storage performances of BCZT sample with other lead-free ferroelectric ceramics, Table 1 summarises the Wtot, Wrec and η of bulk ceramics that have been recently reported at different applied electric fields. In the first five comparisons reported in Table 1, the energy storage performances of BCZT ceramic with the composition Ba0.85Ca0.15Zr0.1Ti0.9O3 under different applied electric fields, at room temperature and the temperature corresponding to the maximal energy storage efficiency (η), are presented. For instance, at room temperature and relatively the same electric field (20 kV cm−1), our sample shows enhanced results compared to those reported by Cai et al.15 Meanwhile, at room temperature, Hanani et al.11 stated a Wrec of 97.4 mJ cm−3 and η of 71.3% in Ba0.85Ca0.15Zr0.1Ti0.9O3 ceramic under 20 kV cm−1. Increasing the applied electric field to 60 kV cm−1 gives higher Wrec of 367.2 mJ cm−3 with η of 67.2%. However, under 60 kV cm−1 and at 107 °C, Wrec reached 414.1 mJ cm−3 with η of 78.6%.11 Besides, in the same BCZT composition, Puli et al.48 achieved a high Wrec of 280 mJ cm−3 and a moderate efficiency of 58.3% at room temperature and under 60 kV cm−1. At room temperature, Zhan et al.50 stated high Wrec of 590 mJ cm−3 and an efficiency of 72.8% under a high applied electric field of 160 kV cm−1 in Ba0.95Ca0.05Zr0.30Ti0.70O3 ceramic.
| Ceramic | Wtot (mJ cm−3) | Wrec (mJ cm−3) | η (%) | E (kV cm−1) | T (°C) | Ref. |
|---|---|---|---|---|---|---|
| BCZT | 202 | 75 | 37 | 25 | 30 | This work |
| BCZT | 85 | 62 | 72.9 | 25 | 130 | This work |
| Ba0.85Ca0.15Zr0.90Ti0.10O3 | 136.7 | 97.4 | 71.3 | 20 | 27 | 11 |
| Ba0.85Ca0.15Zr0.90Ti0.10O3 | 113.8 | 38.6 | 33.9 | 20 | 25 | 15 |
| Ba0.85Ca0.15Zr0.90Ti0.10O3 | 90.2 | 71.2 | 78.9 | 20 | 100 | 15 |
| Ba0.85Ca0.15Zr0.90Ti0.10O3 | 526.6 | 414.1 | 78.6 | 60 | 107 | 11 |
| Ba0.85Ca0.15Zr0.90Ti0.10O3 | 480.3 | 280 | 58.3 | 60 | RT | 48 |
| BaTi0.89Sn0.11O3 | 85.1 | 72.4 | 85.07 | 25 | 30 | 53 |
| BaZr0.05Ti0.95O3 | 302 | 218 | 72 | 50 | RT | 54 |
| Bi0.48La0.02Na0.40K0.10Ti0.98Zr0.90Ti0.10O3 | 1033 | 630 | 61 | 60 | 25 | 55 |
| 0.8[0.9(Bi0.5Na0.5)TiO3–0.1BiScO3]–0.2BaTiO3 | 893.65 | 563 | 63 | 70 | RT | 24 |
| 0.525Bi0.5Na0.5TiO3–0.475Ba0.85Ca0.15Ti0.9Zr0.1O3 | 990 | 640 | 62.81 | 77.2 | RT | 5 |
| Ba0.95Ca0.05Zr0.30Ti0.70O3 | 810.4 | 590 | 72.8 | 160 | RT | 50 |
| 0.85(Bi0.47La0.03Na0.5)0.94Ba0.06TiO3–0.15Sr(Sc0.5Nb0.5)O3 | 2230 | 1830 | 82.32 | 185 | RT | 56 |
Besides, it is necessary to investigate the thermal-stability of energy storage capabilities as a crucial factor for electric devices in practical applications.51 For this purpose, the temperature-dependence of the energy-storage variation (ESV) was assessed by employing the eqn (4),
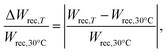 | (4) |
The thermal-evolution of the ESV values in BCZT ceramic is plotted in Fig. 4c. It can be seen that the ESV value of BCZT ceramic process excellent stability less than ±5.5% (Wrec = 75.8–77.2 mJ cm−3) in the temperature range of 30–100 °C. Nevertheless, above 100 °C, the ESV value reached 36.9% due to the ferroelectric–paraelectric phase transition. The obtained results are very promising in comparison to other ferroelectric materials. Xu et al.51 reported that the ESV value of BCZT-0.5 wt% MgO ceramic was ±14.18% despite the high recoverable energy storage Wrec of 93.2 mJ cm−3 in a broad temperature range of 20–120 °C under 35 kV cm−1. Besides, Hanani et al.11 claimed a remarkable ESV value (fluctuation less than ±12.7%) over a temperature range of 27–127 °C under 60 kV cm−1. Besides, Jayakrishnan et al.52 reported that 0.6BaZr0.20Ti0.80O3–0.4Ba0.70Ca0.30TiO3 ceramic exhibits a high variation rate of 46.3%, where Wrec dropped from 121 to 65 mJ cm−3 at 30 °C and 90 °C, respectively, under 25 kV cm−1. Hence, BCZT ceramic presents an excellent thermal-stability over a wide temperature range related to the strengthened diffuse phase transition (DPT) behaviour of BCZT ceramic.
3.6 Electrocaloric effect
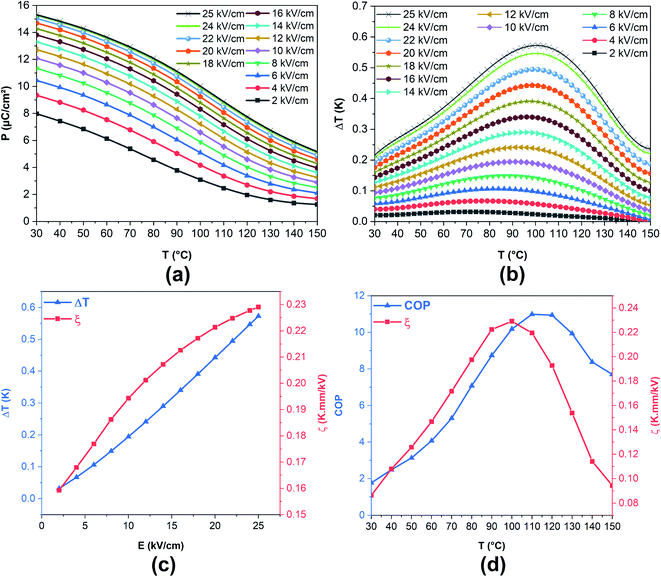
In order to assess the capabilities of BCZT ceramic for eco-friendly solid-state cooling devices, the ECE was investigated by the indirect measurements based on the recorded ferroelectric order parameter P (E, T) determined from the P–E hysteresis loops (see Fig. 3a). At every fixed applied electric field, a fifth-order polynomial fitting of the upper polarisation branches was performed.16 Then, the evolution of the polarisation as a function of the temperature was deduced (see Fig. 5a). Obviously, with increasing the temperature, the polarisation declines gradually then drops at higher temperatures. The isothermal entropy change (ΔS) and the electrocaloric temperature change (ΔT) were estimated by employing the Maxwell relation (eqn (5) and (6)), where, ρ and CP denote the mass density and the specific heat of the sample, respectively. The value of CP was obtained from ref. 20.
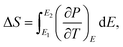 | (5) |
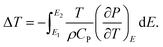 | (6) |
Fig. 5b displays the temperature-dependence of the reversible electrocaloric temperature change (ΔT) under several applied electric fields in BCZT ceramic. The maximum of ECE is closely related to the ferroelectric–paraelectric phase transition resulting in a broad ECE peak exhibiting a maximum around TC. As increasing the applied electric fields, ΔT increases and its maximum shifts toward higher temperatures, indicating that TC shifts up to higher temperatures. At 25 kV cm−1, ΔT achieves a maximum of 0.57 K locates at T = 100 °C and the corresponding ΔS was found to be 0.61 J kg−1 K−1. Afterwards, ΔT diminishes gradually with increasing the temperature, owing to the disruption of the polarisation (i.e., the extracted polarization gradient (∂P/∂T)E above TC). This finding is in accordance with the dielectric properties data. Fig. 5c shows the plots of ΔT versus the applied electric fields, and the corresponding EC responsivity defined as ζ = ΔT/ΔE at the peak temperature. ΔT increases with increasing the applied electric field; in contrast, ζ increases rapidly at low electric fields, then starts to saturate to reach a maximum of 0.23 K mm kV−1 at 25 kV cm−1.
Table 2 compares the EC response of BCZT ceramic with other lead-free ceramics. At 14 kV cm−1, Merselmiz et al.38 reported that Ba0.80Ca0.15Zr0.02Ti0.98O3 sample exhibits high ΔT and ζ of 0.668 K and 0.477 around TC = 112 °C under 14 kV cm−1 determined by the direct method. Moreover, a comparable result of ΔT = 0.565 K and ζ = 0.188 K mm kV−1 was found in Ba0.30Ca0.10Zr0.05Ti0.95O3 ceramic around TC = 119 °C as reported by Ben Abdessalem et al.22 At 60 kV cm−1, Hanani et al.11 stated high ΔT = 1.479 K and ζ = 0.246 K mm kV−1 around TC = 94 °C in Ba0.85Ca0.15Zr0.10Ti0.90O3 ceramic. Wang et al.57 reported comparable ΔT of 0.6 K in Ba0.98Ca0.02Zr0.085Ti0.915O3 ceramic but under a higher electric field of 40 kV cm−1.
| Ceramic | T (°C) | ΔT (K) | ΔE (kV cm−1) | ζ (K mm kV−1) | Ref. |
|---|---|---|---|---|---|
| BCZT | 100 | 0.57 | 25 | 0.23 | This work |
| Ba0.85Ca0.15Zr0.10Ti0.90O3 | 100 | 0.152 | 8 | 0.19 | 19 |
| Ba0.85Ca0.15Zr0.10Ti0.90O3 | 74 | 0.155 | 8 | 0.194 | 11 |
| Ba0.85Ca0.15Zr0.10Ti0.90O3 | 82 | 0.459 | 20 | 0.229 | 11 |
| Ba0.85Ca0.15Zr0.10Ti0.90O3 | 87 | 0.492 | 17 | 0.289 | 16 |
| Ba0.85Ca0.15Zr0.10Ti0.90O3 | 97 | 0.4 | 21.5 | 0.186 | 73 |
| Ba0.85Ca0.15Zr0.10Ti0.90O3 | 94 | 1.479 | 60 | 0.246 | 11 |
| Ba0.80Ca0.15Zr0.02Ti0.98O3 | 112 | 0.668 | 14 | 0.477 | 38 |
| Ba0.80Ca0.20Zr0.02Ti0.98O3 | 112 | 0.68 | 24 | 0.283 | 38 |
| Ba0.30Ca0.10Zr0.05Ti0.95O3 | 119 | 0.565 | 30 | 0.188 | 22 |
| Ba0.98Ca0.02Zr0.085Ti0.915O3 | 85 | 0.6 | 40 | 0.15 | 57 |
| BZT–30BCT | 60 | 0.30 | 20 | 0.15 | 74 |
| BZT–32BCT | 64 | 0.33 | 20 | 0.165 | 75 |
| BaTi0.89Sn0.11O3 | 52 | 0.71 | 25 | 0.284 | 53 |
Moreover, Fig. 5d depicts the thermal-evolution of ζ at 25 kV cm−1, showing a broad peak around 100 °C. It should be mentioned that the electrocaloric effects preserve significant values over a broad temperature span (Tspan). This temperature span represents a crucial parameter for practical cooling applications in which a large ECE can be maintained and is usually given as the full width at half maximum (FWHM) of the ECE peak. It was reported that the diffuse phase transition is directly related to broadened EC peaks under the low electric field.58 The obtained Tspan value is 70 K, which indicates that a large ECE can be maintained over a broad temperature range of 70 K. This can be explained by the diffuse phase transition contribution (γ = 1.74) in diffuse ferroelectrics, where the PNRs are very sensitive to frequency and magnitude of external electric field and can occur in a broad temperature range around TC.59
Another essential parameter to evaluate the ECE materials' ability for application in the solid-state cooling devices is the refrigerant capacity RC = ΔSTspan.11,60 The obtained value of RC was found to be 42.7 J kg−1 at 25 kV cm−1. The coefficient of performance (COP) is considered an essential parameter to estimate the cooling cycle performance and assess the material's efficiency.61,62 The COP is estimated by the eqn (7),61 where Q refers to the isothermal heat,
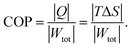 | (7) |
Fig. 5d illustrates the thermal-evolution of the COP from 30 to 150 °C in BCZT ceramic under 25 kV cm−1. The COP is evidenced by a broad peak in the whole temperature range, with a maximum value of 11 at 110 °C, then slightly decreases. The obtained value is comparable to some previous works of Pb-free63–67 and Pb-based61,68–72 materials. For example, Kumar et al.65 presented that 0.97K0.5Na0.5NbO3–0.03LiSbO3 nanocrystalline ceramic demonstrated a COP value of 8.14 under an electric field of 40 kV cm−1. Peng et al.70 obtained a COP value of 3.37 in Nb-doped Pb0.99(Zr0.65Sn0.3Ti0.05)0.98O3 antiferroelectric thin film by using a sol–gel route. In addition, Hanani et al.11 stated a COP value of 6.29 at 92 °C under 55 kV cm−1 in Ba0.85Ca0.15Zr0.10Ti0.90O3 ceramic prepared by hydrothermal method. We conclude that BCZT ceramic is a favourable material for ECE cooling system applications, owing to its enhanced values of ΔT, ζ, Tspan, RC and COP at a moderate applied electric field.
4. Conclusions
The structure, electric, piezoelectric, energy storage and electrocaloric properties of lead-free BCZT ceramic prepared by solid-state reaction route were investigated. The phase transitions in BCZT ceramic were demonstrated through Raman spectroscopy's temperature-dependence, dielectric and ferroelectric measurements. Besides, enhanced piezoelectric properties (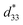 = 234 pm V−1 at 30 °C) and energy storage performances (Wrec = 62 mJ cm−3 and η = 72.9% at 130 °C) were obtained. The recovered energy density's thermal-stability shows an excellent ESV value less than ±5.5% in the temperature range of 30–100 °C, at 25 kV cm−1. Furthermore, enhanced electrocaloric values of ΔT = 0.57 K, ΔS = 0.61 J kg−1 K−1, ζ = 0.23 K mm kV−1, Tspan = 70 °C, RC = 42.7 J kg−1 and COP = 11 in BCZT ceramic were determined by using the Maxwell relation as an indirect method. Hence, the eco-friendly BCZT ceramic results are enhanced and make it a potential candidate for energy storage density capacitors and solid-state electrocaloric cooling technologies.
= 234 pm V−1 at 30 °C) and energy storage performances (Wrec = 62 mJ cm−3 and η = 72.9% at 130 °C) were obtained. The recovered energy density's thermal-stability shows an excellent ESV value less than ±5.5% in the temperature range of 30–100 °C, at 25 kV cm−1. Furthermore, enhanced electrocaloric values of ΔT = 0.57 K, ΔS = 0.61 J kg−1 K−1, ζ = 0.23 K mm kV−1, Tspan = 70 °C, RC = 42.7 J kg−1 and COP = 11 in BCZT ceramic were determined by using the Maxwell relation as an indirect method. Hence, the eco-friendly BCZT ceramic results are enhanced and make it a potential candidate for energy storage density capacitors and solid-state electrocaloric cooling technologies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the generous financial support of CNRST Priority Program PPR 15/2015, and the European Union Horizon 2020 Research and Innovation actions MSCA-RISE-ENGIMA (No. 778072) and MSCA-RISE-MELON (No. 872631). Z. K. and B. R. acknowledge Slovenian Research Agency grant J1-9147 and program P1-0125.References
- P. K. Panda and B. Sahoo, Ferroelectrics, 2015, 474, 128–143 CrossRef CAS.
- T. R. Shrout and S. J. Zhang, J. Electroceram., 2007, 19, 111–124 CrossRef CAS.
- J. Koruza, A. J. Bell, T. Frömling, K. G. Webber, K. Wang and J. Rödel, J. Mater., 2018, 4, 13–26 Search PubMed.
- Z. Hanani, I. Izanzar, M. Amjoud, D. Mezzane, M. Lahcini, H. Uršič, U. Prah, I. Saadoune, M. El Marssi, I. A. Luk’yanchuk, Z. Kutnjak and M. Gouné, Nano Energy, 2021, 81, 105661 CrossRef CAS.
- M. Yao, Y. Pu, L. Zhang and M. Chen, Mater. Lett., 2016, 174, 110–113 CrossRef CAS.
- E. Cross, Nature, 2004, 432, 24–25 CrossRef CAS.
- W. Liu and X. Ren, Phys. Rev. Lett., 2009, 103, 257602 CrossRef.
- X. Liu, Z. Chen, B. Fang, J. Ding, X. Zhao, H. Xu and H. Luo, J. Alloys Compd., 2015, 640, 128–133 CrossRef CAS.
- H. Bao, C. Zhou, D. Xue, J. Gao and X. Ren, J. Phys. D: Appl. Phys., 2010, 43, 465401 CrossRef.
- J. Wu, in Advances in Lead-Free Piezoelectric Materials, Springer Singapore, Singapore, 2018, pp. 247–299 Search PubMed.
- Z. Hanani, S. Merselmiz, D. Mezzane, M. Amjoud, A. Bradeško, B. Rožič, M. Lahcini, M. El Marssi, A. V. Ragulya, I. A. Luk'Yanchuk, Z. Kutnjak and M. Gouné, RSC Adv., 2020, 10, 30746–30755 RSC.
- X. Q. Liu, T. T. Chen, M. Sen Fu, Y. J. Wu and X. M. Chen, Ceram. Int., 2014, 40, 11269–11276 CrossRef CAS.
- Z. Hanani, D. Mezzane, M. Amjoud, A. G. G. Razumnaya, S. Fourcade, Y. Gagou, K. Hoummada, M. El Marssi and M. Gouné, J. Mater. Sci.: Mater. Electron., 2019, 30, 6430–6438 CrossRef CAS.
- V. S. Puli, D. K. Pradhan, D. B. Chrisey, M. Tomozawa, G. L. Sharma, J. F. Scott and R. S. Katiyar, J. Mater. Sci., 2013, 48, 2151–2157 CrossRef CAS.
- W. Cai, Q. Zhang, C. Zhou, R. Gao, S. Zhang, Z. Li, R. Xu, G. Chen, X. Deng, Z. Wang and C. Fu, J. Mater. Sci.: Mater. Electron., 2020, 31, 9167–9175 CrossRef CAS.
- Z. Hanani, S. Merselmiz, A. Danine, N. Stein, D. Mezzane, M. Amjoud, M. Lahcini, Y. Gagou, M. Spreitzer, D. Vengust, Z. Kutnjak, M. El Marssi, I. A. Luk'yanchuk and M. Gouné, J. Adv. Ceram., 2020, 9, 210–219 CrossRef CAS.
- J. Shi, R. Zhu, X. Liu, B. Fang, N. Yuan, J. Ding and H. Luo, Materials, 2017, 10, 1093 CrossRef.
- Y. Zhou, Q. Lin, W. Liu and D. Wang, RSC Adv., 2016, 6, 14084–14089 RSC.
- H. Kaddoussi, A. Lahmar, Y. Gagou, B. Manoun, J. N. Chotard, J. L. Dellis, Z. Kutnjak, H. Khemakhem, B. Elouadi and M. El Marssi, J. Alloys Compd., 2017, 713, 164–179 CrossRef CAS.
- H. Kaddoussi, A. Lahmar, Y. Gagou, B. Asbani, J. L. Dellis, G. Cordoyiannis, B. Allouche, H. Khemakhem, Z. Kutnjak and M. El Marssi, J. Alloys Compd., 2016, 667, 198–203 CrossRef CAS.
- F. Weyland, R. Hayati and N. Novak, Ceram. Int., 2019, 45, 11408–11412 CrossRef CAS.
- M. Ben Abdessalem, I. Kriaa, A. Aydi and N. Abdelmoula, Ceram. Int., 2018, 44, 13595–13601 CrossRef CAS.
- Z. Kutnjak, B. Rožič and R. Pirc, in Wiley Encyclopedia of Electrical and Electronics Engineering, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2015, pp. 1–19 Search PubMed.
- Y. Sun, H. Wang, G. Liu, H. Xie, C. Zhou, G. Chen, C. Yuan and J. Xu, J. Mater. Sci.: Mater. Electron., 2020, 31, 5546–5553 CrossRef CAS.
- W. Cai, Q. Zhang, C. Zhou, R. Gao, F. Wang, G. Chen, X. Deng, Z. Wang, N. Deng, L. Cheng and C. Fu, J. Mater. Sci., 2020, 55, 9972–9992 CrossRef CAS.
- Z. Hanani, E. H. Ablouh, M. 'Barek Amjoud, D. Mezzane, S. Fourcade and M. Gouné, Ceram. Int., 2018, 44, 10997–11000 CrossRef CAS.
- D. A. Tenne, X. X. Xi, Y. L. Li, L. Q. Chen, A. Soukiassian, M. H. Zhu, A. R. James, J. Lettieri, D. G. Schlom, W. Tian and X. Q. Pan, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 174101 CrossRef.
- A. Hamza, F. Benabdallah, I. Kallel, L. Seveyrat, L. Lebrun and H. Khemakhem, J. Alloys Compd., 2018, 735, 2523–2531 CrossRef CAS.
- Z. Hanani, D. Mezzane, M. Amjoud, S. Fourcade, A. G. G. Razumnaya, I. A. A. Luk'yanchuk and M. Gouné, Superlattices Microstruct., 2019, 127, 109–117 CrossRef CAS.
- M. Acosta, N. Novak, W. Jo and J. Rödel, Acta Mater., 2014, 80, 48–55 CrossRef CAS.
- C. Zhao, H. Wu, F. Li, Y. Cai, Y. Zhang, D. Song, J. Wu, X. Lyu, J. Yin, D. Xiao, J. Zhu and S. J. Pennycook, J. Am. Chem. Soc., 2018, 140, 15252–15260 CrossRef CAS.
- M. H. Zhang, K. Wang, J. S. Zhou, J. J. Zhou, X. Chu, X. Lv, J. Wu and J. F. Li, Acta Mater., 2017, 122, 344–351 CrossRef CAS.
- A. A. Bokov and Z. G. Ye, in Frontiers of Ferroelectricity: A Special Issue of the Journal of Materials Science, Springer US, Boston, MA, 2007, pp. 31–52 Search PubMed.
- A. Kumar, V. V. Bhanu Prasad, K. C. James Raju and A. R. James, Eur. Phys. J. B, 2015, 88, 287 CrossRef.
- K. Li, X. L. Zhu, X. Q. Liu and X. M. Chen, Appl. Phys. Lett., 2013, 102, 112912 CrossRef.
- P. Muralt, in Encyclopedia of Materials: Science and Technology, Elsevier, 2001, pp. 8894–8897 Search PubMed.
- J. Rödel, K. G. Webber, R. Dittmer, W. Jo, M. Kimura and D. Damjanovic, J. Eur. Ceram. Soc., 2015, 35, 1659–1681 CrossRef.
- S. Merselmiz, Z. Hanani, S. Ben Moumen, A. Matavž, D. Mezzane, N. Novak, Z. Abkhar, L. Hajji, M. Amjoud, Y. Gagou, K. Hoummada, D. Črešnar, Z. Kutnjak and B. Rožič, J. Mater. Sci.: Mater. Electron., 2020, 31, 17018–17028 CrossRef CAS.
- U. Obilor, C. Pascual-Gonzalez, S. Murakami, I. M. Reaney and A. Feteira, Mater. Res. Bull., 2018, 97, 385–392 CrossRef CAS.
- L. Wang, W. Bai, X. Zhao, F. Wen, L. Li, W. Wu, P. Zheng and J. Zhai, J. Mater. Sci.: Mater. Electron., 2019, 30, 9219–9230 CrossRef CAS.
- J. P. Praveen, T. Karthik, A. R. James, E. Chandrakala, S. Asthana and D. Das, J. Eur. Ceram. Soc., 2015, 35, 1785–1798 CrossRef CAS.
- N. Chaiyo, D. P. Cann and N. Vittayakorn, J. Mater. Sci., 2015, 50, 6171–6179 CrossRef CAS.
- N. Pisitpipathsin, P. Kantha, K. Pengpat and G. Rujijanagul, in Ceramics International, Elsevier, 2013, vol. 39, pp. S35–S39 Search PubMed.
- J. P. Praveen, K. Kumar, A. R. James, T. Karthik, S. Asthana and D. Das, Curr. Appl. Phys., 2014, 14, 396–402 CrossRef.
- Y. Zhang, H. Sun and W. Chen, J. Phys. Chem. Solids, 2018, 114, 207–219 CrossRef CAS.
- X. Chen, X. Chao and Z. Yang, Mater. Res. Bull., 2019, 111, 259–266 CrossRef CAS.
- Z. Hanani, D. Mezzane, M. Amjoud, Y. Gagou, K. Hoummada, C. Perrin, A. G. Razumnaya, Z. Kutnjak, A. Bouzina, M. El Marssi, M. Gouné and B. Rožič, J. Mater. Sci.: Mater. Electron., 2020, 31, 10096–10104 CrossRef CAS.
- V. S. Puli, D. K. Pradhan, I. Coondoo, N. Panwar, S. Adireddy, S. Luo, R. S. Katiyar and D. B. Chrisey, J. Phys. D: Appl. Phys., 2019, 52, 255304 CrossRef CAS.
- L. Yang, X. Kong, F. Li, H. Hao, Z. Cheng, H. Liu, J. F. Li and S. Zhang, Prog. Mater. Sci., 2019, 102, 72–108 CrossRef CAS.
- D. Zhan, Q. Xu, D. P. Huang, H. X. Liu, W. Chen and F. Zhang, J. Alloys Compd., 2016, 682, 594–600 CrossRef CAS.
- K. Xu, P. Yang, W. Peng and L. Li, J. Alloys Compd., 2020, 829, 154516 CrossRef CAS.
- A. R. Jayakrishnan, K. V. Alex, A. Thomas, J. P. B. Silva, K. Kamakshi, N. Dabra, K. C. Sekhar, J. Agostinho Moreira and M. J. M. Gomes, Ceram. Int., 2019, 45, 5808–5818 CrossRef CAS.
- S. Merselmiz, Z. Hanani, D. Mezzane, M. Spreitzer, A. Bradeško, D. Fabijan, D. Vengust, M. Amjoud, L. Hajji, Z. Abkhar, A. G. Razumnaya, B. Rožič, I. A. Luk'yanchuk and Z. Kutnjak, Ceram. Int., 2020, 46, 23867–23876 CrossRef CAS.
- T. Badapanda, S. Chaterjee, A. Mishra, R. Ranjan and S. Anwar, Phys. B, 2017, 521, 264–269 CrossRef CAS.
- P. Butnoi, S. Manotham, P. Jaita, C. Randorn and G. Rujijanagul, J. Eur. Ceram. Soc., 2018, 38, 3822–3832 CrossRef CAS.
- J. Xie, Z. Dai, X. Ding, X. Fan, W. Liu, L. Zhang and J. Li, J. Mater. Sci., 2020, 55, 13578–13589 CrossRef CAS.
- J. Wang, T. Yang, S. Chen, G. Li, Q. Zhang and X. Yao, J. Alloys Compd., 2013, 550, 561–563 CrossRef CAS.
- X. Zhang, L. Wu, S. Gao, J. Q. Liu, B. Xu, Y. D. Xia, J. Yin and Z. G. Liu, AIP Adv., 2015, 5, 047134 CrossRef.
- Y. Zhao, X. Q. Liu, S. Y. Wu and X. M. Chen, J. Electroceram., 2019, 43, 106–116 CrossRef CAS.
- S. G. Lu and Q. Zhang, Adv. Mater., 2009, 21, 1983–1987 CrossRef CAS.
- Y. Zhao, X. Hao and Q. Zhang, Ceram. Int., 2016, 42, 1679–1687 CrossRef CAS.
- J. Shi, D. Han, Z. Li, L. Yang, S. G. Lu, Z. Zhong, J. Chen, Q. M. Zhang and X. Qian, Joule, 2019, 3, 1200–1225 CrossRef.
- R. Kumar and S. Singh, J. Alloys Compd., 2018, 764, 289–294 CrossRef CAS.
- B. Peng, Q. Zhang, B. Gang, G. J. T. Leighton, C. Shaw, S. J. Milne, B. Zou, W. Sun, H. Huang and Z. Wang, Energy Environ. Sci., 2019, 12, 1708–1717 RSC.
- R. Kumar and S. Singh, Sci. Rep., 2018, 8, 3186 CrossRef.
- R. Kumar, A. Kumar and S. Singh, Sustainable Energy Fuels, 2018, 2, 2698–2704 RSC.
- R. Kumar, D. Khurana, A. Kumar and S. Singh, Ceram. Int., 2018, 44, 20845–20850 CrossRef CAS.
- E. Defay, S. Crossley, S. Kar-Narayan, X. Moya and N. D. Mathur, Adv. Mater., 2013, 25, 3337–3342 CrossRef CAS.
- H. Gao, X. Hao, Q. Zhang, S. An and L. B. Kong, J. Mater. Sci.: Mater. Electron., 2016, 27, 10309–10319 CrossRef CAS.
- B. Peng, M. Zhang, S. Tang, J. Jiang, W. Zhao, B. Zou, N. Luo, Q. Zhang, G. J. T. Leighton, C. Shaw, L. Liu and W. Sun, Ceram. Int., 2020, 46, 4300–4306 CrossRef CAS.
- Y. Zhao, X. Hao and Q. Zhang, ACS Appl. Mater. Interfaces, 2014, 6, 11633–11639 CrossRef CAS.
- X. Hao, Y. Zhao and Q. Zhang, J. Phys. Chem. C, 2015, 119, 18877–18885 CrossRef CAS.
- S. Patel, P. Sharma and R. Vaish, Phase Transitions, 2016, 89, 1062–1073 CrossRef CAS.
- Y. Bai, X. Han and L. Qiao, Appl. Phys. Lett., 2013, 102, 1–5 Search PubMed.
- M. Sanlialp, V. V. Shvartsman, M. Acosta and D. C. Lupascu, J. Am. Ceram. Soc., 2016, 99, 4022–4030 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra09707a |
| This journal is © The Royal Society of Chemistry 2021 |