Open Access Article
Open Access ArticleElectronic phase-crossover and room temperature ferromagnetism in a two-dimensional (2D) spin lattice†
A. K. Nair and
S. J. Ray *
*
Department of Physics, Indian Institute of Technology Patna, Bihta 801106, India. E-mail: ray@iitp.ac.in; ray.sjr@gmail.com
First published on 4th January 2021
Abstract
Tuning of system properties such as electronic and magnetic behaviour through various engineering techniques is necessary for optoelectronic and spintronic applications. In our current work, we employ first-principles methodologies along with Monte-Carlo simulations to comprehensively study the electronic and magnetic behaviour of 2-dimensional (2D) Cr2Ge2Te6 (Tc = 61 K), uncovering the impact of strain and electric field on the material. In the presence of strain, we were able to achieve high temperature magnetic ordering in the layer along with observable phase crossover in the electronic state of the system, where the system exhibited transference from semiconducting to half-metallic state. Finally, on coupling strain and electric field remarkable increase in Curie temperature (Tc) ∼ 331 K (above 5-fold enhancement from pristine configuration) was observed, which is very well above room temperature. Our inferences have shed light on a relatively new type of coupling method involving strain and electric field which may have tremendous implications in the development of 2D spintronic architecture.
I Introduction
The emergence of two-dimensional (2D) materials has paved the way for the development of several nanoelectronic and spintronic devices.1 Extensive studies were conducted to explore the electronic properties of these materials which is tunable through the presence of doping,2,3 strain,4–6 vacancy7–9 and electric field5,10,11 etc. In addition, van der Waals heterostructure of these 2D materials can be employed to generate engineered properties for desired applications.12 The presence of spontaneous magnetism in 2D materials could effectively pave its way in spintronics,13 which was however limited to the observation of edge-magnetism or vacancy/doping induced magnetism,14 localised in nature. To establish a long range magnetic ordering (LRMO) in two-dimension, anisotropy is required to establish an energy gap in the spin wave spectrum, overcoming the thermally induced magnon excitation, as theoretically predicted through Onsager's model15 and Mermin–Wagner–Hohenberg theorem.16,17 However, the experimental discovery of intrinsic magnetism was recently made in several 2D nanocrystals18–20 with critical temperature (Tc) below 100 K.The technological operation of a spintronic device favours ferromagnetic materials with room-temperature magnetic ordering21 and several of the 2D magnetic materials do not fit the criterion in terms of either being intrinsically antiferromagnetic or not processing a high ordering temperature. However, the magnetic properties can be fine-tuned, as desired, through the application of a few engineering techniques.22,23 Cr2Ge2Te6 (CGT) is a newly discovered 2D magnetic material which has gained great attention recently because of its ability to be exfoliated to the monolayer limit24 similar to that of CrI3.25 Moreover, recent investigations have shown the feasibility of formation of stable heterostructures with several other 2D materials like graphene,26 CrI3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 and topological insulators,28,29 observation of photoluminescence30 and magneto-optical effects.31 However, the experimental Tc ∼ 61 K20,32 of CGT is well-below room temperature, which is too low for practical spintronics applications. The Tc changes with the change of layer thickness between 40 K to 68 K.32 In this work, we have explored the possibility of using non-invasive external stimuli like strain and electric field to fine-tune the electronic and magnetic behaviour and change the Tc. Through extensive first-principles based calculations and Monte Carlo (MC) simulations, we have investigated the electronic and magnetic properties of CGT under different strain and electric field conditions. We are able to observe high temperature ferromagnetism (FM) sustaining upto a temperature as high as ∼312 K and interesting phase transitions at different parts of the phase diagram. The combination of strain and electric field is a noteworthy mechanism to tune the system properties, which is an unexplored method to the best of our knowledge.
27 and topological insulators,28,29 observation of photoluminescence30 and magneto-optical effects.31 However, the experimental Tc ∼ 61 K20,32 of CGT is well-below room temperature, which is too low for practical spintronics applications. The Tc changes with the change of layer thickness between 40 K to 68 K.32 In this work, we have explored the possibility of using non-invasive external stimuli like strain and electric field to fine-tune the electronic and magnetic behaviour and change the Tc. Through extensive first-principles based calculations and Monte Carlo (MC) simulations, we have investigated the electronic and magnetic properties of CGT under different strain and electric field conditions. We are able to observe high temperature ferromagnetism (FM) sustaining upto a temperature as high as ∼312 K and interesting phase transitions at different parts of the phase diagram. The combination of strain and electric field is a noteworthy mechanism to tune the system properties, which is an unexplored method to the best of our knowledge.
II Methodology
First-principles based density functional theory (DFT) calculations were used to investigate the electronic structure and magnetic properties of CGT.33,34 The present methodology involved spin-polarised generalised gradient approximation (SGGA) of the Perdew–Burke–Ernzerhof35 (PBE) exchange correlation functional. Maximum energy cutoff limit for numerical accuracy was achieved with 150 Ry along with a Monkhorst–Pack36 k-grid of 9 × 9 × 1 in the reciprocal space for the Brillouin zone. The wave-functions were expanded within a double-ζ polarised basis set under periodic boundary conditions for strain based calculations and Neumann boundary conditions were implemented in the case of electric field applied along the z-direction. In order to account for the on-site Coulomb interaction (U) between the 3d electrons of the Cr-ion, U = 4 eV was taken into account. The van der Waal's interaction was incorporated via semi-empirical corrections by Grimme D2 and D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 within the GGA.
37 within the GGA.
CGT belongs to space group 162 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1m) having a hexagonal lattice structure with optimised lattice constants of a0 = b0 = 6.8275 Å. These values were obtained by geometry optimisation with a numerical convergence criterion set with a tolerance of 10−6 eV in energy and 10−3 eV Å−1 in force per atom. A 2 × 2 × 1 supercell of the central structure was prepared for calculations of electronic and magnetic properties. A vacuum space of 20 Å was constructed in the z-direction to eliminate the interaction between the mirror layers. Each Cr atom is surrounded by six neighbouring Te atoms, while each Ge atom is bonded to nearby three Te atoms as shown in Fig. 1. In the present exercise, the electronic and magnetic properties of the system was studied under the influence of biaxial strain. Externally applied strain along a specific direction is defined by, S = (b − b0)/b0, where b(b0) is the lattice constant in strained (unstrained) condition. Here we applied biaxial strain (Sb) on the 2 × 2 × 1 supercell of CGT over a range of −8 to 20%. The electric field was applied along the z-direction (Ez), by placing the material between two electrodes and applying equal but opposite voltages (Vz) to them. Statistical Monte Carlo (MC) simulation was used to conduct analysis of the magnetic behaviour of the system considering the 2D Ising model38 of the hexagonal lattice of CGT. The MC simulation was performed on a 100 × 100 supercell of CGT with 105 iterations and 105 MC equilibration sweeps. On the basis of the above information, studies were performed as a function of various strain and electric field cases which are explained later.
1m) having a hexagonal lattice structure with optimised lattice constants of a0 = b0 = 6.8275 Å. These values were obtained by geometry optimisation with a numerical convergence criterion set with a tolerance of 10−6 eV in energy and 10−3 eV Å−1 in force per atom. A 2 × 2 × 1 supercell of the central structure was prepared for calculations of electronic and magnetic properties. A vacuum space of 20 Å was constructed in the z-direction to eliminate the interaction between the mirror layers. Each Cr atom is surrounded by six neighbouring Te atoms, while each Ge atom is bonded to nearby three Te atoms as shown in Fig. 1. In the present exercise, the electronic and magnetic properties of the system was studied under the influence of biaxial strain. Externally applied strain along a specific direction is defined by, S = (b − b0)/b0, where b(b0) is the lattice constant in strained (unstrained) condition. Here we applied biaxial strain (Sb) on the 2 × 2 × 1 supercell of CGT over a range of −8 to 20%. The electric field was applied along the z-direction (Ez), by placing the material between two electrodes and applying equal but opposite voltages (Vz) to them. Statistical Monte Carlo (MC) simulation was used to conduct analysis of the magnetic behaviour of the system considering the 2D Ising model38 of the hexagonal lattice of CGT. The MC simulation was performed on a 100 × 100 supercell of CGT with 105 iterations and 105 MC equilibration sweeps. On the basis of the above information, studies were performed as a function of various strain and electric field cases which are explained later.
III Results and discussion
A Electronic properties
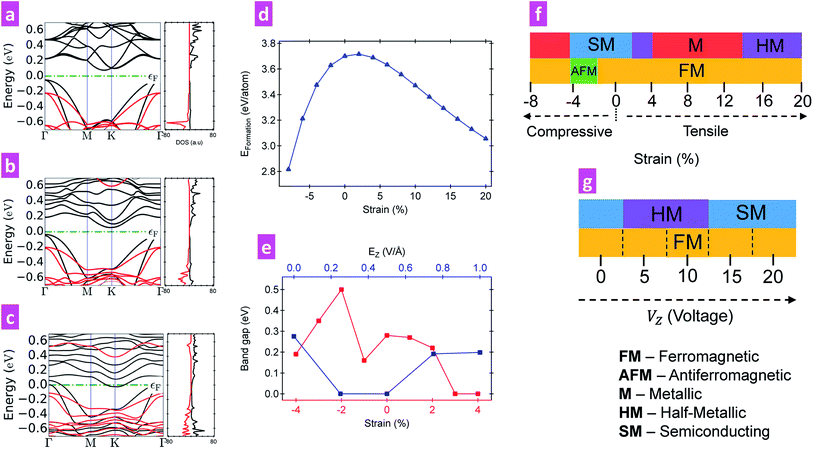
First, we looked at the variation of the electronic structure of CGT as a function of strain and electric field as shown in Fig. 2. Unstrained CGT exhibits a semiconducting character with a direct bandgap of 0.28 eV for both spin-↑ and spin-↓ states, while spin-↑ being the majority type near the Fermi level (EF) as shown in Fig. 2a. However, the bandgap starts decreasing on applying tensile strain and it turns metallic at Sb > 3%. This information can also be confirmed from the density of states (DOS) behaviour where the conduction and valence band edges move closer to the Fermi level (EF) for Sb = 2% (Fig. 2b). At Sb = 4%, spin-↑ states are present at the Fermi level, while it offers a gap for the spin-↓ states, a signature of half-metallic behaviour as shown in Fig. 2c, which is also noticed in the spin density of states (SDOS) behaviour. Further, it is observed that the system maintains its semiconducting nature in the compressive strain regime with a maximum band gap of 0.5 eV at Sb = −2%, which decreases beyond this value. The variation of bandgap of CGT on applying tensile and compressive strain is depicted in Fig. 2e. Considering the effect of spin orbit coupling (SOC),39 a direct band gap opening of 0.36 eV is observed for unstrained CGT. The diagrammatic representation of the two band structures (with SOC and without SOC) is provided in Section S5 of the ESI.†40Exfoliation energy is an important parameter to be considered while fabricating 2D structures from their bulk counterparts. In our present work, we have calculated the exfoliation energy of n-layer CGT (Eexf(n))41 and have observed that the energies fall below the range of commonly exfoliated materials, which proves that CGT can be experimentally exfoliated. The detailed information is included in the Section S3 of the ESI.†40 The stability of the system was studied by analysing the formation energy of CGT as shown in Fig. 2d. The formation energy (Eform) was calculated using eqn (1) as,
| Eform = (mECr + nEGe + pETe − ECr2Ge2Te6)/(m + n + p) | (1) |
Apart from strain, another way of influencing the electronic properties is through the application of an external electric field. The bandgap decreases from 0.28 eV → 0 eV at Ez = 0.25 V Å−1 (Fig. 2e). The metallic nature remains upto Ez = 0.5 V Å−1 as well. However, on further increasing the field to Ez = 0.75 V Å−1, a direct band gap opening of 0.19 eV was noticed, which more or less remained the same upto Ez = 1 V Å−1. Changing the polarity of the electric field did not disturb this scenario. The electronic and magnetic phase diagram displayed in Fig. 2f and g shows that CGT is semiconducting between the strain range Sb = −4% to Sb = 2%, while being half-metallic at Sb = 3% → 4%, Sb = 14% and beyond this. Metallic region is found between the strain regimes Sb = −6% → Sb = −8% and Sb = 5% → Sb = 12%. Similarly the phase diagram with electric field applied on unstrained CGT (displayed in Fig. 2f) shows that CGT is half-metallic between Ez = 0.25 V Å−1 → 0.5 V Å−1, while remaining semiconducting elsewhere. The system is also observed to be antiferromagnetic for the strain range from Sb = −2% to Sb = −4% and stays in the FM state at other values of strain studied in this work. Also the material remains ferromagnetic throughout even on exposing the system to variable electric field. Such a diagram can be very useful in phase designing of the system through strain and electric field tuning.
B Magnetic properties
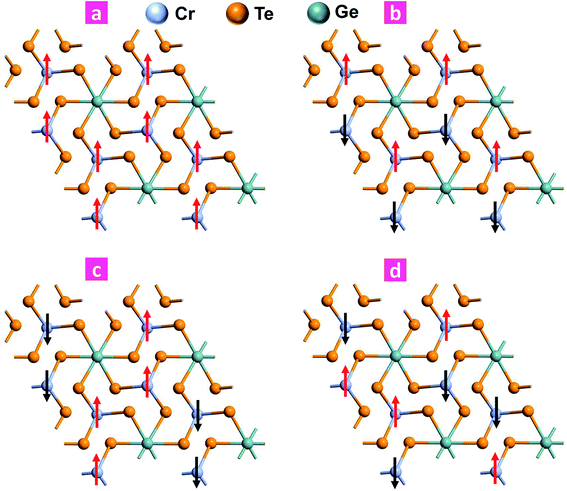
In order to study the magnetic properties as a function of biaxial strain, we considered all the theoretically possible and distinct magnetic configurations to explore the preferred magnetic ground state exhibited by CGT. The arrangements consisted of one ferromagnetic (i) FM and 3 antiferromagnetic configurations which are named as (ii) AFM1, (iii) AFM2, (iv) AFM3 respectively as portrayed in Fig. 1. The difference between the FM and AFM ground states is expressed in the form of exchange energy calculated using eqn (2) as given below,| ΔE = EFM − EAFM | (2) |
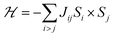 | (3) |
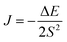 | (4) |
The result of a typical MC simulation has been illustrated in Fig. 3 for the unstrained condition. An FM → PM phase transition at a temperature of 61 K can be inferred from the magnetisation curve, which is also well in agreement with the experimentally reported value.47 The critical temperature can be estimated accurately from the specific heat peak in Fig. 3a as well. The sharp peak in the susceptibility curve in Fig. 3b demonstrates the divergence of the first derivative of the order parameter, characteristics of a 2nd order phase transition. Comparing with the work conducted on similar system, it is observed that in ref. 5, the electronic and magnetic properties of have been reported over a limited strain and electric field range and it does not offer any information on the critical temperature, phase transition etc. The results in ref. 4 offers a detailed overview on the magnetic state, critical temperature on the sister compound Cr2Ge2Se6 over a strain range upto 7%. The present work offers a unique perspective by combining the effect of strain and electric field on the electronic and magnetic properties of Cr2Ge2Te6 over a larger strain range (∼20%), which has not been covered before in any of these studies.
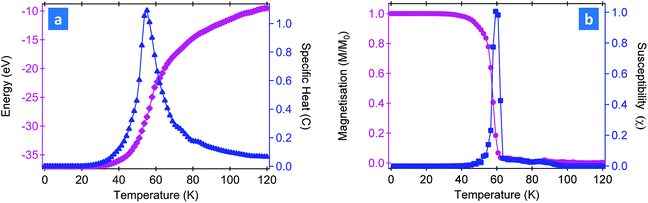 | ||
| Fig. 3 Temperature dependence of various thermodynamic parameters obtained through Monte Carlo simulations: (a) energy and specific heat, (b) magnetisation and magnetic susceptibility. | ||
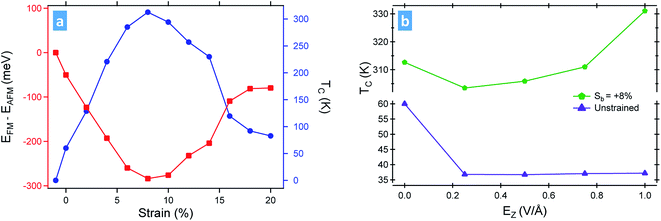
Fig. 4a portrays the energy difference between the FM and AFM state for various strain cases along with the strain dependence of Tc in the FM phase. In the unstrained case, negative ΔE indicates CGT to be FM, which agrees with the experimental observation.32 Under the application of a tensile strain, the Tc gets enhanced rapidly with a maximum of 312 K at Sb = 8%. The rate of enhancement of Tc between unstrained → Sb = 8% is 32 K/% strain, which shows a significantly high rate of enhancement. However, for strains above Sb = 10%, a gradual drop in Tc is observed with an average rate of reduction ∼19 K/% strain from Sb = 8% → 20%, finally falling to a Tc of 83 K at Sb = 20%. These results indicate the existence of a high degree of FM ordering existing in CGT with a five fold enhancement in the Tc on the application of strain from the unstrained state. Strain dependent studies on CrXTe3 (X = Si, Ge) nanosheets have reported similar enhancement on Tc (35.7 K → 57.2 K for CrGeTe3 and 91.7 K → 108.9 K for CrSiTe3 in the presence of 8% strain).48 The magnetic moment in CGT is primarily contributed by the Cr-atoms, which in the unstrained case offers a moment ∼4.46 μB and this value stays of similar order of magnitude over a large strain range. The presence of a room temperature FM ordering through the application of strain and the strain tunability in Tc can facilitate the application of CGT in designing various spin circuits. Magneto-anisotropic energy (MAE) is an important parameter to be considered while analyzing the magntic properties of a system and provides essential information regarding the easy and hard axis of magnetization of materials. For the present case, we have calculated the MAE for different strain percentages of CGT and it was observed that in the unstrained condition, the spins prefer to stay along the in-plane direction. Further information is provided in Section S6 of the ESI.†40
The electric field dependence of the Tc is shown in Fig. 4b. In the unstrained case, Tc drops sharply at Ez > 0, which does not show significant changes between Ez = 0.25 V Å−1 → 1 V Å−1. However, in the presence of strain of Sb = 8%, Tc shows interesting variation with the change in Ez. We observed that as the electric field increases there is a gradual decrease in Tc, with a value of 303 K at Ez = 0.25 V Å−1. However, with further increment in Ez, Tc increases monotonically reaching a value of 331 K for an applied field of Ez = 1 V Å−1. The Tc value is higher than the maximum Tc estimated only in the presence of strain, with 5.5 times higher than the value from the pristine configuration, suggesting the association of electric field and strain offers superior enhancement of Tc and the FM properties in CGT. It was also observed that swapping the direction of electric field also offers a similar Tc behaviour. The massive escalation in Tc through coupling strain with electric field is a note-worthy mechanism for enhancing the ferromagnetic ordering temperature, which is by far an unexplored option to the best of our knowledge. The electric field effect on the material is understood by analysing the projected density of states (PDOS) of the system. Details regarding the same are included in Section S7 of the ESI.†40
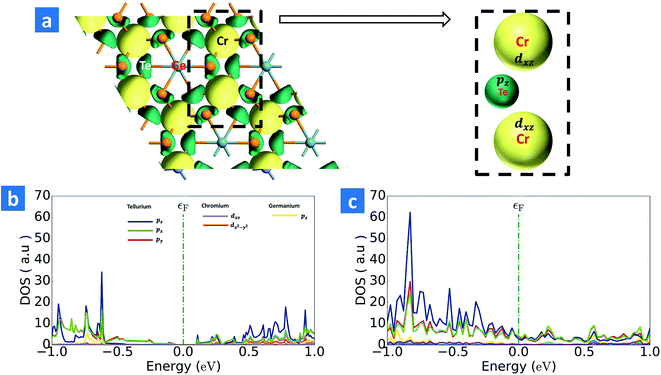
The existence of a sustainable magnetic ordering in CGT is facilitated through the exchange interaction between the Cr atoms, mediated via tellurium atoms as seen from the electron density iso-surface plot in Fig. 5a. The viable path for indirect exchange is through Te–Cr–Te bonds and the projected density of states (PDOS) analysis revealed that the dxz/dx2−y2 orbitals of Cr and pz/px orbitals of Te contribute primarily towards this as observed from Fig. 5b. Furthermore, it could be seen that as the strain is increased the orbital contributions from the Te atoms increases dramatically near the Fermi level, owing to the high Tc observed at Sb = 8% as displayed in Fig. 5c. The degree of orbital overlap determines the strength of exchange interaction (J) which further promotes an increase in Tc. The extent of the overlap is maximum at Sb = 8% and further overlap extension breaks down as we go beyond 8% strain, which then results in the decrease of Tc. There was a decrease in Tc observed when unstrained CGT was exposed to electric field. The reason for this also lies in the superexchange between the Cr atoms via Te atom. There is a drastic decrease in the density of states of the pz and px orbitals of Te on the application of electric field. However strained (Sb = 8%) CGT on interaction with electric field showed an escalation in critical temperature. In this scenario there is an increase in the DOS of all the components of p-orbitals (pz, px, py) of Te atoms at the Fermi level which is responsible for the enhancement of Tc.
Superexchange is basically an indirect exchange mechanism occurring in ionic solids since there is no direct overlap between the magnetic metal atoms (Cr atoms in our case). It is mediated via a non-magnetic atom (Te atom in this case) which is placed between the two magnetic ions. This indirect exchange allows in lowering of the kinetic energy of the system by allowing the unpaired electrons on the metal atoms to be easily delocalized over the whole structure through the non-magnetic atom. It is a second order process and is derived from the second-order perturbation theory. From a mechanical point of view, the angle of the Cr–Te–Cr bond changes in the presence of strain, which as per Goodenough–Kanamori rule49,50 can lead to a varied degree of ferromagnetism as the bond angle deviates from 180°. Under such circumstance, the antiferromagnetic coupling between the Cr and Te atoms stays proportional to (∼t2/δε), where t is the hopping term between Te-4p and Cr-3d orbitals and δε is the energy difference between them.4 While it was observed that t stays of similar value, δε gets reduced in the presence of strain. This leads to an enhancement of the AFM coupling between Cr and Te atoms, strengthening the FM coupling between Cr atoms involved in the superexchange path of Cr–Te–Cr. This explains the enhancement of the Tc upto Sb = 8%. The present study involves exposing the material to a variety of excitation, like a large value of strain and electric field and the material is found to be stable under such conditions. In an experimental situation, pre-stretched substrates can be used for applying strain on a 2D material or special substrates with 3D-nanostructure can be prepared upon which a 2D material can be transferred. Upon restoration of such substrates from flat condition, relatively high value of strain could be achieved. Other possible systems where high compressive strain could be expected is when one 2D layer edge is anchored, and locally a scanning microscopy probe tip is used to compress the system. The present results offers direction for tuning the magnetic phase as well Tc of a 2D magnetic system without causing permanent changes to the structure, which can have immense importance for future spintronics device development.
IV Conclusion
We have investigated the influence of strain and electric field on the electronic and magnetic behaviour of a novel 2D magnetic material Cr2Ge2Te6 through first-principles based calculations. Under the influence of biaxial strain, the material goes through a semiconductor → half-metallic phase and FM → AFM transition as well as rapid changes in the Tc, suggesting the existence of a high temperature ferromagnetic ordering which is unique in such 2D materials. The origin of such behaviour lies in the strength of overlap between various orbitals of Cr mediated via the Te atom in the superexchange process across Cr–Te–Cr path. Further enhancement in Tc is possible when the material is exposed to electric field, leading to a Tc ∼ 331 K, nearly 6 times from the initial unstrained condition. Our current approach offers a novel route of engineering the electronic and magnetic properties of a 2D material in a non-destructive manner which is essential for future magneto-electronic and spintronic device applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the Department of Science and Technology, India through the INSPIRE scheme (Ref: DST/INSPIRE/04/2015/003087), ECR Grant (Ref: ECR/2017/002223) and CRG Grant (Ref: CRG/2019/003289). SJR sincerely acknowledges the support provided by UGC-DAE Consortium for Scientific Research (Ref: CSR-IC-263 and CRS-M-321) and Indian Institute of Technology Patna.References
- A. Chaudhury, S. Majumder and S. J. Ray, Phys. Rev. Appl., 2019, 11, 024056 CrossRef CAS
.
- M. Sun, Y. Hao, Q. Ren, Y. Zhao, Y. Du and W. Tang, Solid State Commun., 2016, 242, 36–40 CrossRef CAS
.
- A. K. Nair, P. Kumari, M. Venkata Kamalakar and S. J. Ray, Phys. Chem. Chem. Phys., 2019, 21, 23713–23719 RSC
.
- X.-J. Dong, J.-Y. You, B. Gu and G. Su, Phys. Rev. Appl., 2019, 12, 014020 CrossRef CAS
.
- K. Wang, T. Hu, F. Jia, G. Zhao, Y. Liu, I. V. Solovyev, A. P. Pyatakov, A. K. Zvezdin and W. Ren, Appl. Phys. Lett., 2019, 114, 092405 CrossRef
.
- S. J. Ray and M. Venkata Kamalakar, Phys. Chem. Chem. Phys., 2018, 20, 13508–13516 RSC
.
- P. Srivastava, K. Hembram, H. Mizuseki, K.-R. Lee, S. S. Han and S. Kim, J. Phys. Chem. C, 2015, 119, 6530–6538 CrossRef CAS
.
- Y. Liu, C. Xiao, Z. Li and Y. Xie, Adv. Energy Mater., 2016, 6, 1600436 CrossRef
.
- S. Rani and S. J. Ray, Phys. Chem. Chem. Phys., 2020, 22, 11452–11459 RSC
.
- S. Zhang, N. Wang, S. Liu, S. Huang, W. Zhou, B. Cai, M. Xie, Q. Yang, X. Chen and H. Zeng, Nanotechnology, 2016, 27, 274001 CrossRef
.
- S. Rani and S. J. Ray, Carbon, 2019, 144, 235–240 CrossRef CAS
.
- S. Rani and S. J. Ray, Carbon, 2020, 173, 493–500 CrossRef
.
- J. F. Dayen, S. J. Ray, O. Karis, I. J. Vera-Marun and M. V. Kamalakar, Appl. Phys. Rev., 2020, 7, 011303 CAS
.
- P. Kumari, S. Majumder, S. Rani, A. K. Nair, K. Kumari, M. Venkata Kamalakar and S. J. Ray, Phys. Chem. Chem. Phys., 2020, 22, 5893–5901 RSC
.
- L. Onsager, Phys. Rev., 1944, 65, 117–149 CrossRef CAS
.
- N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133–1136 CrossRef CAS
.
- P. C. Hohenberg, Phys. Rev., 1967, 158, 383 CrossRef CAS
.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273 CrossRef CAS
.
- J.-U. Lee, S. Lee, J. H. Ryoo, S. Kang, T. Y. Kim, P. Kim, C.-H. Park, J.-G. Park and H. Cheong, Nano Lett., 2016, 16, 7433–7438 CrossRef CAS
.
- V. Carteaux, D. Brunet, G. Ouvrard and G. Andre, J. Phys.: Condens. Matter, 1995, 7, 69 CrossRef CAS
.
- M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M.-H. Phan and M. Batzill, Nat. Nanotechnol., 2018, 13, 289–293 CrossRef CAS
.
- A. K. Nair, S. Rani, M. Venkata Kamalakar and S. J. Ray, Phys. Chem. Chem. Phys., 2020, 22, 12806–12813 RSC
.
- S. Rani, A. K. Nair, M. Venkata Kamalakar and S. J. Ray, J. Phys.: Condens. Matter, 2020, 32, 415301 CrossRef CAS
.
- W. Xing, Y. Chen, P. M. Odenthal, X. Zhang, W. Yuan, T. Su, Q. Song, T. Wang, J. Zhong and S. Jia, et al., 2D Materials, 2017, 4, 024009 CrossRef
.
- Y. Liu and C. Petrovic, Phys. Rev. B, 2018, 97, 014420 CrossRef CAS
.
- J. Zhang, B. Zhao, Y. Yao and Z. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 165418 CrossRef
.
- C. Xu, J. Feng, H. Xiang and L. Bellaiche, npj Comput. Mater., 2018, 4, 1–6 CrossRef CAS
.
- L. Alegria, H. Ji, N. Yao, J. Clarke, R. J. Cava and J. R. Petta, Appl. Phys. Lett., 2014, 105, 053512 CrossRef
.
- M. Mogi, A. Tsukazaki, Y. Kaneko, R. Yoshimi, K. S. Takahashi, M. Kawasaki and Y. Tokura, APL Mater., 2018, 6, 091104 CrossRef
.
- Y. Fang, S. Wu, Z. Z. Zhu and G. Y. Guo, Phys. Rev. B, 2018, 98, 125416 CrossRef CAS
.
- K. L. Seyler, D. Zhong, D. R. Klein, S. Gao, X. Zhang, B. Huang, E. Navarro-Moratalla, L. Yang, D. H. Cobden, M. A. McGuire and W. Yao, Nat. Phys., 2018, 14, 277–281 Search PubMed
.
- C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang and Y. Wang, et al., Nature, 2017, 546, 265–269 CrossRef CAS
.
- S. Smidstrup, T. Markussen, P. Vancraeyveld, J. Wellendorff, J. Schneider, T. Gunst, B. Verstichel, D. Stradi, P. A. Khomyakov, U. G. Vej-Hansen and M. E. Lee, J. Phys.: Condens. Matter, 2019, 32, 015901 CrossRef
.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo and A. Dal Corso, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef
.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS
; S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef
.
- J. V. Selinger, Introduction to the theory of soft matter: from ideal gases to liquid crystals, Springer, 2015 Search PubMed
.
- C. He, M. Cheng and W. X. Zhang, Mater. Res. Express, 2018, 5, 065059 CrossRef
.
- A. K. Nair, et al., See ESI† for additional results on electronic phase-crossover and room temperature ferromagnetism in a two-dimensional (2D) spin lattice.
- T. Li, C. He and W. Zhang, Energy Storage Mater., 2020, 25, 866–875 CrossRef
.
- Y. Sun, Z. Zhuo, X. Wu and J. Yang, Nano Lett., 2017, 17, 2771–2777 CrossRef CAS
.
- L-M. Yang, I. A. Popov, T. Frauenheim, A. I. Boldyrev, T. Heine, V. Bacic and E. Ganz, Phys. Chem. Chem. Phys., 2015, 17, 26043–26048 RSC
.
- C. He, M. Zhang, T. T. Li and W. X. Zhang, J. Mater. Chem. C, 2020, 8, 6542–6551 RSC
.
- M.-W. Lin, H. L. Zhuang, J. Yan, T. Z. Ward, A. A. Puretzky, C. M. Rouleau, Z. Gai, L. Liang, V. Meunier and B. G. Sumpter, et al., J. Mater. Chem. C, 2016, 4, 315–322 RSC
.
- N. Sivadas, M. W. Daniels, R. H. Swendsen, S. Okamoto and D. Xiao, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 235425 CrossRef
.
- M. Lohmann, T. Su, B. Niu, Y. Hou, M. Alghamdi, M. Aldosary, W. Xing, J. Zhong, S. Jia and W. Han, et al., Nano Lett., 2019, 19, 2397–2403 CrossRef CAS
.
- X. Li and J. Yang, J. Mater. Chem. C, 2014, 2, 7071–7076 RSC
.
- J. B. Goodenough, Phys. Rev., 1955, 100, 564 CrossRef CAS
.
- J. Kanamori, J. Appl. Phys., 1960, 31, S14–S23 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra09726h |
| This journal is © The Royal Society of Chemistry 2021 |