Open Access Article
Open Access ArticleThe importance of intramolecular hydrogen bonds on the translocation of the small drug piracetam through a lipid bilayer†
João T. S. Coimbra ,
Ralph Feghali,
Rui P. Ribeiro‡
,
Maria J. Ramos
,
Ralph Feghali,
Rui P. Ribeiro‡
,
Maria J. Ramos and
Pedro A. Fernandes
and
Pedro A. Fernandes *
*
LAQV, REQUIMTE, Departamento de Química e Bioquímica, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre, s/n, 4169-007 Porto, Portugal. E-mail: pafernan@fc.up.pt
First published on 4th January 2021
Abstract
The number of hydrogen bond donors and acceptors is a fundamental molecular descriptor to predict the oral bioavailability of small drug candidates. In fact, the most widely used oral bioavailability rules (such as the Lipinsky's rule-of-five and the Veber rules) make use of this molecular descriptor. It is generally assumed that hydrogen bond donors and acceptors impact on passive diffusion across cell membranes, a fundamental event during drug absorption and distribution. Although the relationship between the number of these motifs and the probability of having good oral bioavailability has been studied and described for more than 20 years, little attention has been given to their spatial distribution in the molecule. In this paper, we used molecular dynamics to describe the effect of intramolecular hydrogen bonding on the passive diffusion of a small drug (piracetam) through a lipid membrane. The results indicated that the formation of an intramolecular hydrogen bond decreases the barrier for translocation by ca. 4 kcal mol−1 and increases the permeability of the tested molecule, partially compensating the desolvation penalty arising from the penetration of the drug into the biological membrane core. This effect was apparent in simulations where the formation of this interaction was prevented with the help of modified potentials, and in simulations with a similar compound to piracetam that was not able to form this intramolecular hydrogen bond due to a larger distance between the hydrogen bond donor and acceptor groups. These results were also supported by coarse-grained methods, which are becoming an important resource for sampling a larger chemical space of molecules, with reduced computational effort. Furthermore, entropy and enthalpy derived profiles were also obtained as the compounds translocated across the membrane, suggesting that, even though the process of formation of internal hydrogen bonds is entropically unfavorable, the enthalpic gain is such that the formation of these interactions is beneficial for the passive diffusion across cell membranes.
Introduction
Hydrogen bonds are important interactions in biochemistry as these can play key roles in molecular recognition,1–3 structural stability,3,4 enzyme catalysis,5–7 and drug partition and permeability.8–11 The existence of functional groups in a drug that are capable of forming hydrogen bonds, can increase its solubility and the ability to establish important interactions with its biomolecular targets, driving potent binding and selectivity.12However, too many hydrogen bond donors/acceptors can have a deleterious effect on the drug's membrane partition and permeability.12 These polar groups can decrease the affinity toward the hydrophobic membrane region and also increase the water desolvation penalty upon penetration of the drug.12 Since a drug, apart from having the desired bioactivity, needs to demonstrate favorable pharmacokinetics, a proper balance between lipophilicity and hydrophilicity is thus crucial. In that regard, drug-like character predictors, such as Lipinski's rule-of-five (Ro5)13 or Veber's rules14 have been using the number of hydrogen bond donors/acceptors as a molecular descriptor. Conversely, recent studies have shown that in the post Ro5 era, drug candidate attrition due to poor pharmacokinetics and/or bioavailability has decreased significantly.15–17
More recently, interest has been spiking for drugs that lie outside the Ro5 criteria.18 There have been a few compounds that while outside the Ro5 chemical space, have still shown favorable cell permeation and oral bioavailability. Furthermore, it has been also shown that the Ro5 properties have been inflating with time.19
There have been a few strategies to increase the cell permeability outside the Ro5 chemical space, and these are mainly related to the reduction or shielding of polarity by N-methylation, bulky side chains and intramolecular hydrogen bonds (IMHBs).18 IMHBs can be formed, when a hydrogen bond donor and acceptor are in proximity in the same molecule. These interactions can work as molecular switches in drugs and may create two sets of conformations: (i) open conformations that should be more soluble in water, and (ii) closed conformations that can shield polarity relative to the open conformation, and thus result in higher lipophilicity and membrane permeability.20 IMHBs have been recognized as an efficient strategy to limit the negative impact on the pharmacokinetics of a drug, while not necessarily preventing the adoption of a different conformation upon binding with its biomolecular target.9 Several studies have now shown improved membrane permeability resultant from IMHBs, including small molecules and compounds outside the Ro5 chemical space, such as cyclic peptides and macrocycles.21
Due to the intrinsic flexibility that is granted by IMHB, their experimental characterization is still limited.22 In this regard, computational simulations have provided important information on these interactions extending the limits of current experiments.18,22 Molecular dynamics (MD) simulations, for instance, can offer a practical solution to efficiently sample the conformational space of molecules that are able to form IMHBs, and that can display different sets of conformations depending on the properties of the surrounding media.23
This work attempts to get a finer, atomic-level understanding of the influence of IMHB on the membrane translocation with MD simulations. For that, we have chosen a small drug, 2-oxo-1-pyrrolidine acetamide (PCT, piracetam) that serves as a good model for the study. PCT is a small and polar molecule that shows a bioavailability close to 100%, despite its hydrophilicity (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Poct of −1.54 determined by the “shake flask” method).24,25 In previous MD simulations we have already shown that PCT is able to form an IMHB between the oxo group in the pyrrolidine ring structure and the amide group, while at the center of the bilayer.26
Poct of −1.54 determined by the “shake flask” method).24,25 In previous MD simulations we have already shown that PCT is able to form an IMHB between the oxo group in the pyrrolidine ring structure and the amide group, while at the center of the bilayer.26
In this work, we have employed all-atom MD simulations to quantify the impact of the IMHB in the free energy profile of the membrane translocation of PCT, which has not been previously addressed. We have done so by also studying the translocation of a related compound, 3-oxo-1-pyrrolidine acetamide (here labelled as PCM). The two studied molecules are represented in Fig. 1. The two molecules are isomers that share most properties important for permeation (molecular weight, number of HBDA, number of rotatable bonds), but PCM cannot form an IMHB due to a higher distance between the donor and acceptor groups in the molecule. By comparing the free energy profiles for the translocation of the two molecules, we highlight the influence of this IMHB on the membrane translocation process. Using flat-bottom potentials, we have also restrained PCT and prevented the formation of the IMHB as the compound migrates from the water phase to the bilayer's center. In this way, we wanted to evaluate how much the chemical modification in PCM was affecting the free energy profile due to collateral electronic or stereochemical effects.
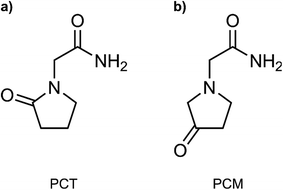 | ||
| Fig. 1 Compounds evaluated in this study. (a) 2-oxo-1-pyrrolidine acetamide (PCT, piracetam); (b) 3-oxo-1-pyrrolidine acetamide (here labelled as PCM). | ||
Lastly, to get a better understanding of the thermodynamic driving forces for the membrane translocation of PCT and PCM, and using both all-atom and coarse-grained (CG) MD simulations, we have also spatially resolved the entropy and enthalpy profiles upon translocation. Coarse-grained (CG) models have been successfully employed in the past to explore drug-membrane translocation.27 Due to its reduced computational effort, the CG approach is often considered when one needs to work with large scale models and/or if the system requires extensive sampling. The latter applies here, as a proper thermodynamic characterization of the translocation process requires extensive sampling. Hence, the combination of all-atom and CG MD simulations would increase the confidence in our conclusions. Furthermore, these near-atomic resolution methods have been successfully employed in high-throughput MD simulations to explore the drug-membrane permeability across a large chemical space of drug-like compounds.28
Methodology
System modeling
Our all-atom hydrated bilayer model system was composed of 64 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) lipids (32 lipids per leaflet), a hydration level of 70 water molecules per lipid, and NaCl ions (ca. 0.15 M). It was assembled using the CHARMM-GUI interface.29–31 For describing the lipids, we have used the SLipids force field,32,33 which has been shown to reproduce very accurately the structure of biological membranes and the energetics of membrane associated events, such as drug partition.34 This force field has been also demonstrated to be compatible with the AMBER force fields.35 We employed the TIP3P water model36 and used ff99SBildn37 ion parameters present in GROMACS.38–40 After an initial minimization and equilibration of the system, we have inserted two replicas of the studied compounds at different bilayer depths in the simulation box: one of the replicas was inserted in the water phase, and the other at the center of the lipid bilayer (see next sections for details). The compounds were parameterized with the general AMBER force field (GAFF)41 following a standard procedure, i.e. the atomic point charges were derived following a restrained electrostatic potential (RESP) procedure42 at the HF/6-31G(d) level of theory, to be coherent with the rest of the force field. The antechamber43 and Gaussian09 (ref. 44) software were used for this regard. Structure and topology files were converted to GROMACS compatible extension by using the ACPYPE tool.45Coarse-grained (CG) hydrated bilayer systems were also generated with the CHARMM-GUI interface, and using the MARTINI 2.0 force field for lipids and polarizable water.46,47 A total of 128 DOPC lipids (64 lipids per leaflet), and 2562 polarizable water beads were employed, again with a 0.15 M ionic concentration. The PCT and PCM molecules were also parameterized with the MARTINI force field, using the AUTO-MARTINI scheme.48 The CG topology files for PCT and PCM are provided in the ESI.† For adding the solute molecules in the hydrated bilayer system, we have employed the same protocol as for the all-atom simulations.
Molecular dynamics simulations parameters
The all-atom simulations were performed with the GROMACS 2018 software, with the Verlet cut-off scheme. A non-bonded cut-off value of 1.2 nm was employed. The LINCS constraint algorithm49 was applied to all bonds involving hydrogen atoms, which allowed for an integration time step of 2 fs. Temperature was set to 298.15 K with the Nose–Hoover thermostat (1.0 ps time constant for coupling),50,51 and a semi-isotropic pressure scaling to 1 atm was maintained with the Parrinello–Rahman barostat (5 ps time constant for coupling).52,53 During the NPT equilibration, the Berendsen barostat was employed.54 Dispersion corrections were applied to energy and pressure terms. Periodic boundary conditions were considered, and long range electrostatic interactions were treated by a Particle Mesh Ewald (PME) scheme.55 The center of mass motion was removed in a linear fashion and individually for the upper and lower leaflets and the rest of the system (including the solvent, ions and the two solute molecules).The CG MD simulations were also performed with GROMACS 2018 software using the Verlet cut-off scheme. A non-bonded cut-off of 1.1 nm was employed. Temperature was set to 298.15 K with the v-rescale thermostat (1.0 ps time constant for coupling),56 and a semi-isotropic pressure scaling to 1 atm was maintained with the Parrinello–Rahman barostat (12 ps time constant for coupling). A 10 fs integration time step was employed. Long range electrostatic interactions were treated by a reaction-field scheme using a relative dielectric constant of 2.5. The center of mass motion was removed in a linear fashion for the entire system.
Umbrella sampling simulations and analysis
The hydrated bilayers coming from CHARMM-GUI were minimized and equilibrated in the NVT and NPT ensembles. Subsequently, an NPT conventional MD simulation of 300 ns was run. From the density profiles and as in previous works,57–59 we have defined a four-region model to aid in the analysis of the PMFs. Region I contained only the hydrophobic lipid tails. Region II contained both hydrophobic tails and the initial portion of the polar headgroup density, ending where the lipid tail density intercepted the choline density. Region III contained most of the charged phosphate and choline density. Finally, region IV was composed primarily of bulk water, and a small portion of the lipid's headgroup density.Two replicas of each compound were inserted at different bilayer depths using the last structure of the previous run – one in the water phase and the other near the bilayer's center. The interactions with the hydrated bilayer system were then gradually switched on during 20 ns, with the compounds harmonically restrained to the initial positions relative to the bilayer's COM (with a harmonic force constant of 477.7 kcal mol−1 nm−2). Afterwards, a constant pulling simulation of 50 ns was performed to sample the desired translocation coordinate (pulling rate of −0.000074 nm ps−1). The translocation coordinate in this case was defined by the COM distance between the solute and the lipid bilayer and was discretized into 38 sampling windows spaced by 0.1 nm. This comprised the COM distances of [−3.5; 0.2] nm and [−0.2; 3.5] nm, depending on whether the compound started in the water phase or near the center of the bilayer. Then production runs were performed for 160 ns (with a harmonic force constant of 358.3 kcal mol−1 nm−2). The binding free energy, 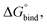 was then derived from the energy profile using eqn (1):60–62
was then derived from the energy profile using eqn (1):60–62
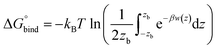 | (1) |
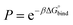 | (2) |
For the calculation of the binding free energies we have considered the energy profiles produced from the last 100 ns of each window of the production runs. These were assessed with the weighted histogram analysis method (WHAM) tool63,64 present in GROMACS 2018. A bootstrapping analysis (200 bootstraps) was also performed to assess for the error of the energy profile. Unsymmetrized energy profiles are shown as ESI† to assess convergence (see ESI, Fig. S1†).
For spatially resolving the enthalpy and entropy profiles as the compounds translocate the bilayer, we have used the finite difference (FD) of the free energy with respect to temperature.60,65 The free energy was decomposed in its entropic and enthalpic components using eqn (3) and (4):
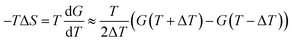 | (3) |
| ΔH = ΔG + TΔS | (4) |
The FD approach has been described to perform generally well, provided that enough sampling is performed and that sufficiently large temperature gaps are considered.65 In this case, the umbrella sampling simulations were run at three additional temperatures – 283.15 K, 313.15 K and 328.15 K. A total of 180 ns per window were run for each of the mentioned temperatures (with a harmonic force constant of 358.3 kcal mol−1 nm−2). Initial configurations of each umbrella window were obtained after the previous production runs at 298.15 K. By combining different temperature pairs to calculate the entropic component of translocation, we were able to estimate the uncertainty of our calculations from the standard deviation of these multiple estimates.
The protocol for the coarse-grained simulations was very similar to the all-atom simulations. The only difference resided on the simulated time scales. For the umbrella sampling production runs at 298.15 K, each window was simulated for 220 ns. For the spatially resolved entropy and enthalpy profiles, each window from the three additional temperatures was also simulated for 220 ns. In the case of the coarse-grained simulations a harmonic force constant of 477.7 kcal mol−1 nm−2 was always employed. Analysis of the free energy profiles was conducted using the last 150 ns of the production runs.
The permeability coefficient was calculated using the inhomogeneous solubility-diffusion model (ISDM),66,67 in which the resistivity, R, and permeability, Pm, are obtained via eqn (5):
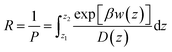 | (5) |
For the position-dependent diffusivities, D(z), we have used the generalized Langevin method, using eqn (6):
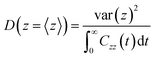 | (6) |
Although the ISDM has led to varied results for the permeability of large solutes,8 its applicability to small permeants has been deemed fit.72 So, for the purposes of this study we have decided to include the permeability data for PCT and PCM using only the ISDM.
Using flat-bottom potentials, we have also restrained PCT and prevented the formation of the IMHB as the compound migrates from the water phase to the bilayer's center. Therefore, for the entire translocated distance, we have defined a flat-bottom potential, where at an interatomic distance of the oxo group of the pyrrolidine ring and the nitrogen atom of the amide group below ca. 0.4 nm, a harmonic potential with a force constant of 1194.2 kcal mol−1 nm−2 was employed.
We used the GROMACS native analysis tools to analyze other aspects, such as the polar surface area (PSA) and hydrogen bonds along the bilayer's normal. Visual inspection was attained with the VMD 1.9.3 software.73
Results and discussion
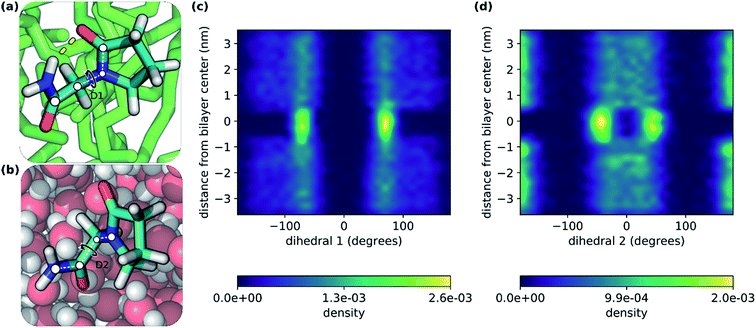
In this study, we have explored the translocation of the small drug piracetam (PCT) across a hydrated phospholipidic bilayer model system, to study the impact of an IMHB in the permeation of this molecule. In a previous study, we have observed that, in aqueous solvent, the hydrogen donor and acceptor groups of PCT form hydrogen bonds with water molecules. But, when PCT dives deeply into the center of the membrane, its hydrogen bond donor and acceptor groups make an IMHB, compensating, at least in part, for the desolvation cost, reducing its polar surface area and overall favoring the interaction with the bilayer's hydrophobic core.26In Fig. 2, we can see two conformations of PCT derived from the MD simulations done here: (i) where the IMHB is formed and that is more prevalent in the hydrophobic core of the bilayer (Fig. 2a); and (ii) an extended conformation where the IMHB is not formed (Fig. 2b). In Fig. 2, we have also represented the behavior of two dihedral angles that describe the two flexible bonds present in PCT (Fig. 2c and d). In accordance with previous studies, we saw that as PCT approached the bilayer center, the populations for the two dihedral angles were more focused around the specific values that allow for the formation of an IMHB.
We have decided to extend this study, to quantify the impact of the IMHB to the translocation of PCT (including its partition and permeability) and also measure the thermodynamic quantities that are influencing this process, by decomposing the free energy profile into its enthalpic and entropic components.
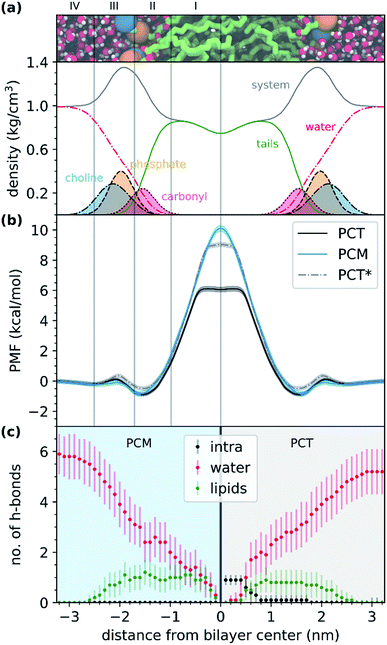
Fig. 3a shows the representation of the hydrated bilayer system and partial density profiles for the different functional groups or molecules in the system, followed by the translocation profile of PCT in Fig. 3b, in which we have obtained a profile similar to the one of our previous work.26 As PCT approaches the bilayer from the water phase, and after a small decrease in the free energy profile to −0.2 kcal mol−1, we observed a very small increase in region III to 0.1 kcal mol−1. Then, we saw a shallow minimum (ca. −0.9 kcal mol−1) in the most heterogeneous region of the lipid bilayer, region II, that should dominate the partition of this compound to the bilayer. Then the free energy profile increased to a maximum of 6.1 kcal mol−1 in region I of the bilayer, finding a plateau while at the center.
From the analysis of the hydrogen bonds (h-bond) profiles along the translocated coordinate in Fig. 3c, we observed the formation of an IMHB in region I of the hydrated bilayer system. We also observed that at ca. 0.5 nm from the bilayer center, PCT was not establishing any h-bonds with water or lipid molecules. The polar surface area (PSA) analysis (see ESI, Fig. S1†), also shows that while in region I, PCT decreases its PSA (from 64.8 ± 1.6 Å2 in the water phase to 60.0 ± 1.6 Å2 in the center), thus, in principle, this should favor the affinity for this region.
To measure the impact of the IMHB in the partition and permeability of PCT, we have then modified the chemical structure of PCT, by changing the oxo group to a different position in the pyrrolidine ring structure (see Fig. 1b). In this way, the modified compound, which we have labelled as PCM, was not able to form the IMHB due to the distance between the hydrogen bond donor and acceptor groups.
As the modified PCM molecule went from the water phase to the lipid bilayer headgroups (region IV, III and II), we observed a very similar profile to that of PCT (see Fig. 3b). However, as the compound penetrated deeply into the membrane and approached the bilayer center (region I), the free energy profile changed in relation to PCT, increasing more and up to a maximum of 10.1 kcal mol−1 (4 kcal mol−1 above PCT). Furthermore, and in contrast with PCT, we did not observe a plateau for PCM, while in region I. The free energy of transfer of PCM rose continually. This can be explained by looking at the h-bond profiles in Fig. 3c, because PCT replaces the lost hydrogen bonds it was making with the solvent by an IMHB, whereas PCM cannot make such compensation. Comparing the two free energy profiles, and if the difference comes essentially from the IMHB, this means that an IHMB can lower the free energy barrier for translocation by as much as 4 kcal mol−1.
In Table 1, we summarize the partition and permeability coefficients for both compounds, together with the average PSA in water (at 3.4 nm from the bilayer center) and at the bilayer's center (at 0.0 nm). Altogether, our results suggest that PCM and PCT have a very similar partition to this bilayer system, but they present distinct permeability coefficients, dominated by the high energy barrier at the middle of the bilayer. In fact, PCT showed a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pm almost 2 times higher than PCM, when determined by the ISDM. We also saw that the permeability estimate should be dominated by the free energy profile, because the diffusivity calculations gave essentially the same results for both molecules, as expected by their similar structure (see ESI, Fig. S2†). The constant PSA profile of PCM and the hydrogen bond analysis along the translocation coordinate, also indicated that PCM was not forming an IMHB.
Pm almost 2 times higher than PCM, when determined by the ISDM. We also saw that the permeability estimate should be dominated by the free energy profile, because the diffusivity calculations gave essentially the same results for both molecules, as expected by their similar structure (see ESI, Fig. S2†). The constant PSA profile of PCM and the hydrogen bond analysis along the translocation coordinate, also indicated that PCM was not forming an IMHB.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P), permeability (log
P), permeability (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pm) and polar surface area (PSA) of the tested compounds (PCT and PCM) in the DOPC hydrated bilayer system
Pm) and polar surface area (PSA) of the tested compounds (PCT and PCM) in the DOPC hydrated bilayer system
| Compound | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pm/cm s−1 Pm/cm s−1 |
PSA (at z = 3.4 nm)/Å2 | PSA (at z = 0.0 nm)/Å2 |
|---|---|---|---|---|
| PCT | 0.07 ± 0.05 | −3.34 | 64.8 ± 1.6 | 60.0 ± 1.6 |
| PCM | 0.05 ± 0.04 | −5.82 | 65.6 ± 1.4 | 65.2 ± 1.5 |
Then, we have studied the translocation of PCT, while applying a flat-bottom potential to impair the formation of the IMHB in this molecule. We have done so, by restraining the interatomic distance of the nitrogen atom of the amide group and the oxo group of the pyrrolidine ring, to values that do not allow the formation of the IMHB in PCT (see Methods section). Even though we focused the discussion in the PCM molecule in this work, because PCM is synthesizable and experimentally testable, the artificially restrained PCT molecule, confirms that the difference in the translocation profiles of PCT and PCM was due to the IMHB and not due to the different chemical properties that the modification could induce (for instance, due to different point charges of the molecules).
We observed that the PMF for the restrained PCT molecule increased to 9.0 kcal mol−1 in the middle of the bilayer (3 kcal mol−1 more than PCT and close to the PCM value of 10.1 kcal mol−1). This result suggested that the main difference in the free energy profiles of PCT and PCM was mainly due to the formation of the IMHB.
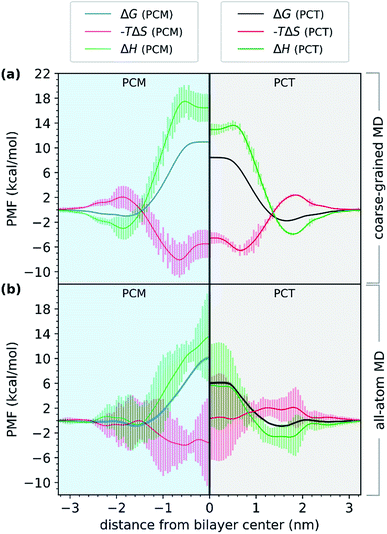
Additionally, we have also decomposed the free energy profile in its two components: enthalpic and entropic. We have done so, for both PCT and PCM molecules. Since the enthalpic and entropic components are difficult to obtain due to their difficult convergence,60,65 we proposed to evaluate these profiles using both all-atom simulations and coarse-grained molecular dynamics (CGMD) simulations. In CGMD, the molecular representation of the system was simplified, and we ended up with less degrees of freedom.
First, we evaluated the PMF of PCT and PCM using a coarse-grained model. Comparing the results with those from all-atom simulations in Fig. 4, we observed a very similar trend. Even though the free energy minimum are more pronounced for the CG simulations and the PCT and PCM molecules differ in their partition to the bilayer, the energy barrier for crossing, measured by the difference between the minimum and maximum values of the free energy profile, is still higher for the PCM molecule, by almost 2.0 kcal mol−1. A different perspective of Fig. 4 is given in ESI (see Fig. S3†) for comparing the free energy profiles and their components as calculated by the all-atoms and coarse-grained physical models.
In Fig. 4, we have represented the entropic (−TΔS) and enthalpic (ΔH) profiles that have been derived from coarse-grained (Fig. 4a) and all-atom (Fig. 4b) MD simulations. These profiles were calculated for both PCT and PCM compounds. Considering the CGMD simulations results, we observed that the major difference between the PCT and PCM molecules was in the ΔH component. We saw that in the center of the bilayer, ΔH increased to 18.2 kcal mol−1 in the case of PCM, and just 14.1 kcal mol−1 in the case of PCT. Hence, the CGMD simulations indicated that the PCM translocation is enthalpically unfavorable in the center of the bilayer, when compared with PCT. The same tendency was found for the all-atom MD simulations, even though the errors of this estimate were much higher. This result would make sense, considering that PCM, in contrast to PCT, cannot establish an IMHB. Furthermore, PCT should also present more favorable interactions with the membrane hydrophobic core, because the IMHB that is formed while PCT is at the center of the bilayer also decreases the PSA of PCT in comparison with PCM.
As for the entropic component, represented as −TΔS, and considering the CGMD simulations, the profiles were very similar, with PCM showing only a slightly more favorable entropic profile (on average), as it approached the bilayer. When considering the all-atom MD simulations, the results were different. The entropic profile of PCM seemed to be more favorable than PCT, as both molecules approached the bilayer. However, we can see that the errors were higher for these estimates, so any conclusions should be drawn carefully. It would make sense that PCM would present a more favorable entropic profile, if considering that it presented (on average) one more h-bond with water molecules, and that it was not able to establish an IMHB while at the center. Consequently, the desolvation of PCM as it translocated the bilayer would release more water molecules and the conformational flexibility of PCM would be also higher than PCT's, because the geometry of the molecule is not constrained by an IMHB. Nonetheless, the unfavorable enthalpic profile of PCM seemed to dominate the entropic gain, thus decreasing the permeability of this molecule when compared with PCT.
Altogether, our results suggested that the difference between the barriers of PCT and PCM, while at the center of the bilayer, are dominated by enthalpy. Furthermore, the partition of both molecules to the bilayer's polar region, seemed to be enthalpically favored. Compared to other studies in the literature,60 we have also found a favorable entropic component (−TΔS) as the compounds approached the middle of the bilayer, and an unfavorable −TΔS as the compound approached the highest density region of the system. Others have suggested that this effect was mostly due to the acyl chains' conformational entropy and the available free volume distribution in the membrane.60 Even though, these estimates are affected by large errors (in particular for the all-atom simulations), a combination with CGMD simulations allowed us to provide a more robust interpretation to the enthalpic and entropic profiles, increasing the confidence in our conclusions.
Conclusions
In this study, we have used MD simulations to describe the effects of an intramolecular hydrogen bond (IMHB) on the passive diffusion of a small drug (piracetam) through a lipid membrane. We have done so, by performing chemical modifications on the structure of piracetam (PCT), and in this way, preventing the formation of the IMHB. The new compound, PCM, presented the same partition constant to the membrane model, but showed a very different permeability coefficient. In fact, the permeability of PCM was much lower than PCT, due to the higher free energy for the transfer. The reduction in the free energy barrier for the transfer was calculated in 4 kcal mol−1. This reinforced that this IMHB was very important for the translocation of piracetam.These results were also confirmed, by using flat-bottom potentials to inhibit the formation of this IMHB in PCT. With this test, we confirmed that the differences in the transfer free energy profile between PCT and PCM were essentially due to the absence of the internal hydrogen bond, and not due to other factors, such as different point atomic charges on the molecules.
By combining all-atom and coarse-grained MD simulations, we also decomposed the free energy profiles into their enthalpic and entropic components. Our results suggested that the main free energy difference between PCT and PCM was enthalpically driven, with PCM showing a more unfavorable enthalpy in the middle of the membrane. This is supported by the fact that PCT forms an IMHB as it approaches the middle of the bilayer. The inherent reduction on the PSA upon formation of the IMHB should also protect polar groups from a very hydrophobic environment, thus favoring the interactions with the core of the membrane.
Altogether, we have shown the potential of MD simulations, from all-atom to coarse-grained levels of resolution, to spatially resolve thermodynamic profiles as the compounds translocate hydrated bilayer systems. This allowed us to extract both thermodynamic and kinetic information for the translocation process. We have also shown the potential of MD simulations, of not only measuring the effect of orthogonal degrees of freedom to the translocation of molecules, but also the effects of modifications in the permeant to the same process.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Applied Molecular Biosciences Unit – UCIBIO, which is financed by national funds from FCT/MCTES – Portuguese Foundation for Science and Technology within the scope of the project UID/Multi/04378/2019 and by the Associate Laboratory for Green Chemistry Unit – LAQV, which is financed by national funds from FCT/MCTES within the scope of the project UIDB/50006/2020. The work was also supported by the European Union (FEDER funds through COMPETE), and by “Programa Operacional Regional do Norte” (NORTE 2020) under the PORTUGAL 2020 Partnership Agreement, through the European Regional Development Fund (ERDF): project NORTE-01-0145-FEDER-000024. JTSC has received financial support from the scientific employment stimulus – individual call of 2018 (CEECIND/01374/2018). We acknowledge PRACE for awarding us access to MareNostrum at Barcelona Supercomputing Center (BSC), Spain. We thank Dr Óscar Passos for technical assistance.References
- D. Santos-Martins and S. Forli, Charting Hydrogen Bond Anisotropy, J. Chem. Theory Comput., 2020, 16(4), 2846–2856 CrossRef CAS.
- S. W. Pedersen, S. B. Pedersen, L. Anker, G. Hultqvist, A. S. Kristensen, P. Jemth and K. Stromgaard, Probing backbone hydrogen bonding in PDZ/ligand interactions by protein amide-to-ester mutations, Nat. Commun., 2014, 5, 3215 CrossRef.
- A. V. Morozov and T. Kortemme, Potential Functions for Hydrogen Bonds in Protein Structure Prediction and Design, Adv. Protein Chem., 2005, 72, 1–38 CrossRef.
- C. N. Pace, H. L. Fu, K. L. Fryar, J. Landua, S. R. Trevino, D. Schell, R. L. Thurlkill, S. Imura, J. M. Scholtz, K. Gajiwala, J. Sevcik, L. Urbanikova, J. K. Myers, K. Takano, E. J. Hebert, B. A. Shirley and G. R. Grimsley, Contribution of hydrogen bonds to protein stability, Protein Sci., 2014, 23(5), 652–661 CrossRef CAS.
- R. P. P. Neves, P. A. Fernandes and M. J. Ramos, Mechanistic insights on the reduction of glutathione disulfide by protein disulfide isomerase, Proc. Natl. Acad. Sci. U.S.A., 2017, 114(24), E4724–E4733 CrossRef CAS.
- A. R. Calixto, M. J. Ramos and P. A. Fernandes, Conformational diversity induces nanosecond-timescale chemical disorder in the HIV-1 protease reaction pathway, Chem. Sci., 2019, 10(30), 7212–7221 RSC.
- L. Simon and J. M. Goodman, Enzyme Catalysis by Hydrogen Bonds: The Balance between Transition State Binding and Substrate Binding in Oxyanion Holes, J. Org. Chem., 2010, 75(6), 1831–1840 CrossRef CAS.
- C. J. Dickson, V. Hornak, R. A. Pearlstein and J. S. Duca, Structure-Kinetic Relationships of Passive Membrane Permeation from Multiscale Modeling, J. Am. Chem. Soc., 2017, 139(1), 442–452 CrossRef CAS.
- S. B. Rafi, B. R. Hearn, P. Vedantham, M. P. Jacobson and A. R. Renslo, Predicting and Improving the Membrane Permeability of Peptidic Small Molecules, J. Med. Chem., 2012, 55(7), 3163–3169 CrossRef CAS.
- W. Shinoda, Permeability across lipid membranes, Biochim. Biophys. Acta Biomembr., 2016, 1858(10), 2254–2265 CrossRef CAS.
- T. Rezai, J. E. Bock, M. V. Zhou, C. Kalyanaraman, R. S. Lokey and M. P. Jacobson, Conformational flexibility, internal hydrogen bonding, and passive membrane permeability: Successful in silico prediction of the relative permeabilities of cyclic peptides, J. Am. Chem. Soc., 2006, 128(43), 14073–14080 CrossRef CAS.
- A. Alex, D. S. Millan, M. Perez, F. Wakenhut and G. A. Whitlock, Intramolecular hydrogen bonding to improve membrane permeability and absorption in beyond rule of five chemical space, Medchemcomm, 2011, 2(7), 669–674 RSC.
- C. A. Lipinski, F. Lombardo, B. W. Dominy and P. J. Feeney, Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings, Adv. Drug Delivery Rev., 1997, 23(1–3), 3–25 CrossRef CAS.
- D. F. Veber, S. R. Johnson, H. Y. Cheng, B. R. Smith, K. W. Ward and K. D. Kopple, Molecular properties that influence the oral bioavailability of drug candidates, J. Med. Chem., 2002, 45(12), 2615–2623 CrossRef CAS.
- D. Cook, D. Brown, R. Alexander, R. March, P. Morgan, G. Satterthwaite and M. N. Pangalos, Lessons learned from the fate of AstraZeneca's drug pipeline: a five-dimensional framework, Nat. Rev. Drug Discov., 2014, 13(6), 419–431 CrossRef CAS.
- I. Khanna, Drug discovery in pharmaceutical industry: productivity challenges and trends, Drug Discov. Today, 2012, 17(19–20), 1088–1102 CrossRef.
- I. Kola and J. Landis, Can the pharmaceutical industry reduce attrition rates?, Nat. Rev. Drug Discov., 2004, 3(8), 711–715 CrossRef CAS.
- P. Matsson, B. C. Doak, B. Over and J. Kihlberg, Cell permeability beyond the rule of 5, Adv. Drug Delivery Rev., 2016, 101, 42–61 CrossRef CAS.
- P. D. Leeson and B. Springthorpe, The influence of drug-like concepts on decision-making in medicinal chemistry, Nat. Rev. Drug Discov., 2007, 6(11), 881–890 CrossRef CAS.
- B. Kuhn, P. Mohr and M. Stahl, Intramolecular Hydrogen Bonding in Medicinal Chemistry, J. Med. Chem., 2010, 53(6), 2601–2611 CrossRef CAS.
- G. Caron, J. Kihlberg and G. Ermondi, Intramolecular hydrogen bonding: An opportunity for improved design in medicinal chemistry, Med. Res. Rev., 2019, 39(5), 1707–1729 CrossRef CAS.
- F. Colizzi, A. Hospital, S. Zivanovic and M. Orozco, Predicting the Limit of Intramolecular Hydrogen Bonding with Classical Molecular Dynamics, Angew. Chem. Int. Ed., 2019, 58(12), 3759–3763 CrossRef CAS.
- J. Witek, B. G. Keller, M. Blatter, A. Meissner, T. Wagner and S. Riniker, Kinetic Models of Cyclosporin A in Polar and Apolar Environments Reveal Multiple Congruent Conformational States, J. Chem. Inf. Model., 2016, 56(8), 1547–1562 CrossRef CAS.
- C. Altomare, S. Cellamare, A. Carotti, G. Casini, M. Ferappi, E. Gavuzzo, F. Mazza, P. A. Carrupt, P. Gaillard and B. Testa, X-Ray Crystal-Structure, Partitioning Behavior, and Molecular Modeling Study of Piracetam-Type Nootropics - Insights into the Pharmacophore, J. Med. Chem., 1995, 38(1), 170–179 CrossRef CAS.
- B. Winblad, Piracetam: A review of pharmacological properties and clinical uses, CNS Drug Rev., 2005, 11(2), 169–182 CrossRef CAS.
- R. P. Ribeiro, J. T. S. Coimbra, M. J. Ramos and P. A. Fernandes, Diffusion of the small, very polar, drug piracetam through a lipid bilayer: an MD simulation study, Theor. Chem. Acc., 2017, 136, 46 Search PubMed.
- H. A. L. Filipe, M. Javanainen, A. Salvador, A. M. Galvao, I. Vattulainen, L. M. S. Loura and M. J. Moreno, Quantitative Assessment of Methods Used To Obtain Rate Constants from Molecular Dynamics Simulations-Translocation of Cholesterol across Lipid Bilayers, J. Chem. Theory Comput., 2018, 14(7), 3840–3848 CrossRef CAS.
- R. Menichetti, K. H. Kanekal and T. Bereau, Drug-Membrane Permeability across Chemical Space, ACS Cent. Sci., 2019, 5(2), 290–298 CrossRef CAS.
- S. Jo, T. Kim, V. G. Iyer and W. Im, CHARMM-GUI: a web-based graphical user interface for CHARMM, J. Comput. Chem., 2008, 29(11), 1859–1865 CrossRef CAS.
- E. L. Wu, X. Cheng, S. Jo, H. Rui, K. C. Song, E. M. Davila-Contreras, Y. F. Qi, J. M. Lee, V. Monje-Galvan, R. M. Venable, J. B. Klauda and W. Im, CHARMM-GUI Membrane Builder Toward Realistic Biological Membrane Simulations, J. Comput. Chem., 2014, 35(27), 1997–2004 CrossRef CAS.
- Y. F. Qi, H. I. Ingolfsson, X. Cheng, J. Lee, S. J. Marrink and W. Im, CHARMM-GUI Martini Maker for Coarse-Grained Simulations with the Martini Force Field, J. Chem. Theory Comput., 2015, 11(9), 4486–4494 CrossRef CAS.
- J. P. M. Jambeck and A. P. Lyubartsev, Derivation and Systematic Validation of a Refined All-Atom Force Field for Phosphatidylcholine Lipids, J. Phys. Chem. B, 2012, 116(10), 3164–3179 CrossRef.
- J. P. M. Jambeck and A. P. Lyubartsev, An Extension and Further Validation of an All-Atomistic Force Field for Biological Membranes, J. Chem. Theory Comput., 2012, 8(8), 2938–2948 CrossRef.
- M. Paloncyova, G. Fabre, R. H. DeVane, P. Trouillas, K. Berka and M. Otyepka, Benchmarking of Force Fields for Molecule-Membrane Interactions, J. Chem. Theory Comput., 2014, 10(9), 4143–4151 CrossRef CAS.
- A. P. Lyubartsev and A. L. Rabinovich, Force Field Development for Lipid Membrane Simulations, Biochim. Biophys. Acta Biomembr., 2016, 1858(10), 2483–2497 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of Simple Potential Functions for Simulating Liquid Water, J. Chem. Phys., 1983, 79(2), 926–935 CrossRef CAS.
- E. J. Sorin and V. S. Pande, Exploring the helix-coil transition via all-atom equilibrium ensemble simulations, Biophys. J., 2005, 88(4), 2472–2493 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- D. Van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, GROMACS: Fast, flexible, and free, J. Comput. Chem., 2005, 26(16), 1701–1718 CrossRef CAS.
- H. J. C. Berendsen, D. Vanderspoel and R. Vandrunen, Gromacs - a Message-Passing Parallel Molecular-Dynamics Implementation, Comput. Phys. Commun., 1995, 91(1–3), 43–56 CrossRef CAS.
- J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25(9), 1157–1174 CrossRef CAS.
- C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges - the Resp Model, J. Phys. Chem., 1993, 97(40), 10269–10280 CrossRef CAS.
- J. M. Wang, W. Wang, P. A. Kollman and D. A. Case, Automatic atom type and bond type perception in molecular mechanical calculations, J. Mol. Graph. Model., 2006, 25(2), 247–260 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. W. Sousa da Silva and W. F. Vranken, ACPYPE - AnteChamber PYthon Parser interfacE, BMC Res. Notes, 2012, 5, 367 CrossRef.
- S. O. Yesylevskyy, L. V. Schafer, D. Sengupta and S. J. Marrink, Polarizable Water Model for the Coarse-Grained MARTINI Force Field, PLoS Comput. Biol., 2010, 6(6), e1000810 CrossRef.
- D. H. de Jong, G. Singh, W. F. D. Bennett, C. Arnarez, T. A. Wassenaar, L. V. Schafer, X. Periole, D. P. Tieleman and S. J. Marrink, Improved Parameters for the Martini Coarse-Grained Protein Force Field, J. Chem. Theory Comput., 2013, 9(1), 687–697 CrossRef CAS.
- T. Bereau and K. Kremer, Automated Parametrization of the Coarse-Grained Martini Force Field for Small Organic Molecules, J. Chem. Theory Comput., 2015, 11(6), 2783–2791 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, LINCS: A linear constraint solver for molecular simulations, J. Comput. Chem., 1997, 18(12), 1463–1472 CrossRef CAS.
- S. Nose, A Molecular-Dynamics Method for Simulations in the Canonical Ensemble, Mol. Phys., 1984, 52(2), 255–268 CrossRef CAS.
- W. G. Hoover, Canonical Dynamics - Equilibrium Phase-Space Distributions, Phys. Rev. A, 1985, 31(3), 1695–1697 CrossRef.
- M. Parrinello and A. Rahman, Polymorphic Transitions in Single-Crystals - a New Molecular-Dynamics Method, J. Appl. Phys., 1981, 52(12), 7182–7190 CrossRef CAS.
- S. Nose and M. L. Klein, Constant Pressure Molecular-Dynamics for Molecular-Systems, Mol. Phys., 1983, 50(5), 1055–1076 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. Vangunsteren, A. Dinola and J. R. Haak, Molecular-Dynamics with Coupling to an External Bath, J. Chem. Phys., 1984, 81(8), 3684–3690 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, Particle Mesh Ewald - an N.Log(N) Method for Ewald Sums in Large Systems, J. Chem. Phys., 1993, 98(12), 10089–10092 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126(1), 014101 CrossRef.
- J. L. MacCallum, W. F. D. Bennett and D. P. Tieleman, Distribution of amino acids in a lipid bilayer from computer simulations, Biophys. J., 2008, 94(9), 3393–3404 CrossRef CAS.
- J. T. S. Coimbra, N. F. Bras, P. A. Fernandes, M. Rangel and M. J. Ramos, Membrane partition of bis-(3-hydroxy-4pyridinonato) zinc(ii) complexes revealed by molecular dynamics simulations, RSC Adv., 2018, 8(48), 27081–27090 RSC.
- S. J. Marrink, A. H. de Vries and A. E. Mark, Coarse grained model for semiquantitative lipid simulations, J. Phys. Chem. B, 2004, 108(2), 750–760 CrossRef CAS.
- J. L. MacCallum and D. P. Tieleman, Computer simulation of the distribution of hexane in a lipid bilayer: Spatially resolved free energy, entropy, and enthalpy profiles, J. Am. Chem. Soc., 2006, 128(1), 125–130 CrossRef CAS.
- J. P. M. Jambeck and A. P. Lyubartsev, Implicit inclusion of atomic polarization in modeling of partitioning between water and lipid bilayers, Phys. Chem. Chem. Phys., 2013, 15(13), 4677–4686 RSC.
- C. Neale, W. F. D. Bennett, D. P. Tieleman and R. Pomes, Statistical Convergence of Equilibrium Properties in Simulations of Molecular Solutes Embedded in Lipid Bilayers, J. Chem. Theory Comput., 2011, 7(12), 4175–4188 CrossRef CAS.
- S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, The Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules .1. The Method, J. Comput. Chem., 1992, 13(8), 1011–1021 CrossRef CAS.
- J. S. Hub, B. L. de Groot and D. van der Spoel, g_wham-A Free Weighted Histogram Analysis Implementation Including Robust Error and Autocorrelation Estimates, J. Chem. Theory Comput., 2010, 6(12), 3713–3720 CrossRef CAS.
- S. Jo, C. Chipot and B. Roux, Efficient Determination of Relative Entropy Using Combined Temperature and Hamiltonian Replica-Exchange Molecular Dynamics, J. Chem. Theory Comput., 2015, 11(5), 2234–2244 CrossRef CAS.
- J. M. Diamond and Y. Katz, Interpretation of Nonelectrolyte Partition-Coefficients between Dimyristoyl Lecithin and Water, J. Membr. Biol., 1974, 17(2), 121–154 CrossRef CAS.
- S. J. Marrink and H. J. C. Berendsen, Simulation of Water Transport through a Lipid-Membrane, J. Phys. Chem., 1994, 98(15), 4155–4168 CrossRef CAS.
- G. Hummer, Position-dependent diffusion coefficients and free energies from Bayesian analysis of equilibrium and replica molecular dynamics simulations, New J. Phys., 2005, 7, 34 CrossRef.
- D. Bemporad, J. W. Essex and C. Luttmann, Permeation of small molecules through a lipid bilayer: A computer simulation study, J. Phys. Chem. B, 2004, 108(15), 4875–4884 CrossRef CAS.
- M. Orsi, W. E. Sanderson and J. W. Essex, Permeability of Small Molecules through a Lipid Bilayer: A Multiscale Simulation Study, J. Phys. Chem. B, 2009, 113(35), 12019–12029 CrossRef CAS.
- T. S. Carpenter, D. A. Kirshner, E. Y. Lau, S. E. Wong, J. P. Nilmeier and F. C. Lightstone, A Method to Predict Blood-Brain Barrier Permeability of Drug-Like Compounds Using Molecular Dynamics Simulations, Biophys. J., 2014, 107(3), 630–641 CrossRef CAS.
- C. T. Lee, J. Comer, C. Herndon, N. Leung, A. Pavlova, R. V. Swift, C. Tung, C. N. Rowley, R. E. Amaro, C. Chipot, Y. Wang and J. C. Gumbart, Simulation-Based Approaches for Determining Membrane Permeability of Small Compounds, J. Chem. Inf. Model., 2016, 56(4), 721–733 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graph. Model., 1996, 14(1), 33–38 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Complementary figures (Fig. S1–S3) and coarse-grained topology files. See DOI: 10.1039/d0ra09995c |
| ‡ Current address: Department of Biotechnology, University of Verona, Strada Le Grazie 15, I-37134 Verona, Italy. |
| This journal is © The Royal Society of Chemistry 2021 |