Open Access Article
Open Access ArticleThe origin of the regiospecificity of acrolein dimerization†
Ramiro F. Quijano-Quiñones *a,
Jareth Guadarrama-Morenoa,
Mariana Quesadas-Rojasbc,
Gonzalo J. Mena-Rejón
*a,
Jareth Guadarrama-Morenoa,
Mariana Quesadas-Rojasbc,
Gonzalo J. Mena-Rejón d,
Carolina S. Castro-Seguraa and
David Cáceres-Castillo
d,
Carolina S. Castro-Seguraa and
David Cáceres-Castillo d
d
aLaboratorio de Química Teórica, Facultad de Química, Universidad Autónoma de Yucatán, Mérida, Yucatán, Mexico. E-mail: ramiro.quijano@correo.uady.mx
bPosgrado en Ciencias del Mar y Limnología, UNAM, Mexico
cEscuela Nacional de Educación Superior, UNAM, Mérida, Mexico
dLaboratorio de Química Farmaceútica, Facultad de Química, Universidad Autónoma de Yucatán, Mérida, Yucatán, Mexico
First published on 16th February 2021
Abstract
Acrolein dimerization is a intriguing case since the reaction does not occur to form the electronically preferred regioisomeric adduct. Various explanations have been suggested to rationalize this experimental regioselectivity, however, none of these arguments had been convincing enough. In this work, the hetero Diels–Alder acrolein dimerization was theoretically investigated using DFT and MP2 methods. The influence of nucleophilic/electrophilic interactions and non-covalent interactions (NCI) in the regiospecificity of the reaction were analyzed. Our results show that the NCI at the transition state are the key factor controlling the regiospecificity in this reaction. Besides, we found that the choice of calculation method can have an effect on the prediction of the mechanism in the reaction, as all DFT methods forecast a one-step hetero Diels–Alder acrolein dimerization, while MP2 predicts a stepwise description for the lower energy reaction channel.
1 Introduction
Non-covalent interactions (NCI) are everywhere in organic chemistry and biological systems. Although these interactions are weak, the combined effect becomes significant. Furthermore, in chemical reactions, single NCI or NCI acting in synergy contribute to differential stabilization of transition states where the differences between the activation energy are small.1–4 Even the importance of the NCI in organic chemistry, their impact in the Diels–Alder (DA) and hetero Diels–Alder (HDA) selectivity has not been studied as deep as the role of nucleophilic/electrophilic interaction and the Secondary Orbital Interactions (SOIS). The DA and HDA cycloadditions are two of the most important reactions used for the synthesis of cyclic compounds, with the high regio- and stereo-selectivity being some of the relevant issues of these reactions.5 Thus, a deeper understanding of the factors controlling the selectivity is crucial to design a more rational and efficient synthesis of cyclic and heterocyclic compounds.Traditionally, the endo rule has been explained mainly by SOIS, but, in recent years these interactions have been subject to controversy and NCI have been invoked to rationalize endo/exo stereoselectivities.6 Nevertheless, the influence of NCI on the regiochemical outcomes in DA and HDA, on the contrary to the one exerted by stereochemical factors, remains unclear. Since the first documented example of regiospecificity controlled by NCI in DA reactions between substituted acetylenes and tetrazines by Cioslowski et al. in 1993,3 few examples of DA and HDA regioselectivity mainly controlled by NCI have been reported. And many questions regarding the influence of NCI in regiocontrolling this type of reactions remain unanswered.
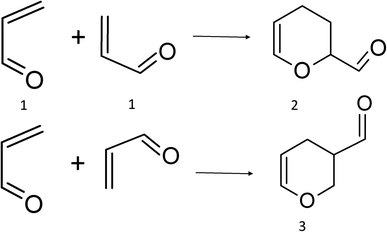
As is well known, acrolein thermally dimerizes through a regiospecific HDA cycloaddition (Scheme 1), producing exclusively isomer 27–10 and it is a textbook example of the regioselectivity of Diels–Alder reactions.11 The activation barrier energy for this reaction has been measured in a non-polar solvent (19.6 kcal mol−1, heptane) and is almost unaffected by the polarity of the media, indicating a non-polar mechanism. The proximity of the electron-withdrawing group to the unsaturated bond confers to acrolein strong electrophilicity,10,11 and the resonance forms of 1, indicate that the beta carbon is the most electrophilic atom, whereas the oxygen atom is the most nucleophilic. This is in complete agreement with the calculated reactivity index for this moiety.12 Therefore, according to electrophile–nucleophile interactions, adduct 3 should be the preferred regioisomeric product.
Until now, various explanations such as HOMO/LUMO interacting orbitals and SOIS has been adduced by different authors to rationalize the dimerization regioselectivity in acrolein dimerization.10,13–18 Even the regiospecific acrolein dimerization has been used as an example of the frontier orbital approach validity to regiochemical issues. But, due to the small differences in the coefficients of the HOMO/LUMO interacting orbitals,10,11 the FMO model could not explain the unique formation of the adduct 2. Thus, the origin of the regioselectivity in this reaction remains unclear.
In this work, we report the influence of the NCI in the regiospecificity of acrolein dimerization. To this end, we performed an accurate theoretical study on the NCI in the transition states imply in acrolein dimerization. The NCI was studied through the reduced gradient isosurfaces. The strength of the NCI was quantified by integrating their ρ(r) in defined ranges. The results show that the regiospecificity in the acrolein dimerization is being primarily controlled by the NCI. It is important to note that the analysis of the changes in electron density of the NCI along the reaction channels lies within the recent proposed Molecular Electron Density Theory (MEDT).19
2 Computational details
Full geometry optimizations for all the stationary points (TS, reactants, products) were performed using Gaussian 09.20 Since several studies have shown that, both, the transition state geometries and the activation energies depend on the theoretical method used in the geometry optimization,21–24 we employ the MP2 method and the M06-2X, B3LYP, ωB97X, and ωB97X-D functionals, along with the medium size 6-31+g(d,p) basis set. The meta-GGA M06-2X25 functional was applied since it was constructed to treat dispersion with more accuracy than older functionals and consequently performs very well in van der Waals complexes and describe successfully the π → σ transformations in reactions such as Diels–Alder and [3 + 2] cycloadditions.25–27 The medium size 6-31+G(d,p) basis set was used since different studies have shown that the description of medium-range interactions does not improve when a larger basis set is used.28–30 In addition, the M06-2X/6-31+G(d,p) level of theory has been used successfully in the theoretical study of the reactivity and selectivity of the Diels–Alder reaction.1,31,32 The ωB97X-D33 is one of the most reliable meta-GGA functionals in computational chemistry and includes long-range corrections and empirical dispersion terms using Grimme's D2 dispersion model, and is currently one of the best DFT methods for NCI calculation.34 In several benchmarks using different test sets, the M062X and wb97xd functionals have been proven to perform very well for NCI.27,34–41 Furthermore, it has been shown that the M062x functional works well in complexes governed by van der Waals interactions.41 Besides, the wB97X, and B3LYP functionals, and MP2 method were chosen for comparative purposes.Since the experimental activation energy9 was measured in an inert solvent and the experimental results show that the activation energy was almost unaffected by the solvent polarity, all calculation was made in the gas phase. Zero-point vibrational energy corrections were applied without scaling for all the examined structures.
The nature of all the stationary points was determined by diagonalizing the Hessian matrix at the same level. The reactants and products were identified from the vibrational analysis with all normal modes had real frequencies, and the TS with only one normal mode with imaginary frequency, corresponding to the movement in the direction of the reaction coordinate. Also, the intrinsic reaction coordinate (IRC) calculations were performed.42
The global electrophilicity index (ω) was calculated from the chemical potential (μ) and the chemical hardness (η) using the expression ω = (μ2/2η) according to Parr et al.43 The ω indicates the stabilization in energy when the chemical system acquires an additional charge from the surroundings. The η and the μ quantities can be approached in terms of the electron energy of the frontier molecular orbitals HOMO (EH) and LUMO (EL) as:
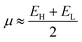 | (1) |
| η ≈ EL − EH | (2) |
In contrast to ω, several approaches have been established for the calculations of the nucleophilicity index (N). In this work, we have used the empirical approach to nucleophilicity proposed by Domingo et al.44 since there is evidence of its capability to predict the nucleophilic behaviour of organic molecules,45 in this scheme N is defined as
| N = EHOMO(Nucleophile) − EHOMO(TCE) | (3) |
To characterize the most nucleophilic/electrophilic centers, we calculated the spin density on the radical anion of the electrophile and the radical cation of the nucleophile, using the Gaussian 09 (ref. 20) code, whereas the Spartan16 (ref. 46) software was used to generate the spin density maps. Then, the Parr function local reactivity indexes were calculated using the following equations.12
| P+(r) = ρrcS(r) | (4) |
| P−(r) = ρraS(r) | (5) |
| Nk = NP−K |
| ωk = ωP+K |
To study the influence of NCI in the activation energy of acrolein dimerization, calculations of the reduced density gradient was performed. In this method, the maximum variations in the contributions to the Laplacian, along with the axes, correspond to the eigenvalues (λi) of the electron-density Hessian matrix. The sign of λ2 enables us to distinguish between the different types of weak interaction (repulsive and attractive), while the electron density lets us assess the interaction strength. We depict the low gradient isosurfaces, over the range of −0.5 < Sig(λ2) ρ < 0.5. Such NCI calculations were performed using the NCIPLOT program,47 and the resulting isosurfaces were visualized with Visual Molecular Dynamics (VMD) software.48
Finally, he NBO analysis to calculate the global electron density transfer (GEDT) was performed with the version included in Gaussian 09.49–53
3 Results and discussion
The study was divided into three parts, first, the geometrical parameters and GEDT, as well the reactivity indexes of acrolein were examined. Then, an analysis of the effect that the theoretical level of calculation has in the energetics of the acrolein dimerization was done. Finally, an exhaustive study of the factors controlling the stabilization of the transition states was performed.3.1. Geometrical, GEDT, and reactivity index analysis
The two acrolein molecules can react to produce the ortho and meta regioisomers (2 and 3, respectively) through different channels. For each channel, four transition states are possible: transoid (T) or cisoid (C) conformations, and exo (X) and endo (N) approximations.The eight possible TS are depicted in Fig. 1 where the label of each transition state is formed by combined all the symbols for the different combinations. To analyse the evolution of the potential energy surface for the dimerization in all reaction channels, we localize the eight TS (Fig. 1). Since results with all the functionals were qualitatively the same, only those obtained the results with M06-2X are presented, for simplicity.
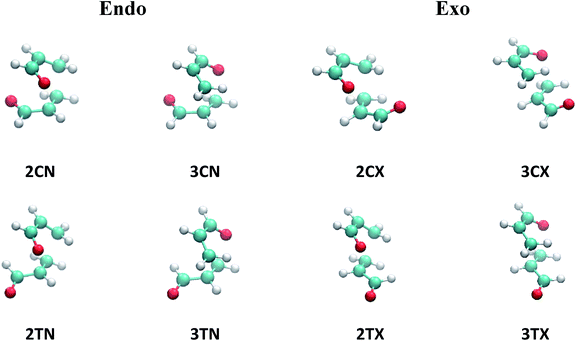 | ||
| Fig. 1 Transition state structures for acrolein cycloaddition dimerization at the M06-2X level of theory. | ||
We calculated the distance of selected bonds (Scheme 2), the asynchronicity degrees (Δd), and the GEDT for all TS. The GEDT was computed by sharing the natural charges obtained from the NBO analysis.20,49
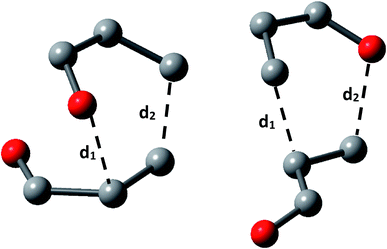 | ||
| Scheme 2 Nomenclature for selected bond lengths in the transition state structures for acrolein dimerization. | ||
The results, collected in Table 1, display that the beta carbon bond (d2) is the more developed in all the TS and show that all TS belongs to asynchronous process with the lowest energy TS 2CN presenting the higher asynchronicity degree (Δd). The GEDT at the most favourable TS 2CN (0.06e), allowed us to establish that acrolein dimerization as a non-polar reaction within the scale introduced by Domingo et al.54 Besides, has been established that with the increase of the polar character of DA reaction, the nucleophilic–electrophilic interactions at the TS are the mainly factor controlling reaction, whereas in a non-polar DA reaction this interactions cannot predict the regioselectivity.54 It is important to note, that the non-polarity of this reaction is in agreement with the experimental results. Finally, the global reactivity indexes of the acrolein, which show that this moiety is a good electrophile (ω = 1.6 eV) and good nucleophile (N = 1.5 eV).
| d1 | d2 | Δd | GEDT | |
|---|---|---|---|---|
| 2CN | 2.30 | 1.87 | 0.43 | 0.06 |
| 2TN | 2.17 | 2.00 | 0.17 | 0.09 |
| 2CX | 2.21 | 1.93 | 0.28 | 0.10 |
| 2TX | 2.16 | 1.98 | 0.18 | 0.10 |
| 3CN | 2.24 | 1.92 | 0.32 | 0.04 |
| 3TN | 2.13 | 2.01 | 0.12 | 0.07 |
| 3CX | 2.18 | 1.99 | 0.19 | 0.06 |
| 3TX | 2.14 | 2.01 | 0.13 | 0.06 |
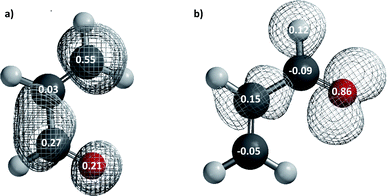
In order to check the conclusions based on the GEDT values, we have calculated Parr functions (Fig. 2) which are in consensus with those calculated in the ref. 12 using a B3LYP/6-31G* method. The Parr functions indicate the most nucleophilic centre in the dienophile, is the alpha conjugated carbon atom (P−K = 0.15) whereas the beta conjugated carbon (P+K = 0.55) is the most electrophilic center in the diene. Therefore, as we expected from above results, the Parr indices cannot be used to predict the regioselectivity in this polar reaction. Thus, it is necessary to explore alternative factors that can explain the experimental observations, by analysing the transition states.
3.2. Energetic analysis
The adduct 2 in endo approximation is both the preferred path (more negative Ea), and product (lesser Ereacc) with all the DFT methods used (see Table 2), in agreement with the selectivity of the acrolein dimerization. It is important to note that, despite the calculated experimental product ratio is explained very well by the DFT activation energies, non-statistical dynamics post-transition state may also occur.55–58 For instance, bispericyclic transition structure has been reported for several DA dimerization reactions59–65 even in natural product dimers.59,61| TS | MP2 | B3LYP | M06-2X | ωB97X-D | ωB97X | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ea | Ereacc | Ea | Ereacc | Ea | Ereacc | Ea | Ereacc | Ea | Ereacc | |
| 2CN | 9.8* | −24.9 | 20.5 | −16.8 | 16.7 | −30.0 | 17.8 | −28.1 | 21.1 | −29.4 |
| 2CX | 14.5 | −25.2 | 22.3 | −16.2 | 19.1 | −30.4 | 20.2 | −28.2 | 23.3 | −29.4 |
| 2TN | 19.2 | −22.9 | 26.1 | −14.7 | 23.0 | −28.2 | 23.9 | −26.3 | 26.9 | −27.8 |
| 2TX | 19.9 | −23.2 | 26.8 | −14.1 | 23.8 | −28.6 | 24.6 | −26.4 | 27.6 | −27.8 |
| 3CN | 18.3 | −24.3 | 23.9 | −14.9 | 18.9 | −29.1 | 20.9 | −26.7 | 23.7 | −27.9 |
| 3CX | 20.9 | −23.1 | 25.0 | −14.9 | 20.9 | −28.0 | 22.6 | −26.3 | 25.4 | −27.1 |
| 3TN | 21.7 | −22.2 | 26.7 | −12.7 | 22.2 | −27.3 | 23.5 | −24.9 | 26.1 | −26.3 |
| 3TX | 22.0 | −21.1 | 26.6 | −12.8 | 22.6 | −26.1 | 24.0 | −24.4 | 26.6 | −25.5 |
It is known that the B3LYP functional overestimated the Ea in DA and HDA reactions where the number of double bonds is reduced, since this functional cannot provide a balanced description of reaction that involve double to single bond transitions, as it energetically favours π-orbitals over σ-orbitals.26,66,67 For these reasons, in the acrolein dimerization case, B3LYP predicts reaction energies less exothermic than all the other methods, as we can check in Table 2. However, surprisingly, the B3LYP functional provide the best fit between the calculated activation energy and the experimental activation energy. Considering the factors discussed above, this B3LYP's good performance could be due to the well-known error cancellation in this functional68,69 rather than a good description of the electronic density on this system.
It is also notable that MP2 does not predict a one-step HDA reaction for the lower activation energy 2CN channel, as all attempts to find one-step pathways were unsuccessful. Instead, it predicts a stepwise reaction where the rate-limiting step of the mechanism is the first step with a Ea = 9.8 kcal mol−1, in clear disagreement with the experimental activation energy.8,9 In contrast, each one of the TS calculated with DFT methods belong to a one-step HDA cycloaddition reaction. Moreover, all DFT methods show that cisoid conformation lead to more stable products and transition states, compared to transoid conformations, whereas this result is not predicted by MP2, neither in the activation energies nor in the transition states. The MP2's failure in the description of this reaction suggests that any MP2 prediction about DA and HDA mechanism should be taken carefully, and we suggest the use of another method to confirm the results for the MP2's geometry optimization of the TS.
The ωb97X functional overestimated the activation energy of the all TS respect to the ωb97X-D results by 2.3 (3TX) up to 3.3 kcal mol−1 (2CN). As the ωb97X functional is a version of the ωb97X-D functional without empirical dispersion correction, the differences between the results of both functionals are likely caused by London dispersion interactions. These results indicate that the NCI may play an important role in the stabilization of the transition states for acrolein dimerization, and could be the explanation of the regiospecificity of this reaction.
3.3. Factors involved in the stabilization of the transition states of acrolein dimerization
To establish the role that the NCI play in the stereoelectronic interactions at the TS, an exhaustive study of the changes of the electron density of NCI as well as the energies associated with these changes along the reaction path was performed.In this sense, the quantification of the NCI is of crucial importance for understanding their importance in the chemical structure and reactivity. The integration of ρ(r) is defined range allows an estimation of the strength of the NCI70,71 and recently, the relationship between the NCI integrals and interaction between two fragments has been addressed.72,73 Therefore to analyse how NCI are involved in the stabilization of the transition states, a set of calculations have been performed integrating the electronic density of the NCI in the range corresponding to attractive (−0.1 < sign(λ2)ρ(r) < −0.02) and vdW interactions (−0.02 < sign(λ2)ρ(r) < 0.02) using the code NCIPLOT4.47 As results with all the functionals were qualitatively the same, for simplicity only the results with M06-2X are presented.
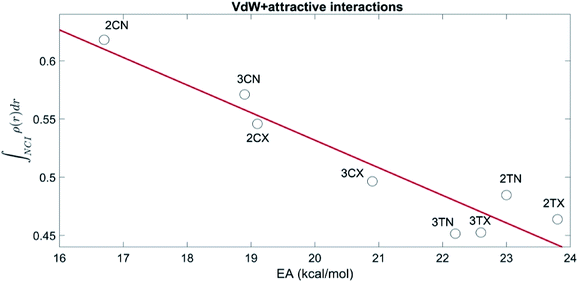
Fig. 3, shows the relation between the sum of the vdW and attractive integrals and the activation energy of all transition states and show that the NCI correctly account for the preference of the cisoid over the transoid conformations. Moreover, the energetic preference of all the TS is explained adequately by the NCI, as there is a significant linear correlation (R = −0.94, p = 0.003) between the NCI and the activation barriers.
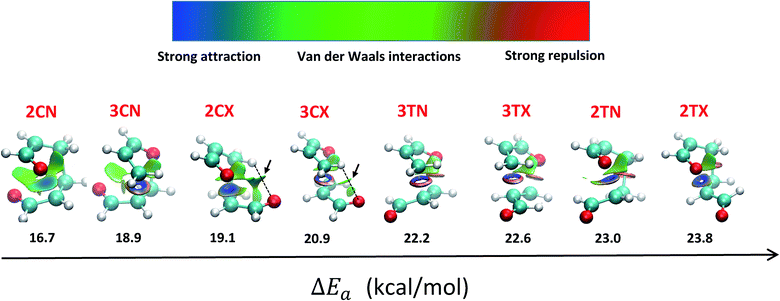
Accordingly to the above outcomes, a NCI analysis through the reduced gradient density was performed on the transition state structures calculated at the M06-2X method, to establish the favourable NCI appearing between both fragments. By analysing the low gradient isosurfaces (Fig. 4), we can observe cisoid/endo transition states (2CN and 3CN) have more covalent interactions, respect to exo and transoid transition states. This is likely due to their more compact shape that allows more direct interaction between both fragments.
Furthermore, the NCI are more pronounced in TS 2CN, as the oxygens of both carbonyl groups can interact with the carbon of the carbonyl from the other acrolein moiety, forming a carbonyl–carbonyl interaction (CO⋯CO).74 This interaction accounts for the stabilization of 2CN respect to other reaction channels.
Even though in exo approximation the atoms are further away than in endo approximation, in the cisoid/exo transition states (2CX and 3CX) a weak hydrogen bond (HB) is formed with a bond length and bond angle of 2.56 Å and 112.8° for 3CX; and 2.49 Å and 131.1° for 2CX. This HB explains the energy stabilization of these transition states, respect to the transoid TS, where neither hydrogen bonding, nor the oxygen (dienophile)–carbon (diene) interactions are possible.
In summary, the analysis of the changes in electron density of the NCI along the reaction channels show that the regiospecificity observed in acrolein dimerization can be explained by NCI analysis of the TS, and clarifies the theoretical endo/exo preferences. Finally, all the NCI calculated in this work belong to regions with low density and low reduced gradient but with no zero gradients, therefore their study was not possible using an atom-in-molecules (AIM) approach.75,76
4 Conclusions
The analysis based on the GEDT and conceptual density functional index allows to establish that acrolein dimerization as non-polar reaction. The NCI integrals and the low gradient isosurfaces show that NCI play an essential role in the mechanistic pathway, and explains adequately the experimental regiospecificity and the endo/exo theoretical selectivity found in acrolein dimerization. Therefore, the NCI analysis clarifies satisfactorily the regiospecificity in this reaction. The energetic study of the different models used in this work, show that the MP2's fails in the prediction of the experimental activation energy and the stepwise description of the mechanism reaction associated with the 2CN channel, suggest that any MP2-based prediction about the DA and HDA mechanisms should be made carefully.Author contributions
Conceptualization, R. F. Q.-Q.; formal analysis, R. F. Q.-Q., M. Q.-R.; funding acquisition, R. F. Q.-Q., M. Q.-R., D. C.-C., G. J. M.-R., and C. S. C.-S.; investigation, R. F. Q.-Q., J. G.-M.; writing—original draft, R. F. Q.-Q.; writing—review & editing, G. J. M.-R., M. Q.-R., C. C.-S., D. C.-C., validation, C. C.-S.; methodology, M. Q.-R, J. G.-M., G. J. M.-R., and D. C.-C.; resources, M. Q.-R., R. F. Q.-Q.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the research project 256657 granted by the Consejo Nacional de Ciencia y Tecnología – México (CONACYT) and by the research project LANCAD-UNAM-DGTIC-094 granted by the Universidad Nacional Autonoma de Mexico. The authors are grateful to Romina Quijano and Oliver Lown for the English review of the manuscript and to DGTIC-UNAM for supercomputer time.Notes and references
- M. T. Blyth and M. L. Coote, J. Org. Chem., 2019, 84, 1517–1522 CrossRef
.
- D. Cáceres Castillo, G. J. Mena Rejón, C. S. Castro Segura and R. F. Quijano Quiñones, Mol. Phys., 2020, 118, 6 CrossRef
.
- J. Cioslowski, J. Sauer, J. Hetzenegger, T. Karcher and T. Hierstetter, J. Am. Chem. Soc., 1993, 115, 1353 CrossRef CAS
.
- M. Orlandi, J. A. S. Coelho, M. J. Hilton, F. Dean-Toste and M. S. Sigman, J. Am. Chem. Soc., 2017, 139, 6803–6806 CrossRef CAS
.
- J. Fleming, Pericyclic reaction, Oxford University Press, 2015 Search PubMed
.
- J. I. García, J. A. Mayoral and L. Salvatella, Acc. Chem. Res., 2000, 33, 658–664 CrossRef
.
- G. Desimoni and G. Tacconi, Chem. Rev., 1975, 75, 651–692 CrossRef CAS
.
- J. Sauer and R. Sustmann, Angew. Chem., Int. Ed., 1980, 19, 779–807 CrossRef
.
- G. Jenner, J. Rimmelin, S. Libs and F. Antoni, Tetrahedron, 1976, 32, 1107–1111 CrossRef CAS
.
- L. Toma, P. Quadrelli and P. Caramella, Tetrahedron Lett., 2001, 42, 731–733 CrossRef CAS
.
- J. Fleming, Frontier Orbitals and Organic Chemical Reactions, Wiley, 1976, p. 4 Search PubMed
.
- L. R. Domingo, P. Pérez and J. A. Sáez, RSC Adv., 2013, 3, 1486–1494 RSC
.
- R. B. Woodward and T. J. Katz, Tetrahedron, 1959, 5, 70–89 CrossRef CAS
.
- L. Salem, J. Am. Chem. Soc., 1968, 90, 5530 Search PubMed
.
- S. B. Bowlus and J. A. Katzenellenbogen, J. Org. Chem., 1974, 39, 3309–3314 CrossRef CAS
.
- O. Eisenstein, J. M. Lefour, N. T. Anh and R. F. Hudson, Tetrahedron, 1977, 33, 523–531 CrossRef CAS
.
- A. Devaquet and L. Salem, J. Am. Chem. Soc., 1969, 91, 3793 CrossRef CAS
.
- V. Bachler and F. Mark, Tetrahedron, 1977, 33, 2857–2861 CrossRef CAS
.
- L. R. Domingo, Molecules, 2016, 21, 1319 CrossRef
.
- Gaussian 09, Revision E. 01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed
.
- N. Q. Su, P. Pernot, X. Xu and A. Savin, J. Mol. Model., 2017, 23, 65 CrossRef
.
- X. Xu, I. M. Alecu and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 1667–1676 CrossRef CAS
.
- L. Simón and J. M. Goodman, Org. Biomol. Chem., 2011, 9, 689–700 RSC
.
- P. Verma and D. G. Truhlar, Trends Chem., 2020, 2, 302–318 CrossRef CAS
.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS
.
- S. N. Pieniazek, F. R. Clemente and K. N. Houk, Angew. Chem., Int. Ed., 2008, 47, 7746–7749 CrossRef CAS
.
- E. G. Hohenstein, S. T. Chill and C. D. Sherrill, J. Chem. Theory Comput., 2008, 4, 1996–2000 CrossRef CAS
.
- K. Ramírez-Gualito, N. López-Mora, H. A. Jiménez-Vázquez, J. Tamariz and G. Cuevas, J. Mex. Chem. Soc., 2013, 57, 267–275 Search PubMed
.
- B. J. Lynch, Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2003, 107, 1384–1388 CrossRef CAS
.
- A. D. Boese, J. M. L. Martin and N. C. Handy, J. Chem. Phys., 2003, 119, 3005–3014 CrossRef CAS
.
- B. J. Levandowski and K. N. Houk, J. Am. Chem. Soc., 2016, 138, 16731–16736 CrossRef CAS
.
- A. Lozynskyi, B. Zimenkovsky, A. Karkhut, S. Polovkovych, A. K. Gzella and R. Lesyk, Tetrahedron Lett., 2016, 57, 3318–3321 CrossRef CAS
.
- J. Da Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC
.
- K. E. Riley, M. Pitončák, P. Jurecčka and P. Hobza, Chem. Rev., 2010, 110, 5023–5063 CrossRef CAS
.
- G. Paytakov, T. Dinadayalane and J. Leszczynski, J. Phys. Chem. A, 2015, 119(7), 1190–1200 CrossRef CAS
.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed
.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS
.
- D. Josa, J. Rodríguez-Otero, E. M. Cabaleiro-Lago and M. Rellán-Piñeiro, Chem. Phys. Lett., 2013, 557, 170–175 CrossRef CAS
.
- L. A. Burns, Á. V. Mayagoitia, B. G. Sumpter and C. D. Sherrill, J. Chem. Phys., 2011, 134, 084107 CrossRef
.
- A. L. Parrill and K. B. Lipkowitz, Reviews in Computational Chemistry Volume 29, John Wiley & Sons, New Jersey, 2016 Search PubMed
.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Theory Comput., 2012, 8, 1929–1934 CrossRef CAS
.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS
.
- R. G. Parr and S. Liu Szentpály, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS
.
- L. R. Domingo, E. Chamorro and P. Pérez, J. Org. Chem., 2008, 73, 4615–4624 CrossRef CAS
.
- L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, Molecules, 2019, 24, 4159 CrossRef
.
- Spartan'16, Wavefunction Inc., Irvine Search PubMed
.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef
.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS
.
- A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066 CrossRef CAS
.
- A. E. Reed and F. Weinhold, J. Chem. Phys., 1985, 83, 1736 CrossRef CAS
.
- A. E. Reed, R. B. Weinstock and F. J. Weinhold, Chem. Phys., 1985, 83, 735 CAS
.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS
.
- L. R. Doming, RSC Adv., 2014, 4, 32415–32428 RSC
.
- L. R. Domingo and J. A. Sáez, Org. Biomol. Chem., 2009, 7, 3576–3583 RSC
.
- D. H. Ess, S. E. Wheeler, R. G. Iafe, L. Xu, N. Celebi-Oelcuem and K. N. Houk, Angew. Chem., Int. Ed., 2008, 47, 7592–7601 CrossRef CAS
.
- S. R. Hare and D. J. Tantillo, Pure Appl. Chem., 2017, 89, 679–698 CAS
.
- N. Mandal and A. Datta, J. Phys. Chem. B, 2018, 122, 1239–1244 CrossRef CAS
.
- N. Mandal and A. Datta, J. Org. Chem., 2018, 83, 11167–11177 CrossRef CAS
.
- T. Wang and T. R. Hoye, Nat. Chem., 2015, 7, 641–645 CrossRef CAS
.
- Z. Yang, L. Zou, Y. Yu, F. Liu, X. Dong and K. N. Houk, Chem. Phys., 2018, 514, 120–125 CrossRef CAS
.
- B. Liu, S. Fu and C. Zhou, Nat. Prod. Rep., 2020, 37, 1627–1660 RSC
.
- P. Caramella, P. Quadrelli and L. Toma, J. Am. Chem. Soc., 2002, 124, 1130–1131 CrossRef CAS
.
- P. Quadrelli, S. Romano, L. Toma and P. Caramella, J. Org. Chem., 2003, 68, 6035–6038 CrossRef CAS
.
- L. Toma, S. Romano, P. Quadrelli and P. Caramella, Tetrahedron Lett., 2001, 42, 5077–5080 CrossRef CAS
.
- P. Quadrelli, S. Romano, L. Toma and P. Caramella, Tetrahedron Lett., 2002, 43, 8785–8789 CrossRef CAS
.
- S. N. Pienaziek and K. Houk, Angew. Chem., Int. Ed., 2006, 45, 1442–1445 CrossRef
.
- M. Linder and T. Brinck, Phys. Chem. Chem. Phys., 2013, 15, 5108–5114 RSC
.
- P. Winget and T. J. Clark, Comput. Chem., 2004, 25, 725–733 CrossRef CAS
.
- J. Cioslowski, M. Schimeczek, G. Liu and V. Stoyanov, J. Chem. Phys., 2000, 113, 9377–9389 CrossRef CAS
.
- W. Neuhauser, D. Haltrich, K. D. Kulbe and B. Nidetzky, Biochemistry, 1998, 37, 1116–1123 CrossRef CAS
.
- J. Černý and P. Hobza, Phys. Chem. Chem. Phys., 2007, 9, 5291–5303 RSC
.
- F. Peccati, E. Desmedt and J. Contreras García, Comput. Theor. Chem., 2019, 115, 23–26 CrossRef
.
- R. Boto, F. Peccati, R. Laplaza, C. Quan, A. Carbone, J.-P. Piquemal, Y. Maday and J. Contreras-García, ChemRxiv, 2019, 1–31 Search PubMed
.
- B. Sahariah and B. Kanta-Sarma, Chem. Sci., 2019, 10, 909–917 RSC
.
- R. A. Boto, J. Contreras-García, J. Tierny and J. P. Piquemal, Mol. Phys., 2016, 114, 1406–1414 CrossRef CAS
.
- J. R. Lane, J. Contreras-García, J. P. Piquemal, B. J. Miller and H. G. Kjaergaard, J. Chem. Theory Comput., 2013, 9, 3263–3266 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra10084f |
| This journal is © The Royal Society of Chemistry 2021 |