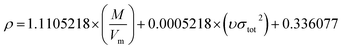DOI:
10.1039/D0RA10241E
(Paper)
RSC Adv., 2021,
11, 12066-12073
Two models to estimate the density of organic cocrystals†
Received
4th December 2020
, Accepted 8th March 2021
First published on 24th March 2021
Abstract
Two models for predicting the density of organic cocrystals composed of energetic organic cocrystals and general organic cocrystals containing nitro groups were obtained. Sixty organic cocrystals in which the ratio of component molecules is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were studied as the dataset. Model-I was based on the artificial neural network (ANN) to predict the density of the cocrystals, which used (six) input parameters of the component molecules. The root mean square error (RMSE) of the ANN model was 0.033, the mean absolute error (MAE) was 0.023, and the coefficient of determination (R2) was 0.920. Model-II used the surface electrostatic potential correction method to predict the cocrystal density. The corresponding RMSE, MAE, and R2 were 0.055, 0.045, and 0.716, respectively. The performance of Model-I is better than that of Model-II.
1 were studied as the dataset. Model-I was based on the artificial neural network (ANN) to predict the density of the cocrystals, which used (six) input parameters of the component molecules. The root mean square error (RMSE) of the ANN model was 0.033, the mean absolute error (MAE) was 0.023, and the coefficient of determination (R2) was 0.920. Model-II used the surface electrostatic potential correction method to predict the cocrystal density. The corresponding RMSE, MAE, and R2 were 0.055, 0.045, and 0.716, respectively. The performance of Model-I is better than that of Model-II.
1 Introduction
Nowadays, with the development of modern national defense and military industry, research on energetic materials (EMs) has attracted considerable attention. Pure crystals of EMs could not meet the needs of today's military development; therefore, numerous researchers have put their hearts into the study of energetic cocrystals (ECCs). ECCs are built by combining an energetic molecule with one or more molecules through non-covalent interactions in the same lattice. ECCs show great performance with high energy and low sensitivity compared with pure EMs.
For example, Yang1 has prepared a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystal explosive by combining 2,4,6,8,10,12-hexanitrohexaazaisowurtzitane (CL-20) and benzotrifuroxan (BTF), and the cocrystal exhibits excellent performance compared with the pure components. Bolton2 et al. have discovered and characterized an ECC, which is composed of CL-20 and 2,4,6-trinitrotoluene (TNT) at a molar ratio of 1
1 cocrystal explosive by combining 2,4,6,8,10,12-hexanitrohexaazaisowurtzitane (CL-20) and benzotrifuroxan (BTF), and the cocrystal exhibits excellent performance compared with the pure components. Bolton2 et al. have discovered and characterized an ECC, which is composed of CL-20 and 2,4,6-trinitrotoluene (TNT) at a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. This cocrystal combines the economic and stability factors of TNT with the density and power of CL-20 into a homogenous energetic compound with high explosive power and excellent insensitivity. Xue3 et al. have found that the cocrystal of CL-20/HMX can mediate the thermal stability of the pure crystal. Zhang and Guo4 have discovered and characterized five novel 1
1. This cocrystal combines the economic and stability factors of TNT with the density and power of CL-20 into a homogenous energetic compound with high explosive power and excellent insensitivity. Xue3 et al. have found that the cocrystal of CL-20/HMX can mediate the thermal stability of the pure crystal. Zhang and Guo4 have discovered and characterized five novel 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio cocrystals, which were composed of BTF and a variety of energetic materials. They found that not all cocrystals exhibited excellent performance in comparison with pure BTF.
1 molar ratio cocrystals, which were composed of BTF and a variety of energetic materials. They found that not all cocrystals exhibited excellent performance in comparison with pure BTF.
The solid-state density of the energetic material is the primary physical factor in detonation performance. The energy is usually characterized by detonation velocity and pressure, which are proportional to the density according to the Kamlet–Jacobs equations.5 For ECC research, the high density cocrystals are our research goal. The loading density of a cocrystal explosive is determined by chemical composition, crystal packing, and intermolecular binding strength. However, the relationship between the cocrystal density and the pure component density is uncertain. Kira et al.6 have researched 17 cocrystals of the benchmark energetic material, TNT, and many of these cocrystals have a density in between those of both components. However, this is not always the case, and some cocrystals have a density higher than those of two pure crystals. Therefore, it is important to choose the appropriate compound to get the cocrystal that has a high density. Nowadays, numerous researchers have obtained cocrystals with some excellent properties by numerous experimental attempts and it is time consuming and dangerous. So, it is urgent to find an accurate model to predict the cocrystal density before the experimental operation.
Zhang7 et al. have supplied a method (eqn (1)) for calculating the cocrystal density, and they supposed that the systems are composed of mixtures of pure components. mi is the mass of component i, and d298K,i is the density of component i.
| |
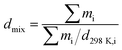 | (1) |
This equation only supplied a rough calculation of the cocrystal density. Strictly speaking, the density of the mixture of pure components is different from that of the cocrystal of pure components because the mixture density does not consider the intermolecular interactions between the pure components.
Fathollahi et al.8 have built models for predicting the densities of the energetic cocrystals using artificial neural network and multiple linear regression (MLR) based on three dragon descriptors (Ms, Elu, and RTm). In their study, while building the model, a cocrystal descriptor is denoted by CD (eqn (2)), and R1 and R2 are the mole fractions of the first and second components, respectively. D1 and D2 are the descriptors of the first and second components, respectively.
| | |
CD = (R1 × D1) + (R2 × D2)
| (2) |
The correlation coefficient (R2) of the ANN and MLR models (for the whole dataset) was 0.9716 and 0.9309, respectively. The average absolute relative deviation of the ANN model for the complete dataset was 2.48%.
Zohari9 has researched the relationship between the densities of energetic cocrystals through a quantitative structure–property relationship (QSPR) model (eqn (3)).
| | |
ρ = 1913 + 0.017sp + 0.003OB + 0.008DU − 0.0128nAT + 0.136ρ+
| (3) |
where
ρ is the density of the compound in g cm
−3, sp is the sum of the atomic polarizabilities, OB is the value of the oxygen balance, DU is the degree of unsaturation of the compound,
nAT is the number of atoms, and
ρ+ is a correction factor. The research methodology provides a new model that can relate the density of an energetic co-crystal to several molecular structural descriptors, which are calculated by the Dragon
10 software. Dragon is a well-known software that can supply the calculation of more than 1600 molecular descriptors from several input formats (MDL, SYBYL, HyperChem, and Smiles). The determination coefficient (
R2) of the derived correlation was 0.937.
Krishna et al.11 have developed a model for predicting the density of cocrystals using artificial neural network based on some descriptors, such as mass weight, binding energy, melting point, and pKa.
In these existing models about the prediction of the density of the energetic cocrystals, most models did not consider the interactions between the two components of the cocrystals, so these models are not accurate enough to predict the density of the energetic cocrystals. In the present study, to predict the density of the energetic cocrystal, we chose the energetic organic cocrystals that have been synthesized as the main research objects. To increase the dataset and enhance the credibility of the model, some general organic cocrystals, which contain nitro groups and whose densities are higher than 1.4 g cm−3 and the ratio of whose components is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, were also selected as the dataset.
1, were also selected as the dataset.
The two models to predict the densities of ECCs were built. For Model-I, we used the ANN model to predict the density of the organic cocrystal that uses three input parameters as the factors affecting the density of the organic cocrystal. For Model-II, we have used the Politzer12,13 method, which was based on the molecular surface electrostatic potential (MESP) to predict the energetic cocrystal density. The method based on MESP has always been used to predict the density of the pure energetic compound. In the present study, we tried to predict the density of the cocrystal. In order to compare the prediction results with those of Model-I, the same dataset as Model-I was used as the research object.
2 Methods and calculations
In the present study, our major objective is to look for suitable expression parameters, so directly referring to the ref. 11, the ANN was selected as the machine learning algorithm. The ANN model was built as shown in Fig. 1, which includes an input layer, a hidden layer, weights, a sum function, an activation function, and an output layer. The input layer acts as the training sample, and the number of nodes in the input layer is the sample size.
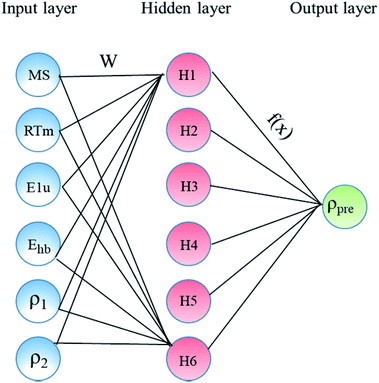 |
| | Fig. 1 Architecture of the constructed ANN model consists of three main layers: input, hidden, and output layers. | |
The hidden layer is the operation black box used for connecting the input layer and output layer, and the number of nodes and number of layers can be customized. The output layer is the calculation result, which is mainly used for different calculations with the expected output. Through error feedback, the weights between the nodes of the hidden layer are adjusted, and then the new result is the output. The error feedback is repeated until the error is within the allowed range. Table 1 lists the main parameters used in the ANN model using the MATLAB toolbox. This includes network topology, training algorithm, and the number of data points of each dataset (training, test, and validation). In the present study, only one hidden layer network was chosen because the number of the samples is only 60, and it is too few.
Table 1 The network parameters in the MATLAB toolbox
| Topology |
6 inputs, 1 output, and 1 hidden layer with 3 neurons (6 × 3 × 1) |
| Data |
Training set: 42 randomly selected cocrystals |
| Test set: 9 randomly selected cocrystals |
| Validation set: 9 randomly selected cocrystals |
| Beginning function |
log-sigmoid |
| Training algorithm |
Levenberg–Marquardt |
| Loss function conditions |
Minimum MSE |
| Stopping condition |
The network stops in one of three ways: validation check > 10, minimum gradient < 10−7, momentum speed > 1010 |
The names of the components of the 60 organic cocrystals are listed in Table S1 (see ESI).† The three input parameters of the 60 organic cocrystals, that is, the densities of the two components that make up the cocrystals, ρ1 and ρ2, the strongest hydrogen bond interaction (Ehb), and the three dragon descriptors (Ms, RTm, and E1u)8 are listed in Table S2 (see ESI).† The strongest hydrogen bond interaction (Ehb) can be calculated using the following formula.14,15
| | |
αmax = 0.0000162 × MEPmax2 + 0.00962 × MEPmax
| (4) |
| | |
βmax = 0.000146 × MEPmin2 − 0.00930MEPmin
| (5) |
where MEP
max and MEP
min are the maximum and minimum values on the map of electrostatic potential surface (MEPS) of the gaseous molecule.
αmax and
βmax are the parameters of the strongest hydrogen bond donor and acceptor, respectively. Suppose that the cocrystal A
mB
n is formed by the compounds A and B.
| | |
E(max,A) = −α(max,A)β(max,A)
| (7) |
| | |
E(max,B) = −α(max,B)β(max,B)
| (8) |
| | |
E(max,AB1) = −α(max,A)β(max,B)
| (9) |
| | |
E(max,AB2) = −α(max,B)β(max,A)
| (10) |
and
| | |
E(max,AB) = min(E(max,AB1),E(max,AB2))
| (11) |
| | |
ΔEA = E(max,AB) − E(max,A)
| (12) |
| | |
ΔEB = E(max,AB) − E(max,B)
| (13) |
and
where
E(max,A) and
E(max,B) denote the pairing energies of the strongest hydrogen bond between A–A and B–B in the pure crystal of compounds A and B.
E(max,AB) denotes those in cocrystal A
mB
n. Δ
Emax denotes the energy difference. The higher the −Δ
Emax, the more probable is the formation of the cocrystal. −Δ
Emax is taken as the criterion to indicate the possibility of cocrystal formation. The method based on the above description can be called the strongest intermolecular site pairing energy method (SISPE). The corresponding computations were implemented in multiwfn3.6.
16 The program multiwfn can realize the electronic wavefunction analysis.
Normalization is to facilitate the rapid learning of neural networks and grasp the logical relationship between the data. Therefore, before performing the artificial neural network calculation, all inputs (descriptors values) were normalized between −1 and +1 using the following equation:
| |
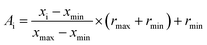 | (15) |
where
xi is the input or output of the model,
Ai is the normalized value of
xi,
xmin and
xmax are the minimum and maximum values of
xi, respectively, and
rmin and
rmax describe the limits of the range where
xi should be scaled.
Model-II is based on the surface electrostatic potential correction method. The following eqn (16) reflects the features of the molecules' surface electrostatic potentials.
| |
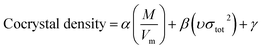 | (16) |
where
M is the molecular mass and
Vm is the volume of the isolated gas phase molecule that is enclosed by the 0.001 au contour of its electronic density. The
υσtot2 reflects the features of the molecules' surface electrostatic potentials. The two parameter values of
Vm and
υσtot2 can be computed using the Multiwfn software, and the value of
M can be calculated according to the cocrystal molecular formula. The calculation values of
M,
Vm, and
υσtot2 for the 60 cocrystals are listed in Table S3 (see ESI).
†
In order to assess the prediction results of the artificial neural network model and the surface electrostatic potential correction model, the relative percentage error (Re%) of the 60 cocrystal samples in the artificial neural network model and the surface electrostatic potential correction model were calculated, respectively. The RMSE, MAE, and R2 of the artificial neural network model and the surface electrostatic potential correction model were also calculated. The specific calculation of Re%, RMSE, MAE, and R2 are showed in the following formula.
| |
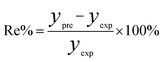 | (17) |
| |
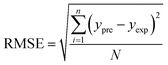 | (18) |
| |
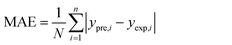 | (19) |
| |
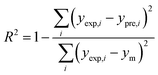 | (20) |
where the predicted value of the cocrystal density was abbreviated as
ypre. The corresponding experimental value of the cocrystal density was abbreviated as
yexp, the mean values of the experimental densities of all the cocrystals was abbreviated as
ym, and
N represents the total number of the cocrystals.
3 Results and discussion
The training set was 42 randomly selected cocrystals, the test set was 9 randomly selected cocrystals, and the validation set was 9 randomly selected cocrystals in the ANN model. The dataset whose serial numbers ranged from 1 to 42 was taken as the training set. The dataset whose serial numbers ranged from 43 to 51 was taken as the test set. The dataset whose serial numbers ranged from 52 to 60 was taken as the validation set. The descriptors (ρ1, ρ2, ΔEhb, Ms, RTm, and E1u) were taken as the input data and trained.
ρ1 and ρ2 are the experimental densities of the cocrystals from the Cambridge Structural Database. They are calculated according to the experimental crystal cell parameters or are directly determined by experimental measurements. ΔEhb is the energy difference of the strongest hydrogen bond interactions. Ms, RTm, and E1u are the dragon descriptors, and they have been indicated that they have a relation to the density in the ref. 8. For the choice of the descriptor, one method is that the important descriptors are decided by the relative analysis from thousands of descriptors. The other method is that the important descriptor with the physical meaning is directly selected by the expert's experiences. In the present study, six parameters were selected mainly according to the ref. 8, 11 and 15. The ANN model was taken as Model-I. Table 2 lists the predicted density using the artificial neural network model (ρANN), experimental density (ρexp), and relative percentage error (Re%) of the 60 organic cocrystals. From Table 2, it can be seen that the predicted densities agree well with the experimental densities for all the cocrystals in the research study. The maximum absolute value of Re% is 6.48%, and the smallest absolute value of Re% is 0%. 88.3% of the absolute value of Re% of all 60 cocrystals was less than 3%, and 8.3% was between 3 and 5, and 3.3% was more than 5. The RMSE, MAE, and R2 of 60 cocrystal densities predicted by the ANN model were 0.033, 0.023, and 0.920, respectively. 88.3% of the total results had an error of less than 0.05 g cm−3. The RMSE and MAE of 50 energetic cocrystals, according to the prediction results of the ref. 9 were 0.077 and 0.066. In order to compare, R2 of 50 energetic cocrystals from the ref. 9 was also calculated according to eqn (20), and the value was 0.825. 40% of the total results had an error of less than 0.05 g cm−3. The densities of 50 energetic cocrystals from the ref. 9 were predicted according to the method of the ref. 8, and the RMSE, MAE, and R2 were 0.490, 0.413, and 0.023, respectively. 40% of the total results had an error of less than 0.05 g cm−3. From the view of RMSE, MAE, R2, and the error range, the ANN model in the present work has a better prediction performance.
Table 2 The prediction results of the 60 organic cocrystals using artificial neural network models (g cm−3 for the density units)
| No. |
Co-formers |
Ref. code |
ρexp |
ρANN |
Re% |
| Training dataset |
| 1 |
CL-20:TNT |
IZUZUZ |
1.911 |
1.930 |
0.994 |
| 2 |
CL-20:AZ2 |
TETTAQ |
1.939 |
1.938 |
−0.052 |
| 3 |
CL-20:NEX-1 |
WEPGEG |
1.882 |
1.874 |
−0.425 |
| 4 |
CL-2:TODAAZ |
HIVGAW |
1.971 |
1.958 |
−0.660 |
| 5 |
CL-20:BQN |
ROSMOD |
1.737 |
1.745 |
0.461 |
| 6 |
CL-20:DNB |
TIVJUF |
1.880 |
1.881 |
0.053 |
| 7 |
CL-20:4,5-MDNI |
NILCIX |
1.882 |
1.877 |
−0.266 |
| 8 |
HMX:PNO |
WEPTAP |
1.700 |
1.697 |
−0.176 |
| 9 |
HMX:FA |
ZEZHET |
1.687 |
1.687 |
0 |
| 10 |
BTF:TNA |
ZEVNUL |
1.811 |
1.819 |
0.442 |
| 11 |
BTF:MATNB |
GEXMON |
1.804 |
1.814 |
0.554 |
| 12 |
BTF:TNA |
GEXMIH |
1.884 |
1.867 |
−0.902 |
| 13 |
TNT:NNAP |
TOZMUS |
1.539 |
1.565 |
1.689 |
| 14 |
TNT:1-BN |
URIJAH |
1.737 |
1.698 |
−2.245 |
| 15 |
TNT:Ant |
URIJEL |
1.515 |
1.532 |
1.122 |
| 16 |
TNT:9-BN |
URIJIP |
1.688 |
1.715 |
1.600 |
| 17 |
TNT:Per |
URIJUB |
1.531 |
1.536 |
0.327 |
| 18 |
TNT:T2 |
URIKEM |
1.677 |
1.675 |
−0.119 |
| 19 |
TNT:DMB |
URILEN |
1.501 |
1.508 |
0.466 |
| 20 |
ABA:TNT |
URILUD |
1.594 |
1.589 |
−0.314 |
| 21 |
MACIC:TZM |
ACERAD |
1.605 |
1.623 |
1.121 |
| 22 |
MBD:MTNB |
DIFZOK |
1.522 |
1.480 |
−2.760 |
| 23 |
PM:UREA |
EFOZAB03 |
1.644 |
1.648 |
0.243 |
| 24 |
MC:PC |
FIXROV01 |
1.606 |
1.661 |
3.425 |
| 25 |
NDT:THTZT |
FOYSUJ |
1.664 |
1.657 |
−0.421 |
| 26 |
IDT:NTZ |
FUFSOQ |
1.644 |
1.651 |
0.426 |
| 27 |
DNBA:BA |
GAUTAM15 |
1.697 |
1.655 |
−2.475 |
| 28 |
PZ:OA |
GUDSUV |
1.609 |
1.627 |
1.119 |
| 29 |
TNP:MDNI |
HARJOB |
1.769 |
1.768 |
−0.057 |
| 30 |
NF:CA |
LEWTAK |
1.627 |
1.627 |
0 |
| 31 |
NF:UREA |
ORUXUV |
1.661 |
1.652 |
−0.542 |
| 32 |
NPO:PA |
OWIYEZ |
1.682 |
1.653 |
−1.724 |
| 33 |
UREA:CA |
PANVUV |
1.672 |
1.654 |
−1.077 |
| 34 |
PZCX:DHXBED |
PAQNOM |
1.628 |
1.608 |
−1.229 |
| 35 |
DNPA:ODADA |
QARQUY |
1.775 |
1.772 |
−0.169 |
| 36 |
TNP:TAD |
QONYUP |
1.685 |
1.655 |
−1.780 |
| 37 |
IZO:DLTA |
RUWPEG |
1.656 |
1.648 |
−0.483 |
| 38 |
IZO:LTA |
UHACIQ |
1.631 |
1.646 |
0.920 |
| 39 |
IZO:LTA |
UHAFEP |
1.607 |
1.616 |
0.560 |
| 40 |
DNBZA:TZ |
UNAWUD |
1.640 |
1.655 |
0.915 |
| 41 |
TZTM:HP |
YAFFUJ |
1.636 |
1.635 |
−0.061 |
| 42 |
BM:TNP |
YUQHEY |
1.616 |
1.663 |
2.908 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Test dataset |
| 43 |
CL-20:MTNP |
QAPNAZ |
1.932 |
1.928 |
−0.207 |
| 44 |
CL-20:GTA |
XAQFUS |
1.650 |
1.571 |
−4.788 |
| 45 |
CL-20:NFQN |
ROSMIX |
1.774 |
1.659 |
−6.483 |
| 46 |
DHDS:TZM |
ACETEJ |
1.625 |
1.655 |
1.846 |
| 47 |
AB:MTNB |
FONHOH |
1.442 |
1.513 |
4.924 |
| 48 |
DNBA:TA |
IJAKAH |
1.635 |
1.655 |
1.223 |
| 49 |
NMI:NMI |
ITIXUE |
1.660 |
1.657 |
−0.181 |
| 50 |
AN:HP |
JOZZED |
1.614 |
1.647 |
2.045 |
| 51 |
Urea:OA |
UROXAM |
1.679 |
1.605 |
−4.407 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Validation dataset |
| 52 |
CL-20:DNG |
JABYOD |
1.750 |
1.770 |
1.143 |
| 53 |
HMX:PDCA |
ZEZGOC |
1.630 |
1.658 |
1.718 |
| 54 |
BTF:TNB |
GEXMED |
1.806 |
1.838 |
1.772 |
| 55 |
TNT:DMDBT |
URIKUC |
1.496 |
1.523 |
1.805 |
| 56 |
TNT:PDA |
URILAJ |
1.578 |
1.561 |
−1.077 |
| 57 |
TNT:TNB |
NIBJUF |
1.640 |
1.653 |
0.793 |
| 58 |
DNBZA:NA |
AWUDEB |
1.607 |
1.671 |
3.983 |
| 59 |
PZCX:OA |
UZODUK |
1.628 |
1.651 |
1.413 |
| 60 |
TZA:NDTZI |
VAZBIJ |
1.790 |
1.698 |
−5.140 |
In order to compare the prediction results of the two models, 42 cocrystals used in Model-I were also used as the training set in Model-II, and the rest were used for verification. The three parameters α, β, and γ in eqn (16) were obtained by the least-squares method.
The specific formula is as follows:
| |
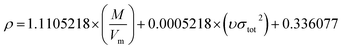 | (21) |
The predicted densities of the 60 cocrystals using the surface electrostatic potential correction model are presented in Table 3. Table 3 lists the predicted densities using the surface electrostatic potential correction model (ρP), experimental densities (ρexp), and relative percentage errors (Re%) of the 60 cocrystals. From Table 3, it can be seen that the predicted densities are also in good agreement with the experimental densities for all the cocrystals in the study. The maximum absolute value of Re% is 8.346%, and the smallest absolute value of Re% is 0.094%. In the 60 predicted results of the cocrystal densities, 60% of the absolute values of Re% was between 0 and 3, 28.3% was between 3 and 5, and 11.67% was greater than 5. The RMSE, MAE, and R2 of 60 cocrystal densities predicted by the surface electrostatic potential correction model are 0.055, 0.045, and 0.716, respectively. 65.0% of the total results had an error of less than 0.05 g cm−3. According to the ref. 17, for CHNO molecular crystals, the RMSE, MAE, and R2 of 36 molecular crystals are 0.045, 0.036, and 0.918, respectively. 77.8% of the total results had an error of less than 0.05 g cm−3. According to the ref. 18, an R2 value greater than 0.5 indicates the significant predictivity of the model. In the ref. 17, Politzer et al. categorized the quality of the density predictions according to the criteria provided by Kim et al.,18 that is, (a) “excellent” (having an error less than 0.03 g cm−3), (b) “informative” (having an error between 0.03 and 0.05 g cm−3), (c) “barely usable” (an error between 0.05 and 0.10 g cm−3), and (d) “deceptive” (error greater than 0.10 g cm−3). Compared to the pure energetic crystal, the prediction based on MESP exhibits worse performance. However, according to the ref. 17, Model-II was also acceptable.
Table 3 Prediction results of the 60 organic cocrystals using surface electrostatic potential correction models (g cm−3 for the density unit)
| |
Co-formers |
Ref. code |
ρexp |
ρP |
Re% |
| 1 |
CL-20:TNT |
IZUZUZ |
1.911 |
1.853 |
−3.023 |
| 2 |
CL-20:DNG |
JABYOD |
1.750 |
1.811 |
3.464 |
| 3 |
CL-20:MTNP |
QAPNAZ |
1.932 |
1.882 |
−2.574 |
| 4 |
CL-20:AZ2 |
TETTAQ |
1.939 |
1.877 |
−3.213 |
| 5 |
CL-20:NEX-1 |
WEPGEG |
1.882 |
1.898 |
0.837 |
| 6 |
CL-20:GTA |
XAQFUS |
1.650 |
1.749 |
6.010 |
| 7 |
CL-2:TODAAZ |
HIVGAW |
1.971 |
1.878 |
−4.721 |
| 8 |
CL-20:NFQN |
ROSMIX |
1.774 |
1.812 |
2.155 |
| 9 |
CL_20:BQN |
ROSMOD |
1.737 |
1.839 |
5.864 |
| 10 |
CL-20:DNB |
TIVJUF |
1.880 |
1.860 |
−1.070 |
| 11 |
CL-20:4,5-MDNI |
NILCIX |
1.882 |
1.849 |
−1.770 |
| 12 |
HMX:PNO |
WEPTAP |
1.700 |
1.698 |
−0.094 |
| 13 |
HMX:FA |
ZEZHET |
1.687 |
1.741 |
3.205 |
| 14 |
HMX:PDCA |
ZEZGOC |
1.630 |
1.698 |
4.164 |
| 15 |
BTF:TNA |
ZEVNUL |
1.811 |
1.876 |
3.612 |
| 16 |
BTF:TNB |
GEXMED |
1.806 |
1.823 |
0.940 |
| 17 |
BTF:MATNB |
GEXMON |
1.804 |
1.807 |
0.178 |
| 18 |
BTF:TNA |
GEXMIH |
1.884 |
1.820 |
−3.414 |
| 19 |
TNT:NNAP |
TOZMUS |
1.539 |
1.627 |
5.740 |
| 20 |
TNT:1-BN |
URIJAH |
1.737 |
1.740 |
0.151 |
| 21 |
TNT:Ant |
URIJEL |
1.515 |
1.565 |
3.305 |
| 22 |
TNT:9-BN |
URIJIP |
1.688 |
1.712 |
1.404 |
| 23 |
TNT:Per |
URIJUB |
1.531 |
1.540 |
0.616 |
| 24 |
TNT:T2 |
URIKEM |
1.677 |
1.556 |
−7.213 |
| 25 |
TNT:DMDBT |
URIKUC |
1.496 |
1.544 |
3.187 |
| 26 |
TNT:PDA |
URILAJ |
1.578 |
1.623 |
2.882 |
| 27 |
TNT:DMB |
URILEN |
1.501 |
1.585 |
5.585 |
| 28 |
TNT:TNB |
NIBJUF |
1.640 |
1.744 |
6.364 |
| 29 |
ABA:TNT |
URILUD |
1.594 |
1.636 |
2.632 |
| 30 |
MACIC:TZM |
ACERAD |
1.605 |
1.621 |
1.027 |
| 31 |
DHDS:TZM |
ACETEJ |
1.625 |
1.667 |
2.555 |
| 32 |
DNBZA:NA |
AWUDEB |
1.607 |
1.633 |
1.648 |
| 33 |
MBD:MTNB |
DIFZOK |
1.522 |
1.589 |
4.434 |
| 34 |
PM:UREA |
EFOZAB03 |
1.644 |
1.574 |
−4.243 |
| 35 |
MC:PC |
FIXROV01 |
1.606 |
1.614 |
0.470 |
| 36 |
AB:MTNB |
FONHOH |
1.442 |
1.509 |
4.618 |
| 37 |
NDT:THTZT |
FOYSUJ |
1.664 |
1.685 |
1.237 |
| 38 |
IDT:NTZ |
FUFSOQ |
1.644 |
1.676 |
1.931 |
| 39 |
DNBA:BA |
GAUTAM15 |
1.697 |
1.555 |
−8.347 |
| 40 |
PZ:OA |
GUDSUV |
1.609 |
1.577 |
−1.977 |
| 41 |
TNP:MDNI |
HARJOB |
1.769 |
1.745 |
−1.367 |
| 42 |
DNBA:TA |
IJAKAH |
1.635 |
1.679 |
2.712 |
| 43 |
NMI:NMI |
ITIXUE |
1.660 |
1.668 |
0.504 |
| 44 |
AN:HP |
JOZZED |
1.614 |
1.579 |
−2.151 |
| 45 |
NF:CA |
LEWTAK |
1.627 |
1.670 |
2.634 |
| 46 |
NF:UREA |
ORUXUV |
1.661 |
1.689 |
1.673 |
| 47 |
NPO:PA |
OWIYEZ |
1.682 |
1.729 |
2.806 |
| 48 |
UREA:CA |
PANVUV |
1.672 |
1.680 |
0.477 |
| 49 |
PZCX:DHXBED |
PAQNOM |
1.628 |
1.649 |
1.302 |
| 50 |
DNPA:ODADA |
QARQUY |
1.775 |
1.708 |
−3.761 |
| 51 |
TNP:TAD |
QONYUP |
1.685 |
1.652 |
−1.930 |
| 52 |
IZO:DLTA |
RUWPEG |
1.656 |
1.645 |
−0.686 |
| 53 |
IZO:LTA |
UHACIQ |
1.631 |
1.617 |
−0.873 |
| 54 |
IZO:LTA |
UHAFEP |
1.607 |
1.630 |
1.420 |
| 55 |
DNBZA:TZ |
UNAWUD |
1.640 |
1.689 |
3.015 |
| 56 |
Urea:OA |
UROXAM |
1.679 |
1.691 |
0.707 |
| 57 |
PZCX:OA |
UZODUK |
1.628 |
1.613 |
−0.942 |
| 58 |
TZA:NDTZI |
VAZBIJ |
1.790 |
1.705 |
−4.740 |
| 59 |
TZTM:HP |
YAFFUJ |
1.636 |
1.562 |
−4.515 |
| 60 |
BM:TNP |
YUQHEY |
1.632 |
1.649 |
1.028 |
While the Politzer model was built, the Politzer parameters were calculated based on the packing unit structure of the experimental crystal. However, in fact, while the model was used, the packing unit structure of the experimental crystal was not obtained, and it was only obtained by theoretical optimization. In order to compare the error caused by the packing unit structure, the densities of the six cocrystals were predicted based on the packing unit structures coming from the experimental cocrystals, which were theoretically optimized and unoptimized, respectively.
The specific calculated values are shown in Table 4 and 5, respectively. By comparing the predicted densities of the cocrystals based on the optimized and unoptimized packing unit structures, it could be found that the Re% of the predicted density values was comparable with that of the predicted density values based on the unoptimized cocrystals. Therefore, the Politzer model built in the present study can be used to predict the densities of the cocrystals.
Table 4 Parameters and the predicted density of the 6 optimized cocrystalsa
| Co-formers |
Ref. code |
M |
Vm |
M/Vm |
υσtot2 |
ρexp |
ρpre |
Re% |
| M are in g mol−1, Vm in Å3, the υσtot2 in (kcal mol)2 and all the density units are in g cm−3. |
| CL-20:AZ2 |
TETTAQ |
672.320 |
498.763 |
1.348 |
42.282 |
1.939 |
1.992 |
2.733 |
| TNT:NNAP |
TOZMUS |
400.302 |
361.863 |
1.106 |
35.107 |
1.539 |
1.620 |
5.263 |
| TNT:1-BN |
URIJAH |
434.201 |
359.316 |
1.208 |
28.743 |
1.737 |
1.777 |
2.303 |
| TNT:DMDBT |
URIKUC |
431.363 |
421.063 |
1.044 |
24.216 |
1.496 |
1.524 |
1.872 |
| TNT:PDA |
URILAJ |
341.275 |
310.756 |
1.079 |
31.515 |
1.578 |
1.578 |
0 |
| TNT:DMB |
URILEN |
365.297 |
344.786 |
1.059 |
24.105 |
1.501 |
1.547 |
3.065 |
Table 5 Parameters and the predicted density of the 6 unoptimized cocrystalsa
| Co-formers |
Ref. code |
M |
Vm |
M/Vm |
υσtot2 |
ρexp |
ρpre |
Re% |
| M are in g mol−1, Vm in Å3, υσtot2 in (kcal mol)2, and all the density units are in g cm−3. |
| CL-20:AZ2 |
TETTAQ |
672.320 |
492.017 |
1.366 |
45.318 |
1.939 |
1.929 |
−0.516 |
| TNT:NNAP |
TOZMUS |
400.302 |
349.462 |
1.145 |
37.773 |
1.539 |
1.574 |
2.274 |
| TNT:1-BN |
URIJAH |
434.201 |
347.532 |
1.249 |
31.624 |
1.737 |
1.741 |
0.23 |
| TNT:DMDBT |
URIKUC |
431.363 |
401.162 |
1.075 |
26.426 |
1.496 |
1.461 |
−2.34 |
| TNT:PDA |
URILAJ |
341.275 |
299.556 |
1.139 |
43.138 |
1.578 |
1.564 |
−0.887 |
| TNT:DMB |
URILEN |
365.297 |
328.383 |
1.112 |
26.551 |
1.501 |
1.521 |
1.332 |
In order to compare the relative accuracy of the artificial neural network model and the surface electrostatic potential correction model in predicting the cocrystal density, the differences between the absolute values of the Re% of the two models were calculated. Table 6 shows the values of RANN%, RP%, and the differences between the absolute values of RANN% and RP% (|RANN%| − |RP%|). The regression performance of the two models for predicting the densities of the cocrystals is shown in Fig. 2. When the value of |RANN%| − |RP%| is negative, it indicates that the artificial neural network model is more accurate in predicting the density value of the cocrystal.
Table 6 Comparison of the prediction results of the two organic cocrystal density prediction models
| No. |
Co-formers |
Ref. code |
RANN% |
Rp% |
|RANN%| − |RP%| |
| 1 |
CL-20:TNT |
IZUZUZ |
0.994 |
−3.023 |
−2.029 |
| 2 |
CL-20:DNG |
JABYOD |
−0.052 |
3.464 |
−3.412 |
| 3 |
CL-20:MTNP |
QAPNAZ |
−0.425 |
−2.574 |
−2.149 |
| 4 |
CL-20:AZ2 |
TETTAQ |
−0.660 |
−3.213 |
−2.553 |
| 5 |
CL-20:NEX-1 |
WEPGEG |
0.461 |
0.837 |
−0.376 |
| 6 |
CL-20:GTA |
XAQFUS |
0.053 |
6.010 |
−5.957 |
| 7 |
CL-2:TODAAZ |
HIVGAW |
−0.266 |
−4.721 |
−4.455 |
| 8 |
CL-20:NFQN |
ROSMIX |
−0.176 |
2.155 |
−1.979 |
| 9 |
CL-20:BQN |
ROSMOD |
0 |
5.864 |
−5.864 |
| 10 |
CL-20:DNB |
TIVJUF |
0.442 |
−1.070 |
−0.628 |
| 11 |
CL-20:4,5-MDNI |
NILCIX |
0.554 |
−1.770 |
−1.216 |
| 12 |
HMX:PNO |
WEPTAP |
−0.902 |
−0.094 |
0.808 |
| 13 |
HMX:FA |
ZEZHET |
1.689 |
3.205 |
−1.516 |
| 14 |
HMX:PDCA |
ZEZGOC |
−2.245 |
4.164 |
−1.919 |
| 15 |
BTF:TNA |
ZEVNUL |
1.122 |
3.612 |
−2.49 |
| 16 |
BTF:TNB |
GEXMED |
1.600 |
0.940 |
0.66 |
| 17 |
BTF:MATNB |
GEXMON |
0.327 |
0.178 |
0.149 |
| 18 |
BTF:TNA |
GEXMIH |
−0.119 |
−3.414 |
−3.295 |
| 19 |
TNT:NNAP |
TOZMUS |
0.466 |
5.740 |
−5.274 |
| 20 |
TNT:1-BN |
URIJAH |
−0.314 |
0.151 |
0.163 |
| 21 |
TNT:Ant |
URIJEL |
1.121 |
3.305 |
−2.184 |
| 22 |
TNT:9-BN |
URIJIP |
−2.760 |
1.404 |
1.356 |
| 23 |
TNT:Per |
URIJUB |
0.243 |
0.616 |
−0.373 |
| 24 |
TNT:T2 |
URIKEM |
3.425 |
−7.213 |
−3.788 |
| 25 |
TNT:DMDBT |
URIKUC |
−0.421 |
3.187 |
−2.766 |
| 26 |
TNT:PDA |
URILAJ |
0.426 |
2.882 |
−2.456 |
| 27 |
TNT:DMB |
URILEN |
−2.475 |
5.585 |
−3.11 |
| 28 |
TNT:TNB |
NIBJUF |
1.119 |
6.364 |
−5.245 |
| 29 |
ABA:TNT |
URILUD |
−0.057 |
2.632 |
−2.575 |
| 30 |
MACIC:TZM |
ACERAD |
0 |
1.027 |
−1.027 |
| 31 |
DHDS:TZM |
ACETEJ |
−0.542 |
2.555 |
−2.013 |
| 32 |
DNBZA:NA |
AWUDEB |
−1.724 |
1.648 |
0.076 |
| 33 |
MBD:MTNB |
DIFZOK |
−1.077 |
4.434 |
−3.357 |
| 34 |
PM:UREA |
EFOZAB03 |
−1.229 |
−4.243 |
−3.014 |
| 35 |
MC:PC |
FIXROV01 |
−0.169 |
0.470 |
−0.301 |
| 36 |
AB:MTNB |
FONHOH |
−1.780 |
4.618 |
−2.838 |
| 37 |
NDT:THTZT |
FOYSUJ |
−0.483 |
1.237 |
−0.754 |
| 38 |
IDT:NTZ |
FUFSOQ |
0.920 |
1.931 |
−1.011 |
| 39 |
DNBA:BA |
GAUTAM15 |
0.560 |
−8.347 |
−7.787 |
| 40 |
PZ:OA |
GUDSUV |
0.915 |
−1.977 |
−1.062 |
| 41 |
TNP:MDNI |
HARJOB |
−0.061 |
−1.367 |
−1.306 |
| 42 |
DNBA:TA |
IJAKAH |
2.908 |
2.712 |
0.196 |
| 43 |
NMI:NMI |
ITIXUE |
−0.207 |
0.504 |
−0.297 |
| 44 |
AN:HP |
JOZZED |
−4.788 |
−2.151 |
2.637 |
| 45 |
NF:CA |
LEWTAK |
−6.483 |
2.634 |
3.849 |
| 46 |
NF:UREA |
ORUXUV |
1.846 |
1.673 |
0.173 |
| 47 |
NPO:PA |
OWIYEZ |
4.924 |
2.806 |
2.118 |
| 48 |
UREA:CA |
PANVUV |
1.223 |
0.477 |
0.746 |
| 49 |
PZCX:DHXBED |
PAQNOM |
−0.181 |
1.302 |
−1.121 |
| 50 |
DNPA:ODADA |
QARQUY |
2.045 |
−3.761 |
−1.716 |
| 51 |
TNP:TAD |
QONYUP |
−4.407 |
−1.930 |
2.477 |
| 52 |
IZO:DLTA |
RUWPEG |
1.143 |
−0.686 |
0.457 |
| 53 |
IZO:LTA |
UHACIQ |
1.718 |
−0.873 |
0.845 |
| 54 |
IZO:LTA |
UHAFEP |
1.772 |
1.420 |
0.352 |
| 55 |
DNBZA:TZ |
UNAWUD |
1.805 |
3.015 |
−1.21 |
| 56 |
Urea:OA |
UROXAM |
−1.077 |
0.707 |
0.37 |
| 57 |
PZCX:OA |
UZODUK |
0.793 |
−0.942 |
−0.149 |
| 58 |
TZA:NDTZI |
VAZBIJ |
3.983 |
−4.740 |
−0.757 |
| 59 |
TZTM:HP |
YAFFUJ |
1.413 |
−4.515 |
−3.102 |
| 60 |
BM:TNP |
YUQHEY |
−5.140 |
1.028 |
4.112 |
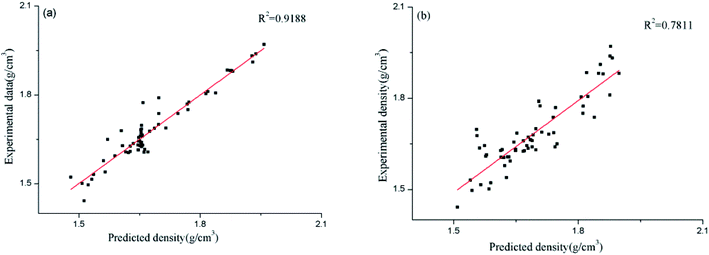 |
| | Fig. 2 Predicted densities of the cocrystals vs. experimental data for all the datasets ((a) for the ANN model, and (b) for the Politzer model). | |
However, the surface electrostatic potential correction model is more accurate in predicting the density value of the cocrystal. From Table 6, it can be seen that among the 60 cocrystals, 18 are positive values, accounting for 30%, and 42 are negative values, accounting for 70%. According to the RMSE and MAE values of the two models calculated above, it is also found that both values of the artificial neural network model are smaller than those obtained using the surface electrostatic potential correction model. From Fig. 2, it can also be seen that the performance of the artificial neural network model is better than that of the surface electrostatic potential correction model. Therefore, in these two models, the density value of the cocrystal predicted by the artificial neural network model is relatively accurate. However, the surface electrostatic potential correction model is more convenient to predict the cocrystal density because it provides a unique and specific formula for calculating the cocrystal density. It is also simple and time-saving to calculate the two parameters of the surface electrostatic potential correction model.
4 Conclusions
In this study, two types of prediction models for the organic cocrystal density were established. One is the artificial neural network model, and the other is the surface electrostatic potential correction model. For the artificial neural network model, the maximum absolute value of Re% is 6.483%, and the smallest absolute value of Re% is 0. 88.3% of 60 cocrystals for the absolute values of Re% were less than 3%. The RMSE and MAE of 60 organic cocrystal densities predicted by the artificial neural network model are 0.033 and 0.023, respectively. For the surface electrostatic potential correction model, maximum absolute value of Re% is 8.346%, and smallest absolute value of Re% is 0.094%. In the 60 predicted results of the cocrystal densities, 60% of the absolute values of Re% were between 0 and 3, 28.3% was between 3 and 5, and 11.67% was greater than 5. The RMSE and MAE of the 60 cocrystal densities predicted by the surface electrostatic potential correction model are 0.055 and 0.045, respectively.
To compare the prediction accuracy of the two models, the values of |RANN%| − |RP%| were also calculated. By comparing the values of Re%, RMSE, MAE, and |RANN%| − |RP%|, it can be inferred that the artificial neural network model is more accurate than the surface electrostatic potential correction model. However, the surface electrostatic potential correction model is more convenient and practical than the artificial neural network model. Therefore, the two models could be selected according to the actual requirements.
Conflicts of interest
The authors declare there are no conflicts of interest regarding the publication of this paper.
Acknowledgements
The authors acknowledge the support of the National Natural Science Foundation of China (21805303).
Notes and references
- Z. W. Yang, H. Z. Li, X. Q. Zhou, C. Y. Zhang, H. huang, J. S. Li and F. D. Nie, Cryst. Growth Des., 2012, 12, 5155–5158 CrossRef CAS.
- O. Bolton and A. J. Matzger, Angew. Chem., Int. Ed., 2011, 50, 8960–8963 CrossRef CAS.
- X. G. Xue, Y. Ma, Q. Zeng and C. Y. Zhang, J. Phys. Chem. C, 2017, 121, 4899–4908 CrossRef CAS.
- H. B. Zhang, C. Y. Guo, X. C. Wang, J. J. Xu, X. He, Y. Liu, X. F. Liu, H. Huang and J. Sun, Cryst. Growth Des., 2013, 13(2), 679–687 CrossRef CAS.
- L. Kazandjian and J. F. Danel, Propellants, Explos., Pyrotech., 2006, 31, 20–24 CrossRef CAS.
- K. B. Landenberger and A. J. Matzger, Cryst. Growth Des., 2010, 10, 5341–5347 CrossRef CAS.
- C. Y. Zhang, Y. F. Cao, H. Z. Li, Y. Zhou, J. H. Zhou, T. Gao, H. B. Zhang, Z. W. Yang and G. Jiang, CrystEngComm, 2013, 15, 4003–4014 RSC.
- M. Fathollahi and H. Sajady, Struct. Chem., 2018, 29, 1119–1128 CrossRef CAS.
- Z. Narges and G. F. Mohammadkhani, Cent. Eur. J. Energ. Mater., 2020, 17(1), 31–48 CrossRef.
- I. V. Tetko, J. Gasteiger, R. Todeschini, A. Mauri, D. Livingstone, P. Ertl, V. A. Palyulin, E. V. Radchenko, N. S. Zefirov, A. S. Makarenko, V. Y. Tanchuk and V. V. Prokopenko, Virtual computational chemistry laboratory – design and description, J. Comput.-Aided Mol. Des., 2005, 19, 453–463 CrossRef CAS PubMed.
- G. R. Krishna, U. Marko, Z. Jacek and Å. C. Rasmuson, Cryst. Growth Des., 2018, 18, 133–144 CrossRef.
- P. Politzer, J. Martinez, J. S. Murray, M. C. Concha and A. Toro-labbé, Mol. Phys., 2009, 107, 2095–2101 CrossRef CAS.
- A. Nirwan, A. Devi and V. D. Ghule, J. Mol. Model., 2018, 24, 166 CrossRef PubMed.
- D. Musumeci, C. A. Hunter, R. Prohens, S. Scuderi and J. F. McCabe, Chem. Sci., 2011, 2, 883 RSC.
- J. H. Zhou, M. B. Chen, W. M. Chen, L. W. Shi, C. Y. Zhang and H. Z. Li, J. Mol. Struct., 2014, 1072, 179–186 CrossRef CAS.
- T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- P. Politzer, J. Martinez, J. S. Murray, M. C. Concha and A. Toro-Labbé, Mol. Phys., 2009, 107(19), 2095–2101 CrossRef CAS.
- C. K. Kim, S. G. Cho, C. K. Kim, H. Y. Park, H. Zhang and H. W. Lee, J. Comput. Chem., 2008, 29(11), 1818–1824 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra10241e |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Li Zhaob,
Liang-Wei Shic and
Pei-Cheng Luo*b
*a,
Li Zhaob,
Liang-Wei Shic and
Pei-Cheng Luo*b
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were studied as the dataset. Model-I was based on the artificial neural network (ANN) to predict the density of the cocrystals, which used (six) input parameters of the component molecules. The root mean square error (RMSE) of the ANN model was 0.033, the mean absolute error (MAE) was 0.023, and the coefficient of determination (R2) was 0.920. Model-II used the surface electrostatic potential correction method to predict the cocrystal density. The corresponding RMSE, MAE, and R2 were 0.055, 0.045, and 0.716, respectively. The performance of Model-I is better than that of Model-II.
1 were studied as the dataset. Model-I was based on the artificial neural network (ANN) to predict the density of the cocrystals, which used (six) input parameters of the component molecules. The root mean square error (RMSE) of the ANN model was 0.033, the mean absolute error (MAE) was 0.023, and the coefficient of determination (R2) was 0.920. Model-II used the surface electrostatic potential correction method to predict the cocrystal density. The corresponding RMSE, MAE, and R2 were 0.055, 0.045, and 0.716, respectively. The performance of Model-I is better than that of Model-II.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystal explosive by combining 2,4,6,8,10,12-hexanitrohexaazaisowurtzitane (CL-20) and benzotrifuroxan (BTF), and the cocrystal exhibits excellent performance compared with the pure components. Bolton2 et al. have discovered and characterized an ECC, which is composed of CL-20 and 2,4,6-trinitrotoluene (TNT) at a molar ratio of 1
1 cocrystal explosive by combining 2,4,6,8,10,12-hexanitrohexaazaisowurtzitane (CL-20) and benzotrifuroxan (BTF), and the cocrystal exhibits excellent performance compared with the pure components. Bolton2 et al. have discovered and characterized an ECC, which is composed of CL-20 and 2,4,6-trinitrotoluene (TNT) at a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. This cocrystal combines the economic and stability factors of TNT with the density and power of CL-20 into a homogenous energetic compound with high explosive power and excellent insensitivity. Xue3 et al. have found that the cocrystal of CL-20/HMX can mediate the thermal stability of the pure crystal. Zhang and Guo4 have discovered and characterized five novel 1
1. This cocrystal combines the economic and stability factors of TNT with the density and power of CL-20 into a homogenous energetic compound with high explosive power and excellent insensitivity. Xue3 et al. have found that the cocrystal of CL-20/HMX can mediate the thermal stability of the pure crystal. Zhang and Guo4 have discovered and characterized five novel 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio cocrystals, which were composed of BTF and a variety of energetic materials. They found that not all cocrystals exhibited excellent performance in comparison with pure BTF.
1 molar ratio cocrystals, which were composed of BTF and a variety of energetic materials. They found that not all cocrystals exhibited excellent performance in comparison with pure BTF.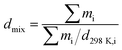
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, were also selected as the dataset.
1, were also selected as the dataset.
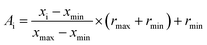
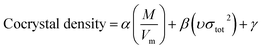
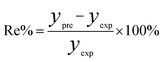
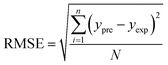
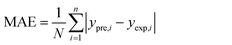
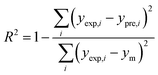
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)