Open Access Article
Open Access ArticleControlling the aqueous growth of urea crystals with different growth inhibitors: a molecular-scale study
M. K. Singh *ab
*ab
aTheory & Simulation Laboratory, Human Resource Development Section, Raja Ramanna Centre for Advanced Technology, Indore, India. E-mail: mksingh@rrcat.gov.in; Tel: +91-731-248-8677
bHomi Bhabha National Institute, Raja Ramanna Centre for Advanced Technology, Department of Atomic Energy, Indore, India
First published on 6th April 2021
Abstract
Molecular scale understanding of the mechanism of solution-mediated nucleation and the growth of crystalline materials in the presence of growth inhibitors together with the process parameters continues to attract the interest of the scientific community though much headway has been made in recent years. Growth inhibitors can be added to solution of a crystallizing parent molecule to alter the rate of growth of different crystal faces, size and shape of the crystalline materials. In this work, we investigated the effects of a number of shape-controlling inhibitors, such as acetone, biuret and biurea, on the growth kinetics of the various faces of aqueous-grown urea crystals as a means to predictably control the crystal growth morphology. We combined the adsorption energy landscape of various auxiliaries with the kinetics of the molecular growth processes to develop an analytical model to compute the rate of growth as a function of supersaturation and the additive concentration. The model relates the kinetic and thermodynamic aspects of the adsorption of the solute, solvent and additive to provide a quantitative description of the crystal growth. Ab initio periodic dispersion-corrected density functional theory using the hybrid exchange–correlation functional was employed to determine the interfacial structure of the adsorption of various auxiliaries at crystalline surfaces. The calculated adsorption energies of different auxiliaries were employed to examine the role played by these auxiliaries during the aqueous crystallization of urea crystals containing small amounts of additives. Our results showed that the growth of (110), (111) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces were nearly unaltered by the addition of moderate amounts of acetone as it has lower adsorption energies with the surfaces of these faces. Nevertheless, the presence of acetone in the solution reasonably impeded the growth of the (001) face. The addition of biuret or biurea in the solution led to a higher adsorption energy at (001) and (111) faces. Consequently, the low concentration of these additives severely obstructed the growth of (001) and (111) faces as most of the adsorption sites were occupied by these additives. On the other hand, these additives were weakly adsorbed at the (110) face and, hence, the growth of the (110) face largely remained unaltered. Moreover, unlike biuret, biurea considerably inhibited the growth of the (
) faces were nearly unaltered by the addition of moderate amounts of acetone as it has lower adsorption energies with the surfaces of these faces. Nevertheless, the presence of acetone in the solution reasonably impeded the growth of the (001) face. The addition of biuret or biurea in the solution led to a higher adsorption energy at (001) and (111) faces. Consequently, the low concentration of these additives severely obstructed the growth of (001) and (111) faces as most of the adsorption sites were occupied by these additives. On the other hand, these additives were weakly adsorbed at the (110) face and, hence, the growth of the (110) face largely remained unaltered. Moreover, unlike biuret, biurea considerably inhibited the growth of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) face. Our results are in agreement with the experimental and computational results reported in the literature.
) face. Our results are in agreement with the experimental and computational results reported in the literature.
1 Introduction
Controlling the polymorphism and particle morphology of fine chemicals and active pharmaceutical ingredients poses a difficult challenge to the chemical and pharmaceutical industries in order to regulate key properties, such as the growth/dissolution kinetics and bioavailability.1,2 It is becoming increasingly clear that shape-controlling growth inhibitors (hereafter referred as additives) – a foreign molecule that selectively binds to the growing face –, the solvent, composition of the mother phase and crystallization conditions, such as supersaturation, temperature, and cooling rate, play primary roles in determining the kinetics of the growing surface, properties, shape and size of the material. However, the ability to design crystalline materials with desired properties based on their structural understanding is still limited. During crystallization, particular (or tailor-made) additives or solvents selectively interfere with the growing crystal surface (hereafter referred as the surface) because of the high degree of specificity in the interaction of the additives with different growing surfaces. As a result, the relative growth rates of crystal faces can be altered largely, leading to drastic changes in the growth morphology. The adsorption energies of a number of auxiliaries present in the mother phase and their corresponding concentrations greatly affect the kinetics of the growing surface by inhibiting the crystal growth perpendicular to these faces.3–9 Molecular scale understanding of the role of the solvent, additive and crystallization conditions would allow us to control the evolution of the growth morphologies and polymorphism. Inevitably, our ability to control the crystallization and polymorph formation can take the form of a careful choice of solvent, additive and accurate monitoring of the crystallization process parameters.10,11 The rate of incorporation of the crystalline solute material (hereafter referred as the solute) into the growing surface steps depends on supersaturation, the temperature, additive concentration and adsorption energies of the solute, solvent and additive. On the other hand, auxiliaries, such as the solvent and additive adsorbed on the kink sites in a step ledge or surface terrace, either by blocking the movement of the growing steps or by incorporating in the surface, can disrupt the intermolecular interactions. The monomolecular surface steps generally have regular structures in pure solution. However, the presence of additive in the growth solution often generates irregular macro steps, which results in a reduction in the step velocity. To this end, a quantitative understanding of this will not only lead to being able to engineer the crystal growth morphology and desired properties1,2,11 with the judicious use of the right solvent and additive, but will also help us to design new crystalline materials with the desired properties. The accurate prediction of the evolution of the growth morphology requires precise control over the kinetics and of the thermodynamic factors during the crystallization process, which will ultimately control the rate of growth and growth morphology.Predicting the role of the solvent, additive and external growth parameters to elucidate the face-dependent growth and dissolution dynamics has attracted considerable interest over the past two decades. Nevertheless, the present understanding of the crystallization mechanism through which the solvent interacts with the surface is still far from complete.12 Also not well understood is the role of the solvent during crystallization, such as whether the solvent inhibits3–5 or promotes13–17 the crystal growth. In the inhibition model hypothesis, solvent molecules preferentially adsorb on the growth sites, which would disrupt the attachment of the solute to that particular crystal face.5–9 The incorporation of the solute requires the removal of the bound solvent from the surface, which would require overcoming an additional energy barrier. The alternative hypothesis proposes that the interaction of the solvent with specific crystal faces lower the energy barrier for the 2D nucleation by reducing the edge energy and this would cause a resultant increase in the growth rate of the crystal faces.13–17 For some systems, e.g. (R,S)-alanine and γ-glycine crystallizing from aqueous solution, the experimentally observed faster growing face along their polar axis can only be explained using a complex and distinct relay-type mechanism.5 Nevertheless Tilbury et al.18 proposed mechanistic models that go well beyond the inhibition mechanism, and that can capture rough growth, 2D nucleation, and BCF spiral growth. On the computational front, Nielsen et al.19,20 investigated the attachment and detachment frequencies of solvated growth units to determine the rate of displacement normal to the face. Woensdregt21 depicted the solvent as an impurity that is preferentially adsorbed on the crystalline interface. Liu et al.22–26 carried out molecular dynamic simulations to predict the growth shape of urea crystals from water and put forward the idea of an effective growth unit. Subsequently, Gnanasambandam and Rajagopalan27 extended this idea to predict the shape of aqueous-grown α-glycine crystals by fully accounting for the effects of the solvent. On the other hand, Doherty et al.28–30 predicted the supersaturation-dependent shapes of many organic crystals by examining the detailed Burton–Cabrera–Frank spiral growth mechanism31 and by considering additional terms to represent the solvent-induced surface energy. Wireko et al.32 and Anwar et al.33,34 performed molecular dynamic simulations to examine the effect of the solvent towards asymmetrical growth along the polar axis of α-resorcinol crystal and showed that water has a stronger interaction on the slower growing face and, thus, their results supported the inhibition model of crystal growth. Piana et al.35,36 exploited multi-scale modelling to study the effect of the solvent, degree of supersaturation and extended defects to predict the growth shape of a urea crystal grown from a water and methanolic solution. Tóth37 determined molecular rate constants to obtain the growth of urea in water and methanol by combining a genetic algorithm with kinetic Monte Carlo simulations. Recently, we employed density functional theory to calculate the adsorption energies of the solvent and solute at the solvent–surface interface to study the solvent-induced habit modification of different molecular crystals.38–41 A comprehensive account of molecular modelling techniques and computational chemistry was made by Myerson42 and Docherty and Meenan.43
In general, additives can affect the nucleation and growth of flat faces in two distinct ways, either by impeding the incorporation of crystalline materials by hindering the subsequent absorption of further layers of the solute,44,45 or, in some instances, they can even promote13–17,46–48 the rate of crystallization by decreasing the surface free energy. With some exceptions, it is generally thought that the increase in an additive's concentration would result in a decrease in the particle size.49 These effects of growth additives are generally related to a decrease in the kinetic coefficient, resulting in a change in the free energy of the growing surface. We envisage that the additive plays a similar role as the solvent during crystallization and it can either inhibit5–9 or promote48 the nucleation and crystal growth. The selective adsorption of tailor-made additives at a given face causes growth inhibition of the face, which is consistent with the mechanism of action of a solvent on crystal growth. In contrast to the solvent effect on the crystallization mechanism, it has been observed that trace amounts of additives can greatly alter the rate of crystallization, where even the magnitude of the interactions of the additive and solvent to a specific surface are comparable. The effect of additives on the morphology can be fairly explained by a two-step mechanism of adsorption and inhibition of growth of that specific face.50 Accordingly, additives bind to surface steps in the growth spirals, leading to a drastic reduction in the growth of specific faces, consequently altering the crystal morphology. The pinning models51–55 of impurity adsorption offer a qualitative understating of the effect of adsorption of a low impurity concentration on the growth kinetics. The immobile impurity is adsorbed all over the surface terrace and obstructs the advancing step edge caused by its structure becoming deformed, which ultimately leads to the altered step velocity.51 Nevertheless, Kubota–Mullin's model52–55 was used to investigate the adsorption of mobile impurities on the crystal surface, which retard its growth by blocking the available active growth sites. Relatively large and immobile impurities, such as organic dyes, eventually hamper the growth of surface steps, ultimately leading to a reduction in the growth velocity. However, observations made by atomic force microscopy56–58 showed an abrupt increase in step velocity. This evidently raises serious question about the validity of the Gibbs–Thomson effect, which is the basis of the pinning model. It is also noteworthy that pinning models can be reasonably successfully used to study the kinetic aspect of the adsorption of impurities, but ignore the thermodynamics of the crystallization process. In recent years, the stereochemical approach5,59 has been put forward to investigate the role of tailor-made additives on the crystallization and dissolution of many molecular crystals. A computational molecular modelling technique60,61 was developed by Clydesdale et al.62–64 to study the effect of additives on the crystal morphology. Recently, Poornachary et al.65–67 studied the influence of the solution speciation of “tailor-made” additives to control the stereoselective habit modification in molecular crystals. Recently, Sangwal68 compiled a comprehensive description of the role played by additives during the nucleation, growth and aggregation of crystals. Amjad69 discussed in detail the interaction of polymeric and non-polymeric inhibitors with a variety of scale-forming crystals.
With the motivation to glean insights into the role of different additives to determine the rate of growth and, hence, the morphology of crystals, we examined the growth of a urea crystal in an aqueous medium containing small amount of acetone, biuret and biurea as habit modifiers. In the present work, we addressed the local concentrations of the solute, solvent and additive at the interface and their corresponding adsorption energies, as well as externally controllable crystallization parameters, such as supersaturation and temperature, to determine the rate of growth of a number of faces of the urea crystal. Biurea and biuret were chosen due to their higher structural compatibility to the urea molecule. Consequently, it is anticipated that they would become more efficient50 and could significantly alter the growth morphology of the urea crystal. On the other hand, the urea lattice has a lower structural compatibility with the acetone molecule, while also having a comparable size and, thus, the presence of acetone provides mere steric hindrance during growth. It is expected that it would only marginally alter the morphology of the urea crystal. It was established that the dynamics of the advancing steps depends on several kinetic and thermodynamic factors, such as supersaturation, temperature, and the adsorption energy of the solute, solvent and additive, at the surface and the additive concentration. With this in mind, we investigated the kinetic and thermodynamic aspects of the adsorption of the aforementioned growth inhibitors on the flat faces of crystals to study the growth morphology of the urea crystal. Different configurations of additives on the surface were explored to obtain the adsorption energy of the rate-limiting molecule. Ab initio density functional method (DFT) using the hybrid exchange–correlation functional was employed to obtain the adsorption energy of the solute, solvent and different additives at the surface. It was experimentally observed that the presence of trace amounts of biuret significantly inhibited the growth of the fast-growing (001) face of the aqueous-grown urea crystal. This was largely due to the formation of strong and specific hydrogen bonds between biuret and the exposed lattice sites on the (001) face.70 In contrast, the growth of the slow-growing (110) face largely remained unaffected because of the lower and nonspecific interaction of biuret than the water on the (110) face.70–72 Our results showed that the presence of a small amount of biurea with the growing crystallites resulted in a severe drop in the rate of growth of the (111), (001) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces. Moreover, the incorporation of biuret also inhibited the growth of the (111) and (001) faces, leaving small change in the growth of the (
) faces. Moreover, the incorporation of biuret also inhibited the growth of the (111) and (001) faces, leaving small change in the growth of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) face. In contrast to these, the addition of a moderate amount of acetone into the mother phase only mildly affected the growth of the (001) and (111) faces. In all cases, we observed that the growth of the (110) face remained largely unaffected by the presence of these additives, even in a moderate amount.
) face. In contrast to these, the addition of a moderate amount of acetone into the mother phase only mildly affected the growth of the (001) and (111) faces. In all cases, we observed that the growth of the (110) face remained largely unaffected by the presence of these additives, even in a moderate amount.
The rest of the paper is organized in the following manner. The kinetic and thermodynamics affecting the rate of growth are briefly discussed in Section 2, followed by a discussion of the computational method in Section 3. The results are discussed in Section 4, while the paper is concluded in Section 5.
2 Methodology
As stated earlier in the introduction to this paper, we aimed to examine how the kinetics and thermodynamics of the molecular growth processes containing different growth inhibitors affect the rate of crystallization. In order to study the kinetic and thermodynamic factors on the solvent and additive-controlled crystallization, we briefly describe an analytical model employed to calculate the rate of growth. The surface comprised flat regions and raised partial layers called terraces and steps, respectively.73 The solvated solute molecule in solvent-assisted crystallization diffuses towards the interfacial region through the mother nutrient before it is adsorbed into the surface steps. It also re-orients itself according to the surface structure before being absorbed. The surface-adsorbed solvent and additive then obstruct the movement of advancing steps, resulting in a delay in growth. The growth of crystal faces, Rred(hkl) is usually governed by a spiral growth mechanism and given by,31,74,75| Rred(hkl) = vkinkstep(hkl)d(hkl)/λ0(hkl) | (1) |
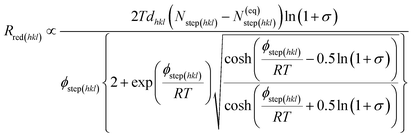 | (2) |
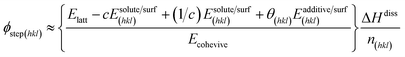 | (3) |
The fourth term in the numerator of the above expression represents a growth hindrance from the adsorption of the additive on the surface. With a saturated mol fraction of the solute concentration ceq, the supersaturation σ can be approximated as,
| σ = (c − ceq)/ceq | (4) |
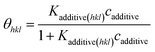 | (5) |
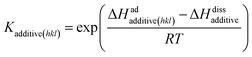 | (6) |
 | (7) |
| ΔEsolvent/surf(hkl) = Esolvent/surf(hkl) − Esolute/surf(hkl) | (8) |
| ΔEadditive/surf(hkl) = Eadditive/surf(hkl) − Esolute/surf(hkl) | (9) |
The third term in the denominator of eqn (7) represents the growth hindrance contributed by the surface-adsorbed additive. Detailed derivation of the above growth rate expression is described in detail elsewhere.41 It is evident from eqn (2), (3) and (7) that the step energy and rate of growth greatly depend on several kinetic and thermodynamic factors, like the supersaturation, solubility, surface coverage of the additive, and adsorption energy different auxiliaries present during crystallization. These energetics are accurately obtained using periodic ab initio density functional theory.
3 Computational method
We now provide a brief description of the computational details employed to calculate the adsorption energies and interfacial structures of the solute–surface, solvent–surface and additive–surface on various faces of the urea crystal. With this in mind, we employed periodic dispersion-corrected density functional theory with the B3LYP exchange–correlation functional (hereafter referred as DFT-B3LYP-D) as implemented in CRYSTAL14 (ref. 80 and 81) code to calculate the structure and energies. It has been widely demonstrated that the hybrid functionals and, in particular, the B3LYP functional can precisely determine the structure, energy and vibrational properties of molecules and solids.82–84 Civalleri et al.84 showed that the adsorption energy and vibrational frequency shift of CO adsorbed on the MgO(001) surface could be accurately obtained with the DFT-B3LYP-D method. The computed structures and lattice energies of different molecular crystals using the B3LYP functional are in good agreement with experimental data.85–87 This clearly shows that the results obtained with the DFT-B3LYP-D level of theory are better than the Hartree–Fock or exchange–correlation functional within the local density approximation and the generalized gradient approximation. In the present calculations, we employed finite atom-centred basis sets that lead to a basis sets superposition error (BSSE). This gives a spurious extra-binding that mimics the dispersion energy and, thereby exaggerates the dispersion correction.88,89 Ordinary BSSE tends to cancel the missing dispersive interactions in small and moderate basis sets. The dispersion-corrected density functional theory using the B3LYP exchange–correlation functional with BSSE correction has been employed to study the structure and the lattice energies of different molecular crystals and the results have shown that the computed lattice energies and lattice parameters are in good agreement with the corresponding experimental results.84 We also show that the crystal cell parameters and lattice energy of different molecular crystals obtained with DFT-B3LYP-D using a moderate basis set (6-31G(d,p)) gave close agreement with the corresponding experimental value.87 The application of smaller basis sets yields a larger basis set superposition error that leads to an over-correction of the lattice energy. On the other hand, the application of larger basis sets, like triple zeta polarization, gives structural parameters close to the experimental results, but the lattice energy is largely exaggerated. Taking all this into account, we employed the DFT-B3LYP-D method with the 6-31(d,p)90 all-electron basis set (hereafter referred as DFT-B3LYP-D/6-31(d,p)) for all the calculations reported in the paper. The counterpoise (CP) method, as proposed by Boys and Bernardi,91 was used to obtain the BSSE. The massive parallel implementation of CRYSTAL14 code is ideally suited to study a larger assembly of atoms with lower symmetry. The implementation effectively utilized high-performance computing resources and showed that a nearly linear scaling was achievable with large processor counts.92 The shrinking factor of 64 was used to define a mesh of points in the irreducible Brillouin zone to meet the convergence criteria.93,94 The detailed description of the computational parameters employed in the present calculation has been reported elsewhere.41 The energy optimization of the lattice parameters and atomic coordinates was carried out by means of analytical energy gradients.95,96Ab initio determination of the structure and adsorption energy of the auxiliaries adsorbed on the surface also required a consideration of the dispersion forces in the DFT calculations.82,84,86,97 An empirical correction term proposed by Grimme98 for long-range dispersion interactions in DFT calculations was thus added to the total energy and is given by,
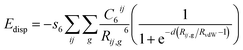 | (10) |
4 Results and discussion
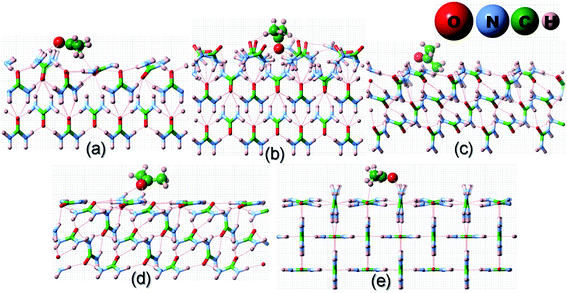
Having discussed the computational method to obtain the adsorption energy of the additive, we now briefly describe the adsorption of a low coverage of different additives, like biurea, biuret and acetone, on the different faces of the urea crystal. In Fig. 1, we show the structures of: (a) acetone, (b) biuret and (c) biurea. It is evident from Fig. 1 that biurea and biuret molecules have a higher structural compatibility to the urea molecule, and it is expected that they would play a dominant role in affecting the growth morphology of the urea crystal. On the contrary, acetone has a lower structural compatibility with the urea molecule, and would not alter the growth morphology to a large extent. The interaction between these molecular additives and urea surfaces are primarily dominated by hydrogen bonding at the interface. The potential energy surface, particularly for hydrogen-bonded complexes, would comprise many local minima and predicting the most stable structure is crucial to accurately determine the adsorption energy.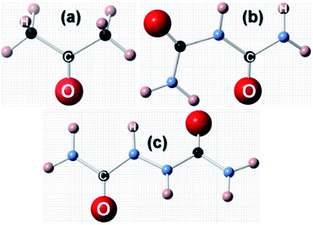 | ||
| Fig. 1 Molecular structures of three structurally related additives: (a) acetone, (b) biuret and (c) biurea molecules, showing the structural incompatibility/compatibility with the urea molecule. | ||
It has been shown that each symmetry site on the crystalline surface has an equal opportunity for additive adsorption closest to the surface.102 The adsorption of a low coverage of additives on various faces of the urea crystal was achieved by constructing a 3 × 3 supercell and exchanging the host molecule (urea) with a single additive molecule at each symmetry site and removing all other host molecules from the molecular layer103 that contain the additive.104 The 3D unit cell of the urea crystal comprises two urea molecules101 and, therefore, a 2D unit cell of (001), (110), (111) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces would comprise two distinct orientations of urea molecules,103,105 and, consequently, it is anticipated that the additive could also be adsorbed on the surface of these faces in two different orientations. To determine the most stable interfacial structures, we employed the ab initio evolutionary-based algorithm as implemented in USPEX code.106–108 The interfacial structures constructed by exchanging the host molecule with an additive molecule served as guess structures for the USPEX code. The application of suitable heredity, mutation and transmutation operators yielded next-generation trail interfacial structures that were structurally relaxed: first using the GULP109,110 code at the atomistic scale and subsequently, all the stable and metastable structures obtained using GULP were further relaxed using CRYSTAL14 (ref. 80 and 81) at the DFT-B3LYP-D/6-31G(d,p) level of theory. The energy ranking provided by the CRYSTAL14 code was used to obtain the lowest energy configuration. The 2D cell parameters of the crystal faces were fixed to their experimental value during the energy minimization process.
) faces would comprise two distinct orientations of urea molecules,103,105 and, consequently, it is anticipated that the additive could also be adsorbed on the surface of these faces in two different orientations. To determine the most stable interfacial structures, we employed the ab initio evolutionary-based algorithm as implemented in USPEX code.106–108 The interfacial structures constructed by exchanging the host molecule with an additive molecule served as guess structures for the USPEX code. The application of suitable heredity, mutation and transmutation operators yielded next-generation trail interfacial structures that were structurally relaxed: first using the GULP109,110 code at the atomistic scale and subsequently, all the stable and metastable structures obtained using GULP were further relaxed using CRYSTAL14 (ref. 80 and 81) at the DFT-B3LYP-D/6-31G(d,p) level of theory. The energy ranking provided by the CRYSTAL14 code was used to obtain the lowest energy configuration. The 2D cell parameters of the crystal faces were fixed to their experimental value during the energy minimization process.
Before we proceed to compute the rate of growth of different faces of the urea crystal in an aqueous solution containing a small amount of additives, we first present the results of our calculated adsorption energies (Eadditive/surf(hkl)) of different additives adsorbed on the (001), (110), (111) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces in low coverage. The fully relaxed structures of the adsorption of acetone, biuret and biurea on different faces of urea crystal can be seen in Fig. 2–4, respectively. In Table 1, we compiled the calculated adsorption energies in different configurations of acetone, biuret and biurea in partially and fully relaxed interfacial structures on the above-mentioned faces. For the partially relaxed additive–surface interface, the geometry of the additive molecule adsorbed on different faces was only allowed to relax; whereas, in the structure of the additive and other urea molecules that constitute a slab, only the bottom layer of the slab was relaxed in full relaxation. As noted earlier, the unit cell of a urea crystal comprises two urea molecules; consequently, in the partially relaxed structure, we obtained two distinct configurations of the additive molecule on each face. We carried out full structural relaxation of the interfacial structure as we noted that the adsorption of the additive on the surface would also alter the surface structure, particularly in the case of a strongly interacting additive. Interestingly our results showed that the two configurations of the additive adsorbed on either (110), (111) or (
) faces in low coverage. The fully relaxed structures of the adsorption of acetone, biuret and biurea on different faces of urea crystal can be seen in Fig. 2–4, respectively. In Table 1, we compiled the calculated adsorption energies in different configurations of acetone, biuret and biurea in partially and fully relaxed interfacial structures on the above-mentioned faces. For the partially relaxed additive–surface interface, the geometry of the additive molecule adsorbed on different faces was only allowed to relax; whereas, in the structure of the additive and other urea molecules that constitute a slab, only the bottom layer of the slab was relaxed in full relaxation. As noted earlier, the unit cell of a urea crystal comprises two urea molecules; consequently, in the partially relaxed structure, we obtained two distinct configurations of the additive molecule on each face. We carried out full structural relaxation of the interfacial structure as we noted that the adsorption of the additive on the surface would also alter the surface structure, particularly in the case of a strongly interacting additive. Interestingly our results showed that the two configurations of the additive adsorbed on either (110), (111) or (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces were reduced to a single configuration. However, it is evident from Fig. 2–4(a, b) and Table 1 that the fully relaxed interfacial structure comprising either acetone, biuret or biurea adsorbed on the (001) face retained two distinct configurations, namely configuration 1 and configuration 2.
) faces were reduced to a single configuration. However, it is evident from Fig. 2–4(a, b) and Table 1 that the fully relaxed interfacial structure comprising either acetone, biuret or biurea adsorbed on the (001) face retained two distinct configurations, namely configuration 1 and configuration 2.
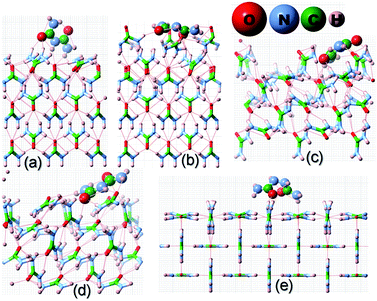 | ||
| Fig. 3 Same as Fig. 2 but for the adsorption of a biuret molecule on different surfaces of the urea crystal. | ||
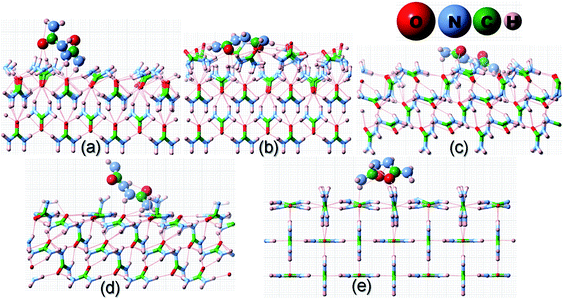 | ||
| Fig. 4 Same as Fig. 2 but for the adsorption of a biurea molecule on different surfaces of the urea crystal. | ||
| Face | Configuration no. | Eadditive/surf(hkl) (kJ mol−1) of | |||||
|---|---|---|---|---|---|---|---|
| Acetone | Biuret | Biurea | |||||
| Partially relaxed | Fully relaxed | Partially relaxed | Fully relaxed | Partially relaxed | Fully relaxed | ||
| (001) | 1 | −11.6 | −17.9 | −27.8 | −29.7 | −28.7 | −32.1 |
| 2 | −42.1 | −23.6 | −30.9 | −32.7 | −56.2 | −44.4 | |
| (110) | 1 | −14.3 | −15.7 | −21.2 | −24.5 | −23.1 | −28.8 |
| 2 | −14.9 | −22.4 | −34.7 | ||||
| (111) | 1 | −14.5 | −17.8 | −22.0 | −34.5 | −29.9 | −40.4 |
| 2 | −17.5 | −29.8 | −31.4 | ||||
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) ) |
1 | −18.8 | −15.4 | −16.5 | −30.4 | −34.3 | −38.5 |
| 2 | −19.7 | −29.5 | −35.6 | ||||
The adsorption energies of the strongly bound acetone molecule in the fully relaxed structure on (001), (110), (111), and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces were −23.6, −15.7, −17.8 and −15.4 kJ mol−1, respectively. On the other hand, the corresponding adsorption energies of biuret and biurea were −32.7, −24.5, −34.5, −30.4 kJ mol−1 and −44.4, −28.8, −40.4, −38.5 kJ mol−1, respectively. These can be compared with the adsorption energies of the strongly bound water molecule adsorbed in a liquid-like structure on the (001), (110), (111) and (
) faces were −23.6, −15.7, −17.8 and −15.4 kJ mol−1, respectively. On the other hand, the corresponding adsorption energies of biuret and biurea were −32.7, −24.5, −34.5, −30.4 kJ mol−1 and −44.4, −28.8, −40.4, −38.5 kJ mol−1, respectively. These can be compared with the adsorption energies of the strongly bound water molecule adsorbed in a liquid-like structure on the (001), (110), (111) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces, which were −9.8, −28.3, −10.1 and −6.5 kJ mol−1, respectively.41 Our calculated adsorption energy of biuret on different faces of the urea crystal were in good agreement with the results obtained using well-tempered meta-dynamics simulation.71,72 These results gave us confidence to employ the above-mentioned method to carry out calculations of the adsorption energy for acetone and biurea on the above-mentioned faces. It is worth mentioning that our previous41 calculations of the adsorption energies of biuret on different faces of urea crystal were slightly higher than the results reported in the present paper. This could be anticipated as the structure of the different interfaces were predicted by the ab initio evolutionary-based method.106–108 Note that the method employed in this paper for obtaining the interfacial structures is more rigorous in nature than the method employed previously.41 Nonetheless, in our previous study,41 we constructed several configurations of biuret positioned on different faces by exchanging the host molecule for a biuret molecule on a symmetry site.
) faces, which were −9.8, −28.3, −10.1 and −6.5 kJ mol−1, respectively.41 Our calculated adsorption energy of biuret on different faces of the urea crystal were in good agreement with the results obtained using well-tempered meta-dynamics simulation.71,72 These results gave us confidence to employ the above-mentioned method to carry out calculations of the adsorption energy for acetone and biurea on the above-mentioned faces. It is worth mentioning that our previous41 calculations of the adsorption energies of biuret on different faces of urea crystal were slightly higher than the results reported in the present paper. This could be anticipated as the structure of the different interfaces were predicted by the ab initio evolutionary-based method.106–108 Note that the method employed in this paper for obtaining the interfacial structures is more rigorous in nature than the method employed previously.41 Nonetheless, in our previous study,41 we constructed several configurations of biuret positioned on different faces by exchanging the host molecule for a biuret molecule on a symmetry site.
It is evident from Fig. 2 and Table 1 that acetone would be positioned lying flat on the surfaces of (110), (111), (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) and (001) in the configuration and, thus, it would result in a lower adsorption energy of acetone on the surface of these faces. Moreover, it is evident from Fig. 3 and 4 that biuret and biurea would also be lying down flat on the surface of the (110) face, which would also result in a lower adsorption energy. On the contrary, biuret and biurea were strongly adsorbed on the (001), (111) and (
) and (001) in the configuration and, thus, it would result in a lower adsorption energy of acetone on the surface of these faces. Moreover, it is evident from Fig. 3 and 4 that biuret and biurea would also be lying down flat on the surface of the (110) face, which would also result in a lower adsorption energy. On the contrary, biuret and biurea were strongly adsorbed on the (001), (111) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces. We employed eqn (5) to compute the surface coverage of the adsorption of acetone, biuret and biurea on the different faces relative to the (110) face in the fully relaxed structure, and the same is reported in Table 2. At lower concentrations of acetone in the aqueous solution of urea, the surface coverages on the (001), (111), and (
) faces. We employed eqn (5) to compute the surface coverage of the adsorption of acetone, biuret and biurea on the different faces relative to the (110) face in the fully relaxed structure, and the same is reported in Table 2. At lower concentrations of acetone in the aqueous solution of urea, the surface coverages on the (001), (111), and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces were 42.1, 2.4 and 0.9 times higher than those of the (110) face, respectively. On the other hand, the corresponding relative surface coverages at a low concentration of biuret and biurea on these faces were 27.6, 57.1, 10.7 and 539.4, 108.0, 50.4, respectively. Our results show that the surface coverage is increased by increasing the additive concentrations. At moderate concentrations of acetone, the relative surface coverages on the (001), (111) and (
) faces were 42.1, 2.4 and 0.9 times higher than those of the (110) face, respectively. On the other hand, the corresponding relative surface coverages at a low concentration of biuret and biurea on these faces were 27.6, 57.1, 10.7 and 539.4, 108.0, 50.4, respectively. Our results show that the surface coverage is increased by increasing the additive concentrations. At moderate concentrations of acetone, the relative surface coverages on the (001), (111) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces were in the same order of magnitude. Nonetheless, the relative surface coverage at a moderate concentration of biuret and biurea on these faces followed the same trends as at a low concentration of these additives. It is worth noting that the incorporation of biuret to the aqueous solution will severely impede the growth of (001) and (111) faces. Moreover, it also slightly delays the growth of (
) faces were in the same order of magnitude. Nonetheless, the relative surface coverage at a moderate concentration of biuret and biurea on these faces followed the same trends as at a low concentration of these additives. It is worth noting that the incorporation of biuret to the aqueous solution will severely impede the growth of (001) and (111) faces. Moreover, it also slightly delays the growth of (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces because of the huge difference in relative surface coverage on these faces. Furthermore, the growth of (001), (111) and (
) faces because of the huge difference in relative surface coverage on these faces. Furthermore, the growth of (001), (111) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces was severely inhibited by the addition of biurea in the aqueous solution. However, in either case the growth of the (110) face was hardly affected by the addition of these additives.
) faces was severely inhibited by the addition of biurea in the aqueous solution. However, in either case the growth of the (110) face was hardly affected by the addition of these additives.
| Face | Configuration no. | Surface coverage containing | |||||
|---|---|---|---|---|---|---|---|
| Acetone of concentration | Biuret of concentration | Biurea of concentration | |||||
| Low | Moderate | Low | Moderate | Low | Moderate | ||
| (001) | 1 | 2.5 | 1.8 | 8.1 | 11.0 | 3.8 | 4.5 |
| 2 | 24.3 | 3.7 | 27.6 | 24.0 | 539.4 | 46.5 | |
| (110) | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| (111) | 2.4 | 1.8 | 57.1 | 39.0 | 108.0 | 37.0 | |
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) ) |
0.9 | 0.9 | 10.7 | 11.0 | 50.4 | 28.5 | |
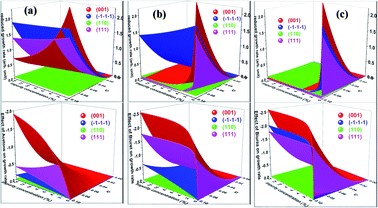
Having calculated the adsorption energy and relative surface coverage of the different additives, we now turn to compute the rate of growth of the different faces of urea from an aqueous medium containing a small amount of additive. The adsorption energies of the solute and solvent (water) on the different faces of urea crystal are reported elsewhere.41 It is evident from eqn (2), (3), (5) and (6) that the enthalpy of dissolution of an additive (ΔHdissadditive) is an important quantity to determine the step energy and rate of growth from a solution containing such an additive. The aqueous enthalpies of dissolution of acetone111,112 and biuret113 were −10.5 and −26.1 kJ mol−1, respectively. Nevertheless, the dissolution enthalpy of biurea is not readily available in scientific literature, and as a result, we estimated the same from the aqueous solubility data, and it was found to be −28.0 kJ mol−1. We employed eqn (2) along with the results presented in Table 1 and the adsorption energies of solutes and solvents discussed elsewhere41 to compute a reduced rate of growth of the aforementioned faces as a function of the supersaturation and additive concentrations at 25 °C, as shown in Fig. 5 (top). The growth hindrance arising primarily due to the additive in the vapour phase was obtained by subtracting the growth rate in a pure aqueous solution containing the solute and solvent (binary phase) from the rate of growth in an impure aqueous solution comprising the solute, solvent and additive (ternary phase), as shown in Fig. 5 (bottom). In Fig. 6, we show the relative rate of growth as a function of the supersaturation and additive concentration, which represents the ratio of the growth rate in the impure and pure aqueous solutions.
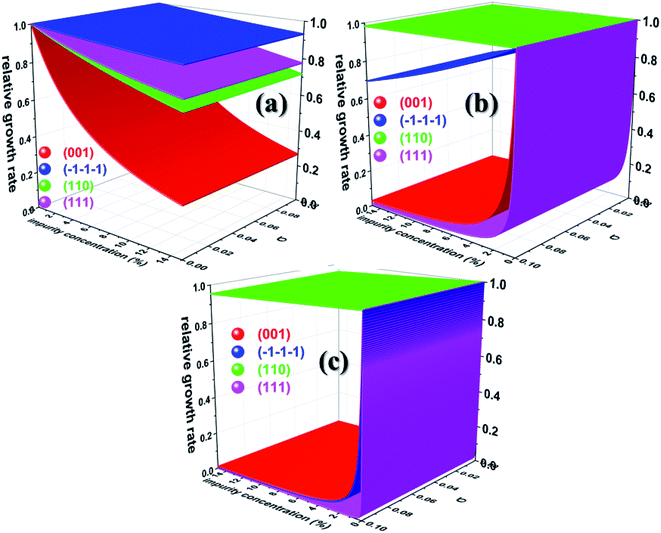 | ||
| Fig. 6 Calculated relative growth rate of different faces of urea crystal containing (a) acetone (b) biuret and (c) biurea as functions of the impurity concentration and supersaturation at 25 °C. | ||
Before we discuss the effect of different additives and their concentrations on the aqueous crystallization of urea crystal, we first briefly discuss the growth of different faces of urea crystal in pure aqueous solution in order to put our work into proper perspective. It can be concluded from eqn (2) that the higher adsorption energy of either the solvent or additive would inhibit the growth of the face, as solute molecules need to cross a high-energy barrier before getting absorbed. It is readily clear from Fig. 5 that the reduced aqueous growth rate of (001) and (110) faces in the presence of different additives was the highest and lowest, respectively, as the adsorption energy of a water molecule on these faces was the lowest and highest, respectively. The disruption of the solvent–surface interface on the (110) face leads to difficulty in the direct incorporation of the solute to the lattice and consequently the growth is rate-determined by the nucleation of a stable crystalline 2D nucleus on its surface. In contrary, the lower adsorption energy of water on the (001), (111) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces would eventually lead to a continuous growth of these faces and the rate-determining step of the growth is controlled by the diffusion of the solute towards the surface, which is consistent with the results of MD simulations.35,36,71,72
) faces would eventually lead to a continuous growth of these faces and the rate-determining step of the growth is controlled by the diffusion of the solute towards the surface, which is consistent with the results of MD simulations.35,36,71,72
We now discuss the additive-controlled crystallization of aqueous growth of urea crystal. It can be seen from Fig. 5a and 6 and the results presented in Table 1 that the addition of even moderate amounts of acetone in the growth medium did not appreciably obstruct the growth of even the fastest growing (001) face. It is also evident from Fig. 6a that the growth of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) face remained practically independent of the addition of a moderate amount of acetone in the growth medium. On the other hand, the presence of acetone marginally reduced the growth rate of (111), (110) and (001) faces. It is interesting to note that the adsorption energy of acetone on the (110) face was lower than the adsorption energy of water. However, the adsorption energy of acetone on the (001), (111) and (
) face remained practically independent of the addition of a moderate amount of acetone in the growth medium. On the other hand, the presence of acetone marginally reduced the growth rate of (111), (110) and (001) faces. It is interesting to note that the adsorption energy of acetone on the (110) face was lower than the adsorption energy of water. However, the adsorption energy of acetone on the (001), (111) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces was higher than the adsorption energy of water on the respective faces. It is clear from Fig. 6 that the addition of acetone in the aqueous solution of urea slightly affected the rate of growth of these faces. It is clear from Table 1 that the adsorption energies of either biuret or biurea were considerably higher than that of water on the (001), (111) and (
) faces was higher than the adsorption energy of water on the respective faces. It is clear from Fig. 6 that the addition of acetone in the aqueous solution of urea slightly affected the rate of growth of these faces. It is clear from Table 1 that the adsorption energies of either biuret or biurea were considerably higher than that of water on the (001), (111) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces, which enable a better efficacy of these additives in controlling the rate of growth of the above-mentioned faces. It can be seen from Fig. 5b and c and the results presented in Table 1 that the presence of biurea in the aqueous solution of urea most severely reduced the rate of growth of the (001) face than that of biuret even at their lower concentration. This was largely due to the fact that the former has more adsorption energy than the latter. On the contrary, it is evident from Fig. 5 and 6 that the reduce growth and relative growth rate of the (110) face were nearly unaffected by the adsorption of biuret, which is in agreement with the experimental observation.70 This can be rationalised by considering the higher adsorption energy of the strongly bound water molecule than the adsorption energy of biuret (see Table 1); thus the adsorption sites available at the (110) face were largely occupied by the water molecules. Interestingly, even a higher concentration of biuret did not appreciably impede the growth of the (110) face. Moreover, the modest increase in biuret concentration substantially decreased the growth rate of the (001) and (111) faces. On the other hand, the adsorption energy of biurea at (110) was slightly higher than the adsorption energy of the strongly bound water molecule at the surface and thus, growth was barely obstructed by the addition of a moderate amount of biurea (cf. Fig. 6c). The growth of the (001) and (111) and (
) faces, which enable a better efficacy of these additives in controlling the rate of growth of the above-mentioned faces. It can be seen from Fig. 5b and c and the results presented in Table 1 that the presence of biurea in the aqueous solution of urea most severely reduced the rate of growth of the (001) face than that of biuret even at their lower concentration. This was largely due to the fact that the former has more adsorption energy than the latter. On the contrary, it is evident from Fig. 5 and 6 that the reduce growth and relative growth rate of the (110) face were nearly unaffected by the adsorption of biuret, which is in agreement with the experimental observation.70 This can be rationalised by considering the higher adsorption energy of the strongly bound water molecule than the adsorption energy of biuret (see Table 1); thus the adsorption sites available at the (110) face were largely occupied by the water molecules. Interestingly, even a higher concentration of biuret did not appreciably impede the growth of the (110) face. Moreover, the modest increase in biuret concentration substantially decreased the growth rate of the (001) and (111) faces. On the other hand, the adsorption energy of biurea at (110) was slightly higher than the adsorption energy of the strongly bound water molecule at the surface and thus, growth was barely obstructed by the addition of a moderate amount of biurea (cf. Fig. 6c). The growth of the (001) and (111) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces were exceedingly hindered by the increase in biurea concentration. From the above observation, it can be concluded that the adsorption of a small amount of either biurea or biuret at the (001) face at a lower supersaturation absolutely terminated the growth of that face.
) faces were exceedingly hindered by the increase in biurea concentration. From the above observation, it can be concluded that the adsorption of a small amount of either biurea or biuret at the (001) face at a lower supersaturation absolutely terminated the growth of that face.
Nevertheless, Salvalaglio et al.71,72 observed a slight decrease in the rate of growth of the (110) face by the addition of acetone in the aqueous growth of urea crystal in their MD simulation, which was primarily attributed to steric hindrance. It is also interesting to note that increasing the additive concentration in the aqueous solution of urea decreased the aqueous solubility of urea and, hence, it is anticipated that the rate of growth would be further reduced by increasing the additive concentration. It is noteworthy that the steric hindrance arising due to the presence of the additive near the interface and the reduction in aqueous solubility of urea that occurs due to the addition of the additive were neglected in our calculations. It is also apparent from Fig. 6 that the rate of growth of the (111) face is lower than its Freidel opposite (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) face at all supersaturations, additive concentrations and saturation temperatures, and, hence, the (
) face at all supersaturations, additive concentrations and saturation temperatures, and, hence, the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) face is never observed in additive-assisted aqueous-growth morphologies of the urea crystal. This could be attributed to the fact that the former face possesses a higher adsorption energy of water and additives than the latter face (see Table 1). It can be concluded from Table 1 and Fig. 6 that the additives considered in this paper would strongly retard the growth of the (111) face more than that of the (
) face is never observed in additive-assisted aqueous-growth morphologies of the urea crystal. This could be attributed to the fact that the former face possesses a higher adsorption energy of water and additives than the latter face (see Table 1). It can be concluded from Table 1 and Fig. 6 that the additives considered in this paper would strongly retard the growth of the (111) face more than that of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
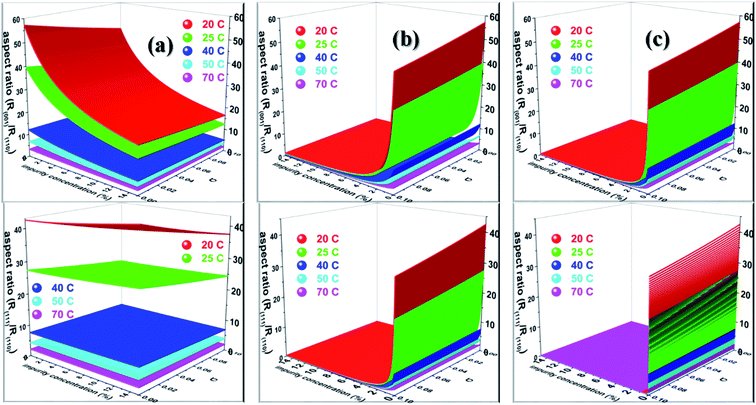
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) face. Considering the above discussion, we envisage that the growth morphology of urea would be drastically modified by the addition of either biurea or biuret by ceasing the growth along the [001] and [111] directions. The top and bottom of Fig. 7 show the predicted aspect ratio AR1 = (Rred(001)/Rred(110)) and AR2 = (Rred(111)/Rred(110)), respectively, of aqueous-grown urea crystals at different saturation temperatures containing (a) acetone, (b) biuret and (c) biurea as functions of σ and different additive concentrations. Fig. 7a clearly demonstrates that AR1 was slowly decreased and AR2 became nearly independent with increasing the acetone concentration. Moreover, our results show that the aspect ratio also decreased with increasing the degree of supersaturation. Notwithstanding, it is clear from Fig. 7b and c that the presence of a small amount of either biurea or biuret drastically reduced the aspect ratio. It also became clear that biurea could more severely reduce the aspect ratio than biuret. The shape of urea crystal became plate-like at a moderate concentration of either biurea or biuret. It is quite clear that an increase in saturation temperature also resulted in an increase in the growth rates but a decrease in the aspect ratio.
) face. Considering the above discussion, we envisage that the growth morphology of urea would be drastically modified by the addition of either biurea or biuret by ceasing the growth along the [001] and [111] directions. The top and bottom of Fig. 7 show the predicted aspect ratio AR1 = (Rred(001)/Rred(110)) and AR2 = (Rred(111)/Rred(110)), respectively, of aqueous-grown urea crystals at different saturation temperatures containing (a) acetone, (b) biuret and (c) biurea as functions of σ and different additive concentrations. Fig. 7a clearly demonstrates that AR1 was slowly decreased and AR2 became nearly independent with increasing the acetone concentration. Moreover, our results show that the aspect ratio also decreased with increasing the degree of supersaturation. Notwithstanding, it is clear from Fig. 7b and c that the presence of a small amount of either biurea or biuret drastically reduced the aspect ratio. It also became clear that biurea could more severely reduce the aspect ratio than biuret. The shape of urea crystal became plate-like at a moderate concentration of either biurea or biuret. It is quite clear that an increase in saturation temperature also resulted in an increase in the growth rates but a decrease in the aspect ratio.
5 Summary and conclusions
In summary, we examined different growth additives like acetone, biuret and biurea in order to study the aqueous crystallization of the urea crystal. The additive–surface configurations on different faces were obtained using an evolutionary-based algorithm. The structure and adsorption energies of various configurations of additives on different faces of urea crystal were calculated using a periodic dispersion-corrected density functional method. The kinetic and thermodynamic aspects of the adsorption of various auxiliaries present in the crystallizing media were related to the kinetics of the molecular growth processes on the flat faces of the crystals. We derived an analytical growth rate expression related to the kinetic and thermodynamic aspects of the adsorption of the solute, solvent and additive on the flat faces of the crystals to compute the rate of growth of the different faces of urea crystal as functions of the additive concentration and supersaturation.Our results show that the lower bonding of acetone with the surfaces of the (110), (111), (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) and (001) faces were due to the geometry of the adsorbed acetone molecule that was positioned lying flat on the surfaces. Consequently, the rate of growth of the (110), (111) and (
) and (001) faces were due to the geometry of the adsorbed acetone molecule that was positioned lying flat on the surfaces. Consequently, the rate of growth of the (110), (111) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) faces were nearly unaltered by the presence of moderate amounts of acetone in the solution. However, a moderate concentration of acetone reasonably hampered the growth of the (001) face. The optimized interfacial structure showed that biuret and biurea attained flat positions at the (110) face, which resulted in a weak interaction with the face and, hence, it was expected that the growth of the face would remain largely unaltered. On the other hand, the adsorption of biuret and biurea on the (001) and (111) faces was remarkably stronger than that on the (110) face. Additionally, biurea also inhibited the growth of the (
) faces were nearly unaltered by the presence of moderate amounts of acetone in the solution. However, a moderate concentration of acetone reasonably hampered the growth of the (001) face. The optimized interfacial structure showed that biuret and biurea attained flat positions at the (110) face, which resulted in a weak interaction with the face and, hence, it was expected that the growth of the face would remain largely unaltered. On the other hand, the adsorption of biuret and biurea on the (001) and (111) faces was remarkably stronger than that on the (110) face. Additionally, biurea also inhibited the growth of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) face significantly. Our results show that the growths of the (001) and (111) face were severely hampered by the addition of a small amount of biurea or biuret additive. This was largely due to the higher adsorption energy of these additives at the (001) and (111) faces and, thus, the available adsorption sites were mostly occupied by either biurea or biuret additive. We believe that our results presented in the paper will enable experimentalists to control the various process parameters for the predictive design of crystal growth experiments as well as the additive-controlled nucleation and growth processes. We are currently applying the methodology discussed in this paper to investigate the experimentally observed asymmetrical growth and dissolution along the polar axis of many acentric materials to elucidate the role played by different solvents and tailor-made additives towards the unidirectional growth and dissolution of these materials. Details will be published in due course.
) face significantly. Our results show that the growths of the (001) and (111) face were severely hampered by the addition of a small amount of biurea or biuret additive. This was largely due to the higher adsorption energy of these additives at the (001) and (111) faces and, thus, the available adsorption sites were mostly occupied by either biurea or biuret additive. We believe that our results presented in the paper will enable experimentalists to control the various process parameters for the predictive design of crystal growth experiments as well as the additive-controlled nucleation and growth processes. We are currently applying the methodology discussed in this paper to investigate the experimentally observed asymmetrical growth and dissolution along the polar axis of many acentric materials to elucidate the role played by different solvents and tailor-made additives towards the unidirectional growth and dissolution of these materials. Details will be published in due course.
Conflicts of interest
The author declares no competing financial and conflicts of interest.Acknowledgements
The author wish to thank Shri D. Das and Shri. S. V. Nakhe for their encouragement and invaluable support. The support and motivation also received from Dr Arup Banerjee and Dr Aparna Chakrabarti are kindly acknowledged. The author would like to acknowledge efforts of Computer Division staff that enabled effective utilization of centralized scientific computing resources for carrying out computations reported in this paper/article.References
- R. C. Snyder, S. Veesler and M. F. Doherty, Cryst. Growth Des., 2008, 8, 1100 CrossRef CAS.
- N. Variankaval, A. S. Cote and M. F. Doherty, AIChE J., 2008, 54, 1682 CrossRef CAS.
- D. Kaminski, N. Radenovic, M. A. Deij, W. J. P. van Enckevort and E. Vlieg, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 245404 CrossRef.
- D. Kaminski, N. Radenovic, M. A. Deij, W. J. P. van Enckevort and E. Vlieg, Cryst. Growth Des., 2006, 6, 588 CrossRef CAS.
- I. Weissbuch, L. Addadi and L. Leiserowitz, Science, 1991, 253, 637–645 CrossRef CAS PubMed.
- I. Weissbuch, R. Popovitibiro, M. Lahav and L. Leiserowitz, Acta Crystallogr., Sect. B: Struct. Sci., 1995, 51, 115 CrossRef.
- A. F. Wells, Discuss. Faraday Soc., 1949, 5, 197 RSC.
- Z. Berkovitch-Yellin, J. Am. Chem. Soc., 1985, 107, 8239 CrossRef CAS.
- R. J. Davey, B. Milisavljevic and J. R. Bourne, J. Phys. Chem., 1988, 92, 2032 CrossRef CAS.
- P. Dandekar, Z. B. Kuvadia and M. F. Doherty, Annu. Rev. Mater. Res., 2013, 43, 359 CrossRef CAS.
- M. A. Lovette, A. R. Browning, D. W. Griffin, J. P. Sizemore, R. C. Snyder and M. F. Doherty, Ind. Eng. Chem. Res., 2008, 47, 9812 CrossRef CAS.
- E. Vlieg, M. Deij, D. Kaminski, H. Meekes and W. van Enckevort, Faraday Discuss., 2007, 136, 57 RSC.
- J. R. Bourne and R. J. Davey, J. Cryst. Growth, 1976, 36, 278 CrossRef CAS.
- J. R. Bourne and R. J. Davey, J. Cryst. Growth, 1976, 36, 287 CrossRef CAS.
- P. Bennema and J. P. van Eerden, Morphology of Crystals, Terra Scientific Publishing Co., Tokyo, 1977, pp. 1–75 Search PubMed.
- L. J. W. Shimon, M. Vaida, L. Addadi, M. Lahav and L. Leiserowitz, J. Am. Chem. Soc., 1990, 112, 6215 CrossRef CAS.
- P. Bennema and G. Gilmer, Crystal Growth: An Introduction, ed. P. Hartman, North-Holland, Amsterdam, 1973, p. 274 Search PubMed.
- C. J. Tilbury and M. F. Doherty, AIChE J., 2017, 63, 1338 CrossRef CAS.
- A. E. Nielsen, Pure Appl. Chem., 1981, 53, 2025 CAS.
- A. E. Nielsen, J. Cryst. Growth, 1984, 67, 289 CrossRef CAS.
- C. F. Woensdregt, Faraday Discuss., 1993, 95, 97 RSC.
- X. Y. Liu and P. Bennema, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 765 CrossRef CAS PubMed.
- X. Y. Liu, E. S. Boek, W. J. Briels and P. Bennema, Nature, 1995, 374, 342 CrossRef CAS.
- X. Y. Liu, E. S. Boek, W. J. Briels and P. Bennema, J. Chem. Phys., 1995, 103, 3747 CrossRef CAS.
- X. Y. Liu and P. Bennema, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 2314 CrossRef CAS PubMed.
- X. Y. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 2810 CrossRef CAS.
- S. Gnanasambandam and R. Rajagopalan, CrystEngComm, 2010, 12, 1740 RSC.
- D. Winn and M. F. Doherty, AIChE J., 1998, 44, 2501 CrossRef CAS.
- V. Bisker-Leib and M. F. Doherty, Cryst. Growth Des., 2001, 1, 455 CrossRef CAS.
- M. A. Lovette and M. F. Doherty, Cryst. Growth Des., 2012, 12, 656 CrossRef CAS.
- W. K. Burton, N. Cabrera and F. C. Frank, Philos. Trans. R. Soc., A, 1951, 243, 299 CrossRef.
- F. C. Wireko, L. J. W. Shimon, F. Frolow, Z. Berkovitch-Yellin, M. Lahav and L. Leiserowitz, J. Phys. Chem., 1987, 91, 472 CrossRef CAS.
- M. Hussain and J. Anwar, J. Am. Chem. Soc., 1999, 121, 8583 CrossRef CAS.
- S. Khoshkhoo and J. Anwar, J. Chem. Soc., Faraday Trans., 1996, 92, 1023 RSC.
- S. Piana and J. D. Gale, J. Am. Chem. Soc., 2005, 127, 1975 CrossRef CAS PubMed.
- S. Piana, M. Reyhani and J. D. Gale, Nature, 2005, 438, 70 CrossRef CAS PubMed.
- G. Tóth, Cryst. Growth Des., 2008, 8, 3959 CrossRef.
- M. K. Singh and A. Banerjee, Cryst. Growth Des., 2013, 13, 2413 CrossRef CAS.
- M. K. Singh, S. K. Sharma and A. Banerjee, CrystEngComm, 2013, 15, 8493 RSC.
- M. K. Singh, CrystEngComm, 2017, 17, 7731 RSC.
- M. K. Singh and V. S. Tiwari, Cryst. Growth Des., 2015, 15, 3220 CrossRef CAS.
- A. S. Myerson, Molecular Modelling Applications in Crystallization, Cambridge University Press, Cambridge, 1999 Search PubMed.
- R. Docherty and P. Meenan, The Study of Molecular Materials using Computational Chemistry, ed. A. S. Myerson, Cambridge University Press, Cambridge, 1999, pp. 106–165 Search PubMed.
- I. Weissbuch, L. J. W. Shimon, K. M. Landau, R. Popovitz-Biro, Z. Berkovitch-Yellin, L. Addadi, M. Lahav and L. Leiserowitz, Pure Appl. Chem., 1986, 58, 947 CAS.
- I. Weissbuch, R. Popovitz-Biro, M. Lahav and L. Leiserowitz, Acta Crystallogr., Sect. B: Struct. Sci., 1995, 51, 115 CrossRef.
- K. Sangwal, Prog. Cryst. Growth Charact., 1996, 32, 3 CrossRef CAS.
- X. Yang, G. Qian, X. Duan and X. Zhou, Cryst. Growth Des., 2013, 13, 1295 CrossRef CAS.
- R. Dowling, R. J. Davey, R. A. Curtis, G. Han, S. K. Poornachary, P. S. Chow and R. B. H. Tan, Chem. Commun., 2010, 46, 5924 RSC.
- F. Wang, G. Y. Xu, Z. Q. Zhang, S. Song and S. L. Dong, J. Colloid Interface Sci., 2006, 293, 394 CrossRef CAS PubMed.
- L. Addadi, Z. Berkovitchyellin, N. Domb, E. Gati, M. Lahav and L. Leiserowitz, Nature, 1982, 296, 21 CrossRef CAS.
- N. Cabrera and D. A. Vermilyea, Growth and Perfection of Crystals, ed. R. H. Doremus, B. W. Roberts and D. Turnbull, John Wiley & Sons, Inc., New York, 1958, p. 393 Search PubMed.
- N. Kubota and J. W. Mullin, J. Cryst. Growth, 1995, 152, 203 CrossRef CAS.
- N. Kubota, M. Yokota and J. W. Mullin, J. Cryst. Growth, 2000, 212, 480 CrossRef CAS.
- K. Sangwal, J. Cryst. Growth, 1999, 203, 197 CrossRef CAS.
- K. Sangwal, J. Cryst. Growth, 2002, 242, 215 CrossRef CAS.
- H. H. Teng, P. M. Dove, C. A. Orme and J. J. De Yoreo, Science, 1998, 282, 724 CrossRef CAS PubMed.
- L. N. Rashkovich, N. V. Gvozdev, M. I. Sil'nikova, I. Yaminski and A. A. Chernov, Crystallogr. Rep., 2001, 46, 860 CrossRef.
- A. A. Chernov, J. Cryst. Growth, 2004, 264, 499 CrossRef CAS.
- L. Addadi, Z. Berkovitch-Yellin, I. Weissbuch, J. van Mil, L. J. W. Simon, M. Lahav and L. Leiserowitz, Angew. Chem., Int. Ed. Engl., 1985, 24, 466 CrossRef.
- G. Clydesdale, R. Docherty and K. J. Roberts, Crystal Growth of Organic Materials, Proceedings of the 3rd International Workshop on the Crystal Growth of Organic Materials (CGOM3), Washington, DC, August 27–31, 1995, ed. A. S. Myerson, D. A. Green and P. Meenan, Oxford University Press, New York, 1996, p. 43 Search PubMed.
- G. Clydesdale, R. Docherty and K. J. Roberts, HABIT95, Quantum Chemistry Program Exchange (QCPE), Bloomington, IN 47405, program number 670, 1996 Search PubMed.
- G. Clydesdale, G. B. Thomson and E. M. Walker, Cryst. Growth Des., 2005, 5, 2154 CrossRef CAS.
- G. Clydesdale, K. J. Roberts, K. Lewtas and R. Docherty, J. Cryst. Growth, 1994, 141, 443 CrossRef CAS.
- G. Clydesdale, K. J. Roberts and R. Docherty, J. Cryst. Growth, 1994, 135, 331 CrossRef CAS.
- S. K. Poornachary, P. S. Chow, R. B. H. Tan and R. J. Davey, Cryst. Growth Des., 2007, 7, 254 CrossRef CAS.
- S. K. Poornachary, P. S. Chow and R. B. H. Tan, J. Cryst. Growth, 2008, 310, 3034 CrossRef CAS.
- S. K. Poornachary, G. Lau, P. S. Chow, R. B. H. Tan and N. George, Cryst. Growth Des., 2011, 11, 492 CrossRef CAS.
- K. Sangwal, Additive and Crystallization Processes: From Fundamental to Application, John Wiley & Sons, Inc., England, 2007, pp. 73–174 Search PubMed.
- A. Amjad, Advances in Crystal Growth Inhibition Technologies, ed. A. Amjad, Kluwer Academic Publishers, New York, 2002 Search PubMed.
- R. Davey, W. Fila and J. Garside, J. Cryst. Growth, 1986, 79, 607 CrossRef CAS.
- M. Salvalaglio, T. Vetter, F. Giberti, M. Mazzotti and M. Parrinello, J. Am. Chem. Soc., 2012, 134, 17221 CrossRef CAS PubMed.
- M. Salvalaglio, T. Vetter, M. Mazzotti and M. Parrinello, Angew. Chem., Int. Ed., 2013, 52, 13369 CrossRef CAS PubMed.
- A. A. Chernov, Contemp. Phys., 1989, 30, 251 CrossRef CAS.
- A. A. Chernov, Modern Crystallography III, Springer-Verlag, New York, 1984 Search PubMed.
- P. Bennema, Handbook of Crystal Growth, ed. D. T. J. Hurle, Elsevier Science Publishers, Amsterdam, 1993, ch. 7, vol. 1a, pp. 477–581 Search PubMed.
- H. Cuppen, Ph.D. thesis, Radboud University Nijmegen, The Netherlands, 2005.
- M. A. Lovette and M. F. Doherty, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 021604 CrossRef PubMed.
- J. Osśik, Adsorption, PWN, Warsaw, 1982 Search PubMed.
- R. J. Davey and J. W. Mullin, J. Cryst. Growth, 1974, 26, 45 CrossRef CAS.
- R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D'Arco, Y. Noel, M. Causa, M. Rerat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287 CrossRef CAS.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco, M. Llunell, M. Causà and Y. Noël, CRYSTAL14 User's Manual, University of Torino, Torino, 2014 Search PubMed.
- S. Feng and T. Li, J. Chem. Theory Comput., 2006, 2, 149 CrossRef CAS PubMed.
- F. Corá, M. Alfredsson, G. Mallia, D. S. Middlemiss, W. C. Mackrodt, R. Dovesi and R. Orlando, Struct. Bonding, 2004, 113, 171 CrossRef.
- B. Civalleri, L. Maschio, P. Ugliengoa and C. M. Zicovich-Wilsonb, Phys. Chem. Chem. Phys., 2010, 12, 6382 RSC.
- B. Civalleri, C. M. Zicovich-Wilson, L. Valenzano and P. Ugliengo, CrystEngComm, 2008, 10, 405 RSC.
- B. Civalleri, K. Doll and C. M. Zicovich-Wilson, J. Phys. Chem. B, 2007, 111, 26 CrossRef CAS PubMed.
- M. K. Singh, J. Cryst. Growth, 2014, 396, 14 CrossRef CAS.
- A. Johansson, P. Kollman and S. Rotherberg, Theor. Chim. Acta, 1973, 29, 167 CrossRef CAS.
- J. P. Daudey, P. Claverieand and J. P. Malrieu, Int. J. Quantum Chem., 1974, 8, 1 CrossRef CAS.
- W. J. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, Wiley, New York, 1986 Search PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- A. Erba, J. Baima, I. Bush, R. Orlando and R. Dovesi, J. Chem. Theory Comput., 2017, 13, 5019 CrossRef CAS PubMed.
- G. Gilat, J. Comput. Phys., 1972, 10, 432 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- K. Doll, N. M. Harrison and V. R. Saunders, Int. J. Quantum Chem., 2001, 82, 1 CrossRef CAS.
- K. Doll, R. Dovesi and R. Orlando, Theor. Chem. Acc., 2004, 112, 394 Search PubMed.
- J. F. Dobson, K. McLennan, A. Rubio, J. Wang, T. Gould, H. M. Le and B. P. Dinte, Aust. J. Chem., 2001, 54, 513 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. D. Cox and G. Pilcher, Thermochemistry of Organic and Organometallic Compounds, Academic Press, New York, 1970 Search PubMed.
- S. Swaminathan, B. M. Craven and R. K. McMullan, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1984, 40, 300 CrossRef.
- A. I. Kitaigorodskii, Mixed Crystals, Springer-Verlag, Berlin, 1984 Search PubMed.
- M. K. Singh, A. Banerjee and P. K. Gupta, J. Cryst. Growth, 2012, 343, 77 CrossRef CAS.
- J. J. Lu and J. Ulrich, Cryst. Res. Technol., 2003, 38, 63 CrossRef CAS.
- M. K. Singh, A. Banerjee and P. K. Gupta, Cryst. Growth Des., 2012, 12, 732 CrossRef CAS.
- A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704 CrossRef PubMed.
- A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, Comput. Phys. Commun., 2013, 184, 1172 CrossRef CAS.
- A. R. Oganov, A. O. Lyakhov and M. Valle, Acc. Chem. Res., 2011, 44, 227 CrossRef CAS PubMed.
- J. D. Gale, Z. Kristallogr., 2005, 220, 552 Search PubMed.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291 CrossRef CAS.
- E. W. Washburn, N. R. Council, C. J. West, I. C. S. Unions, C. Hull and N. A. Sciences, International Critical Tables (ICT), National Research Council, 1929, vol. 5, pp. 148–150 Search PubMed.
- V. D. Kiselev, I. I. Shakirova, L. N. Potapova, H. A. Kashaeva and D. A. Kornilov, Dataset Papers in Chemistry, Hindawi Publishing Corporation, 2013, pp. 823638 Search PubMed.
- A. L. Voskov, T. S. Babkina, A. V. Kuznetsov and I. A. Uspenskaya, J. Chem. Eng. Data, 2012, 57, 3225 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |