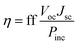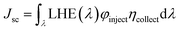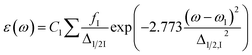DOI:
10.1039/D0RA10613E
(Paper)
RSC Adv., 2021,
11, 5556-5567
The influence of the shape and configuration of sensitizer molecules on the efficiency of DSSCs: a theoretical insight†
Received
17th December 2020
, Accepted 4th January 2021
First published on 29th January 2021
Abstract
The sensitizer is an active component of dye sensitized solar cell (DSSC) technology, which is highly influential for the performance of DSSCs. The present study attempts to investigate the relationship between the shape of the sensitizer molecule and efficiency of DSSCs. Specifically, 17 different structures were investigated, and classified into four categories based on the shape of the dye molecule, namely L-shaped (linear), V-shaped, X-shaped and Y-shaped, and into two different categories based on the donor moiety. The five of studied structures contained a triphenylamine (TPA) donor moiety, and twelve structures contained carbazole (CAR) donor moiety. Parameters related to the performance of DSSCs such as absorption spectra, intramolecular charge transfer indices, frontier molecular orbitals, light harvesting efficiency, excited-state lifetime, exciton binding energy, electrostatic potential, charge transfer and electron injection ability were studied using results obtained from electronic structure calculations. The analysis of these various parameters showed that the linear-shaped and V-shaped sensitizers possess better photon absorption ability, and the V-shaped structure is best suited shape for applications in high performance DSSCs.
1. Introduction
Energy plays a vital role in global economy, and thus energy scarcity will cause critical issues in almost all the aspects of daily life. Currently, it is important to identify energy production methods that are more efficient and environmental friendly.1,2 The production of renewable energy provides a solution to both energy demands and environmental concerns.3 In this case, solar energy harvesting using photovoltaic technology seems to be a very viable choice.4–6 Since conventional silicon-based technology is expensive, research is focused on comparatively cheaper photovoltaic technologies such as perovskite solar cells (PSCs), dye sensitised solar cells (DSSCs), organic solar cells (OSC), and quantum dot solar cells (QDSC). These new generation solar cell technologies are characterised by good flexibility, low production costs and biodegradability. However, new generation photovoltaic technology has not achieved the required efficiency for its wide applicability.
Among the available photovoltaic technologies, dye sensitised solar cells (DSSCs) are a promising technology. Although the efficiency level of DSSCs is modest under full light conditions, they are the best choice under dim light conditions.7 Also, DSSCs offer decent scope for improvement in efficiency chiefly by tuning the opto-electronic properties of the dye material, which is an active component of this technology with tuneable substitutions and structural modifications.8–10 There are two main factors that determine the power conversion efficiency (PCE) of DSSCs, namely, the short circuit current (Jsc) and the open circuit voltage (Voc). The electronic properties of a sensitizer molecule directly impact Jsc since the sensitizer is responsible for harvesting solar light, and thereby accounts for the number of charge carriers produced and injected into the oxide layer.11,12 On the other hand, the dye molecule can influence the Voc of DSSCs through its participation in energy level alignment and control over recombination losses. Numerous experimental and theoretical studies have reported with the aim of improving solar cell efficiency based on its structure and compositional tuning.8,9,12–21 These efforts have led to a gradual increase in the efficiency of DSSCs, where the maximum efficiency of up to 14.3% was achieved under full light conditions,22 while efficiency up to 28.9% has been reported under dim light conditions.23 Hence, structural and compositional modifications are common strategies to improve the efficiency of DSSCs, particularly manipulating the shape of the dye molecule, and there are several reports on the effect of the shape of dye molecules on the performance of DSSCs.13–15,18–21,24–28
The implications of shape modifications of the sensitizer molecule on the efficiency of DSSCs is not straightforward, and thus it is difficult to develop a benchmark shape for a sensitizer that results in high efficiency in DSSCs. This is because the shape of the dye can influence several factors that are related to the PCE of DSSCs, where it can have a positive impact on certain parameters, while the same shape may have a negative impact on other parameters. For instance, a branched sensitizer (instead of linear sensitizer) can be helpful in decreasing the energy quenching effect that occurs between dye molecules and screening TiO2–electrolyte interactions, but it may reduce the dye loading on the surface of TiO2, thereby reducing the amount of charge generated. Also, it is known that the frontier molecular orbital patterns and their energies responsible for the opto-electronic properties of dye molecules strongly depend on the shape of the dye molecule and functional groups present on it. Therefore, it is important to develop a design that balances different aspects of the sensitizer towards high PCE. In this direction, Yuezhen et al.19 performed an experimental study to investigate the impact of the shape of the sensitizer on the PCE of DSSC, particularly focusing on the angle between the donor and acceptor moieties (flare angle). Their study concluded that the dyes with a larger flare angle of about 150.6° between the donor and acceptor units are suitable for DSSC applications. There are several other studies that investigated sensitizers of different shapes, such as X-shaped, Y-shaped, linear, branched, H-shaped, V-shaped, and rod-shaped sensitizers,5,10,13–15,18–21,24–28 most of which were carried out independently, lack consistency in the description rules for the sensitizer molecular shape and do not present any insight into how sensitizers of different shapes differ under identical conditions of examination to reach a benchmark on the shape of the sensitizer.
To form consolidated conclusions, a collective study that encompasses several shapes of dyes in a uniform platform must be performed. Thus, this study is an attempt to achieve this goal and will present more clarity on the design strategy for sensitizers and their relationship with the PCE. In the present work, electronic structure calculations were performed on 17 different structures, which can be classified into four categories based on their shape, namely linear-shaped, V-shaped, X-shaped and Y-shaped sensitizers. The studied structures can also be classified in terms of their donor moieties, namely triphenylamine (TPA)-based sensitizers and carbazole (CAR)-based sensitizers. One of the studied sensitizers (TPAL1) was previously reported by Kuan-Fu Chen et al.29 and was shown to provide a modest PCE of 4.40%, while the other sensitizers were newly designed. This study was limited to investigating the opto-electronic properties of the individual sensitizer molecules, such as their absorption spectrum, intra-molecular charge transfer and other parameters related to the Jsc and Voc.
2. Theoretical background and methodology
The power conversion efficiency (PCE) is a measure of the performance of any type of solar cell, which refers to the percentage of incident light that a solar cell can harvest. The PCE (η) is given by the expression30| |
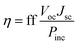 | (1) |
where ff is the fill factor of the solar cell, Voc is the open circuit voltage, Jsc is the short circuit current and Pinc refers to the power of incident solar radiation flux. In the above expression, Voc and Jsc are parameters that can be tuned to improve the PCE. Although the expression for the PCE is generic for all photovoltaic technologies, the Voc and Jsc are dependent on the components of the specific technology.
The short-circuit current (Jsc) of a DSSC is given by31
| |
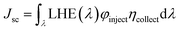 | (2) |
where LHE (
λ) refers to the light harvesting efficiency at a particular absorption wavelength,
λ, of a dye molecule,
φinject refers to the electron injection efficiency and
ηcollect is the charge collection efficiency. It should be noted that the LHE (
λ) is completely a sensitizer-dependent factor, whereas
φinject is partially dependent on the sensitizer and
ηcollect is a parameter that is dependent on the recombination lifetime and diffusion transit time. LHE (
λ) can be calculated through electronic structure calculations of the photo-excitation occurring in a system with a known ground state electronic structure, which is given by the expression
32where
f refers to the oscillator strength, which corresponds to the spectrum. The excited state (fluorescence) lifetime of a dye is calculated through the expression
33where
f is the oscillator strength and
E is the excitation energy. The electron injection efficiency of the dye can be evaluated through the change in the Gibbs free energy, which corresponds to the electron injection,
34 Δ
Ginject| | |
ΔGinject = Edye* − ECB = (Edye − E0–0) − ECB
| (5) |
where
Edye* refers to the excited-state oxidation potential energy of the dye,
Edye refers to the ground state oxidation potential energy,
ECB refers to the conduction band edge of the semiconductor (TiO
2) and
E0–0 refers to the vertical electronic transition energy.
The open circuit voltage (Voc) depends on the energy level alignment between layers (dye–TiO2 substrate and dye–electrolyte interface) and the recombination loss. These factors can be analyzed through the results of the electronic structure calculations. In addition to the above parameters, which are directly related to the magnitude of Voc and Jsc, the reorganization energy and excited state lifetime of a dye molecule are also important. The reorganization energy (Ereorg) of the dye while undergoing oxidation is given by35
| | |
Ereorg = [E+(g0) − E+(g+)] + [E0(g+) − E0(g0)]
| (6) |
where
E+(
g0) is the total energy of the cationic state in the neutral geometry,
E+(
g+) is the total energy of the cationic state in the cationic geometry,
E0(
g+) is the total energy of the neutral molecule in the cationic geometry, and
E0(
g0) is the total energy of the neutral molecule in the neutral geometry.
The ground state geometry of the selected dye molecules was optimised at the B3LYP36,37/6-311G(d,p) level of theory, where B3LYP is recognised as an accurate functional for structural optimisations.38 A benchmark study with different DFT functionals was carried out to identify the best suited functional for orbital energy analysis (see Table S2 in the ESI†). Among them, the HOMO energy obtained from the B3LYP functional closely agrees with the vertical ionisation potential of TPAL1 (Koopmans' theorem). Hence, the orbital energy, orbital pattern, and fragment orbital coefficients for carrying out the charge decomposition analysis (CDA) were computed at the B3LYP/6-311G(d,p) level of theory. The reorganisation energy was calculated at the B3LYP/6-311G(d,p) level of theory to optimize cationic geometry and to perform the single point energy calculations, as mentioned in eqn (6). With the available experimental results of TPAL1,29 the benchmarking of the time-dependent density functional theory (TD-DFT) calculations of the absorption spectrum showed that the CAM-B3LYP39 functional with the 6-311G(d,p) basis set provides results that are closer to the experimental results (see ESI, Table S1†). Hence, TD-DFT calculations were carried out at the CAM-B3LYP/6-311G(d,p) level of theory for the studied dye molecules. The abovementioned electronic structure calculations were performed using the conductor-like polarisable continuum model (CPCM) to incorporate the effects of acetonitrile solvent (ε = 35.688).40 Acetonitrile solvent was taken as the solvent medium since it has been recognized and widely used as a solvent41 for solution processing of sensitizer molecules. All the electronic structure calculations were carried out using the Gaussian 09 package.42
The Multiwfn programming package43 was used to perform the charge decomposition analysis (CDA),44 charge density difference (CDD) analysis and plotting the electrostatic potential maps. The charge density difference (CDD) module was used to compute photoinduced charge transfer based on the TD-DFT calculated data. The absorption spectra computed from TD-DFT calculations were plotted using the SWizard software.45 The graph was plotted as molar extinction coefficient against wavelength. The program computed the molar extinction coefficient from the oscillator strength of the spectral lines and provided the half band width of 3000 cm−1 through following expression:
| |
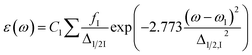 | (7) |
where
ε is the molar extinction coefficient in M
−1 cm
−1;
ω −
ω1 represents the electronic transition energy,
fI and
Δ1/2 are the oscillator strength and the half band width, respectively.
3. Results and discussion
Fig. 1(a) and (b) depict the structures of the designed 17 sensitizer molecules. A detailed discussion on the selection of molecules and the design strategy is provided in the ESI, Section S1.† The structures of the studied 17 sensitizer molecules were optimized at the B3LYP/6-311G(d,p) level of theory and are shown in Fig. S2.† The frequency calculations performed at this level of theory showed that the optimized structures are global minima on their potential energy surface.
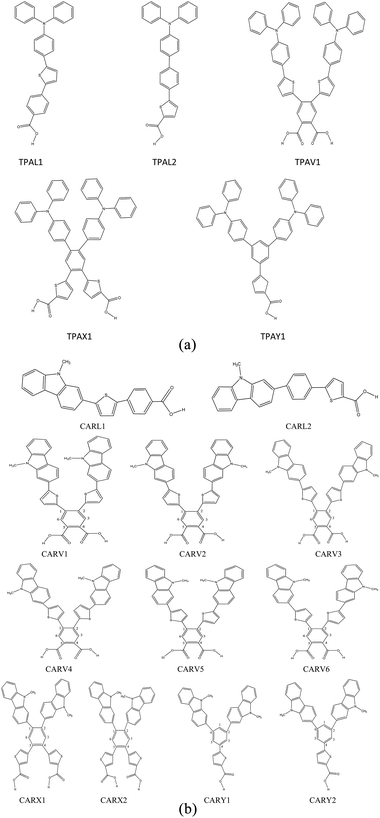 |
| | Fig. 1 (a) Molecular structure of the studied triphenylamine (TPA) derivatives with various shapes. (b) Molecular structures of the studied carbazole derivatives with different shapes. | |
3.1 Absorption spectra
The absorption spectrum of a sensitizer is a crucial factor that directly influences its light harvesting capacity. In general, it is desirable for a sensitizer to have an absorption maximum centered between 500–600 nm (ref. 46) so that its absorption spectrum will match with AM 1.5 solar spectrum irradiance. However, it is challenging to design and synthesize metal-free sensitizers with spectral maxima in this range with a broader spectral coverage. Most of the metal-free sensitizers show a spectral maximum (λmax) centered below 500 nm and almost all of them have a very narrow spectral distribution. The absorption spectra of the studied TPA- and CAR-based sensitizers are shown in Fig. 2(a) and (b), and the corresponding data is presented in Tables 1 and 2, respectively.
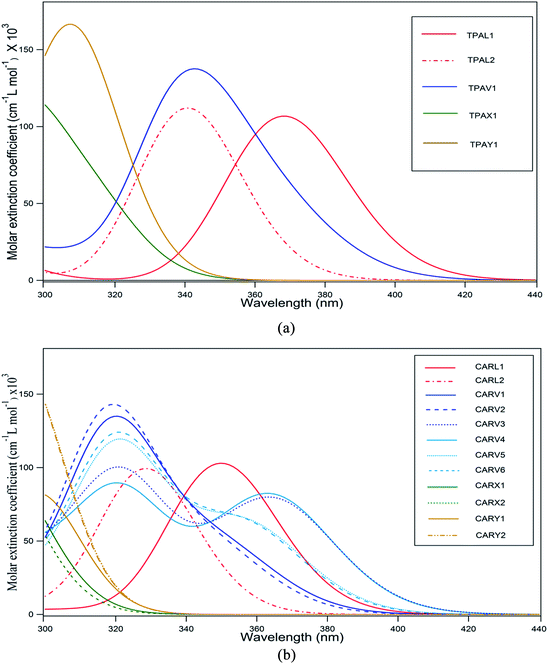 |
| | Fig. 2 (a) Absorption spectra of TPA-based sensitizers with different shapes computed at the CAM-B3LYP/6-311G(d,p) level of theory in acetonitrile solvent medium (the spectra were simulated using a Gaussian distribution centered at the computed absorption wavelength). (b) Absorption spectra of CAR-based sensitizers with different shapes computed at the CAM-B3LYP/6-311G(d,p) level of theory in acetonitrile solvent medium (the spectra were simulated using a Gaussian distribution centered at the computed absorption wavelength). | |
Table 1 Computed absorption wavelength (nm), energy (eV) and oscillator strength (a.u.) of the TPA-based derivatives in acetonitrile solvent medium. In the orbital transitions, H and L represent the HOMO and LUMO, respectively
| Molecule |
λ (nm) |
Absorption energy (eV) |
f (a.u.) |
Orbital transition |
| TPAL1 |
368 |
3.37 |
1.47 |
H → L (73%) |
| H−1 → L (14%) |
| H → L+1 (10%) |
| TPAL2 |
341 |
3.64 |
1.55 |
H → L (59%) |
| H−1 → L (22%) |
| H → L+1 (14%) |
| TPAV1 |
340 |
3.64 |
1.72 |
H−1 → L (46%) |
| H → L+1 (25%) |
| H → L+2 (12%) |
| H−3 → L (8%) |
| TPAX1 |
295 |
4.21 |
1.24 |
H−1 → L+2 (38%) |
| H → L+3 (28%) |
| TPAY1 |
313 |
3.96 |
1.12 |
H → L (30%) |
| H → L+2 (28%) |
| H → L+1 (27%) |
| H → L+1 (43%) |
| 305 |
4.07 |
1.01 |
H−2 → L (25%) |
Table 2 Computed absorption wavelength (nm), energy (eV) and oscillator strength (a.u.) of the CAR-based derivatives in acetonitrile solvent medium. In the orbital transitions, H and L represent the HOMO and LUMO, respectively
| Molecule |
λ (nm) |
Absorption energy (eV) |
f (a.u.) |
Orbital transition |
| CARL1 |
350 |
3.54 |
1.42 |
H → L (80%) |
| CARL2 |
329 |
3.77 |
1.37 |
H → L (64%) |
| H−2 → L (21%) |
| CARV1 |
320 |
3.87 |
1.68 |
H−1 → L (43%) |
| H → L+1 (25%) |
| CARV2 |
319 |
3.89 |
1.78 |
H−1 → L (80%) |
| H → L+1 (64%) |
| H−3 → L (21%) |
| CARV3 |
365 |
3.40 |
1.08 |
H → L (78%) |
| 322 |
3.85 |
1.25 |
H → L+1 (35%) |
| H−1 → L (24%) |
| H−3 → L (19%) |
| CARV4 |
364 |
3.41 |
1.12 |
H → L (78%) |
| 322 |
3.85 |
1.10 |
H → L+1 (35%) |
| H−1 → L (24%) |
| H−3 → L (19%) |
| CARV5 |
321 |
3.86 |
1.50 |
H−1 → L (40%) |
| H → L+1 (27%) |
| CARV6 |
321 |
3.86 |
1.56 |
H−1 → L (37%) |
| H → L+1 (28%) |
| H−3 → L (12%) |
| CARX1 |
278 |
4.46 |
1.11 |
H−3 → L+1 (25%) |
| H → L+3 (23%) |
| H−2 → L+3 (20%) |
| CARX2 |
278.5 |
4.45 |
1.21 |
H−3 → L+1 (28%) |
| H → L+3 (22%) |
| H−2 → L+3 (21%) |
| CARY1 |
298 |
4.16 |
1.03 |
H−4 → L (70%) |
| H−3 → L (16%) |
| CARY2 |
264 |
4.70 |
1.00 |
H−3 → L+1 (28%) |
| H−3 → L+2 (34%) |
| H−2 → L+1 (29%) |
| H−1 → L+3 (15%) |
It was observed that the TPA donors was more beneficial for the molar absorption coefficient of the sensitizer than the CAR donors. For both cases, the spectra were plotted for wavelengths above 300 nm. As shown in Fig. 1(a), the spectral maximum for TPAL1 was located at 368 nm, which is the highest λmax among the TPA-based sensitizers. The reason for the linear-shaped sensitizer, TPAL1, having the highest λmax is that the electronic transition corresponding to λmax is from the HOMO to LUMO and the energy gap is low, whereas for the other shaped sensitizers, the orbitals adjacent to the frontier molecular orbitals (FMO) also significantly contribute as dominating transitions. For instance, in the TPAL2 and CARL2 sensitizers where thiophene is placed adjacent to the –COOH group, the contribution from the HOMO to LUMO transition to the dominant peak is relatively less, resulting in a blue shift in the spectrum with respect to TPAL1 and CARL1, respectively. Among the CAR-based sensitizers, the maximum wavelength (λmax) of 365 nm and 364 nm was observed for CARV3 and CARV4, respectively. It should be noted that for CARV3 and CARV4, the electronic transition corresponding to λmax is dominantly from the HOMO to LUMO (approximately 80%), as in the case of CARL1. With respect to λmax of CARL1, the λmax of CARV3 and CARV4 is red shifted by 14 nm. Besides, these two sensitizers have a dominant peak at around 322 nm. Thereby, CARV3 and CARV4 showed a wider spectral distribution than that of other studied sensitizers. It was observed that the CARV1, CARV2, CARV5 and CARV6 molecules have a relatively higher molar absorption coefficient corresponding to λmax. Among the V-shaped sensitizers, the distinct optical behavior of CARV3 and CARV4 is related to the orientation of the thiophene rings, which are oriented oppositely and outwards from the π bridge. The spectral distribution of the X- and Y-shaped sensitizers was unsatisfactory for application as active components in photovoltaic devices since the λmax of these sensitizers is below or around 300 nm. It should be noted that the transitions in these sensitizers were characterized with less participation of HOMO and LUMO. Thus, these results indicate the importance of the orientation of the donor and acceptor groups on optical behavior of the sensitizer molecule. Further, it is conclusive from the absorption spectral properties that the linear-shaped and V-shaped sensitizers are good contributors for better light harvesting ability across the UV-visible region.
3.2 Frontier molecular orbital distribution
Fig. 3(a) and (b) show the spatial distribution pattern of the frontier molecular orbitals (FMO), HOMO and LUMO of the TPA- and CAR-based sensitizer molecules of different shapes. Studying the distribution pattern of the FMO is useful to understand the opto-electronic properties of a molecule because these orbitals are directly involved in charge transport properties, optical behavior and the interaction with nearby molecules. Hence, by analyzing the distribution of FMO, qualitative predictions can be made on the performance of dye molecules for DSSC applications. Further, it is also important to analyze the orbitals adjacent to the FMO, such as HOMO−1, HOMO−2, HOMO−3, LUMO+1, LUMO+2, and LUMO+3, which have a significant contribution to the spectral behavior of a molecule, particularly for X- and Y-shaped molecules (see Tables 1 and 2). For DSSCs where the configuration of the sensitizer molecule is the push–pull type, it is desirable to have a segregated HOMO and LUMO distribution. This distribution will favor intramolecular charge transfer, and it is also desirable to have the LUMO distribution on the acceptor moiety, which will support stable anchoring of the sensitizer on the semiconductor (TiO2) surface. As shown in Fig. 3(a) and (b), the studied X- and Y-shaped TPA- and CAR-based sensitizers have a segregated HOMO and LUMO distribution. Also, it was observed that the molecular structure in which the thiophene moiety is positioned adjacent to the anchoring group possesses a high orbital coefficient of LUMO around the anchoring moiety. The distribution of the HOMO−1 and LUMO+1 orbitals of the studied sensitizers is shown in Fig. S1(a) and (b),† respectively. Upon comparing the HOMO and LUMO distribution with the HOMO−1 and LUMO+1 distributions, it was observed that the HOMO and LUMO distribution favors charge separation more than the HOMO−1 and LUMO+1 orbitals since these orbitals do not show a good segregated distribution as that of the HOMO and LUMO.
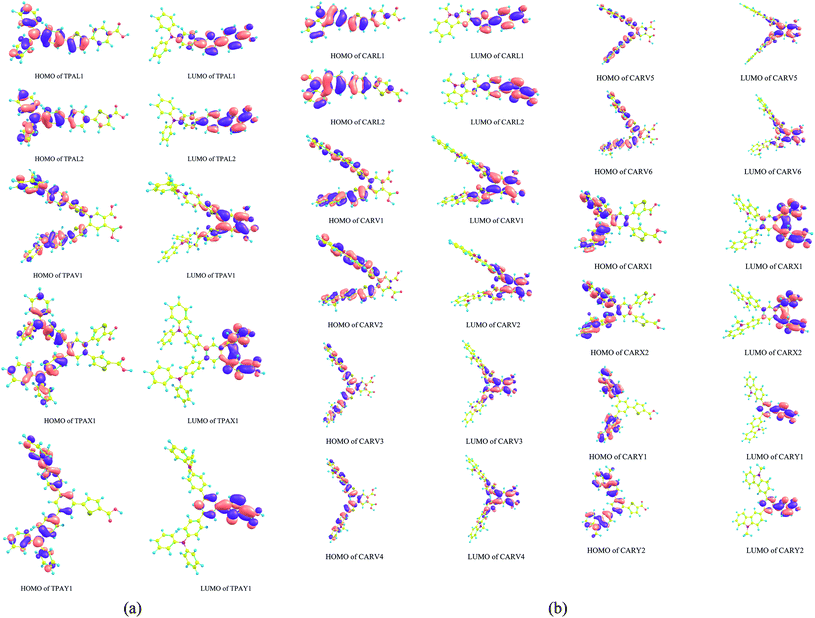 |
| | Fig. 3 (a) HOMO and LUMO distribution patterns in the triphenylamine-based derivatives with different shapes computed at the B3LYP/6-311G(d,p) level of theory. (b) HOMO and LUMO distribution patterns in the carbazole-based derivatives with different shapes computed at the B3LYP/6-311G(d,p) level of theory. | |
To quantify the observed orbital pattern, a charge decomposition analysis (CDA) was carried out. The CDA analysis was carried out by partitioning the sensitizer molecule into three fragment components, namely donor, π and acceptor. The contribution of these fragments to the FMOs was analyzed and summarized in Tables 3 and 4. It was observed that the π fragment of all the studied sensitizers has a significant contribution on the LUMO of the sensitizer molecule. In the X- and Y-shaped TPA and CAR derivatives and in the TPAL2 sensitizer (linear-shaped TPA derivative), the contribution of the π fragment on the HOMO of the sensitizer molecule is absent (contribution falls below 10%). This is the reason for the segregated distribution of the HOMO and LUMO in the X- and Y-shaped structures, and in the TPAL2 molecule. It was found that in the linear-shaped molecules, the positioning of thiophene adjacent to the anchoring moiety (–COOH) decreases the amount of orbital contribution from the π fragment on the HOMO of the sensitizer. A similar observation was also found for the V-shaped and X-shaped sensitizers, where the X-shaped sensitizer with the same molecular composition shows better HOMO–LUMO segregation than the V-shaped sensitizers. Hence, according to the FMO and CDA analysis, it was observed that placing the thiophene moiety adjacent to the anchoring group is a potential strategy to design a sensitizer structure with a segregated HOMO and LUMO distribution. However, by comparing the absorption spectrum of the L1 and L2 sensitizers, and the V-shaped and X-shaped sensitizers, it was observed that placing the thiophene moiety nearer to the –COOH group blue shifts the absorption spectrum. It should be noted that although the molecular composition in both configurations, TPAL1 and TPAL2 (for the TPA-based sensitizers) and CARL1 and CARL2 (for the CAR-based sensitizers) is same, the fragment orbital (FO) contribution percentage for the HOMO and LUMO composition in each case is different. Specifically, the fragment orbital contribution orbital for the HOMO and LUMO formation is dependent on the shape of the sensitizer. For instance, as given in Table 4 although the molecular structure and composition (C26N2H20) of the donor fragment in the V-, X- and Y-shaped sensitizers of CAR derivatives is same, the fragment orbital (FO) contribution from the donor fragment on the HOMO and LUMO of the sensitizer is different in each case. It is important to note that the shape and distribution of the electron density of each contributing fragment orbital will influence the formation of the frontier molecular orbitals (HOMO and LUMO) of the sensitizer molecule. We found that since the linear combination of fragment orbital (LCFO) approach accounts for the symmetry of the combined FO, the angle at which the combining fragment orbital approaches each other becomes the decisive factor over molecular orbital formation. Thereby, the shape of the sensitizer has a direct influence on the opto-electronic properties of the sensitizer molecule since the angle of approach of the combining fragment orbital depends on the shape of the molecule.
Table 3 Charge decomposition analysis of triphenylamine-based sensitizers computed at the B3LYP/6-311G(d,p) level of theory
| Dye |
HOMOa |
LUMOa |
| Orbital contribution from donor fragment |
Orbital contribution from π-bridge fragment |
Orbital contribution from acceptor fragment |
Orbital contribution from donor fragment |
Orbital contribution from π-bridge fragment |
Orbital contribution from acceptor fragment |
| Fragment orbital (FO) contribution to the HOMO or LUMO of the sensitizer, where H, S and L represent HOMO, singly occupied molecular orbital (SOMO) and LUMO of the fragment, respectively. |
| TPAL1 |
FO(S−1) → 38% |
FO(H−1) → 12% |
— |
— |
FO(L+1) → 68% |
FO(S+1) → 12% |
| FO(S) → 37% |
| TPAL2 |
FO(S−1) → 44% |
— |
— |
— |
FO(L+1) → 62% |
FO(S+1) → 15% |
| FO(S) → 44% |
| TPAV1 |
FO(H) → 73% |
FO(H−1) → 11% |
— |
— |
FO(L+2) → 67% |
FO(L+2) → 16% |
| TPAX1 |
FO(H) → 89% |
— |
— |
— |
FO(L+2) → 41% |
FO(L+1) → 20% |
| FO(L+4) → 28% |
| TPAY1 |
FO(H−1) → 84% |
— |
— |
— |
FO(S+2) → 68% |
FO(S+1) → 18% |
Table 4 Charge decomposition analysis of carbazole-based sensitizers computed at the B3LYP/6-311G(d,p) level of theory
| Dye |
HOMOa |
LUMOa |
| Donor fragment contribution |
π-bridge fragment contribution |
Acceptor fragment contribution |
Donor fragment contribution |
π-bridge fragment contribution |
Acceptor fragment contribution |
| Fragment orbital (FO) contribution to the HOMO or LUMO of the sensitizer, where H, S and L represent HOMO, singly occupied molecular orbital (SOMO) and LUMO of the fragment, respectively. |
| CARL1 |
FO(S−1) → 27% |
FO(H−1) → 23% |
— |
— |
FO(L+1) → 71% |
FO(S+1) → 14% |
| FO(S) → 24% |
FO(L) → 12% |
| CARL2 |
FO(S−1) → 36% |
FO(H−1) → 11% |
— |
— |
FO(L+1) → 62% |
FO(L) → 16% |
| FO(S) → 33% |
| CARV1 |
FO(H−4) → 25% |
FO(H−1) → 27% |
— |
— |
FO(L+2) → 67% |
FO(L+2) → 15% |
| FO(H−3) → 22% |
FO(L) → 18% |
| CARV2 |
FO(H−4) → 22% |
FO(H−1) → 27% |
— |
— |
FO(L+2) → 68% |
FO(L+2) → 16% |
| FO(H−3) →25% |
FO(L) → 18% |
| CARV3 |
FO(H−4) → 20% |
FO(H−1) → 27% |
— |
— |
FO(L+2) → 68% |
FO(L+2) → 14% |
| FO(H−3) → 20% |
FO(L) → 25% |
| CARV4 |
FO(H−4) → 19% |
FO(H−1) → 26% |
— |
— |
FO(L+2) → 68% |
FO(L+2) → 14% |
| FO(H−3) → 22% |
FO(L) → 24% |
| CARV5 |
FO(H−4) → 24% |
FO(L) → 43% |
— |
— |
FO(L+2) → 65% |
FO(L+2) → 14% |
| FO(H−3) → 19% |
| CARV6 |
FO(H−4) → 24% |
FO(H−1) → 27% |
— |
— |
FO(L+2) → 68% |
FO(L+2) → 15% |
| FO(H−3) → 19% |
FO(L) → 22% |
| CARX1 |
FO(H) → 84% |
— |
— |
— |
FO(L+2) → 42% |
FO(L+1) → 20% |
| FO(L+4) → 27% |
| CARX2 |
FO(H) → 84% |
— |
— |
— |
FO(L+2) → 42% |
FO(L+1) → 20% |
| FO(L+4) → 27% |
| CARY1 |
FO(H−2) → 89% |
— |
— |
— |
FO(S+2) → 68% |
FO(S+1) → 18% |
| FO(H−1) → 10% |
| CARY2 |
FO(H−1) → 80% |
— |
— |
— |
FO(S+2) → 67% |
FO(S+1) → 19% |
3.3 Energy of frontier molecular orbital
The energy of the frontier molecular orbital has high importance on the performance of solar cells since the energy gap between the HOMO and LUMO has a direct impact on the light harvesting capacity of the sensitizer, and thereby impacts the Jsc of the DSSC.47 The energy level diagram of the FMO of the studied TPA- and CAR-based sensitizers is illustrated in Fig. 4(a) and (b). It was observed that the TPA-based sensitizers have a lower band gap than that of the CAR-based sensitizers. The analysis of the diagrams showed that the energy level alignment on the studied sensitizers is shape dependent. In both cases, the linear- and V-shaped sensitizers show a lower band gap than the X- and Y-shaped sensitizers, while the V-shaped and X-shaped sensitizers possess the same molecular composition. Hence, the linear- and V-shaped sensitizers are more likely to result in a better photocurrent. Upon analyzing the HOMO and LUMO energy levels based on shape, we found that the relatively high HOMO energy of the linear-shaped sensitizers and relatively lower lying LUMO in the V-shaped sensitizers are responsible for the lower energy gap in these two cases.
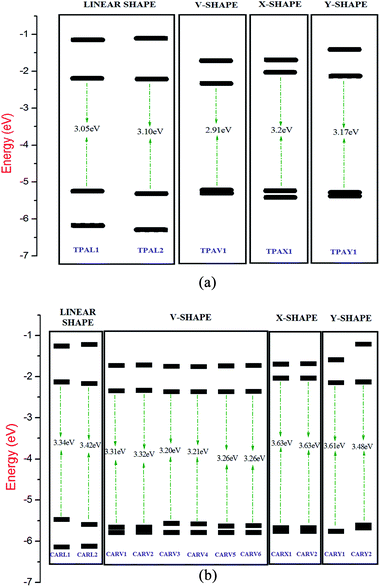 |
| | Fig. 4 (a) Energy level diagram of the frontier molecular orbital of the TPA-based sensitizers with different shapes calculated at the B3LYP/6-311G(d,p) level. The energy gap values are presented in eV. (b) Energy level diagram of the frontier molecular orbital of the CAR-based sensitizers with different shapes calculated at the B3LYP/6-311G(d,p) level. The energy gap values are presented in eV. | |
It was also important to study whether the sensitizers have a suitable HOMO and LUMO energy with respect to the conduction band edge of the semiconductor substrate and redox potential of the electrolyte. Efficient electron injection from the sensitizer to the TiO2 substrate requires the energy of the LUMO of the sensitizer molecule to be higher than the energy of the conduction band edge of the TiO2 substrate. Similarly, for the regeneration of the dye by the electrolyte, the HOMO of the sensitizer should lie lower than the energy of the redox potential of the electrolyte. In the present study, we compared the energy level alignment of the sensitizers with the widely used TiO2 semiconductor substrate48 (−4.0 eV) and I−/I3− redox electrolyte49 (−4.7 eV). It was found that the HOMO energy of the studied TPA- and CAR-based sensitizers is sufficiently lower than the redox potential of the I−/I3− redox couple, and the LUMO of the studied sensitizers is high enough to facilitate electron injection into the conduction band of TiO2. Specifically, all the studied sensitizers, irrespective of their shape, show optimal FMO energy levels for the electron injection and dye regeneration processes.
3.4 Charge transfer indices
All the studied structures belong to the donor–π bridge–acceptor architecture. These structures exhibit push–pull property, which will facilitate the intramolecular charge transfer as a photon excites the molecule. Specifically, when an electron is excited from the HOMO to LUMO, there will be a temporary redistribution of charges (holes and electrons), which is crucial in the generation of a photocurrent. Hence, in the present study, the charge transfer indices corresponding to the first mode of transition (S0 → S1) were studied using the charge density difference (CDD) analysis module available in the Multiwfn package, and the results are summarized in Table 5. According to the tabulated values, we found that the amount of charge transferred per transition mode is high (around 0.95e) in the linear-shaped sensitizers and the charge transfer is relatively less the in X-shaped molecules. By analyzing the transition dipole moment of the studied sensitizers, we observed that in terms of charge transport properties, the TPAL1, TPAL2, TPAV1, CARV3 and CARV4 sensitizers exhibit good charge transport properties, and the TPA-based sensitizers are clearly superior to the CAR-based sensitizers. On comparing their shapes, it was observed that the charge transporting ability of the linear-shaped and V-shaped sensitizers is comparable and the X-shaped sensitizers show the lowest intramolecular charge transporting ability. The barycenter of the hole and electron distribution after excitation of the sensitizer was plotted and is shown in Fig. S2.† Well separated barycenters are preferred for obtaining good efficiency, and a barycenter of electrons nearer to the anchoring group ensures good electron injection into the TiO2 substrate. According to Fig. S2,† it can be inferred that the V-shaped sensitizers have good charge distribution characteristics for electron injection into the TiO2 substrate. In terms of overlap integral and t-index (a computed measure of the ground state and excited state charge density), it was observed that in comparison with the linear-shaped sensitizers, the V-shaped sensitizers have a relatively higher t-index value and lower overlap integral, showing that the V-shaped sensitizers are a better option with less recombination possibilities. Hence, based on the EDD analysis, it was observed that the linear- and V-shaped sensitizers are well suited as light-harvesting sensitizers, and particularly the V-shaped sensitizers are slightly better.
Table 5 Computed charge density difference (CDD) indices, charge transfer distance (DCT) (Å), amount of charge transfer (qct), difference in transition dipole movement due to excitation (cm), t-index (Å) and overlap integral of the triphenylamine- and carbazole-based sensitizersa
| Molecule |
DCT (Å) |
qct (e) |
10−29μCT (C m) |
t (Å) |
Overlap integral |
| Transition mode = 1. |
| TPAL1 |
2.15 |
0.96 |
1.30 |
2.37 |
0.48 |
| TPAL2 |
2.79 |
0.95 |
1.68 |
2.18 |
0.46 |
| TPAV1 |
2.77 |
0.94 |
1.65 |
3.56 |
0.41 |
| TPAX1 |
2.29 |
0.89 |
1.29 |
3.76 |
0.36 |
| TPAY1 |
2.07 |
0.93 |
1.21 |
4.71 |
0.37 |
| CARL1 |
2.06 |
0.96 |
1.25 |
2.07 |
0.49 |
| CARL2 |
2.32 |
0.96 |
1.40 |
1.85 |
0.48 |
| CARV1 |
1.85 |
0.91 |
1.07 |
3.45 |
0.42 |
| CARV2 |
1.89 |
0.93 |
1.10 |
3.57 |
0.43 |
| CARV3 |
2.45 |
0.93 |
1.43 |
3.54 |
0.38 |
| CARV4 |
2.41 |
0.93 |
1.41 |
3.36 |
0.38 |
| CARV5 |
1.80 |
0.92 |
1.04 |
3.45 |
0.42 |
| CARV6 |
1.86 |
0.93 |
1.09 |
3.29 |
0.43 |
| CARX1 |
1.05 |
0.83 |
0.56 |
3.67 |
0.42 |
| CARX2 |
1.02 |
0.90 |
0.58 |
3.89 |
0.47 |
| CARY1 |
1.94 |
0.84 |
1.03 |
1.47 |
0.34 |
| CARY2 |
2.00 |
0.85 |
1.08 |
2.98 |
0.35 |
3.5 Light harvesting efficiency, fluorescence lifetime, free energy change for electron injection, reorganisation energy and exciton binding energy
The parameters that are directly related with the Jsc and Voc of a DSSC, such as light harvesting efficiency (LHE), excited state lifetime (τ), change in Gibbs free energy for electron injection, (ΔGinject) and reorganisation energy were calculated using the electronic structure calculations and are summarized in Table 6. The LHE was calculated from the oscillator strength corresponding to the dominant electronic transition of a sensitizer molecule. As discussed in Section 3.3, CARV1, CARV2, CARV5 and CARV6 have a high oscillator strength at around the wavelength of 320 nm, and hence these sensitizers have high LHE in that region of the spectrum. In general, it was observed that the studied linear- and V-shaped sensitizers possess a high LHE at the respective λmax (although comparatively less in CARV3 and CARV4). The LHE of the X- and Y-shaped sensitizers was comparatively less than that of the other sensitizers. The decay of an electron from the excited state to ground state is an important competing process against the process of electron injection by an excited dye molecule into the conduction band of TiO2, where a dye with a longer excited-state lifetime offers greater possibility of electron injection.50 Hence, the excited-state lifetime of the studied sensitizers was calculated based on eqn (4). It was observed that the excited-state lifetime is dependent on the structure of the sensitizer. For instance, between TPAL1 and TPAL2, the difference in the excited state lifetime is 0.26 ns. In the case of CARL1 and CARL2, the difference is 0.28 ns. Among the V-shaped sensitizers, CARV4 exhibits the highest excited-state lifetime of 1.41 ns. A highly negative ΔGinject indicates high spontaneity (exoergic) for electron injection by the sensitizer into the semiconductor.51 As presented in Table 6 for all the studied sensitizer molecules, the ΔGinject is negative, showing the possibility of spontaneous electron injection. It was observed that the linear- and V-shaped dyes show the least spontaneity, and the X-shaped sensitizers have high spontaneity. However, the difference between the lowest and highest calculated ΔGinject is only 0.7 eV. The reorganisation energy corresponding to the oxidation of the studied sensitizers was calculated using eqn (6), which measures the change in energy of the sensitizer due to the presence of excess charge. It should be noted that in DSSCs, the sensitizer acts as a p-type material by donating an electron to the substrate, thereby reducing itself, and is regenerated later by the electrolyte. As presented in Table 6, the Y- and X-shaped sensitizers exhibit a relatively low reorganisation energy. However, similar to the ΔGinject, the maximum difference between the reorganisation energy of the sensitizers is only 0.24 eV. Also, the exciton binding energies of the studied sensitizers was calculated using the formula Eb = Eg − Ex = ΔEH–L − E1, where ΔEH–L represents the energy gap value and E1 represents the optical gap of the sensitizer. For high conversion energy, it is desirable to have a sensitizer with a low exciton binding energy.52 It was observed that the X- and Y-shaped sensitizers have a low exciton binding energy (less than 1.7 eV for the TPA-based dyes and less than 2.0 eV for the CAR-based dyes), whereas the exciton binding energy of the L- and V-shaped dyes has slightly higher values (greater than 1.8 for the TPA-based dyes and greater than 2.0 eV for the CAR-based dyes). The values of the exciton binding energy obtained in the present study are slightly higher than that reported for similar dyes in the previous studies.53,54 Also, from the analysis of the ΔGinject, reorganisation energy and exciton binding energy (Eb), we observed that the X-shaped and Y-shaped sensitizer molecules are efficient in harvesting captured light energy. However, since the light capturing process proceeds before the harvesting process, we conclude that the linear and V-shaped sensitizers are better for DSSC applications.
Table 6 Calculated light harvesting efficiency (LHE), excited state lifetime (τ in ns), Gibbs free energy for electron injection (ΔGinject in eV), reorganization energy (in eV) and exciton binding energy (Eb in eV)
| Molecule |
Light harvesting efficiency (LHE) |
τ (ns) |
ΔGinject (eV) |
Reorganization energy (eV) |
Exciton binding energy (Eb, eV) |
| TPAL1 |
0.96 |
1.38 |
−2.35 |
0.2 |
2.0 |
| TPAL2 |
0.97 |
1.12 |
−2.53 |
0.17 |
1.83 |
| TPAV1 |
0.98 |
1.01 |
−2.35 |
0.18 |
1.86 |
| TPAX1 |
0.94 |
1.05 |
−2.92 |
0.15 |
1.68 |
| TPAY1 |
0.92 |
1.31 |
−2.82 |
0.12 |
1.62 |
| CARL1 |
0.96 |
1.29 |
−2.34 |
0.3 |
2.12 |
| CARL2 |
0.96 |
1.18 |
−2.36 |
0.21 |
2.01 |
| CARV1 |
0.98 |
0.9 |
−2.14 |
0.27 |
2.12 |
| CARV2 |
0.98 |
0.8 |
−2.18 |
0.26 |
1.91 |
| CARV3 |
0.94 |
1.24 |
−2.13 |
0.31 |
2.13 |
| CARV4 |
0.92 |
1.41 |
−2.14 |
0.36 |
2.13 |
| CARV5 |
0.97 |
1.03 |
−2.19 |
0.36 |
2.13 |
| CARV6 |
0.97 |
1.00 |
−2.14 |
0.28 |
2.13 |
| CARX1 |
0.92 |
1.04 |
−2.64 |
0.29 |
1.98 |
| CARX2 |
0.94 |
1.00 |
−2.65 |
0.2 |
1.98 |
| CARY1 |
0.91 |
1.29 |
−2.51 |
0.15 |
1.95 |
| CARY2 |
0.90 |
1.04 |
−2.68 |
0.12 |
1.75 |
The interaction of the dye on the surface of TiO2, the dye–electrolyte interaction and the aggregation of the dye on the surface of TiO2 are crucial factors,55 which highly influence the performance of DSSCs. In the present work, the two-dimensional electrostatic potential (ESP) map computed at the B3LYP/6-311G(d,p) level of theory was used to study the active sites for the dye–TiO2 and dye–electrolyte interactions. In the ESP map (shown in Fig. S3†), the blue regions correspond to the electron-deficient regions (electron-accepting regions) and the yellow or white regions correspond to the electron-rich region (electron donating). It was observed that the electron-deficient region on the studied V-shaped and X-shaped sensitizers was oriented towards the anchoring site, and this distribution of charge density can be beneficial for the vertical adsorption of sensitizers on the surface of TiO2 since from previous works it is well established that TiO2 has a greater affinity for electron deficient groups.56 Further, it was observed that the regions around the double-bonded oxygen atom, sulfur in the thiophene rings, nitrogen atom in the donor moieties and lateral edges of the conjugated rings are more likely to be electrophilic, where electrolyte–dye interactions can favorably occur. Further, it is expected that the branched structure of the V-shaped sensitizers can be useful in creating space for electrolyte–dye interactions57 and to prevent dye–dye aggregation by limiting the π–π interaction between adjacent dye molecules,58 thereby reducing the quenching effect.
4. Conclusion
A collective study on 17 sensitizer molecules was performed as a systematic attempt to identify potential shapes for the application of sensitizer molecules in dye sensitized solar cells (DSSCs). Based on the analysis of various parameters obtained from electronic structure calculations, we found that the linear- and V-shaped sensitizers outperform the X and Y-shaped sensitizers in most of the crucial parameters, where especially, the linear and V-shaped sensitizers show good photon absorption ability. By considering the drawback of π–π aggregation in linear-shaped sensitizers, we recommend the V-shaped design for sensitizers to achieve the best performance in DSSCs. It was observed that positioning the thiophene group adjacent to the anchoring group segregates the HOMO–LUMO distribution significantly, which is advantageous; however, it blue shifts the absorption spectrum, which can limit the photon absorption ability of the dye molecule. Further, we observed that the triphenylamine donor is more advantageous than the carbazole donor in terms of photon absorption ability. We hope that the present study, which was limited to the electronic structure properties of selected isolated dye molecules, will be useful to design and synthesize efficient dye molecules to achieve better power conversion efficiencies in DSSCs.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Authors are thankful to the University Grants Commission, New Delhi, India, for providing funds to establish High Performance Computing facility, under the Center with Potential for Excellence in Particular Area (CPEPA) scheme [grant no. 2-8/2016 (NS/PE) dated 03.10.2016]. Author, S. Krishnan sincerely thanks University Grants Commision (UGC) for providing the financial support through Basic Science Research (BSR) scheme.
References
- P. B. L. Neto, O. R. Saavedra and D. Q. Oliveira, Renewable Energy, 2020, 147, 339–355 CrossRef.
- P. J. Burke, J. Widnyana, Z. Anjum, E. Aisbett, B. Resosudarmo and K. G. H. Baldwin, Energy Policy, 2019, 132, 1216–1228 CrossRef.
- E. Guelpa, A. Bischi, V. Verda, M. Chertkov and H. Lund, Energy, 2019, 10, 2–21 CrossRef.
- X. Li, X. Zhang, J. Hua and H. Tian, Mol. Syst. Des. Eng., 2017, 2, 98–122 RSC.
- T. Lehtola and A. Zahedi, Sustain. Energy Technol. Assess., 2019, 35, 25–31 Search PubMed.
- N. Sangiorgi, A. Sangiorgi, A. Dessì, L. Zani, M. Calamante, G. Reginato, A. Mordini and A. Sanson, Sol. Energy Mater. Sol. Cells, 2019, 204, 110209 CrossRef.
- M. A. Sabuj and N. Rai, Mol. Syst. Des. Eng., 2020, 5, 1477–1490 RSC.
- S. Ashrafa, R. Sud, J. Akhtarc, H. M. Siddiqib, A. Shujae, K. A. Al-Saadf, S. Y. Al-Qaradawif and A. El-Shafeid, Dyes Pigm., 2019, 171, 107754 CrossRef.
- N. Manfredi, B. Cecconi and A. Abbotto, Eur. J. Org. Chem., 2014, 7069–7086 CrossRef CAS.
- Y. Tanga, Y. Wang, H. Song, Q. Liu, X. Lid, Y. Cai and Y. Xie, Dyes Pigm., 2019, 171, 107776 CrossRef.
- Z.-D. Sun, J.-S. Zhao, Z. Mei and X.-H. Ju, J. Mol. Model., 2019, 25, 300 CrossRef PubMed.
- S. Yamamoto, A. Zhang, M. J. Stillman, N. Kobayashi and M. Kimura, Chem.–Eur. J., 2018, 22, 1–10 Search PubMed.
- M. Harikrishnan, V. Sadhasivam, A. Siva, S. Anandan, V. Subbiah and S. Murugesan, J. Phys. Chem. C, 2019, 123, 21959–21968 CrossRef CAS.
- B. L. Watson, B. D. Sherman, A. L. Moore, T. A. Moore and D. Gusta, Phys. Chem. Chem. Phys., 2015, 17, 15788–15796 RSC.
- E. Aslan, M. Karaman, G. Yanalak, M. Can, F. Ozel and I. H. Patir, Dyes Pigm., 2019, 171, 107710 CrossRef CAS.
- T. Duan, K. Fan, T. Peng, C. Zhong, Y. He and X. Chen, Synth. Met., 2016, 211, 19–24 CrossRef CAS.
- M. K. R. Fischer, S. Wenger, M. Wang, A. Mishra, S. M. Zakeeruddin, M. Gratzel and P. Bauerle, Chem. Mater., 2009, 22, 1836–18445 CrossRef.
- J. M. Parka, C. Y. Jungb, Y. Wang, H. D. Choib, S. J. Parkb, P. Oub, W.-D. Janga and J. Y. Jaungb, Dyes Pigm., 2019, 170, 107568 CrossRef.
- Y. Wu, Q. Zhang, X. Tian, J. Li, X. Lu, D. Li, B. Xu, Y. Wu and K. Guo, J. Mater. Chem. A, 2019, 7, 1974–1981 CAS.
- F. Zhang, J. Fan, H. Yu, Z. Ke, C. Nie, D. Kuang, G. Shao and C. Su, J. Org. Chem., 2019, 80, 9034–9040 CrossRef PubMed.
- H. Zhang, Z.-E. Chen, J. Hu and Y. Hong, Electrochim. Acta, 2018, 295, 934–941 CrossRef.
- K. Kakiage, Y. Aoyama, T. Y. K. Oya, J.-i. Fujisawab and M. Hanaya, Chem. Commun., 2015, 51, 15894–15897 RSC.
- M. Freitag, J. Teusher, Y. Saigilli and X. Zhang, Nat. Photonics, 2017, 11, 372–378 CrossRef CAS.
- D. D. Babu, R. Su, A. El-Shafei and A. V. Adhikari, RSC Adv., 2016, 6, 30205–30216 RSC.
- T. Duana, K. Fanb, T. Peng, C. Zhongb, Y. Hea and X. Chenb, Synth. Met., 2016, 211, 19–24 CrossRef.
- H. Jia, K. Shen, X. Ju, M. Zhang and H. Zheng, New J. Chem., 2016, 40, 2799–2805 RSC.
- Q. Li, J. Shi, S. Li, C. Zhong, F. Guo, M. Peng, J. Hua, J. Qina and Z. Li, J. Mater. Chem., 2012, 2012, 6689–6696 RSC.
- A. Yuvapragasam, N. Muthukumarasamy, S. Agilan, D. Velauthapillai, T. S. Senthil and S. Sundaram, J. Photochem. Photobiol., B, 2015, 148, 223–231 CrossRef CAS PubMed.
- K.-F. Chen, Y.-C. Hsu, Q. Wu, M.-C. P. Yeh and S.-S. Sun, Org. Lett., 2008, 11, 377–380 CrossRef PubMed.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- B. O. Regan and M. Gratzel, Nature, 1991, 353, 737–740 CrossRef.
- M. K. Nazeeruddin, A. Kay, I. Rodicio, R. Humphry-Baker, E. Muller, P. Liska, N. Vlachopoulos and M. Gratzel, J. Am. Chem. Soc., 1993, 115, 6382–6390 CrossRef CAS.
- T. L. Bahers, T. Pauporte, G. Scalmani, C. Adamo and I. Ciofini, Phys. Chem. Chem. Phys., 2009, 11, 11276–11284 RSC.
- J. Preat, A. Hagfeldt and E. A. Perpete, Energy Environ. Sci., 2011, 4, 4537–4549 RSC.
- H. L. Tavernier, A. V. Barzykin, M. Tachiya and M. D. Fayer, J. Phys. Chem. B, 1998, 102, 6078–6088 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, E. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- F. M. Rajab, J. Nanomater., 2015, 2016, 8 Search PubMed.
- J. Wu, Z. Lan, J. Lin, M. Huang, Y. Huang, L. Fan and G. Luo, Chem. Rev., 2015, 115, 2136–2173 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, M. C. X. Li, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, O. K. Y. Honda, T. V. H. Nakai, K. Throssell, J. A. Montgomery, J. E. P. Peralta Jr, M. B. F. Ogliaro, E. B. J. J. Heyd, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- M. Xiao and T. Lu, J. Adv. Phys. Chem., 2015, 4, 111–124 CrossRef CAS.
- S. I. Gorelsky and A. B. P Lever, J. Organomet. Chem., 2001, 635, 187–196 CrossRef CAS.
- K. Portillo-Cortez, A. Martínez, A. Dutt and G. Santana, J. Phys. Chem. A, 2019, 123, 10930–10939 CrossRef CAS PubMed.
- V. K. Singh, R. K. Kanaparthi and L. Giribabu, RSC Adv., 2014, 4, 6970–6984 RSC.
- J.-i. Fujisawa, T. Eda and M. Hanaya, Chem. Phys. Lett., 2017, 685, 23–26 CrossRef CAS.
- G. Boschloo and A. Hagfeldt, Acc. Chem. Res., 2009, 42, 1819–1826 CrossRef CAS PubMed.
- J.-H. Luo, Q.-S. Li, L.-N. Yang, Z.-Z. Sun and Z.-S. Li, RSC Adv., 2014, 4, 20200–20207 RSC.
- R. Katoh, Ambio, 2012, 41, 143–148 CrossRef CAS PubMed.
- B.-G. Kim, C.-G. Zhen, E. J. Jeong, J. Kieffer and J. Kim, Adv. Funct. Mater., 2012, 22, 1606–1612 CrossRef CAS.
- M. A. M. Rashid, D. Hayati, K. Kwak and J. Hong, Nanomaterials, 2020, 10, 914–937 CrossRef PubMed.
- P. Li, Z. Wang, C. Song and H. Zhang, J. Mater. Chem. C, 2017, 5, 11454–11465 RSC.
- G. Pepe, J. M. Cole, P. G. Waddel and J. I. Perrya, Mol. Syst. Des. Eng., 2016, 1, 416–435 RSC.
- P. Ganesan, V. S. Rajadurai, J. Sivanadanam, V. Ponnambalam and R. Rajalingam, J. Photochem. Photobiol., A, 2013, 271, 31–44 CrossRef CAS.
- Y.-Q. Yan, Y.-Z. Zhu, P.-P. Dai, J. Han, M. Yan and J.-Y. Zheng, New J. Chem., 2020, 44, 12909–12915 RSC.
- J. Yang, P. Ganesan, J. l. Teuscher, T. Moehl, Y. J. Kim, C. Yi, P. Comte, K. Pei, T. W. Holcombe, M. K. Nazeeruddin, J. Hua, S. M. Zakeeruddin, H. Tian and M. Gratzel, J. Am. Chem. Soc., 2014, 136, 5722–5730 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra10613e |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*