Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A novel three-dimensional electroosmotic micromixer based on the Koch fractal principle
Siyue Xiongab,
Xueye Chen *a and
Jinyuan Wangc
*a and
Jinyuan Wangc
aCollege of Transportation, Ludong University, Yantai, Shandong 264025, China. E-mail: xueye_chen@126.com
bFaculty of Mechanical Engineering and Automation, Liaoning University of Technology, Jinzhou, Liaoning 121001, China
cDepartment of Information Engineering, Chaoyang Teachers College, Chaoyang, Liaoning 12200, China
First published on 6th April 2021
Abstract
Micromixers are extensively used in the field of biochemistry. In this study, based on the Koch fractal principle, a new type of micromixer is designed. To improve the mixing performance of the micromixer, under the action of fractal and electric field, irregular alternating eddy currents were generated in the microchannel to improve the mixing of fluids. Using COMSOL Multiphysics 5.4, by changing the fractal structure, direct current (DC) voltage size, electrode spacing, electrode configuration, and numerical calculations were determined, and a micromixer with excellent mixing effect was obtained. In particular, when the electroosmotic micromixer has three groups of alternately placed electrode pairs and Re = 0.01, the mixing efficiency can reach 99%.
1 Introduction
In recent years, the integration of micro-scale sample preparation, separation and detection into a micro-scale chip has attracted researchers attention.1–4 Among them, the micro scale fluid mixing has always been a hot issue in the field of scientific research; therefore, a micromixer has become an important component of the chip laboratory system.5–8 Therefore, to improve the mixing efficiency of the fluid in the micromixer, researchers usually change the geometry of the micromixer or add external conditions to improve the mixing efficiency of the working fluid.9–11Generally, micromixers are divided into two types according to their working principles: passive and active.12 The passive micromixer has the advantages of simple structure, low manufacturing difficulty and easy integration. Because it is not affected by external forces, the mixing process primarily depends on molecular diffusion.13 The mixing of samples in the microchannel is generally realized using the influence of chaotic convection, although the passive micromixer has the advantages of simple structure, low manufacturing difficulty, and easy integration.14 However, because of its large physical size and poor controllability for fluids, it has not been extensively used in the research process.15 In contrast, the active micromixer has a greater application prospect. Active micromixers usually use some additional active components to mix different fluids, such as magnetic field, electric field and pressure field, to achieve effective mixing of different fluid samples.16–18 In the active micromixer, electroosmotic micromixer is widely used because of its simple structure and easy integration.19,20 Jalili et al. conducted a numerical study on an active micromixer driven by osmotic pressure. The optimal value of the effective parameters of the original micromixer is obtained, and it is applied to the micromixer with different obstacle shapes in the mixing chamber. The results show that the mixing quality largely depends on the inlet velocity of the fluid, the phase lag of the electrode, frequency and voltage amplitude. Moreover, when the optimal values of these parameters are used, the mixing quality does not depend on the shape of the obstacle.21 Shamloo et al. proposed a new type of T-type electroosmotic micromixer and studied the influence of different parameters on the mixing process. The influence of the aspect ratio of the channel cross-section and the radius and depth of obstacles was also discussed. Note that the triangular cavity with circular conductive barrier is the best geometric configuration; moreover, please check its time transient performance. The results show that the use of these structures can not only increase the mixing index but also reduce the mixing time.22 Usefian et al. proposed a new type of electroosmotic micromixer in the presence of alternating current (AC) and DC electric fields. PDMS is used to make microchips, and gold nanoparticles are used to make electrodes. The results show that, for both DC and AC electric fields, the mixing performance can be controlled by the applied voltage value and the fluid inlet velocity. The conclusion is that by increasing the applied voltage and reducing the inlet velocity, the mixing performance is improved. The experimental results are in good agreement with numerical results in terms of quality.23
There are many studies on the effect of fractal structure and electric field to improve the mixing efficiency of micromixer. In this study, after combining the two factors, we developed a new type of electroosmotic micromixer with the Koch fractal structure. The effects of fractal structure, voltage size, electrode spacing and electrode structure on the mixing performance have also been studied. The simulation results show that the best mixing efficiency of micromixer can reach 99%, which meets our expectation.
2 Micromixer designs
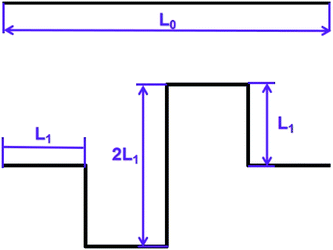
Fractal obstacles are set up on the basis of the Koch fractal. The steps are as follows:(1) Take a line segment with a length of 0.4 mm.
(2) Divide the line segment into four equal parts, keep the quarter line segments at both ends unchanged, then move the second line segment down by 0.1 mm, move the third line up by 0.1 mm, and finally in sequence connect the four segments.
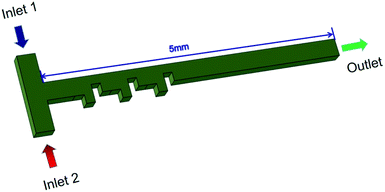
The fractal structure is shown in Fig. 1 and 2 shows the micromixer with fractal structure.
3 Theoretical background
3.1 Governing equations
The fluid dynamics analysis uses the following Navier–Stokes (N–S) equation and continuity equation:
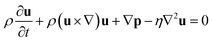 | (1) |
| ∇ × u = 0 | (2) |
The convection–diffusion equation can be used to analyze the mixing of fluids of different concentrations in the microchannel:
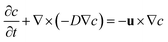 | (3) |
The potential distribution of the electric field can be expressed by the Laplace equation:
| ∇2V = 0 | (4) |
In the above formula, V represents a potential (V).
Adopting electroosmotic velocity boundary conditions, the local slip velocity given by Helmholtz–Smoluchowski is as follows:
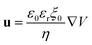 | (5) |
Among them, ε0, εr are the dielectric constant of vacuum and electrolyte solution respectively;ξ0 is the zeta potential of the inner wall of the fixed wall; and V is the electric potential.
The characteristic dimensionless number of the microchannel and the Reynolds number (Re) corresponding to the flow velocity:
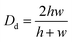 | (6) |
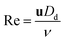 | (7) |
The calculation equation of mixing efficiency is as follows:
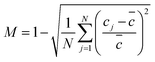 | (8) |
The mixing efficiency is M, N is the total number of sampling points, and cj and ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) are normalized concentration and the expected normalized concentration, respectively. The mixing efficiency ranges from 0 (0%) to 1 (100%).
are normalized concentration and the expected normalized concentration, respectively. The mixing efficiency ranges from 0 (0%) to 1 (100%).
3.2 Finite element modeling
Based on COMSOL Multiphysics 5.4 software, the electrolyte solution incompressibly flows, and the fluid dynamics boundary conditions do not slip on the wall of the micromixer. The outlet pressure of the microchannel is 0 Pa, the sample concentration of the injection port 1 and the injection port 2 is set to C1 = 1 mol L−1 and C2 = 0 mol L−1, the electric field follows the law of conservation of charge, the boundaries of the micromixer are insulated except for the electrode area, zeta potential is −0.1 V, fluid density is 988 kg m−3, relative dielectric constant is 78, ionic solution conductivity is 0.11845 S m−1, dynamic viscosity is 10−3 Pa s, and solution diffusion coefficient is 10−11 m2 s−1. The 3D model of the micromixer was designed using the three-dimensional software Pro/Engineer 5.0.4 Results and discussion
4.1 Grid independence analysis
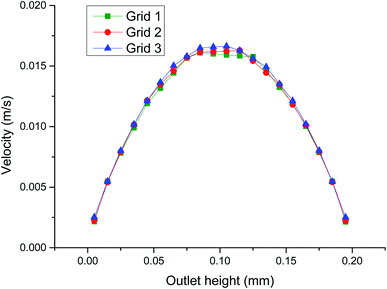
The selection of the grid has a great influence on the simulation results. The correct selection of the grid can improve the accuracy and save the calculation time. Fig. 3 shows the local velocity distribution of the line segment at the exit of the micromixer. The test result increases as the number of grid cells increases. However, the difficulty of simulation will increase as the number of grid cells increases. As per the grid dependency test calculation, the number of grid cells in grid 2 is selected as the best result. According to COMSOL 5.4, the complete grid information of grid 2 selected is counted, and the number of cells is 366 033, the minimum cell mass is 0.001271, and the average element can reach 0.5866, tetrahedron the number of units is 295![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 869, the pyramid cell number is 1816, the prism cell number is 68
869, the pyramid cell number is 1816, the prism cell number is 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 348, and the triangle cell number is 36
348, and the triangle cell number is 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260.
260.
4.2 The effect of electrodes on mixing efficiency
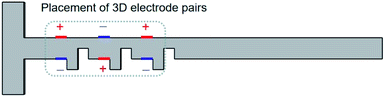
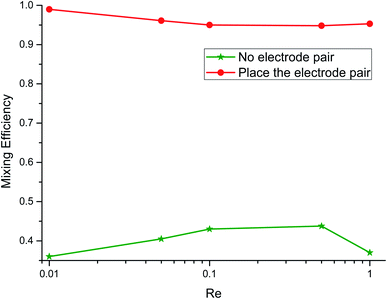
In this study, we compare the passive micromixer with the electroosmotic micromixer with the Koch fractal. As shown in Fig. 4, three pairs of electrodes with opposite polarity are alternately added on the fractal channel wall, and other conditions are the same. Fig. 5 shows that when the Re values are 0.01, 0.05, 0.1, 0.5 and 1, the application of electrodes in the microchannel can effectively improve the mixing efficiency of the solution. Especially, when Re = 0.01, the mixing efficiency can be increased by 64%. Under the action of non-electric field, the fluid mainly flows in laminar flow. The mixing of solution primarily depends on the fractal structure in the microchannel and the diffusion between molecules. At a low Reynolds number, the fractal structure has little effect on the mixing of fluid. When the electric field is applied, the fluid in the microchannel forms a vortex under the action of the electric field. With the help of the fractal structure, the fluid motion path is changed so as to improve the fluid mixing.4.3 The effect of electrode spacing and voltage on mixing efficiency
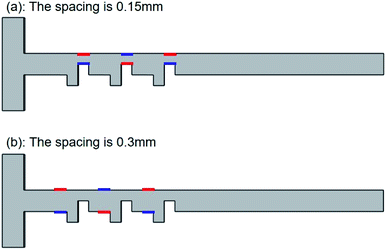
As shown in Fig. 6, red is high potential and blue is low potential. Two groups of electrode pairs were selected to study. The electrode spacing was 0.15 mm and 0.3 mm. It can be seen from the calculation results in Fig. 7 that within the scope of study, the mixing efficiency is effectively improved with the decrease of electrode spacing. As shown in Fig. 7, with the increase of voltage, the mixing efficiency of the two micromixers is effectively improved, especially when the voltage increases from 1 to 3 V. When the voltage is increased, the mixing efficiency is not so obvious.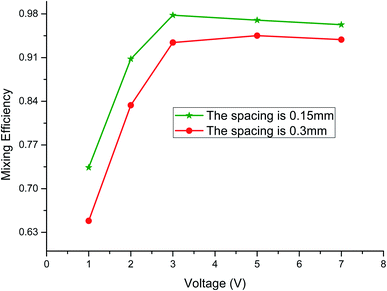 | ||
| Fig. 7 Mixing efficiency of three micromixers with different electrode spacings at different voltage values. | ||
When the electrode spacing is small, the energy efficiency level is higher. With the increase of electrode spacing, the energy efficiency rapidly decreases in the low voltage stage. When the voltage increases, the energy efficiency difference of different electrode spacing will narrow. Because the ions in the diffusion layer of the electric double layer are affected by the horizontal and vertical electric fields, the ions in the diffusion layer will be disturbed, and the viscosity of the fluid will be reduced. Moreover, the ions in the diffusion layer will then drive the surrounding fluid molecules to form a vertical motion with the wall. After reducing the distance between the electrode pairs, the energy efficiency is increased, thus strengthening the convection, which makes the fluid stretch and fold repeatedly in the microchannel and improves the mixing efficiency. Therefore, it is feasible to adjust the electrode spacing and voltage value to control the mixing of the micromixer.
4.4 The effect of electrode configuration on mixing efficiency
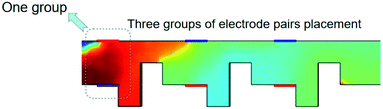
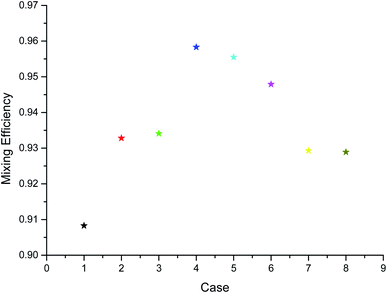
The charge in the microchannel is primarily related to the applied electric field, which can form eddy currents near the electrodes and improve fluid mixing. Therefore, the direction of the electric field has a significant impact on the mixing efficiency. This section studies the influence of different configurations of electrodes on the mixing efficiency. As shown in Fig. 8, the electrodes are divided into three groups. We have studied eight configurations. The two electrodes in each group have opposite potentials, and the external conditions of the eight configurations are exactly the same. The mixing efficiency of the eight configuration outlets is shown in Fig. 9. The best mixing efficiency is the configuration given in Fig. 8, which is about 95%. It can be seen that changing the potential has a great influence on the performance of the mixer. Because the electrodes placed in the micromixer change the fluid from a uniform flow to a non-uniform flow, the fluid is mixed. The potential difference in the microchannel is adjusted to allow more adequate mixing of the working fluid. When an asymmetric potential difference is applied to the flow path, greater disturbances are generated, resulting in complex fluid disturbances. Therefore, the mixing performance of the electroosmotic micromixer can be improved by changing the potential of the microelectrode. Properly placed potential in microchannels can strengthen the fluid to stretch and fold in different directions to achieve the purpose of mixing.4.5 Flow analysis in microchannels
To more intuitively study the effect of the electrode on the fluid on the fractal micromixer, we have selected three velocity streamline diagrams under different voltages, and the streamline density of the three diagrams is equal. The color of the streamline indicates the concentration distribution of the fluid. Fig. 10a shows that when no voltage is applied to the fractal micromixer, the mixing efficiency at this time is not ideal. Because the Reynolds number is low at this time, the mixing of fluids is mainly affected by molecular diffusion and residence time. In the whole process, the fractal hinders the fluid, and the weak chaotic convection promotes the mixing of the fluid. As shown in Fig. 10b, when the voltage is increased to 3 V in the fractal microchannel, the fluid undergoes obvious deflection and folding under the action of the electric field and the fractal structure. From the streamline diagram, due to the action of electric field, the fluid generated a series of chaotic vortices at the fractal, which promoted the mixing of fluid in the microchannel. As shown in Fig. 10c, when the voltage in the microchannel is continuously increased, the chaotic motion of the fluid becomes more intense; therefore, appropriately adjusting the electrode voltage on the fractal structure will help the fluid to mix.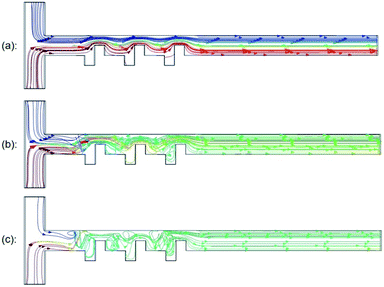 | ||
| Fig. 10 Mixing performance of micromixers. (a) The voltage value is 0 V. (b) The voltage value is 3 V. (c) The voltage value is 10 V. | ||
5 Conclusions
In this study, using the Koch fractal principle and electroosmotic effect to improve the mixing efficiency of the micromixer, it is confirmed that:(1) Alternating electrodes in a micromixer with the Koch fractal structure is a method to generate vortex and enhance mixing.
(2) Because the ions in the diffusion layer of the electric double layer will be affected by the horizontal and vertical electric fields, the ions in the diffusion layer will be disturbed and the viscosity of the fluid will decrease. The surrounding fluid molecules vertically move with the wall. After reducing the distance between the electrode pairs, the energy efficiency is improved, thereby enhancing the convection and making the fluid repeatedly stretch and folding in the microchannel as well as improving the mixing efficiency.
(3) Because the electrodes placed in the micromixer change the fluid from a uniform flow to an uneven flow, the fluids are mixed. When an asymmetric potential difference is applied to the flow path, greater interference will be generated, resulting in complex fluid interference. Therefore, the mixing performance of the electroosmotic micromixer can be improved by changing the potential of the microelectrode. To achieve the purpose of mixing, the placed potential difference will cause the fluid to stretch and fold in different directions.
(4) Because of the fractal structure, the contact surface of the two fluids is increased, the mixing of the fluids is improved, and the microelectrodes can be better placed in the microchannels, which is more conducive to the effect of the electric field, thereby improving the mixing efficiency of the micromixer.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was supported by Young Taishan Scholars Program of Shandong Province of China (tsqn2020), Shandong Provincial Natural Science Foundation (ZR2021JQ).References
- Á. Ríos, M. Zougagh and M. Avila, Miniaturization through lab-on-a-chip: utopia or reality for routine laboratories? A review, Anal. Chim. Acta, 2012, 740, 1–11 CrossRef PubMed.
- N. T. Nguyen and Z. Wu, Micromixers—a review, J. Micromech. Microeng., 2004, 15(2), R1 CrossRef.
- E. O. Adekanmbi and S. K. Srivastava, Dielectrophoretic applications for disease diagnostics using lab-on-a-chip platforms, Lab Chip, 2016, 16(12), 2148–2167 RSC.
- W. Han and X. Chen, Nano-electrokinetic ion enrichment in a micro-nanofluidic preconcentrator with nanochannel's Cantor fractal wall structure, Appl. Nanosci., 2019, 1–11 Search PubMed.
- X. Chen, T. Li and X. Li, Numerical research on shape optimization of microchannels of passive micromixers, IEEE Sens. J., 2016, 16(17), 6527–6532 Search PubMed.
- Z. Wu and X. Chen, Numerical simulation of a novel microfluidic electroosmotic micromixer with Cantor fractal structure, Microsyst. Technol., 2019, 25(8), 3157–3164 CrossRef.
- K. Zhang, Y. Ren and L. Hou, et al., An efficient micromixer actuated by induced-charge electroosmosis using asymmetrical floating electrodes, Microfluid. Nanofluid., 2018, 22(11), 130 CrossRef.
- N. H. A. Le, H. Deng, C. Devendran, N. Akhtar, X. Ma, C. Pouton and T. Alan, Ultrafast star-shaped acoustic micromixer for high throughput nanoparticle synthesis, Lab Chip, 2020, 20(3), 582–591 RSC.
- X. Chen and S. Zhang, 3D micromixers based on Koch fractal principle, Microsyst. Technol., 2018, 24(1), 2627–2636 CrossRef.
- Z. Wu and X. Chen, Numerical simulation of a novel microfluidic electroosmotic micromixer with Cantor fractal structure, Microsyst. Technol., 2019, 25(8), 3157–3164 CrossRef.
- M. K. Manshadi, H. Nikookar, M. Saadat and R. Kamali, Numerical analysis of non-uniform electric field effects on induced charge electrokinetics flow with application in micromixers, J. Micromech. Microeng., 2019, 29(3), 035016 CrossRef CAS.
- M. Bayareh, M. N. Ashani and A. Usefian, Active and passive micromixers: a comprehensive review, Chem. Eng. Process., 2019, 147, 107771 CrossRef.
- R. R. Gidde, P. M. Pawar and B. P. Ronge, et al., Flow field analysis of a passive wavy micromixer with CSAR and ESAR elements, Microsyst. Technol., 2019, 25(3), 1017–1030 CrossRef.
- R. R. Gidde, P. M. Pawar, B. P. Ronge, N. D. Misal, R. B. Kapurkar and A. K. Parkhe, Evaluation of the mixing performance in a planar passive micromixer with circular and square mixing chambers, Microsyst. Technol., 2018, 24(6), 2599–2610 CrossRef CAS.
- W. Hong, H. Shi and Z. Huang, et al., Design and simulation of a passive micromixer with gourd-shaped channel, J. Nanosci. Nanotechnol., 2019, 19(1), 206–212 CrossRef CAS PubMed.
- G. A. Mensing, T. M. Pearce and M. D. Graham, An externally driven magnetic microstirrer: one contribution of 11 to a theme ‘Transport and mixing at the microscale’, Philos. Trans. R. Soc., B, 2004, 362, 1059–1068 Search PubMed.
- T. Zhou, H. Wang and L. Shi, et al., An enhanced electroosmotic micromixer with an efficient asymmetric lateral structure, Micromachines, 2016, 7(12), 218 CrossRef PubMed.
- T. Zhou, X. Ji and L. Shi, et al., Dielectrophoretic interactions of two rod-shaped deformable particles under DC electric field, Colloids Surf., A, 2020, 607, 125493 CrossRef CAS.
- D. Jing and S. Yi, electroosmotic flow in tree-like branching microchannel network, Fractals, 2019, 27(6), 1950095 CrossRef.
- G. Kunti, A. Bhattacharya and S. Chakraborty, Rapid mixing with high-throughput in a semi-active semi-passive micromixer, Electrophoresis, 2017, 38(9–10), 1310–1317 CrossRef CAS PubMed.
- H. Jalili, M. Raad and D. A. Fallah, Numerical study on the mixing quality of an electroosmotic micromixer under periodic potential, Proc. Inst. Mech. Eng., Part C, 2020, 234(11), 2113–2125 CrossRef.
- A. Shamloo, M. Madadelahi and S. Abdorahimzadeh, Three-dimensional numerical simulation of a novel electroosmotic micromixer, Chem. Eng. Process., 2017, 119, 25–33 CrossRef.
- A. Usefian and M. Bayareh, Numerical and experimental study on mixing performance of a novel electro-osmotic micro-mixer, Meccanica, 2019, 54(8), 1149–1162 CrossRef.
| This journal is © The Royal Society of Chemistry 2021 |