 Open Access Article
Open Access ArticleEnhanced lattice distortion, yield strength, critical resolved shear stress, and improving mechanical properties of transition-metals doped CrCoNi medium entropy alloy
Md. Lokman Ali ab
ab
aDepartment of Mechanical Science and Bioengineering, Graduate School of Engineering Science, Osaka University, Osaka 560-8531, Japan. E-mail: m.l.ali@tsme.me.es.osaka-u.ac.jp
bDepartment of Physics, Pabna University of Science and Technology, Pabna-6600, Bangladesh
First published on 6th July 2021
Abstract
The effect of transition-metals (TM) addition on the mechanical properties of CrCoNi medium entropy alloys (MEAs) was investigated. Molecular dynamics (MD) simulations were carried out to evaluate the atomic distortion and yield strength and critical resolved shear stress (CRSS) quantitively. The MD simulation results indicate that the lattice distortion and yield strength agree with the other experimental results. The addition of 4 atomic% of transition metals enhances the lattice distortion and yield strength of the CrCoNi alloy by ∼30% and retains high ductility and strengthening ability. Also, the elastic moduli, anisotropy factor, Pugh's ratio, and the hardness were investigated. Furthermore, we performed MD simulations to obtain the CRSS and the root-mean-square-atomic-displacement (RMSAD) of equiatomic and near-equiatomic CrCoNi MEAs. We demonstrated that an approximately linear relationship exists between the RMSAD and the CRSS for these alloying systems. A more realistic embedded atom method (EAM) potential also verified the universality. These simulation results will be useful in the future development and research of CrCoNi-based quaternary alloys with improved mechanical properties.
1 Introduction
Medium entropy alloys (MEAs) have attracted considerable attention in materials science and solid-state physics due to their exceptional mechanical properties when TM is incorporated and used as a structural material. These properties include high tensile strength, ductility, hardness, and high thermal stability.1,2 A significant challenge has been designing and developing a new MEA with mechanical properties better than the MEAs currently in use. Pure metals are never used and require alloying additions for strength. However, the alloying of several metallic elements usually leads to a large change in hardening. Therefore, several methods to improve yield strength have been made, including precipitation strengthening, grain refining, and dislocation hardening.2–4 Traditional hardening methods increase yield strength while also weakening ductility, which does not overcome the strength–ductility trade-off. Therefore, the effects of adding transition-metals elements on the mechanical properties of CrCoNi MEAs have drawn more attention.4–10Owing to the specific and unique atomic size of multi-principal elements, lattice distortion is a fundamental characteristic of MEAs. In fcc alloys, atomic distortion due to atomic size mismatch and Young's moduli mismatch of additional atoms prevents dislocation movements and plays a leading role in the distinctive solid solution strengthening.11–13 The solid solution strengthening mechanism relies heavily on lattice distortion. Severe lattice distortion is an essential technique for improving yield strength. Sohn et al.14 have produced a CiNiV alloy via extreme lattice distortion, which has a yield strength of nearly 800 MPa. Element V has a greater atomic size than Cr and the fluctuation of the atomic displacement of CoNiV are higher than CoCrNi, which implies an increase in resistance to dislocation. Similar phenomena are documented in (CrCoNi)100−xWx (ref. 15) and (CrCoNi)100−xAlx (ref. 16) single phase fcc medium entropy alloys. CrCoNi MEA was selected in this study as the parent material to be further hardened by adding transition elements. Transition-elements were chosen due to a large atomic size and a modulus different from Cr, Co, and Ni. Transition elements-containing CrCoNi alloys can therefore be anticipated to have a larger yield strength. Also, we calculated the CRSS for the first time of 4% TM-doped (CrCoNi)100−xTMx (TM = W, Mo, Cu, V, Y, and x = 0, 4) MEAs demonstrated the relationship between the RMSAD and the CRSS in the equi- and non equiatomic CrCoNi MEAs using the MD simulations.
To further improve the mechanical properties of MEAs and design new MEAs and understand their potential technological applications. It is necessary to understand the effects of additional element addition on other mechanical properties, including the elastic moduli (bulk, shear, Young's), Pugh's ratio, the Poisson's ratio, the anisotropy factor, and the hardness. However, fewer studies have been carried out on the mechanical properties of the tungsten and molybdenum-doped CrCoNi alloy. The elastic constants, elastic moduli, and the hardness, CRSS are still unexplored in detail. In order to predict the importance of alloys for technological applications, it is useful to consider the mechanical properties of these MEAs, including mechanical stability and ductility. This paper provides essential details on the physical metallurgy of multicomponent medium entropy alloys, which will undoubtedly contribute to a deeper understanding of their fascinating mechanical characteristics.
2 Simulation method
2.1 Interatomic potential
The Lennard-Jones (LJ) potential is useful for the qualitative analysis of the motion of defects in metallic structures, including dislocation glides and vacancy diffusion, although this interatomic interaction ignores the many-body effect. This potential has been commonly used to model an assortment of phases and structural defects, ranging from rare gas materials, metallic liquids, and grain boundaries. We also chose the LJ potential incorporated due to its flexibility in adapting the MSAD and the CRSS of the alloying systems. The LJ potential of the similar element, i is parameterized by the expression below
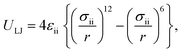 | (1) |
 The LJ potential parameters of the ternary equi and near equiatomic CrCoNi MEA, and transition-metals doped (CrCoNi)96W4, (CrCoNi)96Mo4, (CrCoNi)96Y4, (CrCoNi)96V4 and (CrCoNi)96Cu4 alloys are used in our recent previous work.11 The parameter, σij for MD simulations have been set to 0.2 eV.
The LJ potential parameters of the ternary equi and near equiatomic CrCoNi MEA, and transition-metals doped (CrCoNi)96W4, (CrCoNi)96Mo4, (CrCoNi)96Y4, (CrCoNi)96V4 and (CrCoNi)96Cu4 alloys are used in our recent previous work.11 The parameter, σij for MD simulations have been set to 0.2 eV.
2.2 Molecular dynamics (MD) simulations
In the present work, the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)17 was used for performing the MD simulations. The MD simulations were performed to determine the MSAD values for CrCoNi MEA and TM-doped CrCoNi MEAs in an fcc crystal structure comprised of 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms with a 7.6 × 8.8 × 9.4 nm3 supercell in all three directions under periodic boundary conditions. Fig. 1(a) shows the atoms are colored by the common neighbor analysis (CNA) method. The green atoms denote the face-centered cubic structures. Fig. 1(b) shows the atomic configuration of a TM-doped CrCoNi single-crystal sample, atoms are colored according to the element type. We have used two types of potentials; the first is Lennard-Jones potential, which is recently published in our work,11 and the second is embedded atom method (EAM) potential.8 In the CRSS measurements, the computational cell used for simulations is depicted in Fig. 1(c), along with the crystallographic orientation. A simulation cell consisting of an fcc crystal structure was created with a 50.9 × 21.2 × 9.8 nm3 supercell comprised of 379
000 atoms with a 7.6 × 8.8 × 9.4 nm3 supercell in all three directions under periodic boundary conditions. Fig. 1(a) shows the atoms are colored by the common neighbor analysis (CNA) method. The green atoms denote the face-centered cubic structures. Fig. 1(b) shows the atomic configuration of a TM-doped CrCoNi single-crystal sample, atoms are colored according to the element type. We have used two types of potentials; the first is Lennard-Jones potential, which is recently published in our work,11 and the second is embedded atom method (EAM) potential.8 In the CRSS measurements, the computational cell used for simulations is depicted in Fig. 1(c), along with the crystallographic orientation. A simulation cell consisting of an fcc crystal structure was created with a 50.9 × 21.2 × 9.8 nm3 supercell comprised of 379![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 atoms. The elements are randomly arranged on the fcc lattice. In the x- and y-directions, the periodic boundary conditions were applied, and the free boundary condition were applied in the z-direction. The atomic layers were viewed as rigid bodies on both the lower and upper boundaries, and a constant strain rate was applied at a relative velocity to the upper rigid body with respect to the lower one.
800 atoms. The elements are randomly arranged on the fcc lattice. In the x- and y-directions, the periodic boundary conditions were applied, and the free boundary condition were applied in the z-direction. The atomic layers were viewed as rigid bodies on both the lower and upper boundaries, and a constant strain rate was applied at a relative velocity to the upper rigid body with respect to the lower one.
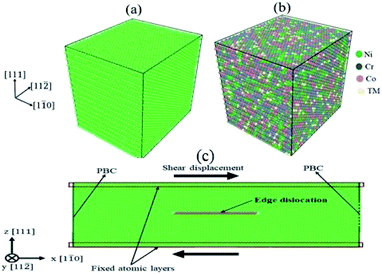 | ||
| Fig. 1 Schematic diagram of (a) (CrCoNi)100−xTMx MEA with atoms colored according to the common neighbor analysis (CNA) method18 in Open Visualization Tool (OVITO)19 to identify the fcc crystal structure (b) model after random initialization of Ni, Co, Cr, and TM (c) supercell with one edge dislocation. | ||
3 Results and discussions
3.1 Lattice distortion, yield strength, MSAD and CRSS
The lattice distortion is a fundamental feature of materials. The lattice distortion is broadly correlated to the atomic size of the constituent elements. The MSAD is widely used to investigate the atomic distortion of CrCoNi, and other reported MEAs, which is consistent with our previous study.11 The lattice distortion of pure elemental Ni and Al is significantly smaller than that of CrCoNi alloy.20 Tong et al.21 measured the lattice friction stress in CrCoNi, CrCoFeNi, and NiCoCrFeMn HEA by X-ray diffraction and observed that the lattice distortion of CrCoNi is much like that in NiCoCrFeMn HEA and larger than that of CrCoFeNi. We employed mean square atomic displacement (MSAD) from ideal regular lattice sites to quantify the degree of lattice distortion.11 It is necessary because resistance to dislocation movement is determined solely by the distorted lattice and tends to yield strength by evaluating the appropriate MSAD results could be predicted. The MSAD values of TM-doped (CrCoNi)96TM4 MEA are much higher than those of the CrCoNi alloy. Also, TM-containing MEAs exhibit large atomic size fluctuations. Therefore, the addition of transition metals is confirmed to produce large atomic distortions, which is the leading cause of the large yield strength.The MSAD values and yield strength of various multi-principal element alloys are presented in Fig. 2(c) and (d). The results show that the addition of W, Mo, Cu, V, Y had similar effects on the yield strength and that the MSAD parameter is an important scaling parameter for the prediction of the yield strength. The MD simulations of the CRSS values for (CrCoNi)100−xTMx alloys are shown in Fig. 2(b). The chemical environment is more complex by adding the TM elements, which may be the main reason for the higher CRSS compared to others.
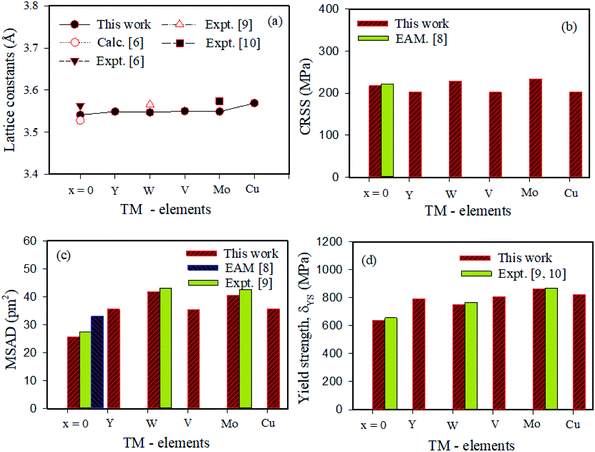 | ||
| Fig. 2 The calculated (a) lattice constants (b) CRSS (c) MSAD and (d) yield strength of (NiCoCr)100−xTMx (TM = W, Mo, Y, V, Cu and x = 0, 4) MEAs. | ||
3.2 RMSAD vs. CRSS
The relationship between the calculated RMSAD and CRSS of the equiatomic and non-equiatomic CrCoNi MEA is shown in Fig. 3(a) and (b). For comparison, each RMSAD was normalized by the Burgers vector length and each CRSS was normalized by the shear moduli of the model. Following the volumetric relaxation, the Burgers vector b is calculated from the supercell size. We found the equi- and non-equiatomic ternary alloy systems follow a linear relationship. The greater the RMSAD, of the alloy, the higher the CRSS, regardless of whether the system is a CrCoNi MEA. We found that, as the number of Cr elements increases, the slope continues to increase. The spatial overlap between the possible dislocation motion wells created by the lattice friction stress becomes more important in the chromium elements of the ternary alloy. Our predicted results mean that the RMSAD calculated by the MD simulations can be a general random alloy CRSS predictor that can strongly support a high-throughput high-strength MEA design. The universality relation was also confirmed by a more realistic embedded atom method (EAM) potential.8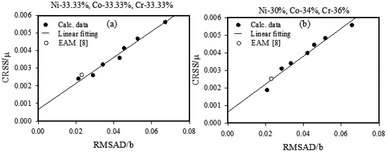 | ||
| Fig. 3 The correlation between the RMSAD and the CRSS for (a) equiatomic and (b) non-equiatomic CrCoNi MEA. | ||
3.3 Mechanical properties
The TM-doped phases elastic constants are obtained and analyzed to ensure the mechanical stability of the TM-doped CrCoNi MEA. The influences on the elastic constants by the TM-doping of (CrCoNi)100−xTMx alloys are presented in Fig. 4(a), demonstrating that all the TM-doped alloys the elastic constants gradually increase. The simulated results indicate that all the (CrCoNi)100−xTMx alloys satisfy the Born-stability conditions.22| C11 − C12 > 0, C11 > 0, C44 > 0, C11 + 2C12 | (2) |
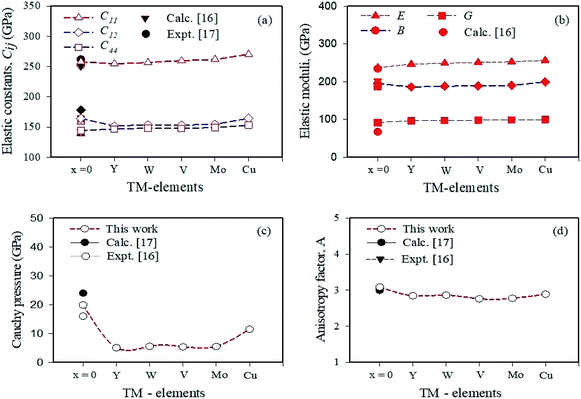 | ||
| Fig. 4 The calculated (a) elastic constants (b) elastic moduli (c) Cauchy pressure and (d) anisotropy factor of (CrCoNi)100−xTMx alloys. | ||
Our predicted elastic constants satisfy the above criteria. Hence, all the doped phases are mechanically stable. The measured elastic constants of the undoped CrCoNi alloy are consistent with the other theoretical findings showing the reliability of the present calculations.6,7
The behavior of elastic constants in response to TM addition suggests that TM-doped CrCoNi alloys are mechanically strengthened. The Cauchy pressure (C12 − C44) is a useful indicator to predict the ductility and brittleness of the alloys. This indicator's positive or negative value denotes the ductile or brittle behavior of a solid, respectively.23 The simulated results of the Cauchy pressure of the (CrCoNi)100−xTMx alloys are positive, which shows that all the MEAs have a ductile nature. Using the simulated elastic constants, an investigation of the mechanical parameters including the bulk moduli (B), shear moduli (G), Young's moduli (E) and the anisotropy factor (A) of TM-doped CrCoNi MEAs were conducted. These parameters can be directly calculated with the Voigt–Reuss–Hill approximation method.24 The bulk and shear modulus can predict materials resistance to changing their volume and shape, respectively.25 The Young's modulus shows the stiffness of materials the higher the value of E, the more rigid the materials are. The variations in the B, G, and E of the (CrCoNi)100−xTMx alloys are given in Fig. 4(b). The values of B, G, and E increases monotonically as the transition-metals doping. The simulation results for the B, G, and E of all the alloys studied are comparatively high and hence suitable for technological applications. The anisotropy factor has essential implications in solid-state physics and materials science. Hossain et al.26 reported that when A's value is equal to one, the alloys will be isotropic, and when the value of A is greater or less than one, the alloys will be anisotropic. The simulation results for A are not one, indicating that the TM-doped MEAs are anisotropic. The effects of TM-doped MEAs on the anisotropy factor are shown in Fig. 4(d), showing that the degree of crystal anisotropy increases as the transition-metals adding.
3.4 Ductility analysis of (CrCoNi)100−xTMx MEAs
The ratio of bulk moduli (B) to shear moduli (G) is commonly referred to as Pugh's ratio, which is used to predict an alloys failure mode. For classifying the ductility and brittleness of alloys, the critical value of Pugh's ratio is 1.75.22 The simulation results for Pugh's ratio of all the (CrCoNi)100−xTMx alloys indicate ductile behavior as the value of B/G is higher than the critical value. After the TM-doping in CrCoNi MEA, the value of Pugh's ratio is slightly decreased. However, the calculated of Pugh's ratio of the TM-doped CrCoNi MEA is still higher than the critical value of 1.75, and the alloy should therefore exhibit a ductile response, similar to the undoped CrCoNi MEA. Fig. 5(a) presents the B/G ratios of the (CrCoNi)100−xTMx alloys and indicates that the alloys become slightly brittle as the transition-metals doping. Another useful measure for predicting the ductility and brittleness of solids is the Poisson ratio ν. The critical value separating the ductility and brittleness of a solid is 0.26.26,27 The computed results of Poisson's ratio of all studied alloys are higher than the critical value implying the materials are ductile. The Poisson's ratio of TM-doped alloys slightly decreased as TM-content adding, as shown in Fig. 5(b), which indicates the alloys have become more brittle.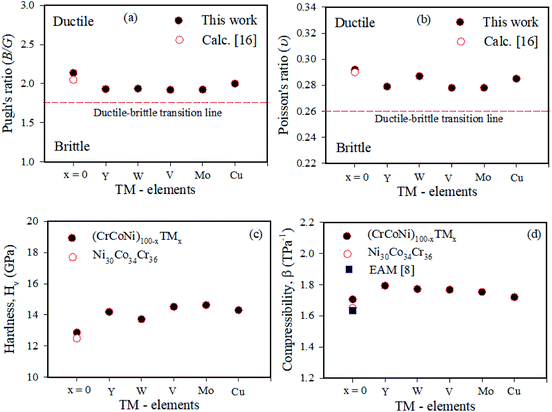 | ||
| Fig. 5 The calculated (a) Pugh's ratio (b) Poisson's ratio (c) hardness and (d) compressibility of (CrCoNi)100−xTMx alloys. | ||
3.5 Hardness and compressibility analysis of (CrCoNi)100−xTMx MEAs
Fig. 5(c) shows the effects of the addition of TM on the Vickers hardness of the (CrCoNi)100−xTMx MEAs. It can be shown that when the TM-elements were adding, the Vickers hardness values increases. The CrCoNi MEA had the lowest Vickers hardness value, 12.2 GPa, and the highest hardness value, 14.1 GPa, was measured for the (CrCoNi)96Mo4 alloy. Similar findings were also reported by Wu et al.28 on other alloying systems, and they noted that it is important to understand the existence of the alloying elements. The variations of the atomic size, lattice distortion, and Young's moduli of the alloying components will influence the hardness of the alloys, i.e., strengthening. As the atomic size and Young's moduli variations increase, the Vickers hardness values progressively increase. Tungsten, molybdenum, copper, yttrium has a much larger atomic radius and Young's modulus than Co, Cr, and Ni. Therefore, the Vickers hardness variation is greatly affected by the effective atomic size and Young's modulus. In this study, when TM is added to the CrCoNi alloy, Young's modulus variation increases due to the high modulus and atomic size of W, Mo, Cu, V, and Y, thus increasing the hardness. Therefore, the (CrCoNi)96TM4 alloy is expected to show the highest hardness of alloys studied, which matches the results shown in Fig. 4(b). Linear compressibility is an important parameter to measure the relative volume change of solids. The calculated values of TM-doped MEAs as shown in Fig. 5(d). It can be seen that the compressibility is positive; that is, an increased pressure compresses the alloy to a smaller volume. This condition is required for the mechanical stability of materials.294 Conclusions
The mechanical properties of (CrCoNi)100−xTMx (TM = W, Mo, Cu, V, Y and x = 0, 4) alloys have been systemically investigated using molecular dynamics (MD) simulations. The addition of transition-metals (TM) into the CoCrNi alloys significantly improved the mechanical properties. The simulation results presented here captured the effects of the addition of TM on CrCoNi fcc alloys. The following main conclusions can be drawn:The lattice distortion of (CrCoNi)96TM4 alloys dramatically increased. TM-doping in the CrCoNi alloys impeded the dislocation motion, which contributed to the high yield strength. Overall 4 atomic% TM-additions improved the yield strength of CrCoNi by about ∼30% and retained the high ductility. Direct MD analysis of the relationship between the CRSS – and the lattice distortion (CRSS–MSAD) of equi- and non-equiatomic CrCoNi alloy is discussed. The elastic moduli of the (NiCoCr)96TM4 alloy were higher than that of the CrCoNi alloy. The Vickers hardness of the (CrCoNi)96TM4 alloy was higher than that of the CrCoNi alloys.
Data availability
The data sets generated and/or analyzed in this study are available from the corresponding author on reasonable request.Conflicts of interest
There are no conflicts of interest to declare.Notes and references
- I. Moravcik, L. Gouvea, J. Cupera and I. Dlouhy, J. Alloys Compd., 2018, 748, 979–988 CrossRef CAS.
- P. Sathiyamoorthi, J. Moon, J. W. Bae, P. Asghari-Rad and H. S. Kim, Scr. Mater., 2019, 163, 152–156 CrossRef CAS.
- G. Laplanche, A. Kostka, C. Reinhart, J. Hunfeld, G. Eggeler and E. George, Acta Mater., 2017, 128, 292–303 CrossRef CAS.
- Y. Zhao, T. Yang, Y. Tong, J. Wang, J. Luan, Z. Jiao, D. Chen, Y. Yang, A. Hu, C. Liu and J.-J. Kai, Acta Mater., 2017, 138, 72–82 CrossRef CAS.
- M. Komarasamy, S. Shukla, N. Ley, K. Liu, K. Cho, B. McWilliams, R. Brennan, M. L. Young and R. S. Mishra, Mater. Sci. Eng. A, 2018, 736, 383–391 CrossRef CAS.
- K. Jin, Y. Gao and H. Bei, Mater. Sci. Eng. A, 2017, 695, 74–79 CrossRef CAS.
- B. Yin, S. Yoshida, N. Tsuji and W. A. Curtin, Nat. Commun., 2020, 11, 2507 CrossRef CAS PubMed.
- Q.-J. Li, H. Sheng and E. Ma, Nat. Commun., 2019, 10, 3563 CrossRef.
- Z. Wu, W. Guo, K. Jin, J. D. Poplawsky, Y. Gao and H. Bei, J. Mater. Res., 2018, 33, 3301–3309 CrossRef CAS.
- R. Chang, W. Fang, J. Yan, H. Yu, X. Bai, J. Li, S. Wang, S. Zheng and F. Yin, J. Mater. Sci. Technol., 2021, 62, 25–33 CrossRef.
- M. L. Ali, S. Shinzato, V. Wang, Z. Shen, J. ping Du and S. Ogata, Mater. Trans., 2020, 61, 605–609 CrossRef CAS.
- Y. Ye, C. Liu, H. Wang and T. Nieh, Acta Mater., 2018, 147, 78–89 CrossRef CAS.
- K. Ming, X. Bi and J. Wang, Scr. Mater., 2017, 137, 88–93 CrossRef CAS.
- S. S. Sohn, D. G. Kim, Y. H. Jo, A. K. da Silva, W. Lu, A. J. Breen, B. Gault and D. Ponge, Acta Mater., 2020, 194, 106–117 CrossRef CAS.
- R. Chang, W. Fang, X. Bai, C. Xia, X. Zhang, H. Yu, B. Liu and F. Yin, J. Alloys Compd., 2019, 790, 732–743 CrossRef CAS.
- M. P. Agustianingrum, S. Yoshida, N. Tsuji and N. Park, J. Alloys Compd., 2019, 781, 866–872 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- N. Lümmen and T. Kraska, Modell. Simul. Mater. Sci. Eng., 2007, 15, 319–334 CrossRef.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
- S. Yoshida, T. Bhattacharjee, Y. Bai and N. Tsuji, Scr. Mater., 2017, 134, 33–36 CrossRef CAS.
- Y. Tong, K. Jin, H. Bei, J. Ko, D. Pagan, Y. Zhang and F. Zhang, Mater. Des., 2018, 155, 1–7 CrossRef CAS.
- S. Pugh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823–843 CrossRef CAS.
- D. G. Pettifor, Mater. Sci. Technol., 1992, 8, 345–349 CrossRef CAS.
- R. Hill, Proc. Phys. Soc. A., 1952, 65, 349–354 CrossRef.
- S. Huang, R.-Z. Li, S.-T. Qi, B. Chen and J. Shen, Phys. Scr., 2014, 89, 065702 CrossRef CAS.
- K. M. Hossain, M. Zahid Hasan and M. Lokman Ali, Results Phys., 2020, 19, 103337 CrossRef.
- M. Z. Rahaman and M. L. Ali, Chin. J. Phys., 2018, 56, 1386–1393 CrossRef CAS.
- Z. Wu, H. Bei, G. Pharr and E. George, Acta Mater., 2014, 81, 428–441 CrossRef CAS.
- R. Lakes and K. W. Wojciechowski, Phys. Status Solidi B, 2008, 245, 545–551 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |
