Open Access Article
Open Access ArticleStudy of charge transfer mechanism and dielectric relaxation of all-inorganic perovskite CsSnCl3
Mohamed Ben Bechir *a and
Mohamed Houcine Dhaoub
*a and
Mohamed Houcine Dhaoub
aLaboratory of Spectroscopic and Optical Characterization of Materials (LaSCOM), Faculty of Sciences, University of Sfax, BP1171 – 3000, Sfax, Tunisia. E-mail: mohamedbenbechir@hotmail.com
bDepartment of Physics College of Science Qassim University, Buraydah, Almolaydah 51452-P.O.Box: 6644, Saudi Arabia
First published on 21st June 2021
Abstract
In the field of commercialization, lead-free metal halide perovskite materials are becoming more popular these days because of their prospective use in solar cells and also in other optoelectronic applications. In this paper, a non-toxic CsSnCl3 metal halide is successfully synthesized via the slow evaporation solution growth technique. Such systematic characterizations as differential scanning calorimetry (DSC) measurements, dielectric measurements, and variable-temperature structural analyses indicate that CsSnCl3 goes through a reversible phase transformation at T = 391/393 K from the monoclinic to the cubic system. Optical measurements of CsSnCl3 reveal a direct band-gap value of about 3.04 eV. The study of the charge transfer mechanism of CsSnCl3 is carried out based on Elliott's theory. The conduction mechanism in CsSnCl3 is interpreted through the following two approaches: the non-overlapping small polaron tunneling (NSPT) model (monoclinic phase) and the overlapping large polaron tunneling (OLPT) model (cubic phase). Moreover, the high dielectric constant of CsSnCl3 which is associated with a low dielectric loss makes it a possible candidate for energy harvesting devices.
1. Introduction
Metal halide perovskite materials of the well-known formula AMX3 (where A = a cation, M = a metal ion, and X = a halogen anion) have recently attracted researchers' attention owing to their marked solar cell potency with astonishing optoelectronic proprieties including a vast range of absorption spectra, improved optical absorption, tunable bandgap, high charge-carrier mobility and low effective mass.1–3 The researchers have started the application of these semiconducting materials which are also widespread in the field of such electronic devices as LEDs (Light Emitting Diodes) and photodetectors, and the devices that are largely employed for solar-to-fuel energy conversion.4–6 In addition, these metal halide perovskites are inexpensive and widely available on Earth. As a consequence, these semiconductors would be more appropriate and favorable to the solar cell application relative to the Si-based photovoltaic (PV) technology.3 Nevertheless, most of the halide perovskites with superlative properties are composed of lead (Pb) which has a damaging effect on the environment.7–9 Eco-friendly energy sources have caught much attention because of environmental contamination and the global energy crisis. Hence, a big number of experimental and theoretical works have been carried out in the last few years to replace Pb with a convenient metal cation.10–13 In the perovskite structure, using Sn2+ instead of Pb2+ removes the toxicity of the halide inorganic material but provides more pronounced phase instability.Furthermore, The CsSnX3 compounds are direct bandgap semiconductors with good hole mobilities. Moreover, these Metal halide perovskite materials have small excitation binding energies, high values of the optical absorption coefficient, and the range of bandgap values was 1–3 eV.14,15 All these properties make the CsSnX3 compounds promising candidates for optoelectronic nanodevices. Lately, solar cells using CsSnX3 have been made, and until now the maximum power conversion efficiency (PCE) is up to 9.13% (CsSnBr3 based device).16–18 In addition to the application in PV, the important physical properties of CsSnX3 also enable these compounds to be good for different applications, such as ferroelectricity, photoluminescence, and X-ray detectors. Hao et al. have noted that the CsSnI3 compound had important photoluminescence characteristics, and the tunable photoluminescence covered the whole visible to the near-infrared zone.19,20
This paper focuses on CsSnCl3, a comparatively stable but less studied member of the CsSnX3 family. Nonetheless, extensive investigations on its structural and dielectric properties are very important to evaluate the compatibility of inorganic materials with the field of next-generation photovoltaics and optoelectronics. Multiple researchers have concentrated on the synthesis and optical/optoelectronic characterization of metal halide perovskite materials21 through which charge transport plays a key role in the efficiency of the electrical and the optoelectronic devices. Nonetheless, a thorough knowledge of the electrical transport mechanism is still missing along with the dielectric behavior of CsSnCl3.22
Dielectric spectroscopy is broadly employed to gather information on the AC conduction mechanism and dielectric relaxation in a vast frequency range of different temperatures. The dielectric properties can be examined by establishing multiple parametric tools such as complex impedance, dielectric permittivity, electrical modulus, and also AC conductivity. The qualitative representation frequently provides the latest insight into the field of dielectric behavior. In the material, non-localized (known as long-range conductivity) and localized conduction (also known as dielectric relaxation) processes can, for instance, be marked by either the absence or the presence of the relaxation peak from the imaginary modulus plots. Specific transport mechanism can be defined using the activation energy and the relaxation time for material. The behavior of the dielectric parameter was previously investigated on perovskite oxide materials, amorphous transition metal oxide semiconductors, ionically conducting polymers, and conducting glasses.23–25
The synthesis is reported in this paper along with the structural and optical characterization of CsSnCl3. This paper offers an in-depth investigation of dielectric and electrical properties as this perovskite is relatively unexplored. Impedance spectroscopy is a very suitable and practical tool to research dielectric properties. The temperature and frequency-dependent dielectric study of CsSnCl3 can give in-depth information concerning the performance of the localized charge carriers, conduction mechanism, permittivity, loss factor, etc. Very little literature about the extensive research on AC conductivity, and dielectric relaxation of CsSnCl3 is available. In this paper, the study of dielectric relaxation with impedance spectroscopy, electrical modulus and conductivity of CsSnCl3 has been thoroughly conducted as a function of frequency and temperature. Using different theoretical models, the results of the dielectric researches have been carefully scrutinized. In-depth discussions on the AC and DC conductivity, dielectric loss, dielectric constant, impedance study, and also electrical modulus of this perovskite material are reported in this paper.
2. Experimental section
2.1. Materials
Cesium chloride (Sigma-Aldrich, ≥98.0%) and Tin(II) chloride (Sigma-Aldrich, reagent grade, 98%) were employed as received without further purification.2.2. Synthesis
The CsSnCl3 compound was synthesized by the evaporation at room temperature method with stoichiometric quantities of CsCl (0.94 g, 0.0055 mol) and SnCl2 (1.05 g, 0.0055 mol) in deionized water (50 mL) according to the following equation:| CsCl + SnCl2 → CsSnCl3 |
The solution obtained was slowly evaporated at room temperature. The product was purified by different successive recrystallizations. Throughout these steps, the crystal quality improved, and transparent single crystals of CsSnCl3 were obtained and chosen for further experiments.
2.3. Characterization
The differential scanning calorimetric study (DSC) was carried out on a Perkin-Elmer Diamond DSC apparatus in the temperature range of 300–500 K with a rate of 5 K min−1 under a nitrogen (N2) atmosphere.A small quantity of CsSnCl3 crystals was ground mechanically in an agate mortar with a pestle to obtain fine powders so as the powder X-ray diffraction (PXRD). The PXRD analysis was conducted by means of a Rigaku MiniFlex 600 benchtop diffractometer using a Cu Kα line radiation (λ = 1.54 Å) in the 2θ = 10°–60° range with a 0.04° step size at 303 and 403 K.
Thermogravimetric (TG) analysis was done at a range of heating rates from 300 to 900 K with a Perkin Elmer Pyris 6 in a closed perforated aluminum pan under an N2 gas flow. The TG analysis was made on powder from the obtained CsSnCl3 crystals.
Ultraviolet-visible diffuse reflectance measurement was conducted on a PerkinElmer Lambda 950 UV-Vis spectrophotometer, whereas the UV-Vis absorption spectrum was carried out on a single crystal of the material at room temperature.
A small quantity of CsSnCl3 crystals was ground mechanically in an agate mortar with a pestle to obtain fine powders so as to measure the complex impedance. CsSnCl3 pellet (0.93 mm thickness) was prepared under a nitrogen (N2) atmosphere (at room temperature) with a hydraulic press of 8 mm diameter under a 50 Torr pressure, and the relative density was found to be equal to 93%. The resulting pellet was put between two copper electrodes. In order to make good electrical contact between the sample and the electrodes, the pellet was coated with silver paint. AC conductivity and dielectric relaxation were investigated by the TH2828A impedance analyzer (frequency range 10−1–106 Hz) associated with a temperature controller (TP94, Linkam, Surrey, UK) from 303 K to 483 K at a heating rate of 2 K min−1. The measured AC voltage was 0.5 V.
3. Results and discussion
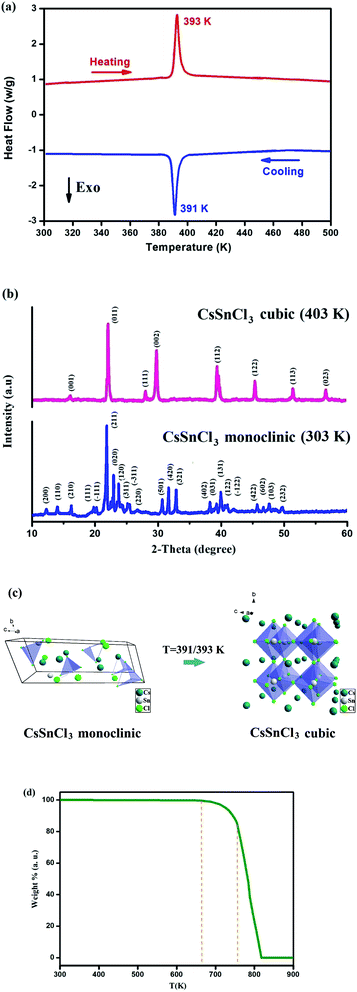
3.1. Temperature-dependent structural analysis
The DSC measurement of both heating and cooling is an effective way to measure the temperature-triggered phase transition. The DSC curve for CsSnCl3 demonstrates an endothermic peak which takes place at 393 K and also an exothermic peak found at 391 K as shown in Fig. 1(a). The sharp reversible peaks confirm that they ought to be first-order phase transitions. The phase transition at T = 391/392 K is confirmed by the PXRD pattern at 303 and 403 K (Fig. 1(b)).The crystal structure of CsSnCl3 was obtained at 303 K using powder X-ray diffraction. The diffractogram is shown in Fig. 1(b). All the peaks seen in this diffractogram were indexed with the Celeref. 3 software by the least square method from the powder data.26 The PXRD pattern proves that CsSnCl3 crystallizes at 303 K in the monoclinic system with the space group P21/n and has the unit cell parameters a = 16.089 (2) Å, b = 7.419 (5) Å, c = 5.739 (4) Å and β = 93.4°. On the other hand, CsSnCl3 crystallizes at 403 K in the cubic system with the space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and the refined unit-cell parameters: a = 5.579 (3) Å, and V = 173.64 (Å3). The parameters values found in both phases are in accord with the values of the literature.27,28
m and the refined unit-cell parameters: a = 5.579 (3) Å, and V = 173.64 (Å3). The parameters values found in both phases are in accord with the values of the literature.27,28
As indicated in Fig. 1(c), the molecular structure of CsSnCl3 for the two alternative phases (monoclinic and cubic) is obtained by the Vesta software. The thermogravimetric analysis data of CsSnCl3 indicates no mass loss between 300 and 670 K, which confirms that the as-prepared perovskite is thermally stable up to 670 K as shown in Fig. 1(d). The decomposition of CsSnCl3 takes place in two steps with a final temperature of about 820 K.
3.2. Optical properties
The study of the optical properties of perovskite materials in photovoltaic (PV) technologies plays a big part in understanding the optoelectronic nature of these technologies. In fact, UV-Vis spectroscopy is an accurate and convenient method to learn about the absorption behavior, get the various optical parameters, and clarify the band structure of semiconductor materials.29 With the help of optical absorption studies, these characteristics can simply be identified by examining the interaction between the incident photons and the treated compounds.The optical absorption of the CsSnCl3 perovskite was determined by means of a UV-Vis spectrophotometer in the 250–800 nm wavelength range. Fig. 2(a) illustrates the absorption spectrum of the compound. The optical bandgap is a major factor in such fields of science as photovoltaics, solar cells, lasers, photoluminescence, and diodes.30,31 Finding out whether the optical bandgap nature is direct or not represents, nonetheless, one of the most prominent features of perovskite materials.32
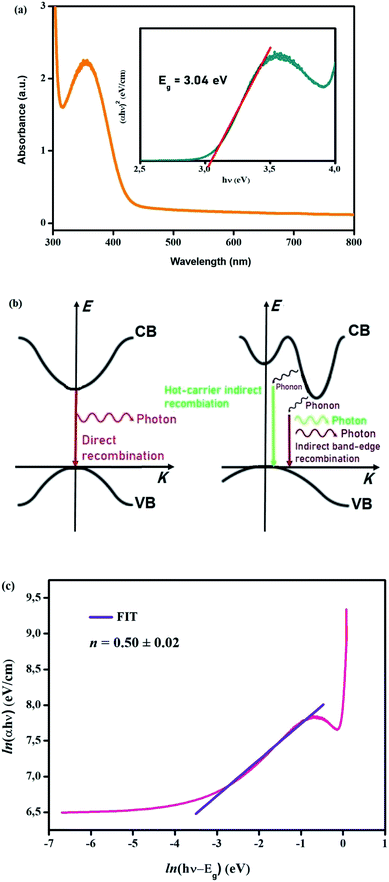 | ||
| Fig. 2 (a) Absorbance spectrum of CsSnCl3. The inset presents the Tauc plot for CsSnCl3. (b) Direct and indirect band gaps. (c) Plot of ln(αhυ) vs. ln(hυ′′ − Eg). | ||
Overall, the character of the bandgap transition in semiconductor materials is experimentally identified by examining the absorption spectrum and calculating the optical absorption coefficient (α) of the compound. α could be found out from the absorption measurements bearing in mind that (e) refers to the cell thickness through the Beer–Lambert law:33
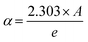 | (1) |
α is generally related to the photon energy (hν) using the Tauc relation which is shown by the following equation.34,35
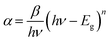 | (2) |
The calculation of the optical bandgap Eg is on the basis of the following Tauc formula:
| (αhν)1/n = β(hν − Eg) | (3) |
After plotting (αhν)2 and (αhν)1/2 as a function of the photon energy (hν), the most appropriate and satisfactory plot is obtained when n = 1/2. The direct transition is chosen in accordance with the Tauc equation. Consequently,
| (αhν)2 = β(hν − Eg) | (4) |
As illustrated in the inset of Fig. 2(a), the bandgap Eg value could be calculated by means of the extrapolation of the linear portion to α = 0.36 Eg is found to be equivalent to 3.04 eV, proving that CsSnCl3 is a potential candidate for optoelectronics.
In order to check the transition mode of the optical strip for our compound, the following equation is used to express:37
ln(αhν) = ln(β) + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(hν − Eg) ln(hν − Eg)
| (5) |
Accordingly, Fig. 2(c) displays the plot of the variation ln(αhν) as a function of ln(hν − Eg). This curve provides a straight line where the slope is the power factor (n) which recognizes the type of optical transition mode.37 In accordance with both Fig. 2(c) and eqn (5), the following linear relation is obtained:
| ln(αhν) = 8.28 + 0.5 ln(hν − 3.04); (n ≈ 1/2) | (6) |
Therefore, the direct optical band transition mode of our material is verified. The determined value of the transition power factor (n) is almost equivalent to 1/2, which is in accord with the estimated mode.
3.3. Impedance spectroscopy results
Complex impedance spectroscopy (CIS) is a principal and successful procedure used in order to study the electrical behavior of a material. It provides information on the movement of ions within CsSnCl3, the relaxation time, and the electrical conductivity.The complex frequency-dependent impedance represents a non-destructive technique that demonstrates the bulk (grain), the grain boundary, and the electrode contribution in the material when applying the time-reversed electric field.38 When an alternating field is forced, the charge carrier generally tends to become active and causes dipole orientation, charge displacement, and space charge formation. Hence, the contribution of grains, grain boundaries, and electrodes to the charge transport within the compound can be distinguished using the complex impedance study. The frequency-dependent impedance can be illustrated through eqn (7):
| Z(ω) = Z′(ω) + jZ′′(ω) | (7) |
Fig. 3(a) indicates the frequency variation in the real part (Z′) of the complex impedance with various temperatures. In both phases, It is noticed that Z′ decreases when frequency and temperature go up, which shows the negative temperature coefficient of the resistance (NTCR)-type behavior within the compound.39,40 This type of behavior propounds that an increase in AC conductivity is possible owing to the rise in the mobility of charge carriers and also to the reduction in the trapped charge density in CsSnCl3. Z′ is temperature-independent in the high-frequency region, which points to the existence of space charge in the material. Space charge has less time to relax as soon as frequency augments. Hence, the fact that space charge polarization drops leads to a merging of curves at high frequency.41 Fig. 3(b) displays the loss factor variation (Z′′) in the whole frequency range of various temperatures. In both regions (monoclinic and cubic systems), this variation shows the basic charge transport mechanism and the relaxation process in CsSnCl3 as a function of temperature. The immobile species/electrons at low temperatures and defects/vacancies at high temperatures seem to be the reasons behind the relaxation process. For each spectrum, a well-defined characteristic peak which was traditionally known as the “relaxation frequency” is noticed. The broadness peak shows a sharp deviation from an ideal Debye nature. The motion of charge carriers over a long-range which is essentially the cause of the transportation below the loss peak frequency contributes to the motion of the localized carriers above the relaxation frequency. With the rise of the temperature, the movement of the relaxation peak towards the high-frequency regime points to the thermally-dependent relaxation mechanism. Additionally, the peak height is reduced with temperature, suggesting the decrease in the grain and grain boundary resistance with temperature.42
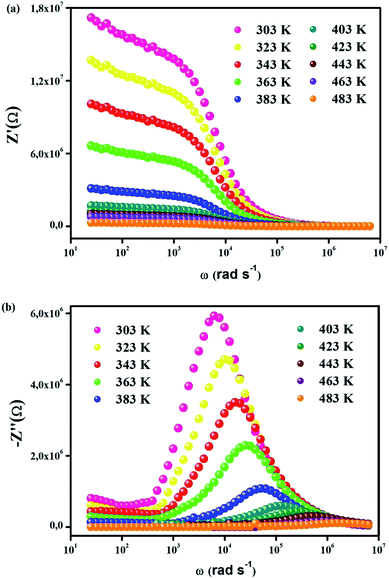 | ||
| Fig. 3 (a) Real part of impedance (Z′) vs. frequency, (b) imaginary part of impedance (Z′′) vs. frequency. | ||
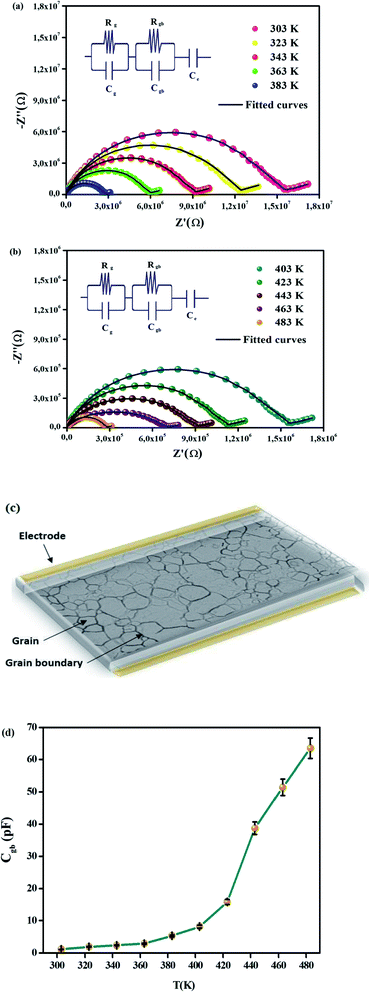
The Cole–Cole plot in the temperature range of 303–483 K is illustrated in Fig. 4(a) and (b). It is worth mentioning that for both phases, the depressed semicircles have their centers below the real axis. This shows the non-Debye type of behavior in CsSnCl3.42 The decrease in the radii of the semicircles with the elevation of temperature in the Cole–Cole plot points once again to the NTCR behavior of the material.43 Besides, this proves that the conduction process is thermally activated and that the compound possesses semiconducting proprieties. Three distinct semicircles which are most importantly in view of the contribution of electrode–material interface, grains, and grain boundaries ideally emerge in the Nyquist diagram. The semicircle in the high-frequency region indicates the contribution of the grain, whereas the semicircle in the low-frequency region denotes the contribution of grain boundaries. The semicircle in the ultra-low-frequency area shows the contribution owing to the electrode–material interface. Differentiating the involvement of grains and grain boundaries from the single depressed semicircle is deeply ambiguous. Consequently, the Maxwell–Wagner equivalent circuit model comprised of a parallel combination of a number of resistors (R) and capacitors (C) is used in order to distinguish the contribution of the grains and grain boundaries from the single semicircle. The impedance spectra of all temperatures are fitted with the help of the ZView Software. The desired circuit model is acquired in that case by linking two parallel RC elements in series, the straight line after the semicircle can be interpreted with the constant phase element (CPE) according to the double layer capacity of an inhomogeneous electrode surface (the inset of Fig. 4(a) and (b)). The diameter of the semicircle, i.e. the intersection point on the real axis, decreases significantly with the rise in temperature as illustrated in Fig. 4(a) and (b). This confirms the improvement in DC conductivity with higher temperatures.44 A schematic representation of grains and grain boundaries in the material is illustrated in Fig. 4(c). The ZView software has been used to fit the experimental data in our paper in order to assess these parameters. It is noted that the value of Rgb is higher than the value of Rg for all temperatures as expressed in Table 1 which demonstrates that the grain boundaries have more contributions to the total resistance since R = Rg + Rgb. In fact, the grain boundaries in perovskite materials are more resistive than the grains. Because of polarization, the distinction between these two resistive values triggers a substantial growth in the number of space charges at the grain boundaries also known as the Maxwell–Wagner effect.45
| T (K) | Rg (kΩ) | Cg (nF) | Rgb (kΩ) | Cgb (pF) | Ce (μF) | αe |
|---|---|---|---|---|---|---|
| 303 | 101.21 | 1.78 | 1268.69 | 1.13 | 0.0642 | 0.4763 |
| 323 | 84.55 | 2.32 | 9445.87 | 1.96 | 0.0809 | 0.4712 |
| 343 | 61.88 | 2.87 | 765.48 | 2.42 | 0.0117 | 0.4521 |
| 363 | 40.18 | 3.14 | 498.23 | 2.96 | 0.212 | 0.4637 |
| 383 | 23.61 | 3.96 | 304.21 | 5.35 | 0.468 | 0.4895 |
| 403 | 9.35 | 4.42 | 171.56 | 8.16 | 0.852 | 0.4535 |
| 423 | 7.57 | 5.35 | 93.42 | 15.82 | 1.078 | 0.4637 |
| 443 | 5.54 | 6.63 | 63.98 | 38.75 | 1.747 | 0.4856 |
| 463 | 3.70 | 7.05 | 47.85 | 51.42 | 2.311 | 0.4825 |
| 483 | 1.93 | 7.89 | 23.67 | 63.52 | 2.759 | 0.4909 |
The variation in grain boundary capacitance (Cgb) which is shown in Fig. 4(d) tends to go up with temperature. Grain boundary capacitance could be expressed as follows: Cgb = (εgbA)/d, where εgb refers to the intrinsic dielectric constant at the grain boundary. Hence, Cgb depends on the barrier-layer width (d), which is proportional to the ratio of trapped charge carriers in free carrier density.38 The layer width becomes fairly small at high temperatures since trapped charge carriers drop as soon as the temperature rises. In fact, because of this behavior, grain boundary capacitance grows with temperature.
3.4. Dielectric properties
The dielectric response of any material could be illustrated through the following complex dielectric constant:| ε(ω) = ε′(ω) + jε′′(ω) | (8) |
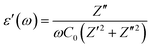 | (9) |
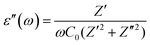 | (10) |
The difference between the dielectric constants is investigated as a function of frequency in the temperature range of 303–483 K. For both phases, Fig. 5(a) and (b) confirm that, in the low-frequency region, the dielectric constant is wide at a certain temperature and slowly goes down with the rise in frequency. Both ε′(ω) and ε′′(ω) play a big part in the ionic conduction process which is controlled by four main types of polarization, viz. ionic, electronic, orientational, and interfacial.
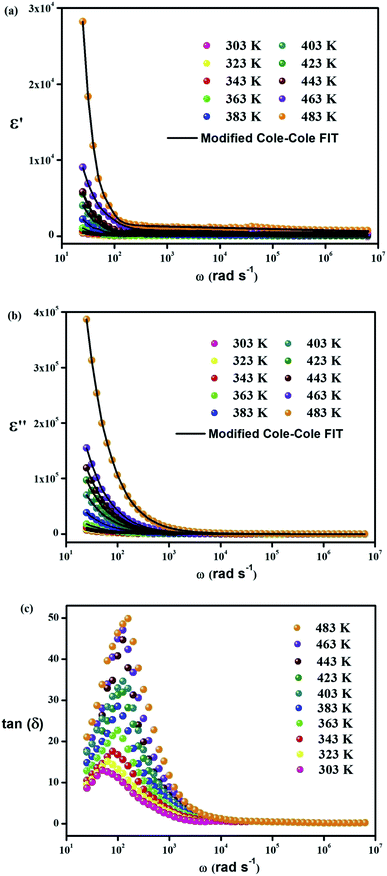 | ||
Fig. 5 (a) Frequency-dependent real part of dielectric permittivity. (b) Frequency-dependent imaginary part of dielectric permittivity. (c) tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ vs. angular frequency spectra of CsSnCl3. δ vs. angular frequency spectra of CsSnCl3. | ||
Ionic and electronic polarizations refer to the deformational component of polarizability, whereas orientational and interfacial polarizations represent the relaxation component of polarizability.46 The variation in the real part of permittivity with frequency could be interpreted via Maxwell–Wagner interfacial polarization, which is in accord with Koop's phenomenological theory.47
The material in this model is expected to include conducting grains that are separated by poorly conducting grain boundaries. Therefore, to restrain their flow, charge carriers get trapped at the interface of grain boundaries.47,48 The exchange of electrons between the ions belonging to the same molecules occurs in the interfacial polarization process. The deformities and imperfections found in the material are the reason for changing the position and the distribution of positive and negative space charges. Influenced by the applied electric field, positive and negative charges shift towards the negative and positive poles of the applied field respectively.49
We note that for the two phases (monoclinic and cubic system), electrons can reach the grain boundary regime through hopping (Fig. 5(a)) in the low-frequency region but they are accumulated at the grain boundary position and cause polarization due to the high grain boundary resistance. On the other hand, electrons cannot follow the alternation of the applied field at high frequency, which avoids further accumulation of electrons even if they move in the reverse direction. Consequently, the possibility of arriving at the grain boundary diminishes for electrons when frequency increases which thin polarization.49 At the mid-frequency region, the variation in ε′(ω) can be typified by the appearance of a hump on account of the relaxation process. The movement of the hump position with temperature to the low-frequency region puts forth a temperature-dependent dielectric response. However, at high frequency, the value of ε′(ω) does not change considerably. This “unrelaxed” value of permittivity shows the atomic and electronic polarization. The CsSnCl3 perovskite crystal includes Cs+, Sn2+, and Cl− ions which play a big part in its polarization. Therefore, the real part of the dielectric constant ε′(ω) goes down with the decline in temperature, which is probably because of the low responsive nature of the participating ions and the conducting electrons at low temperature.
Among various popular theoretical models, the modified Cole–Cole model has been used with DC conductivity to examine the variation in the dielectric constant and the dielectric loss as a function of frequency for different temperatures.50 Per the modified Cole–Cole model, the complex permittivity is shown as follows:
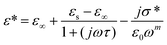 | (11) |
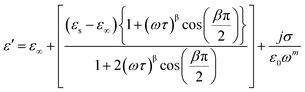 | (12) |
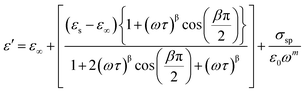 | (13) |
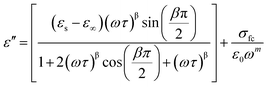 | (14) |
The experimental data of ε′ and ε′′ are fitted with the modified Cole–Cole equation. The obtained values of such various parameters as β, m, σsp, σfc, and τ are mentioned in Table 2. According to Table 2, it is obvious that the values of space charge conductivity (σsp) and free charge conductivity (σfc) go up as soon as the temperature rises. The value of β which is between 0 and 1 further proves the non-Debye nature. The relaxation time declines the moment the temperature climbs.
| T (K) | Parameter | |||||||
|---|---|---|---|---|---|---|---|---|
| fmax | τ | β | m | σsp | σfc | a | b | |
| 303 | 1.45 × 104 | 6.89 × 10−5 | 0.659 | 0.789 | 3.57 × 10−5 | 8.56 × 10−4 | 0.578 | 0.503 |
| 323 | 2.76 × 104 | 3.62 × 10−5 | 0.785 | 0.806 | 8.91 × 10−5 | 9.89 × 10−4 | 0.598 | 0.552 |
| 343 | 4.95 × 104 | 2.02 × 10−5 | 0.795 | 0.813 | 2.68 × 10−4 | 1.65 × 10−3 | 0.612 | 0.621 |
| 363 | 7.68 × 104 | 1.30 × 10−5 | 0.801 | 0.825 | 6.35 × 10−4 | 4.48 × 10−3 | 0.633 | 0.675 |
| 383 | 1.35 × 105 | 7.36 × 10−6 | 0.875 | 0.847 | 9.15 × 10−4 | 7.31 × 10−3 | 0.678 | 0.699 |
| 403 | 4.13 × 105 | 2.41 × 10−6 | 0.657 | 0.869 | 4.88 × 10−3 | 1.45 × 10−2 | 0.745 | 0.728 |
| 423 | 5.02 × 105 | 1.99 × 10−6 | 0.854 | 0.911 | 9.09 × 10−3 | 3.68 × 10−2 | 0.789 | 0.743 |
| 443 | 6.28 × 105 | 1.59 × 10−6 | 0.932 | 0.936 | 3.72 × 10−2 | 5.51 × 10−2 | 0.825 | 0.762 |
| 463 | 7.83 × 105 | 1.27 × 10−6 | 0.912 | 0.942 | 5.03 × 10−2 | 7.08 × 10−2 | 0.869 | 0.789 |
| 483 | 8.78 × 105 | 1.13 × 10−6 | 0.928 | 0.966 | 8.68 × 10−2 | 9.74 × 10−2 | 0.881 | 0.825 |
The loss tangent represents the ratio of the dielectric loss and the real part of the dielectric constant. Fig. 5(c) illustrates the variation in the loss tangent with frequency for a particular range of temperature (tan(δ) = ε′(ω)/ε′′(ω)). For the two regions, the loss tangent decreases when the frequency rises and then becomes constant in the high-frequency region at a given temperature. The appearance of the peaks in the low-frequency region may be caused by the dominant dipolar polarization. Loss tangent values increase and peaks thus move as soon as the temperature climbs, which proves that dipolar polarization is a thermally controlled mechanism. The loss peak ultimately emerges the moment the hopping frequency corresponds obviously to the frequency of an applied external AC field. In addition, the hopping mechanism propounds that the electrical conductivity is elevated with temperature which brings about the thermally activated charge carriers.
3.5. Modulus analysis
The detailed complex modulus spectra have been examined to study the relaxation procedure in CsSnCl3. The complex electric modulus which is essentially the reciprocal of complex permittivity suggested by Macedo is an incredibly simple tool to research the electrical relaxation mechanism of space charge distribution by stopping the effect of electrodes. The electric modulus mainly shows the electric field relaxation in the material as soon as the dielectric displacement is continuous. The electric modulus is expressed through the following equation:
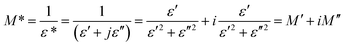 | (15) |
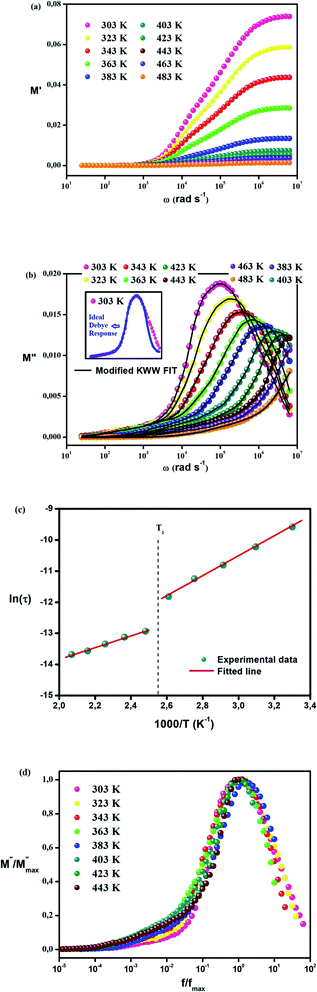
Fig. 6(a) describes the real part of the electric modulus spectra as a function of frequency for different temperatures. The variation in M′ with frequency illustrates that M′ obtains an extremely small value (almost zero) in the low-frequency region for all temperatures. This behavior along with the sigmoidal nature of M′ is caused by the long-range mobility of charge carriers in the conduction mechanism and the negligence of the electrode polarization. There is a minor change in the peak of M′ with the increase in temperature along the high-frequency region.
Fig. 6(b) illustrates the variation in the imaginary part of the electric modulus M′′ with frequency at various temperatures. For both phases, M′′ obtains its maximum value at a particular temperature, causing a peak at a certain frequency which amounts to the relaxation frequency. In the low-frequency region, no peak occurs while there is a significant peak that is noticed in the high-frequency region. In the low-frequency region, charge carriers can move easily over a long distance showing the successful charge carrier hopping from one site to another. However, charge carriers are restricted in their potential well and make a controlled motion in the high-frequency region. As a result, the peak occurrence provides information concerning the transition from long-range to short-range mobility of charge carriers. The peaks in M′′ tend to move to the high-frequency region with a rise in temperature, which can be set out by the hopping mechanism. The non-Debye response of the sample is demonstrated by the asymmetrical nature of the peaks in M′′. To interpret the asymmetric nature of peaks in the imaginary part of the electric modulus, a KWW equation is used as follows (16):51–55
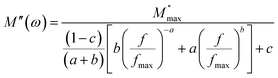 | (16) |
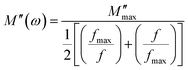 | (17) |
The relaxation time is estimated via eqn (18);
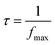 | (18) |
The average activation energy of the charge carriers could be calculated based on the Arrhenius equation as stated in eqn (19);
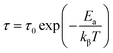 | (19) |
The phase transition appearing in DSC diagrams from the monoclinic to the cubic system is confirmed by the change of the curve slope at T = 391/393 K (Fig. 6(c)). 0.27 and 0.16 eV represent the derived activation energy from the slope of the least square fitting of ln τ vs. 1000/T plot for the phase 1 (CsSnCl3 monoclinic) and 2 (CsSnCl3 cubic), successfully. Additionally, this demonstrates that, in CsSnCl3, the conduction mechanism is on account of the thermally-stimulated charge carriers.56
Fig. 6(d) displays the variation in the normalized imaginary part of the electric modulus with the normalized frequency of the examined sample for various temperatures. The peak positions of the normalized spectrum show the transition from long-range mobility to short-range mobility of charge carriers as well as the hopping method of charge carriers as previously explained in detail in the case of M′′ spectra.57 The coincidence of the peaks at all temperatures emphasizes the temperature-independent performance of dynamic processes occurring in the sample.
3.6. AC electrical conductivity
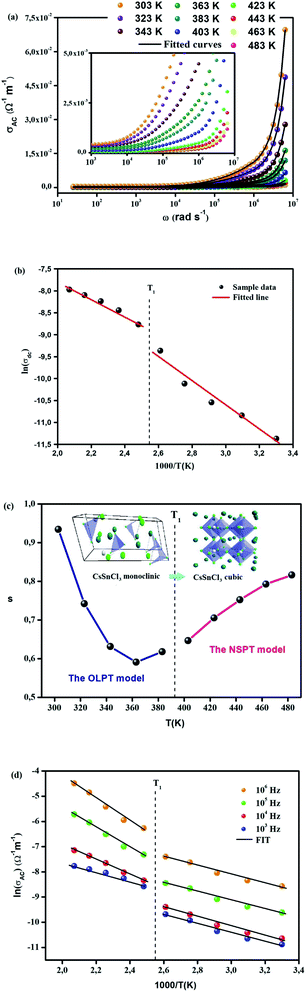
Fig. 7(a) exhibits the variation in temperature-dependent AC conductivity as a function of frequency. The AC electrical conductivity is estimated using of the following relation σac = ωε′ε0 tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ where ε0 denotes the permittivity of free space. In our work, the estimated conductivity in the low-frequency region is ascribed to DC conductivity, whereas conductivity in the high-frequency region is caused by AC conductivity. Due to the contribution of frequency-independent and temperature-dependent DC conductivity, the curves tend to be flattened in the low-frequency region.54 Nevertheless, the curves of the electrical conductivity become a lot larger and point to a strong frequency dispersion with the rise in frequency, which is on account of the contribution of AC conductivity. In this type of variation, the frequency at which the transition of conductivity occurs is known as “frequency hopping” (ωP). The latter tends to move to the high-frequency region when the temperature climbs. The spotted frequency-independent DC conductivity and frequency-dependent AC conductivity can be illuminated by the theory of the jump relaxation model (JRM) propounded by Funke.58 Per this theory, the ions in the low-frequency region can hop successfully to their neighboring sites. Long-term availability supports these successful jumps which result in a long-range translational motion of ions devoted to DC conductivity but both successful and unsuccessful hopping occur in the high-frequency region.
δ where ε0 denotes the permittivity of free space. In our work, the estimated conductivity in the low-frequency region is ascribed to DC conductivity, whereas conductivity in the high-frequency region is caused by AC conductivity. Due to the contribution of frequency-independent and temperature-dependent DC conductivity, the curves tend to be flattened in the low-frequency region.54 Nevertheless, the curves of the electrical conductivity become a lot larger and point to a strong frequency dispersion with the rise in frequency, which is on account of the contribution of AC conductivity. In this type of variation, the frequency at which the transition of conductivity occurs is known as “frequency hopping” (ωP). The latter tends to move to the high-frequency region when the temperature climbs. The spotted frequency-independent DC conductivity and frequency-dependent AC conductivity can be illuminated by the theory of the jump relaxation model (JRM) propounded by Funke.58 Per this theory, the ions in the low-frequency region can hop successfully to their neighboring sites. Long-term availability supports these successful jumps which result in a long-range translational motion of ions devoted to DC conductivity but both successful and unsuccessful hopping occur in the high-frequency region.
The hopping ion can jump back to its initial site (forward–backward–forward motion) causing an unsuccessful hopping. However, in successful hopping, the excited jumping ion hops to a new site and becomes steady in the new position while the neighboring ions become relaxed with this stationary ion. The ratio of successful and unsuccessful hopping increases in the high-frequency region leading to dispersive conductivity there. The measured electrical conductivity is attributed to Jonscher's power law-i.e. the universal dielectric response (UDR) model which was suggested by Jonscher;59
| σAC(ω) = σDC + σ0fs | (20) |
However, σDC values are calculated at various temperatures by non-linear curve fitting of σAC using the UDR model. The activation energy (Ea) of CsSnCl3 are further estimated based on the ln σDC vs. 1000/T plot (Fig. 7(b)) via the Arrhenius equation:
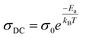 | (21) |
The phase transition is confirmed by the change of the slope of a curve at T = 391/393 K. The energy activation values of CsSnCl3 were found to be 0.23 (phase 1) and 0.16 eV (phase 2), which are so close to the values obtained from the M′′ spectra.
A convenient pattern based on the various theoretical models associating it with s(T) behavior may be proposed to establish the conduction mechanism in the CsSnCl3 compound.60 Several patterns which are in agreement with the literature are suggested based on two distinctive procedures, typical barrier hopping, and quantum mechanical tunneling, or a mixture of the two. Besides, it is thought that atoms or electrons (or polarons) are carriers in various ways. The diverse models are the quantum mechanical tunneling (QMT), the correlated barrier hopping (CBH), the non-overlapping small-polaron tunneling (NSPT) and also the overlapping large polaron tunneling (OLPT).61–63
Fig. 7(c) presents the temperature dependence of the exponent s which confirms the phase transition appearing in DSC diagrams at T = 391/393 K from the monoclinic to the cubic system:
−Phase 1 (CsSnCl3 cubic): the exponent s reaches a minimum value when the temperature rises and then increases slightly. Accordingly, the (OLPT) model is well-chosen.
−Phase 2 (CsSnCl3 monoclinic): the exponent s increases with the temperature, which demonstrates that the (NSPT) model is the suitable one.
In fact, within CsSnCl3, negatively charged chloride ions exist in the environment of Cs+ and Sn2+ ions but the two charge centers do not coincide, which results in a partially polar material. The polaron is formed as soon as the localized charge comes close to the compound and moves to the nearest neighboring positions. After the movement of the polaron to a new configuration, it either is stable at that position (“successful hop”) or shifts towards the reverse direction so as to get a partially relaxed configuration also known as “unsuccessful hop”. At low frequency, the non-dispersive behavior of the AC conductivity emerges owing to the successful hopping of the polaron. However, with the increase in frequency, some hops become unsuccessful. Accordingly, conductivity becomes dispersive at a high frequency. In the majority of the inorganic halide perovskite materials, a polaron is believed to be caused by lattice distortion64 which is ignored in the quantum mechanical tunneling of electrons. When the polarons are formed because of adding a charge carrier to a site, they can trigger a high degree of local lattice distortion. These polarons are so confined that their cloud distortions do not overlap. The AC conductivity at high temperatures is explained by the tunneling of carriers or polarons trapped at structural defects.
The AC conductivity in the OLPT model is ensured by the polaron tunneling mechanism. An overlap of the polaron distortion clouds comes off. The spatial extent of the polaron is wider than the interatomic spacing in the case of large polarons for which the overlap of the potential wells at the neighboring sites can occur because of the long-range character of the Coulomb interaction. Consequently, the polaron hopping energy diminishes, making an impact on the loss as a function of frequency since the activation energy related to the motion of the charge carriers between the various sites decreases as shown through:62
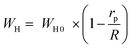 | (22) |
WH0 is expressed as follows:60
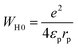 | (23) |
The AC conductivity is presented through the following equation:60
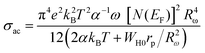 | (24) |
| (R′ω)2 + (βWH0 + ln(ωτ0))R′ω − βWH0r′p = 0 | (25) |
In the OLPT model, s corresponds to the following equation:62
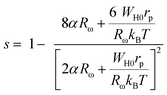 | (26) |
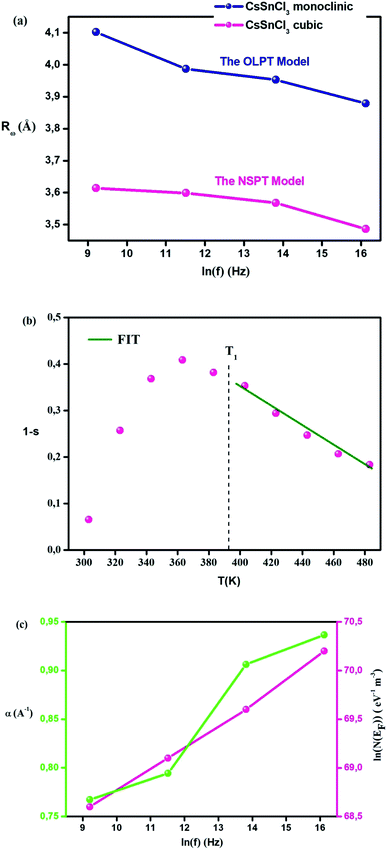
The theoretical calculations of the OLPT approach which is used in phase 1 (Fig. 7(d)) fit well with the experimental data (eqn (24)). Table 3 presents the values of α, WH0, N(EF), rP, and Rω. WH and εP values are calculated in eqn (22) and (23), respectively as mentioned in Table 3. The obtained values of N(EF) are logical for localized states. α values are of the same order as discussed by Murawski et al.62 Fig. 8(a) shows the variation of the tuning distance “Rω” which decreases with frequency as a function of ln(f) (phase 1).
| Frequency (Hz) | |||||
|---|---|---|---|---|---|
| 103 | 104 | 105 | 106 | ||
| The OLPT model | α (Å−1) | 0.59 | 0.63 | 0.69 | 0.74 |
| WH0 (eV) | 0.48 | 0.43 | 0.42 | 0.41 | |
| N (cm−3) | 7.98 × 1026 | 1.14 × 1027 | 2.68 × 1027 | 3.85 × 1027 | |
| rp (Å) | 1.12 | 1.08 | 1.01 | 0.98 | |
| Rω (Å) | 4.10 | 3.98 | 3.95 | 3.87 | |
| εp (F m−1) | 1.11 × 10−9 | 2.80 × 10−9 | 3.69 × 10−9 | 5.75 × 10−9 | |
| WH (eV) | 0.32 | 0.30 | 0.28 | 0.27 | |
| The NSPT model | α (Å−1) | 0.76 | 0.81 | 0.86 | 0.92 |
| N(EF) (eV−1 cm−3) | 6.68 × 1029 | 8.74 × 1029 | 2.68 × 1030 | 4.01 × 1030 | |
| Rω (Å) | 3.61 | 3.59 | 3.56 | 3.48 | |
In the NSPT model, the exponent s could be calculated via the following equation:65
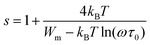 | (27) |
For the great values of Wm/kBT, s changes into:
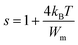 | (28) |
The curve fitting (Fig. 8(b)) is employed to calculate the value of Wm, which is equivalent to 0.161 eV.
In the NSPT model, the activation energy for polaron transfer (Wm) does not depend on the intersite separation65 since small polarons are confined in such a way that their cloud distortions do not overlap. For the NSPT model, the AC conductivity is expressed as follows.63
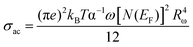 | (29) |
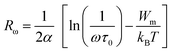 | (30) |
Fig. 7(d) shows the temperature dependence of ln(σAC) at various frequencies. This figure indicates that the fit accords with the experimental data (phase 2). The dissimilar parameters calculated for the (NSPT) model are mentioned in Table 3.
The values of the density of states N(EF) are adequate for the localized states.65 Fig. 8(c) illustrates the variation in the parameters α and N(EF) as a function of frequency. The increase in the two parameters α and N(EF) with the frequency is noticed, which is in agreement with the literature.53
Table 3 shows the values of Rω interpreted based on eqn (30). Fig. 8(a) confirms the variation in Rω as a function of frequency. It is obvious that the values of the tunneling distance for the two phases have the same range of the interatomic spacing Cs–Cl (3.55–4.14 Å).27 Moreover, the value of the tunneling distance diminishes faster when frequency increases. This behavior proposes that the charge carriers shift from the long-distance toward the short-distance tunneling. This behavior can be the reason for the rise in N(EF) (∼1030 eV−1 cm−3) with the frequency.60 The values of Rω (3.48–4.10 Å) and the distances Cs–Cl (3.55–4.14 Å) are close, which implies that due to the mobility of Cs+ in the compound, the AC conductivity is ensured by large or small polaron motion.
4. Conclusions
In summary, CsSnCl3 has been synthesized using the slow evaporation solution growth technique. Phase transformation (from monoclinic to cubic) has been assured by PXRD and DSC measurements and demonstrated by the study of the dielectric properties. The direct bandgap of this sample was 3.04 eV. A general investigation has been conducted on complex impedance, relative permittivity, complex modulus and AC conductivity for the 10−1–106 Hz frequency range with various temperatures. The frequency dependence of the AC conductivity which was explained by Jonscher's law has been researched as a function of temperature. The conduction mechanism which was interpreted by several models based on Elliott's theory might be assigned in phase 1 to tbibhe overlapping large polaron tunneling (OLPT) model and to the non-overlapping small polaron tunneling (NSPT) model in phase 2. The analysis of these various models (OLPT and NSPT) for which Elliott's variables were calculated suggested that the mobility of Cs+ ions ensured the alternative current conduction in CsSnCl3 via the tunneling mechanism.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for the financial support provided by the Ministry of Higher Education and Scientific Research of Tunisia. We would also like to express our thanks to Sabriya Mbarek, an English Language Teacher at the Faculty of Science - Sfax, Tunisia for proofreading this paper.References
- Q. Jiang, L. Q. Zhang, H. L. Wang, X. L. Yang, J. H. Meng, H. Liu, Z. G. Yin, J. L. Wu, X. W. Zhang and J. B. You, Nat. Energy, 2017, 2, 16177 CrossRef CAS.
- Q. Jiang, Y. Zhao, X. W. Zhang, X. L. Yang, Y. Chen, Z. M. Chu, Q. F. Ye, X. X. Li, Z. Z. Yin and J. B. You, Nat. Photonics, 2019, 13, 460 CrossRef CAS.
- W. Zhang, G. E. Eperon and H. J. Snaith, Nat. Energy, 2016, 1, 1 Search PubMed.
- P. Sadhukhan, S. Kundu, A. Roy, A. Ray, P. Maji, H. Dutta, S. K. Pradhan and S. Das, Cryst. Growth Des., 2018, 18, 3428 CrossRef CAS.
- S. Ananthakumar, J. R. Kumar and S. M. Babu, J. Photonics Energy, 2016, 6, 42001 CrossRef.
- P. Maji, A. Ray, P. Sadhukhan, A. Roy and S. Das, Mater. Lett., 2018, 227, 268 CrossRef CAS.
- A. Babayigit, et al., Sci. Rep., 2016, 6, 18721 CrossRef CAS PubMed.
- G. E. Eperon, et al., ACS Nano, 2015, 9, 9380 CrossRef CAS.
- A. Babayigit, et al., Nat. Mater., 2016, 15, 247 CrossRef CAS.
- M. Roknuzzaman and K. Ostrikov, et al., Sci. Rep., 2017, 7, 14025 CrossRef PubMed.
- L. Peedikakkandy and P. Bhargava, RSC Adv., 2016, 6, 19857 RSC.
- T. C. Jellicoe, et al., J. Am. Chem. Soc., 2016, 138, 2941 CrossRef CAS PubMed.
- H. Ayatullahah, et al., Acta Phys. Polym., 2013, 124, 102 CrossRef.
- L. Huang and W. R. L. Lambrecht, Phys. Rev. B, 2013, 88, 165203 CrossRef.
- X. Mao, L. Sun, T. Wu, T. Chu, W. Deng and K. Han, J. Phys. Chem. C, 2018, 122, 7670 CrossRef CAS.
- M. H. Kumar, S. Dharani, W. L. Leong, P. P. Boix, R. R. Prabhakar, T. Baikie, C. Shi, H. Ding, R. Ramesh, M. Asta, M. Graetzel, S. G. Mhaisalkar and N. Mathews, Adv. Mater., 2014, 26, 7122 CrossRef CAS PubMed.
- H. Xu, J. Duan, Y. Zhao, Z. Jiao, B. He and Q. Tang, J. Power Sources, 2018, 399, 76 CrossRef CAS.
- D. Sabba, H. K. Mulmudi, R. R. Prabhakar, T. Krishnamoorthy, T. Baikie, P. P. Boix, S. Mhaisalkar and N. Mathews, J. Phys. Chem. C, 2015, 119, 1763 CrossRef CAS.
- I. Chung, J.-H. Song, J. Im, J. Androulakis, C. D. Malliakas, H. Li, A. J. Freeman, J. T. Kenney and M. G. Kanatzidis, J. Am. Chem. Soc., 2012, 134, 8579 CrossRef CAS PubMed.
- F. Hao, C. C. Stoumpos, D. H. Cao, R. P. H. Chang and M. G. Kanatzidis, Nat. Photonics, 2014, 8, 489 CrossRef CAS.
- J. Islam and A. K. M. Akther Hossain, Sci. Rep., 2020, 10, 14391 CrossRef CAS PubMed.
- P. Maji, A. Ray, P. Sadhukhan, S. Chatterjee and S. Das, J. Appl. Phys., 2018, 124, 124102 CrossRef.
- S. Das and A. Ghosh, J. Phys. Chem. B, 2017, 121, 5422 CrossRef CAS PubMed.
- C. Tealdi, G. Chiodelli, L. Malavasi, G. Flor, C. Fisica, I. C. N. R. Unita, V. Taramelli and I. Pavia, J. Mater. Chem., 2004, 14, 3553 RSC.
- T. Paul and A. Ghosh, J. Appl. Phys., 2017, 121, 135106 CrossRef.
- See http://mill2.chem.ucl.ac.uk/tutorial/lmgp/celref.htm.
- F. R. Poulsen and S. E. Rasmussen, Acta Chem. Scand., 1970, 24, 150 CrossRef CAS.
- K. Yamada, Y. Kuranaga, K. Ueda, S. Goto, T. Okuda and Y. Furukawa, Bull. Chem. Soc. Jpn., 1998, 71, 127 CrossRef CAS.
- S. A. Khan, F. S. Al-Hazmi, S. Al-Heniti, A. S. Faidah and A. A. Al-Ghamdi, Curr. Appl. Phys., 2010, 10, 145 CrossRef.
- J. Lv, M. Xu, S. Lin, X. Shao, X. Zhang, Y. Liu, Y. Wang, Z. Chen and Y. Ma, Nano Energy, 2018, 51, 489 CrossRef CAS.
- N. Kobayashi, H. Kuwae, J. Oshima, R. Ishimatsu, S. Tashiro, T. Imato, C. Adachi, S. Shoji and J. Mizuno, J. Lumin., 2018, 200, 19 CrossRef CAS.
- R. Kalthoum, M. Ben Bechir and A. Ben Rhaiem, Phys. E, 2020, 124, 114235 CrossRef CAS.
- S. M. H. Qaid, B. A. Al-Asbahi, H. M. Ghaithan, M. S. AlSalhi and A. S. Al dwayyan, J. Colloid Interface Sci., 2020, 563, 426 CrossRef CAS PubMed.
- J. Tauc, in Amorphous and Liquid Semiconductors, ed. J. Tauc, Plenum Press, London and New York, 1974 Search PubMed.
- S. K. Gagandeep, B. S. Lark and H. S. Sahota, Nucl. Sci. Eng., 2000, 134, 208 CrossRef.
- G. S. Shahane, B. M. More, C. B. Rotti and L. P. Deshmukh, Mater. Chem. Phys., 1997, 47, 263 CrossRef CAS.
- D. Bhattacharya, S. Chaudhuri and A. K. Pal, Vacuum, 1992, 43, 313 CrossRef.
- H. Rahmouni, M. Smari, B. Cherif, E. Dhahri and K. Khirouni, Dalton Trans., 2015, 44, 10457 RSC.
- P. Maji, S. Chatterjee and S. Das, Ceram. Int., 2015, 45, 6012 CrossRef.
- D. K. Pattanayak, R. K. Parida, N. C. Nayak, A. B. Panda and B. N. Parida, J. Mater. Sci.: Mater. Electron., 2018, 29, 6215 CrossRef CAS.
- D. K. Pradhan, P. Misra, V. S. Puli, S. Sahoo, D. K. Pradhan and R. S. Katiyar, J. Appl. Phys., 2014, 115, 243904 CrossRef.
- A. Ray, A. Roy, S. De, S. Chatterjee and S. Das, J. Appl. Phys., 2018, 123, 104102 CrossRef.
- Y. Mateyshina, A. Slobodyuk, V. Kavun and N. Uvarov, Solid State Ionics, 2018, 324, 196 CrossRef CAS.
- A. Dhara, S. Sain, S. Das and S. K. Pradhan, Mater. Res. Bull., 2018, 97, 169 CrossRef CAS.
- T. Wang, J. Hu, H. Yang, L. Jin, X. Wei, C. Li, F. Yan and Y. Lin, J. Appl. Phys., 2017, 121, 084103 CrossRef.
- C. R. Cena, A. K. Behera and B. Behera, J. Adv. Ceram., 2016, 5, 84 CrossRef CAS.
- C. G. Koops, Phys. Rev., 1951, 83, 121 CrossRef CAS.
- M. Ahmad, M. A. Rafiq, K. Rasool, Z. Imran and M. M. Hasan, J. Appl. Phys., 2013, 113, 043704 CrossRef.
- P. Thongbai, S. Tangwancharoen, T. Yamwong and S. Maensiri, J. Phys.: Condens. Matter, 2008, 20, 395227 CrossRef.
- D. K. Rana, S. K. Singh, S. K. Kundu, S. Roy, S. Angappane and S. Basu, New J. Chem., 2019, 43, 3128 RSC.
- P. Thongbai, S. Tangwancharoen, T. Yamwong and S. Maensiri, J. Phys.: Condens. Matter, 2008, 20, 395227 CrossRef.
- S. Patra, P. Sengupta, A. Ray, A. Roy and S. Das, Ceram. Int., 2018, 44, 14236 CrossRef CAS.
- J. Liu, C.-G. Duan, W.-G. Yin, W. N. Mei, R. W. Smith and J. R. Hardy, J. Chem. Phys., 2003, 119, 2812 CrossRef CAS.
- X. Z. Zuo, J. Yang, B. Yuan, D. P. Song, X. W. Tang, K. J. Zhang, X. B. Zhu, W. H. Song, J. M. Dai and Y. P. Sun, J. Appl. Phys., 2015, 117, 114101 CrossRef.
- D. K. Rana, S. K. Singh, S. K. Kundu, S. Roy, S. Angappane and S. Basu, New J. Chem., 2019, 43, 3128 RSC.
- P. Sengupta, P. Sadhukhan, A. Ray, R. Ray, S. Bhattacharyya and S. Das, J. Appl. Phys., 2020, 127, 204103 CrossRef CAS.
- B. E. Jun, H. K. Kim, Y. H. Hwang, B. C. Choi, J. H. Jeong, J. S. Bae and C. H. Kim, J. Korean Phys. Soc., 2006, 49, 2408 CAS.
- D. K. Pradhan, P. Misra, V. S. Puli, S. Sahoo, D. K. Pradhan and R. S. Katiyar, J. Appl. Phys., 2014, 115, 243904 CrossRef.
- N. Vol, Nature, 1977, 267, 673 CrossRef.
- M. Ben bechir and A. Ben Rhaiem, Phys. E, 2021, 130, 114686 CrossRef CAS.
- M. Ben bechir and A. Ben Rhaiem, Phys. E, 2020, 120, 114032 CrossRef CAS.
- M. Ben bechir and A. Ben Rhaiem, J. Solid State Chem., 2021, 296, 122021 CrossRef CAS.
- M. Ben Bechir, K. Karoui, M. Tabellout, K. Guidara and A. Ben Rhaiem, J. Appl. Phys., 2014, 115, 203712 CrossRef.
- P. Maji, S. Chatterjee and S. Das, Ceram. Int., 2019, 5, 6012 CrossRef.
- M. Ben Bechir, K. Karoui, M. Tabellout, K. Guidara and A. Ben Rhaiem, J. Appl. Phys., 2014, 115, 153708 CrossRef.
| This journal is © The Royal Society of Chemistry 2021 |