TM₄B₁₈^0/− (TM = Hf, Ta, W, Re, Os): new structure construction with TM doped B wheel units

Abstract

We report the global search for the lowest energy structures of the transition metal (TM) doped B clusters, TM₄B₁₈^0/− (TM = Hf, Ta, W, Re, Os) and their electronic properties. A combination of the comprehensive genetic algorithm (CGA) method with density functional theory (DFT) calculations shows that they are composed of four planar TM@B₉ wheel units by sharing B atoms, except for Os₄B₁₈^0/−, which consists of two types of planar molecular wheels of Os@B₇ and Os@B₈. Among these nanoclusters, it is found that the Ta₄B₁₈ cluster has a closed-shell with a large HOMO–LUMO gap of 2.61 eV. Adaptive natural density partitioning analysis (AdNDP) reveals that the Ta₄B₁₈ cluster has σ antiaromaticity and π aromaticity, i.e., a conflicting aromaticity. The simulated photoelectron spectra (PES) of all anionic clusters are also provided for future experimental investigations.

---

1. Introduction

As an adjacent element of carbon (C), boron (B) has three valence electrons (2s²2p¹), and possesses a diverse and complex range of chemistry. Due to the characteristic of electron deficiency, B aggregates into various structures by sharing electrons and easily forms multicenter-two electron (mc–2e) bonds, which lead to various cluster structures.^1–3 In the past decade, combining experimental and theoretical calculations, it was found that small and medium-sized pure B clusters could have the planar,^4–6 quasi-planar,^7–9 double ring,^10,11 cage-like,^12–15 bilayer,^16,17 and core–shell¹⁸ structures. The B_n⁻ clusters possess the planar or quasi-planar structures form up to the size of n ∼ 38, whereas the neutral counterparts from n = 20 exhibit a transition from the planar to the double-ring tubular shape.¹⁹ The discoveries of planar B₃₆^0/−,⁹ fullerene-like B₄₀^0/− (ref. 15) and bilayer B₄₈^0/− (ref. 17) represent three major breakthroughs in the study of boron clusters. The planar B₃₆ proves the viability of monolayer boron sheets with hexagonal vacancies, which leads to the concept of borophene. The cage-like B₄₀ can be regarded as a boron analogue of C₆₀ (ref. 20) and the bilayer B₄₈ can be extended to a two-dimensional bilayer phase.¹⁶

Doping transition-metal (TM) atoms is known as an effective approach to stabilize pure B clusters and to change their geometries and electronic properties. Up to now, the doping of B clusters with different numbers of metal atoms has led to many novel structures, e.g. (i) planar molecular wheel,^21–23 (ii) half-sandwich,²⁴ inverse sandwich^25,26 and inverse triple-decker²⁷ clusters, (iii) drum-like structures,^28–30 (iv) the endohedral boron cages,^31–34 and (v) metallo-borospherenes.^35–38

Doping single TM atom into small-sized B clusters produces perfect TM-centered monocyclic B wheel clusters such as Co@B₈⁻,²¹ Rh@B₉⁻,²² and Ta@B₁₀⁻.²³ The 10 coordination number (CN) of Ta@B₁₀⁻ is known as the highest number among the planar species. With the increase of the number of B atoms, the structure growth pattern changes into the half-sandwich structures and the metal-centered B drum structures, such as Rh@B₁₂⁻,²⁴ Co@B₁₆⁻,²⁸ Rh@B₁₈⁻,²⁹ and Ta@B₂₀⁻.³⁰ Some highly stable endohedral B cages are also predicted by theoretical calculations, for example, Mo@B₂₂,³² W@B₂₄,³³ and Co@B₄₀⁻.³⁴

A new class of di-metal-doped inverse sandwich complexes, including La₂B₇⁻,²⁵ Pr₂B₈⁻,²⁶ and La₂B₉⁻,²⁵ have been observed by photoelectron spectra (PES) and density functional theory (DFT) calculations. Because of the unique (d–p)δ bond between metallic 5d orbitals and B_n rings, these lowest energy structures exhibit a higher level of stability than the other isomers. The first icosahedral clusters of M₂B₁₀ (M = Rh, Ir)³⁹ were found in the theoretical investigations. Moreover, the PES results combined with DFT calculations has confirmed that the La₃B₁₄⁻ cluster has a La–B₈–La–B₈–La inverse triple-decker structure, which is used to assemble 1D lanthanide B nanowires.²⁷ More recently, the first metallo-borospherenes La₃B₁₈⁻ and Tb₃B₁₈⁻ (D_3h)³⁵ were observed in the experiment, and the calculations confirmed that their structures are composed of two B₆ triangles linked together at their three corners with three B₂ units. The core–shell spherical trihedral metallo-borospherene La₃&[B₂@B₁₈]⁻ (ref. 36) and the smallest metallo-borospherene Ta₃B₁₂⁻ (ref. 37) were subsequently predicted. Among them, the D_3h Ta₃B₁₂⁻ compound is first metallo-borospherene with σ + π + δ triple aromaticity. The perfect core–shell La₄[B@B₄@B₂₄]^0/+/− clusters have been theoretically proposed to possess four equivalentinter-connected B₆ triangles on the cage surface.³⁸

In this work, we report the schematic study of the four TM atoms doped B₁₈ clusters, TM₄B₁₈^0/− (TM = Hf, Ta, W, Re, Os). These clusters can be thought that they are built up with four TM doped B wheel units by sharing B atoms on their peripheral ring. Among them, the bonding pattern shows this Ta₄B₁₈ has 50 skeleton electrons on the cage surface suggesting a spherical aromatic system with filled 1s + 1p + 1d + 2s + 1f + 2p + 2d molecular orbitals. It is also found that the ground-state structure of Ta₄B₁₈ shows a conflicting aromaticity.

2. Computational methods

The optimization of the lowest energy structures of TM₄B₁₈^0/− (TM = Hf, Ta, W, Re, Os) were conducted using our developed comprehensive genetic algorithm (CGA) code⁴⁰ incorporated with DFT calculations (CGA-DFT). The all-electron method with double-ζ numerical plus polarization d-function (DND) basis sets and the Perdew–Burke–Enzerhof (PBE) functional within the generalized gradient approximation (GGA)⁴¹ were used during each step of CGA using DMol³ package.⁴² Each structure was optimized without any symmetry constraint. The CGA code randomly generated sixteen initial parent configurations for each cluster system. The new structures were created by mating, perturbation, and exchange of the atom type of a pair of different types of atoms.⁴³ In order to achieve the global minimum of potential energy surface (PES), all cluster systems had at least 3000 iterations.

After the global search of CGA-DFT, the low-energy isomers were more accurately optimized by Gaussian16 program⁴⁴ for TM₄B₁₈^0/− (TM = Hf, Ta, W, Re, Os). The previous studies proved the feasibility of the PBE0 functional⁴⁵ to describe the energy differences between different isomers of TM doped B clusters.^{35,37,39,46–48} Moreover, our previous study of the single TM atom doped B_n (n = 7–10) clusters⁴⁹ also confirmed that PBE0 functional can precisely describe the interactions between TM atom and B atom by comparing with the high-level CCSD(T)⁵⁰ results. For basis set, the 6-311G* was proved enough to describe B atom in our study of pure boron clusters.⁵¹ We further calculated the equilibrium bond lengths and vibrational frequencies of TM (TM = Hf, Ta, W, Re, Os) dimer under the different basis sets and found that the def2-TZVP basis set is more suitable for TM atom (see Table S1†). Therefore, PBE0 functional combined with 6-311G* basis set for B and def2-TZVP basis set for TM atoms were chosen for our systems. Furthermore, chemical bonding analyses were performed using the adaptive natural density partitioning (AdNDP 2.0) program.⁵²

3. Results and discussion

3.1. Lowest energy structures of TM₄B₁₈^0/− (TM = Hf, Ta, W, Re, Os)

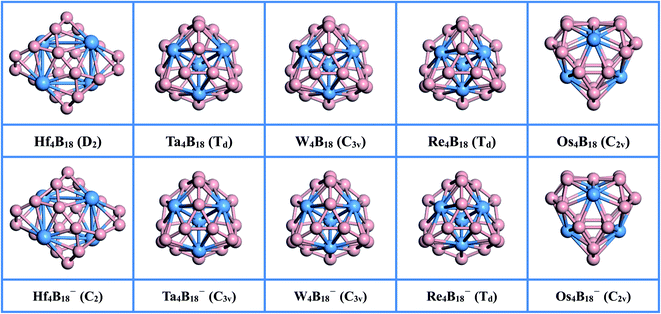
The optimized lowest energy structures of neutral TM₄B₁₈ (TM = Hf, Ta, W, Re, Os) clusters and corresponding anionic species, along with their point group symmetries with 0.1 Å tolerance, are presented in Fig. 1. More information about the low-lying isomer structures is given in Fig. S1 of the ESI.† The summary of the structural and electronic properties of the ground state in both neutral and anionic series is listed in Table 1. All ground states are found to be singlet or doublet with exception of the Re₄B₁₈ cluster, which has the triplet states of spin multiplicity.

Fig. 1 The lowest energy structures of TM₄B₁₈ (TM = Hf, Ta, W, Re, Os) clusters (upper panel) and corresponding anionic clusters (lower panel). The point group symmetry of each cluster is presented in parentheses. The blue and pink spheres are TM and B, respectively.

Table 1 The structural and electronic properties of TM₄B₁₈^0/− (TM = Hf, Ta, W, Re, Os) clusters. The minimum and maximum distances between TM atoms, between TM and B, and between B atoms are shown with their average distance values (R_TM–TM, R_TM–B, and R_B–B, respectively in Å). The average charge transfer the TM atom to the B cage (Q_TM, in |e|), binding energies per atom (E_b, in eV), HOMO–LUMO energy gap (E_HL, in eV), and the lowest vibrational frequency (ω_min, in cm⁻¹) are also presented

	Min–Max (RTM–TM)	Min–Max (RTM–B)	Min–Max (RB–B)	QTM	Eb	EHL	ωmin
Hf4B18 (D2)	3.132–3.560 (3.346)	2.378–2.458 (2.419)	1.533–1.783 (1.635)	1.148	5.80	2.60	120.33
Hf4B18^− (C2)	3.106–3.541 (3.324)	2.379–2.468 (2.421)	1.537–1.792 (1.640)	1.007	5.89	1.54	64.17
Ta4B18 (Td)	3.011 (3.011)	2.351–2.358 (2.353)	1.565–1.697 (1.631)	0.487	6.02	2.61	158.80
Ta4B18^− (C3v)	2.946–3.073 (3.010)	2.332–2.378 (2.358)	1.565–1.701 (1.634)	0.383	6.13	1.70	121.59
W4B18 (C3v)	2.609–2.912 (2.761)	2.294–2.365 (2.333)	1.555–1.720 (1.629)	0.068	6.16	2.41	136.90
W4B18^− (C3v)	2.666–2.831 (2.749)	2.315–2.352 (2.332)	1.562–1.706 (1.629)	−0.042	6.30	1.87	126.07
Re4B18 (Td)	2.571–2.574 (2.573)	2.298–2.359 (2.319)	1.568–1.694 (1.629)	−0.166	6.10	1.85	216.66
Re4B18^− (Td)	2.541–2.561 (2.554)	2.289–2.391 (2.326)	1.570–1.712 (1.639)	−0.189	6.26	1.37	153.41
Os4B18 (C2v)	—	2.104–2.250 (2.170)	1.564–1.766 (1.681)	−0.089	5.95	1.69	102.89
Os4B18^− (C2v)	—	2.108–2.278 (2.170)	1.576–1.759 (1.687)	−0.190	6.09	1.55	111.05

---

As shown in the upper panel of Fig. 1, the lowest energy configuration of the neutral Hf₄B₁₈ has D₂ symmetry and it is composed of four twisted umbrella-like Hf@B₉ units by sharing the B atoms on their rings. The distances between the Hf atoms are in the range of 3.132 to 3.560 Å, and the average bond length between metal atoms (R_TM–TM) is 3.346 Å. The bonding lengths between each Hf atom and its neighboring B atoms are in between 2.378 and 2.458 Å, and the average bond length between metal atom and B (R_TM–B) is 2.419 Å. The distances between B atoms are in between 1.533 and 1.783 Å, which smallest value is slightly shorter than the B=B double bond (1.56 Å)⁵³ and the largest value is longer than the typical B–B single bond (1.70 Å).⁵³ Besides, the natural population analysis (NPA) shows that each Hf serves as the donor of 1.148 |e| to the B₁₈ skeleton, implying the formation of typical charge-transfer Hf₄⁴⁺B₁₈⁴⁻ complexes.

The Ta₄B₁₈ forms a structure with the highly-symmetric point group of T_d with the electronic state of ¹A₁. The Ta₄B₁₈ is composed of the previously reported the four planar molecular Ta@B₉ wheels⁴⁷ by sharing the B atoms on the rings. The total energy of this structure is much lower than the second low-lying isomers (C₂) by 1.114 eV at the levels of PBE0/TZVP (see Fig. S1†). The interatomic distance between Ta atoms is 3.011 Å. The bonding lengths between each Ta atom and B atoms are in the range of 2.351 to 2.358 Å, which are slightly shorter than those in the freestanding Ta@B₉ (2.39 Å),⁴⁷ and the lengths between adjacent B atoms (1.565–1.697 Å) are longer than Ta@B₉ (1.54 Å)⁴⁷ at the PBE0 levels, suggesting that doping more Ta atom weakens the interaction between B atoms and strengthen the Ta and B bonding. The Ta₄B₁₈ also can be regarded as the Ta₄ cluster in the middle bonded with the B atoms. We found that the lowest energy structure of Ta₄ cluster has a tetrahedral structure with T_d symmetry and its bonding length is 2.541 Å, which is significantly shorter than that of Ta₄ moiety (3.011 Å) in Ta₄B₁₈. It shows that the strong interaction between Ta and B atoms weakens the bonding strength between Ta atoms, resulting in longer lengths. Moreover, NPA shows each Ta atom donates 0.487 |e| to the B₁₈ skeleton forming a covalent bond due to the larger B electronegativity.

For the lowest energy structures of W₄B₁₈ and Re₄B₁₈, their geometric configurations are very similar to the Ta₄B₁₈ cluster. Doping Re atoms into the B₁₈ framework leads to a magnetic cluster Re₄B₁₈ (T_d) with the triplet states of spin multiplicity. The influence of atomic radius and magnetic moment makes it have a higher symmetry than W₄B₁₈ (C_3v). The average distances of W₄B₁₈ between W atoms (R_TM–TM), and between W and B atoms (R_TM–B), are 2.761 and 2.333 Å, respectively. For the Re₄B₁₈ cluster, the R_TM–TM and R_TM–B are 2.573 Å and 2.319 Å, respectively. It can be seen that R_TM–TM and R_TM–B of the Re₄B₁₈ cluster are shorter than those of the W₄B₁₈ cluster, but the average bond length between B atoms (R_B–B) is the same (1.629 Å). For Re₄B₁₈, compared with the previously reported planar molecular wheel Re@B₉,⁵⁴ we find that the bonding length of Re₄B₁₈ (1.568–1.694 Å) between adjacent B atoms are longer than the Re@B₉ (1.543–1.571 Å) at the PBE0 levels.

The optimized structure of Os₄B₁₈ is a hollow cage-like structure with C_2v symmetry, which is very different from the other TM₄B₁₈ (TM = Hf, Ta, W, Re) clusters. The Os₄B₁₈ is insufficient to support the large spherical B skeleton due to the further reduction of metal atomic radius. Therefore, the lowest energy structure of cage-like Os₄B₁₈ is assembled by two types of planar molecular wheels of Os@B₇ and Os@B₈, and the Os atoms on cage surface with the coordination numbers (CN) are 7 and 8. Moreover, the bonding length between B atoms are in the range of 1.564 to 1.766 Å, and the average (R_B–B) is 1.681 Å, which is very close to the single bond value. The bonding lengths between each Os atom and its neighboring B atom are in the range of 2.104–2.250 Å, and the R_TM–B is 2.170 Å. It can be seen from Table 1 that the average distance between Os and B atoms (R_TM–B) becomes shorter rapidly when the size of metal atom decreases, which leads to a tighter bond between the TM and B atom. The coordinates of the lowest energy structures of TM₄B₁₈ (TM = Hf, Ta, W, Re, Os) are listed in Table S2 of the ESI.†

All corresponding global minima of anionic clusters are exhibited in the lower panel of Fig. 1. The geometric structures of TM₄B₁₈⁻ (TM = Hf, Ta, W, Re, Os) are very similar to their corresponding neutral clusters. However, owing to the Jahn–Teller effect, the capture of one additional electron results in the low point group symmetries for Hf and Ta. The lowest energy structure of Hf₄B₁₈⁻ has C₂ symmetry, and each Hf atom transfers fewer electrons (1.007 |e|) to the B₁₈ skeleton than the neutral. The structures of TM₄B₁₈⁻ (TM = Ta, W, Re) are very similar like the neutral ones and consist of planar molecular wheels of the TM@B₉ unit. However, compared with the corresponding neutral clusters, their R_TM–TM is shorter and R_B–B is slightly longer. NPA shows each TM atom donates electrons to the B₁₈ skeleton in the range of −0.189 |e| to 0.383 |e|, which forms the typical covalent bonds. The structure of Os₄B₁₈⁻ (C_2v) is also a hollow cage-like structure, its R_TM–B and R_B–B are little changed. The coordinates of all anionic clusters are listed in Table S3 of the ESI.† The TM₄B₁₈^0/− (TM = Hf, Ta, W, Re, Os) clusters can be thought that they are constructed with four TM doped B wheel units by sharing B atoms. This approach could be a new pathway to produce various TM doped B cluster structures.

To gain a better understanding of the stability of these nanoclusters, we further examined the electronic properties. The binding energies per atom (E_b) is regarded as an effective parameter to evaluate the thermodynamic stability of a cluster, which is calculated by

E_b = (4E_TM + 18E_B − E_TM4B18^−/0)/22 (1)

In the eqn (1), E_TM4B18^−/0, E_TM and E_B represent the total energy of TM₄B₁₈^−/0 (TM = Hf, Ta, W, Re, Os) clusters, a TM atom, and a B atom, respectively. Here, the larger E_b value implies the more favorable thermodynamic stability of a cluster. In neutral clusters, the W₄B₁₈ has a maximum E_b value of 6.16 eV, while the Hf₄B₁₈ has a minimum E_b value (5.80 eV). The E_b values of TM₄B₁₈ (Ta, W, Re) are larger than those of others, so these clusters have a higher thermodynamic stability. The same trend is observed for the corresponding anions. As a reflection of the energy cost for an electron jumping from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO), the HOMO–LUMO energy gap (E_HL) can reveal the chemical stability of a cluster. In comparison with cage-like Ta₃B₁₂⁻ which possess a E_HL of 2.50 eV with three equivalent Ta@B₈ octagons sharing two eclipsed B₃ triangles at the top and bottom interconnected by three B₂ units on the waist,³⁷ the lowest energy structures of Hf₄B₁₈ and Ta₄B₁₈ possess a large E_HL of 2.60 and 2.61 eV, respectively, being less chemically reactive than others. For all anionic clusters, due to the trapping of an electron, the E_HL of these species is decreased and significantly less than the neutral clusters. Among them, the W₄B₁₈⁻ cluster has the largest E_HL value of 1.87 eV, while the E_HL of the Re₄B₁₈⁻ cluster is the smallest, only 1.37 eV. Moreover, vibrational frequency calculations confirm that there are no imaginary frequencies for all these ground-state structures, and the corresponding lowest frequencies are listed in Table 1.

3.2. Bonding analysis

The structural and electronic properties of TM₄B₁₈^0/−(TM = Hf, Ta, W, Re, Os) nanoclusters shows that the neutral Ta₄B₁₈ and Hf₄B₁₈ clusters are chemically more inert than the others (larger E_HL)⁵⁵ but relatively the Ta₄B₁₈ has larger E_b (thermodynamically more stable)⁵⁶ than Hf₄B₁₈. Based on this analysis, we further investigate the bonding properties of the Ta₄B₁₈ cluster. The molecular orbital (MO) energy-level diagram and the relevant MOs of Ta₄B₁₈ derived from the Ta₄ moiety and B₁₈ skeleton, which is presented in Fig. 2. It shows the interactions between the orbitals of the four Ta atoms and the group orbitals of the B₁₈ skeleton. Among them, LUMO, HOMO and HOMO − n represent the energy-levels of the Ta₄B₁₈ cluster, respectively. LUMO′, LUMO + n′, HOMO′ and HOMO − n′ represent the energy-levels of Ta₄ moiety. LUMO′′, LUMO + n′′, HOMO′′ and HOMO − n′′ represent the energy-levels of the B₁₈ skeleton. Since the global minimum of B₁₈ is a planar structure, the stabilization of the 3D B₁₈ framework is entirely due to its strong bonding with the Ta₄ moiety. The 3D B₁₈ skeleton has a small HOMO–LUMO gap of 0.85 eV. The addition of four Ta atoms results in a closed-shell Ta₄B₁₈ with a large HOMO–LUMO gap of 2.61 eV. It is noted that the T_d symmetry of Ta₄B₁₈ leads to the feature level of LUMO, HOMO, HOMO − 1 and HOMO − 2 are triple degenerates. Furthermore, we find that the LUMO + 2′ of Ta₄ moiety is unoccupied and mainly becomes the LUMO orbital of Ta₄B₁₈. For the occupied MOs of Ta₄B₁₈, HOMO, HOMO − 1 and HOMO − 2 are formed from LUMO + 2′′ (σ orbits), LUMO + 3′′ (σ orbits), and HOMO − 1′′ (π orbits) of B₁₈ framework, respectively. The HOMO − 3 is a σ + π hybrid orbital, which derives from the mixing of LUMO + 1′ (π orbit) with LUMO + 1′′ (σ orbit). The HOMO − 4 of σ + σ hybrid orbital is formed from two σ orbit of HOMO − 2′ and HOMO − 4′′. Moreover, the Ta atom in Ta₄B₁₈ has total on-site Wiberg bond order (WBO) of 5.82, which well supporting the spherical coordination interactions between Ta₄ moiety and B₁₈ skeleton.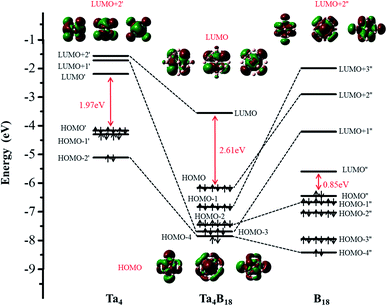

Fig. 2 The Kohn–Sham molecular orbital correlation diagram for Ta₄B₁₈. It shows the interactions between the orbitals of the Ta₄ atoms and the group orbitals of the B₁₈ skeleton.

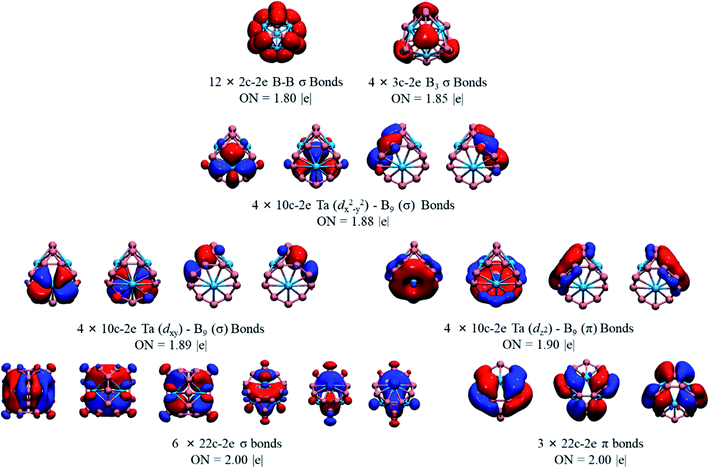
We also performed a chemical bonding analysis of the spherical Ta₄B₁₈ using the AdNDP method. As depicted in Fig. 3, the Ta₄B₁₈ cluster contains 12 localized bonds and 25 delocalized bonds, ordered by occupation number (ON) ranging from 1.80 |e| to 2.00 |e|. The 12 localized B–B bonds are all 2c–2e σ bonds on the peripheral edge of the B₁₈ skeleton, which are mainly composed of B 2s/2p electrons, and their ONs are 1.80 |e|. Among the 25 delocalized bonds, there are 4 equivalent 3c–2e σ bonds on the B₃ triangles (ON = 1.85 |e|). The three sets of the delocalized 10c–2e Ta–B₉ bonds (ON = 1.88–1.90 |e|) over the boron skeleton, which includes 4 equivalent Ta (d_x²−y²)–B₉ (σ) bonds, 4 equivalent Ta (d_xy)–B₉ (σ) bonds, and 4 equivalent Ta (d_z²)–B₉ (π) bonds. As shown in the bottom row of Fig. 3, there are 9 totally delocalized 22c–2e bonds distributed on the entire spherical skeleton with ON = 2.00 |e|. Among them, 6 are σ and the other 3 are π bonds. Therefore, the Ta₄B₁₈ cluster has 10 delocalized σ bonds in total (4 equivalent 3c–2e σ bonds plus 6 equivalent 22c–2e bonds), leading to the σ antiaromaticity according to 4n (n = 5) Hückel's rule. Meanwhile, the 3 totally delocalized π-bonds (22c–2e bonds) satisfies the Hückel rules of 4n + 2 (n = 1) of π aromaticity. Thus, Ta₄B₁₈ is a conflicting aromatic system with 20 σ and 6 π totally delocalized electrons. Note that 50 skeletal electrons are distributed on the cage surface is a magic number for a closed-shell three-dimensional spherical structure in which the 25 delocalized orbitals are completely filled with electron pairs leading to a closed-shell 1S²1P⁶1D¹⁰2S²1F¹⁴2P⁶2D¹⁰ configuration.

Fig. 3 AdNDP bonding patterns of Ta₄B₁₈, with the occupation numbers (ON).

3.3. Simulated photoelectron spectra of TM₄B₁₈⁻ (TM = Hf, Ta, W, Re, Os)

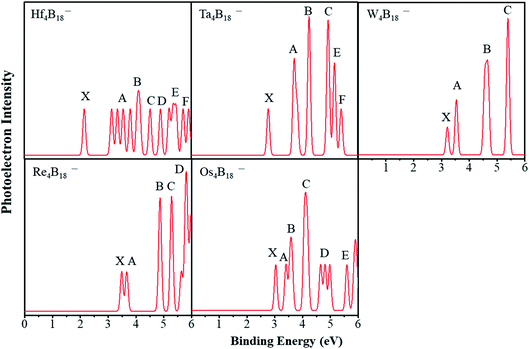
Photoelectron spectra (PES) can be used as the fingerprints about the electronic structures of nanoclusters. Therefore, we simulated the PES of TM₄B₁₈⁻ (TM = Hf, Ta, W, Re, Os) anionic clusters, hoping to help experimentally determine these lowest energy structures.

First, we consider the simulated PES of Ta₄B₁₈⁻ and Re₄B₁₈⁻ by comparing with the experimentally reported of Ta@B₉⁻ and Re@B₉⁻. As displayed in Fig. 4, the spectral features are labeled X, A, B, etc. In each spectrum, the X peak represents the vertical detachment energy (VDE) which denotes the transition from the anionic ground-state to the neutral ground-state, and the other (A, B, etc.) peaks indicate transitions to the excited state of the neutral complexes. The VDE of Ta₄B₁₈⁻ is approximately 2.77 eV. After this first peak, there are five peaks between 3.5 eV and 5.5 eV. In the experimental spectrum of Ta@B₉⁻, the first X peak is located at around 3.64 eV,⁴⁷ indicating the structure of Ta₄B₁₈⁻ assembled by Ta@B₉⁻ has the lower electron binding energy. For the simulated spectrum of Re₄B₁₈⁻, the first two peaks are somewhat weak and close each other. The experimental PES of Re@B₉⁻ also shows two close peaks at 4.02 eV and 4.34 eV,⁵⁴ respectively. These lower binding energies of Re₄B₁₈⁻ are similar to those of Ta₄B₁₈⁻ by comparison with the experimental results. Presumably, this is caused by the interaction between planar molecular unit wheels (Ta@B₉ and Re@B₉).

Fig. 4 The simulated photoelectron spectra of TM₄B₁₈⁻ (TM = Hf, Ta, W, Re, Os) clusters.

The PES of Hf₄B₁₈⁻ is simulated and shows a compact spectral pattern, and the first peak is approximately 2.16 eV, following by four consecutive peaks of the same intensity. There are four major peaks (X, A, B and C) of the simulated spectrum of W₄B₁₈⁻, and the VDE is approximately 3.19 eV. The simulated spectrum of Os₄B₁₈⁻ also presents a compact spectral pattern with a VDE of 3.02 eV. To provide detailed data for the future experiment, we further calculated the vertical ionization potentials (VIP) and vertical electron affinities of neutral clusters, and adiabatic detachment energy (ADE) of anionic clusters, which are shown in Table 2. The W₄B₁₈ shows a larger VIP value (7.52 eV) and VEA value (2.82 eV) than others. The Re₄B₁₈ shows a larger ADE value of 3.07 eV than others. However, the spherical Ta₄B₁₈ has a large VIP value (7.37 eV) and a moderate VEA value (2.46 eV).

Table 2 Vertical ionization potentials (VIP), vertical electron affinities (VEA), vertical detachment energy (VDE), and adiabatic detachment energy (ADE) of TM₄B₁₈^0/− (TM = Hf, Ta, W, Re, Os) clusters. All energies are in eV

	VIP^a	VEA^b		VDE^c	ADE^d
a Vertical ionization energy from the ground state of the neutral to the ground state of the cation.b Vertical electronic affinity from the ground state of the neutral to the ground state of the anion.c Vertical detachment energy from the ground state of the anion to the ground state of the neutral.d Adiabatic detachment energy from the ground state of the anion to the ground state of the neutral.
Hf4B18 (D2)	6.65	1.53	Hf4B18^− (C2)	2.16	1.88
Ta4B18 (Td)	7.37	2.46	Ta4B18^− (C3v)	2.77	2.65
W4B18 (C3v)	7.52	2.82	W4B18^− (C3v)	3.19	3.01
Re4B18 (Td)	7.25	2.13	Re4B18^− (Td)	3.49	3.07
Os4B18 (C2v)	6.77	2.90	Os4B18^− (C2v)	3.02	2.97

---

4. Conclusion

We carried out unbiased search for the lowest energy structures of TM₄B₁₈^0/− clusters (TM = Hf, Ta, W, Re, Os). The structural analysis shows that they are composed of the four planar molecular TM@B₉ wheel units sharing the B atoms except for Os₄B₁₈^0/−, which has a hollow cage-like structure assembled by two types of planar molecular wheels of Os@B₇ and Os@B₈ due to the reduction of the atomic radius. According the electronic properties, spherical Ta₄B₁₈ has large E_b and E_HL. The chemical bonding analyses showed that it has the σ antiaromaticity with 4n (n = 5) and π aromaticity with 4n + 2 (n = 1) from Hückel's rule, resulting in a conflicting aromatic system. Finally, the PES of all anionic clusters was simulated which provides predictive information for future experimental investigations.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Research Funds for the Central Universities of China (DUT20RC(5)014), and the Supercomputing Center of Dalian University of Technology.

References

1. A. I. Boldyrev and L.-S. Wang, Phys. Chem. Chem. Phys., 2016, 18, 11589–11605.
2. J. Zhao, Q. Du, S. Zhou and V. Kumar, Chem. Rev., 2020, 120, 9021–9163.
3. D. Li, J. Gao, P. Cheng, J. He, Y. Yin, Y. Hu, L. Chen, Y. Cheng and J. Zhao, Adv. Funct. Mater., 2020, 30, 1904349.
4. H.-J. Zhai, A. N. Alexandrova, K. A. Birch, A. I. Boldyrev and L. Wang, Angew. Chem., Int. Ed., 2003, 42, 6004–6008.
5. A. P. Sergeeva, D. Y. Zubarev, H.-J. Zhai, A. I. Boldyrev and L.-S. Wang, J. Am. Chem. Soc., 2008, 130, 7244–7246.
6. W. Huang, A. P. Sergeeva, H.-J. Zhai, B. B. Averkiev, L.-S. Wang and A. I. Boldyrev, Nat. Chem., 2010, 2, 202–206.
7. W.-L. Li, Y.-F. Zhao, H.-S. Hu, J. Li and L.-S. Wang, Angew. Chem., Int. Ed., 2014, 126, 5646–5651.
8. W.-L. Li, Q. Chen, W.-J. Tian, H. Bai, Y.-F. Zhao, H.-S. Hu, J. Li, H.-J. Zhai, S.-D. Li and L.-S. Wang, J. Am. Chem. Soc., 2014, 136, 12257–12260.
9. Z. A. Piazza, H.-S. Hu, W.-L. Li, Y.-F. Zhao, J. Li and L.-S. Wang, Nat. Commun., 2014, 5, 3113.
10. B. Kiran, S. Bulusu, H.-J. Zhai, S. Yoo, X. C. Zeng and L.-S. Wang, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 961–964.
11. X. Wu, L. Sai, S. Zhou, P. Zhou, M. Chen, M. Springborg and J. Zhao, Phys. Chem. Chem. Phys., 2020, 22, 12959–12966.
12. J. Zhao, X. Huang, R. Shi, H. Liu, Y. Su and R. B. King, Nanoscale, 2015, 7, 15086–15090.
13. Y.-J. Wang, Y.-F. Zhao, W.-L. Li, T. Jian, Q. Chen, X.-R. You, T. Ou, X.-Y. Zhao, H.-J. Zhai, S.-D. Li, J. Li and L.-S. Wang, J. Chem. Phys., 2016, 144, 064307.
14. J. Lv, Y. Wang, L. Zhu and Y. Ma, Nanoscale, 2014, 6, 11692–11696.
15. H.-J. Zhai, Y.-F. Zhao, W.-L. Li, Q. Chen, H. Bai, H.-S. Hu, Z. A. Piazza, W.-J. Tian, H.-G. Lu, Y.-B. Wu, Y.-W. Mu, G.-F. Wei, Z.-P. Liu, J. Li, S.-D. Li and L.-S. Wang, Nat. Chem., 2014, 6, 727–731.
16. L. Sai, X. Wu, N. Gao, J. Zhao and R. B. King, Nanoscale, 2017, 9, 13905–13909.
17. W.-J. Chen, Y.-Y. Ma, T.-T. Chen, M.-Z. Ao, D.-F. Yuan, Q. Chen, X.-X. Tian, Y.-W. Mu, S.-D. Li and L.-S. Wang, Nanoscale, 2021, 13, 3868–3876.
18. J. Zhao, L. Wang, F. Li and Z. Chen, J. Phys. Chem. A, 2010, 114, 9969–9972.
19. T. Jian, X. Chen, S.-D. Li, A. I. Boldyrev, J. Li and L.-S. Wang, Chem. Soc. Rev., 2019, 48, 3550–3591.
20. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163.
21. C. Romanescu, T. R. Galeev, W.-L. Li, A. I. Boldyrev and L.-S. Wang, Angew. Chem., Int. Ed., 2011, 50, 9334–9337.
22. W.-L. Li, C. Romanescu, T. R. Galeev, Z. A. Piazza, A. I. Boldyrev and L.-S. Wang, J. Am. Chem. Soc., 2012, 134, 165–168.
23. C. Romanescu, T. R. Galeev, W.-L. Li, A. I. Boldyrev and L.-S. Wang, Acc. Chem. Res., 2013, 46, 350–358.
24. I. A. Popov, W.-L. Li, Z. A. Piazza, A. I. Boldyrev and L.-S. Wang, J. Phys. Chem. A, 2014, 118, 8098–8105.
25. T.-T. Chen, W.-L. Li, J. Li and L.-S. Wang, Chem. Sci., 2019, 10, 2534–2542.
26. W.-L. Li, T.-T. Chen, D.-H. Xing, X. Chen, J. Li and L.-S. Wang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6972–E6977.
27. T.-T. Chen, W.-L. Li, W.-J. Chen, J. Li and L.-S. Wang, Chem. Commun., 2019, 55, 7864–7867.
28. I. A. Popov, T. Jian, G. V. Lopez, A. I. Boldyrev and L.-S. Wang, Nat. Commun., 2015, 6, 8654.
29. T. Jian, W.-L. Li, X. Chen, T.-T. Chen, G. V. Lopez, J. Li and L.-S. Wang, Chem. Sci., 2016, 7, 7020–7027.
30. W.-L. Li, T. Jian, X. Chen, H.-R. Li, T.-T. Chen, X.-M. Luo, S.-D. Li, J. Li and L.-S. Wang, Chem. Commun., 2017, 53, 1587–1590.
31. P. Jin, Q. Hou, C. Tang and Z. Chen, Theor. Chem. Acc., 2015, 134, 13.
32. Y. Wang, X. Wu and J. Zhao, J. Cluster Sci., 2018, 29, 847–852.
33. J. Lv, Y. Wang, L. Zhang, H. Lin, J. Zhao and Y. Ma, Nanoscale, 2015, 7, 10482–10489.
34. J. Liu, Y. Zhang, C. Li, W. Jin, G. Lefkidis and W. Hübner, Phys. Rev. B, 2020, 102, 024416.
35. T.-T. Chen, W.-L. Li, W.-J. Chen, X.-H. Yu, X.-R. Dong, J. Li and L.-S. Wang, Nat. Commun., 2020, 11, 2766.
36. X.-Y. Zhao, M. Yan, Z. Wei and S.-D. Li, RSC Adv., 2020, 10, 34225–34230.
37. Y. Zhang, X.-Y. Zhao, M. Yan and S.-D. Li, RSC Adv., 2020, 10, 29320–29325.
38. X.-Q. Lu, C.-Y. Gao, Z. Wei and S.-D. Li, J. Mol. Model., 2021, 27, 130.
39. W.-y. Liang, J. Barroso, S. Jalife, M. a. Orozco-Ic, X. Zarate, X. Dong, Z.-h. Cui and G. Merino, Chem. Commun., 2019, 55, 7490–7493.
40. J. Zhao, R. Shi, L. Sai, X. Huang and Y. Su, Mol. Simul., 2016, 42, 809–819.
41. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
42. B. Delley, J. Chem. Phys., 2000, 113, 7756–7764.
43. L. Sai, L. Tang, J. Zhao, J. Wang and V. Kumar, J. Chem. Phys., 2011, 135, 184305.
44. M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson and H. Nakatsuji, Gaussian 16, Revision A. 03, Gaussian. Inc., Wallingford CT, 2016.
45. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
46. W.-L. Li, A. S. Ivanov, J. Federic, C. Romanescu, I. Cernušák, A. I. Boldyrev and L.-S. Wang, J. Chem. Phys., 2013, 139, 104312.
47. C. Romanescu, T. R. Galeev, W.-L. Li, A. I. Boldyrev and L.-S. Wang, J. Chem. Phys., 2013, 138, 134315.
48. B. L. Chen, W. G. Sun, X. Y. Kuang, C. Lu, X. X. Xia, H. X. Shi and G. Maroulis, Inorg. Chem., 2018, 57, 343–350.
49. X. Wu, Y. Wang, X. Zhao, S. Zhou, S. Li, M. Chen and J. Zhao, Eur. Phys. J. Plus, 2021, 136, 328.
50. G. D. Purvis and R. J. Bartlet, J. Chem. Phys., 1982, 76, 1910.
51. F. Li, P. Jin, D.-e. Jiang, L. Wang, S. B. Zhang, J. Zhao and Z. Chen, J. Chem. Phys., 2012, 136, 074302.
52. N. V. Tkachenko and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2019, 21, 9590–9596.
53. P. Pyykkö, J. Phys. Chem. A, 2015, 119, 2326–2337.
54. T.-T. Chen, W.-L. Li, H. Bai, W.-J. Chen, X.-R. Dong, J. Li and L.-S. Wang, J. Phys. Chem. A, 2019, 123, 5317–5324.
55. J.-L. Bredas, Mater. Horiz., 2014, 1, 17–19.
56. M. Rahm, T. Zeng and R. Hoffmann, J. Am. Chem. Soc., 2019, 141, 342–351.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra02525b

---