Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Crystal engineering with copper and melamine†
Ignacio Bernabé Vírseda a,
Shiraz Ahmed Siddiqui
a,
Shiraz Ahmed Siddiqui b,
Alexander Prado-Rollerc,
Michael Eistererd and
Hidetsugu Shiozawa
b,
Alexander Prado-Rollerc,
Michael Eistererd and
Hidetsugu Shiozawa *ab
*ab
aJ. Heyrovsky Institute of Physical Chemistry, Czech Academy of Sciences, Dolejskova 3, 182 23 Prague 8, Czech Republic. E-mail: hide.shiozawa@jh-inst.cas.cz; Tel: +420-26605-3755
bFaculty of Physics, University of Vienna, Boltzmanngasse 5, 1090 Vienna, Austria. E-mail: hidetsugu.shiozawa@univie.ac.at; Fax: +43-1-4277-9726; Tel: +43-1-4277-72601
cInstitute of Inorganic Chemistry, Faculty of Chemistry, University of Vienna, Währinger Straße 42, Austria
dAtominstitut, TU Wien, Stadionallee 2, 1020 Vienna, Austria
First published on 7th July 2021
Abstract
Coordination complexes and polymers are central in inorganic and materials chemistry as a variety of metal centers and coordination geometries lead to a diverse range of interesting properties. Here, size and structure control of gem-like quality monocrystals is demonstrated at room temperature. Using the same set of precursors, the copper-to-melamine molar ratio is adjusted to synthesize either a novel coordination complex of dinuclear copper and melamine (Cu2M1), or a barely-studied coordination polymer of zigzag copper–chlorine chains (Cu4M1). Crystals of the former are dark green and square with a size up to 350 μm across. The latter is light green, octagonal, and as large as 5 mm across. The magnetic properties of both crystals reflect the low-dimensional arrangements of copper. The magnetic susceptibility of Cu2M1 is modelled with a spin-1/2 dimer, and that of Cu4M1 with a spin-1/2 one-dimensional Ising chain. Controlled synthesis of such quality magnetic crystals is a prerequisite for various magnetic and magneto-optical applications.
Advanced crystal engineering continues to draw the attention of the scientific community. This discipline is leading to new crystalline materials, and is focusing on finding strategies and logical ways to control their properties. Coordination chemistry plays an important role in crystal engineering as it allows the creation of various coordination compounds, e.g. metal complexes, coordination polymers or metal–organic frameworks, by designing the coordination between ligands and metal ions.1–3 While the d orbitals of the metal ions promote directional bonding, there has been widespread use of polyamines, carboxylates, pyridyl and cyano groups as ligands.4
Coordination compounds are considered useful in a great deal of applications, such as energy transfer, gas storage and separation, heterogeneous catalysis, proton conduction, biomedical applications and chemical sensing.5,6 Molecular magnets based on coordination compounds play an essential role in information storage in quantum computing.7 Single crystals based on Mn and Fe can serve as information storage elements in a dynamic random-access memory device in which decoding and reading the information could be realized by fast electron spin resonance pulses.8
In the present paper, it is demonstrated how molar ratios can affect reactions among precursor solutes and solvents. As an example, copper chloride and melamine are dissolved in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of methanol and dimethyl sulfoxide (DMSO) at room temperature. The structure of melamine is shown in Fig. 1b. Melamine-based coordination polymers reported previously include a fluorescent coordination polymer based on Cu(I) and melamine, which is highly stable and suitable for detection of nitro aromatic compounds in aqueous media.9 Also, a cationic coordination polymer based on Ag(I) and melamine was used for selective anion exchange.10
1 mixture of methanol and dimethyl sulfoxide (DMSO) at room temperature. The structure of melamine is shown in Fig. 1b. Melamine-based coordination polymers reported previously include a fluorescent coordination polymer based on Cu(I) and melamine, which is highly stable and suitable for detection of nitro aromatic compounds in aqueous media.9 Also, a cationic coordination polymer based on Ag(I) and melamine was used for selective anion exchange.10
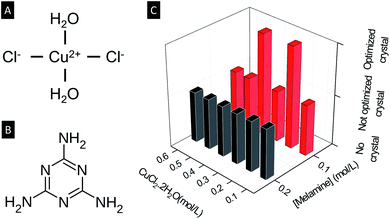 | ||
| Fig. 1 Schematic diagram of (A) CuCl2·2H2O and (B) melamine. (C) Crystal growth at room temperature with various concentrations of CuCl2·2H2O and melamine. | ||
It is found that two kinds of large crystals grow at optimized concentrations and molar ratio between copper chloride and melamine. At an optimal concentration of melamine of 0.1 mol L−1, a copper to melamine ratio in the range 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 2
1 to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, leads to the formation of a new copper complex composed of all available elements and molecules, i.e. copper, chlorine, melamine, methanol and DMSO. With a copper to melamine ratio in the range 3
1, leads to the formation of a new copper complex composed of all available elements and molecules, i.e. copper, chlorine, melamine, methanol and DMSO. With a copper to melamine ratio in the range 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 4
1 to 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, both melamine and methanol are passivated, leading to the formation of a coordination polymer with zigzag copper–chlorine chains with each copper coordinated by three chlorines and two DMSO. Both of them are large single crystals with low-dimensional spin structures and are candidate materials for magnetic and sensing applications.
1, both melamine and methanol are passivated, leading to the formation of a coordination polymer with zigzag copper–chlorine chains with each copper coordinated by three chlorines and two DMSO. Both of them are large single crystals with low-dimensional spin structures and are candidate materials for magnetic and sensing applications.
All synthesis was carried out at room temperature (around 25 °C) by mixing a methanol solution of CuCl2·2H2O and a DMSO solution of melamine at different concentrations and molar ratio. The concentrations of CuCl2·2H2O tested are 0.8, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, 0.05 and 0.025 mol L−1, and the concentrations of melamine are 0.05, 0.1 and 0.2 mol L−1. See ESI 1† for more details on the synthesis procedures and optimization. In each case, 2 mL of a methanol solution of CuCl2 was placed in a 5 mL glass vial, then 2 mL of a DMSO solution of melamine was added to the CuCl2 solution. The results are summarized qualitatively in Fig. 1 where ‘no crystal’ refers to the condition in which no solids are formed, while ‘not optimized crystal’ refers to the condition in which crystals grow but their quantity and/or size are not as large as the ‘optimized crystal’.
The two optimal conditions are (ρCuCl2, ρMelamine) = (0.2 mol L−1, 0.1 mol L−1) for crystals named Cu2M1, and (0.4 mol L−1, 0.1 mol L−1) for crystals named Cu4M1, where ρCuCl2 is the concentration of CuCl2·2H2O in methanol and ρMelamine (mol L−1) is the concentration of melamine in DMSO. Crystals are formed only within the concentration window 0.05 mol L−1 ≤ ρCuCl2 ≤ 0.6 mol L−1 and 0.1 mol L−1 ≤ ρMelamine ≤ 0.2 mol L−1. The fact that no crystal growth can be achieved at high concentrations of both cations, Cu(II) and anions Cl−, can be attributed to the high ionic strength that reduces the mobility of the ions in the solution,11 hindering the metal to ligand coordination. On the contrary, when the concentration is low, the mobility is high, but the nucleation of the crystal does not occur since the critical nucleation concentration is surpassed, and the collisions between both ligand and metal are less probable.12
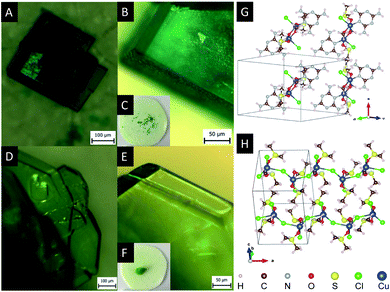
Fig. 2 shows the micrographs of crystals Cu2M1 and Cu4M1, formed at the optimal conditions. For Cu2M1, dark green rectangular crystals with truncated edges are formed in 5 hours with sizes as large as 350 μm in length (see panels A, B and C). As for Cu4M1, light green octagonal crystals as large as 5 mm across are formed in 48 hours (panels D, E and F). This demonstrates that only doubling the concentration of CuCl2·2H2O can drastically alter the morphology of the formed crystal.
X-ray diffraction analysis of a Cu4M1 single crystal reveals the structure of the coordination complex (formula Cu((CH3)2SO)2Cl2)*, that was previously reported (CCDC deposition number 1142844),13 but not much was reported regarding its properties.14,15 The determined structure of Cu4M1, illustrated in Fig. 2H, consists of copper, chlorine and DMSO and is an orthorhombic system. As for its structure, it consists of serpent-like Cu–Cl chains. Each copper has a trigonal ligand geometry with a crystallographic point group of D3h symmetry:16 bonded to two dimethyl sulfoxide molecules through a Cu–O bond with a length of 1.95 Å, forming a O–Cu–O angle of 173.67°, and to three chlorine atoms in the a–c plane. One of the chlorines is out of the zigzag chain and the other two are in the chain. Cl–Cu–Cl angles are 146.46°, 112.22° and 101.32°. The length of the three Cu–Cl bonds (2.75 Å) are longer than the covalent Cu–Cl bond length (2.3 Å) in CuCl2, indicating the weak covalent bonding.13 Fig. 3 shows the inter- and intramolecular bonds. The bond lengths [Å] and the bond angles [°] are also given. It highlights that the zigzag chain results in a (red marked) “cap”. In the area marked in red, two other intramolecular bonds have also been detected (shaded green). The cap encloses a neighbouring strain and it is characterised by several intermolecular interactions (shaded yellow).
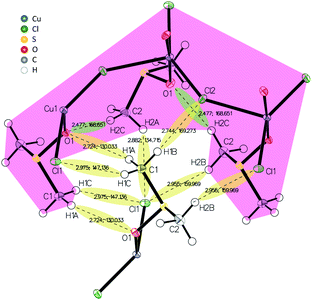 | ||
| Fig. 3 Inter- and intramolecular bonds visualized in the crystal structure of Cu4M1 drawn with 50% displacement ellipsoid. | ||
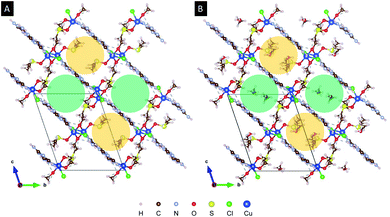
X-ray diffraction analysis of a single crystal of Cu2M1 reveals that it is a coordination complex consisting of copper, chlorine, melamine, DMSO and methanol, as shown in Fig. 2G. The empirical formula of the coordination complex is (Cu(C3H6N6)(OCH3)((CH3)2SO)Cl)2. See ESI 2† for more details on the structural analysis. To the best of our knowledge, this crystalline structure has not been previously reported, only some similar examples as reported by Chen et al., (2006) (CCDC deposition numbers 280091 and 280092),17 Goodgame et al., (1999) (CCDC deposition number 134810),18 and Wiles et al., (2006).19 In our Cu2M1 complex, two copper atoms are bridged by the oxygen atoms of two methoxides, forming an angle O–Cu–O of 77.88°. Each copper has a distorted square pyramidal ligand geometry with a crystallographic point group of C4v symmetry.16 At the top of the square base pyramids is a chlorine Cu–Cl bond (2.63 Å). The basal plane of the pyramids consists of two Cu–O bonds (1.93 Å) where each copper coordinates with the oxygen of methoxide, another Cu–O bond (1.95 Å) which links copper with a molecule of DMSO by its oxygen, and a Cu–N bond (1.98 Å) that coordinates copper with a nitrogen of the pyridine ring of melamine. The two melamines are in the same plane which is outside of the basal plane of the two pyramids. Melamines of the adjacent Cu2M1 molecules are hydrogen bonded to one another, constituting a global two-dimensional layer of melamine. The packing view along (1 1 1) in Fig. 4 shows that every dimer (red shaded area) is surrounded by six neighbouring dimers in the plane. The shaded areas within the plane show the seven intermolecular interactions in yellow, and the two intramolecular interactions in green.
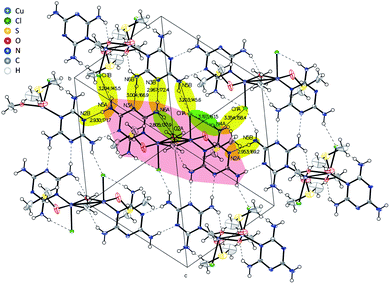 | ||
| Fig. 4 Inter- and intramolecular bonds visualized in the crystal structure of Cu2M1 drawn with 50% displacement ellipsoid. | ||
Packing of melamine layers along (1 0 0) leads to two types of one-dimensional void accessible by the solvents (DMSO and MeOH). Fig. 5 compares the structure model for Cu2M1 viewed along the “a” axis without co-crystallised solvents in panel (a), with the methanol-filled model pictured in panel (b). The green-shaded void is along the visible radius in panel (a). This sterically influenced void allows the two different types of solvents (DMSO and MeOH) used during the synthesis to co-crystallise in a disordered way. The second type of void (yellow-shaded) is intruded by the coordinated DMSO and limits the available space in which only MeOH can be modelled. See ESI 2 for more details.†
The crystal structures of Cu2M1 and Cu4M1 accommodate low-dimensional coordinations of copper, namely, the dinuclear copper molecular unit in Cu2M1 and the zigzag copper–chlorine chain in Cu4M1. The low-dimensional nature of the exchange coupling among copper spins are of particular interest for their potential magnetic applications.
The temperature dependence of the magnetic moment per copper in units of μB for a dinuclear Cu–melamine complex Cu2M1 sample (33.7 mg of Cu2M1 crystals encapsulated in a gelatin capsule) in an applied magnetic field of 1 T is shown in Fig. 6A. As planar crystals are stacked horizontally, the magnetic field is applied normal to the crystal plane for the majority of crystals. The net magnetism of the dinuclear Cu–melamine complex is much smaller than the dashed curve showing Curie’s Law for a paramagnetic 1/2 spin, with an effective magnetic moment of 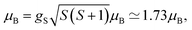 indicating the presence of strong antiferromagnetic coupling. The magnetic susceptibility as a function of temperature can be analysed using the Bleaney–Bowers equation for an exchange-coupled pair of S = 1/2 spins20,21
indicating the presence of strong antiferromagnetic coupling. The magnetic susceptibility as a function of temperature can be analysed using the Bleaney–Bowers equation for an exchange-coupled pair of S = 1/2 spins20,21
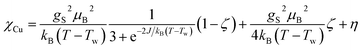 | (1) |
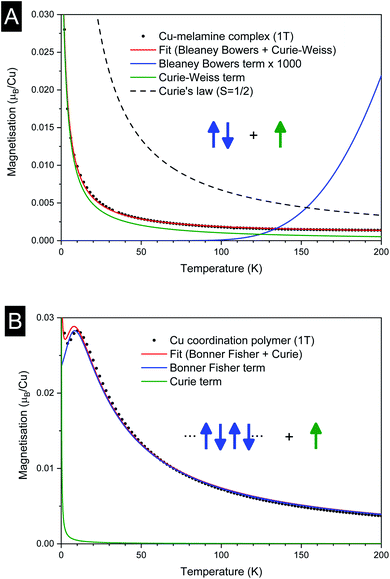 | ||
| Fig. 6 Magnetisation versus temperature for (A) dinuclear Cu–melamine complex Cu2M1, and (B) 1D-Cu coordination polymer Cu4M1. | ||
As shown in Fig. 6B, the magnetization of a planar single crystal of copper coordination polymer Cu4M1 (24.0 mg) in the magnetic field applied normal to the crystal plane, exhibits a maximum of 0.0285 μB at 10 K. Provided that the exchange coupling is anisotropic and strong along the zigzag copper–chlorine–copper chain, the temperature dependence of the magnetic susceptibility can be evaluated based on the exchange Hamiltonian Ĥ = − ∑ijJijŜiŜj taking exchange coupling between any two adjacent spins in a one-dimensional spin chain into account.22–26 The Bonner–Fisher equation derived from the above Hamiltonian for a S = 1/2 Heisenberg chain27,28 together with a paramagnetic term, is as follows in eqn (2),
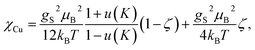 | (2) |
The structure analysis reveals that with a Cu–melamine ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (0.4 mol L−1 of CuCl2·2H2O in methanol and 0.1 mol L−1 of melamine in DMSO) copper coordination polymer Cu4M1 is formed despite the presence of melamine. During their synthesis at room temperature, the pH of the media evolves differently in the 2
1 (0.4 mol L−1 of CuCl2·2H2O in methanol and 0.1 mol L−1 of melamine in DMSO) copper coordination polymer Cu4M1 is formed despite the presence of melamine. During their synthesis at room temperature, the pH of the media evolves differently in the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 4
1 and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixed solutions.30 Although evaluating pH values of organic and aprotic solvents is a complicated task, their relative changes upon chemical reactions are worth noting. Since there is no OH− in the precursor solvents, the pH is only related to the presence of H+. The pH value of 0.2 mol L−1 of CuCl2·2H2O in methanol, 0.4 mol L−1 of CuCl2·2H2O in methanol and 0.1 mol L−1 of melamine before mixing are 1.03 ± 0.03, 0.62 ± 0.04 and 9.64 ± 0.02, respectively. The pH of the 2
1 mixed solutions.30 Although evaluating pH values of organic and aprotic solvents is a complicated task, their relative changes upon chemical reactions are worth noting. Since there is no OH− in the precursor solvents, the pH is only related to the presence of H+. The pH value of 0.2 mol L−1 of CuCl2·2H2O in methanol, 0.4 mol L−1 of CuCl2·2H2O in methanol and 0.1 mol L−1 of melamine before mixing are 1.03 ± 0.03, 0.62 ± 0.04 and 9.64 ± 0.02, respectively. The pH of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 4
1 and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solutions just after mixing are 5.96 ± 0.03 and 5.56 ± 0.02, respectively. After the formation of crystals of the dinuclear copper–melamine complex Cu2M1, the pH of the 2
1 solutions just after mixing are 5.96 ± 0.03 and 5.56 ± 0.02, respectively. After the formation of crystals of the dinuclear copper–melamine complex Cu2M1, the pH of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solution remains unchanged within the confidence interval (5.94 ± 0.03). (This statistical parameter is determined by a “t of Student” distribution with 95% confidence interval, for which it is considered five simultaneous measurements.) On the contrary, the pH of the 4
1 solution remains unchanged within the confidence interval (5.94 ± 0.03). (This statistical parameter is determined by a “t of Student” distribution with 95% confidence interval, for which it is considered five simultaneous measurements.) On the contrary, the pH of the 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solution is increased to 6.14 ± 0.03 after the formation of crystals of copper coordination polymer Cu4M1. This increase can be attributed to a reduction of H+ as a result of protonation of melamine which is initially deprotonated in pure DMSO. This leaves passivated neutral melamine which does not get coordinated with Cu(II) ions. Likewise, the pH barely changes in the 2
1 solution is increased to 6.14 ± 0.03 after the formation of crystals of copper coordination polymer Cu4M1. This increase can be attributed to a reduction of H+ as a result of protonation of melamine which is initially deprotonated in pure DMSO. This leaves passivated neutral melamine which does not get coordinated with Cu(II) ions. Likewise, the pH barely changes in the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solution because melamine ions react with Cu(II) before being protonated. Hence, the proton concentration needs to be optimised for the formation of copper coordination polymer Cu4M1.
1 solution because melamine ions react with Cu(II) before being protonated. Hence, the proton concentration needs to be optimised for the formation of copper coordination polymer Cu4M1.
In order to justify the above-mentioned scenario, the synthesis of copper coordination polymer Cu4M1 has been attempted by mixing a methanol solution of CuCl2·2H2O with aprotic DMSO whose pH value is adjusted by adding anhydrous acetic acid. It is found that crystals of the same copper coordination polymer are formed in the solution without melamine when the pH is adjusted to 9.64 ± 0.02, while no crystals are formed without acetic acid. Thus, the concentration of protons plays an important role in the coordination of DMSO and chlorine with copper ions in the presence of methanol.
In summary, a novel copper–melamine complex and a copper coordination polymer have been synthesized selectively by adjusting the concentrations of copper(II) chloride dihydrate and melamine in a mixed solution of methanol and DMSO at room temperature. Crystals of copper–melamine complex Cu2M1 formed with a Cu–melamine ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 are green and square shaped with sizes as large as 350 μm across. The hydrogen-bonded two-dimensional lattice is composed of planes of melamine and one-dimensional pores along the a-axis that accommodate solvent molecules. Crystals of copper coordination polymer Cu4M1 formed with a Cu–melamine ratio of 4
1 are green and square shaped with sizes as large as 350 μm across. The hydrogen-bonded two-dimensional lattice is composed of planes of melamine and one-dimensional pores along the a-axis that accommodate solvent molecules. Crystals of copper coordination polymer Cu4M1 formed with a Cu–melamine ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 are light green gem-like octagonals and can grow as large as 5 mm across. The lattice is composed of Cu–Cl zigzag chains and has no porosity. Both Cu2M1 and Cu4M1 exhibit low-dimensional magnetic properties. The magnetic susceptibility of Cu2M1 can be modelled well based on the Hamiltonian for paired spins of 1/2, and that of Cu4M1 based on a spin-1/2 anti-ferromagnetic Ising chain. The well-controlled synthesis of the high quality and large monocrystals demonstrated in the present study will pave the way for future research on spintronic applications of inorganic and organic–inorganic hybrid materials.
1 are light green gem-like octagonals and can grow as large as 5 mm across. The lattice is composed of Cu–Cl zigzag chains and has no porosity. Both Cu2M1 and Cu4M1 exhibit low-dimensional magnetic properties. The magnetic susceptibility of Cu2M1 can be modelled well based on the Hamiltonian for paired spins of 1/2, and that of Cu4M1 based on a spin-1/2 anti-ferromagnetic Ising chain. The well-controlled synthesis of the high quality and large monocrystals demonstrated in the present study will pave the way for future research on spintronic applications of inorganic and organic–inorganic hybrid materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
H. S. acknowledges support from the Austrian Science Fund (FWF) P30431–N36 and the Czech Science Foundation (GACR) project 19-15217 S. This work was supported in part by the Austrian Federal Ministry of Education, Science and Research (BMBWF), OeAD-GmbH and the Ministry of Education, Youth and Sports (MEYS) of the Czech Republic, through the Scientific & Technological Cooperation (WTZ) program, No. CZ 18/2019 and 8J19AT026.Notes and references
- H. J. Cleaves, Encyclopedia of Astrobiology, Springer Berlin Heidelberg, Berlin, Heidelberg, 2011, p. 1183 Search PubMed.
- S. R. Batten, N. R. Champness, X.-M. Chen, J. Garcia-Martinez, S. Kitagawa, L. Öhrström, M. O’Keeffe, M. P. Suh and J. Reedijk, Pure Appl. Chem., 2013, 85, 1715–1724 CAS.
- M. Bazargan, M. Mirzaei, M. Aghamohamadi, M. Tahmasebi and A. Frontera, J. Mol. Struct., 2020, 1202, 127243 CrossRef CAS.
- M. Safaei, M. M. Foroughi, N. Ebrahimpoor, S. Jahani, A. Omidi and M. Khatami, Trac. Trends Anal. Chem., 2019, 118, 401–425 CrossRef CAS.
- M. G. Campbell, D. Sheberla, S. F. Liu, T. M. Swager and M. Dincă, Angew. Chem., Int. Ed., 2015, 54, 4349–4352 CrossRef CAS.
- S. Yuan, L. Feng, K. Wang, J. Pang, M. Bosch, C. Lollar, Y. Sun, J. Qin, X. Yang, P. Zhang, Q. Wang, L. Zou, Y. Zhang, L. Zhang, Y. Fang, J. Li and H. C. Zhou, Adv. Mater., 2018, 30, 1–35 Search PubMed.
- P. P. Liu, L. Sheng, X. Q. Song, W. Y. Xu and Y. A. Liu, Inorg. Chim. Acta, 2015, 434, 252–257 CrossRef CAS.
- M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793 CrossRef CAS.
- Y. Zhang, Q. Yang, X. Li, C. Miao, Q. Hou and S. Ai, CrystEngComm, 2020, 22, 5690–5697 RSC.
- A. Baraka, H. Hatem, M. S. El-Geundi, H. Tantawy, K. Karaghiosoff, M. Gobara, A. Elbeih, M. Shoaib, M. A. Elsayed and M. M. Kotb, J. Solid State Chem., 2019, 274, 168–175 CrossRef CAS.
- W. Peng, H. Li, Y. Liu and S. Song, J. Mol. Liq., 2017, 230, 496–504 CrossRef CAS.
- N. Stock and S. Biswas, Chem. Rev., 2012, 112, 933–969 CrossRef CAS PubMed.
- R. D. Willett and K. Chang, Inorg. Chim. Acta, 1970, 4, 447–451 CrossRef CAS.
- S. Becker, M. Dürr, A. Miska, J. Becker, C. Gawlig, U. Behrens, I. Ivanović-Burmazović and S. Schindler, Inorg. Chem., 2016, 55, 3759–3766 CrossRef CAS.
- H. Chebbi, M. Chebbi, A. Guesmi and Y. Arfaoui, J. Struct. Chem., 2016, 57, 1104–1110 CrossRef CAS.
- R. Flurry, Symmetry Groups, Prentice-Hall, 1980, pp. 115–127 Search PubMed.
- C. Chen, C. W. Yeh and J. D. Chen, Polyhedron, 2006, 25, 1307–1312 CrossRef CAS.
- D. M. L. Goodgame, I. Hussain, A. J. P. White and D. J. Williams, J. Chem. Soc., Dalton Trans., 1999, 2899–2900 RSC.
- A. B. Wiles, D. Bozzuto, C. L. Cahill and R. D. Pike, Polyhedron, 2006, 25, 776–782 CrossRef CAS.
- B. Bleaney, Rev. Mod. Phys., 1953, 25, 161–162 CrossRef.
- B. Figgis and R. Martin, J.Chem. Soc., 1956, 3837–3846 RSC.
- J. Bonner and M. Fisher, Phys. Rev., 1964, 135, A640 CrossRef.
- J. Hall, W. Marsh, R. Weller and W. Hatfield, Inorg. Chem., 1981, 20, 1033–1037 CrossRef CAS.
- J. Borrasalmenar, E. Coronado, J. Curely, R. Georges and J. Gianduzzo, Inorg. Chem., 1994, 33, 5171–5175 CrossRef CAS.
- S. Dalai, P. Mukherjee, G. Rogez, T. Mallah, M. Drew and N. Chaudhuri, Eur. J. Inorg. Chem., 2002, 3292–3297 CrossRef CAS.
- N. Marino, D. Armentano, G. De Munno, J. Cano, F. Lloret and M. Julve, Inorg. Chem., 2012, 51, 4323–4334 CrossRef CAS PubMed.
- M. E. Fisher, Am. J. Phys., 1964, 32, 343–346 CrossRef.
- W. E. Estes, D. P. Gavel, W. E. Hatfield and D. J. Hodgson, Inorg. Chem., 1978, 17, 1415–1421 CrossRef CAS.
- R. Feyerherm, S. Abens, D. Günther, T. Ishida, M. Meißner, M. Meschke, T. Nogami and M. Steiner, J. Phys.: Condens. Matter, 2000, 12, 8495–8509 CrossRef CAS.
- W. Ostwald, Z. Phys. Chem., 1900, 34U, 495–503 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2061869 and 2061868. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1ra02903g |
| This journal is © The Royal Society of Chemistry 2021 |