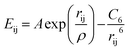Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A high throughput computational investigation of the solid solution mechanisms of actinides and lanthanides in zirconolite†
Stavrina Dimosthenous a,
Christopher M. Handley
a,
Christopher M. Handley ab,
Lewis R. Blackburna,
Colin L. Freemana and
Neil C. Hyatt
ab,
Lewis R. Blackburna,
Colin L. Freemana and
Neil C. Hyatt *a
*a
aDepartment of Materials Science and Engineering, The University of Sheffield, Mappin Street, Sheffield, UK. E-mail: stavrinadimosthenous@gmail.com; n.c.hyatt@sheffield.ac.uk
bThe Digital Research Service, The School of Computing, Jubilee Campus, The University of Nottingham, Nottingham, UK
First published on 20th July 2021
Abstract
In this work, we perform a theoretical investigation of the actinide and lanthanide solid solution mechanisms of zirconolite-2M, prototypically CaZrTi2O7, as a candidate immobilisation matrix for plutonium. Solid solution energies were calculated using static atomistic simulations by means of the General Utility Lattice Program, for formulations of relevance to ceramic wasteform deployment, with substitution on the Ca2+ and Zr4+ sites by Ce4+, Pu4+, Th4+, and U4+, and appropriate charge balance by substitution of Al3+ or Fe3+ on Ti4+ sites. In simple solid solutions involving substitution on the Zr4+ site, we found that whereas substitution of Ce4+, U4+ and Pu4+ were energetically favoured, substitution of Th4+ was not energetically favoured. For more complex solid solutions involving Ce4+, Pu4+, Th4+, and U4+ substitution on the Ca2+ site, we found the most energetically favoured scheme involved co-substitution of Al3+ or Fe3+ on the five-fold co-ordinate Ti4+ site in the zirconolite-2M structure. Comparison of these computational data with experimental evidence, where available, demonstrated broad agreement. Consequently, this study provides useful insight into formulation design and the efficacy of Ce4+, U4+ and Th4+ as Pu4+ surrogates in zirconolite-2M ceramic wasteforms for plutonium disposition.
1 Introduction
The UK holds the world's largest inventory of separated civil plutonium, forecast to reach 140 tons at the end of reprocessing operations.1 UK government policy is to manage this material to a safe and secure end point, the preferred strategy for which is reuse in mixed oxide (MOX) fuel in light water reactors. However, should this strategy not prove implementable, immobilisation of the inventory will be required, along with the fraction of material known to be unsuitable for MOX fuel manufacture.Numerous natural and synthetic materials have been proposed as wasteforms for the immobilisation of actinides, these including ceramics, glasses, and glass-ceramics.2–6 Geological disposal of actinides places greater emphasis on the performance of the wasteform and near field barriers, so as to assure adequate containment of fissile material over the required timescales, which, in the geological context, are comparably short.2–5,7 Zirconolite, prototypically CaZrTi2O7, is a naturally occurring mineral and the dominant actinide bearing phase in the SYNROC C ceramic wasteform;8,9 it is known to be highly resistant to alteration and dissolution.10,11 As a result, zirconolite is an attractive material for plutonium immobilisation and its potential as a wasteform has been well established.8,12–15 The zirconolite-2M polytype structure (space group C2/c), adopted by the prototypical composition CaZrTi2O7, comprises alternating layers of CaO8 and ZrO7 polyhedra aligned parallel to (110); parallel to the [001] direction, these polyhedra are interleaved 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 with hexagonal tungsten bronze motifs formed by corner sharing TiO6 and TiO5 polyhedra.16,17 The 2M nomenclature thus signifies a monoclinic unit cell with a two layer repeat sequence along [001]; other zirconolite polytype structures with different interlayer relationships are known, as discussed below.
1 with hexagonal tungsten bronze motifs formed by corner sharing TiO6 and TiO5 polyhedra.16,17 The 2M nomenclature thus signifies a monoclinic unit cell with a two layer repeat sequence along [001]; other zirconolite polytype structures with different interlayer relationships are known, as discussed below.
The use of Pu in laboratory based studies is hazardous, challenging and expensive. Consequently, Ce, U and Th are frequently used as inactive or low active surrogates to emulate the behaviour of Pu in laboratory based studies.18,19 This is due to the similarity of the ionic size of Ce4+, U4+, Th4+ and Pu4+ and to CeO2, PuO2, ThO2, and UO2 all having a common fluorite crystal structure and exhibiting solid solution at any ratio, implying similar solid state chemistry.20–23
In this work we aim to investigate the plutonium immobilisation potential of zirconolite-2M by atomistic simulations. Previous simulation based studies of zirconolite-2M at the atomistic level have focused on studying the defect chemistry of actinide additions,24 and within the regime of molecular dynamics for investigations the radiation damaged structure, and crystalline to amorphous phase transition, arising from α-decay of Pu.25–27 More recently, Ce and actinide solid solution mechanisms in zirconolite-2M were studied at the electronic structure level, within the density functional theory (DFT) regime.28 Importantly, the DFT investigation of Tanti et al. broadly agreed with findings of the atomistic simulations of Gilbert et al. for Ce-substituted zirconolite-2M. The choice of methodology and accuracy level is a critical consideration in such investigations. The broad agreement between DFT and atomistic simulations shows that we can obtain accurate insight with the atomistic approach. Further, given the low computational cost, it is feasible to simulate relatively large lattices at the atomistic level employing an innovative high-throughput workflow described herein.
Our investigation develops and extends a previous computational study of the defect chemistry of zirconolite-2M,24 with regard to incorporation of Ce3+/4+ and Pu3+/4+. In this contribution we expand the previous study by examining the solid solution of Pu4+ and its typical surrogates, Ce4+, U4+, Th4+, on the Ca2+ and Zr4+ sites, at concentrations greater than point defects, with necessary charge compensation provided by Al3+ and Fe3+ substitution on the Ti4+ sites.
We focus on the Pu4+ oxidation state which has been shown to be the dominant species in fluorite related zirconolite-2M and pyrochlore structured ceramics synthesised under conditions relevant to wasteform manufacture.29–33 Under conditions of hot isostatic pressing with PuO2 as a feedstock, synthesis of the zirconolite ceramic wasteform will be under the redox control of the Fe/FeO buffer imposed by the stainless steel can. Consideration of Ellingham diagrams shows that this will not be sufficient to effect PuO2/Pu2O3 reduction.34 Indeed, Pu3+ is stabilised by annealing only under strongly reducing 5% H2/N2, or 5% H2/Ar, which is not relevant to the technological focus of wasteform manufacture by hot isostatic pressing.31,32
2 Theory
The work presented in this paper examines three substitution schemes to investigate Pu and surrogate incorporation in zirconolite-2M. The substitution schemes are based on compositions relevant to optimisation of zirconolite ceramic formulations. We used the supercell approach to study the defects of the system. Here, the defects are added as absolute concentrations in a solid solution, and our concentration values can therefore be directly compared to experimental compositions. This differs from previous work on this system24 that used a Mott–Littleton method where the substitution defects were effectively at infinite dilution.In the first substitution scheme, we replaced Zr4+ sites in prototypical zirconolite-2M with Ce4+, Pu4+, Th4+ and U4+. The chemical reaction for the substitution scheme was as follows,
| CaZrTi2O7 + xMO2 → CaZr1−xMxTi2O7 + xZrO2 |
The second substitution scheme targeted the substitution of Ce4+, Pu4+, Th4+ and U4+ on the Ca2+ site, with charge balance provided by replacing 2Ti4+ sites with Al3+, for every Ca2+ ion replaced.35–37 The second substitution scheme followed the reaction,
| CaZrTi2O7 + xMO2 + xAl2O3 → Ca1−xMxZrTi2−2xAl2xO7 + xCaO + 2xTiO2 |
There are three unique Ti4+ sites in the zirconolite-2M structure that may accommodate charge balancing cations such as Al3+. An illustration of the Ti4+ site orientations and coordination is shown in Fig. 1, where example Ti(1), Ti(2) and Ti(3) sites are coloured in green, yellow and fuschia respectively, with Ca and Zr omitted for clarity. The Ti(1) and Ti(3) sites adopt octahedral co-ordination by O2−, whereas the Ti(2) site adopts a trigonal bipyramidal configuration by O2−. The Ti(2) site is partially occupied, with a 50% probability of lying either side of the site axis.16
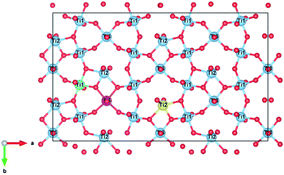 | ||
| Fig. 1 Ti4+ site orientation in our base zirconolite-2M system (Ca2+, Zr4+ hidden). Ti sites are labelled, example Ti(1), Ti(2) and Ti(3) sites are coloured green, yellow and fuchsia, respectively. The Ti(1) and Ti(3) sites have octahedral coordination, whereas the Ti(2) site has trigonal bipyramidal co-ordination and is 50% occupied. Figure generated in VESTA.40 | ||
Experimental studies have shown that charge balancing ions are generally preferentially accommodated in the 5-fold coordinate Ti(2) site.36–38 Although, in some instances, charge balancing species such as Cr3+ have been shown to preferentially adopt 6-fold Ti4+ sites as may be expected from consideration of crystal field stabilisation energy.34 Therefore, this substitution scheme needs to consider potential preferential substitution of the charge balancing ions for particular Ti4+ sites. To address this question, we considered 6 different Al3+ site combinations: two Ti(1) sites; two Ti(2) sites; two Ti(3) sites; one Ti(1) and one Ti(2); one Ti(1) and one Ti(3); and one Ti(2) and one Ti(3).
The third substitution scheme was identical to the second scheme, however, the reaction was charge balanced with Fe3+.39 The third substitution scheme followed the reaction,
| CaZrTi2O7 + xMO2 + xFe2O3 → Ca1−xMxZrTi2−2xFe2xO7 + xCaO + 2xTiO2 |
3 Method
All the calculations in this work were performed with the General Utility Lattice Program (GULP).41 Ions are treated as charged spheres represented by their formal charge42 with a coulombic attraction/repulsion. Short range interactions between ions are described with Buckingham potentials of the form,where rij is the distance between two ions i and j, and A, ρ and C6 are parametrised constants specific to each interaction pair, as summarised in Table 1.
| Interaction | A (eV) | ρ (Å) | C6 (eV Å6) | Ref. |
|---|---|---|---|---|
| O2−–O2− | 25.410 | 0.6937 | 32.320 | 48 |
| Ca2+–O2− | 2272.741 | 0.2986 | 0.000 | 48 |
| Zr4+–O2− | 7290.347 | 0.2610 | 0.000 | 49 |
| Ti4+–O2− | 4545.823 | 0.2610 | 0.000 | 49 |
| Al3+–O2− | 2409.505 | 0.2649 | 0.000 | 48 |
| Fe3+–O2− | 3219.335 | 0.2641 | 0.000 | 48 |
| Ce4+–O2− | 2409.505 | 0.3260 | 0.000 | 49 |
| Pu4+–O2− | 752.224 | 0.4007 | 0.000 | 24 |
| Th4+–O2− | 8638.5 | 0.2856 | 70.000 | 50 |
| U4+–O2− | 9296.65 | 0.2796 | 90.000 | 50 |
The polarisability of the system is described by the shell model43 where the charged core interacts with a massless “shell” via a spring constant, k. Only O2− was polarised in this study so the interaction potentials presented in Table 1 are cation–anion core–shell interaction potentials. The shell model data for O2− are presented in Table 2.
| Effective charge (core/shell) | k (eV Å−2) | Ref. |
|---|---|---|
| 0.513/−2.513 | 20.53 | 51 |
The model zirconolite lattice is the stoichiometric 2M polytype taken from the work of Gilbert et al.,24 based on the structure published by Rossell.17 For our simulations the structure was expanded to a 2 × 2 × 2 supercell (704 atoms). The calculations were performed at constant pressure and the structure and atomic positions were optimised using a Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm.44–47
Substitution sites were randomly chosen. Our base zirconolite-2M system was composed of 704 atoms, 64 of those were Zr4+, 64 were Ca2+, 128 were Ti4+ (64 Ti(1), 32 Ti(2), 32 Ti(3)). For the first solid solution scheme, we chose to produce 30 random site substitution configurations. For the second solid solution scheme we produced 120 random configurations per site combination, e.g. CeTi(1)Ti(1). That is, for every substitution introduced to the system we replaced one Ca2+ site at random and two of the chosen type of Ti4+ sites at random with Al3+. For the third solid solution scheme, our aim was to directly compare Al3+ and Fe3+ as charge balancing species. Therefore, we made a direct substitution of Fe3+ on the sites that were occupied by Al3+ in the second solid solution scheme. The structures remained identical, otherwise. In our simulations we considered substitution concentrations of 3, 6, 9, 12, 15, 18 and 21%. In practice, this was the percentage of the number of atoms of the element in the cell to be replaced by the substitution rounded to the nearest integer, which was 2, 4, 6, 8, 10, 12 and 13 sites for Zr4+ and Ca2+, and 4, 8, 12, 20, 24 and 26 sites for Ti4+, when considering Al3+ and Fe3+ charge compensation. For a cell of 704 atoms, there were 64 Zr4+ and 64 Ca2+ sites that were potential substitution sites. Therefore, we were able to sample a wide range of configurations without artificial symmetry restrictions and provide data that could be compared to experimental investigation. Importantly, the upper substitution limit in this study concentration approximates that required for wasteform deployment.
Once the groundstate energy for each randomly substituted lattice was obtained we calculated the solution energy, that is the enthalpy of solid solution, for each substitution scheme. The calculation was based on the reactions presented in Section 2. We obtained the energy of each component by performing a geometry optimisation calculation on each structure, we assumed the polymorph of TiO2 to be rutile.
Configurations that failed to optimise were removed from the spread of data. The solution energies were averaged. For an optimised spread the ground state energy differed by 2 eV to 3 eV. Each point on the graphs presented in Fig. 3 is the average solution energy for the denoted M4+ concentration. Each line presented in Fig. 4 and 5 is the trend in the average solution energy over all substitutions for each scheme. Where the trend in the solution energy of a substitution did not follow the global trend in the scheme, it is presented separately on the same graph with a dashed line.
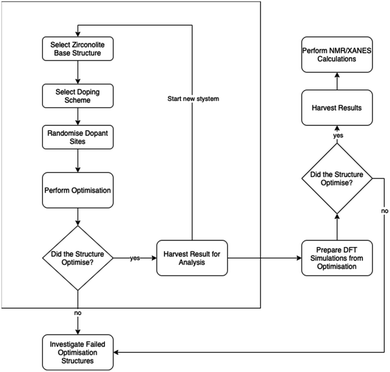
To perform the above randomisation of site substitution in structures for each solid solution scheme, we wrote Python based software to enable the automation of the generation of the structures that are then passed to a high-performance computer server, enabling us to rapidly perform simulations and, from the following analysis, provide meaningful suggestions for material synthesis. An example time frame would be about 1–12 hours per simulation on a single core, with simulations queued as an array job; this resulted in about 2 days for the 120 simulation cell analyses from queueing to data clean-up and analysis. The above workflow is illustrated in Fig. 2.
Importantly, Fig. 2 extends the work performed in this study to a pipeline workflow for high-throughput materials discovery. Enclosed within the box is the work performed within this paper. Outside of the box are future steps that can be performed where more expensive computational methods are applied. This demonstrates the method of use computationally cheaper methods – force fields – to scan the search space of crystal structure to quickly provide targets for investigation by more expensive methods. Within the context of the work here, this is beneficial when it is impractical to physically synthesise all possible solid solution stoichiometries. Within the wider context of materials science, our method has application to the exploration of similar materials e.g. high entropy alloys, capacitor ceramics, perovskites. Furthermore, the use of this initial screening can then direct subsequent, more costly, ab initio simulations, where the initial screening method has narrowed down the range of target compositions. The full calculation outputs are presented in the associated ESI.†
4 Results
4.1 CaZr1−xMxTi2O7 (M = Ce, Pu, Th, U)
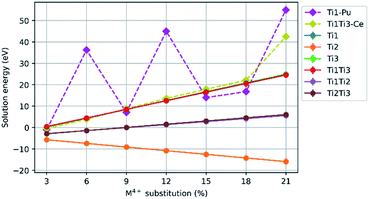
Fig. 3 shows the mean solution energy for the following scheme, plotted against Ce, Pu, Th, and U concentration.| CaZrTi2O7 + xMO2 → CaZr1−xMxTi2O7 + xZrO2 |
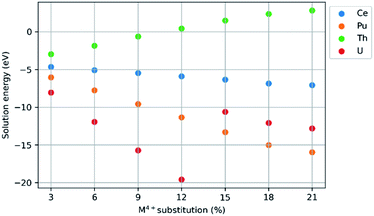 | ||
| Fig. 3 Comparison of solution energy as a function of M4+ substitution on the Zr4+ site (M = Ce, Pu, Th, U). | ||
The solution energies of Ce4+ and Pu4+ substitution on the Zr4+ site become progressively more negative with increasing Ce4+ and Pu4+ concentration; the slope for Pu4+ is greater than for Ce4+. In contrast, for Th4+ substitution, an increase in solution energy is observed with increasing concentration. The solution energy for U4+ substitution initially follows a downward trend, however, beyond a U concentration of 12%, there is an abrupt increase in solution energy. Thereafter, the solution energies for U4+ substitution follow a downward trend despite the discontinuity in solution energy from 12–15% concentration.
4.2 Ca1−xMxZrTi2−2xAl2xO7 (M = Ce, Pu, Th, U)
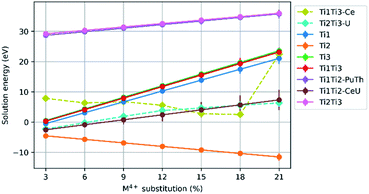
Results for Ce4+, Pu4+, Th4+ and U4+ substitution on the Ca2+ site and charge balance by replacement of Ti4+ with Al3+, are presented in Fig. 4. The mean solution energies are plotted against M4+ substitution concentration, with Al3+ as the charge balancing species substituted on sites Ti(1)Ti(1), Ti(2)Ti(2), Ti(3)Ti(3), Ti(1)Ti(2), Ti(1)Ti(3), and Ti(2)Ti(3). The solution energies of particular substitution schemes which do not follow the general trends are plotted separately with their own dashed lines. There is an upward trend in solution energy with increasing Ce, Pu, Th and U concentration for all schemes involving substitution on either the Ti(1) or Ti(3) sites, and the solution energy is always positive above an M4+ concentration of 6%. The solution energy only decreases with increasing M4+ concentration when charge balancing with Al3+ on the Ti(2)Ti(2) site combination, for which the solution energy is always negative.While Pu4+ substitution with Al3+ charge balance on two Ti(1) sites follows the general trend of the other substitutions, where the solution energy increases with increasing concentration, we observe maxima in the solution energy at 6%, 12% and 21% M4+ concentration. In the case of Al3+ charge balance on the combination of Ti(1) and Ti(3) sites, Ce4+ substitution did not follow the trend of Pu4+, Th4+ and U4+ so the data for it is plotted individually on the graph.
4.3 Ca1−xMxZrTi2−2xFe2xO7 (M = Ce, Pu, Th, U)
Fig. 5 shows the results for substitution of Ce4+, Pu4+, Th4+ and U4+ substitution on the Ca2+ site of the zirconolite-2M structure with charge balance by replacement of Ti4+ with Fe3+. The mean solution energies are plotted against M4+ substitution concentration, with Fe3+ as the charge balancing species substituted on sites Ti(1)Ti(1), Ti(2)Ti(2), Ti(3)Ti(3), Ti(1)Ti(2), Ti(1)Ti(3), and Ti(2)Ti(3). Again, the solution energies of particular substitution schemes which do not follow the general trends are plotted separately with their own dashed lines.The general trends in solution energy with Fe3+ as a charge balancing species are similar to those of Al3+. All substitution schemes showed an increase in solution energy with increasing M4+ concentration, with two exceptions. In the case of Ce4+ substitution with Fe3+ charge balancing on the Ti(1)Ti(3) site, the solution energy decreased with increased Ce4+ concentration, however, we observe a large increase in solution energy in the compositional interval between 18–21% Ce4+ incorporation. Whereas, in the case of U4+ substitution with Fe3+ charge balancing on Ti(2)Ti(3) sites, the solution energies for each compositional interval are much lower than for counterpart M4+ substitutions.
5 Discussion
The negative solution energies presented in Fig. 3 suggest that zirconolite-2M may fully accommodate Ce4+, U4+, Th4+ and Pu4+ on the Zr4+ site at low to moderate concentrations, which is in broad agreement with experimental validations for corresponding CaZr1−xMxTi2O7 solid solutions (M = Ce, U, Th, Pu). Furthermore, as the concentration of substitution is increased, the mixing of Ce4+, U4+ and Pu4+ is increasingly favoured, but only up to a value of 15% in the case of U4+, where we observe a discontinuity in solution energy. The observed discontinuity in solution energy for U4+ is consistent with the apparent solid solution limit of U in the zirconolite-2M structure as reported by Vance et al.13 Transformation to the zirconolite-4M polytype structure was reported in excess of approximately 15% U4+ substitution in the Zr4+ site of the zirconolite-2M structure.13 The 4M polytype also crystallises in the space group C2/c and is commonly described as an intergrowth of zirconolite-2M and pyrochlore-type layers, parallel to the [001] axis, resulting in a doubling of the unit cell.52 The zirconolite-4M phase remains the dominant structure in the CaZr1−xUxTi2O7 system up to a value of approximately 40% substitution, after which the cubic pyrochlore CaUTi2O7-type structure is preferred. Similar solid solution limits for Ce in the corresponding CaZr1−xCexTi2O7 system were reported by Blackburn et al.53 and Begg et al.54 with the Ce inventory preferentially accommodated in the zirconolite-4M structure above 20% incorporation. However, it must be recognised that the tendency of Ce4+ to undergo reduction to Ce3+, when processing under inert or reducing conditions, does not permit formation of zirconolite-4M in the same solid solution, rather a Ce-rich CaTiO3 phase is preferentially formed.53 Nevertheless, targeting equimolar Ce3+ substitution between Ca2+ and Zr4+ sites, i.e. Ca1−xZr1−xCe2xTi2O7 was observed to yield a transformation to zirconolite-4M.55 Begg et al. fabricated the CaZr1−xPuxTi2O7 solid solution confirming that Pu4+ was preferentially accommodated in the 4M structure at around 15% incorporation, consistent with data for Ce4+ and U4+.56 Consequently, simulation studies of substituent reduction and polytype transitions of zirconolite are necessary.It follows that a similar trend would be expected for Pu in the data presented in Fig. 3, however, a continuous trend of negative solution energy was observed. It should be noted that a number of configurations did fail to optimise in our simulations, suggesting that certain defect arrangements are highly unfavourable. This may correspond to experimental observations, in which the 2M structure becomes less favourable towards high substitution concentrations, possibly due to substituent proximity within a lattice. Our observation that Ce4+ and Pu4+ substitute favourably for Zr4+ in zirconolite is further supported by the observations of Gilbert et al.24 These data indicate that, whilst Ce remains a safe and practical analogue for Pu in wasteform development trials, it cannot fully replicate the substitution behaviour of Pu in zirconolite. Despite a similar trend to Pu4+ and U4+ at low concentrations, a clear variation in the solution energy, as a function of substitution, was observed. Nevertheless, the limitations of Ce–Pu surrogacy have been previously discussed in the context of Pu immobilisation in ceramic materials.57,58
In contrast, the substitution of Th4+ for Zr4+ produces a continuous positive upward trend in solution energy, which becomes positive above 9% Th substitution, suggesting that Th4+ may have a narrow solid solution range in the zirconolite-2M structure. These data are consistent with recent observations by Blackburn et al.59 in which it was confirmed that the solubility of Th4+ in the CaZr1−xThxTi2O7 solid solution was limited to 10% substitution for Zr4+, with Th4+ preferentially accommodated in a pyrochlore-structured phase between 0.10 ≤ x ≤ 0.50. The single phase pyrochlore compound CaZr0.40Th0.60Ti2O7 was produced when targeting x = 0.60. Interestingly, a phase transition to the zirconolite-4M structure, as reported in analogue Ce and U solid solutions, was not observed.
The data presented in Fig. 4 and 5 demonstrate that the substitution of Ce4+, U4+, Th4+ and Pu4+ in the Ca2+ site, with charge balance provided by Al3+ and Fe3+ is favoured at M4+ concentrations around 3%. Yet, these solid solutions become rapidly unfavourable, tending towards positive solution energy with the exception of the substitution scheme in which charge compensators were accommodated in the Ti(2) site. This substitution scheme follows a downward trend in solution energy, suggesting that surrogate species may be accommodated in the Ca2+ site up to a 21% substitution, with Al3+ and Fe3+ preferentially accommodated in the Ti(2) site, consistent with some experimental observations. Loiseau et al.60 fabricated the Ca1−xNdxZrTi2−xAlxO7 solid solution, confirming that zirconolite-2M was produced as a single phase in the compositional range x ≤ 0.60, with Nd3+ deployed as a trivalent actinide surrogate, and further substitution resulted in the formation of the orthorhombic 3O polytype. Rietveld refinement of a zirconolite-2M structural model, in which Al3+ was constrained in the Ti(2) site, was refined against powder X-ray diffraction data for Ca0.7Nd0.3ZrTi1.7Al0.3O7, confirmed that Al3+ preferentially occupied this site relative to Ti(1) and Ti(3). Similarly, Fe3+ was demonstrated by Whittle et al.37 to substitute for Ti(2) in the CaZrTi2−2xNbxFexO7 solid solution, however, it must be recognised that no surrogate as targeted to replace Ca2+. Conversely, Fe K-edge XANES has failed to resolve any preferential occupation of Fe3+ between Ti(1)/Ti(3) and Ti(2) sites in the Ca1−xHoxZrTi2−xFexO7.61 Similarly, Forder et al.62 resolved Fe3+ coordination in single phase zirconolite-2M (targeting Ca1−xCexZrTi2−2xFe2xO7) using 57Fe Mössbauer spectroscopy, confirming that whilst Fe3+ occupied both 5- and 6-fold coordination Ti4+ sites, occupation of the Ti(2) site was preferred at low Fe3+ concentration. Previous simulation studies did not identify a significant preference of Fe3+ in any particular Ti4+ site of zirconolite-2M.24 Cr3+ coordination was probed by Blackburn et al. in the Ca1−xCexZrTi2−2xCr2xO7 system, with deconvolution of the pre-edge Cr K-edge XANES region consistent with Cr3+ arranged in 6-fold coordination, inferring occupation in the octahedral Ti(1) and Ti(3) sites, as expected from consideration of crystal field stabilisation energy.63
The variation in dominant charge compensation mechanism and preferential site occupancy of charge compensation species in zirconolite-2M may be attributed to a several factors, not limited to: the choice of Pu surrogate deployed, the valence state, electronic structure and ionic radius of the charge compensation cation, and the partial oxygen pressure imposed during the fabrication route, which has been systematically demonstrated to influence both surrogate oxidation state and partitioning in the zirconolite-2M structure. This work also provided some evidence that, in line with experimental observations, Pu4+ may be favourably accommodated on the Ca2+ site in the zirconolite structure, whereas substitution of Ce4+ may be unfavourable in some instances. However, it is important to note that the underlying mechanism constraining the site occupancy of Ce within zirconolite-2M is controlled by the prevailing redox conditions imposed during synthesis, and is not entirely governed by the chosen solid solution regime. Whereas Pu4+ is readily incorporated in the zirconolite-2M phase under oxidising conditions, Ce4+ has a tendency to partially reduce to Ce3+ regardless of sintering environment. For example, synthesis of the CaZr1−xCexTi2O7 and Ca1−xCexZrTi2−2xCr2xO7 solid solutions in air consistently resulted in partial reduction of the Ce4+ inventory to Ce3+. It is this underlying auto-reduction tendency, that does not present itself with Pu under such conditions, that is the limiting factor in Ce–Pu surrogacy. Near single phase zirconolite-2M materials with nominal composition Ca0.8Pu0.2HfTi1.6Al0.4O7 and Ca0.8Pu0.2ZrTi1.8Al0.2O7 have been previously reported by both conventional sintering and hot pressing techniques, targeting Pu4+ and Pu3+ respectively.20,64 Analysis of the compositionally analogous Ca1−xCexZrTi2−2xAl2xO7 solid solution, at x = 0.10, has been observed to produce a minor perovskite phase, attributed to partial Ce3+ speciation-2M.65 The differences between simulated Ce4+ and Pu4+ substitution behaviour suggests that clustering and localised substituent–substituent interactions, which would be present in the current work yet excluded from previous data,24 may be key for stabilising the substituents. The combined presence of numerous defects may relieve the localised stress they create, as opposed to lone, or few, defects.28 This may also explain the data presented by Ji et al.61 where the incorporation of Ln3+ species in the Ca2+ site would lead to a weaker binding energy with Fe3+ defects distributed across the Ti4+ sites, and thus preferential occupation of Fe3+ within any specific Ti4+ site was not reported. It remains clear that in the present study, and as has been confirmed in a selection of laboratory investigations, that low valence charge balancing cations preferentially occupy the trigonal biprymidal TiO5 site. It follows that the partially occupied nature of this site (50% occupied), relative to Ti(1) and Ti(3), permits the accommodation of cations of varied size.
From examination of the collective substituent behaviour we establish that at low concentrations (e.g. 3%) a selection of charge compensated substitution schemes are viable within the zirconolite-2M phase, and it has been experimentally determined that environmental conditions, chemical activity and ion mobility may dictate the solid solution mechanisms that occur. As the nominal concentration of substitution is increased, it is to be expected that clustering of defects will occur in either the Zr4+ site or Ca2+ site, facilitated by charge compensation on the Ti(2) site. The investigation presented herein shows that substitution schemes involving the Ca2+ site reach lower solution energies when charge balancing with Al3+ on the Ti(2) site, this requires further computational work to elucidate, an interpretation is that Al3+ being smaller than Fe3+ can be accommodated more easily. Nevertheless, these data support the deployment of zirconolite-2M as a potential single host phase for the immobilisation of Pu oxides, and are in general agreement with a selection of recent publications concerning the solid solution behaviour of Ce, U, Th and Pu.
6 Conclusions
We have demonstrated trends in the energetics of zirconolite-2M solid solutions with Ce4+, Pu4+, Th4+, and U4+ cations that are in general agreement with published experimental data concerning the deployment of zirconolite-2M as a host for actinides. Consequently, we have shown that atomistic simulations can effectively guide the formulation development of these materials, and inform experimental validation. For example, using the high throughput methodology developed and reported here, it is possible to rapidly screen many solid solution schemes in silico and evaluate their relative stability, to guide more resource intensive ab initio simulations and laboratory investigation for validation. Indeed, this method should have much wider utility in the exploration in the optimisation of functional materials such as high entropy alloys, capacitor ceramics, and perovskite catalysts. Our investigations have also shown that Ce is not a direct analogue for the actinide cations such as Pu, as has been validated in a number of wasteform development trials.Author contributions
S. D. – data curation, investigation, formal analysis, methodology, software, visualization, writing – original draft, writing – review & editing. C. M. H. – conceptualization, formal analysis, investigation, methodology, software, writing – review & editing. L. R. B. – investigation, validation, writing – review & editing. C. L. F. – project administration, resources, supervision, writing – review & editing. N. C. H. – conceptualization, funding acquisition, project administration, resources, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for financial support from the Nuclear Decommissioning Authority and EPSRC under grant reference EP/S01019X/1 and EP/R511754/1. This research utilised the HADES/MIDAS facility at the University of Sheffield established with financial support from EPSRC and BEIS, under grant EP/T011424/1.66 The computational work was made possible by the resources provided by Research-IT at the University of Sheffield. We would also like to extend our gratitude to Ondřej Krejčí for invaluable input on the presentation of this work.Notes and references
- N. C. Hyatt, npj Mater. Degrad., 2020, 4, 28 CrossRef CAS.
- W. J. Weber, R. C. Ewing, C. A. Angell, G. W. Arnold, A. N. Cormack, J. M. Delaye, D. L. Griscom, L. W. Hobbs, A. Navrotsky, D. L. Price, A. M. Stoneham and M. C. Weinberg, J. Mater. Res., 1997, 12, 1948–1978 CrossRef.
- W. J. Weber, R. C. Ewing, C. R. A. Catlow, T. D. de la Rubia, L. W. Hobbs, C. Kinoshita, H. Matzke, A. T. Motta, M. Nastasi, E. K. H. Salje, E. R. Vance and S. J. Zinkle, J. Mater. Res., 1998, 13, 1434–1484 CrossRef CAS.
- R. C. Ewing, Earth Planet. Sci. Lett., 2005, 229, 165–181 CrossRef CAS.
- R. C. Ewing, Prog. Nucl. Energy, 2007, 49, 635–643 CrossRef CAS.
- N. C. Hyatt and M. I. Ojovan, Materials, 2019, 12, 3611 CrossRef CAS PubMed.
- R. C. Ewing, C. R. Geosci., 2011, 343, 219–229 CrossRef CAS.
- A. E. Ringwood, S. E. Kesson, N. G. Ware, W. Hibberson and A. Major, Nature, 1979, 278, 219–223 CrossRef CAS.
- W. Lutze and R. C. Ewing, Radioactive waste forms for the future, North-Holland, 1988 Search PubMed.
- K. P. Hart, E. R. Vance, M. W. A. Stewart, J. Weir, M. L. Carter, M. Hambley, A. Brownscombe, R. A. Day, S. Leung, C. J. Ball, B. Ebbinghaus, L. Gray and T. Kan, MRS Proceedings, 1997, 506, 161 CrossRef.
- K. Zhang, B. Luo and H. Zhang, Mater. Res. Express, 2019, 6, 115526 CrossRef.
- R. F. Haaker and R. C. Ewing, Naturally occurring crystalline phases: analogues for radioactive waste forms, Richland, WA (United States), 1981 Search PubMed.
- E. R. Vance, G. R. Lumpkin, M. L. Carter, D. J. Cassidy, C. J. Ball, R. A. Day and B. D. Begg, J. Am. Ceram. Soc., 2002, 85, 1853–1859 CrossRef CAS.
- X. Deschanels, V. Picot, B. Glorieux, F. Jorion, S. Peuget, D. Roudil, C. Jégou, V. Broudic, J. N. Cachia, T. Advocat, C. Den Auwer, C. Fillet, J. P. Coutures, C. Hennig and A. Scheinost, J. Nucl. Mater., 2006, 352, 233–240 CrossRef CAS.
- L. R. Blackburn, D. J. Bailey, S.-K. Sun, L. J. Gardner, M. C. Stennett, C. L. Corkhill and N. C. Hyatt, Adv. Appl. Ceram., 2021, 120, 69–83 CrossRef CAS.
- B. M. Gatehouse, I. E. Grey, R. J. Hill and H. J. Rossell, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1981, 37, 306–312 CrossRef.
- H. J. Rossell, Nature, 1980, 283, 282–283 CrossRef CAS.
- M. C. Stennett, C. L. Corkhill, L. A. Marshall and N. C. Hyatt, J. Nucl. Mater., 2013, 432, 182–188 CrossRef CAS.
- B. D. Begg, E. R. Vance and G. R. Lumpkin, MRS Proceedings, 1997, 506, 79 CrossRef.
- B. D. Begg and E. R. Vance, MRS Proceedings, 1996, 465, 333 CrossRef.
- C. Dickson and F. Glasser, Cem. Concr. Res., 2000, 30, 1619–1623 CrossRef CAS.
- W. A. Lambertson, M. H. Mueller and F. H. Gunzel, J. Am. Ceram. Soc., 1953, 36, 397–399 CrossRef CAS.
- P. W. Tasker, Le Journal de Physique Colloques, 1980, 41, C6-488–C6-491 CrossRef.
- M. Gilbert and J. H. Harding, Phys. Chem. Chem. Phys., 2011, 13, 13021 RSC.
- L. Veiller, J.-P. Crocombette and D. Ghaleb, J. Nucl. Mater., 2002, 306, 61–72 CrossRef CAS.
- H. R. Foxhall, K. P. Travis, L. W. Hobbs, S. C. Rich and S. L. Owens, Philos. Mag., 2013, 93, 328–355 CrossRef CAS.
- H. R. Foxhall, K. P. Travis and S. L. Owens, J. Nucl. Mater., 2014, 444, 220–228 CrossRef CAS.
- J. Tanti and N. Kaltsoyannis, J. Nucl. Mater., 2021, 543, 152525 CrossRef CAS.
- J. A. Fortner, A. J. Kropf, A. J. Bakel, M. C. Hash, S. B. Aase, E. C. Buck and D. B. Chamberlain, MRS Proceedings, 1999, 608, 401 CrossRef.
- J. A. Fortner, A. J. Kropf, R. J. Finch, A. J. Bakel, M. C. Hash and D. B. Chamberlain, J. Nucl. Mater., 2002, 304, 56–62 CrossRef CAS.
- C. Nästren, R. Jardin, J. Somers, M. Walter and B. Brendebach, J. Solid State Chem., 2009, 182, 1–7 CrossRef.
- D. J. Gregg, Y. Zhang, S. C. Middleburgh, S. D. Conradson, G. Triani, G. R. Lumpkin and E. R. Vance, J. Nucl. Mater., 2013, 443, 444–451 CrossRef CAS.
- S. Finkeldei, M. C. Stennett, P. M. Kowalski, Y. Ji, E. de Visser-Týnová, N. C. Hyatt, D. Bosbach and F. Brandt, J. Mater. Chem. A, 2020, 8, 2387–2403 RSC.
- R. L. Miller and G. A. Reimann, Thermodynamics of gas-metal-slag equilibria for applications in in situ and ex situ vitrification melts, 1993 Search PubMed.
- P. Loiseau, D. Caurant, N. Baffier, L. Mazerolles and C. Fillet, J. Nucl. Mater., 2004, 335, 14–32 CrossRef CAS.
- G. R. Lumpkin, K. R. Whittle, C. J. Howard, Z. Zhang, F. J. Berry, G. Oates, C. T. Williams and A. N. Zaitsev, MRS Proceedings, 2006, 932, 53.1 CrossRef.
- K. R. Whittle, N. C. Hyatt, K. L. Smith, I. Margiolaki, F. J. Berry, K. S. Knight and G. R. Lumpkin, Am. Mineral., 2012, 97, 291–298 CrossRef CAS.
- F. J. Berry, G. R. Lumpkin, G. Oates and K. R. Whittle, Hyperfine Interact., 2006, 166, 363–366 CrossRef.
- M. R. Gilbert, C. Selfslag, M. Walter, M. C. Stennett, J. Somers, N. C. Hyatt and F. R. Livens, IOP Conf. Ser.: Mater. Sci. Eng., 2010, 9, 012007 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS.
- M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Clarendon Press, 1954 Search PubMed.
- B. G. Dick and A. W. Overhauser, Phys. Rev., 1958, 112, 90–103 CrossRef.
- C. G. Broyden, Mathematics of Computation, 1970, 24, 365 CrossRef.
- R. Fletcher, Comput. J., 1970, 13, 317–322 CrossRef.
- D. Goldfarb, Mathematics of Computation, 1970, 24, 23 CrossRef.
- D. F. Shanno, Mathematics of Computation, 1970, 24, 647 CrossRef.
- T. S. Bush, J. D. Gale, C. R. A. Catlow and P. D. Battle, J. Mater. Chem., 1994, 4, 831 RSC.
- S. M. Woodley, P. D. Battle, J. D. Gale and C. R. A. Catlow, Phys. Chem. Chem. Phys., 1999, 1, 2535–2542 RSC.
- M. Nadeem, M. J. Akhtar, R. Shaheen, M. N. Haque and a Y. Khan, J. Mater. Sci. Technol., 2001, 17, 638–642 CAS.
- C. R. A. Catlow, in Solid State Chemistry Techniques, Clarendon Press, 1987, ch. 7 Search PubMed.
- A. A. Coelho, R. W. Cheary and K. L. Smith, J. Solid State Chem., 1997, 129, 346–359 CrossRef CAS.
- L. R. Blackburn, S. Sun, L. J. Gardner, E. R. Maddrell, M. C. Stennett and N. C. Hyatt, J. Nucl. Mater., 2020, 535, 152137 CrossRef CAS.
- B. D. Begg, E. R. Vance, R. Day, M. Hambley and S. D. Conradson, MRS Proceedings, 1996, 465, 325 CrossRef.
- C. Meng, X. Ding, W. Li, J. Zhao and H. Yang, J. Mater. Sci., 2016, 51, 5207–5215 CrossRef CAS.
- B. D. Begg, R. A. Day and A. Brownscombe, MRS Proceedings, 2000, 663, 259 CrossRef.
- P. A. Bingham, R. J. Hand, M. C. Stennett, N. C. Hyatt and M. T. Harrison, MRS Proceedings, 2008, 1107, 421 CrossRef.
- M. V. Zamoryanskaya and B. E. Burakov, MRS Proceedings, 2000, 663, 301 CrossRef.
- L. R. Blackburn, S. Sun, L. J. Gardner, E. R. Maddrell, M. C. Stennett, C. L. Corkhill and N. C. Hyatt, J. Am. Ceram. Soc., 2020, 2 Search PubMed.
- P. Loiseau, D. Caurant, N. Baffier and C. Fillet, MRS Proceedings, 2002, 757, II6.3 CrossRef.
- S. Ji, M. Su, C. Liao, S. Ma, Z. Wang, K. Shih, C. Chang, J. Lee, T. Chan and Y. Li, J. Am. Ceram. Soc., 2020, 103, 1463–1475 CrossRef CAS.
- S. D. Forder, P. A. Bingham, O. J. McGann, M. C. Stennett and N. C. Hyatt, Hyperfine Interact., 2013, 217, 83–90 CrossRef CAS.
- L. R. Blackburn, S.-K. Sun, S. M. Lawson, L. J. Gardner, H. Ding, C. L. Corkhill, E. R. Maddrell, M. C. Stennett and N. C. Hyatt, J. Eur. Ceram. Soc., 2020, 40, 5909–5919 CrossRef CAS.
- E. R. Vance, C. J. Ball, R. A. Day, K. L. Smith, M. G. Blackford, B. D. Begg and P. J. Angel, J. Alloys Compd., 1994, 213–214, 406–409 CrossRef.
- L. R. Blackburn, S. K. Sun, L. J. Gardner, E. R. Maddrell, M. C. Stennett and N. C. Hyatt, MRS Adv., 2020, 5, 93–101 CrossRef CAS.
- N. C. Hyatt, C. L. Corkhill, M. C. Stennett, R. J. Hand, L. J. Gardner and C. L. Thorpe, IOP Conf. Ser.: Mater. Sci. Eng., 2020, 818, 012022 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra02914b |
| This journal is © The Royal Society of Chemistry 2021 |