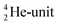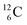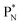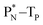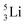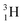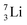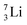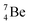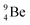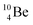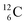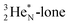Open Access Article
Open Access ArticleSynchronizing chemistry, quantum mechanics and radioactivity in a revolutionary renewed atom model. Part 1: the elements where Z is 1–10 (H, He, Li, Be, B, C, N, O, F, Ne)
Gerard W. M. Visser and
Albert D. Windhorst *
*
Amsterdam UMC, Vrije Universiteit Amsterdam, Dept. Radiology & Nuclear Medicine, De Boelelaan 1117, 1081HV Amsterdam, The Netherlands. E-mail: ad.windhorst@amsterdamumc.nl
First published on 19th August 2021
Abstract
The alliance between the reigning quantum mechanical atom model and chemistry still is a difficult one when it comes to an adequate explanation for e.g. the covalent bond, inversion, chirality, or hydrogen bonds. Overruling Rutherford's extrapolation from gold to hydrogen, an atom model is described that provides improved answers to these phenomena while the hybridization principle and the covalent bond are re-defined by giving neutrons a much more prominent role than they have in the reigning quantum mechanical model. It is postulated that a neutron is not just there to assist the strong force in surpassing the repulsive coulombic forces between the protons in the nucleus, but the neutron is the modus operandi of molecular geometry, and as such plays a part in chemical reactivity, bond length and bond strength.
1 Introduction
Based on the experience that an atom contains positive and negative charges, Thomson was the first to design a model of the atom (1904).1,2 The positive charge formed a ball of even density, with the negatively charged electrons floating in the ball and forming regular geometric patterns by mutual repulsion. From the famous experiment (bombarding thin gold foils with alpha particles) performed by his students, Rutherford concluded in 1911 that Thompson's model required a serious adjustment: the complete positive charge and almost the entire mass of an atom are concentrated in a very small volume, the dense inner core of an atom, the nucleus.3 This solar system model (electrons revolving in circular or elliptical orbits around the nucleus like planets around the sun) evolved via Bohr4 and Schrodinger/Heisenberg5,6 into the quantum mechanical atom model of today. This means a model with orbitals/probability clouds (areas within which an electron can be encountered) instead of orbits of an electron, and with neutrons plus protons bound together by the so-called strong force in the nucleus, accounting for 99.9% of the atom's mass. This strong force surpasses the Coulomb repulsion between the protons; if not, the nucleus of the atom converts to an energetically better situation by radioactive decay. In the latter case, the so-called weak nuclear force plays a role.With respect to chemical aspects, the octet rule (1916) had been implemented as the closed shell principle, the “Aufbau principle” had seen the light, and Pauling7 had developed the hybridization concept (sp3 for single-bonded carbon, sp2 for double-bonded carbon, sp1 for triple-bonded carbon) as a proposition to account for the otherwise inexplicable fact that e.g. CH4 contains four equal CH-bonds. This hybridization concept also solved the issue of how a p-electron crosses a node and passes through the positively charged nucleus. A covalent bond became the result of overlap between two orbitals (two interfering waves, each with one electron) and two paired electrons, inversion (e.g. the NH3 molecule) and hydrogen bonds became the result of spontaneous tunneling.8,9 Even empty orbitals could exhibit chemical reactivity such as the empty p-orbital of boron and alumina, and empty d-orbitals in case of octet rule disobeying compounds like H3PO4, H2SO4 or HClO4. The octet rule disobeying HNO3 remained a nuisance, because nitrogen's quantum number n = 2 forbids the presence of d-orbitals; only a Lewis structure remained descriptive for this compound.10
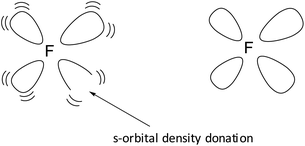
At around the time Ogilvie questioned the whole orbital concept,11 we added an extra dimension to Pauling's geometric s-electron hybridization parameter. Organic fluorine chemistry is rather unusual and numerous dichotomies exist.12 Some of these are accounted for by hypotheses like ‘double-bond no-bond resonance’13 or ‘large repulsion integrals in the carbon-fluorine region’.14 In an attempt to improve on this, we launched the concept of the s-orbital density deficiency of the F-atom as the driving force of its chemical behavior.15–17 This concept was based on the quantum mechanical fact that lone pairs require more than their s-share in the sp3-hybridization process.18 Since F possesses three lone pairs, we postulated (1) that the F-atom is urgently in need for additional s-orbital density via its bonding orbital, to release this tension (see Fig. 1), and (2) that the hydrogen atom and the carbon atom are the perfect s-orbital density donors for the F-atom.
According to this concept, the F-atom in F2 is the most s-orbital density deficient, leading to a weak F–F bond and extreme reactivity; in CH3COOF this situation is slightly better and therefore it reacts less vigorous. Over and above that, although being the most electronegative element in the periodic system, when present as fluoride in water, the F-atom immediately shares its extra electron to form HF in exchange for s-orbital density, whereas fluoride is a strong nucleophile in the absence of H2O. The concept also made clear why in organic chemistry the F-atom prefers to be bound to sp3-carbon over sp2-carbon: the sp2-carbon atom had to use a great deal of its s-orbital density to construct the double bond and, therefore, its s-orbital density donor ability towards fluorine is diminished.
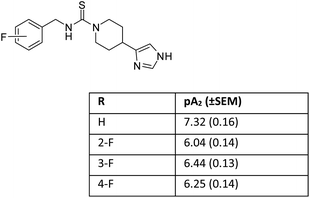
Later on, we reported that in a series of mono-substituted benzyl analogues of thioperamide, the aromatic F-derivatives showed, in contrast to computer predictions, a factor 10 less in vitro activity than its H, Cl, Br, and I counterparts (Fig. 2).19
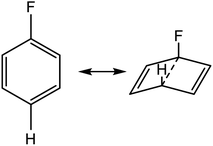
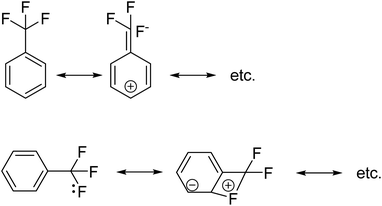
We postulated that the aromatic ring of the fluor derivative was not flat anymore,20 because F had forced the sp2-carbon of the aromatic ring to re-hybridize into a sp3-like carbon, leading to a Dewar benzene-like structure with reduced affinity for the receptor. In addition, we argued that also for fluorobenzene itself the literature data21 (ipso angle increase and apparent bond shortening plus angle decrease for C2 and C3) strongly point to a non-flat configuration (Fig. 3 and 4).
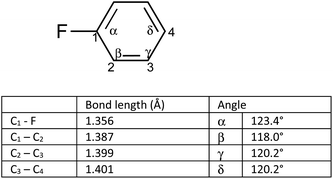 | ||
| Fig. 4 Apparent bond shortening and angle changes when projected in flat fluorobenzene (angles and bond lengths are from 21). | ||
The last decennia we have tried to find an adequate explanation for the re-hybridization phenomenon. We gradually came to the inevitable conclusion that the reigning atom model needed adjustment, and hereto some serious ‘out of the box thinking’ was required. Besides finding a concrete answer to the fluorine problem, it would be an added bonus when at the same time this renewed atom model would also comprise an adequate solution for phenomena like inversion, chirality and hydrogen bonds, and the reason for stability and instability of an atom. In this paper we report our proposal for such an atom model adjustment. The renewed atom model is based on the key premise that Rutherford's extrapolation of the findings for the heavy gold atom (Z = 79) to the lighter atoms, is not correct.
2 The new model
2.1 Central thesis and definitions
In this part 1 paper we discuss our proposition for the atom configuration of the elements with Z = 1–10. We will just stick to the level of protons and neutrons held together by the strong force via quarks. Production and decay of their radioactive isotopes are used as confirmation of the proposed atom structure.The new model will be discussed along the following lines:
(2) This flexible constellation of neutrons and protons is strictly organized. Two protons are always separated from each other by a neutron; two neutrons are always separated from each other by a proton.
(3) In each constellation a neutron can bind to three protons at most, a proton can bind to three neutrons at most, because each have three strong force related quarks.
(4) In the strictly organized constellation of neutrons and protons each electron remains revolving in a probability cloud around its proton.
(5) A “square” proton or “square” neutron can be part of the strictly organized constellation of neutrons and protons. A square proton is defined as a proton that carries an electron that is too low in energy to chemically bind to another atom and therefore needs to become activated by a neutron (hybridization); a square neutron is defined as a neutron that is too low in energy to activate a square proton or to take part in hybridization.
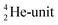 . Throughout the paper, the two neutrons of the
. Throughout the paper, the two neutrons of the 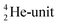 will be called the anchor neutron side and will be drawn on top; the two protons of the
will be called the anchor neutron side and will be drawn on top; the two protons of the 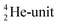 will be called the anchor proton side and will be drawn on the low side (Fig. 5). Subunits at the anchor neutron side will bear the subscript N, subunits at the anchor proton side subscript P.
will be called the anchor proton side and will be drawn on the low side (Fig. 5). Subunits at the anchor neutron side will bear the subscript N, subunits at the anchor proton side subscript P.Nomenclature used for the subunits at the basic building block:
(a) PN is a proton at the anchor neutron side of the basic building block; NP is a neutron at the anchor proton side;
(b) DN is a subunit consisting of a neutron and a proton at the anchor neutron side; DP is the same subunit at the anchor proton side;
(c) TP is a subunit consisting of two neutrons and a proton at the anchor proton side; a TN subunit is only present in extremely short-living radioisotopes.
(d) 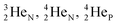 and
and 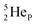 are subunits consisting of two protons and one, two or three neutrons, respectively, at the anchor (N or P) sides, and correspond chemically with a lone pair and quantum mechanically with a filled subshell;
are subunits consisting of two protons and one, two or three neutrons, respectively, at the anchor (N or P) sides, and correspond chemically with a lone pair and quantum mechanically with a filled subshell; 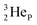 and
and 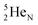 are only present in extremely short-living radioisotopes.
are only present in extremely short-living radioisotopes.
(e) The * in subunits 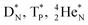 and
and 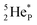 indicate that they bear a square neutron; PN and
indicate that they bear a square neutron; PN and 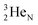 nearly always bear a square proton.
nearly always bear a square proton.
(f) A covalent bond implies formation of a “chemical” helium-unit between a PN, DN, DP or TP subunit of one atom and one of the subunits of the other atom.
(g) In the figures, the neutrons are depicted yellow, the protons blue; square neutrons are depicted as yellow stars, square protons as blue stars; in unstable atoms, neutrons are depicted pink, protons red. For the sake of clarity, in atoms Z = 5 and higher, the anchor neutrons of the basic building 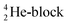 are depicted white, the anchor protons dark grey.
are depicted white, the anchor protons dark grey.
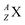 wherein mass number A represents the number of protons plus neutrons, atomic number Z the number of protons, and X the element.
wherein mass number A represents the number of protons plus neutrons, atomic number Z the number of protons, and X the element.– A nuclear reaction is denoted as X (a, b) Y wherein X is the target element, a is the incoming particle, b is the outgoing particle and Y the newborn isotope; as a consequence of the impact, radioisotopes produced in a cyclotron or neutron generator do not contain square protons or square neutrons.
– Because in the new model every proton is separated by a neutron and visa versa (thesis 2, vide supra), the newborn proton formed after β−-decay requires a shift within the constellation of the atom (away from the proton to which the disintegrated neutron was attached). The newborn neutron formed after β+-decay needs a likewise transfer (away from the neutron to which the disintegrated proton was attached).
– An isomeric transition (IT) is a transfer of a neutron within the constellation of the atom to an energetically more favorable position (often temporarily better).
– Electron capture (EC) implies a transfer of the newborn neutron away from the neutron to which the proton was attached before capturing its electron.
Most of the production routes and decay modes can be found in the book Radionuclide Transformations.22 Because individual referring to physicists involved in accurate determination of half-lives and isotope abundancies would make the reference list extremely long, we would like to thank them warmly here.
2.2 The new model at work: the carbon atom (Z = 6)
In organic chemistry, atom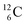 can be regarded as the central atom of the hybridization principle. Therefore, as a first illustration of the new atom model the constellation of
can be regarded as the central atom of the hybridization principle. Therefore, as a first illustration of the new atom model the constellation of 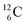 is described (Fig. 6).
is described (Fig. 6).
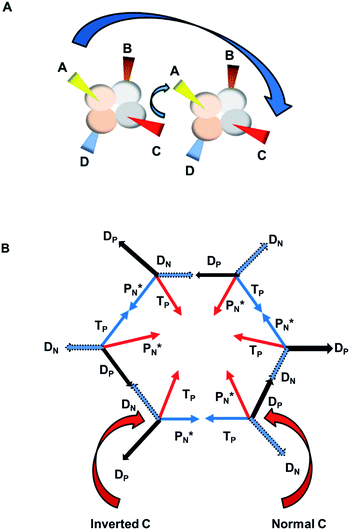
The 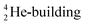 block contains as subunits at the anchor neutron side a
block contains as subunits at the anchor neutron side a 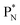 and a DN, at the anchor proton side a DP and a TP. The anchor
and a DN, at the anchor proton side a DP and a TP. The anchor 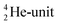 can flip, leading to chemical inversion in so-called SN2 reactions. The atom exhibits stereo isomerism in case four different chemical groups are bound to the atom: the inverted constellation is the enantiomer of the non-inverted one (Fig. 6).
can flip, leading to chemical inversion in so-called SN2 reactions. The atom exhibits stereo isomerism in case four different chemical groups are bound to the atom: the inverted constellation is the enantiomer of the non-inverted one (Fig. 6).
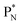 with TP and DN with DP. This represents the common symmetrical sp3-hybridization and is present in the tetrahedral compound CH4 (and covers at the same time the observed subtle difference in bond strength of the four C–H bonds of the CH4 molecule23). The second mode of hybridization is
with TP and DN with DP. This represents the common symmetrical sp3-hybridization and is present in the tetrahedral compound CH4 (and covers at the same time the observed subtle difference in bond strength of the four C–H bonds of the CH4 molecule23). The second mode of hybridization is 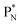 with DN and TP with DP. In this hybridization mode, the distance between the anchor protons is slightly larger and is present in e.g. staggered carbon–carbon chains with the hybridized
with DN and TP with DP. In this hybridization mode, the distance between the anchor protons is slightly larger and is present in e.g. staggered carbon–carbon chains with the hybridized  bearing the hydrogen atoms.
bearing the hydrogen atoms.Multiple bonds formed in the new model are intrinsically the concretization of the banana or bent bonds, whose description had already been shown to be energetically superior to the symmetry-restricted σ, π bond representation of Hückel.24–27
The subunits (PN, DN, TP, DP) can form several double and triple bonds combinations, dependent on the history of the sample and the chemical group R. One may, however, expect the most energetically balanced, symmetrical molecule to be formed, especially at higher temperatures. In that case, the favorite combinations in double bonds, therefore, will be (1) DP with TP, and TP with DP, (2) 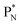 with TP, and TP with
with TP, and TP with 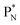 or (3) DP with DN, and DN with DP. Option (1) will be the case in e.g. ethylene (C2H4) with the hydrogen atoms at the hybridized
or (3) DP with DN, and DN with DP. Option (1) will be the case in e.g. ethylene (C2H4) with the hydrogen atoms at the hybridized 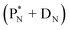 . Allenes provide an elegant example of option (2) and (3) in this respect, because in allenes the central carbon atom possesses both favorite symmetrical combinations, giving rise to the well-known two-bladed propeller geometry.28
. Allenes provide an elegant example of option (2) and (3) in this respect, because in allenes the central carbon atom possesses both favorite symmetrical combinations, giving rise to the well-known two-bladed propeller geometry.28
The favorite combination in triple bonds will be DP with TP, TP with DP, and DN with DN wherein the neutron of TP is hybridized with 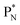 . In e.g. acetylene (C2H2) this
. In e.g. acetylene (C2H2) this 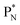 bears the hydrogen atom. Molecule N2 also possesses this triple bond combination (vide infra, paragraph 2.4).
bears the hydrogen atom. Molecule N2 also possesses this triple bond combination (vide infra, paragraph 2.4).
The structure of benzene is an intriguing one in the new model. As shown in Fig. 7A, when a symmetrical double bond is created between A and C of two ‘normal’ carbon atoms, B and D end up in a cis-position. So formation of the symmetrical double bond 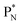 with TP and TP with
with TP and TP with 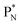 , leads to a cis-position of the DP's (and cis-position for the DN's). The same symmetrical double bond, but with one of the carbon atoms inverted, leads to a trans-position of the DP's. By combining alternatingly three “normal” and three “inverted” carbon atoms in the way shown in Fig. 7B, for benzene a fascinating structure is obtained wherein a double bond between
, leads to a cis-position of the DP's (and cis-position for the DN's). The same symmetrical double bond, but with one of the carbon atoms inverted, leads to a trans-position of the DP's. By combining alternatingly three “normal” and three “inverted” carbon atoms in the way shown in Fig. 7B, for benzene a fascinating structure is obtained wherein a double bond between 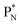 and TP can be formed to the left and to the right. Or in other words, a resonance system is created that answers the famous Kekulé benzene-structure problem from 1865.29,30 Other examples of
and TP can be formed to the left and to the right. Or in other words, a resonance system is created that answers the famous Kekulé benzene-structure problem from 1865.29,30 Other examples of 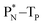 resonance, namely between C and O, will be dealt with in paragraph 2.4.
resonance, namely between C and O, will be dealt with in paragraph 2.4.
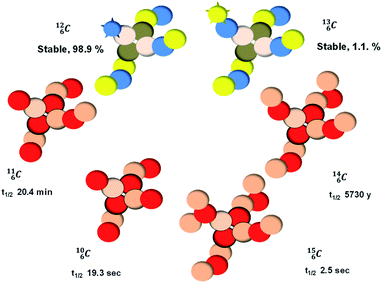
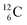 , atom
, atom 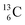 bears a
bears a 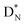 instead of a
instead of a 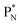 . This constellation of a carbon atom appears to be stable also, but the abundancy of
. This constellation of a carbon atom appears to be stable also, but the abundancy of 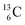 is not high (1.1% abundance) (Fig. 8).
is not high (1.1% abundance) (Fig. 8).
The well-known long-living carbon isotope 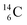 (t1/2 of 5730 y, decays to
(t1/2 of 5730 y, decays to 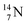 ) bears two DN's and two TP's. In the
) bears two DN's and two TP's. In the 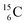 atom there is no obvious place for the additional neutron: an exotic TN is formed, and this isotope decays immediately (t1/2 2.5 s, decays to
atom there is no obvious place for the additional neutron: an exotic TN is formed, and this isotope decays immediately (t1/2 2.5 s, decays to 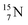 ). Radioisotope
). Radioisotope 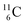 (t1/2 20.4 min, decays to
(t1/2 20.4 min, decays to 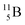 ) bears, compared to
) bears, compared to 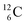 , a DP instead of a TP, while in radioisotope
, a DP instead of a TP, while in radioisotope 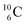 (t1/2 19.3 s, decays to
(t1/2 19.3 s, decays to 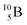 ) also the neutron at the DN is missing (Fig. 8). From the latter constellation, it can be concluded that
) also the neutron at the DN is missing (Fig. 8). From the latter constellation, it can be concluded that 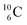 is the last carbon isotope that can chemically react as carbon. For the radioisotopes
is the last carbon isotope that can chemically react as carbon. For the radioisotopes 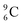 and
and 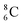 there is no obvious place for the proton, and these radioisotopes are therefore extremely fast deteriorating nuclei, ending up as α-particles, mostly via proton loss.
there is no obvious place for the proton, and these radioisotopes are therefore extremely fast deteriorating nuclei, ending up as α-particles, mostly via proton loss.
In the new atom model, the weak nuclear force is transformed into a stability rule for each anchor side. The carbon isotopes 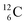 and
and 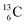 allow the deriving of these stability rules. The summarized subunits at the anchor proton side of the carbon isotopes
allow the deriving of these stability rules. The summarized subunits at the anchor proton side of the carbon isotopes 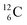 and
and 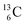 give n = 3, p = 2, with n for neutron and p for proton. When n = 2, p = 2
give n = 3, p = 2, with n for neutron and p for proton. When n = 2, p = 2 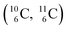 or n = 4, p = 2
or n = 4, p = 2 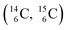 , the atom is instable. So our new model indicates that in order to be stable, the summarized number of neutrons at the anchor proton side should exceed that of protons by exactly one i.e. should follow the stability rule n = p + 1. Applying the same approach for the anchor neutron side, and counting a square neutron or proton for ½, the stability rule for
, the atom is instable. So our new model indicates that in order to be stable, the summarized number of neutrons at the anchor proton side should exceed that of protons by exactly one i.e. should follow the stability rule n = p + 1. Applying the same approach for the anchor neutron side, and counting a square neutron or proton for ½, the stability rule for 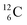 and
and 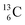 appears to be n = p − ½, namely n = 1, p = 1½ for
appears to be n = p − ½, namely n = 1, p = 1½ for 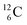 and n = 1½, p = 2 for
and n = 1½, p = 2 for 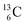 . Because radioisotopes produced in a cyclotron or neutron generator do not contain square protons or square neutrons (vide supra 1.1), the four carbon radioisotopes
. Because radioisotopes produced in a cyclotron or neutron generator do not contain square protons or square neutrons (vide supra 1.1), the four carbon radioisotopes 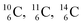 and
and 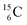 deviate from the anchor neutron stability rule as well. In the new atom model, conversion will, therefore, take place until the new-born constellations comply to both rules.
deviate from the anchor neutron stability rule as well. In the new atom model, conversion will, therefore, take place until the new-born constellations comply to both rules.
2.3 The elements Z = 1–6
For an insight in how we arrived at the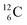 atom constellation, and for a demonstration of the general applicability of the stability rules, first a short overview of the atom configuration of the elements with Z = 1–6 in the new model.
atom constellation, and for a demonstration of the general applicability of the stability rules, first a short overview of the atom configuration of the elements with Z = 1–6 in the new model.
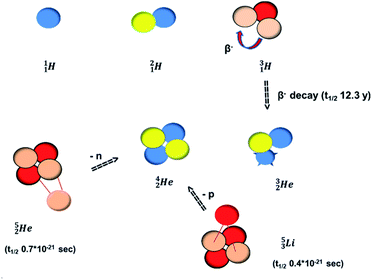
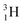 (t1/2 12.3 y), also called tritium, and its daughter
(t1/2 12.3 y), also called tritium, and its daughter 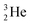 (Fig. 9).
(Fig. 9).
At the same time, the 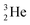 -atom can be taken as the prototype of an atom that bears a square proton (Fig. 9). Because of this square proton, the
-atom can be taken as the prototype of an atom that bears a square proton (Fig. 9). Because of this square proton, the 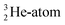 is stable and in fact it is the only stable atom in the periodic system with more protons than neutrons. Its abundancy is only 1.34 × 10−4%, so most probably originating solely from the decay of cosmic-produced
is stable and in fact it is the only stable atom in the periodic system with more protons than neutrons. Its abundancy is only 1.34 × 10−4%, so most probably originating solely from the decay of cosmic-produced 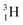 . With the noble gas
. With the noble gas 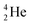 , a unit consisting of two neutrons and two protons alternatingly linked with each other, the first row ends. When adding an additional neutron at the anchor proton side, forming
, a unit consisting of two neutrons and two protons alternatingly linked with each other, the first row ends. When adding an additional neutron at the anchor proton side, forming 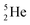 , the neutron is immediately emitted (t1/2 0.7 × 10−21 s).
, the neutron is immediately emitted (t1/2 0.7 × 10−21 s).
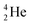 as building block, it appears that the addition of a proton as the only subunit is not accepted (Fig. 9): from the thus assembled
as building block, it appears that the addition of a proton as the only subunit is not accepted (Fig. 9): from the thus assembled 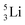 the proton is immediately emitted (t1/2 0.4 × 10−21 s). Adding a proton to the anchor neutron side requires compensation in the form of a neutron at the anchor proton side. What is more, the latter new neutron as well as the new proton are shared to evenly divide the burden of the new situation. With this shared neutron between the anchor protons, two stable isotopes of lithium exist:
the proton is immediately emitted (t1/2 0.4 × 10−21 s). Adding a proton to the anchor neutron side requires compensation in the form of a neutron at the anchor proton side. What is more, the latter new neutron as well as the new proton are shared to evenly divide the burden of the new situation. With this shared neutron between the anchor protons, two stable isotopes of lithium exist: 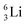 (abundancy 7.6%) bearing a shared
(abundancy 7.6%) bearing a shared 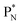 at the anchor neutron side, and
at the anchor neutron side, and 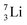 (abundancy 92.4%) bearing a shared
(abundancy 92.4%) bearing a shared 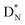 at the anchor neutron side (Fig. 10 and 11).
at the anchor neutron side (Fig. 10 and 11).
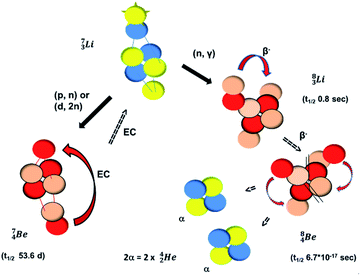
Introduction of a neutron at each anchor proton is too much: when the anchor proton side of 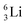 is hit by a neutron the composite atom breaks down into
is hit by a neutron the composite atom breaks down into 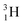 and an α-particle
and an α-particle 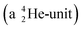 ,31 whereas with the (n, γ) reaction on
,31 whereas with the (n, γ) reaction on 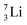 , giving
, giving 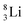 , a radioisotope with a t1/2 of 0.8 s is produced.32
, a radioisotope with a t1/2 of 0.8 s is produced.32
Concerning the stability rules, 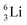 and
and 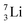 both follow the new rules, with n = 1, p = 0 at the anchor proton side, and n = 0, p = ½ and n = ½, p = 1 at the anchor neutron side, respectively.
both follow the new rules, with n = 1, p = 0 at the anchor proton side, and n = 0, p = ½ and n = ½, p = 1 at the anchor neutron side, respectively. 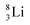 possesses with n = 2, p = 0 at the anchor proton side a neutron too much. Notably, for
possesses with n = 2, p = 0 at the anchor proton side a neutron too much. Notably, for  and
and 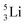 neither β−-decay nor β+-decay leads to a stable situation, leaving emission of the additional neutron and proton, respectively, as the only option.
neither β−-decay nor β+-decay leads to a stable situation, leaving emission of the additional neutron and proton, respectively, as the only option.
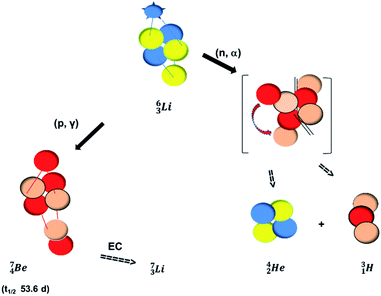
The beryllium (Be) isotopes reveal that the requirements for the addition of the second proton onto the 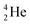 backbone are also very stringent and delicate (Fig. 12). At the anchor proton side, only a constellation wherein the shared neutron is replaced by a shared TP appears acceptable, whereas at the anchor neutron side only a shared
backbone are also very stringent and delicate (Fig. 12). At the anchor proton side, only a constellation wherein the shared neutron is replaced by a shared TP appears acceptable, whereas at the anchor neutron side only a shared 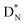 is accepted, yielding the
is accepted, yielding the 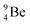 atom (100% abundancy).
atom (100% abundancy).
The proposed 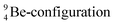 deviates from the Aufbau principle, but is perfectly in accordance with the chemistry of Be: linear molecular geometry i.e. formation of linear compounds. In addition,
deviates from the Aufbau principle, but is perfectly in accordance with the chemistry of Be: linear molecular geometry i.e. formation of linear compounds. In addition, 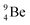 follows with its n = 2, p = 1 at the anchor proton side, and its n = ½, p = 1 at the anchor neutron side the stability rules.
follows with its n = 2, p = 1 at the anchor proton side, and its n = ½, p = 1 at the anchor neutron side the stability rules.
Whereas for lithium the constellation with a shared 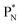 at the anchor neutron side
at the anchor neutron side 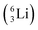 is already a minority, such constellation for beryllium, i.e.
is already a minority, such constellation for beryllium, i.e. 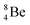 , does not exist. Radioisotope
, does not exist. Radioisotope 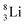 (t1/2 of 0.8 s)33 converts its DN-neutron into a proton at one of the NP's, producing an extremely unstable (t1/2 6.7 × 10−17 s) sort of “open”
(t1/2 of 0.8 s)33 converts its DN-neutron into a proton at one of the NP's, producing an extremely unstable (t1/2 6.7 × 10−17 s) sort of “open” 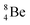 , an atom that, instead of recombining into a constellation with a shared
, an atom that, instead of recombining into a constellation with a shared 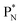 and shared TP, energetically prefers to break down into two α-particles (Fig. 11). A similar sort of break down was observed for the composite atom produced by neutron bombardment of
and shared TP, energetically prefers to break down into two α-particles (Fig. 11). A similar sort of break down was observed for the composite atom produced by neutron bombardment of 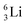 (Fig. 10). Radioisotope
(Fig. 10). Radioisotope 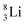 is not the only radioisotope that ends up as α-particles in this way: the boron radioisotopes
is not the only radioisotope that ends up as α-particles in this way: the boron radioisotopes 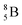 , after β+-decay, and
, after β+-decay, and 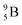 , after proton emission, also end up as α-particles via this “open”
, after proton emission, also end up as α-particles via this “open” 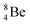 (vide infra). Radioisotope
(vide infra). Radioisotope 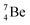 is an unstable Be-isotope with a shared DP between the anchor protons. It can be produced via a (p, γ) reaction on
is an unstable Be-isotope with a shared DP between the anchor protons. It can be produced via a (p, γ) reaction on 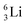 34 and via a (p, n)35 or (d, 2n)36 reaction on
34 and via a (p, n)35 or (d, 2n)36 reaction on 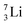 (Fig. 10 and 11). The impact of the proton takes place at the shared neutron between the anchor protons. In the case of the (p, n) on
(Fig. 10 and 11). The impact of the proton takes place at the shared neutron between the anchor protons. In the case of the (p, n) on 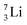 , the neutron at the
, the neutron at the 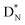 is thrown out; in the (d, 2n) reaction, the second neutron is the neutron from the deuterium particle that is turned aside without interaction with the nucleus. With a t1/2 of 53.6 d, the proton of the shared DP at the anchor proton side of
is thrown out; in the (d, 2n) reaction, the second neutron is the neutron from the deuterium particle that is turned aside without interaction with the nucleus. With a t1/2 of 53.6 d, the proton of the shared DP at the anchor proton side of 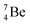 is converted into a square neutron at the shared PN, giving
is converted into a square neutron at the shared PN, giving 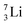 .
.
In radioisotope 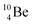 , produced by a (n, γ) reaction on
, produced by a (n, γ) reaction on 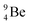 ,37 the shared TP -proton bears a neutron. The atom is unstable, decaying to
,37 the shared TP -proton bears a neutron. The atom is unstable, decaying to 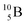 (vide infra), but it is a very slow conversion (t1/2 1.39 × 106 y), most likely owing to the balance and symmetry in the constellation. For radioisotope
(vide infra), but it is a very slow conversion (t1/2 1.39 × 106 y), most likely owing to the balance and symmetry in the constellation. For radioisotope 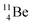 , there is no obvious place for the additional neutron: an exotic TN is formed, yielding a very unstable isotope (t1/2 13.7 s), decaying to
, there is no obvious place for the additional neutron: an exotic TN is formed, yielding a very unstable isotope (t1/2 13.7 s), decaying to 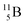 (vide infra).
(vide infra).
The discovery of the neutron in 1932 by Chadwick came from α-bombardment of 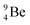 , producing
, producing 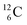 .38 As illustration of our model, nuclear bombardment with α′s or nuclear transformations in which an α-particle is eliminated from the atom, provide in general too many possibilities to be used as proof by logical argument. But because the α-impact on the
.38 As illustration of our model, nuclear bombardment with α′s or nuclear transformations in which an α-particle is eliminated from the atom, provide in general too many possibilities to be used as proof by logical argument. But because the α-impact on the 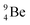 atom from four sides is the same, in this special case we refer to Chadwick's groundbreaking experiment. Upon α-bombardment of
atom from four sides is the same, in this special case we refer to Chadwick's groundbreaking experiment. Upon α-bombardment of 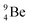 , the impact of the two α-protons takes place at the anchor neutron and at the neutron at the anchor proton side (Fig. 12). The shared DN and TP subunits at the anchor neutron and anchor proton side break open at the side of the impact. One deuteron-fragment from the α-particle binds at the freed NP-neutron at the anchor proton side, the proton of the second deuteron part from the α-particle is incorporated at the freed anchor neutron while the remaining neutron of the second deuteron part of the α-particle is turned aside without interaction with the nucleus.
, the impact of the two α-protons takes place at the anchor neutron and at the neutron at the anchor proton side (Fig. 12). The shared DN and TP subunits at the anchor neutron and anchor proton side break open at the side of the impact. One deuteron-fragment from the α-particle binds at the freed NP-neutron at the anchor proton side, the proton of the second deuteron part from the α-particle is incorporated at the freed anchor neutron while the remaining neutron of the second deuteron part of the α-particle is turned aside without interaction with the nucleus.
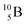 and
and 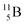 are the first stable atoms that contain four separated subunits: both atoms bear a DN, an NP and a DP, whereas
are the first stable atoms that contain four separated subunits: both atoms bear a DN, an NP and a DP, whereas 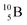 bears as the fourth a
bears as the fourth a 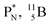 a
a 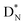 (Fig. 13 and 14). Consequently, the chemical versatility is increased. At the anchor proton side, the DP can combine with the NP and form a (formal) plus situation analogous to the one at the anchor proton side of
(Fig. 13 and 14). Consequently, the chemical versatility is increased. At the anchor proton side, the DP can combine with the NP and form a (formal) plus situation analogous to the one at the anchor proton side of 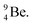 In combination with the DN and the
In combination with the DN and the 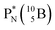 or
or 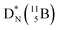 at the anchor neutron side, this leads to the typical trigonal planar molecular geometry of boron compounds. Furthermore, the sole NP represents the empty orbital of boron that exhibits chemical reactivity. NP is capable of binding neutron-deficient ligands like water (as BF3·H2O) or F− (as BF4−) with tetrahedral-like molecular geometry (see also paragraph 2.5).
at the anchor neutron side, this leads to the typical trigonal planar molecular geometry of boron compounds. Furthermore, the sole NP represents the empty orbital of boron that exhibits chemical reactivity. NP is capable of binding neutron-deficient ligands like water (as BF3·H2O) or F− (as BF4−) with tetrahedral-like molecular geometry (see also paragraph 2.5).
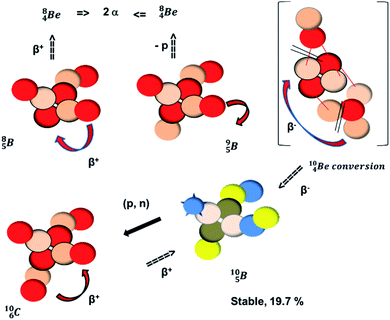 | ||
Fig. 13 Constellation of stable  (1s22s22p) and of radioactive (1s22s22p) and of radioactive  and and  in the new model, including conversions and some illustrative production routes. in the new model, including conversions and some illustrative production routes. | ||
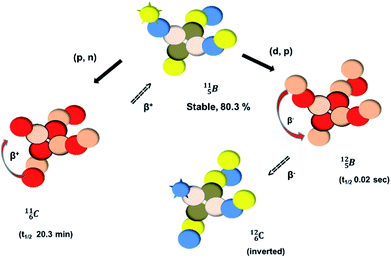 | ||
Fig. 14 Constellation of stable 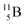 (1s22s22p) and of radioactive (1s22s22p) and of radioactive 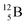 in the new model, including conversions and two illustrative production routes. in the new model, including conversions and two illustrative production routes. | ||
Upon bombardment of 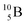 with protons, a (p, n) reaction gives the short living
with protons, a (p, n) reaction gives the short living 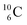 (t1/2 19.5 s).39 This
(t1/2 19.5 s).39 This 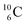 converts back to
converts back to 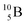 via β+-decay, which means that the
via β+-decay, which means that the 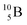 atom is formed as daughter isotope from
atom is formed as daughter isotope from 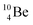 as well as from
as well as from 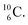 In case of
In case of 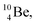 the neutron of the shared TP at the anchor proton side converts into a square proton at the anchor neutron side, while during this process the shared TP and shared DN break open (Fig. 13). In case of
the neutron of the shared TP at the anchor proton side converts into a square proton at the anchor neutron side, while during this process the shared TP and shared DN break open (Fig. 13). In case of 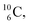 one of the DP protons converts into a neutron (β+-decay) and forms a DN with one of the PN's.
one of the DP protons converts into a neutron (β+-decay) and forms a DN with one of the PN's.
Upon bombardment of 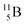 with protons, a (p, n) reaction gives radioisotope
with protons, a (p, n) reaction gives radioisotope 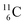 (Fig. 14).40 This carbon radioisotope converts back to
(Fig. 14).40 This carbon radioisotope converts back to 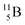 via β+-decay. Radioisotopes
via β+-decay. Radioisotopes 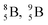 and
and 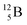 are very instable isotopes:
are very instable isotopes: 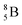 (β+-decay) and
(β+-decay) and 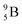 (proton emission) end up via
(proton emission) end up via 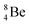 as α-particles, while
as α-particles, while 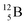 decays to
decays to 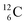 with a t1/2 of 0.02 s. The short half-life of radioisotope
with a t1/2 of 0.02 s. The short half-life of radioisotope 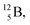 that is produced by a (d, p) reaction on
that is produced by a (d, p) reaction on 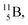 41 confirms that two full DN's at the anchor neutron side together with the fact that the anchor proton side bears three neutrons versus one proton, give rise to severe instability.
41 confirms that two full DN's at the anchor neutron side together with the fact that the anchor proton side bears three neutrons versus one proton, give rise to severe instability.
Both stable boron isotopes 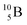 and
and 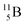 fit with the stability rules, with their n = 2, p = 1 at the anchor proton side, and its n = 1, p = 1½ and its n = 1½, p = 2 at the anchor neutron side, respectively.
fit with the stability rules, with their n = 2, p = 1 at the anchor proton side, and its n = 1, p = 1½ and its n = 1½, p = 2 at the anchor neutron side, respectively.
2.4 Nitrogen (Z = 7), oxygen (Z = 8) and their lone pairs
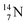 atom at the anchor neutron side possesses as lone pair a
atom at the anchor neutron side possesses as lone pair a 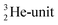 with a square proton (Fig. 15). Nitrogen is the first atom, since Li, that follows the Aufbau principle again (1s22s22p3). Fig. 15 also shows the constellation of the stable
with a square proton (Fig. 15). Nitrogen is the first atom, since Li, that follows the Aufbau principle again (1s22s22p3). Fig. 15 also shows the constellation of the stable 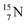 (0.4% abundance), of the instable
(0.4% abundance), of the instable 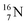 (t1/2 7.1 s, decays to
(t1/2 7.1 s, decays to 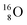 ) and of the instable
) and of the instable 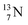 (t1/2 9.96 min, decays to
(t1/2 9.96 min, decays to 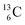 ). The
). The 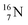 isotope is produced by a (n, γ) or (d, p) on
isotope is produced by a (n, γ) or (d, p) on 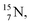 42,43 and by a (n, p) on
42,43 and by a (n, p) on 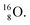 44 These impacts give insight in the position of the second lone pair in the constellation of oxygen (see Fig. 18 in the next paragraph). Atoms
44 These impacts give insight in the position of the second lone pair in the constellation of oxygen (see Fig. 18 in the next paragraph). Atoms 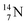 and
and 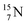 both have n = 3, p = 2 at the anchor proton side, just like
both have n = 3, p = 2 at the anchor proton side, just like 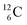 and
and 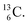 At the anchor neutron side it is n = 2, p = 2½ for
At the anchor neutron side it is n = 2, p = 2½ for 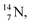 for
for 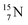 it is n = 2½, p = 3. So both constellations obey the derived stability rules.
it is n = 2½, p = 3. So both constellations obey the derived stability rules.
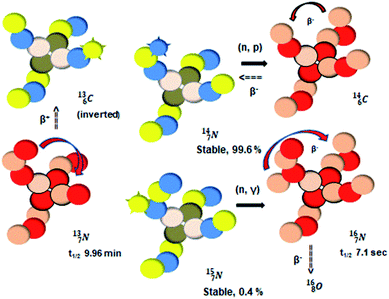 | ||
| Fig. 15 Constellation of the main isotopes of nitrogen (1s22s22p3) in the new model, including conversions. | ||
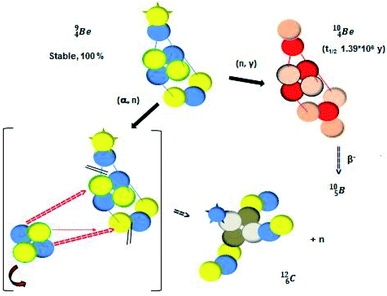
Radioactive 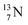 is produced in a cyclotron in various ways (Fig. 16). It is therefore an effectual isotope to demonstrate the consistency of the adjusted atom model in the field of isotope production.
is produced in a cyclotron in various ways (Fig. 16). It is therefore an effectual isotope to demonstrate the consistency of the adjusted atom model in the field of isotope production.
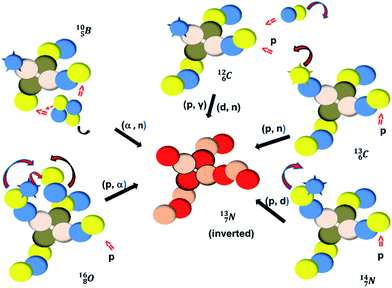 | ||
Fig. 16 Illustration of the consistency in production routes in the new model illustrated by production of  (red arrows indicate the point of impact). (red arrows indicate the point of impact). | ||
The  atom is produced via a (α, n) on
atom is produced via a (α, n) on  45–47 a (d, n) or (p, γ) on
45–47 a (d, n) or (p, γ) on 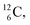 41b,48–50 a (p, n) on
41b,48–50 a (p, n) on 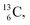 51 a (p, d) on
51 a (p, d) on 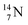
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52 and a (p, α) on
52 and a (p, α) on 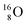
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51 (Fig. 16). In all cases, the impact takes place at the DN-unit (for
51 (Fig. 16). In all cases, the impact takes place at the DN-unit (for 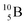 the impact takes place at the DN-unit and the NP-unit in the way described for the α-bombardment of
the impact takes place at the DN-unit and the NP-unit in the way described for the α-bombardment of 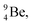 producing
producing 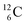 ). The DN is converted into a
). The DN is converted into a 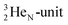 containing a full energy proton (not a square one), which leads to a fast decay (n = 1, p = 3 at the anchor neutron side). After proton impact on
containing a full energy proton (not a square one), which leads to a fast decay (n = 1, p = 3 at the anchor neutron side). After proton impact on 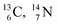 and
and 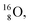 the rule “last in, first out” is followed: for
the rule “last in, first out” is followed: for 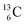 the square neutron of the
the square neutron of the 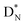 is thrown out, for
is thrown out, for 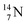 the D*-fragment from the
the D*-fragment from the 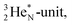 while for
while for 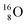 the thrown-out α-particle consists of the deuteron-parts from the
the thrown-out α-particle consists of the deuteron-parts from the 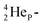 and
and 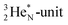 (see next paragraph for the configuration of
(see next paragraph for the configuration of 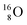 ). In the case of
). In the case of 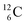 as target material, the combined (d, n) and (p, γ) bombardment,48,49 both producing the same
as target material, the combined (d, n) and (p, γ) bombardment,48,49 both producing the same 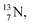 indicate that the proton of the incoming deuteron is built in and its neutron is turned aside without interaction with the nucleus. Notably, for
indicate that the proton of the incoming deuteron is built in and its neutron is turned aside without interaction with the nucleus. Notably, for 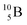 and
and 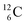 an additional consequence of the impact at DN is the activation of
an additional consequence of the impact at DN is the activation of 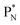 into a full energy proton.
into a full energy proton.
The 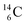 atom, either produced in a neutron generator or in the cosmos, comes from a (n, p) reaction on
atom, either produced in a neutron generator or in the cosmos, comes from a (n, p) reaction on 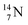 (Fig. 15).53 The neutron is incorporated onto the DP of the
(Fig. 15).53 The neutron is incorporated onto the DP of the 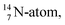 while throwing out the square proton of the
while throwing out the square proton of the 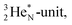 whereas
whereas 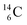 decays back to
decays back to 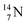 by converting the neutron of the newborn TP into a square proton at the DN, forming the
by converting the neutron of the newborn TP into a square proton at the DN, forming the 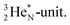
Lastly, atom 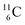 is, in addition to a (p, n) reaction on
is, in addition to a (p, n) reaction on 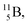 also produced via a (p, α) reaction on
also produced via a (p, α) reaction on 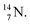 54 This (p, α) on
54 This (p, α) on 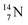 giving
giving 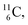 implies the impact of the proton at the TP of the
implies the impact of the proton at the TP of the 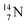 atom. The thrown-out α-particle consists of the deuteron parts from the
atom. The thrown-out α-particle consists of the deuteron parts from the 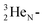 and the TP-unit. Thereby these two carbon isotope productions also follow the rule “last in, first out”.
and the TP-unit. Thereby these two carbon isotope productions also follow the rule “last in, first out”.
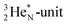 is a chemically quietened lone pair by hybridization with TP, while DN and DP are hybridized as in the CH4-molecule. These hybridized couples can easily flip, leading to the well-known pyramidal inversion of NH3. In the new model no spontaneous tunneling of hydrogen atoms is required.55,56 Notably, in N2, the
is a chemically quietened lone pair by hybridization with TP, while DN and DP are hybridized as in the CH4-molecule. These hybridized couples can easily flip, leading to the well-known pyramidal inversion of NH3. In the new model no spontaneous tunneling of hydrogen atoms is required.55,56 Notably, in N2, the 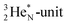 is also chemically quietened via hybridization with TP, and the triple bond of the N2-molecule consists of two mutual DP–TP bonds plus a DN–DN bond. In NH4+, TP is hybridized with DP. At the anchor neutron side, the square proton of the
is also chemically quietened via hybridization with TP, and the triple bond of the N2-molecule consists of two mutual DP–TP bonds plus a DN–DN bond. In NH4+, TP is hybridized with DP. At the anchor neutron side, the square proton of the 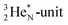 is hybridized with the neutron of DN, forming a symmetrical bridgehead at the anchor neutron side.
is hybridized with the neutron of DN, forming a symmetrical bridgehead at the anchor neutron side.The full-energy proton of the 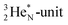 forms the fourth NH-bond (Fig. 17A), whereas the square proton has turned over its electron to this latter hydrogen atom. Notably, the oxygen atom (see next paragraph) can even force both protons of the
forms the fourth NH-bond (Fig. 17A), whereas the square proton has turned over its electron to this latter hydrogen atom. Notably, the oxygen atom (see next paragraph) can even force both protons of the 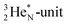 into covalent bond formation, demonstrating the versatility of the
into covalent bond formation, demonstrating the versatility of the 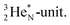
In combination with carbon, the intriguing existence of Z and E (formerly called syn and anti) isomers for N-alkyl substituted imines (R1R2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR3) provides a telling example.57–59 The stereo-isomerism originates from the fact that the double bond between carbon and nitrogen is a symmetrical one (carbon–DP with nitrogen–DN, carbon–DN with nitrogen–DP), but with either a “normal” or an “inverted” nitrogen atom (Fig. 6 and 7A).
NR3) provides a telling example.57–59 The stereo-isomerism originates from the fact that the double bond between carbon and nitrogen is a symmetrical one (carbon–DP with nitrogen–DN, carbon–DN with nitrogen–DP), but with either a “normal” or an “inverted” nitrogen atom (Fig. 6 and 7A).
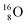 (abundance 99.76%),
(abundance 99.76%), 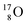 (abundance 0.04%) and
(abundance 0.04%) and 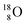 (abundance 0.2%), together with that of the instable oxygen isotopes
(abundance 0.2%), together with that of the instable oxygen isotopes 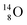 (t1/2 70.6 s),
(t1/2 70.6 s), 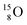 (t1/2 122.2 s) and
(t1/2 122.2 s) and 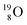 (t1/2 26.5 s).
(t1/2 26.5 s).
 | ||
| Fig. 18 Constellation of the main isotopes of oxygen (1s2 2s2 2p4) in the new model, including production and conversion of the instable ones. | ||
The main oxygen isotope  bears at the anchor neutron side the same DN and the same versatile
bears at the anchor neutron side the same DN and the same versatile  as described above for
as described above for 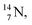 so n = 2, p = 2½. It differs, however, from
so n = 2, p = 2½. It differs, however, from 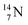 by bearing a
by bearing a 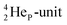 at the anchor proton side instead of a DP. This
at the anchor proton side instead of a DP. This 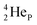 lone pair possesses an intriguing property, it is slightly neutron-deficient and is not closed yet (“open” lone pair). The
lone pair possesses an intriguing property, it is slightly neutron-deficient and is not closed yet (“open” lone pair). The 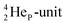 is chemically closed upon interaction with an additional neutron, but not necessarily a neutron from its own constellation. The water molecule forms a beautiful illustration of this latter aspect (vide infra). Notably, one of the protons of this
is chemically closed upon interaction with an additional neutron, but not necessarily a neutron from its own constellation. The water molecule forms a beautiful illustration of this latter aspect (vide infra). Notably, one of the protons of this 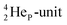 is thrown out in the (n, p) reaction on
is thrown out in the (n, p) reaction on 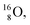 producing
producing 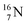 (see Fig. 18).
(see Fig. 18).
With regard to other nuclear aspects, 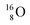 and
and 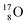 bear with n = 4, p = 3 at the anchor proton side exactly one neutron more than the number of protons, obeying the stability rule. Atom
bear with n = 4, p = 3 at the anchor proton side exactly one neutron more than the number of protons, obeying the stability rule. Atom 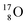 possesses the same anchor neutron subunits as
possesses the same anchor neutron subunits as 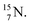 Atom
Atom 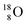 is as neutron-saturated as
is as neutron-saturated as 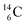 and
and 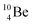 are. The latter radioisotopes slowly convert a neutron into a proton, yielding
are. The latter radioisotopes slowly convert a neutron into a proton, yielding 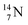 and
and 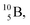 respectively. In case of the
respectively. In case of the 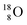 isotope, however, conversion of a neutron into a proton yielding
isotope, however, conversion of a neutron into a proton yielding 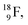 does not occur. In fact, it is the other way around: radioactive
does not occur. In fact, it is the other way around: radioactive 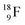 decays to
decays to 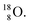 In
In 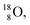 its tenth neutron appears to remain as a square neutron in the
its tenth neutron appears to remain as a square neutron in the 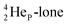 pair, as
pair, as 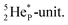 With that,
With that, 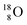 is the first example of an isotope that is stable, despite its n = 4½, p = 3 at the anchor proton side i.e. the first isotope that follows a special anchor proton side stability rule, namely n = p + 1½.
is the first example of an isotope that is stable, despite its n = 4½, p = 3 at the anchor proton side i.e. the first isotope that follows a special anchor proton side stability rule, namely n = p + 1½.
For the 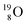 atom, produced either by a (n, γ) or (d, p) reaction on
atom, produced either by a (n, γ) or (d, p) reaction on 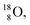 ,60,61 or a (n, p) on
,60,61 or a (n, p) on 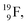 62 there is, like
62 there is, like 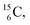 no obvious place for the additional neutron, so again an exotic TN is formed. This
no obvious place for the additional neutron, so again an exotic TN is formed. This 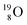 isotope quickly decays (t1/2 26.5 s) to
isotope quickly decays (t1/2 26.5 s) to 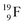 via conversion of the neutron of the
via conversion of the neutron of the 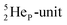 into a proton onto this TN. Isotope
into a proton onto this TN. Isotope 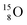 is produced via a (p, n) reaction on enriched
is produced via a (p, n) reaction on enriched 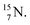 63 The proton impact takes place at the TP while the square neutron of the
63 The proton impact takes place at the TP while the square neutron of the 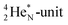 is thrown out (so again last in, first out). Its short half live (t1/2 122.2 s, converts back to
is thrown out (so again last in, first out). Its short half live (t1/2 122.2 s, converts back to 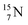 via β+-decay) demonstrates that a n = 3, p = 3 at the anchor proton side is an unacceptable situation. Atom
via β+-decay) demonstrates that a n = 3, p = 3 at the anchor proton side is an unacceptable situation. Atom 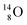 (t1/2 70.6 s) is the last atom configuration that may chemically act like oxygen and decays to
(t1/2 70.6 s) is the last atom configuration that may chemically act like oxygen and decays to 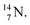 Atoms
Atoms 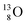 and
and 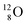 are extremely unstable, these decay to
are extremely unstable, these decay to 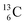 or
or 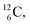 and
and 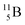 or
or 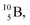 respectively, via β+ and/or proton emission.
respectively, via β+ and/or proton emission.
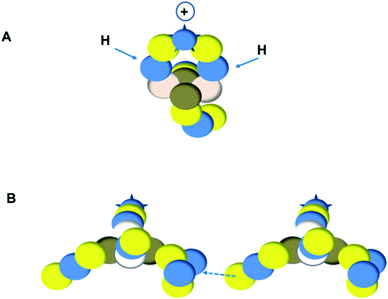
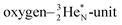 is hybridized with the neutron of the oxygen-DN, forming a symmetrical bridgehead at the anchor neutron side as in NH4+. The full-energy proton of the
is hybridized with the neutron of the oxygen-DN, forming a symmetrical bridgehead at the anchor neutron side as in NH4+. The full-energy proton of the 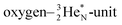 has formed the third OH-bond (Fig. 17A).
has formed the third OH-bond (Fig. 17A).As a gas, the oxygen atom in H2O is hybridized via TP with the 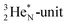 and DN with the
and DN with the 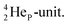 As such, the H2O molecule perfectly fits with the four different energy levels (2 OH-peaks, 2 lone pair peaks) observed in the photo-electronic spectra of H2O (“no rabbit ears on the water”).64
As such, the H2O molecule perfectly fits with the four different energy levels (2 OH-peaks, 2 lone pair peaks) observed in the photo-electronic spectra of H2O (“no rabbit ears on the water”).64
As a liquid, H2O is a temperature-dependent mixture of the gas-phase hybridized form and a hybridized form in which the 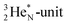 is linked with DN, and in which the TP is not linked intra-atomic with the
is linked with DN, and in which the TP is not linked intra-atomic with the 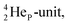 but with the
but with the 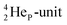 of a neighboring water molecule (Fig. 17B). Such an energetically favorable closure of the 4Hep-unit by a neighboring neutron is the basis for hydrogen bonds, hydrates, and e.g. crystal water.
of a neighboring water molecule (Fig. 17B). Such an energetically favorable closure of the 4Hep-unit by a neighboring neutron is the basis for hydrogen bonds, hydrates, and e.g. crystal water.
As a solid (around zero degrees and lower), the predominant form of H2O will be the fully de-hybridized one, i.e. neutron (“hydrogen”) bonds between TP and the  or
or 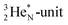 of a neighboring water molecule, and neutron bonds between DN and the
of a neighboring water molecule, and neutron bonds between DN and the 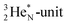 or
or 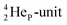 of a neighboring water molecule. This fully de-hybridized form of the water molecule corresponds with expansion, which means a change in volume and, therefore, a change in density. Dissolved cations, but also the
of a neighboring water molecule. This fully de-hybridized form of the water molecule corresponds with expansion, which means a change in volume and, therefore, a change in density. Dissolved cations, but also the 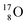 isotope with a square neutron at the
isotope with a square neutron at the 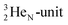 and the
and the 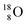 isotope with an additional square neutron at the
isotope with an additional square neutron at the 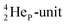 (see Fig. 18) will of course disrupt this hydrogen bond network, and might well be part of the reason behind the geometric variation in hexagonal-shaped snowflakes.
(see Fig. 18) will of course disrupt this hydrogen bond network, and might well be part of the reason behind the geometric variation in hexagonal-shaped snowflakes.
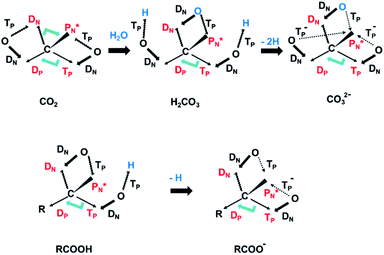 | ||
| Fig. 19 Some illustrative carbon–oxygen combinations in the new model: (a) CO2; (b) H2CO3 and resonance in CO32−; (c) RCOOH and resonance in RCOO− (blue hooked arrow indicates hybridization). | ||
In carbon dioxide (CO2), the DN of each oxygen atom is bound to the hybridized carbon (TP + DP), the TP of each oxygen atom is bound to the hybridized carbon 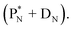 Upon dissolving of CO2 in water, carbonic acid (H2CO3) is formed. In this process, the two oxygen TP's become detached from the carbon
Upon dissolving of CO2 in water, carbonic acid (H2CO3) is formed. In this process, the two oxygen TP's become detached from the carbon 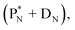 forming two OH-groups, while the oxygen of the incoming H2O molecule becomes bound with its TP to the carbon
forming two OH-groups, while the oxygen of the incoming H2O molecule becomes bound with its TP to the carbon 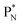 and with its DN to the carbon DN.
and with its DN to the carbon DN.
In ketones, aldehydes and carboxylic acids the double-bonded oxygen atom is bound in the same way to carbon's 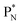 and DN, whereas the anchor proton side of that C-atom is hybridized into the (TP + DP) form. Keto–enol tautomerism and chemical attack on ketones take place at
and DN, whereas the anchor proton side of that C-atom is hybridized into the (TP + DP) form. Keto–enol tautomerism and chemical attack on ketones take place at  whereby the oxygen-TP of the double-bonded oxygen becomes OH or O−. In carboxylic acids (RCOOH), the OH-group is bound with its oxygen–DN to the hybridized carbon (TP + DP). The oxygen–TP of this OH-group loses its hydrogen relatively easily because the oxygen–TP− can form a resonance system with the versatile oxygen–TP plus
whereby the oxygen-TP of the double-bonded oxygen becomes OH or O−. In carboxylic acids (RCOOH), the OH-group is bound with its oxygen–DN to the hybridized carbon (TP + DP). The oxygen–TP of this OH-group loses its hydrogen relatively easily because the oxygen–TP− can form a resonance system with the versatile oxygen–TP plus 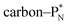 combination of the double-bonded oxygen. Finally, in phenols the OH-group is bound with its oxygen–DN to a DN of the benzene ring, after which the oxygen–TP− becomes part of the resonance system in alkaline solutions.
combination of the double-bonded oxygen. Finally, in phenols the OH-group is bound with its oxygen–DN to a DN of the benzene ring, after which the oxygen–TP− becomes part of the resonance system in alkaline solutions.
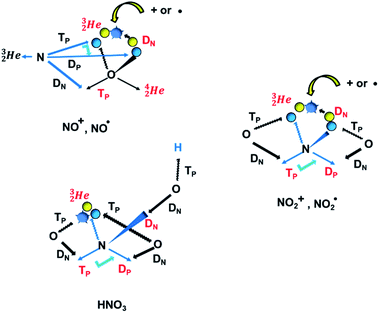 | ||
Fig. 20 Some illustrative nitrogen-oxygen combinations in the new model: (a) NO+/NO˙; (b)  ; (c) HNO3. ; (c) HNO3. | ||
The 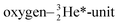 has formed a bridgehead with its DN. The square proton of the
has formed a bridgehead with its DN. The square proton of the 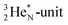 has kept its non-activated low-energy electron, whereas the remaining DN of the
has kept its non-activated low-energy electron, whereas the remaining DN of the 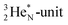 together with the DN form two bonds with the hybridized nitrogen–(TP + DP). The third bond is formed between the oxygen–TP and the nitrogen–DN. In the compound NO+ the square
together with the DN form two bonds with the hybridized nitrogen–(TP + DP). The third bond is formed between the oxygen–TP and the nitrogen–DN. In the compound NO+ the square 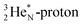 has lost its electron.
has lost its electron.
In 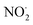 and NO2+,67 the nitrogen atom is the central atom with a bridge-headed
and NO2+,67 the nitrogen atom is the central atom with a bridge-headed 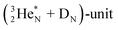 and the square proton of the
and the square proton of the 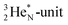 keeping its non-activated low energy electron or not. Each oxygen–TP is bound to the DN's of the bridge-headed
keeping its non-activated low energy electron or not. Each oxygen–TP is bound to the DN's of the bridge-headed 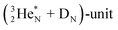 , each oxygen–DN is bound to the hybridized nitrogen–(TP + DP).
, each oxygen–DN is bound to the hybridized nitrogen–(TP + DP).
A final illustrative example is the acid HNO3. This acid is a well-known octet rule disobeying compound (formally N5+ surrounded by 10 electrons) for which a Lewis structure has been developed. In the new atom model, the two double bonded oxygen atoms are bound with their DN to the hybridized nitrogen–(TP + DP) of the nitrogen atom and with their TP to the protons of the 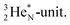 The oxygen of the OH-group bears an H-atom at its TP, and is bound with its DN to the nitrogen–DN (Fig. 20).
The oxygen of the OH-group bears an H-atom at its TP, and is bound with its DN to the nitrogen–DN (Fig. 20).
2.5 Fluorine (Z = 9), neon (Z = 10) and their lone pairs
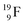 (100% abundance) possesses an open
(100% abundance) possesses an open 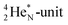 and a closed
and a closed 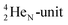 at the anchor neutron side, and, like
at the anchor neutron side, and, like 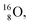 a TP and an open neutron-deficient
a TP and an open neutron-deficient 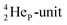 at the anchor proton side (Fig. 21).
at the anchor proton side (Fig. 21).
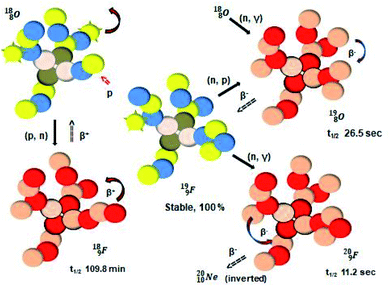 | ||
| Fig. 21 Constellation of the main isotopes of fluorine (1s22s22p5) in the new model, including illustrative conversions. | ||
Closure of the latter unit by a neighboring neutron from an H2O or HF molecule gives rise to a hydrogen bond. With its n = 4, p = 3 at the anchor proton side and n = 3½, p = 4 at the anchor neutron side, 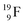 follows the stability rules.
follows the stability rules.
Radioisotope 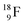 (t1/2 110 min.), a widely known component of PET-chemistry, lacks the square neutron in the
(t1/2 110 min.), a widely known component of PET-chemistry, lacks the square neutron in the 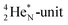 at the anchor neutron side. It is produced by a (p, n) reaction on
at the anchor neutron side. It is produced by a (p, n) reaction on 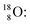 68 the proton impact takes place at the DN, forming a
68 the proton impact takes place at the DN, forming a 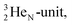 and throws out the square neutron of the
and throws out the square neutron of the 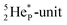 (last in, first out);
(last in, first out); 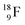 decays via β+-emission back to
decays via β+-emission back to 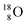 (Fig. 21). Notably,
(Fig. 21). Notably, 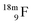 (t1/2 162 nanoseconds, decay to
(t1/2 162 nanoseconds, decay to 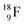 69) is the result of the impact at DN and throwing out the square neutron of the
69) is the result of the impact at DN and throwing out the square neutron of the 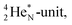 giving two
giving two 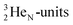 with full energy protons; the IT to
with full energy protons; the IT to 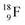 implies the fast shift of a neutron from the
implies the fast shift of a neutron from the 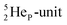 to this very neutron-deficient anchor neutron side as a temporarily better situation. Radioisotope
to this very neutron-deficient anchor neutron side as a temporarily better situation. Radioisotope 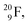 produced by a (n, γ) reaction on
produced by a (n, γ) reaction on 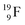 70 appears to be very instable (t1/2 11 s) with its n = 4, p = 4 at the anchor neutron side and its n = 5, p = 3 at the anchor proton side, and decays quickly to
70 appears to be very instable (t1/2 11 s) with its n = 4, p = 4 at the anchor neutron side and its n = 5, p = 3 at the anchor proton side, and decays quickly to 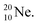 Atom
Atom 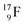 (t1/2 65 s, produced by a (d, n) reaction on
(t1/2 65 s, produced by a (d, n) reaction on 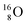 71), bears two
71), bears two 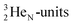 and decays to
and decays to 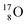 via β+-emission (conversion of a proton from one of the
via β+-emission (conversion of a proton from one of the 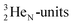 into a square neutron onto the other
into a square neutron onto the other 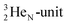 );
); 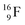 and lower are proton emitters.
and lower are proton emitters.
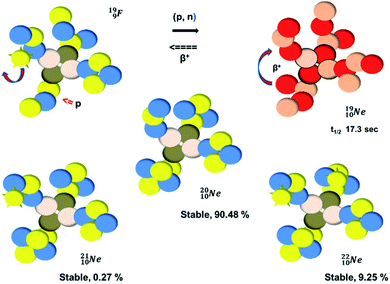
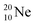 (abundance 90.48%) possesses at the anchor proton side a closed
(abundance 90.48%) possesses at the anchor proton side a closed 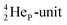 and a
and a 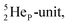 at the anchor neutron side a
at the anchor neutron side a 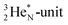 and a closed
and a closed 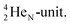 . The
. The 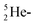 and
and  are hybridized, and so are both
are hybridized, and so are both  (Fig. 22).
(Fig. 22).
 | ||
| Fig. 22 Constellation of the main isotopes of neon (1s22s22p6) in the new model, including one illustrative conversion. | ||
Fig. 22 also shows the constellation of the stable isotopes 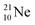 (0.27% abundance) and
(0.27% abundance) and 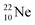 (abundance 9.25%), and of the instable
(abundance 9.25%), and of the instable 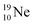 (t1/2 17.3 s). In the
(t1/2 17.3 s). In the 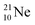 atom, the
atom, the 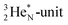 has become a
has become a 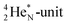 with a square neutron like in
with a square neutron like in 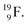 The
The 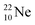 atom bears two
atom bears two 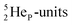 (one with a square neutron) at the anchor proton side, and two
(one with a square neutron) at the anchor proton side, and two 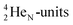 at the anchor neutron side (one with a square neutron). Neon isotopes
at the anchor neutron side (one with a square neutron). Neon isotopes 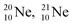 both fit with the stability rules, with their n = 5, p = 4 at the anchor proton side and their n = 3, p = 3½ and n = 3½, p = 4, respectively, at the anchor neutron side. The
both fit with the stability rules, with their n = 5, p = 4 at the anchor proton side and their n = 3, p = 3½ and n = 3½, p = 4, respectively, at the anchor neutron side. The 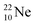 atom is stable with n = 5½, p = 4 at the anchor proton side, and is, therefore, the second isotope that follows the special n = p + 1½ anchor proton side stability rule. As was the case with
atom is stable with n = 5½, p = 4 at the anchor proton side, and is, therefore, the second isotope that follows the special n = p + 1½ anchor proton side stability rule. As was the case with 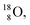 the extra neutron appears to remain as a square neutron in the
the extra neutron appears to remain as a square neutron in the 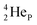 lone pair, as
lone pair, as 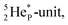 because conversion of a neutron into a proton yielding
because conversion of a neutron into a proton yielding 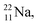 does not occur. Again it is the other way around: radioactive
does not occur. Again it is the other way around: radioactive 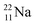 decays to
decays to 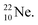
In the short-living radioisotope 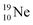 , the
, the 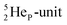 at the anchor proton side is replaced by a
at the anchor proton side is replaced by a 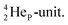 During its production via a (p, n) reaction on
During its production via a (p, n) reaction on 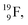 72 proton impact takes place at the TP of
72 proton impact takes place at the TP of 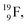 while the square neutron of the
while the square neutron of the 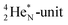 is thrown out. Atom
is thrown out. Atom 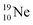 decays back to
decays back to 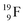 via conversion of a proton from one of the
via conversion of a proton from one of the 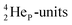 into a square neutron onto the
into a square neutron onto the 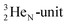 (β+-emission). Radioisotope
(β+-emission). Radioisotope 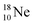 (t1/2 1.7 s) bears two
(t1/2 1.7 s) bears two 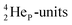 at the anchor proton side, and two
at the anchor proton side, and two 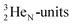 at the anchor neutron side. It decays as a first step to instable
at the anchor neutron side. It decays as a first step to instable 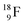 by conversion of a proton of one of the
by conversion of a proton of one of the 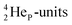 below into a neutron at one of the
below into a neutron at one of the 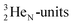 above. The short-living radioisotopes
above. The short-living radioisotopes 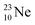 (t1/2 37.1 s), and
(t1/2 37.1 s), and 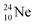 (t1/2 3.38 min) at the right side of
(t1/2 3.38 min) at the right side of 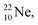 will be dealt with in a forthcoming paper.
will be dealt with in a forthcoming paper.
So in the new model also the last two elements of the 2s2,2p6-series, fluorine and neon, follow the remarkable regularity and consistency with respect to the stability or instability of the atoms. All stable isotopes Z = 3–10 appear to follow a strict n = p − ½ pattern at the anchor neutron side, and a n = p + 1 pattern at the anchor proton side; only for 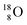 and
and 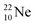 the pattern is n = p + 1½. Any deviation from these patterns leads to conversion. Another regularity is that the EC-decay of radioisotope
the pattern is n = p + 1½. Any deviation from these patterns leads to conversion. Another regularity is that the EC-decay of radioisotope 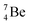 as well as the β+-decay of the nuclear medicine PET-isotopes
as well as the β+-decay of the nuclear medicine PET-isotopes 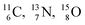 and
and 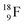 and of radioisotopes
and of radioisotopes 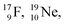 all imply conversion of a full energy proton into a square neutron. Even for
all imply conversion of a full energy proton into a square neutron. Even for 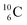 and
and 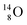 this is the case, although they seem to look like an exception: the newborn square neutron, temporarily bound as a square neutron to both PN's at the anchor neutron side, exchanges energy with the neighboring proton, leaving a
this is the case, although they seem to look like an exception: the newborn square neutron, temporarily bound as a square neutron to both PN's at the anchor neutron side, exchanges energy with the neighboring proton, leaving a 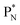 or
or 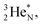 respectively, behind under formation of a DN.
respectively, behind under formation of a DN.
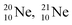 and
and 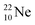 as model, it can be derived that covalent bond formation strives in average for a chemical
as model, it can be derived that covalent bond formation strives in average for a chemical 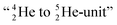 formation at the anchor proton side, and a chemical
formation at the anchor proton side, and a chemical 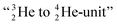 formation at the neutron anchor side. From the fact that F possesses a TP as chemical binding unit, it follows that in case of the F2 molecule a TP with a TP is a very poor bond-proposition, because it would lead to a chemical
formation at the neutron anchor side. From the fact that F possesses a TP as chemical binding unit, it follows that in case of the F2 molecule a TP with a TP is a very poor bond-proposition, because it would lead to a chemical 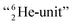 as covalent bond. To avoid formation of an unfavorable chemical
as covalent bond. To avoid formation of an unfavorable chemical 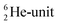 as covalent bond, the TP of the F atom is compelled to hybridize with its
as covalent bond, the TP of the F atom is compelled to hybridize with its 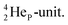 This forces the anchor protons a little closer to each other (and so the anchor neutrons a little further away from each other) creating an energetically disadvantageous tension. The high heat release upon reaction therefore originates from restoring the “normal” distance between the anchor protons and anchor neutrons. For the O2 molecule this bonding aspect is less problematic. The O2 molecule contains a solid bond between both DN's and a more fragile bond between both TP's, the neutrons of which are hybridized with their
This forces the anchor protons a little closer to each other (and so the anchor neutrons a little further away from each other) creating an energetically disadvantageous tension. The high heat release upon reaction therefore originates from restoring the “normal” distance between the anchor protons and anchor neutrons. For the O2 molecule this bonding aspect is less problematic. The O2 molecule contains a solid bond between both DN's and a more fragile bond between both TP's, the neutrons of which are hybridized with their 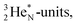 so no
so no 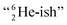 covalent bond, and therefore O2 reacts less extreme. The same holds for hydrogen peroxide (H2O2) and its TP–TP bond. In acetyl hypofluorite (CH3COOF), the F-atom is bound to the TP of the oxygen atom which is hybridized with its
covalent bond, and therefore O2 reacts less extreme. The same holds for hydrogen peroxide (H2O2) and its TP–TP bond. In acetyl hypofluorite (CH3COOF), the F-atom is bound to the TP of the oxygen atom which is hybridized with its 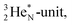 and therefore this F-atom reacts less vigorous than in F2 (approximately as vigorous as H2O2).
and therefore this F-atom reacts less vigorous than in F2 (approximately as vigorous as H2O2).Upon reaction with the carbon atom, the fact that the TP of fluorine strongly prefers covalent 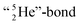 formation leads to subtle conflicts. Upon bond formation with the DP of carbon, the hybridized neutron (from DN or TP) has to be pushed aside. This forced re-hybridization will have its effect on the carbon skeleton. At the anchor neutron side of the carbon atom, bond formation with DN seems fine for the TP of F, but a
formation leads to subtle conflicts. Upon bond formation with the DP of carbon, the hybridized neutron (from DN or TP) has to be pushed aside. This forced re-hybridization will have its effect on the carbon skeleton. At the anchor neutron side of the carbon atom, bond formation with DN seems fine for the TP of F, but a 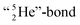 is too much for the carbon–DN. The compromise will be a sort of
is too much for the carbon–DN. The compromise will be a sort of 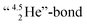 with the hybridized (PN + DN)-units. Bond formation with hybridized PN will in case of a mono-fluorinated aliphatic compound suffer from easy elimination of HF in a process that resembles the keto–enol tautomerism for a carbonyl group. Finally, in the CF3-group (one F at the DP and two F's at the hybridized PN + DN), the TP of the carbon atom has become fully isolated and therefore exhibits more or less the same chemical behavior as the TP of F, which explains e.g. the chemistry of the CF3-group in trifluorotoluene (CF3–C6H5): in CF3–C6H5, the isolated TP of the carbon atom of the CF3-group, bound at the DP of the benzene ring, forces the benzene ring to re-hybridize, while the open neutron-deficient
with the hybridized (PN + DN)-units. Bond formation with hybridized PN will in case of a mono-fluorinated aliphatic compound suffer from easy elimination of HF in a process that resembles the keto–enol tautomerism for a carbonyl group. Finally, in the CF3-group (one F at the DP and two F's at the hybridized PN + DN), the TP of the carbon atom has become fully isolated and therefore exhibits more or less the same chemical behavior as the TP of F, which explains e.g. the chemistry of the CF3-group in trifluorotoluene (CF3–C6H5): in CF3–C6H5, the isolated TP of the carbon atom of the CF3-group, bound at the DP of the benzene ring, forces the benzene ring to re-hybridize, while the open neutron-deficient 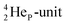 of the fluorine atoms of the CF3-group interacts with the DN-neutron of the neighboring carbon atoms of the benzene ring (the ortho positions). Notably, this explanation according to the new atom model, compiles in an elegant way the ‘double-bond no-bond’ resonance hypothesis, and the hypothesis wherein one of the three F-atoms of the CF3-group has formed a bond with one of the carbon atoms at the ortho-position of the benzene ring (so with F+ formation) (Fig. 23).74,75
of the fluorine atoms of the CF3-group interacts with the DN-neutron of the neighboring carbon atoms of the benzene ring (the ortho positions). Notably, this explanation according to the new atom model, compiles in an elegant way the ‘double-bond no-bond’ resonance hypothesis, and the hypothesis wherein one of the three F-atoms of the CF3-group has formed a bond with one of the carbon atoms at the ortho-position of the benzene ring (so with F+ formation) (Fig. 23).74,75
3 Concluding remarks
This paper describes a revolutionary adjustment of the reigning quantum mechanical atom model for the elements with Z = 1–10. The new atom model is based on the premise that in elements with low Z the mass is not concentrated for 99.9% in a very small dense positive inner core. In the adjusted model, which comprised a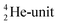 as backbone with various subunits (PN, DN, DP, TP,
as backbone with various subunits (PN, DN, DP, TP,  and
and 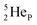 ), the neutron has been given a much more prominent role than it has in the reigning quantum mechanical model. It is not just there to assist the strong force to surpass the repulsive coulombic forces between the protons in the nucleus, but the neutron is the modus operandi of the hybridization principle, molecular geometry and hydrogen bonds, and as such plays a part in chemical reactivity, bond length and bond strength, as shown for F2. Moreover, the neutron plays an important role in the subtle change in the hybridization in the atom constellations of the molecule upon phase transition, as displayed for the boiling H2O molecule.
), the neutron has been given a much more prominent role than it has in the reigning quantum mechanical model. It is not just there to assist the strong force to surpass the repulsive coulombic forces between the protons in the nucleus, but the neutron is the modus operandi of the hybridization principle, molecular geometry and hydrogen bonds, and as such plays a part in chemical reactivity, bond length and bond strength, as shown for F2. Moreover, the neutron plays an important role in the subtle change in the hybridization in the atom constellations of the molecule upon phase transition, as displayed for the boiling H2O molecule.
The atom constellations arising from this new model not only provide an answer to the re-hybridizing power of fluorine, our primary objective. They also appear to be perfectly in accordance with the linear molecular geometry of beryllium, the trigonal planar molecular geometry of boron, and the tetrahedral molecular geometry of carbon, nitrogen and oxygen (including the special lone pairs of the latter two). In addition, the derived atom constellations follow a consistent pattern with respect to the stability of isotopes, the produced radioisotopes thereof, and the respective decay modes of the latter.
Other key topics are the new sound basis for covalent bond formation (formation of a “chemical” He-unit between a PN, DN, DP or TP-subunit with one of the subunits of the other atom), and the re-definition of the hydrogen bond (neutron bond between the TP-subunit of the atom and the neutron-deficient 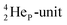 or
or 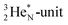 of a neighboring molecule). Furthermore, the new model offers an improved answer to phenomena like the hybridization principle, inversion, chirality, resonance and the secret behind the chemical reactivity of the empty orbital of boron.
of a neighboring molecule). Furthermore, the new model offers an improved answer to phenomena like the hybridization principle, inversion, chirality, resonance and the secret behind the chemical reactivity of the empty orbital of boron.
In a forthcoming “Part II” we will investigate whether the adjusted model still holds for the slightly heavier elements Z = 11–20, and if so, what the configurations of the atoms Na (Z = 11) through Ca (Z = 20) look like in the new approach. And, as a further matter, whether the new model can provide a genuine solution for the occurrence of multiple valencies of the elements P, S, and Cl, with special attention to the well-known “octet-rule violating” compounds H3PO4, H2SO4 and HClO4.
Conflicts of interest
Prof. Dr A. D. Windhorst is editor-in-chief of Nuclear Medicine & Biology.Note added after first publication
This article replaces the version published on 19th August 2021, which contained multiple formatting errors.References
- J. J. Thomson, Phil. Mag. Ser., 1904, 7(39), 237 CrossRef CAS.
- K. Lord, Phil. Mag. Ser., 1902, 3(15), 257 CrossRef.
- E. Rutherford, Phil. Mag. Ser., 1911, 6(21), 669 CrossRef.
- N. Bohr, Phil. Mag. Ser., 1913, 26(151), 1 CrossRef CAS.
- E. Schrodinger, Ann. Phys., 1926, 384(4), 273 CrossRef.
- W. Heisenberg, Z. Phys., 1927, 43(3–4), 172 CrossRef.
- L. Pauling, J. Am. Chem. Soc., 1931, 53(4), 1367 CrossRef CAS.
- M. D. Harmony, Chem. Soc. Rev., 1972, 1, 211 RSC.
- X.-Z. Li, B. Walker and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(16), 6369 CrossRef CAS.
- G. N. Lewis, J. Am. Chem. Soc., 1916, 38, 762 CrossRef CAS.
- J. F. Ogilvie, J. Chem. Educ., 1990, 67(4), 280 CrossRef CAS.
- R. D. Chambers, Fluorine in Organic Chemistry, Wiley-Interscience, John Wiley & Sons, 1973 Search PubMed.
- J. Hine, J. Am. Chem. Soc., 1963, 85(20), 3239 CrossRef CAS.
- P. Politzer and J. W. Timberlake, J. Org. Chem., 1972, 37(22), 3557 CrossRef CAS.
- G. W. M. Visser, Trends Org. Chem., 1993, 4, 379 CAS.
- G. W. M. Visser and J. D. M. Herscheid, 14th Intern. Symp. on Fluorine Chem., 1994, Yokohama, Japan. https://www.researchgate.net/publication/292605267_The_s-orbital_character_deficiency_of_fluorine_as_driving_force_to_react_with_organic_substrates Search PubMed.
- G. W. M. Visser, 11th Eur. Symp. on Fluorine Chem., 1995, Bled, Slovenia. https://www.researchgate.net/publication/295860798_On_the_Chemical_Behaviour_of_Fluorine_The_Unusual_and_Unexpected_made_usual_11th_European_Symposium_on_Fluorine_Chemistry_Bled_1995 Search PubMed.
- H. A. Bent, Chem. Rev., 1961, 61(3), 275 CrossRef CAS.
- A. D. Windhorst, H. Timmerman, E. A. Worthington, G. J. Bijloo, P. H. J. Nederkoorn, W. M. P. B. Menge, R. Leurs and J. D. M. Herscheid, J. Med. Chem., 2000, 43, 1754 CrossRef CAS PubMed.
- G. W. M. Visser, R. P. Klok and A. D. Windhorst, 15th Intern. Symp. on Fluorine Chem., 1997, Vancouver, Canada, https://www.researchgate.net/publication/295860864_Fluorine_and_the_Problem_with_Electrostatic_Effects_15th_International_Symposium_on_Fluorine_Chemistry_Vancouver_August_2-7_1997 Search PubMed.
- G. Portalone, G. Schultz, A. Domenicano and I. Hargittai, J. Mol. Struct., 1984, 118(1–2), 53 CrossRef CAS.
- Radionuclide Transformations – Energy and Intensity of Emissions, Radiation Protection, ICRP PUBLICATION 38, Pergamon Press Ltd., Headington Hill Hall, Oxford, England, 1983 Search PubMed.
- H. H. Voge, J. Chem. Phys., 1948, 16, 984 CrossRef CAS.
- E. Hückel, Z. Phys., 1930, 60(7–8), 423 CrossRef.
- W. E. Palke, J. Am. Chem. Soc., 1986, 108(21), 6543 CrossRef CAS.
- P. A. Schultz and R. P. Messmer, J. Am. Chem. Soc., 1993, 115(21), 10925 CrossRef CAS.
- K. B. Wiberg, Acc. Chem. Res., 1996, 29(5), 229 CrossRef CAS.
- P. Maitland and W. H. Mills, Nature, 1935, 135, 994 CrossRef CAS.
- (a) F. A. Kekulé, Ann. Chem. Pharm., 1886, 137(2), 129 CrossRef; (b) A. Ladenburg, Ber. Dtsch. Chem. Ges., 1869, 2, 140 CrossRef.
- Y. Liu, P. Kilby, T. J. Frankcombe and T. W. Schmidt, Nat. Commun., 2020, 11, 1210 CrossRef CAS PubMed.
- R. D. O'Neal and M. Goldhaber, Phys. Rev., 1940, 58, 574 CrossRef.
- W. L. Imhof, R. G. Johnson, F. J. Vaughn and M. Walt, Phys. Rev., 1959, 114, 1037 CrossRef CAS.
- (a) H. R. Crane, L. A. Delsasso, W. A. Fowler and C. C. Lauritsen, Phys. Rev., 1935, 47, 971 CrossRef CAS; (b) L. A. Delsasso, W. A. Fowler and C. C. Lauritsen, Phys. Rev., 1935, 48, 848 CrossRef CAS; (c) D. S. Bayley and H. R. Crane, Phys. Rev., 1937, 52, 604 CrossRef CAS.
- (a) K. Arai, D. Baye and P. Descouvemont, Nucl. Phys. A, 2002, 699(3), 963 CrossRef; (b) J. J. He, S. Z. Chen, C. E. Rolfs, S. W. Xu, J. Hu, X. W. Ma, M. Wiescher, R. J. deBoer, T. Kajino, M. Kusakabe, L. Y. Zhang, S. Q. Hou, X. Q. Yu, N. T. Zhang, G. Lian, Y. H. Zhang, X. H. Zhou, H. S. Xu and W. L. Zhan, Phys. Lett. B, 2013, 725, 287 CrossRef CAS.
- T. Kobayashi, G. Bengua, K. Tanaka and Y. Nakagawa, Phys. Med. Biol., 2007, 52, 645 CrossRef CAS PubMed.
- L. H. Rumbaugh, R. B. Roberts and L. R. Hafstad, Phys. Rev., 1938, 54, 657 CrossRef CAS.
- (a) D. J Hughes, C. Eggler and C. M. Huddleston, Phys. Rev., 1947, 71, 26 Search PubMed; (b) D. J. Hughes, C. Eggler and B. E. Alburger, Phys. Rev., 1950, 77, 726 CrossRef CAS.
- J. Chadwick, Proc. R. Soc. A, 1932, 136(830), 692 CAS.
- (a) R. Sherr, H. R. Muether and M. G. White, Phys. Rev., 1948, 74, 1239 CAS; (b) R. Sherr, H. R. Muether and M. G. White, Phys. Rev., 1949, 75, 282 CrossRef CAS.
- W. H. Barkas, Phys. Rev., 1939, 56, 287 CrossRef CAS.
- (a) H. R. Crane, L. A. Delsasso, W. A. Fowler and C. C. Lauritsen, Phys. Rev., 1935, 47, 887 CrossRef CAS; (b) W. A. Fowler, L. A. Delsasso and C. C. Lauritsen, Phys. Rev., 1936, 49, 561 CrossRef CAS.
- S. Neelam and R. Chatterjee, Phys. Rev. C, 2015, 92, 044615 CrossRef.
- J. M. Freeman and R. C. Hanna, Nucl. Phys., 1957, 4, 599 CrossRef CAS.
- (a) W. Y. Chang, M. Goldhaber and R. Sagane, Nature, 1937, 139, 962 CrossRef CAS; (b) J. K. Bienlein and E. Kalsch, Nucl. Phys., 1964, 50, 202 CrossRef.
- I. Curie and F. Joliot, Compt. Rend., 1934, 198, 254 CAS.
- C. D. Ellis and W. J. Henderson, Nature, 1935, 135, 429 CrossRef CAS.
- L. N. Ridenour and W. J. Henderson, Phys. Rev., 1937, 52, 889 CrossRef CAS.
- R. N. Hall and W. A. Fowler, The Cross Section for the Radiative Capture of Protons by C-12 near 100 keV, Phys. Rev., 1950, 77, 197 CrossRef CAS.
- W. A. S. Lamb and R. E. Hester, Phys. Rev., 1957, 107, 550 CrossRef CAS.
- D. M. Yost, L. N. Ridenour and K. Shinohara, J. Chem. Phys., 1935, 3, 133 CrossRef CAS.
- (a) R. E. Adamson, Jr, W. W. Buechner, W. M. Preston, C. Goodman and D. M. Van Patter, Phys. Rev., 1950, 80, 985 CrossRef; (b) S. W. Kitwanga, P. Leleux, P. Lipnik and J. Vanhorenbeeck, Phys. Rev. C, 1989, 40, 35 CrossRef CAS PubMed.
- V. A. Muminov, S. Mukhamedov, B. Sultanov and T. Khamrakulov, Izv. Akad. Nauk Uzb. SSR, Ser. Fiz.-Mat. Nauk, 1974, 1, 56 Search PubMed.
- S. Ruben and M. D. Kamen, Phys. Rev., 1941, 59, 349 CrossRef CAS.
- W. H. Barkas, Phys. Rev., 1939, 56, 287 CrossRef CAS.
- Y. Suleymanov, Science, 2019, 366(6471), 1325 CrossRef.
- N. V. Cohan and C. A. Coulson, Trans. Faraday Soc., 1956, 52, 1163 RSC.
- K. Abbaspour Tehrani and N. de Kimpe, Sci. Synth., 2004, 27, 245 Search PubMed.
- M. Raban, J. Chem. Soc. D, 1970, 1415–1416 RSC.
- G. J. Karabatsos and S. S. Lande, Tetrahedron, 1968, 34(10), 3907 CrossRef.
- L. Seren, W. E. Moyer and W. Sturm, Phys. Rev., 1946, 70, 561 CrossRef CAS.
- D. E. Alburger, A. Gallman and D. H. Wilkinson, Phys. Rev., 1959, 116, 939 CrossRef CAS.
- E. B. Paul and R. L. Clark, Can. J. Phys., 1953, 31, 267 CrossRef CAS.
- A. R. Barnett, Nucl. Phys. A, 1968, 120, 342 CrossRef CAS.
- (a) M. Laing, J. Chem. Educ., 1987, 64, 124 CrossRef CAS; (b) M. Ceriotti, W. Fang, P. G. Kusalik, R. H. McKenzie, A. Michaelides, M. A. Morales and T. E. Markland, Chem. Rev., 2016, 116, 7529 CrossRef CAS PubMed.
- S. G. Kukolich, J. Am. Chem. Soc., 1982, 104, 4715 CrossRef CAS.
- N. N. Greenwood and A. Earnshaw, Chemistry of the Elements, Butterworth-Heinemann, 2nd edn, 1997 Search PubMed.
- H. A. Bent, Inorg. Chem., 1963, 2, 747 CrossRef CAS.
- L. A. DuBridge, S. W. Barnes, J. H. Buck and C. V. Strain, Phys. Rev., 1938, 53, 447 CrossRef CAS.
- F. D. Becchetti, J. A. Brown, K. Ashktorab, J. W. Jänecke, W. Z. Liu, D. A. Roberts, R. J. Smith, J. J. Kolata, K. Larrikin, A. Morsad and R. E. Warner, Nucl. Instrum. Methods Phys. Res., Sect. B, 1991, 56–57(part 1), 554 CrossRef.
- (a) S. S. Glickstein and R. G. Winter, Phys. Rev., 1963, 130, 1281 CrossRef; (b) P. Spilling, H. Gruppelaar, H. F. de Vries and A. M. J. Spits, Nucl. Phys. A, 1968, 113, 395 CrossRef CAS.
- (a) H. W. Newson, Phys. Rev., 1935, 48, 790 CrossRef CAS; (b) V. Perez-Mendez and P. Lindenfield, Phys. Rev., 1950, 80, 1097 CrossRef CAS.
- (a) M. G. White, L. A. Delsasso, J. G. Fox and E. C. Creutz, Phys. Rev., 1939, 56, 512–518 CrossRef CAS; (b) G. Schrank and J. R. Richardson, Phys. Rev., 1952, 86, 248 CrossRef CAS.
- L. E. Forslund and N. Kaltsoyannis, New J. Chem., 2003, 27, 1108 RSC.
- J. D. Roberts, R. L. Webb and E. A. McElhill, J. Am. Chem. Soc., 1950, 72(1), 408 CrossRef CAS.
- D. Holtz, Chem. Rev., 1971, 71, 139 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |